伯努利实验数据
伯努利方程实验报告
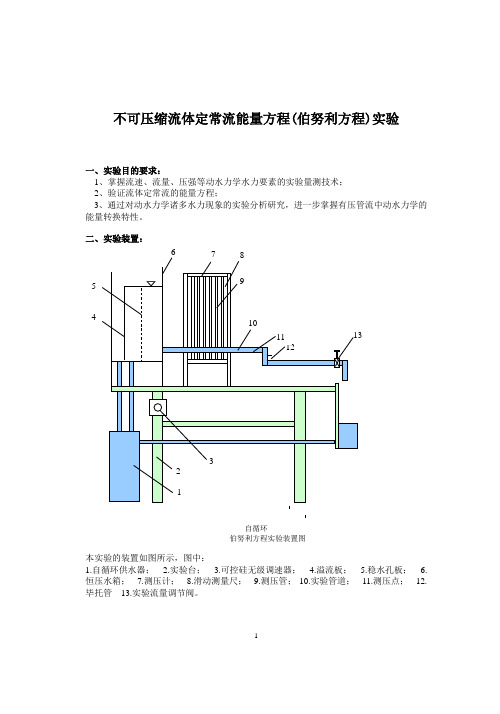
不可压缩流体定常流能量方程(伯努利方程)实验一、实验目的要求:1、掌握流速、流量、压强等动水力学水力要素的实验量测技术;2、验证流体定常流的能量方程;3、通过对动水力学诸多水力现象的实验分析研究,进一步掌握有压管流中动水力学的能量转换特性。
自循环伯努利方程实验装置图本实验的装置如图所示,图中:1.自循环供水器;2.实验台;3.可控硅无级调速器;4.溢流板;5.稳水孔板;6.恒压水箱;7.测压计;8.滑动测量尺;9.测压管;10.实验管道;11.测压点;12.毕托管13.实验流量调节阀。
12 三、实验原理:在实验管路中沿水流方向取n 个过水截面。
可以列出进口截面(1)至截面(i)的能量方程式(i=2,3,.....,,n)W i hg g p Z g g p Z i i i -+++=++12222111νρνρ 选好基准面,从已设置的各截面的测压管中读出g p Z ρ+值,测出通过管路的流量,即可计算出截面平均流速ν及动压g 22ν,从而可得到各截面测管水头和总水头。
四、实验方法与步骤:1、熟悉实验设备,分清各测压管与各测压点,毕托管测点的对应关系。
2、打开开关供水,使水箱充水,待水箱溢流后,检查泄水阀关闭时所有测压管水面是否齐平,若不平则进行排气调平(开关几次)。
3、打开阀13,观察测压管水头线和总水头线的变化趋势及位置水头、压强水头之间的相互关系,观察当流量增加或减少时测压管水头的变化情况。
4、调节阀13开度,待流量稳定后,测记各测压管液面读数,同时测记实验流量(与毕托管相连通的是演示用,不必测记读数)。
5、再调节阀13开度1~2次,其中一次阀门开度大到使液面降到标尺最低点为限,按第4步重复测量。
五、实验结果及要求:1、把有关常数记入表2.1。
2、量测(g pZ ρ+)并记入表2.2。
3、计算流速水头和总水头。
4、绘制上述结果中最大流量下的总水头线和测压管水头线(轴向尺寸参见图2.2,总水头线和测压管水头线可以绘在图2.2上)。
能量方程(伯努利方程)实验

不可压缩流体恒定流能量方程(伯努利方程)实验一、实验背景1726年,伯努利通过无数次实验,发现了“边界层表面效应”:流体速度加快时,物体与流体接触的界面上的压力会减小,反之压力会增加。
为纪念他的贡献,这一发现被称为“伯努利效应”。
伯努利效应适用于包括气体在内的一切流体,是流体作稳定流动时的基本现象之一,反映出流体的压强与流速的关系,即在水流或气流里,如果速度大,压强就小,如果速度小,压强就大。
1738年,在他的最重要的著作《流体动力学》中,伯努利将这一理论公式化,提出了流体动力学的基本方程,后人称之为“伯努利方程”。
书中还介绍了著名的伯努利实验、伯努利原理,用能量守恒定律解决了流体的流动问题,这对流体力学的发展,起到了至关重要的推动作用。
伯努利简介丹尼尔伯努利(Daniel Bernouli,1700~1782),瑞士物理学家、数学家、医学家,被称为“流体力学之父”。
1700年2月8日生于荷兰格罗宁根,1782年3月17日逝世于巴塞尔。
他是伯努利这个数学家族(4代10人)中最杰出的代表,16岁时就在巴塞尔大学攻读哲学与逻辑,后获得哲学硕士学位。
17~20岁时,违背家长要他经商的愿望,坚持学医,并于1721年获医学硕士学位,成为外科名医并担任过解剖学教授。
他在父兄熏陶下最后仍转到数理科学。
伯努利在25岁时应聘为圣彼得堡科学院的数学院士,8年后回到瑞士的巴塞尔,先任解剖学教授,后任动力学教授,1750年成为物理学成教授。
他还于1747年当选为柏林科学院院士,1748年当选为巴黎科学院院士,1750年当选英国皇家学会会员。
在1725~1749年间,伯努利曾十次荣获法国科学院的年度奖。
除流体动力学这一主要领域外,丹尼尔·伯努利的研究领域极为广泛,他的工作几乎对当时的数学和物理学的研究前沿的问题都有所涉及。
他最出色的工作是将微积分、微分方程应用到物理学,研究流体问题、物体振动和摆动问题,因此他被推崇为数学物理方法的奠基人.二、实验目的要求1.验证流体恒定总流的能量方程;2.通过对动水力学诸多水力现象的实验分析,进一步掌握有压管流中动水力学的能量转换特性;3.掌握流速、流量、压强等动水力学水力要素的实验量测技能。
化工原理实验 吸收实验 伯努利方程实验
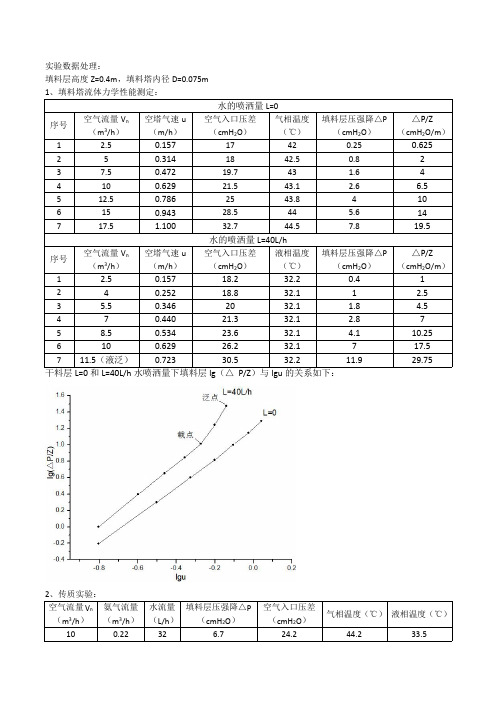
液相温度 填料层压强降△P
(℃)
(cmH2O)
1
2.5
0.157
18.2
32.2
0.4
2
4
0.252
18.8
32.1
1
3
5.5
0.346
20
32.1
1.8
4
7
0.440
21.3
32.1
2.8
5
8.5
0.534
23.6
32.1
4.1
6
10
0.629
26.2
32.1Βιβλιοθήκη 77 11.5(液泛) 0.723
30.5
A 截面-D 截面
0
1
-1
114
115
300
-74
10
128
64
600
66
56
167
278
冲压头为静压头与动压头之和。
在实验导管窗口流量开 600(L/h)时,A 处的静压头为 596 mmH2O 柱,B 处的静压头为 530 mmH2O 柱,PA>PB, 说明 B 处的静压能转化为动能。
0.8
3
7.5
0.472
19.7
43
1.6
4
10
0.629
21.5
43.1
2.6
5
12.5
0.786
25
43.8
4
6
15
0.943
28.5
44
5.6
7
17.5
1.100
32.7
44.5
7.8
水的喷洒量 L=40L/h
序号
能量方程(伯努利方程)实验

能量方程(伯努利方程)实验能量方程(伯努利方程)实验姓名:史亮班级:9131011403学号:913101140327处的7根皮托管测压管测量总水头或12根普通测压管测量测压管水头,其中测点1、6、8、12、14、16和18均为皮托管测压管(示意图见图3.2),用于测量皮托管探头对准点的总水头H ’(=2gu2++r p Z ),其余为普通测压管(示意图见图3.3),用于测量测压管水头。
图3.2 安装在管道中的皮托管测压管示意图 图3.3安装在管道中的普通测压管示意图3.3 实验原理当流量调节阀旋到一定位置后,实验管道内的水流以恒定流速流动,在实验管道中沿管内水流方向取n 个过水断面,从进口断面(1)至另一个断面(i )的能量方程式为:2g v2111++r p Z =fiih r p Z +++2gv 2i=常数 (3.1) 式中:i=2,3,······ ,n ;Z ──位置水头;rp──压强水头; 2gv 2──速度水头;fh ──进口断面(1)至另一个断面(i )的损失水头。
从测压计中读出各断面的测压管水头(r pZ +),通过体积时间法或重量时间法测出管道流量,计算不v2,从同管道内径时过水断面平均速度v及速度水头2g而得到各断面的测压管水头和总水头。
3.4 实验方法与步骤1)观察实验管道上分布的19根测压管,哪些是普通测压管,哪些是皮托管测压管。
观察管道内径的大小,并记录各测点管径至表3.1。
2)打开供水水箱开关,当实验管道充满水时反复开或关流量调节阀,排除管内气体或测压管内的气泡,并观察流量调节阀全部关闭时所有测压管水面是否平齐(水箱溢流时)。
如不平,则用吸气球将测压管中气泡排出或检查连通管内是否有异物堵塞。
确保所有测压管水面平齐后才能进行实验,否则实验数据不准确。
3)打开流量调节阀并观察测压管液面变化,当最后一根测压管液面下降幅度超过50%时停止调节阀门。
伯努利方程实验

伯努利原理(又称伯努利定律或柏努利定律)是流体力学中的一个定律,由瑞士流体物理学家丹尼尔·伯努利于1738年出版他的理论《Hydrodynamica》,描述流体沿着一条稳定、非黏性、不可压缩的流线移动行为。
伯努利原理往往被表述为p+1/2ρv2+ρgh=C,这个式子被称为伯努利方程。
式中p为流体中某点的压强,v为流体该点的流速,ρ为流体密度,g为重力加速度,h为该点所在高度,C是一个常量。
它也可以被表述为p1+1/2ρv12+ρgh1=p2+1/2ρv22+ρgh2。
需要注意的是,由于伯努利方程是由机械能守恒推导出的,所以它仅适用于粘度可以忽略、不可被压缩的理想流体。
原表达形式适于理想流体(不存在摩擦阻力)。
式中各项分别表示单位流体的动能、位能、静压能之差。
假设条件使用伯努利定律必须符合以下假设,方可使用;如没完全符合以下假设,所求的解也是近似值。
•定常流:在流动系统中,流体在任何一点之性质不随时间改变。
•不可压缩流:密度为常数,在流体为气体适用于马赫数(Ma)<0.3。
•无摩擦流:摩擦效应可忽略,忽略黏滞性效应。
•流体沿着流线流动:流体元素沿着流线而流动,流线间彼此是不相交的。
推导过程考虑一符合上述假设的流体,如图所示:流体因受力所得的能量:流体因引力做功所损失的能量:流体所得的动能可以改写为:根据能量守恒定律,流体因受力所得的能量+流体因引力做功所损失的能量=流体所得的动能。
对后可得丹尼尔·伯努利在1726年首先提出时的内容就是:在水流或气流里,如果速度小,压强就大,如果速度大,压强就小。
这个原理当然有一定的限制,但是在这里我们不谈它。
下面是一些通俗些的解释:向AB管吹进空气。
如果管的切面小(像a处),空气的速度就大;而在切面大的地方(像b处),空气的速度就小。
在速度大的地方压力小,速度小的地方压力大。
因为a处的空气压力小,所以C 管里的液体就上升;同时b处的比较大的空气压力使D管里的液体下降。
伯努利方程实验数据(1)

伯努利方程实验数据(1)伯努利方程实验数据是流体静力学和动力学研究中的基础,在航空、建筑、水利等行业都有着广泛应用。
本文旨在通过对伯努利方程实验数据的分析,深入了解流体的物理学特性。
一、伯努利方程实验数据概述伯努利方程描述了在不可压缩流体中,流体速度和流体压力之间的关系。
其公式为P + 1/2ρv² + ρgh = 常数,其中P为流体压强,ρ为流体密度,v为流体速度,g为重力加速度,h为流体对垂直方向上某点的高度。
在实验中,可以通过调整流体速度和位置,来观察伯努利方程中各参数的变化。
二、伯努利方程实验数据分析在实验中,可以通过调节实验装置中的阀门,控制流体速度和流量。
当调节阀门,减小管道截面积时,流量不变,流速升高,压强下降。
当调节阀门,增大管道截面积时,流量增加,流速下降,压强升高。
通过实验数据的分析,可以看出,在管道中的压强P会随着流速v的升高而下降,同时也会受到流体密度ρ和重力加速度g的影响。
在流量不变的情况下,管道中速度越大,管道中的压强就越小。
此外,在实验中也可以观察到在水平流动时,流体速度最大的点是管道的中央位置。
而在垂直向上或向下的流动时,当流速达到最大值时,压强将最小化。
这些观察结果都符合伯努利定理,并且可以直接应用于飞行器设计、建筑物隔音和流体系统优化等实际应用案例中。
三、结论通过伯努利方程实验数据的分析,我们可以更深入地了解流体在管道中的物理特性。
我们可以看到,管道中的流速会对压强产生影响,而流体的密度和重力加速度也会进一步加剧这种影响。
此外,在不同类型的流动情况下,伯努利定理的适用方式也有所不同。
流体力学的基础研究和应用对世界各地的科学技术和工程领域都有着重要的贡献。
实验伯努力方程实验

实验五伯努利方程实验一、实验目的1.观察恒定流条件下,通过管道水流的位置势能、压强势能和动能的沿程转化规律,加深理解能量方程的物理意义及几何意义。
2.学习用比托管和体积法测量流速的技能。
3.学习使用测压管、总压管测水头的实验技能及绘制水头线的方法。
4.验证流体定常流的伯努利方程。
二、实验原理1、理想流体的运动方程(欧拉方程)在恒定流、质量力仅有重力、流体不可压条件下有伯努利积分:(沿流线)。
2、伯努利积分的物理意义是:对于不可压理想流体的恒定流动,总水头(位置水头、压强水头和速度水头之和)或单位重量液体的总机械能(位置势能、压强势能和动能之和)沿流线是保持不变的。
3、伯努利积分可直接运用于恒定元流,重力场中,理想、不可压流体恒定元流的1-1、2-2两个断面上,总水头相等,即:。
4、毕托管利用测压管和总压管(测速管)测得总水头和测管水头之差–速度水头,可用来测量流场中某点的流速,即u=。
图1 毕托管测速原理5、在渐变流的过水断面上,惯性力的分量为零,质量力与压差力的分量在此平面上相互平衡,所以渐变流的过水断面上,压强分布规律与静水中是一样的,即测管水头为常数。
6、理想、不可压流体恒定总流的能量方程为其中1-1、2-2两个过水断面应处于渐变流段中,分别是两断面的动能修正系数。
若考虑实际(粘性)流体流动时的能量损失,则断面1-1是上游断面,断面2-2是下游断面,为断面1-1、2-2之间单位重量流体的能量损失,包括沿程和局部损失。
图2 实验原理图7、定常总流能量方程的各项都是长度量纲,所以可将它们沿程变化的情况几何表示出来,称为水头线。
可分别画出测管水头线和总水头线。
实验装置如图3所示,在自循环恒定管道流上串联变截面圆管和弯管。
在A,B,C,D四个断面管壁上的不同位置各接出四个毕托管,其中的测压管接在管壁上,总压管迎着来流方向放置在管轴处。
管中流速可用尾阀来调节,设置专用量水箱进行流量的量测。
图3 实验装置示意图伯努利实验组件相关参数值(如图所示,单位:mm)图4 伯努利实验组件相关参数1. 认真阅读实验目的要求、实验原理和注意事项。
伯努利方程实验报告

不可压缩流体定常流能量方程(伯努利方程)实验一、实验目的要求:1、掌握流速、流量、压强等动水力学水力要素的实验量测技术;2、验证流体定常流的能量方程;3、通过对动水力学诸多水力现象的实验分析研究,进一步掌握有压管流中动水力学的能量转换特性。
自循环伯努利方程实验装置图本实验的装置如图所示,图中:1.自循环供水器;2.实验台;3.可控硅无级调速器;4.溢流板;5.稳水孔板;6.恒压水箱;7.测压计;8.滑动测量尺;9.测压管;10.实验管道;11.测压点;12.毕托管13.实验流量调节阀。
三、实验原理:在实验管路中沿水流方向取n 个过水截面。
可以列出进口截面(1)至截面(i)的能量方程式(i=2,3,.....,,n)W i hg g p Z g g p Z i i i -+++=++12222111νρνρ选好基准面,从已设置的各截面的测压管中读出g p Z ρ+值,测出通过管路的流量,即可计算出截面平均流速ν及动压g 22ν,从而可得到各截面测管水头和总水头。
四、实验方法与步骤:1、熟悉实验设备,分清各测压管与各测压点,毕托管测点的对应关系。
2、打开开关供水,使水箱充水,待水箱溢流后,检查泄水阀关闭时所有测压管水面是否齐平,若不平则进行排气调平(开关几次)。
3、打开阀13,观察测压管水头线和总水头线的变化趋势及位置水头、压强水头之间的相互关系,观察当流量增加或减少时测压管水头的变化情况。
4、调节阀13开度,待流量稳定后,测记各测压管液面读数,同时测记实验流量(与毕托管相连通的是演示用,不必测记读数)。
5、再调节阀13开度1~2次,其中一次阀门开度大到使液面降到标尺最低点为限,按第4步重复测量。
五、实验结果及要求:1、把有关常数记入表2.1。
2、量测(g pZ ρ+)并记入表2.2。
3、计算流速水头和总水头。
4、绘制上述结果中最大流量下的总水头线和测压管水头线(轴向尺寸参见图2.2,总水头线和测压管水头线可以绘在图2.2上)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1,分析零流速下各测点的能量及侧头位置关系
零流速下,各侧点的能量与侧头位置理论上应该相等,有h=g22
μ
ζ,可得
2,运用伯努利方程,分析各测点的各项能能量
有伯努利方程可得,Z为定值,在流速相等的情况下,管路直径越大,对应的静压头与动压头越大,在等径的情况下,流速越大,能量损失越大,静压头减小,动压头增大
3,分析产生误差的原因
第一,实验读数的误差,
第二,实验仪器的误差
第三,两组流速过于相近而引起的误差
第四,查图的过程引起的误差
4,根据实验数据,可得Hf与u2 成正比
5,当正对的时候,影响流速的主要因素是管经的大小;当垂直的时候,影响流速的主要因素为摩擦损失。
