惯性环节振荡环节二三阶系统的MATLAB仿真
自动控制原理(第2版)(余成波_张莲_胡晓倩)习题全解及MATLAB实验第5章习题解答

第5章频率特性法频域分析法是一种图解分析法,可以根据系统的开环频率特性去判断闭环系统的性能,并能较方便地分析系统参量对系统性能的影响,从而指出改善系统性能的途径,已经发展成为一种实用的工程方法,其主要内容是:1)频率特性是线性定常系统在正弦函数作用下,稳态输出与输入的复数之比对频率的函数关系。
频率特性是传递函数的一种特殊形式,也是频域中的数学模型。
频率特性既可以根据系统的工作原理,应用机理分析法建立起来,也可以由系统的其它数学模型(传递函数、微分方程等)转换得到,或用实验法来确定。
2)在工程分析和设计中,通常把频率特性画成一些曲线。
频率特性图形因其采用的坐标不同而分为幅相特性(Nyquist图)、对数频率特性(Bode图)和对数幅相特性(Nichols图)等形式。
各种形式之间是互通的,每种形式有其特定的适用场合。
开环幅相特性在分析闭环系统的稳定性时比较直观,理论分析时经常采用;波德图可用渐近线近似地绘制,计算简单,绘图容易,在分析典型环节参数变化对系统性能的影响时最方便;由开环频率特性获取闭环频率指标时,则用对数幅相特性最直接。
3)开环对数频率特性曲线(波德图)是控制系统分析和设计的主要工具。
开环对数幅频特性L(ω)低频段的斜率表征了系统的型别(v),其高度则表征了开环传递系数的大小,因而低频段表征系统稳态性能;L(ω)中频段的斜率、宽度以及幅值穿越频率,表征着系统的动态性能;高频段则表征了系统抗高频干扰的能力。
对于最小相位系统,幅频特性和相频特性之间存在着唯一的对应关系,根据对数幅频特性,可以唯一地确定相应的相频特性和传递函数。
4)奈奎斯特稳定性判据是利用系统的开环幅相频率特性G(jω)H(jω)曲线,又称奈氏曲线,是否包围GH平面中的(-l,j0)点来判断闭环系统的稳定性。
利用奈奎斯特稳定判据,可根据系统的开环频率特性来判断闭环系统的稳定性,并可定量地反映系统的相对稳定性,即稳定裕度。
稳定裕度通常用相角裕量和幅值裕量来表示。
实验二-典型环节的时域分析和频域分析

一、 实验名称:典型环节的时域分析和频域分析二、实验目的:(1) 理解、掌握matlab 模拟典型环节的根本方法,包括:比例环节、积分环节、一阶微分环节、惯性环节和振荡环节等。
(2) 熟悉各种典型环节的阶跃响应曲线和频域响应曲线 (3) 理解参数变化对动态特性的影响三、 实验要求:(1) 一人一机,独立完成实验内容 。
(2) 根据实验结果完成实验报告,并用A4纸打印后上交。
四、 时间:2022年11月21日 五、 地点:信自楼234实验报告:一、比例环节的时域分析和频域分析 比例环节的传递函数:()G s k(1) 当k=1:3:10时,绘制系统的阶跃响应曲线,分析k值的影响情况。
程序:for k=1:3:10;num=k;den=1;G=tf(num,den);figure(1);step(G); hold on; %翻开第1个图形窗口,绘制系统的阶跃响应曲线 endfigure(1); legend('k=1','k=4','k=7','k=10'); 曲线:结果分析:时域响应的结果就是把输入信号放大k 倍。
如图,输入信号为幅值为1的阶跃信号,因此,输出是幅值为k 的阶跃信号。
程序:for k=1:3:10;num=k;den=1;G=tf(num,den);figure(1);bode(G);hold on; %翻开第1个图形窗口,绘制系统的阶跃响应曲线 endfigure(1); legend('k=1','k=4','k=7','k=10');曲线:结果分析:比例环节对幅频有影响,输出信号的幅值为输入信号的20*lgk倍。
比例环节对相位没有影响,如图显示,相位特性为一条0度的程度线。
二、积分环节的时域分析和频域分析积分环节的传递函数:1 ()G ss=(1) 当k=1:3:10时,绘制系统()kG ss=的阶跃响应曲线,分析曲线特点。
应用MATLAB绘制系统频率特性曲线

G(s)
稳定性。
s3
5系s22.7统4s的 2奈奎斯特曲线,并利用曲线来判别闭环系统的
解 MATLAB仿真程序代码如下:
num1=[ 2.7];
den1=[1 5 4 2];
sys1=tf(num1,den1);
nyquist(sys1)
title('Nyquist图');
运行后,获得如图1-46所示曲线。
自动控制原理
应用MATLAB绘制系统频率特性曲线
1.1用MATLAB绘制系统开环对数频率特性 对于连续系统,用MATLAB函数绘制系统开环对 数频率特性的函数命令调用格式有 Bode(sys) Bode(sys,w) Bode(sys1,sys2,…,sysN) Bode(sys1,sys2,…,sysN,w) [mag,phase,w]=Bode(sys)
例1-15 绘制一阶惯性环节
的G(s奈) 奎3斯特图。
5s 1
解 MATLAB仿真程序代码如下:
G=tf(3,[5 1]);
nyquist(G);Fra bibliotekhold on;
title('Nyquist图');
运行后,获得如图1-45所示曲线。
图1-45 例1-15系统极坐标曲线图
例1-16 用函数nyquist(sys)绘制开环传递函数为
bode(num,den);hold on;
end
grid
获得振荡环节伯德图如图1-43所示,
图1-43 例1-13开环系统伯德图
如果希望求取控制系统的增益裕量 、相位GM裕量 界频率(也称PM交叉频
率) 、穿越g频率 ,可以使c 用margin函数 计算控制系统的相关稳定裕度值。
自动控制原理实验报告
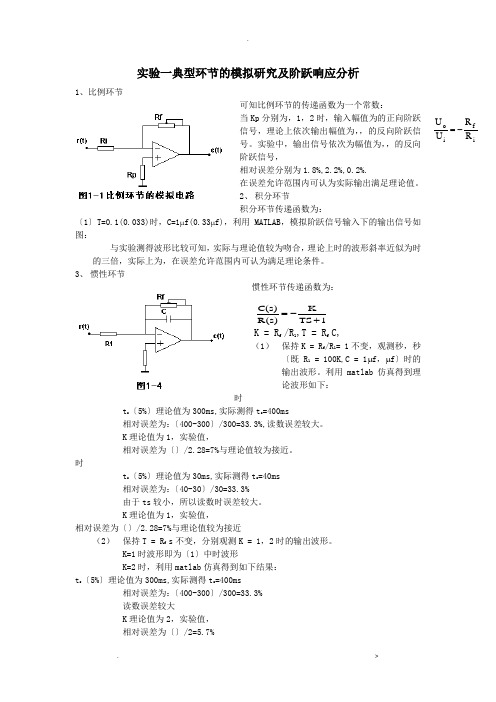
实验一典型环节的模拟研究及阶跃响应分析1、比例环节可知比例环节的传递函数为一个常数:当Kp 分别为,1,2时,输入幅值为的正向阶跃信号,理论上依次输出幅值为,,的反向阶跃信号。
实验中,输出信号依次为幅值为,,的反向阶跃信号,相对误差分别为1.8%,2.2%,0.2%.在误差允许范围内可认为实际输出满足理论值。
2、 积分环节积分环节传递函数为:〔1〕T=0.1(0.033)时,C=1μf(0.33μf),利用MATLAB ,模拟阶跃信号输入下的输出信号如图:与实验测得波形比较可知,实际与理论值较为吻合,理论上时的波形斜率近似为时的三倍,实际上为,在误差允许范围内可认为满足理论条件。
3、 惯性环节惯性环节传递函数为:K = R f /R 1,T = R f C,(1) 保持K = R f /R 1= 1不变,观测秒,秒〔既R 1 = 100K,C = 1μf ,μf 〕时的输出波形。
利用matlab 仿真得到理论波形如下:时t s 〔5%〕理论值为300ms,实际测得t s =400ms 相对误差为:〔400-300〕/300=33.3%,读数误差较大。
K 理论值为1,实验值,相对误差为〔〕/2.28=7%与理论值较为接近。
时t s 〔5%〕理论值为30ms,实际测得t s =40ms 相对误差为:〔40-30〕/30=33.3% 由于ts 较小,所以读数时误差较大。
K 理论值为1,实验值,相对误差为〔〕/2.28=7%与理论值较为接近(2) 保持T = R f s 不变,分别观测K = 1,2时的输出波形。
K=1时波形即为〔1〕中时波形K=2时,利用matlab 仿真得到如下结果:t s 〔5%〕理论值为300ms,实际测得t s =400ms相对误差为:〔400-300〕/300=33.3% 读数误差较大K 理论值为2,实验值, 相对误差为〔〕/2=5.7%if i o R RU U -=1TS K)s (R )s (C +-=与理论值较为接近。
实验三 SIMULINK环境下典型环节阶跃响应仿真及分析

(7)设仿真过程参数:SIMULATION 菜单\PARAMETERS 菜单项。 其中: Start Time 为仿真开始时间, Stop time 为仿真终止时间, Mix Step Size 为仿真最小步长。 Max Step Size 为仿真最大步长。, Tolerance 为仿真精度。 仿真开始前应对 Stop Time 进行修改,如改为 10 秒,50 秒或 200 秒,再根据实际情况进行 调整。
012??ssg积分环节ssg11?微分环节ssg?1比例微分环节pd21??ssg和12??ssg比例积分环节pissg111??和ssg2112??2对典型二阶系统4442???szssg进行仿真分别取00205071观察p?和ts的变化情况
实验三 SIMULINK 环境下典型环节阶跃响应仿真及分析
3.实验总结 初步了解 MATLAB 中 SIMULINK 的使用方法,了解 SIMULINK 下实现典型环节阶跃响应 方法。定性了解各参数变化对典型环节动态特性的影响,实现了实验目的。
S
s2 ,则令 2 s 3s 4
2
为[1];
Denominator 为[1,0]; 例 3-3:要将传递函数变为振荡环节: Denominator 为[1,1,1]; (在此传函中阻尼系数ζ为 0.5) 例 3-4:要将传递函数变为实际微分环节:
1 ,则令 Numerator 为[1]; s s 1
2
s ,则令 Numerator 为[1,0]; s 1
Denominator 为[1,1];
实际微分环节的传递函数为:
K d Td s 1 Td s
分子分母同除以 Td,则为
Kd s s 1 / Td
因此,上式中分子 s 的系数即为 Kd 值,分母中常数项为 Td 的倒数. (6)用鼠标将 step、transfer fcn 及 scope 模块连接。如下图所示:
自动控制原理的MATLAB仿真与实践第5章 线性系统的频域分析

函数模型,如:tf(), zpk(), ss()。 bode(num,den):num,den分别为传递函数的分子与
margin(G);[Gm,Pm,Wcg,Wcp]= margin(G): 直接求出系统G的幅值裕度和相角裕度。 其中:Gm幅值裕度;Pm相位裕度;Wcg幅值裕度 处对应的频率ωc;Wcp相位裕度处对应的频率ωg。
nichols(G);nichols(G,w):绘制单位反馈系统开环传 递尼科尔斯曲线。
20
>>clear; num=[2, 3];den=[1, 2, 5, 7]; %G(s)的分子分母 多项式系数向量
p=roots(den) 求根结果:
%求系统的极点
p=
-0.1981 + 2.0797i
-0.1981 - 2.0797i
-1.6038 可见全为负根,则s右半平面极点数P=0。 绘制Nyquist曲线: >> nyquist(num,den) %绘制Nyquist曲线
本节分别介绍利用MATLAB进行频域绘图和频 率分析的基本方法。
6
5.2.1 Nyquist曲线和Bode图
MATLAB频率特性包括幅频特性和相频特性。 当用极坐标图描述系统的幅相频特性时,通常称为 奈奎斯特(Nyquist)曲线;用半对数坐标描述系 统的幅频特性和相频特性时,称为伯德(Bode) 图;在对数幅值-相角坐标系上绘制等闭环参数( M和N)轨迹图,称为尼克尔斯(Nichols)图。
典型环节时域特性的仿真实验

典型环节时域特性的仿真实验1、通过观察典型环节在单位阶跃信号作用下的动态特性,熟悉各种典型环节的响应曲线。
2 、定性了解各参数变化对典型环节动态特性的影响。
3、初步了解Matlab中Simulink的使用方法。
研究典型环节(比例、积分、微分、惯性、二阶)在阶跃输入信号及白噪声干扰信号输入的响应。
1.1 运行Matlab,在命令窗口“Command Window”下键入“Simulink”后回车,则打开相应的系统模型库;或者点击菜单上的“Simulink”图标,进入系统仿真模型库。
然后点击左上角“创建新文件图标”,打开模型编辑窗口。
1.2 调出模块在系统仿真模型库中,把要求的模块都放置在模型编辑窗口里面。
从信号源模块包(Sources)中拖出1个阶跃信号(step)和1个白噪声信号发生器 (band-limited white noise) ;从输出模块包(Sinks)中拖出1个示波器(Scope);从连续系统典型环节模块包(Continuous) 中拖出1个微分环节(Derivative)和3个传函环节(Transfer Fcn);从数学运算模块包(Math Operations)中拖出1个比例环节(Gain)和1个加法器 (Sum) ;从信号与系统模块包(Signals Routing) 拖出1个汇流排(Mux);所有模块都放置在模型编辑窗口里面。
1.3 模块参数设置双击打开3个传函环节(Transfer Fcn),通过设定参数 (参照图1的数据),分别构成积分、惯性和二阶环节;打开比例环节,设定比例增益为2;打开白噪声信号发生器,设定功率(Noise power)为0.0001,采样时间(Sample time) 为0.05。
1.4 模块连接将各模块连接成如图1所示的仿真模型系统。
图1仿真模型系统22.1 双击Scope打开示波器,点击按钮“”启动仿真,画出输入信号波形图。
2.2 将比例环节的输出端接到汇流排(如图1所示),打开示波器, 点击按钮“”启动仿真,观察比例环节的阶跃响应及对白噪声信号是否敏感,然后画出波形图。
一阶系统及二阶系统时域特性MatLab仿真实验报告

实验一 一阶系统及二阶系统时域特性MatLab 仿真实验一、实验目的1、使学生通过实验中的系统设计及理论分析方法,帮助学生进一步理解自动控制系统的设计与分析方法。
2、熟悉仿真分析软件。
3、利用Matlab 对一、二阶系统进行时域分析。
4、掌握一阶系统的时域特性,理解常数T 对系统性能的影响。
5、掌握二阶系统的时域特性,理解二阶系统重要参数对系统性能的影响。
二、实验设备计算机和Matlab 仿真软件。
三、实验内容1、一阶系统时域特性 一阶系统11)(+=Ts s G ,影响系统特性的参数是其时间常数T ,T 越大,系统的惯性越大,系统响应越慢。
Matlab 编程仿真T=0.4,1.2,2.0,2.8,3.6,4.4系统单位阶跃响应。
2、二阶系统时域特性a 、二阶线性系统 16416)(2++=s s s G 单位脉冲响应、单位阶跃响应、单位正弦输入响应的 Matlab 仿真。
b 、下图为具有一微分负反馈的位置随动系统框图,求出系统的闭环传递函数,根据系统瞬态性能指标的定义利用Matlab 分别计算微分反馈时间常数τ为0,0.0125,0.025时系统的上升时间、峰值时间、最大超调量和调整时间。
C 、二阶线性系统3612362++s s ξ,当ξ为0.1,0.2,0.5,0.7,1.0,2.0时,完成单位阶跃响应的Matlab 仿真,分析ξ值对系统响应性能指标的影响。
四、实验要求1、进入机房,学生要严格遵守实验室规定。
2、学生独立完成上述实验,出现问题,教师引导学生独立分析和解决问题。
3、完成相关实验内容,记录程序,观察记录响应曲线,响应曲线及性能指标进行比较,进行实验分析4、分析系统的动态特性。
5、并撰写实验报告,按时提交实验报告。
五、Matlab 编程仿真并进行实验分析1、一阶系统时域特性实验代码:运行曲线:实验分析:由上图分析可知,一阶系统时间常数越大,图像图线越晚达到常值输出,即时间常数T影响系统参数,时间常数越大,系统的惯性越大,系统响应越慢。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MATLAB仿真
一.典型环节的电模拟及阶跃响应分析
(一)惯性环节
在Simulink中连接系统如下所示:
(1)K=1,T=1,系统的单位阶跃响应的波形如下图所示:
(2)K=1,T=2,系统的单位阶跃响应的波形如下图所示:
(3)T=1,K=2,系统的单位阶跃响应的波形如下图所示:
(二)振荡环节
在Simulink中连接系统如下所示:
(1)T=0.1,ξ=0.1时的单位阶跃响应的波形如下图所示:
(2)T=0.1,ξ=0.5时的单位阶跃响应的波形如下图所示:
(3)T=0.1,ξ=1时的单位阶跃响应的波形如下图所示:
二.二、三阶系统动态分析
(一)二阶系统
在Simulink中连接系统如下图所示:
(1)K1=1,K2=1,T1 =T2=0.1s时系统的单位阶跃响应的波形如下图所示:
(2)K1=5,K2=1,T1 =T2=0.1s时系统的单位阶跃响应的波形如下图所示:
(3)K1=10,K2=1,T1 =T2=0.1s时系统的单位阶跃响应的波形如下图所示:
(二)三阶系统
在Simulink中连接系统如下图所示:
(1)K=1时系统的单位阶跃响应的波形如下图所示:
(2)K=5时系统的单位阶跃响应的波形如下图所示:
(3)K=10时系统的单位阶跃响应的波形如下图所示:。
