第三章 平面力系
第03章+平面力系

物系平衡的特点: ① 当物体系平衡时,组成该系统的每一个物体都处于平 衡状态。 ② 每个单体可列3个平衡方程, 整个系统可列3n个方程 (设物系中有n个物体) 在求解静定的物体系的平衡问题时, 可以选每个物体为研 究对象, 列出全部平衡方程,然后求解;也可以先取整个系统 为研究对象, 列出平衡方程,求出部分未知量,再从系统中选 取某些物体作为研究对象, 列出另外的平衡方程,直至求出所 有的未知量为止。
Fy =0 mO (F )=0
平面平行力系平衡方程的二矩式:
m A (F )=0 mB (F )=0
例3-3 求图示刚架在A、B端所受的约束反力。
解:⑴ 作刚架的受力图。 ⑵ 列出平衡方程:
cos45 å F =0, F 窗 sin45 å F =0, F 窗
x A
y
A
+ F =0 + FB =0
(1)正负号的规定 (2)投影是代数量 (3)力沿轴的分力与力在轴上的投影的区别
Fy Fx cos a = , cos b = F F
讨论:力的投影与分量
y
y
y
F
Fy
O
F
F
Fy
F
O
Fx
x
Fy
O
Fx
x
O
Fx
x
Fx
x
分力Fx=?
⑴ 力F在垂直坐标轴 x、y上的投影与沿轴分 解的分力大小相等。 ⑵ 力F在相互不垂直的轴 x、y‘上的投影与沿 轴分解的分力大小是不相等的。
例3-5 试计算刚架支座A、B的约束反力。
解:⑴ 取整体为研究对象,列出平衡方程:
å å
å
Fx =0, FAx +10kN - FBx =0
第三章平面力系的合成与平衡

滑轮的受力图如图3.10(c)所示。
为了避免解联立方程,选直角坐标系如图所示,使x、 y轴分别与反力NBC、NAB垂直。
∑Fx=0,-NAB+Tcos60°-TBDcos30°=0 得 NAB=Tcos60°-TBDcos30°=-7.33kN NAB为负值,表示该力的实际指向与受力图中所假设 的指向相反。即杆AB受压力作用。再由
R Rx2 Ry2 ( Fx )2 ( Fy )2
tan Ry Fy
Rx
Fx
上式表明了合力在任一轴上的投影,等于各分 力在同一轴上投影的代数和。我们称之为合力投影 定理。
【例3.3】图3.7所示的吊环上作用有3个共面的拉力,各 力的大小分别是T1=3kN、T2=1kN、T3=1.5kN,方向如图
【解】绳AB作用于桩上的拉力是由绳BD传来的。因此先 取结点D为研究对象求出绳BD的拉力。
作用在结点D上的力有已知力F、绳DE的拉力TDE和 绳BD的拉力TDB,这三个力组成一平面汇交力系。结点D 的受力图如图3.11(b)所示。
选直角坐标系如图,使y轴与TDE垂直。列平衡方程
∑Fy=0,TDBsinα-Fcosα=0 得 TDB=Fcotα=4000N 再取结点B为研究对象。作用在结点B上的力有绳BC、 BD和BA的拉力TBC、TBD、TBA,绳BD给两结点D和B的 作用力应大小相等、方向相反,即有TBD=TDB=4000N。 力TBC、TBD、TBA组成一个平面汇交力系,结点B的受力 图如图3.11(c)所示。
3.1 平面汇交力系 3.1.1 力在坐标轴上的投影
设力F作用于物体的A点,如图3.4所示。
工程力学-平面任意力系

R' ( X )2 (Y )2 0
LO mO (Fi ) 0
①一般式 (一矩式)
X 0
平面力系中各力在直角坐标系oxy中
Y 0
各坐标轴上投影的代数和及对任意
点的力矩的代数和均为0。
mO (Fi ) 0
②二矩式
∑X=0 或∑Y=0
mA(Fi ) 0
mB (Fi ) 0
AB O
工程中的桁架结构
桁架的优点:轻,充分发挥材料性能。
桁架的特点:①直杆,不计自重,均为二力杆;②杆端铰接;
力
学 中 的 桁 架 模
基 本 三 角 形
型
③外力作用在节点上。
力
学
中 的 桁 架
简 化 计 算 模
模型
型
力
学
中 的 桁 架
简 化 计 算 模
节点
杆件
模型
型
一、节点法 [例3-3] 已知:如图 P=10kN,求各杆内力?
第三章 平面任意力系
平面任意力系(General coplanar force systems):各力的作用 线在同一平面内,既不汇交为一点又不相互平行的力系叫∼。
[例]
研究方法:把未知力系(平面任意力系)变成已知 力系(平面汇交力系和平面力偶系)
第三章 平面一般力系
§3–1 力向一点平移 §3–2 平面力系的简化 §3–3 平面力系的平衡条件 §3–4 刚体系统的平衡问题 §3–5 考虑有摩擦时物体的平衡问题
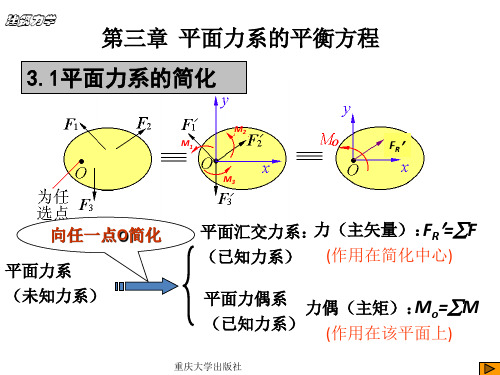
§3-2 平面力系的简化
一、平面力系向作用面内一点简化
O: 简化中心
主矢(Principal vector) R Fi
大小: R' R'x2 R'y2 ( X )2 (Y )2
建筑力学第三章 平面力系的平衡方程
③ FR≠' 0,MO =0,即简化为一个作用于简化中心的合力。这时, 简化结果就是合力(这个力系的合力), FR FR'。(此时
与简化中心有关,换个简化中心,主矩不为零)
重庆大学出版社
建筑力学
④ FR' ≠0,MO ≠0,为最任意的情况。此种情况还可以继续
重庆大学出版社
建筑力学
[例] 已知:Q=7.5kN, P=1.2kN , l=2.5m , a=2m , =30o , 求:
BC杆拉力和铰A处的支座反力?
解:(1)选AB梁为研究对象。
C
(2)画受力图
FAy
FBC
A
FAx
l/2 P
B Q
a
Байду номын сангаас
l
A
l/2 P
B Q
a
l
重庆大学出版社
建筑力学
(3)列平衡方程,求未知量。
静不定问题在材料力学,结构力学,弹性力学中 用变形协调条件来求解。
重庆大学出版社
建筑力学
物系平衡问题的特点: ①物体系统平衡,物系中每个单体也是平衡的。 ②每个单体可列3个(平面任意力系)平衡方程,整个系统
可列3n个方程(设物系中有n个物体)。
解物系问题的一般方法:
机构问题: 个体 个体
个体
“各个击破”
力系中各力对于同一点之矩的代数和。
重庆大学出版社
建筑力学
3.2平面力系的平衡方程及应用
FR=0, MO =0,力系平衡
FR =0 为力平衡
MO =0 为力偶也平衡 平面力系平衡的充要条件为:
理论力学 第三章 平面力系

FBl cos M 0
得
M 20 k N m FB 4.62 kN l cos 5 m cos 30
FA FB 4.62kN
故
目录
第三章 平面力系\力的平移定理
3.3 力的平移定理
作用于刚体上的力,可平行移动到刚体内任一指定点,但必须 在该力与指定点所决定的平面内同时附加一力偶,此附加力偶的矩 等于原力对指定点之矩。 平面一般力系向一点简化的理论基础是力的平移定理。
设平面汇交力系F1、F2、…、Fn中各力在x、y轴上的投影分 别为Xi、Yi,合力FR在x、y轴上的投影分别为XR、YR,利用公式
F Fx Fy Xi Yj
分别计算式FR=F1+F2+…+Fn=ΣF 等号的左边和右边,可得 FR = XR i+YR j 以及 F1+F2+…+Fn=(X1i+Y1j)+(X2i+Y2j)+…+(Xni+Ynj) =(X1+X2+…+Xn)i+(Y1+Y2+…+Yn)j 比较后得到 X R X1 X 2 X n X YR Y1 Y2 Yn Y 目录
返回
第三章 平面力系
如图(a)所示水坝,通常取单位长度坝段进行受力分析,并将坝 段所受的力简化为作用于坝段中央平面内的一个平面力系[图(b)]。
返回
第三章 平面力系
第三章 平面力系
3.1 平面汇交力系的合成与平衡 3.2 平面力偶系的合成与平衡 3.3 力的平移定理 3.4 平面一般力系向一点简化 3.5 平面一般力系的平衡方程及其应用
第三章 平面力系\平面力偶系的合成与平衡
建筑力学(第二版)第3章 平面力系

§ 3 - 1-2 简化结果的分析
■ (3) F′R≠0,M0≠0,原力系可以进一步简化为一个合力,如图3 -2a 所示。为此,只要将力偶M0 用一对等 值、反向、不共线的平行力F″R和FR 表示,且使FR = - F″R = F′R0 = F′R,则力偶臂 如图3 -2b 所示。若使力F″R作用于O 点,则力F′RO和F″R构成一对平衡力,可以去掉这一对平衡力,只剩下作用 于O′点的力FR。显然,力FR 就是原力系的合力,如图3 -2c 所示。因此,在这种情况下,原力系简化的最后结果是 一个合力FR,其大小和方向与主矢F′R相同,合力的作用线离简化中心O 的垂直距离为
§ 3 - 2-2 平面特殊力系的平衡方程
■ 3. 平面平行力系的平衡方程
力系中各力的作用线均相互平行的平面力系称为平面平行力系。设物体受平面平行力系F1,F2,…,Fn 的作用(图 3 -13)。如选取x 轴(或y 轴)与各力垂直,则不论力系是否平衡,每一个力在x 轴(或y 轴) 上的投影恒等于 零,即∑Fx = 0 (或∑Fy =0)。于是,平面平行力系的独立平衡方程的数目只有两个,即
■ 斜梁ABC 为一楼梯的计算简图,如图3 -14a 所示。其上承受的荷载为作用于斜梁AB 中点的集中力F =600 N,作用于C 处的集中力偶M =1. 2 kN·m 及沿梁AB 长度方向的均布荷载q =1 kN/ m,l =1 m, 试求梁A,B 处的约束反力。
§ 例题
■ 例 3-12
■ 塔式起重机如图3 -15 所示。机架重W1 =700 kN,其作用线通 过塔架的中心。最大起重量W2 =200 kN,最大悬臂长为12 m, 轨道AB 的间距为4 m。平衡荷重W3 到机身中心线距离为6 m。试问 :
工程力学教学课件 第3章 平面任意力系
A
MA
FAx
A
简 化
2021/7/22
FAy
11
一、简化结果分析
3.2
平
面 任
F1
A1
F2
O A n A2
M O FR'
O
意
Fn
力
系 的 简 化
1 . F R ' 0 ,M o 0
2 . F R ' 0 ,M O 0
结 果
3 . F R ' 0 ,M O 0 4 . F R ' 0 ,M O 0
的 简 化
此时主矩与简化中心的位置无关。
3、主矢不等于零,主矩等于零 (F R ' 0 ,M O 0 )
结 果
此时平面力系简化为一合力,作用在简化
中心,其大小和方向等于原力系的主矢,即
FRF
2021/7/22
13
一、简化结果分析
3.2 4、主矢和主矩均不等于零 (F R ' 0 ,M O 0 )
平
此时还可进一步简化为一合力。
面
任
FR'
FR'
FR
FR
意 力
O M O O
O
d
O
O
O
d
系 的 简 化
FR'' M O m O ( F R ) F R d F R 'd 于是
d M
F
由主矩的定义知:M O m O (F i)
O ' R
结 所以:
m O (F R ) m O (F i)
果 结论:平面任意力系的合力对作用面内任一点之矩
杆所受的力。
A
45
第3章平面一般力系
第3章 平面任意力系
§3.1 力线平移定理 §3.2 平面任意力系的简化 §3.3 平面任意力系的平衡条件 和平衡方程 §3.4 物体系统的平衡静定 和静不定问题 §3.5 平面桁架
M A / FR 2375.0 / 711.5 d a = AC = = = = 3.52 m o sin ϕ sin ϕ sin 71.6
§3.2 平面任意力系的简化
四、 合力矩定理
平面任意力系的合力对于点O之矩等于原力系对简化中心 O的主矩,即:
M O = M O ( FR ) M O = ∑ M O (F )
第3章 平面任意力系
§3.1 力线平移定理 §3.2 平面任意力系的简化 §3.3 平面任意力系的平衡条件 和平衡方程 §3.4 物体系统的平衡静定 和静不定问题 §3.5 平面桁架
§3.3 平面任意力系的平衡条件和平衡方程
一、 平面任意力系的平衡方程
′ =0 保证物体移动平衡 由于 FR MO=0 为转动平衡
§3.2 平面任意力系的简化
二、主矢和主矩
建立坐标系oxy
′ = F1 x + F2 x + ⋅⋅⋅ + Fnx = ∑ Fx FRx ′ = F1 y + F2 y + ⋅⋅⋅ + Fny = ∑ Fy FRy
y
MO
r ′ FR
α
O
主矢大小 ′ = ( FR ′x )2 + ( FR ′y )2 = ( ∑ Fx )2 + ( ∑ Fy ) 2 FR 主矢方向 r r ′,i ) = cos( FR
-建筑力学第三章平面力系的合成与平衡
平面汇交力系合成与平衡的几何法小 结
几何法解题步骤:1. 取研究对象;2. 画受力图; 3. 作力多边形;4. 选比例尺; 5. 解出未知数。
几何法解题不足: 1. 精度不够,误差大; 2. 作图要求精度高; 3. 不能表达各个量之间的函数关系。
平面汇交力系合成与平衡的另一种方法: 解析法(重点掌 握)。
R0
Rx2
R
2 y
0
或:力系中所有力在各个坐标轴上投影的代
数和分别等于零。
Rx Fx 0 Ry Fy 0
为平衡的充要条件, 也叫平衡方程
解析法求解汇交力系平衡问题的一般步骤:
1.选-对像;即依需选分离体,分离体选取应最好含题设
的已知条件; 2.画-分离体受力图,作到准确无误;
应用力线平移定理,可将刚体上平面任意力系中各个力
的作用线全部平行移到作用面内某一给定点O 。从而这
力系被分解为平面汇交力系和平面力偶系。这种变换的
方法称为力系向给定点O 的简化。点O 称为简化中心。 R0 -----主矢,与简化中心选取无关; M0 ---主矩,与简化中心有关。
2、主矢和主矩 (1)主矢R0
F3 F2
D
C
F2 F4 F3
R
F4
R
F4
E
E
3、汇交力系的合成结果
汇交力系可以合成为一个力,合力作用在力系
的公共作用点,它等于这些力的矢量和,并可由这
力系的力多边形的封闭边表示。
矢量的表达式:R F1 F 2
F1
A F2
F4 F3
F1
A
B F2
R
C
F3
D
F4
n
第三章 平面力系
x'
工程力学 第三章 平面力系
[例] 已知 P=2kN 例 求SCD , RA
解 ①研究AB杆 ②画出受力图 研究 杆 ③选坐标系 ④列平衡方程
∑
RA ⋅ cosφ − SCD ⋅ cos450 = 0 X =0
Y = 0 −P − RA ⋅ sinφ + SCD ⋅ sin450 = 0 ∑
ϕ
工程力学 第三章 平面力系
=
=
=
工程力学 第三章 平面力系
M = FRd = Fd + F2d +L− Fnd = M1 + M2 +LMn 1
M = ∑ Mi = ∑Mi
i= 1
n
平面力偶系平衡的充要条件 M = 0 ,有如下平衡方程
∑ Mi
=0
平面力偶系平衡的必要和充分条件是: 平面力偶系平衡的必要和充分条件是:所有各力偶矩的代数 和等于零. 和等于零.
k=1
n
力在平面直角坐 标系中的解析式
FR = FRxi + FRy j
工程力学 第三章 平面力系
合力投 影定理
合力投影定理: 合力投影定理:平面汇交力系的合力在任一坐标轴 上的投影,等于各分力在同一坐标轴上投影的代数和 代数和。 上的投影,等于各分力在同一坐标轴上投影的代数和。
工程力学 第三章 平面力系
∑Fi = 0
i=1
n
注意 因为力是矢量,其包括大小和方向二个元素。所以 因为力是矢量,其包括大小和方向二个元素。
用封闭力多边形可以求出二个未知元素,即可以有一个力大 封闭力多边形可以求出二个未知元素, 可以求出二个未知元素 小和方向都未知,或者有二个力各有一个未知元素( 小和方向都未知,或者有二个力各有一个未知元素(大小或 方向)。 方向)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章平面力系的平衡问题
§3-1平面力系平衡方程
§3-2 刚体系统的平衡问题、静定、静不定问题
§3-1平面力系的平衡方程
力系平衡的充要条件是主矢主矩同时等于零。
∑F x =0
∑F y =0
∑MO (F )=0
平面力系的平衡方程(基本形式)
即:力系中各力在任选的两直角坐标轴上投影的代数和都等于零,以及力系中各力对任一点之矩的代数和也等于零
平面力系平衡方程的其它形式
两矩一投影:∑MA (F )=0
∑MB (F )=0
∑F x =0
附加条件:X 轴不垂直于A、B 二点的连线。
三矩式:∑MA (F )=0
∑MB (F )=0
∑MC (F )=0
附加条件:A、B、C 三点不共线。
平面力系的平衡方程只有三个独立方程,因此只能求解三个未知量!
平面平行力系
平面平行力系(设各力作用线是平行于y 轴),平衡方程两种形式:
一矩一投影:∑F y =0
∑MO (F )=0
两矩式:∑MA (F )=0
∑MB (F )=0
附加条件:A、B两点的连线不与各力平行
平面汇交力系
平面力偶系
其中113302F q l =×=kN ∑=0x F 0
A M =∑∑=0y F 060cos =−−D F P F Ay 0
360sin 60cos 1=⋅+⋅+⋅−−l F l F l F M M A D D 316.4kN Ax F =kN 300=Ay F m
kN 1188⋅−=A M 0
60sin 1=−+D
F F F Ax 例已知m
1,kN 400,m kN 20,
m kN 20,kN 100===⋅==l F q M P 求:固定端处约束力.
A 解:取型刚架,画受力图.
T 根据平衡条件列方程
习题
已知:梁AD 的支承及受力
如图所示。
F =500 N ,
F A =1000 N ,q =1000
N/m ,M=2000 N ·m ,a
=2m
求:座B 、C 的约束反力
给起重机轮子的约束力。
3
∑=0A M
041424213=+−−B F P P P 0iy F =∑0
321=−−−+P P P F F B A 时
kN 1803=P kN
210=A F kN 870=B
F
§3-2 刚体系统的平衡、静定、静不定概念物体系——由若干个物体通过约束组成的系统。
外力——物体系以外任何物体作用于该系统的力。
内力——物体系内部各物体间互相作用的力。
物体系平衡方程的数目
由n个物体组成的物体系,总共有不多于3n个独立的平衡方程。
静定静不定静不定静不定
静定问题——当系统中未知量数目等于独立平衡方程数目时的问题。
静不定问题——当系统中未知量数目多于独立平衡方程数
目时,不能求出全部未知量的问题。
判断下面结构是否静定?
32.89kN Ax F =0
y F =∑sin 602cos300
Ay B F F ql F −−−=D D 2.32kN
Ay F =−∑=0
A M 22sin 603cos3040
A B M M ql l F l F l −−⋅+⋅−⋅=D D 10.37kN m A M =⋅取整体,画受力图.
0x F =∑
cos 60sin 300
Ax B F F F −−=D D
例
求:A ,E 支座处约束力及BD
杆受力.
已知:DC=CE=CA=CB=2l, R=2r=l,,各构件自
重不计,045.θ=P G
取整体,画受力图.
解:∑=0
E M 02
522=⋅−⋅⋅−l P l F A P F A 825−=0
x F =∑045cos 0
=+A Ex F F 0
y F =∑0
45sin 0=+−A Ey F P F P F Ex 85=P F Ey 8
13=
取DCE 杆,画受力图.
∑=0
C M 02245cos 0=⋅+⋅−⋅−l F l F l F Ex K DB P F DB 8
23=(拉)
例
已知:P 2=2P 1,P =20P 1 ,r , R =2r ,20;α=D
求:物C 匀速上升时,作用于小轮上的力偶矩轴承A ,B 处的约束力.
M
取小轮,画受力图.0x F =∑0y F =∑∑=0A M r P M 110=164.3P F Ax −=19P F Ay −=0'1=−+P F F t Ay 0'=+r Ax F F 0
'=⋅−r F M t
例如图已知q=3 kN/m,F=4 kN,M=2 kN·m。
CD=BD, AC=4m,CE=EA=2 m。
各杆件自重不计,试求A和B处的支座约束力。
2
2
A B
q C
2
2
F
M
D
E30°
解:1.取BC 为研究对象,受力分析如图。
230cos 4=−−°⋅M F F B ()∑=,
0F C M F B = 2.89 kN 2
2B
C
F M
D
30°
F Cx
F Cy
F B
2.取整体为研究对象,受力分析如图。
2
2
A
B
q C
2
2F M D
E
30°
F Ax
F Ay
M A
30°,
0=∑x F F Ay = 0.58 kN
230sin =++°−Ax F q F ,
0=∑y
F
F Ax = 47.5 kN
30cos =++°−Ay B F F F
()∑=,
0F M A
M A = -2 kN·m
30cos 230cos )
30sin 22(30sin 30cos 412=°×°−°+°+°
+×−−F F F q M M B A ()∑=0
F M C
或
230cos 4324=−°+×++−F F q F M M B Ax A 也可以取杆为AC 研究对象, ∑M C =0。
2
2A
B
q C
2
2F M
D
E 30°
F Ax
F Ay
M A
30°
例
已知:构架如图所示,重物重P =10kN,AD =DB =2m ,CD =DE =1.5m ,不计摩擦及杆、滑轮的重量。
求:杆BC 所受的力和杆AB 作用于销钉D 的力。
12.5202.5CB Dx Dy F KN F KN F KN
===
如图已知F=15 kN,M =40 kN·m。
各杆件自重不计,试求D和B处的支座约束力。
讨论题
αA
M
B
E
D
C
F
4m
4m
2m2m
2m
2m
60°
M
D
C
F C
4m 2m α
F D
解:1.先取CD 为研究对象,受力分析如图。
∑=,
0M 0
242
2
=+−D F M F D = 8.95 kN
α
A
M
B
E D
C F
4m
4m
2m
2m
2m
2m
60°
α
B
F B
E F 2m
2m
α
C F C ′
60°2.再取BC ,受力分析如图。
:0=∑x
F 0cos cos 60cos =′−+°−αα
C
B F F F F B = 15.5 k N
错解!
B F Cx
E C F
2m
2m
F By
F Bx
F Cy 60°解:1.先取BC 为研究对象,受力分析如图。
()∑=,
0F M C
4260sin =×−×°By F F F By = 6.5 k N
α
A
M
B
E
D
C
F
4m
4m
2m 2m
2m
2m
60°
正确解答
M
B F Dx
E
D
C F
4m
2m
2m
2m
F By F Bx
F Dy
60°B F Cx
E C F
2m
2m
F By F Bx F Cy
60°()∑=:
0F M B
46460cos 460sin =×−×−×°+×°+Bx By F F F F M 2.再取BCD 为研究对象,受力分析如图。
F Bx = 20.75 k N。
