练习_平面向量基本定理-优质公开课-人教A版必修4精品
新人教A版必修4高中数学2.3.1 平面向量基本定理学案

高中数学 2.3.1 平面向量基本定理学案新人教A版必修4【学习目标】1知识与技能(1)了解平面向量基本定理及其意义,会利用向量基本定理解决简单问题;(2)培养学生分析、抽象、概括的推理能力。
2过程与方法(1)通过平面向量基本定理的得出过程,体会由特殊到一般的思维方法;(2)通过本节学习,体会用基底表示平面内任一向量的方法。
3情感.态度与价值观(1)通过本节学习,培养学生的理性思维,培养学生独立思考及勇于探求、敢于创新的精神、培养主动学习的意识;(2)通过平面向量基本定理的探求过程,培养学生观察能力、抽象概括能力、独立思考的能力,激发学生学习数学的兴趣。
【重点难点】重点:平面向量基本定理的应用难点:对平面向量基本定理的发现和形成过程,数学思想的渗透。
【学习内容】一【知识链接】1. 向量加法与减法有哪几种几何运算法则?2.怎样理解向量的数乘运算λa? (1)模:|λa|=|λ||a|;(2)方向:λ>0时λa 与a方向相同;λ<0时λa与a方向相反;λ=0时λa=03. 向量共线定理 :向量b 与非零向量a共线则:有且只有一个非零实数λ,使b =λa.二【新课导入】情景展示:在物理学中我们知道,力是一个向量,力的合成就是向量的加法运算.而且力是可以分解的,任何一个大小不为零的力,都可以分解成两个不同方向的分力之和.将这种力的分解拓展到向量中来,就会形成一个新的数学理论. 三、小组合作、自主探究 探究(一):平面向量的基本定理探究1:给定平面内任意两个不共线的非零向量1e 、2e ,请你作出向量b =31e +22e 、c =1e -22e .探究2:由探究1可知可以用平面内任意两个不共线的非零向量1e 、2e 来表示向量b ,c 那么平面内的任一向量是否都可以用形如λ11e +λ22e 的向量表示呢?【定理解读】1 、1e 、2e 必须是平面向量的基本定理:如果1e 、2e 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量a ,有且只有一对实数λ1、λ2,使a =λ11e +λ22e .2、λ1,λ2是被a,1e ,2e 的数量 3、基底不唯一,关键是不共线;4、由定理可将任一向量a 在给出基底1e 、2e 的条件下进行分解;5、基底给定时,分解形式唯一.6、λ 1 =0时 ; λ2=0时 ;λ1=0、λ2=0时 。
高中数学--2.3.1-平面向量基本定理--新人教A版必修4PPT课件

思考3:一 个 平 面 内 的 两 个 不 共 线 的 向 量 e 1 、 e 2 与 该 平
面 内 的 任 一 向 量 a 之 间 的 关 系 .
M
C
a
A
e1
e2
O
如 图 O C O M O N
NB
O M 1 O A 1 e 1 O N2O B2e2
O C 1e12e2
即 a1e-1+2e2
有 且 只 有 一 个 实 数 , 使 得 b a .
当 0 时,b 与a 同向, 且| b | 是| a | 的 倍; 当 0 时,b 与a 反向, 且| b | 是| a | 的| | 倍; 当 0 时,b 0 ,且| b| 0 。
-
4
(问题提出) .如图,光滑斜面上一个木块受到的重力为G,下 滑力为F1,木块对斜面的压力为F2,这三个力的 方向分别如何?
解:在 ABCD中,
D
C
AC ABADab
b
M
DB ABADab A
MA 1 AC a b a b
2
2
22
MB 1 DB a b a b
2
2 22
MC 1 AC MA a b
2
22
MD
1
DB
MB
ቤተ መጻሕፍቲ ባይዱ
a
-
b
2
22
aB
13
例3 如图,O A 、O B 不线,APtAB(tR),
向量能够用选取的基底表示.
新疆 王新敞
奎屯
教学重点:
平面内任一向量用两个不共线非零向量表示.
教学难点: 平面向量基本定理的理解.
-
2
你复习了吗?
人教版高中数学必修4(A版) 《平面向量基本定理》课件
b
a
O
B A
b
O
a
与 b 反向
夹角的范围:0 0 ,180 0
a
90 与 垂直, 记作 a b b
A
例2:如图,等边三角形中,求
(1)AB与AC的夹角; (2)AB与BC的夹角。
C
'
C
注意:同起点
120
A
0
60
B
1、若e1,是表示平面内所有向量的一组基底, e2 则下面的四组向量中不能作为基底的是
a
B
向量的夹角:
两个非零向量 a 和 b ,作 OA a ,
AOB OB b ,则
B
b
叫做向量 特别的: a
O
a和
b
O A a 注意:两向量必须 的夹角. 是同起点的
B
a
0
与b
b
B
A
同向
a
180
一、复习旧知,以旧悟新:
(1)求两向量之和的方法是:
(2)向量 b与 a(a 0)共线,则________________
______
当且仅当有唯一一个实数,使b a
二、揭示定理形成, 激发追求新知
设置疑问 导入课题
问题1:给定一个非零向量
能写出什么样的向量?
, e 做线性运算,你
2.已知向量 e1、e2 不共线,实数 x、y 满足(3x-4y)e1+ (2x-3y)e2=6e1+3e2,则 x-y=________.
3.如图,在ABC中, AC, AB的夹角与CA, AB的夹角的关系为
高中数学 第二章 平面向量 2.3.1 平面向量基本定理课件 新人教A版必修4

1.若向量 a,b 不共线,则 c=2a-b,d=3a-2b, 试判断 c,d 能否作为基底. 解:设存在实数 λ,使 c=λd, 则 2a-b=λ(3a-2b), 即(2-3λ)a+(2λ-1)b=0, 由于向量 a,b 不共线, 所以 2-3λ=2λ-1=0,这样的 λ 是不存在的, 从而 c,d 不共线,c,d 能作为基底.
探究点二 用基底表示平面向量
如图所示,在▱ABCD 中,点 E,F
分别为 BC,DC 边上的中点,DE 与 BF 交 于点 G,若A→B=a,A→D=b,试用 a,b 表 示向量D→E,B→F.
[解] D→E=D→A+A→B+B→E =-A→D+A→B+12B→C
=-A→D+A→B+12A→D=a-12b.
4.若 a,b 不共线,且 la+mb=0(l,m∈R),则 l=________, m=________. 答案:0 0 5.若A→D是△ABC 的中线,已知A→B=a,A→C=b,若 a,b 为基底,则A→D=________. 答案:12(a+b)
探究点一 对基底的理解
设 O 是平行四边形 ABCD 两对角线的交点,给出下列向
解:D→E=D→C+C→E=2F→C+C→E=-2C→F+C→E=-2b+a.
B→F=B→C+C→F=2E→C+C→F
=-2C→E+C→F=-2a+b.
用基底表示向量的两种方法 (1基底表示为止. (2)通过列向量方程或方程组的形式,利用基底表示向量的唯一 性求解.
对基底的理解 (1)两个向量能否作为一组基底,关键是看这两个向量是否共 线.若共线,则不能作基底,反之,则可作基底. (2)一个平面的基底若确定,那么平面上任意一个向量都可以由 这组基底唯一线性表示出来,设向量 a 与 b 是平面内两个不共 线的向量,若 x1a+y1b=x2a+y2b,则xy11==yx22.,
新课标人教A版数学必修4全部课件:平面向量的练习题
9 设 a,是两个不同的向量,已 b
知 AB = 2 a+ k b, = a+ 3 b CB k。 8
CD = 2 a- b,若 A , B , D 三点共线,求实数
10 平行四边形 ABCD 中, M , N 分别为 DC 、 BC 的中点, 已知 AM = c, = d,用 c, 表示 AB , 。 AN d AD AB = 2 3
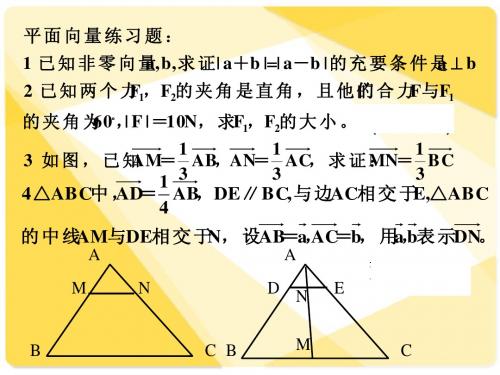
3 如图,已知 AM = AB , AN = AC ,求证:MN = BC 3 3 1 3 4 △ ABC 中, = AB , DE ∥ BC , 与边 AC 相交于 E ,△ ABC AD 4
的中线 AM 与 DE 相交于 N ,设 AB = a, = b,用 a, 表示 DN 。 AC b
A
M N
y B
A
o x
28 .如图 AOE 和 BOE 都是边长为 1的等边 三角形,延长 OB 到 C ,使 | BC | t ( t 0 ).
y A
连 AC 交 BE 于 D . (1)用 t 表示 OC 的坐标 ; . ( 2)求 OD 和 EC 所成的角的大小 . .
O
E
x
D
B
C
29 .已知四边形 ABCD , AB | | AD | , | | BC | | CD | .试用向量方法证明它的 对角线互相垂直 30 .如图,已知; 两条
3 , 5 , 求 A 1 , B 1 , C 1
2 ,3 , 3 , 7 , 4 , 5
ABCD , AB , AD 边长分别为 1, 2 0
24 .已知平行四边形
A 60 ,求 AB CD AC DB AD BC
25 .已知 O 0, , A 1, , B 3, , C 在线段 OB 上,向量 0 2 5 63 105 OA BA AC 与 OB 垂直,求 C 。 , 34 34
人教A版必修四 2.3.1 平面向量基本定理 课件(34张)

其中正确的说法是( B )
A.①②
B.②③
C.①③
D.②
【解析】因为不共线的两个向量都可以作为一组基 底,所以一个平面内有无数多个基底,又零向量和 任何向量共线,所以基底中不含有零向量.因此本 题中,①错,②、③正确,故选 B.
2.在等边三角形 ABC 中,A→B与B→C的夹角等于( C )
A.60°
r ur uur 即 a 1e1 +2 e2.
e1
e2
a
N A
B
C O
uuur uuuur uuur
如图, OC OM ON,
M
uuuur uuur ur uuur uuur uur
因为OM 1OA 1e1,
uuur ur uur
ON 2 OB 2 e2,
所以OC 1e1 2 e2,
数λ1,λ2 ,使
a 1e1 2 e2
说明:① ②
areur1是,e平uur2 面是内两的个任不意共向线量的;向量;
③ λ1,λ2为实数,且唯一确定.
我们把不共线的向量
ur e1
,euur2
叫做这一平面内所有向量
的一组基底.
不共线向量有不同方向,它们的位置关系可用夹角
来表示.关于向量的夹角,我们规定:
那么对于这一平面内的任意向量 有且只有
一对实数
使
.
不共线的向量 叫做表示这一平面内 所有向量的一组基底.
r ur uur
即 a 1e1 +2 e2.
r ur uur
a 1e1 +2e2
这就是说平面内任 r
一向量a都可以表示 ur uur ur uur
成1e1 2 e2 (e1, e2 不共线)的形式.
2015届高考数学一轮复习 平面向量的基本定理及坐标表示练习 新人教A版必修4
必修Ⅳ-07 平面向量的基本定理及坐标表示1.平面向量基本定理:如果12,e e 是同一平面内的两个 ,那么对于这一平面内的任意向量a ,有且只有一对实数12,λλ,使 ,不共线的向量12,e e 叫做表示这一平面内所有向量的一组 .2.向量的夹角与垂直:已知两个 a b 和,作,O A aO B b A O B θ==∠=,则叫做向量a b与的 .向量a b 与的夹角的范围是 .当0θ=时,向量a b 与 ,当θπ=时,向量a b 与 ,当2πθ=时,向量a b 与 .3.把一个向量分解为两个互相垂直的向量,叫做把向量 .4.向量的坐标表示:在平面直角坐标系内,分别取与x 轴,y 轴同方向的两个单位向量,i j 作为基底,对于平面内的一个向量a ,有且只有一对实数,x y 使得 ,我们把有序实数对(,)x y 叫做a 的坐标,记作 , 叫做向量的坐标表示.5.向量的坐标运算:已知1122(,),(,)a x y b x y ==则a b += ,a b -= ;若实数λ,则a λ= .一个向量的坐标等于表示此向量的有向线段的 的坐标减去 的坐标,即:若1122(,),(,)A x y B x y ,则AB = .6.向量相等的坐标关系:若1122(,),(,)a x y b x y ==且a b =,则有 .7.向量共线的坐标表示:若1122(,),(,)a x y b x y ==,且0b ≠,那么当且仅当 时,向量a b 与共线,即12210a b x y x y ⇔-=.8.设112233(,),(,),(,)A x y B x y C x y ===只要证明向量 (答案不唯一),即可判断,,A B C 三点共线.例1.设12,e e 是平面内所有向量的一组基底,则下面四组向量中,不能作为基底的是( )A 1212e e e e +-和B 1221326e e e e --和4C 122122e e e e ++和D 212e e e +和例2.(2008,安徽)若(2,4),(1,3),AB AC ==则BC = ( )A (1,1)B (1,1)--C (3,7)D (3,7)--例7.设O 为ABC ∆内一点,且满足0AO BO CO ++=,则O 为ABC ∆的( )A 外心B 内心C 重心D 垂心例3.(2004,浙江)已知向量(3,4),(sin ,cos ),a b αα==且a b ,则tan α= . 例4.若向量(1,2),(,1),2,2,a b x u a b v a b u v ===+=-且,则x = .例5.已知向量(,12),(4,5),(,10)OA k OB OC k ===-,且,,A B C 三点共线,求实数k 的值.例6.设向量(2,3),(1,2),(9,4)a b c =-==,若c ma nb =+,则求实数,m n 的值.。
2021秋高中数学第二章平面向量2.3.1平面向量基本定理练习(含解析)新人教A版必修4
2.3.1 平面向量根本定理A 级 根底稳固一、选择题1.设e 1,e 2是平面内所有向量的一组基底,那么以下四组向量中,不能作为基底的是( )A .e 1+e 2和e 1-e 2B .3e 1-4e 2和6e 1-8e 2C .e 1+2e 2和2e 1+e 2D .e 1和e 1+e 2解析:B 中,因为6e 1-8e 2=2(3e 1-4e 2), 所以(6e 1-8e 2)∥(3e 1-4e 2),所以3e 1-4e 2和6e 1-8e 2不能作为基底. 答案:B2.在菱形ABCD 中,∠A =π3,那么AB →与AC →的夹角为( )A.π6B.π3C.5π6D.2π3解析:由题意知AC 平分∠BAD ,所以AB →与AC →的夹角为π6.答案:A3.在△ABC 中,点D 在BC 边上,且BD →=2DC →,设AB →=a ,AC →=b ,那么AD →可用基底a ,b 表示为( )A.12(a +b ) B.23a +13b C.13a +23b D.13(a +b ) 解析:因为BD →=2DC →, 所以BD →=23BC →.所以AD →=AB →+BD →=AB →+23BC →=AB →+23(AC →-AB →)=13AB →+23AC →=13a +23b .答案:C4.如图,在△OAB 中,P 为线段AB 上一点,OP →=xOA →+yOB →,且BP →=3PA →,那么( )A .x =23,y =13B .x =13,y =23C .x =14,y =34D .x =34,y =14解析:由BP →=3PA →,得OP →-OB →=3(OA →-OP →),整理,得OP →=34OA →+14OB →,故x =34,y =14.答案:D5.(2021·全国卷Ⅰ)在△ABC 中,AD 为BC 边上的中线,E 为AD 的中点,那么EB →=( ) A.34AB →-14AC → B.14AB →-34AC → C.34AB →+14AC → D.14AB →+34AC → 答案:A 二、填空题6.假设OP 1→=a ,OP 2→=b ,P 1P →=λPP 2→(λ≠-1),那么OP →=________.解析:因为OP →=OP 1→+P 1P →=OP 1+λPP 2→=OP 1→+λ(OP 2→-OP →)=OP 1→+λOP 2→-λOP →, 所以(1+λ)OP →=OP 1→+λOP 2→.所以OP →=11+λOP 1→+λ1+λOP 2→=11+λa +λ1+λb .答案:11+λa +λ1+λb 7.|a |=1,|b |=2,且a -b 与a 垂直,那么a 与b 的夹角为________.解析:如图,作向量OA →=a ,OB →=b ,那么BA →=a -b .由,得OA =1,OB =2,OA ⊥AB ,所以△OAB 为等腰直角三角形,所以∠AOB =45°,所以a 与b 的夹角为45°.答案:45°8.如果3e 1+4e 2=a ,2e 1+3e 2=b ,其中a ,b 为向量,那么e 1=________,e 2=________. 解析:由⎩⎪⎨⎪⎧a =3e 1+4e 2,b =2e 1+3e 2,解得⎩⎪⎨⎪⎧e 1=3a -4b ,e 2=3b -2a .答案:3a -4b 3b -2a 三、解答题9.如下图,平面内有三个向量OA →,OB →,OC →,其中OA →与OB →的夹角为120°,OA →与OC →的夹角为30°,且|OA →|=|OB →|=1,|OC →|=23,假设OC →=λOA →+μOB →(λ,μ∈R).求λ+μ的值.解:如下图,以OA ,OB 所在射线为邻边,OC 为对角线作平行四边形ODCE ,那么OC →=OD →+OE →.在直角△OCD 中,因为|OC →|=23,∠COD =30°,∠OCD =90°,所以|OD →|=4,|CD →|=2,故OD →=4OA →,OE →=2OB →,即λ=4,μ=2,所以λ+μ=6.10.如下图,▱ABCD 中,E ,F 分别是BC ,DC 的中点,G 为DE ,BF 的交点,假设AB →=a ,AD →=b ,试以a ,b 为基底表示DE →,BF →,CG →.解:DE →=AE →-AD →=AB →+BE →-AD →=a +12b -b =a -12b .BF →=AF →-AB →=AD →+DF →-AB →=b +12a -a =b -12a .如下图,连接DB ,延长CG ,交BD 于点O ,点G 是△CBD 的重心,故CG →=CE →+EG →=12CB →+EG →=12CB →+13ED →=-12b -13⎝ ⎛⎭⎪⎫a -12b =-13a -13b .B 级 能力提升1.如果e 1,e 2是平面α内两个不共线的向量,那么以下说法中不正确的选项是( ) ①λe 1+μe 2(λ,μ∈R)可以表示平面α内的所有向量;②对于平面α内任一向量a ,使a =λe 1+μe 2的实数对(λ,μ)有无穷多个;③假设向量λ1e 1+μ1e 2与λ2e 1+μ2e 2共线,那么有且只有一个实数λ,使得λ1e 1+μ1e 2=λ(λ2e 1+μ2e 2);④假设存在实数λ,μ使得λe 1+μe 2=0,那么λ=μ=0.A .①②B .②③C .③④D .②解析:由平面向量根本定理可知,①④是正确的;对于②,由平面向量根本定理可知,一旦一个平面的基底确定,那么任意一个向量在此基底下的实数对是唯一的;对于③,当两向量的系数均为零,即λ1=λ2=μ1=μ2=0时,这样的λ有无数个.答案:B2.如图,向量BP →=14BA →,假设OP →=xOA →+yOB →,那么x -y =________.解析:因为OP →=OB →+BP →=OB →+14BA →=OB →+14(BO →+OA →)=14OA →+34OB →,所以x =14,y =34.所以x -y =-12.答案:-123.设e 1,e 2是不共线的非零向量,且a =e 1-2e 2,b =e 1+3e 2. (1)证明:a ,b 可以作为一组基底;(2)以a ,b 为基底,求向量c =3e 1-e 2的分解式; (3)假设4e 1-3e 2=λa +μb ,求λ,μ的值.(1)证明:假设a ,b 共线,那么存在λ∈R ,使a =λb , 那么e 1-2e 2=λ(e 1+3e 2).由e 1,e 2不共线得,⎩⎪⎨⎪⎧λ=1,3λ=-2,⇒⎩⎪⎨⎪⎧λ=1,λ=-23. 所以λ不存在,故a 与b 不共线,可以作为一组基底.(2)解:设c =ma +nb (m ,n ∈R),得3e 1-e 2=m (e 1-2e 2)+n (e 1+3e 2)=(m +n )e 1+(-2m +3n )e 2.所以⎩⎪⎨⎪⎧m +n =3,-2m +3n =-1,⇒⎩⎪⎨⎪⎧m =2,n =1.所以c =2a +b .(3)解:由4e 1-3e 2=λa +μb ,得4e 1-3e 2=λ(e 1-2e 2)+μ(e 1+3e 2)=(λ+μ)e 1+(-2λ+3μ)e 2.所以⎩⎪⎨⎪⎧λ+μ=4,-2λ+3μ=-3,⇒⎩⎪⎨⎪⎧λ=3,μ=1.故所求λ,μ的值分别为3和1.。
高中数学人教A版必修四全优课堂同步课件2.3.1平面向量基本定理
解: 1→ 1 1→ 1 1 5 → → → OM=OB+BM=b+3BC=b+3· 2BA=b+6(a-b)=6a+6b, → → → → 1→ 1→ 1 1→ 2→ 2 ON=OC+CN=OC+3CD=2OD+3· 2OD=3OD=3(a+b)= 2 2 3a+3b, 1 5 1 1→ 1 → → → → → MN = MC + CN = ( OC - OM ) + 3 CD = 2 (a + b) - 6a+6b + 3
【答案】-1
→ → 4.在等边△ABC 中,向量AB与BC的夹角为________.
【答案】120°
要点阐释 1.平面内任意两个不共线向量都可以作为基底,一旦选定一 组基底,则所给的向量只能唯一地被这组基底表示出来. 2.因为零向量与任意向量共线,所以零向量不会在基底中出 现. 3.在确定两个向量的夹角时,应把两个向量放在同一起点, → → 否则容易出错.如△ABC 中,向量AB与BC的夹角不是角 B,而是 角 B 的补角.
)
【答案】C
(
3 1 2.设 e1,e2 为已知向量, (2x-e1)+4e2-8x=0,则 x 等于 4 ) 1 A.-4e2+ e1 4 1 B.-4e2- e1 4 1 C.4e2+ e1 4 1 D.4e2- e1 4
【答案】D
→ → → 3.在△ABC 中,若BC=λ1AB+λ2AC,则 λ1λ2=________.
人教A版数学必修四2.3.1《平面向量基本定理》授课课件
a
e1
e2
A
O
NB
a OM ON 1e1 2e2
自主探究
确定一对不共线向量 e1,e2 后,是否平面内
任意一个向量都可以用1e1 2 e2来表示呢 ?
(请作图验证你的猜想)
e1 e2
互动辨析
确定一对不共线向量e,e 后,是否平面内
1
2
任意一个向量都可以用 e e 来表示呢?
11
22
两个非零向量 a,b
B
b
AOB 叫做向量
O aA
a 和 b 的夹角.注意:同起点
夹角的范围:(0 180 ) B
a
ObB
0
a
A Bb O
180
A
b
O
a
A
90
辨析练习:如图,等边三角形中,求 (1)AB与AC的夹角; (2)AB与BC的夹角。
C C'
1200
60
A
注意:同起点
B
向量,那么对于这一平面内的任一向
量 a 有且只有一对实数 1、2 ,使
a 1e1 2e2
其中e1,e2 叫做表示这一平面内 所有向量的一组基底 .
抢答:下列说法是否正确?
1.在平面内只有一对基底. ×
2.在平面内有无数对基底. √
3.平面内不共线的任意一对向量,都可作为
基底.
√
4.基底给定时,分解形式唯一.√
自主探究
给定平面内任意两个不共线向量e1,e2, 请你作出向量3e1+2e2和e1-2e2.
e1 e2
设 e1,e2是同一平面内的两个不共线的向量, a 是这一平面内的任一向量。请你将 a 沿着e1、e2 的方向进行分解。并思考:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P
B M
OA, OB .的 分 解 式 为
在l上
OP 1 t OA tOB
并且,满足上式的点 P一 定
O
A
l
证明:设点P在直线 l 上,则由平行向量基本定
理知,存在实数t,使
AP t AB t OB OA
所以O P O A AP O A tO B tO A
A
1 OM OA OB 2
线段这是AB的中点的向量表达式
练习.如图:在
ABCD中,点M是AB的中点,点N在BD上
1 且BN BD,设AB e1, AD e 2 3 1用基底 e1, e 2 表示BN 、 MC
BD e 1解: BN
A M 2求证:M、N、C三点共线。
2
D
C
N
B
e1
2证明:
1 1 BD e 2 e1 3 3 1 1 MC MB BC AB AD e1 e 2 2 2
1 1 1 1 MN BN BM e 2 e1 e1 e1 e 2 3 2M、N、C三点共线。
练习:
已 知A、B是 直 线 l上 任 意 两 点 , O是l外 一 点 ( 如 图 ) 求证:对直线 l上 任 一 点 P, 存在实数 t, 使OP关 于 基 底
1 t O A tO B
即P在l上
设点P满足等式O P 1 t O A tO B, 则AP t AB ,
OP 1 t OA tOB
*
P
B M
*叫做直线 向量等式 l的
向量参数方程式,其中实数t O l 叫做参变数,简称参数 1 在*中,令t ,点M是AB 的中点,则 2
