高考数学课时11对数和对数函数单元滚动精准测试卷文311

合集下载

高中数学-对数与对数函数测试题及答案

高中数学-对数与对数函数测试题及答案高中数学-对数与对数函数测试题满分150分，时间120分钟）班级：__________ 姓名：__________ 成绩：__________ 第Ⅰ卷（选择题，共60分）一、选择题（共12小题，60分）1.对数式loga 25a)b中，实数a的取值范围是（）A。

(∞,5) B。

(2,5) C。

(2,+∞) D。

(2,3)∪(3,5)2.如果lgx lga3lgb5lgc，那么（）A。

x=a+3b-c B。

x=ab/33 C。

x=a+b/3-c/3 D。

x=a-b/3+c/53.设函数y=lg(x^2-5x)的定义域为M，函数y=XXX(x-5)+lgx的定义域为N，则（）A。

M∪N=R B。

M=N C。

M⊊N D。

M⊆N4.已知a = log0.70.8，b = log1.10.9，c = 1.1^9，则a，b，c的大小关系是（）A。

a<c<b B。

b<a<c C。

a<b<XXX<c<a5.若函数y=log2kx^2+4kx+3)的定义域为R，则k的取值范围是（）A。

(3/4,2) B。

(3/4,3/2) C。

(3/4,∞) D。

(-∞,3/4]∪[2,∞)6.设a，b，c∈R，且3a= 4b= 6c，则（）。

A。

a=b+c B。

b=a+c C。

c=a+b D。

a+b+c=0 7.下列函数中，在(0,2)上为增函数的是（）A。

y=log1x+1) B。

y=log2x^2-1) C。

y=log21/x D。

y=log1x^2-4x+5)8.已知函数f(x)=log3x+1)，若f(a)=1，则a=（）A。

2 B。

1 C。

-1 D。

-29.已知loga21，则a的取值范围是（）A。

(0,2/3) B。

(2/3,1) C。

(1,2) D。

(2,∞)10.函数y=34x-3)log0.5的定义域为（）A。

(0,1) B。

2025年高考数学一轮复习课时作业-对数与对数函数【含解析】

2025年高考数学一轮复习课时作业-对数与对数函数【原卷版】(时间:45分钟分值:85分)【基础落实练】1.(5分)计算:lg4+2lg5+log28+823=()A.8B.9C.10D.12.(5分)函数f(x)=log0.5(2 -1)的定义域为()A.(12,1]B.[12,1)C.(-∞,12]D.[1,+∞)3.(5分)若函数y=f(x)是函数y=a x(a>0,且a≠1)的反函数且f(2)=1,则f(x)等于()A.log2xB.12C.lo g12x D.2x-24.(5分)设a=14log213,b=(12)0.3,则有()A.a+b>abB.a+b<abC.a+b=abD.a-b=ab5.(5分)(2023·濮阳模拟)已知a>0且a≠1,函数y=a x的图象如图所示,则函数f(x)=log a(-x+1)的部分图象大致为()6.(5分)(多选题)已知函数f(x)=|log a(x+1)|(a>1),下列说法正确的是()A.函数f(x)的图象恒过定点(0,0)B.函数f(x)在区间(0,+∞)上单调递减C.函数f(x)在区间[-12,1]上的最小值为0D.若对任意x∈[1,2],f(x)≥1恒成立,则实数a的取值范围是(1,2]7.(5分)已知lg2=a,lg3=b,用a,b表示log1815=.8.(5分)(2023·泸州模拟)若函数y=f(x)与y=5x互为反函数,则y=f(x2-2x)的单调递减区间是.9.(5分)已知f(x)=ln(x2+2x+m).若f(x)的值域为R,则实数m的取值范围是.10.(10分)已知f(x)=log a x+log a(4-x)(a>0,且a≠1),且f(2)=2.(1)求a的值及f(x)的定义域;(2)求f(x)在[1,72]上的值域.11.(10分)已知函数f(x)=(log2x)2-log2x-2.(1)若f(x)≤0,求x的取值范围;(2)当14≤x≤8时,求函数f(x)的值域.【能力提升练】12.(5分)(多选题)已知函数f(x)=ln(e2x+1)-x,则()A.f(ln2)=ln52B.f(x)是奇函数C.f(x)在(0,+∞)上单调递增D.f(x)的最小值为ln213.(5分)设实数a,b是关于x的方程|lg x|=c的两个不同实数根,且a<b<10,则abc 的取值范围是.14.(10分)已知f(x)是定义在R上的偶函数,且当x≥0时,f(x)=log a(x+1)(a>0,且a≠1).(1)求函数f(x)的解析式;(2)若-1<f(1)<1,求实数a的取值范围.2025年高考数学一轮复习课时作业-对数与对数函数【解析版】(时间:45分钟分值:85分)【基础落实练】1.(5分)计算:lg4+2lg5+log28+823=()A.8B.9C.10D.1【解析】选B.因为lg4+2lg5=lg4+lg52=lg4+lg25=lg100=2,log28=log223=3, 823=(23)23=22=4,所以lg4+2lg5+log28+823=2+3+4=9.2.(5分)函数f(x)=log0.5(2 -1)的定义域为()A.(12,1]B.[12,1)C.(-∞,12]D.[1,+∞)【解析】选A.由题意,要使函数f(x)=log0.5(2 -1)有意义,则满足log0.5(2x-1)≥0,所以0<2x-1≤1,解得12<x≤1,即函数f(x)的定义域为(12,1].3.(5分)若函数y=f(x)是函数y=a x(a>0,且a≠1)的反函数且f(2)=1,则f(x)等于()A.log2xB.12C.lo g12x D.2x-2【解析】选A.函数y=a x(a>0,且a≠1)的反函数是f(x)=log a x,又f(2)=1,即log a2=1,所以a=2.故f(x)=log2x.4.(5分)设a=14log213,b=(12)0.3,则有()A.a+b>abB.a+b<abC.a+b=abD.a-b=ab【解析】选A.因为a=14log213=-14log23,32<log23<2,所以-12<-14log23<-38,即-12<a<-38,b=(12)0.3>(12)1=12,所以a+b>0,ab<0,所以a+b>ab.5.(5分)(2023·濮阳模拟)已知a>0且a≠1,函数y=a x的图象如图所示,则函数f(x)=log a(-x+1)的部分图象大致为()【解析】选D.由函数y=a x的图象可判断出a>1.当a>1时,y=log a x的图象经过定点(1,0),且为增函数.因为y=log a x与y=log a(-x)的图象关于y轴对称,所以y=log a(-x)的图象经过定点(-1,0),为减函数.而f(x)=log a(-x+1)可以看作y=log a(-x)的图象向右平移1个单位长度得到的.所以f(x)=log a(-x+1)的图象经过定点(0,0),为减函数.6.(5分)(多选题)已知函数f(x)=|log a(x+1)|(a>1),下列说法正确的是()A.函数f(x)的图象恒过定点(0,0)B.函数f(x)在区间(0,+∞)上单调递减C.函数f(x)在区间[-12,1]上的最小值为0D.若对任意x∈[1,2],f(x)≥1恒成立,则实数a的取值范围是(1,2]【解析】选ACD.将(0,0)代入函数f(x)=|log a(x+1)|(a>1),成立,故A正确;当x∈(0,+∞)时,x+1∈(1,+∞),又a>1,所以f(x)=|log a(x+1)|=log a(x+1),由复合函数单调性可知,当x∈(0,+∞)时,f(x)=|log a(x+1)|=log a(x+1)单调递增,故B错误;当x∈[-12,1]时,x+1∈[12,2],所以f(x)=|log a(x+1)|≥log a1=0,故C正确;当x∈[1,2]时,f(x)=|log a(x+1)|=log a(x+1)≥1恒成立,所以由函数为增函数知log a2≥1,解得1<a≤2,故D正确.7.(5分)已知lg2=a,lg3=b,用a,b表示log1815=.【解析】log1815=lg15lg18=lg3+lg5lg2+2lg3= - +12 + .lg2+2lg3=lg3+1-lg2答案: - +12 +8.(5分)(2023·泸州模拟)若函数y=f(x)与y=5x互为反函数,则y=f(x2-2x)的单调递减区间是.【解析】因为y=f(x)与y=5x互为反函数,所以f(x)=log5x,则f(x2-2x)=log5(x2-2x).设μ=x2-2x,则f(μ)=log5μ,由x2-2x>0,解得x<0或x>2,因为f(μ)=log5μ在其定义域上单调递增,又μ=x2-2x在(-∞,0)上单调递减,在(2,+∞)上单调递增,所以y=f(x2-2x)的单调递减区间是(-∞,0).答案:(-∞,0)9.(5分)已知f(x)=ln(x2+2x+m).若f(x)的值域为R,则实数m的取值范围是.【解析】因为f(x)的值域为R,所以x2+2x+m取遍大于0的所有实数,则4-4m≥0,解得m≤1,所以实数m的取值范围是(-∞,1].答案:(-∞,1]10.(10分)已知f(x)=log a x+log a(4-x)(a>0,且a≠1),且f(2)=2.(1)求a的值及f(x)的定义域;【解析】(1)由f(2)=2得,log a2+log a(4-2)=2,解得a=2,所以f(x)=log2x+log2(4-x).由 >0,4- >0,解得0<x<4,故f(x)的定义域为(0,4).(2)求f(x)在[1,72]上的值域.【解析】(2)由(1)及条件知f(x)=log2x+log2(4-x)=log2[x(4-x)]=log2[-(x-2)2+4],设t(x)=-(x-2)2+4,x∈[1,72],则当x=2时,t(x)max=4;当x=1时,t(x)=3;当x=72时,t(x)=74,所以当x∈[1,72]时,t(x)∈[74,4],所以f(x)max=log24=2,f(x)min=log274=log27-2,所以f(x)在[1,72]上的值域为[log27-2,2].11.(10分)已知函数f(x)=(log2x)2-log2x-2.(1)若f(x)≤0,求x的取值范围;【解析】(1)令log2x=t,则y=t2-t-2,t∈R,由f(x)≤0得t2-t-2≤0,解得-1≤t≤2,所以-1≤log2x≤2,解得12≤x≤4,即x的取值范围为[12,4].(2)当14≤x≤8时,求函数f(x)的值域.【解析】(2)当14≤x≤8时,-2≤t≤3,因为y=t2-t-2,则当t=12时,有最小值-94;当t=-2或3时,有最大值4.所以函数f(x)的值域为[-94,4].【能力提升练】12.(5分)(多选题)已知函数f(x)=ln(e2x+1)-x,则()A.f(ln2)=ln52B.f(x)是奇函数C.f(x)在(0,+∞)上单调递增D.f(x)的最小值为ln2【解析】选ACD.f(ln2)=ln(e2ln2+1)-ln2=ln52,A正确;f(x)=ln(e2x+1)-x=ln(e2x+1)-ln e x=ln e2 +1e =ln(e x+e-x),所以f(-x)=ln(e x+e-x)=f(x),所以f(x)为偶函数,B错误;当x>0时,y=e x+e-x在(0,+∞)上单调递增,因此y=ln(e x+e-x)在(0,+∞)上单调递增,C正确;由于f(x)在(0,+∞)上单调递增,又f(x)为偶函数,所以f(x)在(-∞,0]上单调递减,所以f(x)的最小值为f(0)=ln2,D正确.13.(5分)设实数a,b是关于x的方程|lg x|=c的两个不同实数根,且a<b<10,则abc 的取值范围是.【解析】由题意知,在(0,10)上,函数y=|lg x|的图象和直线y=c有两个不同交点(如图),所以ab=1,0<c<lg10=1,所以abc的取值范围是(0,1).答案:(0,1)14.(10分)已知f(x)是定义在R上的偶函数,且当x≥0时,f(x)=log a(x+1)(a>0,且a≠1).(1)求函数f(x)的解析式;【解析】(1)当x<0时,-x>0,由题意知f(-x)=log a(-x+1),又f(x)是定义在R上的偶函数,所以f(-x)=f(x).所以当x<0时,f(x)=log a(-x+1),所以函数f(x)的解析式为f(x)=log ( +1), ≥0,log (- +1), <0.(2)若-1<f(1)<1,求实数a的取值范围.【解析】(2)因为-1<f(1)<1,所以-1<log a2<1,所以log a1 <log a2<log a a.①当a>1时,<2,>2,解得a>2;②当0<a<1时,>2,<2,解得0<a<12.综上,实数a的取值范围为(0,12)∪(2,+∞).。

高考数学专题《对数与对数函数》习题含答案解析

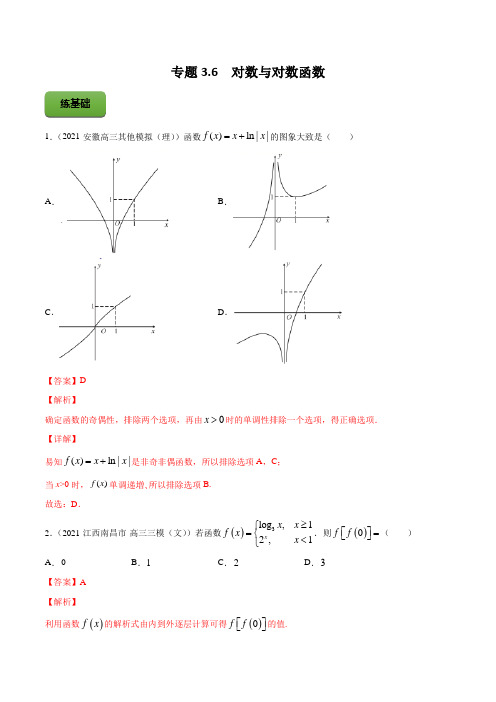
专题3.6 对数与对数函数1．（2021·安徽高三其他模拟（理））函数()ln ||f x x x =+的图象大致是（）A ．B ．C ．D ．【答案】D 【解析】确定函数的奇偶性，排除两个选项，再由0x >时的单调性排除一个选项，得正确选项．【详解】易知()ln ||f x x x =+是非奇非偶函数，所以排除选项A ，C ；当x >0时，()f x 单调递増､所以排除选项B. 故选：D ．2．（2021·江西南昌市·高三三模（文））若函数()3log ,12,1x x x f x x ≥⎧=⎨<⎩．则()0f f ⎡⎤=⎣⎦（） A ．0 B ．1C ．2D ．3【答案】A 【解析】利用函数()f x 的解析式由内到外逐层计算可得()0f f ⎡⎤⎣⎦的值.练基础()3log ,12,1x x x f x x ≥⎧=⎨<⎩，则()0021f ==，因此，()()301log 10f f f ===⎡⎤⎣⎦. 故选：A.3．（2021·浙江高三其他模拟）已知a 为正实数，则“1a >”是“32212log log a a ->”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】C 【解析】利用充分、必要条件的定义，即可推出“1a >”与“32212log log a a ->”的充分、必要关系.【详解】因为32212log log a a ->等价于3222log log a a >，由a 为正实数且1a >，故有32a a >，所以3222log log a a >成立；由a 为正实数，3222log log a a >且函数2log y x =是增函数，有32a a >，故()210a a ->，所以1a >成立. 故选：C ．4．（2021·浙江高三专题练习）已知函数f (x )＝1331,,log 1x x x x ⎧≤⎪⎨>⎪⎩则函数y ＝f (1－x )的大致图象是（）A ．B ．C ．D ．【答案】D 【解析】由()f x 得到()1f x -的解析式，根据函数的特殊点和正负判断即可.因为函数()f x 133,1log ,1x x x x ⎧≤⎪=⎨>⎪⎩，所以函数()1f x -()1133,0log 1,0x x x x -⎧≥⎪=⎨-<⎪⎩，当x ＝0时，y ＝f (1)＝3，即y ＝f (1－x )的图象过点(0，3)，排除A ；当x ＝－2时，y ＝f (3)＝－1，即y ＝f (1－x )的图象过点(－2，－1)，排除B ；当0x <时，()1311,(1)log 10x f x x ->-=-<，排除C ，故选：D ．5．（2021·江苏南通市·高三三模）已知1331311log 5,,log 26a b c ⎛⎫=== ⎪⎝⎭，则a ，b ，c 的大小关系为（） A ．a b c >> B ．b a c >> C ．c b a >> D ．c a b >>【答案】D 【解析】由于1331log g 66lo c ==，再借助函数3log y x =的单调性与中间值1比较即可. 【详解】1331log g 66lo c ==，因为函数3log y x =在()0,∞上单调递增，所以333131log 31log 5log 6log 6a c =<=<<=，因为函数12xy ⎛⎫= ⎪⎝⎭在R 上单调递减，所以10312112b <⎛⎫⎛⎫= ⎪ ⎪⎝⎝⎭=⎭，所以c a b >> 故选：D6．（2021·辽宁高三月考）某果农借助一平台出售水果，为了适当地给鲜杏保留空气呼吸，还会在装杏用的泡沫箱用牙签戳上几个小洞，同时还要在鲜杏中间放上冰袋，来保持泡沫箱内部的温度稳定，这样可以有效延长水果的保鲜时间．若水果失去的新鲜度h 与其采摘后时间t （小时）满足的函数关系式为t h m a =⋅．若采摘后20小时，这种杏子失去的新鲜度为10%，采摘后40小时，这种杏子失去的新鲜度为20%．在这种条件下，杏子约在多长时间后会失去一半的新鲜度（）（已知lg 20.3≈，结果取整数） A ．42小时 B ．53小时 C ．56小时 D ．67小时【答案】D 【解析】利用指数的运算得出1202a =，再利用对数的运算即可求解. 【详解】由题意可得200010m a =⋅，①400020m a =⋅，②②÷①可得202a =，解得1202a =，所以0050tm a =⋅，③③÷①可得205t a -=，所以202025t -=，即20lg 2lg51lg 20.720t -==-=，解得67t ≈（小时）. 故选：D7．【多选题】（2021·辽宁高三月考）已知2log 3a =，34b =，22log 31c =+，则下列结论正确的是（） A ．a c ，即可判断A ；利用222log 3b a==判断B ；利用B 的结论判断C ；利用C 的结论判断D. 【详解】因为2log 31a =>，所以22log 3112c a a c a =+=+<⇒<，即A 不正确；因为33222log 42log 2log 3b a====，所以2ab =，即B 正确；由2ab =可知，21abc c a ==+，C 正确；由1abc a =+可知，2ab c ab b =+，则22bc b =+，即D 正确．故选：BCD.8．【多选题】（2021·山东日照市·高三一模）已知113log 0x x +=，222log 0xx +=，则（） A ．2101x x <<【答案】BC 【解析】根据对数函数的性质可判断AB 正误，由不等式的基本性质可判断CD 正误. 【详解】由131log 0x x =->可得101x <<，同理可得201x <<，因为(0,1)x ∈时，恒有23log log x x <所以122231log log 0x x x x -=-<，即12x x <，故A 错误B 正确；因为1201x x ，所以12lg lg 0x x <<，即210lg lg x x <-<-，由不等式性质可得1221lg lg x x x x -<-，即2112lg lg 0x x x x -<，故C 正确D 错误. 故选：BC9．（2021·浙江高三期末）已知2log 3a =，则4a =________．【答案】9 【解析】把2log 3a =代入4a 可得答案. 【详解】因为2log 3a =，所以222log 3log 34429a ===.故答案为：9.10．（2021·河南高三月考（理））若41log 32a =，则39a a +=___________；【答案】6 【解析】首先利用换底公式表示3log 2a =，再代入39a a +求值.【详解】由条件得331log 4log 22a ==，所以3333log 2log 2log 2log 4393933246a a +=+=+=+=. 故答案为：61．（2021·浙江高三专题练习）如图，直线x t =与函数()3log f x x =和()3log 1g x x =-的图象分别交于点A ，B ，若函数()y f x =的图象上存在一点C ，使得ABC 为等边三角形，则t 的值为（）A B C D ．3【答案】C 【解析】由题意得()3,log A t t ，()3,log 1B t t -，1AB =，根据等边三角形的性质求得C 点的横坐标x t =-，结合A ，B 两点的纵坐标和中点坐标公式列方程t ，解方程即可求得t 的值. 【详解】由題意()3,log A t t ，()3,log 1B t t -，1AB =. 设()3,log C x x ，因为ABC 是等边三角形，所以点C 到直线AB 所以t x -=x t =根据中点坐标公式可得练提升33333log log 11log log log 22t t t t ⎛+-==-= ⎝⎭，所以t -=，解得t =故选：C2．（2021·安徽高三其他模拟（文））已知函数()()14,12ln 1,1xx f x x x ⎧⎛⎫-≤-⎪ ⎪=⎨⎝⎭⎪+>-⎩，若()0f f x <⎡⎤⎣⎦，则x 的取值范围为（） A ．()2,0-B ．21,1e ⎛⎫-∞- ⎪⎝⎭C ．212,1e ⎛⎫-- ⎪⎝⎭D ．()212,11,0e ⎛⎫--⋃-⎪⎝⎭【答案】D 【解析】先由()0f f x <⎡⎤⎣⎦可得出()20f x -<<，然后再分1x ≤-、1x >-两种情况解不等式()20f x -<<，即可得解. 【详解】若()1f x ≤-，则()()1402f x f f x ⎛⎫=-<⎡⎤ ⎪⎣⎦⎝⎭，解得()2f x >-，此时，()21f x -<≤-；若()1f x >-，则()()ln 10f f x f x =+<⎡⎤⎡⎤⎣⎦⎣⎦，可得()011f x <+<，解得()10f x -<<. 综上，()20f x -<<.若1x ≤-，由()20f x -<<可得12402x ⎛⎫-<-< ⎪⎝⎭，可得1242x⎛⎫<< ⎪⎝⎭，解得21x -<<-，此时21x -<<-；若1x >-，由()20f x -<<可得()2ln 10x -<+<，可得2111x e <+<，解得2110x e -<<，此时，2110x e-<<.综上，满足()0f f x <⎡⎤⎣⎦的x 的取值范围为()212,11,0e ⎛⎫--⋃- ⎪⎝⎭. 故选：D.3．（2021·全国高三三模）已知函数()x x f x e e -=+，若()()4561log ,log 6,log 45a f b f c f ⎛⎫=== ⎪⎝⎭，则,,a b c 的大小关系正确的是（）A ．b a c >>B ．a b c >>C ．c b a >>D ．c a b >>【答案】B 【解析】先判断函数的奇偶性，再利用导数判断函数的单调性，最后根据对数函数的性质，结合基本不等式、比较法进行判断即可. 【详解】因为()()xx f x ee f x --=+=，所以()f x 为偶函数，()21x xxxe x eef e --=='-，当0x >时，()0f x '>，函数单调递增，当0x <时，()0f x '<，函数单调递减，()()()()444561log log 5log 5,log 6,log 45a f f f b f c f ⎛⎫==-=== ⎪⎝⎭，因为lg4lg6+>故2222lg4lg6lg 24lg25lg4lg6(lg5)242+⎛⎫⎛⎫⋅<=<= ⎪ ⎪⎝⎭⎝⎭245lg5lg6lg 5lg4lg6log 5log 60lg4lg5lg4lg5-⋅-=-=>⋅所以456log 5log 61log 40>>>>，则.a b c >> 故选：B.4．【多选题】（2021·辽宁高三月考）若1a b >>，则（） A ．log 3log 3a b >，则333311log log 0log log a b a b>>⇒<，即log 3log 3a b <，A 正确；对于B 选项：函数y =x 3在R 上递增，则33a b >，B 错误；对于C 选项：1a b >>，则ab >1，a +b >2，11log ()log log ()1ab abab a ba b a b ab++==+-log 21ab >-，有11log ()log 21ab ab a b+≥-成立，即C 正确；对于D 选项：1112a b a b >>⇒+>+>，而函数1y x =在(0,+∞)上递减，则有11+11a b <+，即D 正确.故选：ACD5．【多选题】（2021·全国高三专题练习（理））已知0a b >>，且4ab =，则（） A ．21a b -> B ．22log log 1a b -> C ．228a b +> D ．22log log 1a b ⋅<【答案】ACD 【解析】利用不等式的性质和基本不等式的应用，结合指数函数与对数函数的单调性，对选项逐一分析判断. 【详解】因为0a b >>，且4ab =，对A ，0a b ->，所以0221a b ->=，故A 正确；对B ，取83,32a b ==，所以2222216log log log log log 219a ab b -==<=，故B 错误；对C ，22a b ≥+，当且仅当a b =取等号，又因为4a b +≥=，当且仅当a b =取等号，所以228a b ≥≥=+，当且仅当a b =取等号，因为0a b >>，所以不能取等号，故C 正确；对D ，当10>>>a b ，22log 0,log 0a b ><，所以22log log 1a b ⋅<；当1a b >>，22log 0,log 0a b >>，所以()()2222222log log log log log 144a b ab a b +⋅≤==，当且仅当a b =取等号，因为0a b >>，所以不能取等号，故D 正确. 故选：ACD.6．【多选题】（2021·湖南高三二模）若正实数a ，b 满足a b >且ln ln 0a b ⋅>，下列不等式恒成立的是（） A ．log 2log 2a b > B ．ln ln a a b b ⋅>⋅ C ．122ab a b ++> D ．log 0a b >【答案】CD 【解析】由已知不等式，求出,a b 之间的关系，结合选项一一判断即可．【详解】由ln ln 0a b ⋅>有01b a <<< 或1a b >> ，对于选项A ，当01b a <<<或1a b >>都有log 2log 2a b < ，选项A 错误；对于选项B ，比如当11,24a b == 时，有211111111ln ln 2ln ln 44424222⎛⎫==⨯= ⎪⎝⎭故ln ln a a b b ⋅>⋅不成立，选项B 错误；对于C ，因为()()1110ab a b a b +--=-->，所以1ab a b +>+ ，则122ab a b ++> ，选项C 正确；对于选项D ，因为ln ln 0a b ⋅>，所以ln log 0ln a bb a=>，选项D 正确，故选：CD ．7．【多选题】（2021·山东临沂市·高三二模）若5log 2a =，1ln 22b =，1ln55c =，则（）A ．a b >B ．b c >C ．c a >D ．2a b >【答案】AB 【解析】对四个选项一一验证：对于A ：利用换底公式，化为同底结构，利用函数的单调性比较大小；对于B ：利用换底公式，化为同底结构，利用函数的单调性比较大小；对于C ：利用不等式的传递性比较大小；对于D ：利用换底公式，化为同底结构，利用函数的单调性比较大小；【详解】对于A ：522221111ln o 21l g 2,log 522log log a b e e ====⨯=，又25e >，且2log y x =为增函数，所以222l l g 5og o e <，所以22251l og 1l og e <，即a b >.故A 正确；对于B：1ln 2ln 2b ==1ln 55c ==因为101052232,525,ln y x =====为增函数，所以b c >；故B 正确；对于C ：因为a b >，b c >，所以a c >，故C 错误；对于D ：因为1ln 22b =，所以212ln 2log b e ==，而521log 2,log 5a == 又5e <，所以22log log 5e <，所以2211log log 5e >，所以2b a >，故D 错误. 故选：AB.8．（2021·浙江高三专题练习）已知函数()f x 满足()(1)f x f x =-+，当(0,1)x ∈时，函数()3xf x =，则13(log 19)f =__________．【答案】2719- 【解析】由()(1)f x f x =-+得函数的周期为2，然后利用周期和()(1)f x f x =-+对13(log 19)f 化简可得13(log 19)f 33927(log 1)(log )1919f f =-+=-，从而可求得结果【详解】解：由题意，函数()f x 满足()(1)f x f x =-+，化简可得()(2)f x f x =+，所以函数()f x 是以2为周期的周期函数，又由(0,1)x ∈时，函数()3xf x =，且()(1)f x f x =-+，则133339(log 19)(log 19)(log 192)(log )19f f f f =-=-+= 327log 193392727(log 1)(log )3191919f f =-+=-=-=-．故答案为：2719-． 9．（2021·千阳县中学高三其他模拟（文））已知函数()()()11330log 0x x f x x x +⎧≤⎪=⎨>⎪⎩，则不等式()1f x >的解集为___________. 【答案】11,3⎛⎫- ⎪⎝⎭【解析】根据分段函数的定义，分段讨论即可求解. 【详解】解：()()()11330log 0x x f x x x +⎧≤⎪=⎨>⎪⎩，()10131x x f x +≤⎧∴>⇔⎨>⎩或130log 1x x >⎧⎪⎨>⎪⎩，解得10-<≤x 或103x <<，即113x -<<， ∴不等式()1f x >的解集为11,3⎛⎫- ⎪⎝⎭.故答案为：11,3⎛⎫- ⎪⎝⎭.10．（2021·浙江丽水市·高三期末）已知()()()1log 1log 01a a a a a ++<<<，则a 的取值范围是__________.【答案】12⎛⎫-+ ⎪ ⎪⎝⎭【解析】通过作差将()()()1log 1log 01a a a a a ++<<<转化为(1)log (1)log 0++-<a a a a ，利用换底公式计算可得[][](1)lg(1)lg lg(1)lg log (1)log lg lg(1)++-+++-=+a a a a a a a a a a ，分别判断每个因式的正负，最终转化为211()124+->a 成立，结合二次函数图像，即可求得a 的取值范围.【详解】∵(1)lg(1)lg log (1)log lg lg(1)a a a aa a a a +++-=-+ 22lg (1)lg lg (1)a aalg a +-=+[][]lg(1)lg lg(1)lg lg lg(1)a a a a a a +-++=+而当01a <<时，lg 0a <，g(0)l 1a +>，1lg(1)lg lglg10a a a a++-=>= 211lg(1)lg lg (1)lg ()24a a a a a ⎡⎤++=+=+-⎢⎥⎣⎦，所以()()()1log 1log 01a a a a a ++<<<即为211lg ()024⎡⎤+->⎢⎥⎣⎦a ，由于lg u 单调递增，所以211()124+->a .211()24u a =+-的图象如图，当1u =时，0a =，1a <<时，12u <<，lg 0u >，可得()()log 1log 10a a a a a +-+<.故答案为：⎫⎪⎪⎝⎭1.（2020·全国高考真题（文））设3log 42a =，则4a-=（）A ．116B ．19C ．18 D ．16【答案】B 【解析】由3log 42a =可得3log 42a=，所以49a =，所以有149a-=，故选：B.2.（2020·全国高考真题（理））设函数()ln |21|ln |21|f x x x =+--，则f (x )（） A ．是偶函数，且在1(,)2+∞单调递增B ．是奇函数，且在11(,)22-单调递减C ．是偶函数，且在1(,)2-∞-单调递增D ．是奇函数，且在1(,)2-∞-单调递减【答案】D 【解析】由()ln 21ln 21f x x x =+--得()f x 定义域为12x x ⎧⎫≠±⎨⎬⎩⎭，关于坐标原点对称，又()()ln 12ln 21ln 21ln 21f x x x x x f x -=----=--+=-，()f x ∴为定义域上的奇函数，可排除AC ；练真题当11,22x ⎛⎫∈-⎪⎝⎭时，()()()ln 21ln 12f x x x =+--， ()ln 21y x =+在11,22⎛⎫- ⎪⎝⎭上单调递增，()ln 12y x =-在11,22⎛⎫- ⎪⎝⎭上单调递减，()f x ∴在11,22⎛⎫- ⎪⎝⎭上单调递增，排除B ；当1,2x ⎛⎫∈-∞-⎪⎝⎭时，()()()212ln 21ln 12ln ln 12121x f x x x x x +⎛⎫=----==+ ⎪--⎝⎭， 2121x μ=+-在1,2⎛⎫-∞- ⎪⎝⎭上单调递减，()ln f μμ=在定义域内单调递增，根据复合函数单调性可知：()f x 在1,2⎛⎫-∞- ⎪⎝⎭上单调递减，D 正确. 故选：D.3．（2020·天津高考真题）设0.80.70.713,,log 0.83a b c -⎛⎫=== ⎪⎝⎭，则,,a b c 的大小关系为（）A ．a b c <，0.80.80.71333b a -⎛⎫==>= ⎪⎝⎭，0.70.7log 0.8log 0.71c =<=，所以1c a b <<<. 故选：D.4.（2019年高考全国Ⅲ卷理）设()f x 是定义域为R 的偶函数，且在()0,+∞单调递减，则A ．f （log 314）＞f （322-）＞f （232-）B ．f （log 314）＞f （232-）＞f （322-）C ．f （322-）＞f （232-）＞f （log 314）D ．f （232-）＞f （322-）＞f （log 314）【答案】C 【解析】()f x 是定义域为R 的偶函数，331(log )(log 4)4f f ∴=．223303322333log 4log 31,1222,log 422---->==>>∴>>，又()f x 在(0，+∞)上单调递减，∴23323(log 4)22f f f --⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭，即23323122log 4f f f --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.故选C ．5.（2020·全国高考真题（理））若2233x y x y ---<-，则（） A ．ln(1)0y x -+> B ．ln(1)0y x -+< C ．ln ||0x y -> D ．ln ||0x y -<【答案】A 【解析】由2233x y x y ---<-得：2323x x y y ---<-，令()23t t f t -=-，2x y =为R 上的增函数，3x y -=为R 上的减函数，()f t ∴为R 上的增函数，x y ∴<，0y x ->，11y x ∴-+>，()ln 10y x ∴-+>，则A 正确，B 错误；x y -与1的大小不确定，故CD 无法确定.故选：A.6.（2019·天津高考真题（文））已知a =log 27，b =log 38，c =0.30.2，则a,b,c 的大小关系为（） A.c log24=2；1<log38<log39=2. 故c<b<a.故选A.。

高中必修一对数与对数函数练习题及答案(2021年整理)

1．高中必修一对数与对数函数练习题及答案(word版可编辑修改)2．3．4．编辑整理：5．6．7．8．9．尊敬的读者朋友们：10．这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高中必修一对数与对数函数练习题及答案(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

11．本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高中必修一对数与对数函数练习题及答案(word版可编辑修改)的全部内容。

12．一、选择题1．若3a =2，则log 38—2log 36用a 的代数式可表示为（）（A)a-2 （B ）3a —(1+a ）2 (C ）5a —2 （D ）3a —a 22。

2log a （M-2N ）=log a M+log a N,则N M 的值为（ ) （A ）41（B ）4 （C ）1 （D ）4或13．已知x 2+y 2=1，x 〉0，y>0,且log a (1+x ）=m ，loga y a n xlog ,11则=-等于（）（A ）m+n （B)m —n (C ）21（m+n) （D ）21(m —n ）4。

已知log 7[log 3(log 2x ）]=0，那么x 21-等于（）（A ）31 （B ）321 （C ）221 （D ）3315．函数y=log 2x —123-x 的定义域是（）（A)（32，1）⋃（1，+∞) （B)（21,1）⋃(1，+∞)（C ）(32，+∞) （D)（21，+∞）6．函数y=log 21(x 2—6x+17）的值域是（）（A ）R （B ）［8，+∞］（C ）（—∞，-3）（D)［3,+∞］7.若log m 9<log n 9〈0,那么m,n 满足的条件是（ )(A ）m>n>1 (B)n>m 〉1（C ）0〈n<m 〈1 （D)0<m<n 〈18.log a 132<，则a 的取值范围是（）(A)（0，32）⋃（1,+∞）（B ）(32，+∞）（C ）(1,32） (D)(0，32）⋃（32,+∞）9．（369a ）4（639a ）4等于（）（A ）a 16 （B ）a 8 （C ）a 4 (D ）a 210．函数f(x)=（a 2—1）x 在R 上是减函数，则a 的取值范围是（）（A)1>a （B ）2<a （C ）a 〈2 (D ）1〈2<a11。

2019年高考数学课时11对数和对数函数单元滚动精准测试卷文011

课时11 对数和对数函数模拟训练（分值：60分建议用时：30分钟） 1．已知log 7[log 3(log 2x )]＝0，那么x 12- 等于( )A.13 B.36 C.24D.33【答案】C【解析】由条件知，log 3(log 2x )＝1，∴log 2x ＝3，∴x ＝8， ∴x12-＝24. 2．设a ＝log 32，b ＝ln2，c ＝512-，则( )A ．a log 33＝12，因此c <a <b .[知识拓展]比较对数式的大小，或证明等式问题是对数中常见题型，解决此类问题的方法很多,①当底数相同时可直接利用对数函数的单调性比较;②若底数不同，真数相同,可转化为同底（利用换底公式）或利用对数函数图象，数形结合解得；③若不同底，不同真数，则可利用中间量进行比较.3.函数的递减区间为（）A.()+∞,1B. ⎥⎦⎤ ⎝⎛∞-43, C. ⎪⎭⎫ ⎝⎛+∞,21 D.⎥⎦⎤ ⎝⎛∞-21,【答案】A4．已知函数（b 为常数），若[)+∞∈,1x 时，0)(≥x f 恒成立，则（）A.1≤bB.1<bC.1≥bD.1=b 【答案】A【解析】因为1≥x ，所以，又1≥x ，0)(≥x f 恒成立，即12≥-b 恒成立，所以1≤b .故选A.5已知函数f (x )满足：当x ≥4时，f (x )＝(12)x；当x ＜4时，f (x )＝f (x ＋1)，则f (2＋log 23)＝( )A.124B.112C.18D.38【答案】A【解析】∵2＜3＜4＝22，∴1＜log 23＜2. ∴3＜2＋log 23＜4，∴f (2＋log 23)＝f (3＋log 23)＝f (log 224)＝(12)2log 24＝22log 24-＝221log 24＝124.6．定义在R 上的奇函数f (x )满足：当x >0时，f (x )＝2010x＋log 2010x ，则方程f (x )＝0的实根个数为( ) A ．1 B ．2 C ．3 D ．4【答案】C7.定义：区间[]21,x x （21x x <）的长度为12x x -.已知函数的定义域为[]b a ,，值域为[]2,0，则区间[]b a ,的长度的最大值为 .【答案】415【解析】由≤0x 5.0log 2≤解得441≤≤x ，所以区间[]b a ,的长度的最大值为415414=-. 8．已知函数f (x )＝⎩⎪⎨⎪⎧3x ＋1x ≤0，log 2x x >0，则使函数f (x )的图象位于直线y ＝1上方的x 的取值范围是________．【答案】{x |－1<x ≤0或x >2} 【解析】当x ≤0时，由3x ＋1>1，得x ＋1>0，即x >－1.∴－1<x ≤0.当x >0时，由log 2x >1，得x >2.∴x 的取值范围是{x |－1<x ≤0或x >2}．9．已知f (x )＝log a 1＋x1－x (a ＞0，且a ≠1)．(1)求f (x )的定义域；(2)判断f (x )的奇偶性并予以证明； (3)求使f (x )＞0的x 的取值范围．10．已知函数f (x )＝log a (2－ax )，是否存在实数a ，使函数f (x )在[0,1]上是关于x 的减函数，若存在，求a 的取值范围．【解析】∵a >0，且a ≠1，∴u ＝2－ax 在[0,1]上是关于x 的减函数．又f (x )＝log a (2－ax )在[0,1]上是关于x 的减函数， ∴函数y ＝log a u 是关于u 的增函数，且对x ∈[0,1]时，u ＝2－ax 恒为正数．其充要条件是⎩⎪⎨⎪⎧a >12－a >0，即1<a <2.∴a 的取值范围是(1,2)．[新题训练] （分值：20分建议用时：10分钟） 11．（10分）求函数的值域和单调区间．【解析】（1）由2x x ->0得01x <<，所以函数的定义域是(0,1)因为0<2x x -=，所以，当01a <<时,，函数的值域为1[log ,)4a +∞．当1a >时,函数的值域为（2）令2t x x =-，则log a y t =，当01a <<时，函数log a y t =在(0,)+∞为减函数，2t x x =-在1(0,]2上是增函数，在1[,1)2上是减函数，故所给函数在在1(0,]2上是减函数，在1[,1)2上是增函数；当1a >时，函数log a y t =在(0,)+∞为增函数，2t x x =-在1(0,]2上是增函数，在1[,1)2上是减函数，故所给函数在在1(0,]2上是增函数，在1[,1)2上是减函数． 12．（10分）若f (x )＝x 2－x ＋b ，且f (log 2a )＝b ，log 2f (a )＝2(a ≠1)． (1)求f (log 2x )的最小值及对应的x 值；(2)x 取何值时，f (log 2x )>f (1)，且log 2f (x )＜f (1)．。

贵州省贵阳高考数学复习对数与对数函数同步练习试题

心尺引州丑巴孔市中潭学校对数与对数函数同步练习一、选择题：〔此题共12小题，每题4分，共48分，在每题给出的四个选项中，只有一项为哪一项符合题目要求的〕 1、32a=，那么33log 82log 6-用a 表示是〔〕A 、2a -B 、52a -C 、23(1)a a -+ D 、 23a a - 2、2log (2)log log a a a M N M N -=+，那么NM的值为〔〕A 、41B 、4C 、1D 、4或1 3、221,0,0x y x y +=>>，且1log (1),log ,log 1y a a a x m n x+==-则等于〔〕A 、m n +B 、m n -C 、()12m n +D 、()12m n -4、如果方程2lg (lg5lg 7)lg lg5lg 70x x +++=的两根是,αβ，那么αβ的值是〔〕A 、lg5lg7B 、lg35C 、35D 、351 5、732log [log (log )]0x =，那么12x-等于〔〕A 、13 B C6、函数2lg 11y x ⎛⎫=- ⎪+⎝⎭的图像关于〔〕A 、x 轴对称B 、y 轴对称C 、原点对称D 、直线y x =对称7、函数(21)log x y -= 〕A 、()2,11,3⎛⎫+∞⎪⎝⎭B 、()1,11,2⎛⎫+∞⎪⎝⎭C 、2,3⎛⎫+∞⎪⎝⎭ D 、1,2⎛⎫+∞ ⎪⎝⎭8、函数212log (617)y x x =-+的值域是〔〕A 、RB 、[)8,+∞ C 、(),3-∞- D 、[)3,+∞9、假设log 9log 90m n <<，那么,m n 满足的条件是〔〕A 、 1 m n >>B 、1n m >>C 、01n m <<<D 、01m n <<< 10、2log 13a<，那么a 的取值范围是〔〕 A 、()20,1,3⎛⎫+∞ ⎪⎝⎭B 、2,3⎛⎫+∞ ⎪⎝⎭C 、2,13⎛⎫ ⎪⎝⎭D 、220,,33⎛⎫⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭11、以下函数中，在()0,2上为增函数的是〔〕A 、12log (1)y x =+ B 、2log y =C 、21log y x=D 、2log (45)y x x =-+12、()log x+1 (01)a g x a a =>≠且在()10-，上有()0g x >，那么1()x f x a +=是〔〕 A 、在(),0-∞上是增加的 B 、在(),0-∞上是减少的 C 、在(),1-∞-上是增加的 D 、在(),0-∞上是减少的二、填空题：〔此题共4小题，每题4分，共16分，请把答案填写在答题纸上〕 13、假设2log 2,log 3,m n a a m n a +=== 。

2025届高考数学一轮复习北师大版多选题专题练：对数运算和对数函数(含解析)

2025届高考数学一轮复习北师大版多选题专题练：对数运算和对数函数A.C. D.4．设,当时,对这三个函数的增长速度进行比较,下列结论中,错误的是( )A.的增长速度最快, 的增长速度最慢B.的增长速度最快, 的增长速度最慢C.的增长速度最快, 的增长速度最慢D.的增长速度最快, 的增长速度最慢5．已知函数，则下列说法正确的是( ).A.B.函数的图象与x 轴有两个交点C.函数的最小值为-434log 9log 2+=212log 3=+5log 3259=225511log 25log log 8log 252⎛⎫⎛⎫++= ⎪⎪⎝⎭⎝⎭()()()22,2,log x f x x g x h x x ===(4,)x ∈+∞()f x ()h x ()g x ()h x ()g x ()f x ()f x ()g x ()2222()log log 3f x x x =--(4)3f =-()y f x =()y f x =D.函数的最大值为46．下列运算正确的是( ).A. B.C.若，则 D.若，则7．下列运算正确的是( ).A. B.C.若，则 D.若，则8．已知，且，下列说法中错误的是( ).A.若，则B.若，则C.若，则D.若，则9．下列运算错误的是( ).A. B.C. D.10．下列运算错误的是( )A.B.C.D.11．若,,且,则( )A. B.C. D.12．下列式子中正确的是( )()y f x =lg(lg10)0=lg(ln e)0=lg 10x =10x =ln e x =2e x=1232=129ln e 4+=3log (lg )1x =1000x=log a c =7cb a =0a >1a ≠M N =log log a a M N =log log a a M N =M N =22log log a a M N =M N =M N =22log log a a M N =11552log 10log 0.252+=42598log 27log 8log 59⨯⨯=23511log 25log log 16169⨯⨯=lg 2lg 5010+=11552log 10log 0.252+=42598log 27log 8log 59⋅⋅=lg 2lg 5010+=((2225log (2log 4-=-1a >1b >lg()lg lg a b a b +=+lg(1)lg(1)0a b -+-=11lg 0a b ⎛⎫+= ⎪⎝⎭lg(1)lg(1)1a b -+-=11lg 1a b ⎛⎫+= ⎪⎝⎭A.若，则B.若C.D.13．在天文学中，星等是衡量天体光度的量，是表示天体相对亮度的数值.天体亮度越强，星等的数值越小，星等的数值越大，天体的亮度就越暗.两颗星的星等与亮度满足的星的亮度为.已知太阳的星等是-26.7，天狼星的星等是-1.45，南极星的星等是-0.72，则( )A.天狼星的星等大约是南极星星等的2倍B.太阳的亮度与天狼星的亮度的比值是10.1C.天狼星的亮度与太阳的亮度的比值是D.天狼星的亮度与南极星的亮度的比值是14．已知且A. B. C. D.15．下列运算正确的是( )A. B.C. D.16．下列运算中正确的是( )A. B.C. D.17．下列运算正确的是( )A. B.C. D.18．下列运算中正确的是( )A. B.C. D.552log 10log 0.252+=42598log 27log 8log 59⨯⨯=lg 2lg5010+=ln 2ln3e 6+=10lg x =10x =25log x =5=±lg(lg10)0=24log 5280+=2152m m -=k ()1,2k E k =10,110-0,29210-0a b >>ln a =22log log a b>2e ab >122ab a b ++<a b b aa b a b >lg 5lg 21+=42log 32log 3=ln πe π=5lg 5lg 2log 2÷=lg5lg 21+=ln πe π=42log 32log 3=2lg 5lg 2log 5÷=52log 10log 0.252s +=42598log 27log 8log 59⨯⨯=lg2lg5010+=ln 2ln36e +=19．下面对函数与在区间上的衰减情况的说法中错误的有( )A.的衰减速度越来越慢，的衰减速度越来越快B.的衰减速度越来越快，的衰减速度越来越慢C.的衰减速度越来越慢，的衰减速度越来越慢D.的衰减速度越来越快，的衰减速度越来越快20．已知，，则的值可能为( )A.B.C.24D.12()log f x x =1()2g x x ⎛⎫= ⎪⎝⎭()0,+∞()f x ()g x ()f x ()g x ()f x ()g x ()f x ()g x ,a b ∈R 249a b ==2a b -8338124参考答案解析：对选项A:,正确;对选项C:,正确;341log 9log 222+=+=2212log 32log 3==-=+555log 3log 3log 9225559===对选项D:,正确;故选:BCD 4．答案：ACD解析：画出函数,,的图象,如图所示,结合图象,可得三个函数,,中,当时,函数增长速度最快,增长速度最慢.所以选项B 正确;选项ACD 不正确.故选：ACD.5．答案：ABC解析：对于A ，，正确；对于B ，，，令，得，即得或，所以或，即的图象与x 轴有两个交点，正确；对于C ，，，当，即时，，正确；对于D ，易知没有最大值.6．答案：AB 解析：7．答案：BCD 解析：8．答案：ACD 解析：()2222(4)log 4log 433f =--=-()222()log 2log 3f x x x =--(0,)x ∈+∞()0f x =()()22log 1log 30x x +-=2log 1x =-2log 3x =12x =2255252511log 25log log 8log log 5log 42log 5log 2252⎛⎫⎛⎫++=⨯=⨯= ⎪⎪⎝⎭⎝⎭()2f x x =()2x g x =()2log h x x =()2f x x =()2x g x =()2log h x x =(4,)x ∈+∞()2x g x =()2log h x x =8x =()f x ()22()log 14f x x =--(0,)x ∈+∞2log 1x =2x =min ()4f x =-()f x9．答案：ABD 解析：对于A ，，故A 错误.对于B ，误.对于C ，，故C 正确.对于D ，，故D 错误.10．答案：ABC解析：对于A ，，A 错误；对于B ，对于C ，，C 错误；对于D ，故选：ABC.11．答案：AB解析:依题意,,由,得,所以,且,即,.故选AB12．答案：CD解析：若，则，故A 错误；若，故B 错误；因为，则，故C 正确；()221111115555552log 10log 0.25log 10log 0.25log 100.25log 252+=+=⨯==-4259lg 27lg8lg 53lg 33lg 2lg 5log 27log 8log 5lg 4lg 25lg 92lg 22lg 52lg 3⨯⨯=⨯⨯=⨯⨯=242235235112lg 54lg 22lg 3log 25log log log 5log 2log 316169lg 2lg 3lg 5----⨯⨯=⨯⨯=⨯⨯=lg 2lg 50lg1002+==()22111155552log 10log 0.25log 100.25log 52+=⨯==-334259222lg 312lg 533log 27log 8log 5lg 215lg 3222g g ⨯⋅⋅=⋅⋅==⨯⨯lg 2lg 50lg1002+==((22221log (2log 12⎛⎫-=--= ⎪⎝⎭1a >1b >lg()lg lg lg()a b a b ab +=+=a b ab +=(1)(1)()1a b ab a b --=-++=111a b=+=[]lg(1)lg(1)lg (1)(1)lg10a b a b -+-=--==11lg 0a b ⎛⎫+= ⎪⎝⎭10lg x =1010x =25log x =12255x ==lg101=lg(lg10)lg10==，故D 正确.故选：CD.13．答案：AC 解析：14．答案：AD解析：对于选项A ：因为，又因为在上单调递增，所以，故A 正确；对于选项B ：因为，解得或，所以或，故B 错误；对于选项C ：因为，且，可得，同号，则有若，同正，可得，则，可得；若，同负，可得，则，可得.综上所述，，又因为在定义域内单调递增，所以，故C 错误；对于选项D ：因为，则，可得在上单调递增，可得，且，，所以，故D 正确.故选AD.15．答案：AC解析：,故选项A 正确;,故选项B 错误;根据对数恒等式可知,,选项C 正确;根据换底公式可得：,故选项D 错误．故选：AC.16．答案：AD解析：对于选项A ，，所以选项A 正确；224log 5log 5422216580+==⨯=⨯0a b >>2log y x =()0,+∞22log log a b >2(ln ln )ln ln 4a b a b +<=()2ln 14ab >()ln 2ab >()ln 2ab <-2e ab >210e ab <<0a b >>ln ln 10a b =>ln a ln b ln a ln b e 1a b >>>()()()1110a b ab a b --=-++>1ab a b +>+ln a ln b 110ea b >>>>()()()1110a b ab a b --=-++>1ab a b +>+1ab a b +>+2x y =122ab a b ++>0a b >>0a b ->a b y x -=()0,+∞0a b a b a b -->>0b a >0b b >a b b a a b a b >()lg 5lg 2lg 52lg101+=⨯==224222log 3log 31log 3log 3log 42log 22===ln πe π=5lg 2log 2lg 2lg 5lg 5==÷()2255552log 10log 0.25log 100.25log 52+=⨯==对于选项B ，误；对于选项C ，，所以选项C 错误；对于选项D ，，所以选项D 正确.故选：AD 17．答案：ABD解析：对于选项A ，，故选项A 正确；对于选项B ，根据对数恒等式可知，故选项B 正确；对于选项C ，，故选项C 错误；对于选项D ，根据换底公式可得，故选项D 正确.故选ABD.18．答案：AD解析:对于选项A,,所以选项A 正确;对于选项B,项C,,所以选项C 错误;对于选项D,, 所以选项D 正确.19．答案：ABD解析：在平面直角坐标系中画出与图象如下图所示，由图象可判断出衰减情况为衰减速度越来越慢，衰减速度越来越慢.20．答案：BC解析：由题意得，，则时，，同理时，334259222lg 3lg 2lg 533log 27log 8log 5lg 2lg 5lg 3222⨯⨯⨯=⨯⨯==⨯⨯lg 2lg50lg1002+==ln 2ln3ln 2ln3e e e 236+=⋅=⨯=lg5lg 2lg(52)lg101+=⨯==224222log 3log 31log 3log 3log 42log 22===2lg 5log 5lg 5lg 2lg 2==÷()2255552log 10log 0.25log 100.25log 52+=⨯==334259222lg3lg2lg533log 27log 8log 5lg2lg5lg3222⨯⨯⨯=⨯⨯==⨯⨯lg2lg50lg1002+==ln 2ln 3ln 2ln 3236e e e +=⋅=⨯=()f x ()g x ()f x ()g x 42log 9log 3a ==3b =±3b =23228a a bb -==3b =-22242a a bb -==故选：BC.。

2025高考数学一轮复习-对数与对数函数-专项训练【含解析】

课时过关检测(十)对数与对数函数【原卷版】1．已知a＝log23，b＝log25，则log415＝()A．2a＋2b B．a＋bC．ab D．12a＋12b2．已知函数y＝f(x)的图象与函数y＝2x的图象关于直线y＝x对称，g(x)为奇函数，且当x＞0时，g(x)＝f(x)－x，则g(－8)＝()A．－5B．－6C．5D．63．已知函数f(x)＝ln x－1x＋1＋a sin x＋2，且f(m)＝5，则f(－m)＝()A．－5B．－3C．－1D．34．2020年12月17日凌晨，嫦娥五号返回器携带月球土壤样品，在预定区域安全着陆．嫦娥五号是使用长征五号火箭发射成功的，在不考虑空气阻力的情况下，火箭的最大速度v(单位：m/s)和燃料的质量M(单位：kg)、火箭(除燃料外)的质量m(单位：kg)的函数关系表达式为v＝212km/s，则燃料的质量与火箭的质量的关系是()A．M＝e6m B．Mm＝e6－1C．ln M＋ln m＝6D．Mm＝e6－15．若函数f(x)＝log a(x＋b)的图象如图所示，其中a，b为常数，则函数g(x)＝a x＋b的图象大致是()6．(多选)已知函数f(x)＝log2x的定义域是[4,8]，则下列函数中与f(x)值域相同的函数是()A．y＝f(x)＋1B．y＝f(x＋1)C．y＝－f(x)D．y＝|f(x)|7．(多选)关于函数f(x)＝ln(1＋x)－ln(3－x)，下列结论正确的是()A．f(x)在(－1,3)上单调递增B．y＝f(x)的图象关于直线x＝1对称C．y＝f(x)的图象关于点(1,0)对称D．f(x)的值域为R8．已知a>0，且a≠1，函数y＝log a(2x－3)＋2的图象恒过点P．若点P也在幂函数f(x)的图象上，则f(x)＝________．9．函数f(x)＝ln(x＋2)＋ln(4－x)的单调递减区间是________．10．已知f(x)是定义在R上的偶函数，且当x≥0时，f(x)＝log a(x＋1)(a>0，且a≠1)．(1)求函数f(x)的解析式；(2)若－1<f(1)<1，求实数a的取值范围．11．已知函数f(x)＝|log2x|，当0<m<n时，f(m)＝f(n)，若f(x)在[m2，n]上的最大值为2，则nm＝()A．2B．52C．3D．412．(多选)函数f(x)＝log a|x－1|在(0,1)上是减函数，那么()A．f(x)在(1，＋∞)上递增且无最大值B．f(x)在(1，＋∞)上递减且无最小值C．f(x)的图象关于直线x＝1对称D．∃a＝2020，满足f(x)在(0,1)上是减函数13．已知函数f(x)满足：①定义域为(－∞，0)∪(0，＋∞)；②值域为R；③f(－x)＝f(x)．写出一个满足上述条件的函数f(x)＝________．14.已知函数f(x)＝log a(3－ax)(a>0，且a≠1)．(1)当x∈[0,2]时，函数f(x)恒有意义，求实数a的取值范围；(2)是否存在这样的实数a，使得函数f(x)在区间[1,2]上单调递减，并且最大值为1？如果存在，试求出a的值；如果不存在，请说明理由．15．设实数a，b是关于x的方程|lg x|＝c的两个不同实数根，且a<b<10，则abc的取值范围是________．16．函数f(x)的定义域为D，若满足①f(x)在D内是单调函数；②存在[a，b]⊆D使f(x)在[a ，b ]上的值域为a 2，b 2，那么就称y ＝f (x )为“半保值函数”，若函数f (x )＝log a (a x ＋t 2)(a ＞0，且a ≠1)是“半保值函数”，求t 的取值范围．课时过关检测(十)对数与对数函数【解析版】1．已知a ＝log 23，b ＝log 25，则log 415＝()A ．2a ＋2bB ．a ＋bC ．abD ．12a ＋12b解析：Dlog 415＝12log 215＝12(log 23＋log 25)＝12a ＋12b ，故选D ．2．已知函数y ＝f (x )的图象与函数y ＝2x 的图象关于直线y ＝x 对称，g (x )为奇函数，且当x ＞0时，g (x )＝f (x )－x ，则g (－8)＝()A ．－5B ．－6C ．5D ．6解析：C由已知，函数y ＝f (x )与函数y ＝2x 互为反函数，则f (x )＝log 2x ．由题设，当x＞0时，g (x )＝log 2x －x ，则g (8)＝log 28－8＝3－8＝－5．因为g (x )为奇函数，所以g (－8)＝－g (8)＝5，故选C ．3．已知函数f (x )＝ln x －1x ＋1＋a sin x ＋2，且f (m )＝5，则f (－m )＝()A ．－5B ．－3C ．－1D ．3解析：C 根据题意，函数f (x )＝ln x －1x ＋1＋a sin x ＋2，则f (－x )＝ln －x －1－x ＋1＋a sin(－x )＋2＝－lnx －1x ＋1－a sin x ＋2，则有f (x )＋f (－x )＝4，故f (m )＋f (－m )＝4，若f (m )＝5，则f (－m )＝－1，故选C ．4．2020年12月17日凌晨，嫦娥五号返回器携带月球土壤样品，在预定区域安全着陆．嫦娥五号是使用长征五号火箭发射成功的，在不考虑空气阻力的情况下，火箭的最大速度v (单位：m/s)和燃料的质量M (单位：kg)、火箭(除燃料外)的质量m (单位：kg)的函数关系表达式为v ＝212km/s ，则燃料的质量与火箭的质量的关系是()A ．M ＝e 6mB ．Mm ＝e 6－1C ．ln M ＋ln m ＝6D ．Mm ＝e 6－1解析：D 依题意可知v ＝212000，可得6，即1＋Mm＝e 6，可得M m ＝e 6－1．如果火箭的最大速度达到12km/s ，则燃料的质量与火箭的质量的关系是M m ＝e 6－1．故选D ．5．若函数f (x )＝log a (x ＋b )的图象如图所示，其中a ，b 为常数，则函数g (x )＝a x ＋b 的图象大致是()解析：D 由f (x )的图象可知0<a <1,0<b <1，∴g (x )的图象应为D ．6．(多选)已知函数f (x )＝log 2x 的定义域是[4,8]，则下列函数中与f (x )值域相同的函数是()A ．y ＝f (x )＋1B ．y ＝f (x ＋1)C ．y ＝－f (x )D ．y ＝|f (x )|解析：BD 函数f (x )＝log 2x 在[4,8]单调递增，f (4)＝log 24＝2，f (8)＝log 28＝3，所以f (x )值域为[2,3]．对于选项A ：y ＝f (x )＋1值域为[3,4]，故选项A 不正确；对于选项B ：因为f (x )＝log 2x 的定义域是[4,8]，所以4≤x ＋1≤8，可得3≤x ≤7，f (x ＋1)＝log 2(x ＋1)∈[2,3]，所以y ＝f (x ＋1)值域为[2,3]，故选项B 正确；对于选项C ：y ＝－f (x )值域为[－3，－2]，故选项C 不正确；对于选项D ：y ＝|f (x )|的值域为[2,3]，故选项D 正确．故选B 、D ．7．(多选)关于函数f (x )＝ln(1＋x )－ln(3－x )，下列结论正确的是()A ．f (x )在(－1,3)上单调递增B ．y ＝f (x )的图象关于直线x ＝1对称C ．y ＝f (x )的图象关于点(1,0)对称D ．f (x )的值域为R 解析：ACD函数f (x )的定义域是(－1,3)，f (x )＝lnx ＋13－x ．令t (x )＝x ＋13－x ＝－4x －3－1(x ≠3)，易知t (x )在(－1,3)上单调递增，所以t (x )>t (－1)＝0，所以f (x )＝ln t (x )在(－1,3)上单调递增，且值域为R ．故A 、D 正确．当x ∈(－2,2)时，1＋x ∈(－1,3)，1－x ∈(－1,3)，f (1＋x )＝ln 2＋x2－x，f (1－x )＝ln2－x2＋x，所以f (1＋x )＝－f (1－x )，f (1＋x )≠f (1－x )．所以y ＝f (x )的图象关于点(1,0)对称．故B 错误，C 正确．故选A 、C 、D ．8．已知a >0，且a ≠1，函数y ＝log a (2x －3)＋2的图象恒过点P ．若点P 也在幂函数f (x )的图象上，则f (x )＝________．解析：设幂函数为f (x )＝x α，因为函数y ＝log a (2x －3)＋2的图象恒过点P (2，2)，则2α＝2，所以α＝12，故幂函数为f (x )＝x 12．答案：x129．函数f (x )＝ln(x ＋2)＋ln(4－x )的单调递减区间是________．解析：＋2>0，－x >0，得－2<x <4，因此函数f (x )的定义域为(－2,4)．f (x )＝ln(x ＋2)＋ln(4－x )＝ln(－x 2＋2x ＋8)＝ln [－(x －1)2＋9]，设u ＝－(x －1)2＋9，又y ＝ln u 是增函数，u ＝－(x －1)2＋9在(1,4)上是减函数，因此f (x )的单调递减区间为(1,4)．答案：(1,4)10．已知f (x )是定义在R 上的偶函数，且当x ≥0时，f (x )＝log a (x ＋1)(a >0，且a ≠1)．(1)求函数f (x )的解析式；(2)若－1<f (1)<1，求实数a 的取值范围．解：(1)当x <0时，－x >0，由题意知f (－x )＝log a (－x ＋1)，又f (x )是定义在R 上的偶函数，∴f (－x )＝f (x )．∴当x <0时，f (x )＝log a (－x ＋1)，∴函数f (x )的解析式为f (x )a (x ＋1)，x ≥0，a (－x ＋1)，x <0(a >0，且a ≠1)．(2)∵－1<f (1)<1，∴－1<log a 2<1，∴log a 1a<log a 2<log a a ．①当a >1，，解得a >2；②当0<a <1，，解得0<a <12．综上，实数a (2，＋∞)．11．已知函数f (x )＝|log 2x |，当0<m <n 时，f (m )＝f (n )，若f (x )在[m 2，n ]上的最大值为2，则n m＝()A ．2B ．52C ．3D ．4解析：D如图所示，根据函数f (x )＝|log 2x |的图象，得0<m <1<n ，所以0<m 2<m <1．结合函数图象，易知当x ＝m 2时f (x )在[m 2，n ]上取得最大值，所以f (m 2)＝|log 2m 2|＝2，又0<m <1，所以m ＝12，再结合f (m )＝f (n )，可得n ＝2，所以nm＝4．故选D ．12．(多选)函数f (x )＝log a |x －1|在(0,1)上是减函数，那么()A ．f (x )在(1，＋∞)上递增且无最大值B ．f (x )在(1，＋∞)上递减且无最小值C ．f (x )的图象关于直线x ＝1对称D ．∃a ＝2020，满足f (x )在(0,1)上是减函数解析：ACD由题意，函数f (x )＝log a |x －1|在(0,1)上是减函数，即f (x )＝log a (1－x )在(0,1)上是减函数，因为y ＝1－x 是减函数，根据复合函数的单调性的判定方法，可得a >1，当x ∈(1，＋∞)时，f (x )＝log a |x －1|＝log a (x －1)，因为y ＝x －1是增函数，根据复合函数的单调性的判定方法，可得函数f (x )在(1，＋∞)上单调递增，且无最大值，所以A 正确，B 错误；又由f (2－x )＝log a |2－x －1|＝log a |x －1|＝f (x )，所以f (x )的图象关于直线x ＝1对称，所以C 正确；由a >1可知，当a ＝2020时，函数f (x )在(0,1)上是减函数，所以D 正确．故选A 、C 、D ．13．已知函数f (x )满足：①定义域为(－∞，0)∪(0，＋∞)；②值域为R ；③f (－x )＝f (x )．写出一个满足上述条件的函数f (x )＝________．解析：f (x )＝ln|x |的定义域为(－∞，0)∪(0，＋∞)，值域为R ，且f (－x )＝ln|－x |＝ln|x |＝f (x )，因此f (x )＝ln|x |符合题意．答案：ln|x |(答案不唯一)15.已知函数f (x )＝log a (3－ax )(a >0，且a ≠1)．(1)当x ∈[0,2]时，函数f (x )恒有意义，求实数a 的取值范围；(2)是否存在这样的实数a ，使得函数f (x )在区间[1,2]上单调递减，并且最大值为1？如果存在，试求出a 的值；如果不存在，请说明理由．解：(1)∵a >0且a ≠1，设t (x )＝3－ax ，则t (x )＝3－ax 为减函数，当x ∈[0,2]时，t (x )的最小值为3－2a ，∵当x ∈[0,2]时，f (x )恒有意义，即x ∈[0,2]时，3－ax >0恒成立．∴3－2a >0，∴a <32．又a >0且a ≠1，∴0<a <1或1<a <32，∴实数a 的取值范围为(0,1)(2)由(1)知函数t (x )＝3－ax 为减函数．∵f (x )在区间[1,2]上单调递减，∴y ＝log a t 在区间[1,2]上单调递增，∴a >1，当x ∈[1,2]时，t (x )的最小值为3－2a ，f (x )的最大值为f (1)＝log a (3－a )，∴－2a >0，a (3－a )＝1，<32，＝32.故不存在这样的实数a ，使得函数f (x )在区间[1,2]上单调递减，并且最大值为1．15．设实数a ，b 是关于x 的方程|lg x |＝c 的两个不同实数根，且a <b <10，则abc 的取值范围是________．解析：由题意知，在(0,10)上，函数y ＝|lg x |的图象和直线y ＝c 有两个不同交点(如图)，∴－lg a ＝lg b ．即ab ＝1,0<c <lg 10＝1，∴abc 的取值范围是(0,1)．答案：(0,1)16．函数f (x )的定义域为D ，若满足①f (x )在D 内是单调函数；②存在[a ，b ]⊆D 使f (x )在[a ，b ]上的值域为a 2，b 2，那么就称y ＝f (x )为“半保值函数”，若函数f (x )＝log a (a x ＋t 2)(a ＞0，且a ≠1)是“半保值函数”，求t 的取值范围．解：∵函数f (x )＝log a (a x ＋t 2)(a ＞0，且a ≠1)是“半保值函数”，且定义域为R ，当a ＞1时，z ＝a x ＋t 2在R 上单调递增，y ＝log a z 在(0，＋∞)上单调递增，可得f (x )为R 上的增函数；当0＜a ＜1时，f (x )仍为R 上的增函数，∴f (x )在定义域R 上为增函数，∴方程log a (a x ＋t 2)＝12x 有两个不同的根，∴a x ＋t 2＝a 12x ，即a x －a 12x ＋t 2＝0，令u ＝a 12x ，u ＞0，即u 2－u ＋t 2＝0有两个不同的正数根，可得1－4t 2＞0，且t 2＞0，1 2，解得t－。

人教A版数学必修一《对数与对数函数》单元测试卷.docx

《对数与对数函数》单元测试卷注意事项：1.考察内容：对数与对数函数 2.题目难度：中等难度题型3.题型方面：8道选择，4道填空，4道解答。

4.参考答案：有详细答案5.资源类型：试题/课后练习/单元测试一、选择题1.三个数0.377,0.3,ln 0.3a b c ===大小的顺序是（）A ．a b c >> B. a c b >>C ．b a c >> D. c a b>>2.已知2x ＝72y＝A ，且1x ＋1y＝2，则A 的值是A ．7B ．7 2C ．±7 2D ．983.若a>0且a ≠1，且143log a <，则实数a 的取值范围是（）A ．0<a<1B ．43a 0<< C ．43a 043a <<>或 D ．43a 0<<或a>14.函数y = log 2 ( x 2– 5x – 6 )单调递减区间是（）A ．⎪⎭⎫ ⎝⎛∞-25,B ．⎪⎭⎫⎝⎛+∞,25C ．()1,-∞-D ．(+∞,6)5.巳知等比数列{}n a 满足0,1,2,n a n >=，且25252(3)nn a a n -⋅=≥，则当1n ≥时，2123221log log log n a a a -+++= ( )Ａ．(21)n n - Ｂ．2(1)n + Ｃ．2n Ｄ．2(1)n -6.若)1()1(32log ,log ,10+-+-==<<a a aa a aQ P a ，则P 与Q 的大小关系是（）A ．P >QB ．P <QC ．P =QD ．P 与Q 的大小不确定7.若函数y = log 12| x + a |的图象不经过第二象限，则a 的取值范围是（）（A ）( 0，+ ∞ )，（B ）[1，+ ∞ ) （C ）( – ∞，0 ) （D ）( – ∞，– 1 ]8.已知函数6s i n c o s 2111)(++⎪⎭⎫⎝⎛+-=x b x a x f x（a 、b 为常数，且1>a ），8)1000o (lg 8=g l f ，则)2lg (lg f 的值是（）(A) 8 (B) 4 (C) -4 (D) 与a 、b 有关的数二、填空题9.对于实数,,a b c ，若在⑴lg 21a c =--⑵lg32a b =-⑶lg 4222a c =--⑷lg5a c =+⑸lg 61a b c =+--中有且只有两个式子是不成立的，则不成立的式子是 10.已知函数()log (0,1)a f x x a a =>≠，若12()()3f x f x -=，则2212()()f x f x -= ． 11.函数2()log (2)f x x =-的单调减区间是．12.已知函数()()()[]111lg 22+++-=x a x a x f 的定义域为()+∞∞-,，则实数a 的取值范围是________________________.三、解答题13.设方程x 2－10x ＋2＝0的两个根分别为α，β，求log 4α2－αβ＋β2(α－β)2的值．14.设关于x 的方程(m+1)x 2-mx+m-1=0有实根时，实数m 的取值范围是集合A ，函数f(x)=lg[x 2-(a+2)x+2a]的定义域是集合B. (1)求集合A ；(2)若A B=B ，求实数a 的取值范围.15.已知函数()ln()(10)xxf x a b a b =->>>.(1) 求函数()f x 的定义域I ；(2) 判断函数()f x 在定义域I 上的单调性，并说明理由；（3）当,a b 满足什么关系时，()f x 在[)1+∞，上恒取正值。

精选-江苏专版2020版高考数学一轮复习课时跟踪检测十对数与对数函数理含解析

课时跟踪检测（十）对数与对数函数一抓基础，多练小题做到眼疾手快．(·淮安调研)函数()＝(－)的定义域为．解析：由－＞，解得＞，所以函数()的定义域为.答案：．函数()＝(－＋)的值域为．解析：令＝－＋＝(－)＋≥，故函数()可化为＝，≥，此函数是一个增函数，其最小值为＝，故()的值域为[，＋∞)．答案：[，＋∞)．计算＋()＝.解析：＋()＝)·)＋＝＋＝＋＝.答案：．(·长沙调研)已知函数＝(＋)－(＞，≠)的图象恒过定点，若点也在函数()＝＋的图象上，则()＝.解析：∵函数＝(＋)－(＞，≠)的图象恒过定点(－，－)，将＝－，＝－代入()＝＋，得－＋＝－，∴＝－，∴()＝－，则()＝－＝－＝.答案：．若函数()＝(\\(－＋，≤，＋，＞))(＞，且≠)的值域是[，＋∞)，则实数的取值范围是．解析：当≤时，＝－＋≥.因为()的值域为[，＋∞)，所以当＞时，＋＞＋≥，所以≥，所以＜≤；当＜＜时，＋＜＋，不合题意．故∈(]．答案：(]．(·镇江期末)已知函数()是定义在上的奇函数，当＞时，()＝－，则不等式()＜的解集是．解析：当＜时，()＝－(－)＝(－)－，()＜，即(－)－＜，解得－＜＜；当＞时，()＝－，()＜，即－＜，解得＞，综上，不等式()＜的解集是(－)∪(，＋∞)．答案：(－)∪(，＋∞)二保高考，全练题型做到高考达标．(·镇江中学调研)函数＝＋(－)的值域为．解析：由题意知，＞且－＞，∴()的定义域是()．∵函数()＝＋(－)＝[(－)]，∴＜(－)≤＝，当且仅当＝时等号成立．∴[(－)]≤，∴函数＝＋(－)的值域为(－∞，]．答案：(－∞，]．(·镇江中学学情调研)已知函数()＝的定义域是，则实数的值为．解析：因为函数()＝的定义域是，所以当＞时，－＞，即＜，所以＜，所以＞.令＝，得＝＝，所以实数的值为.答案：．若函数()＝(－＋＋)在区间(－∞，]上递减，则的取值范围为．解析：令函数()＝－＋＋＝(－)＋＋－，对称轴为＝，要使函数在(－∞，]上递减，则有(\\(＞，≥，))即(\\(－＞，≥，))解得≤＜，即∈[)．答案：[)．(·连云港模拟)已知函数()＝，若()＝，则(－)＝.解析：因为()＝的定义域为－＜＜，所以(－)＝＝－＝－()，所以()为奇函数，所以(－)＝－()＝－.答案：－．函数()＝＋的定义域为．解析：由(\\(－≥，,(－＋－)＞，))得(\\(－≤≤，＞且≠，))故函数定义域为()∪(]．答案：()∪(]．(·苏州调研)若函数()＝(\\(－＋，≤，＋，＞))(＞，且≠)的值域为[，＋∞)，则实数的取值范围是．解析：当≤时，()∈[，＋∞)，所以当＞时，()的取值集合⊆[，＋∞)．当＜＜时，＝，不符合题意；当＞时，＝(＋，＋∞)，若⊆[，＋∞)，则有＋≥，解得＜≤.答案：(]．函数()＝·()的最小值为．解析：依题意得()＝·(＋)＝()＋＝－≥－，当且仅当＝－，即＝时等号成立，因此函数()的最小值为－.答案：－．设函数()＝(\\(，＞，－，＜，))若()＞(－)，则实数的取值范围是．解析：由()＞(－)得(\\(＞，＞))或(\\(＜，－＞－，))即(\\(＞，＞－))或(\\(＜，,－－＞－))解得＞或－＜＜.答案：(－)∪(，＋∞)．已知函数()是定义在上的偶函数，()＝，当＞时，()＝.()求函数()的解析式；()解不等式(－)＞－.解：()当＜时，－＞，则(－)＝(－)．因为函数()是偶函数，所以(－)＝()．所以函数()的解析式为()＝(\\(，＞，，＝，－，＜.))()因为()＝＝－，()是偶函数，所以不等式(－)＞－可化为(－)＞()．又因为函数()在(，＋∞)上是减函数，所以－＜，解得－＜＜，即不等式的解集为(－，)．．(·如东上学期第一次阶段检测)已知函数()＝(＋)＋(－)(＞且≠)，且()＝. ()求的值及()的定义域；()若不等式()≤恒成立，求实数的取值范围．解：()因为()＝，所以＝，故＝，所以()＝(＋)＋(－)，要使函数()有意义，需有(\\(＋＞，－＞，))解得－＜＜，所以()的定义域为(－)．()由()知，()＝(＋)＋(－)＝[(＋)(－)]＝(－＋＋)＝[－(－)＋]，故当＝时，()有最大值，所以的取值范围是[，＋∞)．三上台阶，自主选做志在冲刺名校．(·南京五校联考)已知函数()＝＋－(＜)与()＝＋(＋)，若函数()图象上存在点与函数()图象上的点关于轴对称，则的取值范围是．解析：设点(，)(＜)，则点关于轴的对称点(－，)在函数()的图象上，所以(\\(＝\()＋－()，＝－＋－＋，))消去，可得＋－＝(－)＋(－＋)，所以－＝(－＋)(＜)．令()＝－(＜)，()＝(－)(＜)，问题转化为函数()与函数()的图象在＜时有交点．在平面直角坐标系中分别作出函数()与函数()的图象如图所示．当()＝(－)的图象过点时，＝.由图可知，当＜时，函数()与函数()的图象在＜时有交点．故的取值范围为(－∞，)．答案：(－∞，)．(·昆山测试)已知函数()＝(∈)．()当＝时，求函数()的值域；()当＞时，求函数()的定义域；()若函数()在区间[，＋∞)上是单调增函数，求实数的取值范围．解：()当＝时，()＝，定义域为(－∞，)．因为函数＝(＜)的值域为(，＋∞)，所以()＝的值域为.()因为＞，所以关于的不等式＞⇔(－)(－)＞⇔(－)＞.(*)①若＜＜，则＞，不等式(*)的解为＜或＞；②若＝，则不等式(*)即(－)＞，其解为≠；③若＞，则＜，不等式(*)的解为＜或＞.综上，当＜≤时，函数()的定义域为(－∞，)∪；当＞时，函数()的定义域为∪(，＋∞)．()令()＝，则()＝ ()．因为函数()在[，＋∞)上是单调增函数，且对数的底数＞，所以当∈[，＋∞)时，()＞，且函数()在[，＋∞)上是单调增函数．而()＝＝＝＋，若－≥，则函数()在[，＋∞)上不是单调增函数；若－＜，则函数()在[，＋∞)上是单调增函数．所以＜.①因为函数()在[，＋∞)上是单调增函数，所以要使当∈[，＋∞)时，()＞，必须()＞，即＞，解得＞.②综合①②知，实数的取值范围是.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

课时11 对数和对数函数
模拟训练（分值：60分建议用时：30分钟） 1．已知log 7[log 3(log 2x )]＝0，那么x 12
- 等于( )
A.1
3 B.
36 C.24
D.
33
【答案】C
【解析】由条件知，log 3(log 2x )＝1，∴log 2x ＝3，∴x ＝8， ∴x
12
-＝
2
4
. 2．设a ＝log 32，b ＝ln2，c ＝512
-，则( )
A ．a log 33＝1
2，因此c <a <b .
[知识拓展]比较对数式的大小，或证明等式问题是对数中常见题型，解决此类问题的方法很多,①当底数相同时可直接利用对数函数的单调性比较;②若底数不同，真数相同,可转化为同底（利用换底公式）或利用对数函数图象，数形结合解得；③若不同底，不同真数，则可利用中间量进行比较.
3.函数的递减区间为（）
A.()+∞,1
B. ⎥⎦⎤ ⎝
⎛∞-43, C. ⎪⎭⎫ ⎝⎛+∞,21 D.⎥⎦
⎤ ⎝
⎛∞-2
1,
【答案】A
4．已知函数（b 为常数），若[)+∞∈,1x 时，0)(≥x f 恒成立，则
（）
A.1≤b
B.1<b
C.1≥b
D.1=b 【答案】A
【解析】因为1≥x ，所以，又1≥x ，0)(≥x f 恒成立，即12≥-b 恒成立，
所以1≤b .故选A.
5已知函数f (x )满足：当x ≥4时，f (x )＝(12)x
；当x ＜4时，f (x )＝f (x ＋1)，则f (2＋log 23)＝( )
A.1
24
B.112
C.1
8
D.38
【答案】A
【解析】∵2＜3＜4＝22
，∴1＜log 23＜2. ∴3＜2＋log 23＜4，
∴f (2＋log 23)＝f (3＋log 23)＝f (log 224)＝(12)2log 24＝22log 24
-＝221
log 24＝124
.
6．定义在R 上的奇函数f (x )满足：当x >0时，f (x )＝2010x
＋log 2010x ，则方程f (x )＝0的实根个数为( )
A ．1
B ．2
C ．3
D ．4
【答案】C
7.定义：区间[]21,x x （21x x <）的长度为12x x -.已知函数
的定义域为[]b a ,，值域为
[]2,0，则区间[]b a ,的长度的最大值为 .
【答案】
4
15
【解析】由≤0x 5.0log 2≤解得
441≤≤x ，所以区间[]b a ,的长度的最大值为4
15414=-. 8．已知函数f (x )＝⎩
⎪⎨
⎪⎧
3x ＋1
x ≤0，
log 2x x >0，则使函数f (x )的图象位于直线y ＝1上方的x 的取值范围是
________．
【答案】{x |－1<x ≤0或x >2} 【解析】当x ≤0时，由3x ＋1
>1，得x ＋1>0，即x >－1.
∴－1<x ≤0.
当x >0时，由log 2x >1，得x >2.
∴x 的取值范围是{x |－1<x ≤0或x >2}．
9．已知f (x )＝log a 1＋x
1－x (a ＞0，且a ≠1)．
(1)求f (x )的定义域；
(2)判断f (x )的奇偶性并予以证明； (3)求使f (x )＞0的x 的取值范围．
10．已知函数f (x )＝log a (2－ax )，是否存在实数a ，使函数f (x )在[0,1]上是关于x 的减函数，若存在，求a 的取值范围．
【解析】∵a >0，且a ≠1，
∴u ＝2－ax 在[0,1]上是关于x 的减函数．
又f (x )＝log a (2－ax )在[0,1]上是关于x 的减函数， ∴函数y ＝log a u 是关于u 的增函数，且对x ∈[0,1]时，
u ＝2－ax 恒为正数．
其充要条件是⎩
⎪⎨
⎪⎧
a >1
2－a >0，即1<a <2.
∴a 的取值范围是(1,2)．
[新题训练] （分值：20分建议用时：10分钟） 11．（10分）求函数
的值域和单调区间．
【解析】（1）由2x x ->0得01x <<，所以函数的定义域是(0,1)
因为0<2x x -=
，所以，当01a <<时,
，函数。