指数函数与对数函数单元测试题.docx
指数与对数运算单元测试题(经典全面,一套涵盖)

指数与对数运算单元测试题(经典全面,一
套涵盖)
本文档为指数与对数运算的单元测试题,旨在全面覆盖该主题的经典问题。
下面是一套经过精心设计的测试题,希望对您的研究和理解有所帮助。
第一部分:指数运算
1. 计算 $2^4$ 的值。
2. 将 $8^{\frac{1}{3}}$ 表达为根式。
3. 解方程 $5^x = 125$,并给出结果。
第二部分:对数运算
4. 计算 $\log_{10} 100$ 的值。
5. 将 $\log_2 16$ 表达为指数形式。
6. 解方程 $\log_3 x = 2$,并给出结果。
第三部分:指数与对数运算的性质
7. 对于任意正数 a 和 b,证明 $\log_a b = \frac{\log_c a}{\log_c b}$。
8. 证明 $a^{\log_a b} = b$。
9. 对于任意正数 a、b 和 c,证明 $a^{\log_b c} = c^{\log_b a}$。
第四部分:指数和对数问题的应用
10. 某种细菌每20分钟翻倍,开始时有100个细菌。
经过多少
分钟后,细菌数量将达到1000个?
11. 若投资本金元,年利率为5%,按复利计算,多少年后本金
将增长到元?
12. 若某物品每年贬值20%,初始价值为元,多少年后其价值
将降至5000元以下?
以上是本套指数与对数运算单元测试题的全部内容。
请按照题
目要求逐个回答,并给出详细解答和计算过程。
祝您顺利完成测试!。
(完整版)指数函数对数函数专练习题(含答案).docx
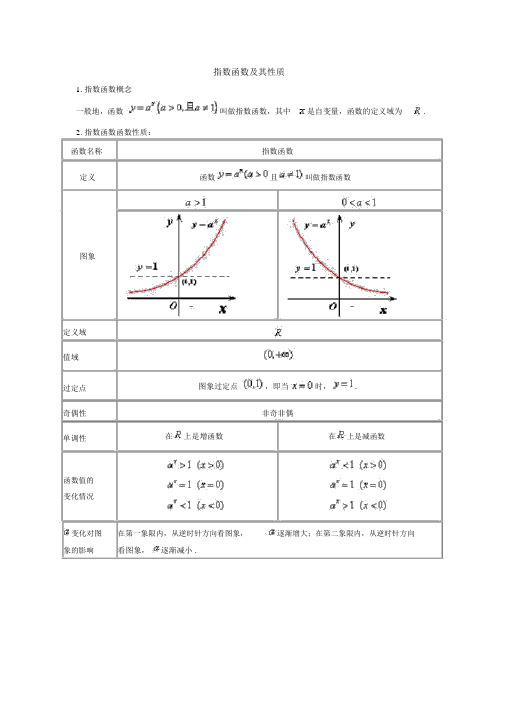
指数函数及其性质1.指数函数概念一般地,函数叫做指数函数,其中是自变量,函数的定义域为.2.指数函数函数性质:函数名称定义图象定义域值域过定点奇偶性单调性函数值的变化情况变化对图象的影响指数函数函数且叫做指数函数图象过定点,即当时,.非奇非偶在上是增函数在上是减函数在第一象限内,从逆时针方向看图象,逐渐增大;在第二象限内,从逆时针方向看图象,逐渐减小 .对数函数及其性质1.对数函数定义一般地,函数叫做对数函数,其中是自变量,函数的定义域.2.对数函数性质:函数名称定义函数对数函数且叫做对数函数图象定义域值域过定点奇偶性图象过定点,即当非奇非偶时,.单调性在上是增函数在上是减函数函数值的变化情况变化对图象的影响在第一象限内,从顺时针方向看图象,看图象,逐渐减小 .逐渐增大;在第四象限内,从顺时针方向指数函数习题一、选择题aa ≤ b,则函数 f ( x ) =1?2x 的图象大致为 ()1.定义运算 a ?b =>b a b2.函数 f ( x ) = x 2-bx + c 满足 f (1 + x ) =f (1 - x ) 且 f (0) =3,则 f ( b x ) 与 f ( c x ) 的大小关系是()xxA . f ( b ) ≤ f ( c ) x xB . f ( b ) ≥ f ( c )xxC . f ( b )> f ( c )D .大小关系随 x 的不同而不同3.函数 y = |2 x - 1| 在区间A . ( - 1,+∞ )C . ( - 1,1)( k - 1, k + 1) 内不单调,则 k 的取值范围是 ()B . ( -∞, 1)D . (0,2)4.设函数 f ( x ) =ln [( x -1)(2 -x)] 的定义域是 ,函数 ( ) = lg(x - 2x -1) 的定义域是 ,Ag xaB若 ?,则正数a 的取值范围 ()ABA . a >3B . a ≥ 3C . a > 5D . a ≥ 5.已知函数 f (x = 3- a x -3, x ≤ 7,若数列 { a n 满足 a n = f (n )(n ∈ * ,且 {a n }是递5 ) a x - 6, x >7. } N) 增数列,则实数a 的取值范围是 ()A . [ 9, 3)B . ( 9, 3) 44C . (2,3)D . (1,3)2x16.已知 a >0 且 a ≠ 1,f ( x ) = x - a ,当 x ∈ ( - 1,1) 时,均有 f ( x )< 2,则实数 a 的取值范围 是( )1 1 A . (0 , 2] ∪ [2 ,+∞ ) B . [ 4, 1) ∪ (1,4]11C . [ 2, 1) ∪ (1,2]D . (0 , 4) ∪ [4 ,+∞ )二、填空题xa7.函数 y = a ( a >0,且 a ≠ 1) 在 [1,2] 上的最大值比最小值大 2,则 a 的值是 ________.8.若曲线 | y | = 2 x + 1 与直线 y =b 没有公共点,则b 的取值范围是 ________.| x|的定义域为9. (2011 ·滨州模拟 ) 定义:区间 [x 1,x 2 ]( x 1<x 2) 的长度为 x 2- x 1. 已知函数 y = 2 [a , b] ,值域为 [1,2] ,则区间 [a , b] 的长度的最大值与最小值的差为 ________.三、解答题10.求函数y=2x2 3x 4 的定义域、值域和单调区间.11.(2011 ·银川模拟 ) 若函数y=a2x+ 2a x-1( a>0 且a≠ 1) 在x∈ [- 1,1]上的最大值为14,求a 的值.12.已知函数f (x) = 3x,(a+ 2) = 18, (x) =λ·3ax-4x的定义域为 [0,1] .f g(1)求 a 的值;(2) 若函数g( x) 在区间 [0,1] 上是单调递减函数,求实数λ的取值范围.1. 解析:由? = a a≤ b x2x x≤0,b a>b x>0 .1答案: A2. 解析:∵f (1 +x) =f (1 -x) ,∴f ( x) 的对称轴为直线x=1,由此得 b=2.又 f (0)=3,∴c=3.∴f ( x)在(-∞,1)上递减,在(1,+∞)上递增.x≥2x≥ 1,∴ (3 x) ≥(2 x) .若 x≥0,则3f f若 x<0,则3x<2x<1,∴f (3x)> f (2x).∴f (3x)≥ f (2x).答案: A3.解析:由于函数 y=|2x-1|在(-∞,0)内单调递减,在(0,+∞)内单调递增,而函数在区间 ( k- 1,k+ 1) 内不单调,所以有答案: Ck-1<0<k+1,解得-1<k<1.4.解析:由题意得: A=(1,2)x x>1x x>1在(1,2)上恒成立,即,a- 2且 a>2,由 A? B知 a- 2x x上恒成立,令x x xln a-2xln2>0 ,所以函数a-2 - 1>0 在 (1,2)u( x)=a- 2- 1,则u′( x) =au ( x ) 在 (1,2) 上单调递增,则 u ( x )> u (1) = a - 3,即 a ≥ 3.答案: B*f ( n ) 为增函数,5. 解析: 数列 { a } 满足 a = f ( n )( n ∈ N ) ,则函数nna >18- 6- ) × 7- 3,所以 3- a >0注意 a>(3,解得 2<a <3.aa8-6> 3- a × 7-3答案: C1 2x1 21 x x21的图象,6. 解析: f ( x )<? x -a < ? x - <a ,考查函数 y = a与 y =x - 2222当 a >1 时,必有 a-1≥1,即 1<a ≤ 2,21 1当 0<a <1 时,必有 a ≥ ,即 ≤a <1,2 2 1 综上, 2≤ a <1 或 1<a ≤ 2. 答案: C7. 解析: 当 a >1 时, y x在 [1,2] 上单调递增,故 2a3x= a a - a = ,得 a = . 当 0<a <1 时, y = a2 22a在 [1,2] 上单调递减,故 a -a = 2,得 a = 2. 故 a =2或 2.1131 3答案: 2或28. 解析: 分别作出两个函数的图象,通过图象的交点个数来判断参数的取值范围.x+1 与直线 y = b 的图象如图所示,由图象可得:如果x+ 1 与直线 y = b曲线 | y | = 2 | y | = 2没有公共点,则 b 应满足的条件是 b ∈ [- 1,1] .答案: [- 1,1]9. 解析: 如图满足条件的区间 [a , b] ,当 a =- 1, b = 0 或 a = 0, b = 1 时区间长度最小,最小值为 1,当 a =- 1,b = 1 时区间长度最大,最大值为2,故其差为 1.答案: 110. 解: 要使函数有意义,则只需- x 2-3x + 4≥ 0,即 x 2+ 3x -4≤ 0,解得- 4≤ x ≤ 1.∴函数的定义域为 { x | -4≤ x ≤ 1} .223225 令 t =- x - 3x + 4,则 t =- x - 3x + 4=- ( x + ) +4,2253∴当-4≤ x ≤ 1 时, t max = 4 ,此时 x =- 2, t min = 0,此时 x =- 4 或 x =1.∴0≤t ≤ 25 . ∴0≤ -x 2- 3x + 4≤ 5 .4 2∴函数 y = ( 1)x 23 x4的值域为 [ 2 , 1] .8223 225由 t =- x - 3x + 4=- ( x + )+4( - 4≤ x ≤ 1) 可知,23当- 4≤ x ≤- 2时, t 是增函数,3当- 2≤ x ≤1 时, t 是减函数.根据复合函数的单调性知:y = ( 1 )x 23 x 4在 [ - 4,- 3 3] 上是减函数,在 [ - ,1] 上是增函数.22 233∴函数的单调增区间是 [ - 2, 1] ,单调减区间是 [ - 4,- 2] . 11. 解: 令x22tt >0y= t+ 2t1= ( t+ 1)2,其对称轴为t =- 1.该二次函数a = ,∴ ,则--在[ - 1,+ ∞ ) 上是增函数.x12①若 a >1,∵x ∈ [ - 1,1] ,∴t = a ∈ [ a , a ] ,故当 t = a ,即 x =1 时, y max =a + 2a - 1=14,解得 a = 3( a =- 5 舍去 ) .②若 0<a <1,∵x ∈ [ - 1,1] ,∴ = x∈1 1=-时,a [ a , ] ,故当 t = ,即 1t a ax12y max = (a + 1) - 2= 14.11∴a =3或- 5( 舍去 ) .1综上可得 a = 3 或 3.12. 解: 法一: (1) 由已知得 a2 aa =log 32.3 += 18? 3 = 2?(2) 此时 g ( x ) = λ·2x - 4 x ,设 0≤ x 1<x 2≤ 1,因为 g ( x ) 在区间 [0,1] 上是单调减函数,所以 g ( x ) - g ( x ) = (2 x - 2x )( λ- 2x - 2x )>0 恒成立,即 λ<2x + 2x 恒成立.1 2 1 2 2 1 2 1由于 2x 2+ 2x 1>2 + 2 = 2,所以实数 λ的取值范围是λ≤ 2.法二: (1) 同法一.(2) 此时 g ( x ) = λ·2x - 4x ,因为 g ( x ) 在区间 [0,1] 上是单调减函数,所以有 g ′( x ) = λln2 ·2x - ln4 ·4x = ln2 [- 2 ·(2x )2+ λ·2x] ≤0 成立.x2 设 2 = u ∈ [1,2] ,上式成立等价于-2u+ λu ≤0 恒成立.因为 u ∈ [1,2] ,只需 λ≤2u 恒成立,所以实数 λ的取值范围是λ≤ 2.对数与对数函数同步练习一、选择题1、已知 3a2 ,那么 log3 8 2log 3 6 用 a 表示是()A 、 a 2B 、 5a2C 、 3a (1 a)2D 、 3a a 22、 2log a (M 2N ) log a Mlog a N ,则M的值为()A 、1NB 、4C 、1D 、 4 或 1413 、 已 知 x 2 y 2 1, x0, y 0 , 且 log a (1 x) m,log a n,则 log a y 等 于1 x()A 、 m nB 、 m nC 、 1m nD 、 1m n224、如果方程 lg 2 x (lg5lg 7)lgx lg5 glg 7 0 的两根是 ,,则 g的值是()A 、 lg5 glg 7B 、 lg35C 、 35D 、13515、已知 log 7[log 3 (log 2 x)] 0,那么 x2等于( )A 、1B 、13 C 、1D 、1322 2336、函数 ylg2 1 的图像关于()1 xA 、 x 轴对称B 、 y 轴对称C 、原点对称D 、直线 yx 对称7、函数 ylog (2 x 1) 3x2 的定义域是()A 、 2,1 U 1,B 、 1,1 U 1,32C 、 2,D 、 1,328、函数 ylog 1 (x 2 6x17) 的值域是()2A 、 RB 、 8,C 、, 3D 、 3,9、若 log m 9 log n 9 0 ,那么 m, n 满足的条件是( )A 、 m n 1B 、 n m 1C 、 0 n m 1D 、 0 m n 110、 log a 2 1,则 a 的取值范围是()3A 、 0, 2U 1,B 、 2,C 、 2,1D 、 0, 2U 2,3333 311、下列函数中,在 0,2 上为增函数的是()A 、 ylog 1 ( x1)B 、 y log 2 x 2 12C 、 ylog 2 1D 、 ylog 1 ( x 2 4x 5)x212、已知 g( x) log a x+1 ( a 0且a 1) 在 10, 上有 g( x)0 ,则 f ( x)a x 1 是( )A 、在 ,0上是增加的 B 、在 ,0 上是减少的C 、在, 1 上是增加的D 、在,0 上是减少的二、填空题13、若 log a 2 m,log a 3 n, a 2 m n 。
最新版精选单元测试《指数函数和对数函数》完整题(含参考答案)
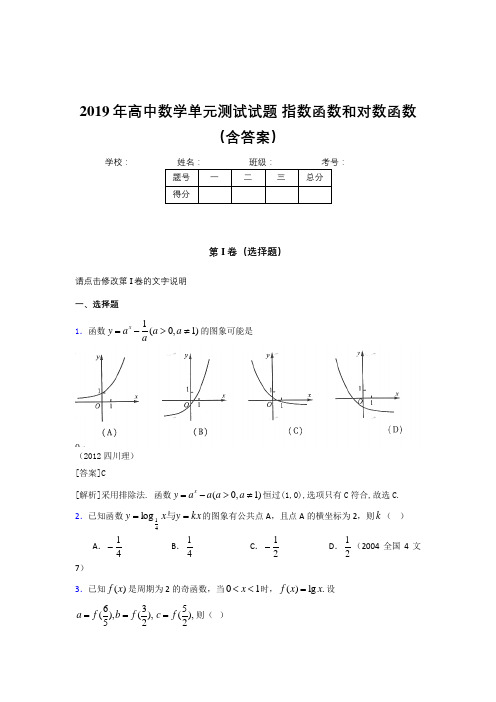
2019年高中数学单元测试试题 指数函数和对数函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题 1.函数1(0,1)xy a a a a=->≠的图象可能是(2012四川理) [答案]C[解析]采用排除法. 函数(0,1)xy a a a a =->≠恒过(1,0),选项只有C 符合,故选C. 2.已知函数kx y x y ==与41log 的图象有公共点A ,且点A 的横坐标为2,则k ( )A .41-B .41 C .21-D .21(2004全国4文7)3.已知()f x 是周期为2的奇函数,当01x <<时,()lg .f x x =设63(),(),52a f b f ==5(),2c f =则( )(A )a b c << (B )b a c << (C )c b a << (D )c a b <<(2006福建文12)4.函数()y f x =的图像与函数2()log (0)g x x x =>的图像关于原点对称,则()f x 的表达式为(D)(A )21()(0)log f x x x=> (B )21()(0)log ()f x x x =<- (C )2()log (0)f x x x =-> (D )2()log ()(0)f x x x =--<(2006全国2理) 解析(x,y)关于原点的对称点为(-x,-y),所以2()l o g (0)g x x x =>⇒2()lo g ()(0)f x x x =--< 故选D 5.定义运算{()()a ab a b b a b ≤⊕=>,则函数()12xf x =⊕的图像是 [答]( )6.设1a >,函数()log a f x x =在区间[,2]a a 上的最大值与最小值之差为12,则a =( )(07全国Ⅰ) AB .2 C.D .4 A7.对于函数①()()12lg +-=x x f ,②()()22-=x x f ,③()()2cos +=x x f .判断如下三个命题的真假:命题甲:()2+x f 是偶函数;命题乙:()()2,∞-在区间x f 上是减函数,在区间()+∞,2上是增函数;命题丙:()()x f x f -+2在()+∞∞-,上是增函数.能使命题甲、乙、丙均为真的所有函数的序号是()(07北京) A .①③ B .①② C . ③D . ② D第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题8. 函数()ln(1)f x x =+的定义域为 ▲ .9.设方程=+-∈=+k k k x x x x 则整数若的根为),21,21(,4200___ .10.已知函数)1(log )(+=x x f a 的定义域和值域都是[0,1],则a 的值是11.用根式的形式表示下列各式(0a >)51a ,43a ,32-a12.比较大小5.05.015,23________________.13.若32n=,则33log 8log 36-=_________________.(用含n 的式子表示) 14.33335555(0.96),0.95,0.95,0.96---由小到大的顺序是____________________15.用二分法求方程x 3-2x -5=0在区间[2,3]上的近似解,取区间中点x 0=2.5, 那么下一个有解区间为 ▲ .16.幂函数的图象过点(4,2),则它的单调递增区间是 ▲ .17. 关于x 的方程ln 1x e x =的实根个数是 ▲ .18. 已知a R +∈,函数2()21f x ax ax =++,若()0f m <,比较大小:(1)f m + ▲ 1.(用“<”或“=”或 “>”连接) .19.若方程1n 2100x x +-=的解为0x ,则不 小于0x 的最小整数是 ★ .520.设a c b a 则,1.1,9.0,9.0312131===、b 、c 按从小到大的排列的顺序为 .21.已知函数2()cos f x x x =-,对于ππ22⎡⎤-⎢⎥⎣⎦,上的任意12x x ,,有如下条件:①12x x >;②2212x x >; ③12x x >.其中能使12()()f x f x >恒成立的条件序号是② .(北京卷13)22. 幂函数()x f 的图象过点()2,2,则()41-f 的值______________.23.方程3log 3=+x x 的解在区间)1,(+n n 内,*n N ∈,则n = ▲ . 24.函数2()23x f x x -=+-的零点个数是 ▲ . 2 25. 函数()lg 2f x x x =+-的零点个数是 ▲ .26.已知函数()21,x f x a b c =-<<,且()()()f a f c f b >>,则下列结论中,必成立的是 (1)0,0,0a b c <<< (2) 0,0,0a b c <≥> (3) 22a c -< (4) 222a c +<关键字:指数函数;含绝对值;数形结合;比较大小27.若全集R U =,函数13-=xy 的值域为集合A ,则=A C U ____________28.函数]3,1[,24)(2-∈+-=x x x x f 的值域是 29.函数12+-=x x y 的值域为30.有一座灯塔A ,观察到海上有两艘轮船,甲船位于灯塔A 的正东方向的D 处向北航行;乙船位于灯塔A 的北偏西30方向的B 处向北偏东60方向航行,甲船行驶5海里,乙船行驶8海里后在点C 处相遇,则点C 处距灯塔A 为___________海里.31.方程2210ax x --=在(0,1)恰有一个零点,则实数a 的取值范围是________; 32.函数2289,[0,3]y x x x =---∈的值域是_______33. 已知函数2()45f x x mx =-+在(,2)-∞上是减函数,则实数m 的取值范围_________.34.求值:00sin 40(tan10= ▲ .35. 已知函数22()log (2)f x x x a =-+的值域为[0,)+∞,则正实数a 等于 236.已知函数f (x )=(13)x -log 2x ,0<a <b <c ,f (a )f (b )f (c )<0,实数d 是函数f (x )的一个零点.给出下列四个判断:①d <a ;②d >b ;③d <c ;④d >c . 其中可能成立的个数为 ________ .三、解答题 37.1.如图,开发商欲对边长为1km 的正方形ABCD 地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路EF (点E F 、分别在BC CD 、上),根据规划要求ECF ∆的周长为2km .(1)设,BAE DAF αβ∠=∠=,试求βα+的大小; (2)欲使EAF ∆的面积最小,试确定点E F 、的位置.2012年春学期期中考试高一数学试题答案一、填空题二、解答题17. (1)1()2cos 2sin 262f x x x x πωωω⎛⎫=+=++ ⎪⎝⎭ --------------------5分R x ∈ ,∴)(x f 的值域为[1,1]- --------------7分(2)∵)(x f 的最小正周期为2π,∴222ππω=,即2ω= ∴)64sin(2)(π+=x x f ∵]2,0[π∈x ,∴]613,6[64πππ∈+x∵)(x f 递减,∴]23,2[64πππ∈+x 由23642πππ≤+≤x ,得到312ππ≤≤x ,∴)(x f 单调递减区间为]3,12[ππ -------15分⑶设11(,)M x y ,22(,)P x y ,则11(,)N x y -,22112x y +=,22222x y +=, 直线MP 与x 轴交点122121(,0)x y x y y y --,122121x y x y m y y -=-, 直线NP 与x 轴交点122121(,0)x y x y y y ++,122121x y x y n y y +=+, …………………14分 222222221221122112211221222221212121(2)(2)2x y x y x y x y x y x y y y y y mn y y y y y y y y -+----====-+--, 故mn 为定值2. …………………16分20. (1)设,BAE DAF αβ∠=∠=,,(01,01)CE x CF y x y ==<≤<≤,则tan 1,tan 1x y αβ=-=-,由已知得:2x y ++=,即2()2x y xy +-=tan tan 112()2()tan()11tan tan 1(1)(1)[22()]x y x y x y x y x y xy x y x y αβαβαβ+-+--+-++=====----+-++-+0,24ππαβαβ<+<∴+=,即.4EAF π∠=(2)由(1)知,1111sin 2cos cos cos cos AEF S AE AF EAF AE AF αβαβ∆=⋅∠=⋅=⋅=211112cos (sin cos )sin 22cos sin 2cos 21cos cos()4πααααααααα===++++- =1)14πα++.38.烟囱向其周围地区散落烟尘而污染环境。
精选单元测试《指数函数和对数函数》完整版考核题(含答案)

2019年高中数学单元测试试题 指数函数和对数函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题1.为了得到函数xy )31(3⨯=的图象,可以把函数xy )31(=的图象 ( )A .向左平移3个单位长度B .向右平移3个单位长度C .向左平移1个单位长度D .向右平移1个单位长度(2004全国4文5)2.已知y =log a (2-ax )在[0,1]上是x 的减函数,则a 的取值范围是( ) A .(0,1) B .(1,2)C .(0,2)D .[2,+∞)(1995全国理11) 3.函数1(0,1)x y a a a a=->≠的图象可能是( )4.已知函数f(x)=ax 2+2ax+4(0<a<3),若x 1<x 2,x 1+x 2=1-a,则( )A .f(x 1)<f(x 2)B .f(x 1)=f(x 2)C .f(x 1)>f(x 2)D .f(x 1)与f(x 2)的大小不能确定(2006陕西)5.函数()(0)f x ax bx c a =++≠的图象关于直线2bx a=-对称。
据此可推测,对任意的非零实数a ,b ,c ,m ,n ,p ,关于x 的方程[]2()()0m f x nf x p ++=的解集都不可能是 A. {}1,2 B {}1,4 C {}1,2,3,4 D {}1,4,16,64 6.已知0,a a >≠,则laa 等于( ) A .2 B .12C .D .与a 的具体数值有关 7.若log a c =,则,,a b c 之间满足 ( ) A .7c b a = B .7c b a = C .7c b a = D .7a b c =8.m,n 是正整数,则11lim 1--→n m x x x =( )A,0 B,1 C,n m D,11--n m (文谱一模)(理)方法一:原式=)1......)(1()1......)(1(lim 21211+++-+++-----→n n m m x x x x x x x =nm,选C方法二:原式=11lim11lim11----→→x x x x nx m x =1/1/|)(|)(==x n x m x x =n m ,选C第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题9.若3()3log 2x f x x =++,则1(30)f -= .10.已知关于x 的函数158)532()(--+-+-=b a x b a x f .如果[]1,1-∈x 时,其图象恒在x 轴的上方,则ab 的取值范围是 ),3()23,(+∞-∞ _11.函数f (x )=(12)2x x -的值域是 ★ .12.函数212log (25)y x x =-+的值域是 ▲13.若118m m-+=,则1122__________m m-+= 1122__________m m--=14.形如________________的函数叫做幂函数,其中________是自变量,________是常数,如2321,2,,,xy y x y x y x y x x =====,其中是幂函数的有___________ ____. 15.函数2()ln(1)f x x x=+-的零点所在的区间是(n ,n +1),则正整数n =______.16.函数12ln y x x=+的单调减区间为 . 17.令113221log ,2,23a b c ===,则,,a b c 的大小关系为18.已知11223a a -+=,求下列 (1)1a a -+ (2) 22a a -+的值。
新版精选《指数函数和对数函数》单元测试考核题完整版(含答案)
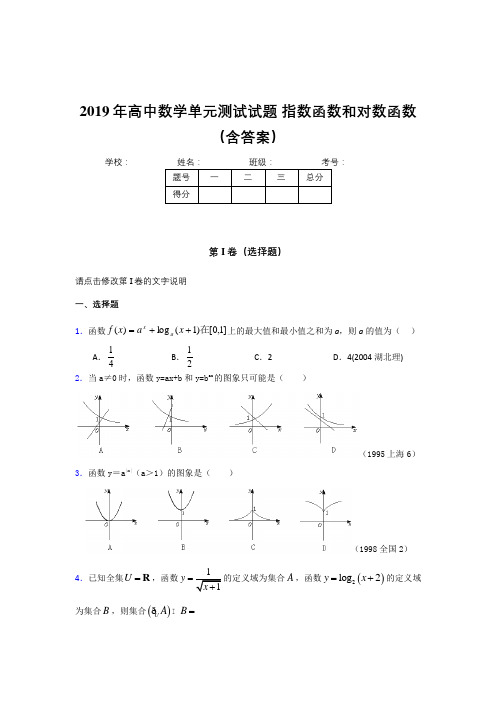
2019年高中数学单元测试试题 指数函数和对数函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题1.函数]1,0[)1(log )(在++=x a x f a x上的最大值和最小值之和为a ,则a 的值为( )A .41 B .21 C .2 D .4(2004湖北理)2.当a ≠0时,函数y=ax+b 和y=b ax的图象只可能是( )(1995上海6)3.函数y =a |x|(a >1)的图象是( )(1998全国2)4.已知全集U =R ,函数y =的定义域为集合A ,函数()2log 2y x =+的定义域为集合B ,则集合()U AB =ðA .()2,1--B .(]2,1--C .(),2-∞-D .()1,-+∞5.若()f x =,则()f x 的定义域为A. (,)1-02B. (,]1-02C. (,)1-+∞2D.(,)0+∞6.设,,a b c 是正数,且346abc==,则----------------------------( ) A.111c a b =+ B.221c a b =+ C.122c a b =+ D.212c a b=+ 7.若函数()log (4)xa f x a =-在区间[1,2]-上单调递减,则实数a 的取值范围是----( )A.2a >B.12a <<C.114a <<或12a << D.以上都不对 8.设函数f (x )=1-x 2+log 12(x -1),则下列说法正确的是 ( )(A )f (x )是增函数,没有最大值,有最小值 (B )f (x )是增函数,没有最大值、最小值 (C )f (x )是减函数,有最大值,没有最小值 (D )f (x )是减函数,没有最大值、最小值第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题9.令113221log ,2,23a b c ===,则,,a b c 的大小关系为10.已知函数b a x a b x x f ++--+=)2()(22是偶函数,则此函数图象与y 轴交点的纵坐标的最大值是 .11.设函数()[)1,,1f x n x n n =-∈+,n N ∈,函数()2log g x x =,则方程()()f x g x =中实数根的个数是关键字:根的个数;数形结合;对数函数12.对于定义在实数集R 上的函数f (x ). 如果存在实数x 0使f (x 0)= x 0,则称x 0叫做函数f (x )的一个“不动点”.若函数f (x )= x 2+ax +1不存在“不动点”,则a 的取值范围是13.已知函数11)(22+-=x x x f ,则)41()31()21()5()4()3()2(f f f f f f f ++++++=14.方程)2(log )12(log 255-=+x x 的解集为15.5lg 20lg )2(lg 2⨯+=16.不等式2log (23)1a x x -+≤-在x R ∈时恒成立,则实数a 的取值范围是__________17.函数12()2x f x x -⎧=⎨-+⎩(0)(0)x x ≤>,若()1f a <,则a 的取值范围是18.若01,1a b <<<-,则函数()xf x a b =+的图象不经过第 象限. 19.若118m m-+=,则1122__________m m-+= 1122__________m m--=20.函数f (x )=(12)2x x -的值域是 ★ .21.函数()2log 3y x =+的定义域为 . 22. 函数28ln y x x =-的单调递减区间为 ▲ .23.如图,有一矩形地块ABCD ,其相邻边长为20m 和50m ,现要在它的短边与长边上各取一点P 与Q ,用周长为80m 的篱笆围出一块直角三角形的花园,则围出部分的最大面积为__________2m .Q PD CBA24.函数lg(3)y x =-的定义域为__________________________ 25.函数))2,0((,cos sin π∈=x x x y 的单调减区间是26.已知函数()35xf x x =+-的零点[]0,x a b ∈,且1b a -=,a ,b N *∈,则a b += .27.已知函数b x a x f x+-=)(的零点))(1,(0Z k k k x ∈+∈,其中常数a ,b 满足493,23==ba ,则k= ▲ . 28.已知幂函数...)(x f y =的图象过点1(2,)4,则1()3f = ____ .29.幂函数()y f x =的图象经过点1(2,)8--,则满足()f x =27的x 的值是 .30.某丹顶鹤自然保护区成立于1984年,第一年(即1984年)在此越冬的丹顶鹤仅有200只,由于保护区环境的改善,在此越冬的丹顶鹤只数y 只与时间(第x 年)可近似的满足关系式2log (1)y a x =+ (a 为常数),则到2014年,在此越冬的丹顶鹤的只数约为 .31.稳定房价是我国今年实施宏观调控的重点,国家最近出台的一系列政策已对各地的房地产市场产生了影响,温州市某房地产介绍所对本市一楼群在今年的房价作了统计与预测:发现每个季度的平均单价y (每平方面积的价格,单位为元)与第x 季度之间近似满足:500sin()9500(0)y ωx ω=+ϕ+>,已知第一、二季度平均单价如右表所示:则此楼群在第三季度的平均单价大约是 元.32. 如果一辆汽车每天行驶的路程比原来多19 km ,那么在8天内它的行程就超过2200 km ,如果它每天行驶的路程比原来少12 km ,那么它行驶同样的路程得花9天多的时间,这辆汽车原来每天行驶的路程(km)范围是 .33.设有半径为3km 的圆形村落,A 、B 两人同时从村落中心出发,B 向北直行,A 先向东直行,出村后不久,改变前进方向,沿着与村落周界相切的直线前进,后来恰与B 相遇.设A 、B 两人速度一定,其速度比为3:1,问两人在何处相遇?34.两灯塔A,B 与海洋观察站C 的距离都等于a (km), 灯塔A 在C 北偏东30°,B 在C 南偏东60°,则A,B 之间相距_____________35. 设{}2,1,0,1,2α∈--,则使幂函数y x α=的定义域为R 且为偶函数的α的值为 ▲三、解答题36.用水清洗一堆蔬菜上残留的农药,对用一定量的水清洗一次的效果作如下假定:用1个单位量的水可洗掉蔬菜上残留农药用量的21,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用x 单位量的水清洗一次以后,蔬菜上残留的农药与本次清洗前残留有农药量之比为函数f (x ).(1)试规定f (0)的值,并解释其实际意义;(2)试根据假定写出函数f (x )应该满足的条件和具有的性质;(3)设f (x )=211x +,现有a (a >0)单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次.试问用哪种方案清洗后蔬菜上的农药量比较少?说明理由.37.某市居民自来水收费标准如下:每户每月用水量不超过4吨时,按每吨1.8元收费;当每户每月用水量超过4吨时,其中4吨按每吨为1.8元收费,超过4吨的部分按每吨3.00元收费。
精选新版《指数函数和对数函数》单元测试完整版考核题(含参考答案)
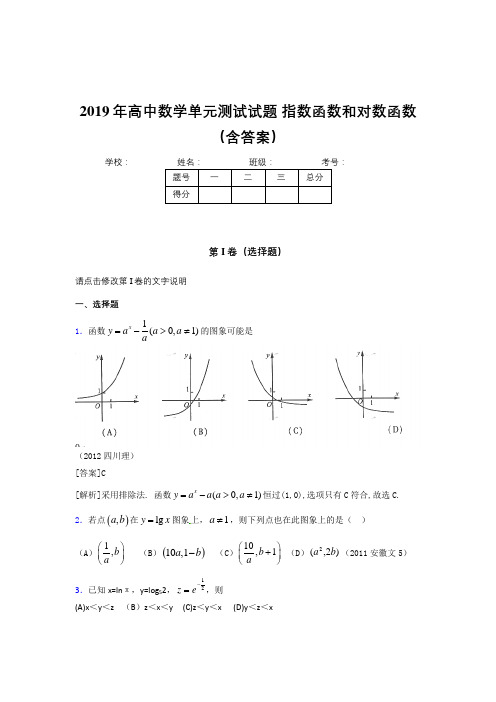
2019年高中数学单元测试试题 指数函数和对数函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题 1.函数1(0,1)xy a a a a=->≠的图象可能是(2012四川理) [答案]C[解析]采用排除法. 函数(0,1)xy a a a a =->≠恒过(1,0),选项只有C 符合,故选C. 2.若点(),a b 在lg y x =图象上,1a ≠,则下列点也在此图象上的是( )(A )1,b a ⎛⎫⎪⎝⎭(B )()10,1a b - (C )10,1b a ⎛⎫+ ⎪⎝⎭ (D ))2,(2b a (2011安徽文5)3.已知x=ln π,y=log 52,21-=ez ,则(A)x <y <z (B )z <x <y (C)z <y <x (D)y <z <x4.定义在R 上的函数f(x)满足f(x)= ⎩⎨⎧>---≤-0),2()1(0),1(log 2x x f x f x x ,则f (2009)的值为( )A.-1B. 0C.1D. 2 (2009山东卷理)【解析】:由已知得2(1)log 21f -==,(0)0f =,(1)(0)(1)1f f f =--=-,(2)(1)(0)1f f f =-=-,(3)(2)(1)1(1)0f f f =-=---=,(4)(3)(2)0(1)1f f f =-=--=,(5)(4)(3)1f f f =-=,(6)(5)(4)0f f f =-=,所以函数f(x)的值以6为周期重复性出现.,所以f (2009)= f (5)=1,故选C.第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题5.已知βαlg ,lg 是方程05lg 2lg 2)5lg 4(lg 2=+++x x 的两根,则αβ⋅=6.已知定义域为D 的函数()f x ,对任意x D ∈,存在正数K ,都有()f x K ≤成立,则称函数()f x 是D 上的“有界函数”。
指数函数和对数函数单元测试题及答案
精品资料欢迎下载指数函数和对数函数单元测试题一选择题1 如果,那么a、 b 间的关系是【】A B C D2已知,则函数的图象必定不经过【】A 第一象限 B第二象限 C 第三象限 D 第四象限3与函数 y =x 有相同图象的一个函数是【】A B,且C D,且4已知函数的反函数为,则的解集是【】A B C D5已知函数在上是 x 的减函数,则 a 的取值范围是【】A B C D6已知函数的值域是,则它的定义域是【】A B C D7已知函数在区间是减函数,则实数 a 的取值范围是【】A B C D8已知,则方程的实数根的个数是【】A 1B 2C 3D 49函数的定义域为 E,函数的定义域为 F,则【】A B C D10 有下列命题:(1)若,则函数的图象关于 y 轴对称;( 2 )若,则函数的图象关于原点对称;( 3)函数与的图象关于x 轴对称;( 4)函数与函数的图象关于直线对称。
其中真命题是【】A ( 1)( 2)B(1)(2)(3) C ( 1)( 3)( 4) D (1)( 2)( 3)( 4)二填空题11函数的反函数是______。
12的定义域是______。
13 函数的单调减区间是________。
14 函数的值域为R,则实数 a 的取值范围是 __________.三解答题1求下列函数的定义域和值域(1)(2)2求下列函数的单调区间(1)(2)3已知函数(1)求的定义域;(2)讨论的单调性;(3)解不等式。
4已知函数(1)证明:在上为增函数;(2)证明:方程=0没有负数根。
参考答案一选择题BADBC BCBDD二填空题 11121314或三解答题1求下列函数的定义域和值域(1)(2)定义域定义域值域值域且2求下列函数的单调区间(1)(2)减区间,增区间减区间,3已知函数(1)求的定义域;( 2)讨论的单调性;( 3)解不等式。
解(1),又,所以,所以定义域。
(2)在上单调增。
(3),,即,所以,所以解集2已知函数(1)证明:在上为增函数;(2)证明:方程=0没有负数根。
精选《指数函数和对数函数》单元测试完整版考核题(含参考答案)
2019年高中数学单元测试试题 指数函数和对数函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题1.为了得到函数xy )31(3⨯=的图象,可以把函数xy )31(=的图象 ( )A .向左平移3个单位长度B .向右平移3个单位长度C .向左平移1个单位长度D .向右平移1个单位长度(2004全国4文5)2.已知()()()2f x x a x b =---,并且βα,是方程()0f x =的两根,实数,,,a b αβ 的大小关系可能是---------------------------------------------------------------------------------------------( ) (A )α<a <b <β (B )a <α<β<b (C )a <α<b <β (D )α<a <β<b3.设()f x 是连续的偶函数,且当x>0时()f x 是单调函数,则满足3()4x f x f x +⎛⎫= ⎪+⎝⎭的所有x 之和为( ) A .3- B .3C .8-D .8(2008辽宁理12)4.设奇函数()f x 在(0)+∞,上为增函数,且(1)0f =,则不等式()()0f x f x x--<的解集为( )A .(10)(1)-+∞,,B .(1)(01)-∞-,,C .(1)(1)-∞-+∞,,D .(10)(01)-,,(2008全国1理)D .由奇函数()f x 可知()()2()0f x f x f x x x--=<,而(1)0f =,则(1)(1)f f -=-=,当0x >时,()0(1)f x f <=;当0x <时,()0(1)f x f >=-,又()f x 在(0)+∞,上为增函数,则奇函数()f x 在(,0)-∞上为增函数,01,10x x <<-<<或第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题5.若12x -≤<,则函数11()2x y -=的值域为 ;6.直角坐标系中横坐标、纵坐标均为整数的点称为格点,如果函数f (x )的图象恰好通过k 个格点,则称函数f (x )为k 阶格点函数.下列函数:①x x f sin )(=;②3)1()(2+-=x x f π;③xx f )31()(=;④.log )(6.0x x f =其中是一阶格点函数的有(填上所有满足题意的序号).7.方程22xx =有 个实数根. 8.433333391624337+--的值为 9.函数212log (253)y x x =-++的单调递增区间是 .10.45sin()33cosππ-+= . 11.若函数)1,0)((log ≠>+=a a b x y a 的图象过两点)0,1(-和)1,0(,则a =_____,b =_____.12.计算:22333948(log log )(log log )+⨯+= . 13.函数1()()1,2x f x x =+∈[1,1]的值域是 ▲ 。
精选《指数函数和对数函数》单元测试完整考试题(含答案)
2019年高中数学单元测试试题 指数函数和对数函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题 1.已知(,)2a ππ∈,1tan()47a π+=则sin cos αα+=_____________. 2.若1x 满足2x+2x=5, 2x 满足2x+22log (x -1)=5, 1x +2x = (A )52 (B)3 (C) 72(D)4(2009辽宁卷理) 【解析】由题意11225x x += ① 22222log (1)5x x +-= ② 所以11252x x =-,121log (52)x x =-即21212log (52)x x =-令2x 1=7-2t,代入上式得7-2t =2log 2(2t -2)=2+2log 2(t -1) ∴5-2t =2log 2(t -1)与②式比较得t =x 2 于是2x 1=7-2x 23.2log 的值为【 D 】A . C .12- D . 12(2009湖南卷文)4.设3.02131)21(,3log ,2log ===c b a ,则A a<b<cB a<c<bC b<c<aD b<a<c (2009天津卷文)5.若log 3log 30a b >>,那么,a b 间的关系是-----------------( ) A.01a b <<< B.1a b << C.01b a <<< D.1b a <<6. 设()833-+=x x f x,用二分法求方程()2,10833∈=-+x x x在内近似解的过程中得()()(),025.1,05.1,01<><f f f 则方程的根落在区间 A A . (1.25,1.5)B . (1,1.25)C .(1.5,2)D .不能确定7.定义在R 上的函数)(x f 既是奇函数,又是周期函数,T 是它的一个正周期.若将方程0)(=x f 在闭区间][T T ,-上的根的个数记为n ,则n 可能为A .0B .1C .3D .5(07安徽)D .第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题8.函数()1f x =-︱x ︱的定义域为 .9.函数x a y =在]1,0[上的最大值与最小值的和为3,求a 值.10.已知sin()3cos(2)απαπ-=--,求3332sin ()5cos (3)33sin ()sin ()cos(2)2πααππαπααπ-+--+--的值11.函数)0(121)(≠+-=x a x f x是奇函数,则a = . 12.已知2,3=,4,...,201121n m+= .13.三个数0.560.56,0.5,log 6由小到大的顺序为 .3.5.065.065.06log <<14.已知lg a 和lg b 是关于x 的方程20x x m -+=的两根,而关于x 的方程2(lg )(1lg )0x a x a --+=有两个相等的实数根,求实数,a b 和m 的值.【例2】1,1000,6100a b m ===-15.设⎪⎩⎪⎨⎧≥-<=-2),1(log 2,2)(231x x x e x f x 则))2((f f 的值为 16.设函数⎪⎩⎪⎨⎧-=-2112)(xx f x 00>≤x x ,若1)(0>x f ,则0x 的取值范围是________________ 17.若集合{|3,},{|41,}xxM y y x R N y y x R ==∈==-∈,则M N 是( )A.MB.NC.∅D.有限集18.函数()x f y =是R 上的奇函数,满足()()x f x f -=+33,当x ∈(0,3)时()x x f 2=,则当x ∈(6-,3-)时,()x f =19. 若曲线y =a |x |与直线y =x +a (a >0)有两个公共点,则a 的取值范围是 (1,+∞) 20.函数2lg(421)y x x =--的定义域是 ★ . (,3)-∞-∪(7,)+∞ 21.已知函数)(x f 是定义在R 上的奇函数,当xx f x --=>21)(,0时,则不等式21)(-<x f 的解集是 )1,(--∞ .22.为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文a ,b ,c ,d 对应密文a +2b ,2b +c ,2c +3d ,4d .例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为 (填上对应的数字).23.已知函数2()cos f x x x =-,对于ππ22⎡⎤-⎢⎥⎣⎦,上的任意12x x ,,有如下条件:①12x x >;②2212x x >; ③12x x >.其中能使12()()f x f x >恒成立的条件序号是② .(北京卷13)24.把长为12厘米的细铁丝截成两段,各自围成一个正三角形,那么这两个正三角形面积之和的最小值是___________ 25.已知函数20134321)(2013432x x x x x x f ++-+-+= ,20134321)(2013432x x x x x x g --+-+-= , 设()(3)(3)=+⋅-F x f x g x ,且函数()F x 的零点均在区间[,](,,)<∈a b a b a b Z 内,则-b a 的最小值为 .26.两灯塔A,B 与海洋观察站C 的距离都等于a (km), 灯塔A 在C 北偏东30°,B 在C 南偏东60°,则A,B 之间相距_____________27.函数2()2,[1,3]f x x x x =-+∈-的值域为 ▲ . 28.已知偶函数()f x 在(0,)π上是增函数,且2(),(),(2)32f f f ππ---的大小关系为________(用“< ”连接)29.已知方程240x x a --=有四个根,则实数a 的取值范围是 .30.已知幂函数()22657m y m m x-=-+在区间()0,+∞上单调递增,则实数m 的值为A .3B .2C .2或3D .2-或3-31.已知1()31xf x a =--是奇函数, 则()f x 的值域为 1122-∞-∞(,)(,+) . 32.3)72.0(-与3)75.0(-的大小关系为_____________33.已知函数)1(log 2-=ax y 在)2,1(单调递增,则a 的取值范围为. 34.函数x y a log =和)1,0(log 1≠>=a a x y a的图象关于 对称.35.设a c b a 则,1.1,9.0,9.0312131===、b 、c 按从小到大的排列的顺序为 .36.设{}12,1,,1,2,32α∈--,则使y x =α为奇函数且在(0,)+∞上单调递减的α值为 ▲ .37.已知定义在R 上的奇函数)(x f ,满足(4)()f x f x -=-,且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间[]8,8-上有四个不同的根1234,,,x x x x ,则1234_________.x x x x +++=【解析】:因为定义在R 上的奇函数,满足(4)()f x f x -=-,所以(4)()f x f x -=-,所以, 由)(x f 为奇函数,所以函数图象关于直线2x =对称且(0)0f =,由(4)()f x f x -=-知(8)()f x f x -=,所以函数是以8为周期的周期函数,又因为)(x f 在区间[0,2]上是增函数,所以)(x f 在区间[-2,0]上也是增函数.如图所示,那么方程f(x)=m(m>0)在区间[]8,8-上有四个不同的根1234,,,x x x x ,不妨设1234x x x x <<<由对称性知1212x x +=-344x x +=所以12341248x x x x +++=-+=-38.计算:(151515log 5log 45log ⋅+39.若{}21,,x x ∈则x =40.方程22xx =有 个实数根. 41.计算lg = ▲ .42.若函数||3([,])x y x a b =∈的值域[1,9],则222a b a +-的取值范围是_________三、解答题43.某工厂生产某种产品,已知该产品的月生产量x (吨)与每吨产品的价格p (元/吨)之间的关系式为:21242005p x =-,且生产x 吨的成本为50000200R x =+(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入─成本)44.某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为)10(≥x x 层,则每平方米的平均建筑费用为x 48560+(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=购地总费用建筑总面积)45.某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.若每辆车的月租金每增加50元,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.(1)当每辆车的月租金定为3600元时,能租出多少辆车?(2)当每辆车的月租金定为多少元时, 租赁公司的月收益最大,最大月收益是多少?46.如图,两个圆形飞轮通过皮带传动,大飞轮1O 的半径为r 2(r 为常数),小飞轮2O 的半径为r ,r O O 421=.在大飞轮的边缘上有两个点A ,B ,满足31π=∠A BO ,在小飞轮的边缘上有点C .设大飞轮逆时针旋转一圈,传动开始时,点B ,C 在水平直线21O O 上. (1)求点A 到达最高点时A ,C 间的距离; (2)求点B ,C 在传动过程中高度差的最大值.47.若函数)(x f y =,如果存在给定的实数对),(b a ,使得b x a f x a f =-+)()(恒成立,则称)(x f y =为“Ω函数”.1.判断下列函数,是否为“Ω函数”,并说明理由: ① 3)(x x f = ② xx f 2)(=2.已知函数x x f tan )(=是一个“Ω函数”,求出所有的有序实数对),(b a (本题满分14分)本题共有2个小题,第1小题满分6分,第二小题满分8分.48.已知32a=,用a 表示33log 4log 6-49.关于x 的方程2a·3-1-x -9-|x -1|-2a -1=0有实数解,求实数a 取值范围。
精选单元测试《指数函数和对数函数》考核题完整版(含参考答案)
2019年高中数学单元测试试题 指数函数和对数函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题1.已知0log log ,10<<<<n m a a a ,则( )A(A)1<n <m (B) 1<m <n (C)m <n <1 (D) n <m <1(2006浙江理)2.已知x 是函数f(x)=2x + 11x-的一个零点.若1x ∈(1,0x ),2x ∈(0x ,+∞),则( )(A )f(1x )<0,f(2x )<0 (B )f(1x )<0,f(2x )>0(C )f(1x )>0,f(2x )<0 (D )f(1x )>0,f(2x )>0(2010浙江文数)(9)3.设232555322555a b c ===(),(),(),则a ,b ,c 的大小关系是( )A .a >c >bB .a >b >cC .c >a >bD .b >c >a (2010安徽文7)4.若正实数,a b 满足b aa b =,且1a <,则有( )(A )a b > (B )a b < (C )a b = (D )不能确定、a b 的大小关系 5.根据表格中的数据,可以断定函数2)(--=x e x f x的一个零点所在的区间是A (—1,0)B (0,1)C (1,2)D (2,3)( )6.设函数f(x)是R 上以5为周期的可导偶函数,则曲线y =f(x)在x =5处的切线的斜率为(07江西)A .-51B .0C .51D .5 B .第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题7.若2lg (x -2y )=lg x +lg y ,则xy的值为 8.定义:区间1212[,]()x x x x <的长度为21x x -,已知函数0.5|log (2)|y x =+定义域为[,]a b ,值域为[0,2],则区间[,]a b 的长度的最大值为 ▲9.求下列函数的定义域:(1))16(log 2)1(x y x -=+; (2))132(log )1_3(-+=x x y x .10.函数3sin ()44y x x ππ=-≤≤的值域是11.3243)1()25(-+--x x 有意义,则x 的取值范围是12.市场营销人员对过去几年某商品的价格及销售数量的关系作数据分析,发现有如下规律:该商品的价格每上涨%(0)x x >,销售数量就减少%kx (其中k 为正常数).目前,该商品定价为a 元,统计其销售数量为b 个,⑴当12k =时,该商品的价格上涨多少,就能使销售的总金额达到最大? ⑵在适当的涨价过程中,求使销售总金额不断增加的k 的取值范围. 13.⑴50%;⑵(0,1)13.已知函数11)(22+-=x x x f ,则)41()31()21()5()4()3()2(f f f f f f f ++++++=14.根据表格中的数据,可以判定方程20x e x --=的一个零点所在的区间为))(1,(N k k k ∈+,则k 的值为 ;15.方程330x x --=的实数解落在长度为1的区间是 16.函数212log (25)y x x =-+的值域是 ▲17.给出幂函数①x x f =)(;②2)(x x f =;③3)(x x f =;④x x f =)(;⑤xx f 1)(=.其中满足条件f 12()2x x +>12()()2f x f x +(021>>x x )的函数的序号是 18.已知函数2,0()2,x x f x x x +⎧=⎨-+>≤⎩,则不等式2()f x x ≥的解集是19.函数y =的值域是20.设函数21(0)()1(0)2x x f x x x -⎧-≤⎪=⎨>⎪⎩,若()1f x >,则x 的取值范围是 .21.若函数213ln()1xy x x+=+-的最大值与最小值分别为M,m ,则M+m= 622.为了预防流感,某学校对教室用药熏消毒法进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y (毫克)与时间t (小时)成正比;药物释放完毕后,y 与t 的函数关系式为at y -⎪⎭⎫ ⎝⎛=161(a 为常数),如图所示,根据图中提供的信息,回答下列问题:(Ⅰ)从药物释放开始,每立方米空气中的含药量y (毫克)与时间t (小时)之间的函数关系式为 .(Ⅱ)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那从药物释放开始,至少需要经过 小时后,学生才能回到教室. (07湖北)⎪⎩⎪⎨⎧>⎪⎭⎫⎝⎛≤≤=-1.0,1611.00101.0t t t y t ,6.023.已知A C A S 则},2,4{},4,3,2{S ===24.函数24)y x =≤≤的值域是_______________(A )[]2,2- (B )[]1,2 (C )[]0,2 (D)⎡⎣25.已知幂函数()f x x α=的图像经过点,则(4)f 的值为__________.26.化简83log 9log 32⨯为_________. 27.函数3222+-=x x y 的单调增区间为 ____________.28.已知集合{1,2},{,},aA B a b ==若1{}2A B =,则A B 为___▲__.29.函数221xx y =+的值域为 .30.已知0.26log 0.2,6a b ==,60.2c =,则,,a b c 的大小关系是______.31.已知log 162x =,则x 等于 ( ) A .±4 B .4 C .256 D .232.已知函数y =a x +2-2(a >0,a ≠1)的图象恒过定点A ,则定点A 的坐标为 . 33.函数2223()(1)mm f x m m x --=--是幂函数,且在(0,)x ∈+∞上是减函数,则实数m = ▲。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
指数函数和对数函数
选择题
1. 下列函数中,值域是(0, +®)的函数是()
1
___ _____________ ____ I
A ・ y = 2"
B ・ y=yj2^—l
C ・ y=yj2x +1
D ・ y=(^)2 x
2. 某种细菌在培养过程中,每20分钟分裂一次(一个分裂为两个).经过3个小时,这种细
菌由1个可繁殖成()
A. 511 个
B. 512 个
C. 1 023 个
D. 1 024 个
3. 如果函数y=
(N —l )寸的定义域为(0, +8)那么d 的取值范围是( )
A. a>0 B- O VQV I
C- a>l D ・心 4•函数y=/(0svl )的图象是(
)
关系是
6. 函数y=a x 在[0,1]上的最大值与最小值的和为3,则Q 等于()
A.|
B. 2
C ・ 4
D.|
7. 在同一平面直角坐标系中,函数fix )=ax 与指数函数的图象可能是()
A • a>b>c
B• b>a>c C. b>c>a D. c>b>a
,则(I 小工的大小
2
5
5•设
=
&如果呃5>吨2>°,那么a 、b 间的关系是()
A 0<a <b<l g \<a<b Q 0<b<a<i D ' < b < a
9. 己知0 VQVl ,bV —l,则函数y = a x
+b 的图象必定不经过() A 第一象限 B 第二象限 C 第三象限
D 第四象限
10. 与函数y = x 有相同图象的一个函数是() A J =
B
y = ai0&aX (a>O f 且QH O ) c
y =
/x D y = i°g° Q "(d>o,且QHO ) 11・函数、 i
y y=|log2x|的图象 是
k V. d
(
L
J y
)
V. 0 1
X
0 A
1 X
B
「 0
A 1 X
D
12已知函数yiog“(2-祇)在(i ,D 上是x 的减函数,则a 的取值范围是(
A (0,2)
B (1,2)
C (I ,©
D t 2^)
13已知函数/(x ) = lo gl (2-log 2x )的值域是(一汽°),则它的定义域是()
2
A {x| x< 2)
B {^|0<x<2} c {x|0<x<4} p {x| 2< x< 4}
14已知函数/(
Q = log ().5("-处+ 3。
)在区间[2,+oo )是减函数,则实数a 的取值范围是
()
A (-汽4]
B [4,+°°)
C (74】
D f-4^l
1
15设3 =斤,贝ij ()
A. —2<x<—1
B. —3<x<—2
C. —1 <x<0 D ・ Ovxvl
16. 函数/(X )=览(* -3兀+ 2)的定义域为E ,函数g (兀)=lg (兀-1) +览(兀-2)的定义
域为F , 则()
A EcF 二 0
B E = F
C E J F D
E ^F
17. 有下列命题:(1)若/(一无)=/(兀),则函数歹=/(兀)的图彖关于y 轴对称;(2)
若 /(—兀)=一/(兀),则函数尸/(Q 的图象关于原点对称;⑶ 函数与了=-/(兀) 的图象关于x 轴对称;(4)函数歹=/(兀)与函数的图象关于直线对称。
其中 真命题是() (3) (4) D (1) (2) (3)
(4) >2b
> 2a
D . 2°
>2a
>2b
(-00,-1)
D. 3
二填空题
1. 指数函数y=j{x )的图象过点(一1, |),则,/[/(2)]= _ ・
2. 当炸[—1,1]时,函数yu )= 3“一2的值域为 ________ ・
3. 已知兀>0时,函数y=(a 2S )x 的值恒大于1,则实数d 的取值范围是 __________ ・
4. (09•江苏文)已知a=^2 I 函数/W=N ,若实数加,斤满足夬肋彳働),则m, n 的大小
关系为 ________ ■
1 1 -1
5•计算:(-)-,-4.(-2)-3+(-)°-9 2
= __________________
2 4 6. y = Jlog*(3兀_ 2)的定义域是 ________ » 7. 方程10创(2无一 1) = 1的解无= _____ o
三解答题
A (1) (2)
B (1) (2) (3)
C (1) 18. 已矢口 lo g L b<\ og 丄 a<\ og 丄 c,贝 ij()
2 2 2
A. 2h >2" >2C
B . 2" >2b >2
C c. 2, 19.
函数/(x) = -^= + lg(3x+l)的定义域是() A /1 — x
(-斗,+°°) (-g'l)
(-舅)
1.判断函数几0=右+扌的奇偶性.
[解析]・・・2"—1工0,・・」工0,定义域{x^R\x^O}
2.求下列函数的定义域和值域
(Dy = (y)x+2 (2)y = 5
3求下列函数的定义域和值域
(1)/(兀)=10逊(4兀-兀2)
2
* (3)y
2x4-1
(2) /(兀)=3荷
4求下列函数的单调区间 1 ..
(1) /(%)七)
(2)
2 吩
5 已知函数f(x) = log a(a x -1)(0 <a< l)
(1)求/(劝的定义域;(2)讨论/(x)的单调性。
3
1 I x
2 + x +2
6.已知疋+无2=3,求X"1+x + 3的值.
7.求函数y=3 —兀"+2x+3 的定义域、值域和单调区间.。
