2018年高一数学寒假作业(人教A版必修2)空间点、直线、平面之间的位置关系word版含答案 (2)
高中数学必修2(人教A版)第二章几点、直线、平面的位置关系2.1知识点总结含同步练习及答案

描述:高中数学必修2(人教A版)知识点总结含同步练习题及答案第二章 点、直线、平面之间的位置关系 2.1 空间点、直线、平面之间的位置关系一、学习任务理解空间点、线、面的位置关系,会用数学语言规范地表述空间点、线、面的位置关系;了解可以作为推理依据的公理和定理,能正确地判断空间线线、线面与面面的位置关系.二、知识清单平面的概念与基本性质 点、线、面的位置关系三、知识讲解1.平面的概念与基本性质平面的概念生活中的一些物体通常呈平面形,课桌面、黑板面、海面都给我们以平面的形象.几何里所说的平面就是从这样的一些物体中抽象出来的,但是几何中的平面是没有厚度、无限延展的.平面的画法我们常常把水平的平面画成一个平行四边形,用平行四边形表示平面,平行四边形的锐角通常画为 ,且横边长等于其邻边长的 倍.如果一个平面被另一个平面遮挡住,为了增强它的立体感,我们常把被遮挡的部分用虚线画出来.平面的表示为了表示平面,常把希腊字母 等等写在代表平面的平行四边形的一个角上,如平面 、平面 ;也可以用代表平面的平行四边形的四个顶点,或者相对的两个顶点的大写英文字母作为这个平面的名称,如图中的平面可以表示为平面 、平面 或者平面 .集合符号在立体几何中的应用以点作为元素,直线和平面都是由点构成的集合.几何中许多符号的规定都是源于将图形视为点集.例如:点 在平面 内,记作 ;点 不在平面 内,记作 .直线 在平面 内,记作 ;直线 不在平面 内,记作 ;直线 与 相交于点 ,记作 ;平面 与平面 相交于直线 ,记作 .平面的基本性质平面的基本性质是由三条公理描述的:公理1 如果一条直线上的两点在一个平面内,那么这条直线在此平面内.45∘2α,β,γαβABCD AC BD A αA ∈αA αA ∉αl αl ⊂αl αl ⊄αl m A l ∩m =A αβa α∩β=a A ∈l A ∈α例题:符号语言:,,且 ,.公理2 过不在一条直线上的三点,有且只有一个平面.推论1 经过一条直线和直线外一点,有且只有一个平面.推论2 经过两条相交直线,有且只有一个平面.推论3 经过两条平行直线,有且只有一个平面.公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.符号语言:,且 ,且 .空间位置关系与几何量的基础平行公理 平行于同一条直线的两条直线互相平行.等角定理 空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.A∈l B∈l A∈αB∈α⇒l⊂αP∈αP∈β⇒α∩β=l P∈l用符号语言表示下列语句.(1)点 在平面 外,点 在平面 内,直线 经过点 ,;(2) 与 交于 , 与 交于 .解:(1),,,.(2),.AαBαl A B平面ABD平面BCD BD平面ABC平面ADC ACa∉αB∈αA∈l B∈l平面ABD∩平面BCD=BD平面ABC∩平面ADC=AC如图所示,在四面体 中,、、、 分别是 、、、 上的点,且 ,求证 ,, 三点共线.ABCD E F G H AB AD BC CDEF∩GH=PB D P2.点、线、面的位置关系证明:因为 ,,所以 ,同理,,又,所以 ,,而 ,所以 ,即 ,, 三点共线.E ∈ABF ∈AD EF ⊂平面 ABD GH ⊂平面 BCD EF ∩GH =P P ∈平面 ABD P ∈平面 BCD 平面 ABD ∩平面 BCD =BD P ∈直线BD B D P 已知:如图,,,.求证:直线 ,, 在同一平面内.证法一:(同一法)因为 ,所以 和 确定一个平面 . 因为 ,所以 .又因为 ,所以 .同理可证 .又 ,,所以 .因此,直线 ,, 在同一个平面内.证法二:(重合法)因为 ,所以 , 确定一个平面 .因为 ,所以 , 确定一个平面 .又因为 ,,所以 .又 ,,所以 .同理可证得 ,,,.所以不共线的三个点 ,, 在平面 内,又在平面 内.所以平面 和平面 重合,即直线 ,, 在同一平面内.∩=A l 1l 2∩=B l 2l 3∩=C l 1l 3l 1l 2l 3∩=A l 1l 2l 1l 2α∩=B l 2l 3B ∈l 2⊂αl 2B ∈αC ∈αB ∈l 3C ∈l 3⊂αl 3l 1l 2l 3∩=A l 1l 2l 1l 2α∩=B l 2l 3l 2l 3βA ∈l 2⊂αl 2A ∈αA ∈l 2⊂βl 2A ∈βB ∈αB ∈βC ∈αC ∈βA B C αβαβl 1l 2l 3结合空间想象回答下列问题:(1) 个平面可以分空间为______部分;(2) 个平面可以分空间为______部分;(3)正方体的各个面延伸后将空间分成______部分.解:(1),;(2),,,;(3).对于(1):当 个平面平行时,分成 部分;当两个面相交时,分成 部分;对于(2):当 个平面两两平行时,分成 部分;当其中两个平面平行,和另外一个平面相交或者三个平面相交于一条直线时,分成 部分;当 个平面两两相交且交线两两平行时,分成 部分;当 个平面两两相交且交线相交于一点时,分成 部分;对于(3):首先,将正方体的四个侧面延伸,可知将空间分成 部分,然后,将正方体的上下底面延伸可知将之前部分分成了 层,每层 部分,共 部分 .233446782723434637389393×9=27若直线 、、 相交于一点,则这 条直线可能确定的平面有( )A. 个 B. 个 C.无数个 D. 个或 个解:D当 、、 三线共面时,平面只有 个;当三线不共面时,任意两条可确定一个平面,共 个.a b c 30113a b c 13描述:例题:点与平面的位置关系平面内有无数个点,平面可以看成点的集合.点 在平面 内,记作 ;点 不在平面 内,记作 .直线与直线的位置关系空间直线与直线的位置关系共有以下两种:共面直线 在同一平面内的两条直线.更进一步,若这两条直线有且只有一个公共点,则称它们是相交直线 ,若这两条直线没有公共点,则称它们是平行直线;异面直线 不同在任何一个平面内的两条直线.直线垂直如果两条直线所成的角是直角,那么我们就说这两条直线互相垂直,记作 .在空间,两条直线垂直包括两种情形:共面垂直和异面垂直.直线与平面的位置关系空间直线与平面的位置关系共有以下三种:直线在平面内 直线上的所有点都在平面内;直线与平面相交 直线与平面有且仅有一个公共点;直线与平面平行 直线与平面没有公共点.平面与平面的位置关系空间平面与平面的位置关系共有以下两种:平行 两个平面没有公共点,则称这两个平面平行;相交 两个平面有一条公共直线,则称这两个平面相交,此时这条公共直线称为这两个平面的交线.A αA ∈αA αA ∉αa ⊥b 如果在两个平面内分别各有一条直线,这两条直线互相平行,那么这两个平面的位置关系是()A.平行 B.相交 C.平行或相交 D.垂直相交解:C可根据题意作图判断,如图所示,分别为两个平面平行、相交的情况 .分别和两条异面直线都相交的两条直线的位置关系是( )A.相交 B.异面 C.异面或相交 D.平行解:C如图所示,可能相交,也可能异面,若两直线平行,则此两条直线确定一个平面,且原两条异面直线均在此平面内,故矛盾 .四、课后作业 (查看更多本章节同步练习题,请到快乐学)若直线 不平行于平面 ,且 ,则( )A. 内的所有直线与 异面 B. 内不存在与 平行的直线 C. 内存在唯一的直线与 平行 D. 内的直线与 都相交解:B依题意,设直线 ,如图. 内的直线若经过点 ,则与直线 相交;若不经过点 ,则与直线 是异面直线,但不可能与 平行.l αl ⊄ααl αl αl αl l ∩α=A αA l A l l 答案:解析:1. 如图,在正方体 中, 是底面正方形 的中心, 是 的中点, 是 上的动点,则直线 、 的位置关系是 .A .平行B .相交C .异面垂直D .异面不垂直C和点 确定平面 ,且 平面 , 判定 与平面 的位置关系,只需判定直线 的位置关系即可.ABCD −A 1B 1C 1D 1O ABCD M D D 1N A 1B 1NO AM ()A 1B 1O O A 1B 1NO ⊂O A 1B 1∴MA O A 1B 1NO 、AM 答案:2. 平行六面体 中,既与 共面也与 共面的棱的条数为 A .B .C .D .C ABCD −A 1B 1C 1D 1AB C C 1()3456答案:3. 正方体 中, 、 、 分别是 、 、 的中点.那么,正方体的过 、 、 的截面图形是 A .三角形B .四边形C .五边形D .六边形D ABCD −A 1B 1C 1D 1P Q R AB AD B 1C 1P Q R ()4. 下列正方体或正四面体中,,,, 分别是所在棱的中点,这四个点不共面的一个图是 P Q R S ()高考不提分,赔付1万元,关注快乐学了解详情。
2018年高一数学寒假作业(人教A版必修2)空间点直线平面之间的位置关系word版含答案

2018年高一数学寒假作业(人教A版必修2)空间点直线平面之间的位置关系A组基础达标(建议用时:30分钟)一、选择题1.(2015·湖北高考)l1,l2表示空间中的两条直线,若p:l1,l2是异面直线,q:l1,l2不相交,则( ) A.p是q的充分条件,但不是q的必要条件B.p是q的必要条件,但不是q的充分条件C.p是q的充分必要条件D.p既不是q的充分条件,也不是q的必要条件2.给出下列说法:①梯形的四个顶点共面;②三条平行直线共面;③有三个公共点的两个平面重合;④三条直线两两相交,可以确定3个平面.其中正确的序号是( )A.①B.①④C.②③D.③④3.(2017·郑州联考)已知直线a和平面α,β,α∩β=l,a⊄α,a⊄β,且a在α,β内的射影分别为直线b和c,则直线b和c的位置关系是( )A.相交或平行B.相交或异面C.平行或异面D.相交、平行或异面4.若空间中四条两两不同的直线l1,l2,l3,l4满足l1⊥l2,l2⊥l3,l3⊥l4,则下列结论一定正确的是( )A.l1⊥l4B.l1∥l4C.l1与l4既不垂直也不平行D.l1与l4的位置关系不确定5.已知正方体ABCDA1B1C1D1中,E,F分别为BB1,CC1的中点,那么异面直线AE与D1F所成角的余弦值为( )A.45B.35C.23D.57二、填空题6.如图737所示,正方体ABCDA1B1C1D1中,M,N分别为棱C1D1,C1C的中点,有以下四个结论:图737①直线AM与CC1是相交直线;②直线AM与BN是平行直线;③直线BN与MB1是异面直线;④直线MN与AC所成的角为60°.其中正确的结论为________.(注:把你认为正确的结论序号都填上)7.(2017·佛山模拟)如图738所示,在正三棱柱ABCA1B1C1中,D是AC的中点,AA1∶AB=2∶1,则异面直线AB1与BD所成的角为________.图7388.如图739,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,则直线EF与正方体的六个面所在的平面相交的平面个数为________.图739三、解答题9.如图7310所示,正方体ABCDA1B1C1D1中,M,N分别是A1B1,B1C1的中点.问:图7310(1)AM 和CN 是否是异面直线?说明理由; (2)D 1B 和CC 1是否是异面直线?说明理由.10.如图7311所示,在三棱锥P ABC 中,PA ⊥底面ABC ,D 是PC 的中点.已知∠BAC =π2,AB =2,AC =23,PA =2.求:图7311(1)三棱锥P ABC 的体积;(2)异面直线BC 与AD 所成角的余弦值.B 组 能力提升(建议用时:15分钟)1.(2017·南昌二模)设α为平面,a ,b 为两条不同的直线,则下列叙述正确的是( )A .若a ∥α,b ∥α,则a ∥bB .若a ⊥α,a ∥b ,则b ⊥αC .若a ⊥α,a ⊥b ,则b ∥αD .若a ∥α,a ⊥b ,则b ⊥α2.如图7312,正方形ACDE 与等腰直角三角形ACB 所在的平面互相垂直,且AC =BC =2,∠ACB =90°,F ,G 分别是线段AE ,BC 的中点,则AD 与GF 所成的角的余弦值为________.图73123.(2016·广州模拟)已知三棱锥A BCD 中,AB =CD ,且直线AB 与CD 成60°角,点M ,N 分别是BC ,AD 的中点,求直线AB 和MN 所成的角.2018年高一数学寒假作业(人教A版必修2)空间点直线平面之间的位置关系答案A组基础达标(建议用时:30分钟)一、选择题1.(2015·湖北高考)l1,l2表示空间中的两条直线,若p:l1,l2是异面直线,q:l1,l2不相交,则( ) A.p是q的充分条件,但不是q的必要条件B.p是q的必要条件,但不是q的充分条件C.p是q的充分必要条件D.p既不是q的充分条件,也不是q的必要条件A [若l1,l2异面,则l1,l2一定不相交;若l1,l2不相交,则l1,l2是平行直线或异面直线,故p⇒q,qD⇒/p,故p是q的充分不必要条件.]2.给出下列说法:①梯形的四个顶点共面;②三条平行直线共面;③有三个公共点的两个平面重合;④三条直线两两相交,可以确定3个平面.其中正确的序号是( )A.①B.①④C.②③D.③④A [显然命题①正确.由三棱柱的三条平行棱不共面知,②错.命题③中,两个平面重合或相交,③错.三条直线两两相交,可确定1个或3个平面,则命题④不正确.]3.(2017·郑州联考)已知直线a和平面α,β,α∩β=l,a⊄α,a⊄β,且a在α,β内的射影分别为直线b和c,则直线b和c的位置关系是( )A.相交或平行B.相交或异面C.平行或异面D.相交、平行或异面D [依题意,直线b和c的位置关系可能是相交、平行或异面.]4.若空间中四条两两不同的直线l1,l2,l3,l4满足l1⊥l2,l2⊥l3,l3⊥l4,则下列结论一定正确的是( )A .l 1⊥l 4B .l 1∥l 4C .l 1与l 4既不垂直也不平行D .l 1与l 4的位置关系不确定D [如图,在长方体ABCD A 1B 1C 1D 1中,记l 1=DD 1,l 2=DC ,l 3=DA .若l 4=AA 1,满足l 1⊥l 2,l 2⊥l 3,l 3⊥l 4,此时l 1∥l 4,可以排除选项A 和C.若取C 1D 为l 4,则l 1与l 4相交;若取BA 为l 4,则l 1与l 4异面;取C 1D 1为l 4,则l 1与l 4相交且垂直.因此l 1与l 4的位置关系不能确定.]5.已知正方体ABCD A 1B 1C 1D 1中,E ,F 分别为BB 1,CC 1的中点,那么异面直线AE 与D 1F 所成角的余弦值为( )A.45B.35 C.23D.57B [连接DF ,则AE ∥DF ,∴∠D 1FD 为异面直线AE 与D 1F 所成的角. 设正方体棱长为a , 则D 1D =a ,DF =52a ,D 1F =52a , ∴cos ∠D 1FD =⎝ ⎛⎭⎪⎫52a 2+⎝ ⎛⎭⎪⎫52a 2-a22·52a ·52a=35.]二、填空题6.如图737所示,正方体ABCD A 1B 1C 1D 1中,M ,N 分别为棱C 1D 1,C 1C 的中点,有以下四个结论:图737①直线AM 与CC 1是相交直线; ②直线AM 与BN 是平行直线; ③直线BN 与MB 1是异面直线; ④直线MN 与AC 所成的角为60°.其中正确的结论为________.(注:把你认为正确的结论序号都填上)③④ [由题图可知AM 与CC 1是异面直线,AM 与BN 是异面直线,BN 与MB 1为异面直线. 因为D 1C ∥MN ,所以直线MN 与AC 所成的角就是D 1C 与AC 所成的角,且角为60°.]7.(2017·佛山模拟)如图738所示,在正三棱柱ABC A 1B 1C 1中,D 是AC 的中点,AA 1∶AB =2∶1,则异面直线AB 1与BD 所成的角为________.图73860° [取A 1C 1 的中点E ,连接B 1E ,ED ,AE ,在Rt △AB 1E 中,∠AB 1E 即为所求, 设AB =1,则A 1A =2,AB 1=3,B 1E =32,AE =32,故∠AB 1E =60°.] 8.如图739,正方体的底面与正四面体的底面在同一平面α上,且AB ∥CD ,则直线EF 与正方体的六个面所在的平面相交的平面个数为________.图7394 [取CD 的中点为G (图略),由题意知平面EFG 与正方体的左、右侧面所在平面重合或平行,从而EF 与正方体的左、右侧面所在的平面平行或EF 在平面内,所以直线EF 与正方体的前、后侧面及上、下底面所在平面相交.故直线EF 与正方体的六个面所在的平面相交的平面个数为4.]三、解答题9.如图7310所示,正方体ABCD A 1B 1C 1D 1中,M ,N 分别是A 1B 1,B 1C 1的中点.问:图7310(1)AM 和CN 是否是异面直线?说明理由; (2)D 1B 和CC 1是否是异面直线?说明理由.[解] (1)AM ,CN 不是异面直线.理由:连接MN ,A 1C 1,AC .因为M ,N 分别是A 1B 1,B 1C 1的中点,所以MN ∥A 1C 1.2分 又因为A 1A 綊C 1C ,所以A 1ACC 1为平行四边形, 所以A 1C 1∥AC ,所以MN ∥AC , 所以A ,M ,N ,C 在同一平面内, 故AM 和CN 不是异面直线.5分 (2)直线D 1B 和CC 1是异面直线.6分理由:因为ABCD A 1B 1C 1D 1是正方体,所以B ,C ,C 1,D 1不共面.假设D 1B 与CC 1不是异面直线, 则存在平面α,使D 1B ⊂平面α,CC 1⊂平面α, 所以D 1,B ,C ,C 1∈α,10分这与B ,C ,C 1,D 1不共面矛盾,所以假设不成立, 即D 1B 和CC 1是异面直线.12分10.如图7311所示,在三棱锥P ABC 中,PA ⊥底面ABC ,D 是PC 的中点.已知∠BAC =π2,AB =2,AC =23,PA =2.求:图7311(1)三棱锥P ABC 的体积;(2)异面直线BC 与AD 所成角的余弦值. [解] (1)S △ABC =12×2×23=23,三棱锥P ABC 的体积为V =13S △ABC ·PA =13×23×2=433.5分 (2)如图,取PB 的中点E ,连接DE ,AE ,则ED ∥BC ,所以∠ADE 是异面直线BC 与AD 所成的角(或其补角).8分在△ADE 中,DE =2,AE =2,AD =2,cos ∠ADE =22+22-22×2×2=34.故异面直线BC 与AD 所成角的余弦值为34.12分B 组 能力提升 (建议用时:15分钟)1.(2017·南昌二模)设α为平面,a ,b 为两条不同的直线,则下列叙述正确的是( ) A .若a ∥α,b ∥α,则a ∥b B .若a ⊥α,a ∥b ,则b ⊥α C .若a ⊥α,a ⊥b ,则b ∥α D .若a ∥α,a ⊥b ,则b ⊥αB [若a ∥α,b ∥α,则a 与b 相交、平行或异面,故A 错误;易知B 正确; 若a ⊥α,a ⊥b ,则b ∥α或b ⊂α,故C 错误;若a ∥α,a ⊥b ,则b ∥α或b ⊂α或b 与α相交,故D 错误.]2.如图7312,正方形ACDE 与等腰直角三角形ACB 所在的平面互相垂直,且AC =BC =2,∠ACB =90°,F ,G 分别是线段AE ,BC 的中点,则AD 与GF 所成的角的余弦值为________.图731236[取DE 的中点H ,连接HF ,GH . 由题设,HF 綊12AD ,∴∠GFH 为异面直线AD 与GF 所成的角(或其补角). 在△GHF 中,可求HF =2,GF =GH =6,∴cos ∠GFH = 2 2+ 6 2- 6 22×2×6=36.]3.(2016·广州模拟)已知三棱锥A BCD 中,AB =CD ,且直线AB 与CD 成60°角,点M ,N 分别是BC ,AD 的中点,求直线AB 和MN 所成的角.[解] 如图,取AC 的中点P .连接PM ,PN ,又点M ,N 分别是BC ,AD 的中点,则PM ∥AB ,且PM =12AB ,PN ∥CD ,且PN =12CD ,所以∠MPN 为AB 与CD 所成的角(或其补角).6分 则∠MPN =60°或∠MPN =120°,①若∠MPN =60°,因为PM ∥AB ,所以∠PMN 是AB 与MN 所成的角(或其补角). 又因为AB =CD ,所以PM =PN ,则△PMN 是等边三角形,所以∠PMN =60°, 即AB 和MN 所成的角为60°.9分②若∠MPN =120°,则易知△PMN 是等腰三角形, 所以∠PMN =30°,即AB 和MN 所成的角为30°. 综上,直线AB 和MN 所成的角为60°或30°.12分。
2018年高一数学寒假作业(人教A版必修2)空间点、直线、平面之间的位置关系word版含答案

2018年高一数学寒假作业(人教A版必修2)空间点、直线、平面之间的位置关系(时间:40分钟)一、选择题1.下列说法正确的是( )A.若a⊂α,b⊂β,则a与b是异面直线B.若a与b异面,b与c异面,则a与c异面C.若a,b不同在平面α内,则a与b异面D.若a,b不同在任何一个平面内,则a与b异面2.(2016·山东高考)已知直线a,b分别在两个不同的平面α,β内。
则“直线a和直线b 相交”是“平面α和平面β相交”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.设A、B、C、D是空间中四个不同的点,下列命题中,不正确的是( ) A.若AC与BD共面,则AD与BC共面B.若AC与BD是异面直线,则AD与BC是异面直线C.若AB=AC,DB=DC,则AD=BCD.若AB=AC,DB=DC,则AD⊥BC4.若空间三条直线a,b,c满足a⊥b,b⊥c,则直线a与c( )A.一定平行B.一定相交C.一定是异面直线D.平行、相交或异面都有可能5.空间四边形的两条对角线互相垂直,顺次连接四边中点的四边形一定是( ) A.空间四边形B.矩形C.菱形D.正方形6.四棱锥P-ABCD的所有侧棱长都为5,底面ABCD是边长为2的正方形,则CD与PA所成角的余弦值为( )A.255B.55C.45D.35二、填空题7.给出下列命题,其中正确的命题有________。
①如果线段AB在平面α内,那么直线AB在平面α内;②两个不同的平面可以相交于不在同一直线上的三个点A,B,C;③若三条直线a,b,c互相平行且分别交直线l于A,B,C三点,则这四条直线共面;④若三条直线两两相交,则这三条直线共面;⑤两组对边相等的四边形是平行四边形。
8.如图为正方体表面的一种展开图,则图中的四条线段AB,CD,EF,GH在原正方体中互为异面直线的对数为________。
9.设a,b,c是空间中的三条直线,下面给出五个命题:①若a∥b,b∥c,则a∥c;②若a⊥b,b⊥c,则a∥c;③若a与b相交,b与c相交,则a与c相交;④若a⊂平面α,b⊂平面β,则a,b一定是异面直线;⑤若a,b与c成等角,则a∥b。
高中数学 必修2(人教版)8.4.2空间点、直线、平面之间的位置关系

要点一 空间两直线的位置关系 1.空间中两条直线的位置关系
Байду номын сангаас
一个 没有 没有
2.异面直线 (1)定义:把不同在___任__一___平面内的两条直线叫做异面直 线. (2)画法:(通常用平面衬托)
状元随笔 1.异面直线的定义表明异面直线不具备确定平面 的条件.异面直线既不相交,也不平行.
跟踪训练2 如果在两个平面内分别有一条直线,且这两条直
线互相平行,那么这两个平面的位置关系是( )
A.平行
B.相交
C.平行或相交 D.以上都不正确
解析:如图,在正方体ABCD - A1B1C1D1中,AB⊂平面 ABCD,C1D1⊂平面A1B1C1D1,C1D1⊂平面CDD1C1,AB∥C1D1, 但平面ABCD∥平面A1B1C1D1,平面ABCD与平面CDD1C1相交.
_0_个__公共点
符号表示 _a_⊂__α__
a_∩__α_=__A
_a_∥__α__
图形表示
状元随笔 直线与平面位置关系的分类 1.按有无公共点分类
2.按是否在平面内进行分类 直线在平面内 直线不在平面内直 直线 线和 和平 平面 面相 平交 行
要点三 平面与平面之间的位置关系 位置关系 两平面平行 两平面相交 公共点 没有公共点 有一条公共直线
解析:由直线与平面的关系可知CD正确. 答案:CD
(2)在如图所示的正方体ABCD -A′B′C′D′中,
①与AB所在直线平行的表面有________个; ②与A′B所在直线平行的表面有________个; ③与A′D′所在直线相交的表面有________个. 解析:①与AB所在直线平行的表面有A′B′C′D′和 DCC′D′; ②与A′B所在直线平行的表面只有DCC′D′; ③与A′D′所在直线相交的表面有DCC′D′和A′B′BA. 答案:①2 ②1 ③2
人教A版高中数学必修二课时作业空间中直线与平面之间的位置关系平面与平面之间的位置关系
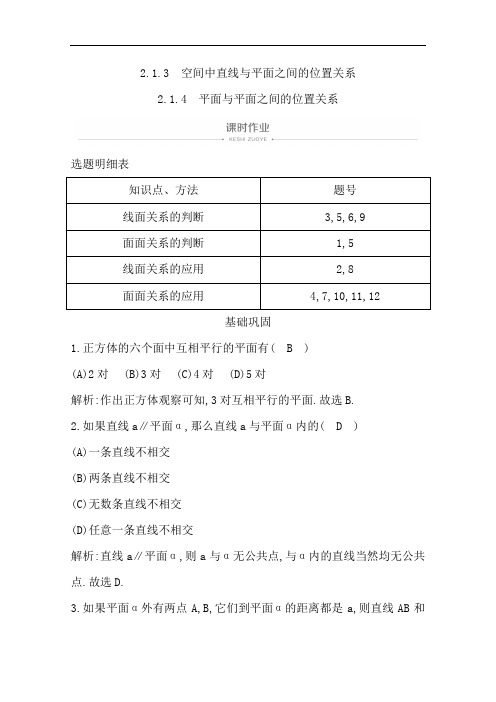
2.1.3 空间中直线与平面之间的位置关系2.1.4 平面与平面之间的位置关系选题明细表知识点、方法题号线面关系的判断3,5,6,9面面关系的判断1,5线面关系的应用2,8面面关系的应用4,7,10,11,12基础巩固1.正方体的六个面中互相平行的平面有( B )(A)2对(B)3对(C)4对(D)5对解析:作出正方体观察可知,3对互相平行的平面.故选B.2.如果直线a∥平面α,那么直线a与平面α内的( D )(A)一条直线不相交(B)两条直线不相交(C)无数条直线不相交(D)任意一条直线不相交解析:直线a∥平面α,则a与α无公共点,与α内的直线当然均无公共点.故选D.3.如果平面α外有两点A,B,它们到平面α的距离都是a,则直线AB和平面α的位置关系一定是( C )(A)平行(B)相交(C)平行或相交(D)AB⊂α解析:结合图形可知选项C正确.4.平面α∥平面β,直线a⊂α,下列四个命题中,正确命题的个数是( B )①a与β内的所有直线平行;②a与β内的无数条直线平行;③a与β内的任何一条直线都不垂直;④a与β无公共点.(A)1 (B)2 (C)3 (D)4解析:借助于长方体模型,可以举出反例说明①③是错误的;利用面面平行的定义进行判断,则有②④是正确的.故选B.5.给出下列几个说法:①过一点有且只有一条直线与已知直线平行;②过一点有且只有一条直线与已知直线垂直;③过平面外一点有且只有一条直线与该平面平行;④过平面外一点有且只有一个平面与该平面平行.其中正确说法的个数为( B )(A)0 (B)1 (C)2 (D)3解析:①当点在已知直线上时,不存在过该点的直线与已知直线平行,故①错;②由于垂直包括相交垂直和异面垂直,因而过一点与已知直线垂直的直线有无数条,故②错;③过棱柱的上底面内的一点任意作一条直线都与棱柱的下底面平行,所以过平面外一点与已知平面平行的直线有无数条,故③错;④过平面外一点与已知平面平行的平面有且只有一个,故④对.故选B.6.下列说法中,正确的个数是( C )①如果两条平行直线中的一条和一个平面相交,那么另一条直线也和这个平面相交;②经过两条异面直线中的一条直线有一个平面与另一条直线平行;③两条相交直线,其中一条与一个平面平行,则另一条一定与这个平面平行.(A)0 (B)1 (C)2 (D)3解析:易知①正确,②正确.③中两条相交直线中一条与平面平行,另一条可能平行于平面,也可能与平面相交,故③错误.选C.7.如图所示,平面ABC与三棱柱ABC A1B1C1的其他面之间有什么位置关系?解:因为平面ABC与平面A1B1C1无公共点,所以平面ABC与平面A1B1C1平行.因为平面ABC与平面ABB1A1有公共直线AB,所以平面ABC与平面ABB1A1相交.同理可得平面ABC与平面ACC1A1及平面BCC1B1均相交.能力提升8.教室内有一根直尺,无论怎样放置,在地面上总有这样的直线与直尺所在的直线( D )(A)异面(B)相交(C)平行(D)垂直解析:若尺子与地面相交,则C不正确;若尺子平行于地面,则B不正确;若尺子放在地面上,则A不正确.所以选D.9.a,b是异面直线,A,B是a上两点,C,D是b上的两点,M,N分别是线段AC,BD的中点,则MN和a的位置关系是( A )(A)异面(B)平行(C)相交(D)以上均有可能解析:若MN与AB平行或相交,则MN与AB共面α.又知C∈直线AM, D ∈直线BD,所以C∈α,D∈α.又A∈α,B∈α,所以a⊂α,b⊂α,与a,b异面矛盾,故选A.10.如果空间的三个平面两两相交,则下列判断正确的是(填序号).①不可能只有两条交线;②必相交于一点;③必相交于一条直线;④必相交于三条平行线.解析:空间的三个平面两两相交,可能只有一条交线,也可能有三条交线,这三条交线可能交于一点.答案:①11.如图,平面α,β,γ满足α∥β,α∩γ=a,β∩γ=b,判断a与b, a 与β的关系并证明你的结论.解:a∥b,a∥β.证明如下:由α∩γ=a知a⊂α且a⊂γ,由β∩γ=b知b⊂β且b⊂γ,因为α∥β,a⊂α,b⊂β,所以a,b无公共点.又因为a⊂γ且b⊂γ,所以a∥b.因为α∥β,所以α与β无公共点.又a⊂α,所以a与β无公共点,所以a∥β.探究创新12.如图,已知平面α和β相交于直线l,点A∈α,点B∈α,点C∈β,且A∉l,B∉l,直线AB与l不平行,那么,平面ABC与平面β的交线与l 有什么关系?证明你的结论.解:平面ABC与平面β的交线与l相交.证明如下:因为AB与l不平行,AB⊂α,l⊂α,所以AB与l是相交直线.设AB∩l=P,则点P∈AB,点P∈l.又因为AB⊂平面ABC,l⊂β,所以P∈平面ABC且P∈平面β,即点P是平面ABC与平面β的一个公共点.而C也是平面ABC与平面β的一个公共点,又因为P,C不重合,所以直线PC就是平面ABC与平面β的交线,即平面ABC∩平面β=直线PC.而直线PC∩l=P,所以平面ABC与平面β的交线与l相交.。
2018版人教A版高中数学必修二同步学习讲义:第二章点、直线、平面之间的位置关系2-1-2含答案精品

1.空间两条互相平行的直线指的是 ( ) A .在空间没有公共点的两条直线 B .分别在两个平面内的两条直线 C .在两个不同的平面内且没有公共点的两条直线 D .在同一平面内且没有公共点的两条直线 答案 D 解析 由平行直线的定义可得.
2.若 OA∥ O′ A′, OB∥ O′B′,且∠ AOB=130 °,则∠ A′ O′ B′为 ( )
2.1.2 空间中直线与直线之间的位置关系
学习目标 1.了解空间中两条直线的位置关系 .2.理解异面直线的概念、 画法 .3.理解并掌握公 理 4 及等角定理 .4.掌握异面直线所成角的概念及异面直线垂直的概念,能求出一些较特殊的 异面直线所成的角.
知识点一 空间两直线的位置关系 思考 在同一平面内,两条直线有几种位置关系? 观察下面两个图形,你能找出既不平行又不相交的两条直线吗?
A . 130 °
B. 50°
C.130 °或 50°
D .不能确定
答案 C
解析 根据定理, ∠ A′ O′ B′与 ∠ AOB 相等或互补, 即∠ A′O′ B′ = 130°或∠ A′O′ B′
= 50°.
3.分别和两条异面直线平行的两条直线的位置关系是
()
A .一定平行
B.一定相交
C .一定异面
(2)计算角:求角度,常利用三角形. (3)确定角:若求出的角是锐角或是直角,则它就是所求异面直线所成的角;若求出的角是钝 角,则它的补角就是所求异面直线所成的角.
跟踪训练 3 在空间四边形 ABCD 中,两条对边 AB= CD=3,E,F 分别是另外两条对边 AD,
BC 上的点,且
AE ED
=
பைடு நூலகம்BF FC
1.判定两直线的位置关系的依据就在于两直线平行、相交、异面的定义.很多情况下,定义 就是一种常用的判定方法.
高中数学(人教A版)必修第二册课后习题:空间点、直线、平面之间的位置关系【含答案及解析】

第八章立体几何初步8.4空间点、直线、平面之间的位置关系8.4.2空间点、直线、平面之间的位置关系课后篇巩固提升必备知识基础练1.如图所示,用符号语言可表示为()A.α∩β=lB.α∥β,l∈αC.l∥β,l⊄αD.α∥β,l⊂α2.在长方体ABCD-A1B1C1D1的六个表面与六个对角面(平面AA1C1C、平面ABC1D1、平面ADC1B1、平面BB1D1D、平面A1BCD1及平面A1B1CD)所在的平面中,与棱AA1平行的平面共有()A.2个B.3个C.4个D.5个,结合图形可知AA1∥平面BB1C1C,AA1∥平面DD1C1C,AA1∥平面BB1D1D.3.(多选题)如图所示,在正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,则以下四个结论正确的是()A.直线AM与CC1是相交直线B.直线AM与BN是平行直线C.直线BN与MB1是异面直线D.直线AM与DD1是异面直线AM与CC1不同在任何一个平面内,直线AM与BN不同在任何一个平面内,故A,B错误;直线BN与MB1不同在任何一个平面内,直线AM与DD1不同在任何一个平面内,故C,D正确.4.如果空间的三个平面两两相交,那么()A.不可能只有两条交线B.必相交于一点C.必相交于一条直线D.必相交于三条平行线,可能相交于一点,也可能相交于一条直线,还可能相交于三条平行线,故选A.5.若两个平面内分别有一条直线,且这两条直线是异面直线,则这两个平面的公共点()A.有有限个B.有无数个C.不存在D.不存在或有无数个,直线AB与直线CC1异面,平面ABCD与平面CDD1C1相交,有无数个公共点;平面ABB1A1与平面CDD1C1平行,没有公共点.6.以下说法正确的是()A.若直线a不平行于平面α,则直线a与平面α相交B.直线a和b是异面直线,若直线c∥a,则c与b一定相交C.若直线a和b都和平面α平行,则a和b也平行D.若点M∈l,点N∈l,N∉α,M∈α,则直线l与平面α相交a不平行于平面α,则直线a与平面α相交,或a⊂α,故A错误;若直线a和b是异面直线,若直线c∥a,则c与b相交或异面,故B错误;若直线a和b都和平面α平行,则a和b可能平行,可能相交,也可能异面,故C错误;若点M,N∈l,N∉α,M∈α,则直线l和平面α相交,故D正确.故选D.7.如图,在正方体ABCD-A1B1C1D1中,所在直线与BD1异面的棱有条.,知在正方体ABCD-A1B1C1D1中,所在直线与BD1异面的棱有CD,A1B1,AD,B1C1,AA1,CC1共6条.8.已知直线a,平面α,β,且a∥α,a∥β,则平面α与β的位置关系是.a∥α,a∥β,所以平面α与β相交(如图①)或平行(如图②).9.过三棱柱ABC-A1B1C1的任意两条棱的中点作直线,其中与平面ABB1A1平行的直线共有条.,与平面ABB1A1平行的直线有6条:D1E1,E1E,ED,DD1,D1E,DE1.10.如图,在长方体ABCD-A1B1C1D1中,面对角线B1D1与长方体的六个面之间的位置关系如何?B1∈平面A1B1C1D1,D1∈平面A1B1C1D1,∴B1D1⊂平面A1B1C1D1.∵B1∈平面BB1C1C,D1∉平面BB1C1C,∴直线B1D1∩平面BB1C1C=B1.同理直线B1D1与平面AA1B1B、平面AA1D1D、平面CC1D1D都相交.在平行四边形B1BDD1中,B1D1∥BD,B1D1与BD无公共点,∴B1D1与平面ABCD无公共点,∴B1D1∥平面ABCD.关键能力提升练11.若a,b是异面直线,且a∥平面α,那么b与平面α的位置关系是()A.b∥αB.b与α相交C.b⊂αD.以上三种情况都有可能a,b是异面直线,且a∥平面α,则根据空间中线面的位置关系可得,b∥a,或b⊂α,或b与α相交.12.(多选题)以下结论中,正确的是()A.过平面α外一点P,有且仅有一条直线与α平行B.过平面α外一点P,有且仅有一个平面与α平行C.过直线l外一点P,有且仅有一条直线与l平行D.过直线l外一点P,有且仅有一个平面与l平行①所示,过点P有无数条直线都与α平行,这无数条直线都在平面β内,过点P有且只有一个平面与α平行,故A错,B正确;如图②所示,过点P只有一条直线与l平行,但有无数个平面与l平行,故C正确,D错.13.(多选题)下列说法中正确的是()A.若直线a不在平面α内,则a∥αB.若直线l上有无数个点不在平面α内,则l∥αC.若l∥α,则直线l与平面α内任何一条直线都没有公共点D.平行于同一平面的两直线可以相交中,直线a也可能与平面α相交,故A错误;B中,直线l与平面α相交时,l上也有无数个点不在平面α内,故B错误;C中,当l∥α时,l与α没有公共点,所以l与α内任何一条直线都没有公共点,故C正确;D中,平行于同一个平面的直线,可以平行也可以相交,也可以是异面直线,故D正确.14.一个正方体的平面展开图如图所示,A,B,C,D为原正方体的顶点,则在原来的正方体中()A.AB∥CDB.AB与CD相交C.AB⊥CDD.AB与CD异面,则在原来的正方体中,由异面直线的定义可知AB与CD异面.故选D.15.下列命题正确的有.(填序号)①若直线与平面有两个公共点,则直线在平面内;②若直线l与平面α相交,则l与平面α内的任意直线都是异面直线;③若直线l与平面α平行,则l与平面α内的直线平行或异面;④若直线a⊂平面α,平面α∩平面β=b,a∥b,则a∥β.显然是正确的;②中,直线l和平面α内过l与α交点的直线都相交而不是异面,所以②是错误的;③中,直线l与平面α没有公共点,所以直线l与平面α内的直线没有公共点,即它们平行或异面,所以③是正确的;因为a∥b,所以a与b无公共点.又因为a⊂α,且α与β的公共点都在直线b上,所以a 与β无公共点,故a与β平行,故④是正确的.16.如图,平面α,β,γ满足α∥β,α∩γ=a,β∩γ=b,判断a与b,a与β的关系,并证明你的结论.∥b,a∥β.证明如下.由α∩γ=a知a⊂α,且a⊂γ,由β∩γ=b知b⊂β,且b⊂γ.∵α∥β,a⊂α,b⊂β,∴a,b无公共点.又∵a⊂γ,且b⊂γ,∴a∥b.∵α∥β,∴α与β无公共点.又a⊂α,∴a与β无公共点,∴a∥β.学科素养创新练17.若直线a不平行于平面α,且a⊄α,则下列结论成立的是()A.平面α内的所有直线与a异面B.平面α内不存在与a平行的直线C.平面α内存在唯一的直线与a平行D.平面α内的直线与a都相交a与平面α相交,则平面α内的直线与a可能相交,也可能异面,不可能平行.故选B.18.(多选题)已知a,b是两条不重合的直线,α,β是两个不重合的平面,则下列说法中正确的是()A.若a∥b,b⊂α,则直线a平行于平面α内的无数条直线B.若α∥β,a⊂α,b⊂β,则a与b是异面直线C.若α∥β,a⊂α,则a∥βD.若α∩β=b,a⊂α,则a,b一定相交中,a∥b,b⊂α,则a∥α或a⊂α,所以不管a在平面内还是平面外,结论都成立,故A正确;B中,直线a与b没有交点,所以a与b可能异面,也可能平行,故B错误;C中,直线a与平面β没有公共点,所以α∥β,故C正确;D中,直线a与平面β有可能平行,所以a,b可能相交,也可能平行,故D错误.。
高中数学 2.1空间点、直线、平面之间的位置关系 新人教A版必修2

公理 3 作用:判定两个平面是否相交的依据。
精品课件
例1、用符号表示下列图形中点、直线、平 面之间的关系。
解 :左边的图中, α∩β=l,a∩α=A,a∩β=B。 右边的图中, α∩β=l,a α,b β, a∩l=P,b∩l=P。
精品课件
新疆 王新敞
奎屯
求证: P 在直线 BD 上新疆 王新敞 奎屯
A
P EH
D
G
B
C
F
精品课件
证明:∵ EH FG P ,∴ PEH , P FG , ∵ E, H 分别属于直线 AB, AD , ∴ EH 平面 ABD,∴ P 平面 ABD, 同理: P 平面 CBD , 又∵平面 ABD 平面 CBD BD ,
集合中“∈”的符号只能用于点与直线,点与平面的关系,“ ”和“∩”的符号只能
用于直线与直线、直线与平面、平面与平面的关系,虽然借用于集合符号,但在读法上仍用
几何语言.(平面α外的直线 a)表示 a (平面α外的直线 a)表示 a 或 a A.
精品课件
问题4:如果直线l与平面α有一个公共点P,直线l是否在平面α内? 直线l不一定在平面α内。
答案:(1)×(2)√(3)×(4)√
精品课件
2.①一条直线与一个平面会有几种位置关系
.
②如图所示,两个平面、,若相交于一点,则会发生什么现象.
③几位同学的一次野炊活动,带去一张折叠方桌,不小心弄坏了桌脚,
有一生提议可将几根一样长的木棍,在等高处用绳捆扎一下作桌脚(如图
所示),问至少要几根木棍,才可能使桌面稳定?
(5)
直线在平面内
aα
直线与平面相交
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年高一数学寒假作业(人教A版必修2)空间点、直线、平面之间的位置关系1.给出下列说法:①梯形的四个顶点共面;②三条平行直线共面;③有三个公共点的两个平面重合;④三条直线两两相交,可以确定3个平面。
其中正确的序号是( )A.① B.①④C.②③ D.③④2.若直线a平行于平面α,则下列结论错误的是( )A.a平行于α内的所有直线B.α内有无数条直线与a平行C.直线a上的点到平面α的距离相等D.α内存在无数条直线与a成90°角3.已知a,b是两条不重合的直线,α,β是两个不重合的平面,则下列命题中正确的是( )A.a∥b,b⊂α,则a∥αB.a,b⊂α,a∥β,b∥β,则α∥βC.a⊥α,b∥α,则a⊥bD.当a⊂α,且b⊄α时,若b∥α,则a∥b4.已知直线a,b,平面α,则以下三个命题:①若a∥b,b⊂α,则a∥α;②若a∥b,a∥α,则b∥α;③若a∥α,b∥α,则a∥b.其中真命题的个数是( )A.0 B.1C.2 D.35.已知直线a与平面α、β,α∥β,a⊂α,点B∈β,则在β内过点B的所有直线中( )A.不一定存在与a平行的直线B.只有两条与a平行的直线C.存在无数条与a平行的直线D.存在唯一一条与a平行的直线6.如图,L,M,N分别为正方体对应棱的中点,则平面LMN与平面PQR的位置关系是( )A.垂直B.相交不垂直C.平行 D.重合7.正方体ABCDA1B1C1D1中,E,F,G分别是A1B1,CD,B1C1的中点,则正确的命题是( )A.AE⊥CGB.AE与CG是异面直线C.四边形AEC1F是正方形D.AE∥平面BC1F8.设l,m,n表示不同的直线,α,β,γ表示不同的平面,给出下列四个命题:①若m∥l,且m⊥α,则l⊥α;②若m∥l,且m∥α,则l∥α;③若α∩β=l,β∩γ=m,γ∩α=n,则l∥m∥n;④若α∩β=m,β∩γ=l,γ∩α=n,且n∥β,则l∥m.其中正确命题的个数是( )A.1 B.2C.3 D.49.如图所示,ABCD A 1B 1C 1D 1是棱长为a 的正方体,M 、N 分别是下底面的棱A 1B 1、B 1C 1的中点,P 是上底面的棱AD 上的一点,AP =a 3,过P 、M 、N 的平面交上底面于PQ ,Q 在CD 上,则PQ =________.10.已知平面α∥平面β,P 是α、β外一点,过点P 的直线m 与α、β分别交于A 、C ,过点P 的直线n 与α、β分别交于B 、D 且PA =6,AC =9,PD =8,则BD 的长为________.11.在正四棱柱ABCD A 1B 1C 1D 1中,O 为底面ABCD 的中心,P 是DD 1的中点,设Q 是CC 1上的点,则点Q 满足条件________时,有平面D 1BQ ∥平面PAO .12.如图E 、F 、G 、H 分别是正方体ABCD A 1B 1C 1D 1的棱BC 、CC 1、C 1D 1、AA 1的中点.求证:(1)EG ∥平面BB 1D 1D ;(2)平面BDF ∥平面B 1D 1H .13.如图,在三棱柱ABC A 1B 1C 1中,点E 在线段B 1C 1上,B 1E =3EC 1,试探究:在AC上是否存在点F ,满足EF ∥平面A 1ABB 1?若存在,请指出点F 的位置,并给出证明;若不存在,请说明理由.14.如图,几何体EABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.(1)求证:BE=DE;(2)若∠BCD=120°,M为线段AE的中点.求证:DM∥平面BEC.(3)在(2)的条件下,在线段AD上是否存在一点N,使得BN∥面DEC,并说明理由.2018年高一数学寒假作业(人教A版必修2)空间点、直线、平面之间的位置关系答案1.给出下列说法:①梯形的四个顶点共面;②三条平行直线共面;③有三个公共点的两个平面重合;④三条直线两两相交,可以确定3个平面。
其中正确的序号是( )A.① B.①④C.②③ D.③④A。
答案:A2.若直线a平行于平面α,则下列结论错误的是( )A.a平行于α内的所有直线B.α内有无数条直线与a平行C.直线a上的点到平面α的距离相等D.α内存在无数条直线与a成90°角解析:选A.若直线a平行于平面α,则α内既存在无数条直线与a平行,也存在无数条直线与a异面且垂直,所以A不正确,B、D正确.又夹在相互平行的线与平面间的平行线段相等,所以C正确.3.已知a,b是两条不重合的直线,α,β是两个不重合的平面,则下列命题中正确的是( )A.a∥b,b⊂α,则a∥αB.a,b⊂α,a∥β,b∥β,则α∥βC.a⊥α,b∥α,则a⊥bD.当a⊂α,且b⊄α时,若b∥α,则a∥b解析:选C.A选项是易错项,由a∥b,b⊂α,也可能推出a⊂α;B中的直线a,b不一定相交,平面α,β也可能相交;C正确;D中的直线a,b也可能异面.4.已知直线a,b,平面α,则以下三个命题:①若a∥b,b⊂α,则a∥α;②若a∥b,a∥α,则b∥α;③若a∥α,b∥α,则a∥b.其中真命题的个数是( )A.0 B.1C.2 D.3解析:选A.对于①,若a∥b,b⊂α,则应有a∥α或a⊂α,所以①不正确;对于②,若a∥b,a∥α,则应有b∥α或b⊂α,因此②不正确;对于③,若a∥α,b∥α,则应有a∥b或a与b相交或a与b异面,因此③是假命题.综上,在空间中,以上三个命题都是假命题.5.已知直线a与平面α、β,α∥β,a⊂α,点B∈β,则在β内过点B的所有直线中( )A.不一定存在与a平行的直线B.只有两条与a平行的直线C.存在无数条与a平行的直线D.存在唯一一条与a平行的直线解析:选D.设直线a和点B所确定的平面为γ,则α∩γ=a,记β∩γ=b,∵α∥β,∴a∥b,故存在唯一一条直线b与a平行.6.如图,L,M,N分别为正方体对应棱的中点,则平面LMN与平面PQR的位置关系是( )A.垂直B.相交不垂直C.平行 D.重合7.正方体ABCD A 1B 1C 1D 1中,E ,F ,G 分别是A 1B 1,CD ,B 1C 1的中点,则正确的命题是( )A .AE ⊥CGB .AE 与CG 是异面直线C .四边形AEC 1F 是正方形D .AE ∥平面BC 1F面BC 1F .8.设l ,m ,n 表示不同的直线,α,β,γ表示不同的平面,给出下列四个命题:①若m ∥l ,且m ⊥α,则l ⊥α;②若m ∥l ,且m ∥α,则l ∥α;③若α∩β=l ,β∩γ=m ,γ∩α=n ,则l ∥m ∥n ;④若α∩β=m ,β∩γ=l ,γ∩α=n ,且n ∥β,则l ∥m .其中正确命题的个数是( )A .1B .2C .3D .4解析:选B.易知①正确;②错误,l 与α的具体关系不能确定;③错误,以墙角为例即可说明,④正确,可以以三棱柱为例证明.9.如图所示,ABCD A 1B 1C 1D 1是棱长为a 的正方体,M 、N 分别是下底面的棱A 1B 1、B 1C 1的中点,P 是上底面的棱AD 上的一点,AP =a 3,过P 、M 、N 的平面交上底面于PQ ,Q 在CD 上,则PQ =________.解析:∵平面ABCD ∥平面A 1B 1C 1D 1,∴MN ∥PQ .∵M 、N 分别是A 1B 1、B 1C 1的中点,AP =a 3, ∴CQ =a 3,从而DP =DQ =2a 3,∴PQ =223a . 答案:223a 10.已知平面α∥平面β,P 是α、β外一点,过点P 的直线m 与α、β分别交于A 、C ,过点P 的直线n 与α、β分别交于B 、D 且PA =6,AC =9,PD =8,则BD 的长为________.解析:根据题意可得到以下如图两种情况:可求出BD 的长分别为245或24. 答案:24或24511.在正四棱柱ABCD A 1B 1C 1D 1中,O 为底面ABCD 的中心,P 是DD 1的中点,设Q 是CC 1上的点,则点Q 满足条件________时,有平面D 1BQ ∥平面PAO .答案:Q 为CC 1的中点12.如图E 、F 、G 、H 分别是正方体ABCD A 1B 1C 1D 1的棱BC 、CC 1、C 1D 1、AA 1的中点.求证:(1)EG∥平面BB1D1D;(2)平面BDF∥平面B1D1H.证明:(1)取B1D1的中点O,连接GO,OB,易证四边形BEGO为平行四边形,故OB∥GE,由线面平行的判定定理即可证EG∥平面BB1D1D.13.如图,在三棱柱ABCA1B1C1中,点E在线段B1C1上,B1E=3EC1,试探究:在AC上是否存在点F,满足EF∥平面A1ABB1?若存在,请指出点F的位置,并给出证明;若不存在,请说明理由.解:法一:当AF=3FC时,FE∥平面A1ABB1.证明如下:在平面A 1B 1C 1内过点E 作EG ∥A 1C 1交A 1B 1于点G ,连接AG .∵B 1E =3EC 1,∴EG =34A 1C 1, 又AF ∥A 1C 1且AF =34A 1C 1,∴FG ∥AB ,又AB ⊂平面A 1ABB 1,FG ⊄平面A 1ABB 1,∴FG ∥平面A 1ABB 1.又EG ⊂平面EFG ,FG ⊂平面EFG ,EG ∩FG =G ,∴平面EFG ∥平面A 1ABB 1.∵EF ⊂平面EFG ,∴EF ∥平面A 1ABB 1.14.如图,几何体E ABCD 是四棱锥,△ABD 为正三角形,CB =CD ,EC ⊥BD .(1)求证:BE=DE;(2)若∠BCD=120°,M为线段AE的中点.求证:DM∥平面BEC.(3)在(2)的条件下,在线段AD上是否存在一点N,使得BN∥面DEC,并说明理由.证明:(1)取BD的中点O,连接CO,EO.由于CB=CD,所以CO⊥BD,又EC⊥BD,EC∩CO=C,CO,EC⊂平面EOC,所以BD⊥平面EOC,因此BD⊥EO,又O为BD的中点,所以BE=DE.又DN ⊄平面BEC ,BC ⊂平面BEC , 所以DN ∥平面BEC .又MN ∩DN =N ,故平面DMN ∥平面BEC ,又DM ⊂平面DMN ,所以DM ∥平面BEC.法二:延长AD ,BC 交于点F ,连接EF.所以DM ∥平面BEC .(3)存在点N 为AD 的中点取AD 的中点N ,连接BN ,O 为BD 的中点 由(2)可知∠DCO =60°,∴∠BDC =30°, 又∵DBN =30°,∴BN ∥DC .DC ⊂面DEC ,∴BN ∥面DEC .。
