随机信号分析基础第二章习题
随机信号分析2习题(供参考)

2.1 由下式定义的两电平二进制过程X(t)=A or – A,(n-1)T<t<nT 式中电平A 或-A 以等概率独立出现,T 为正常数,以及n=0,正负1,正负2,正负3……(1)、画出一个样变函数的草图;(2)、它属于哪一类随机过程?(3)、求一、二维概率密度函数。
(1)(2) 所以是确定的。
(3)2.2 设有下列离散随机过程:X (t )=CC 为随机变量,可能取值为1,2,3,其出现的概率分别为0.6,0.3,0.1(1) 是确定性随机过程?(2 ) 求任意时刻X(t)的一维概密。
解:(1)是(2) 1X(t)2,p(x,t)0.6(1)0.3(2)0.(3)3x x x δδδ⎧⎪==-+-+-⎨⎪⎩2.3 已知随机过程X(t)为 00),t (Xcos )t (X ωω=是标准高斯随机变量是常熟X ,,求X (t )的一维概率密度。
解:发22x x cos(t)(,)(,)())cos(t)2cos (t)d x p x t F x t p dx ωωω'==- 2.4 利用投掷一枚硬币的实验定义随机过程为X(t)=cos πt,出现正面,2t ,出现反面,假设出现正面和反面的概论各位1/2,试确定X(t)的一维分布函数Fx(x;1/2), Fx(x;1),以及二维发布函数Fx(x1,x2;1/2,1).解: x1 x2X :(t=1/2) 0 1Y (t=1) 1 22.5 随机过程X(t)由四条样本函数组成,如图题 2.6,出现的概论分别为p(§1)=1/8,p(§2)=1/4,p(§3)=3/8,p(§4)=1/4,求E[X(t1)],E[X(t2)],E[X(t1)X(t2)]及联合概率密度函数px(x1,x2;t1,t2)。
解:2.6 随机过程X(t)由如题 2.6图所示的三条样本函数曲线组成,并以等概率出现,试求E[X(2)], E[X(6)], E[X(2)X(6)], Fx(x;2),Fx(x;6),Fx(x1,x2;2,6).解:()A or A A A k -=-=∑∞-∞=,;nT t h )t (X k kX1 x2 x3T1=2 3 4 6E[X(2)]=313)643(31=++ E[X(6)]=314)752(31=++ E[X(2) X(6)]=155(3x54x76x2)33++= [])6x ()4x ()3x (31)x,2(f -+-+-=δδδ2.7随机过程X(t)由三条样本函数构成,cost )3,t (X sint;)2,t (X ;1)1,t (X ===ξξξ ,并以等概率出现,求E (X(t)),和 R(t1,t2)解:2.8 已知随机过程X(t) 的均值为m(t), 协方差函数为C(t1,t2), 又知f(t)是确定的时间函数,试求随机过程Y(t)=X(t)+f(t)的均值及协方差。
随机信号分析基础作业题

随机信号分析基础作业题第⼀章1、有朋⾃远⽅来,她乘⽕车、轮船、汽车或飞机的概率分别是0.3,0.2,0.1和0.4。
如果她乘⽕车、轮船或者汽车来,迟到的概率分别是0.25,0.4和0.1,但她乘飞机来则不会迟到。
如果她迟到了,问她最可能搭乘的是哪种交通⼯具?解:()0.3P A =()0.2P B =()0.1P C =()0.4P D =E -迟到,由已知可得(|)0.25(|)0.4(|)0.1(|)0P E A P E B P E C P E D ====全概率公式: ()()()()(P E P E AP E B P E C P E D=+++ 贝叶斯公式:()(|)()0.075(|)0.455()()0.165(|)()0.08(|)0.485()0.165(|)()0.01(|)0.06()0.165(|)()(|)0()P EA P E A P A P A E P E P E P E B P B P B E P E P E C P C P C E P E P E D P D P D E P E ?====?===?===?==综上:坐轮船3、设随机变量X 服从瑞利分布,其概率密度函数为2222,0()0,0X x x X x e x f x x σσ-??>=??式中,常数0X σ>,求期望()E X 和⽅差()D X 。
考察:已知()x f x ,如何求()E X 和()D X ?222222()()()[()]()()()()()()()x x E X x f x dxD XE X m X m f x dxD XE X E X E X x f x dx∞-∞∞-∞∞-∞=?=-=-=-?=6、已知随机变量X 与Y ,有1,3,()4,()16,0XYEX EY D X D Y ρ=====,令3,2,U X Y V X Y =+=-试求EU 、EV 、()D U 、()D V 和(,)Cov U V 。
随机信号分析(常建平,李林海)课后习题答案第二章习题讲解
A与 B独立 , f AB (a, b) f A (a) fB (b)
X (t) A Bt Y(t) A
A Y(t) X (t) Y (t)
B t
01 J1 1 1
t tt
1
xy 1
xy
f XY (x, y; t ) J f AB (a,b) t f AB ( y, t ) t f A ( y) f B ( t )
E X (t) E A cost XH cost EA XH
D X (t) E X 2 (t ) E2 X (t )
方法 2:
D X (t)
D Acost XH D Acost cos2 t DA cos2 t
12
D XH
公式: D aX+ bY a2 D X b2 D Y 2abC XY
RX (t1, t2 )=E Acost1 XH A cost2 XH
f X (x1;0)
1
x12 e 2,
2Байду номын сангаас
A
1
X (t)
~ N (0, )
t 30
2
4
f X ( x2; 3
)=
0
2 2
e
2
x2
2
,
X (t) t
=0,
f ( x3;2
)
0
20
( x3)
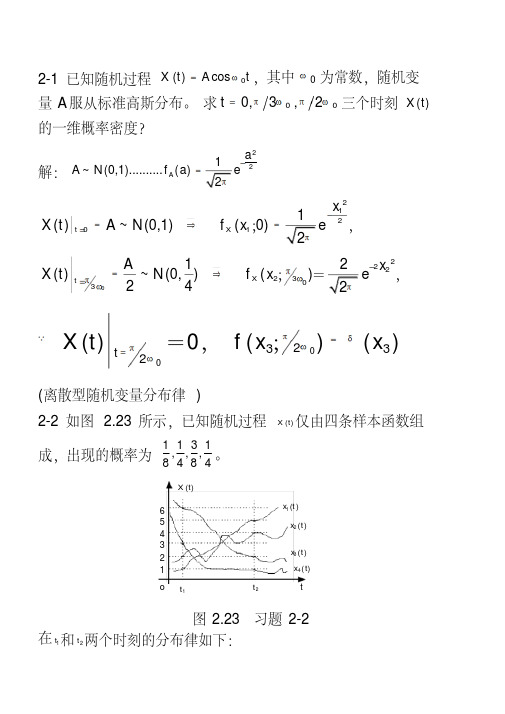
(离散型随机变量分布律 )
2-2 如图 2.23 所示,已知随机过程 X (t) 仅由四条样本函数组
成,出现的概率为
数 RX (t1, t2 ) ?②若已知随机变量相 A, B 互独立,
它们的概率密度分别为 f A (a) 和 f B (b) ,求 X (t) 的一
北邮随机信号分析与处理第2章习题解答_2

1 mX (t ) X (t , e1 ) X (t , e2 ) X (t , e3 ) (1 sin t cos t ) 3 3 3 3
RX (t1 , t2 ) E[ X (t1 ) X (t2 )] 1 (11 sin t1 sin t2 cos t1 cos t2 ) 3 1 [1 cos(t1 t2 )] 3
, X (t N ) xN FX ( x1 ,
, X (t N ) x N |
, xN ; t1 ,
, tN )
因此有 FX ( x1 , , xN ; t1 ,
, t N ) FX |Θ ( x1 , 1 T FX ( x1 , T 0
8
2.22
2 R ( ) e 和 已知平稳随机过程的相关函数 X RX ( ) 2 (1 ) , 1/ 。试求其相关时间 0 。 2 2 0 解: (1) mX lim RX ( ) lim e
RX (0) m 2 RX ( ) mX 因此有 rX ( ) e 2 X 1 r0 rX ( )d e d 0 0 2 2 2 2 R (0) m (2) mX lim RX ( ) 0 X X X 2 RX ( ) mX 1 , ( 1/ ) 因此有 rX ( ) 2 X 1/ 1 r0 rX ( )d (1 )d 0 0 2
常数
RX (t , t | ) E[ X (t ) X (t ) | ]
E[ X (t ) X (t )] RX (t , t )
《随机信号基础》练习题

《随机信号分析》练习题一、 概念题1.叙述随机试验的三个条件。
2.写出事件A 的概率P(A)所满足的三个条件。
3.何谓古典概型?其概率是如何计算的? 4.两个事件独立的充要条件。
5.两个随机变量独立的充要条件。
6.两个随机过程的独立是如何定义的?7.随机变量X 服从正态分布,写出其概率密度函数表达式,并说明其中各个参数的意义。
8.简述一维随机变量分布函数F (x )的性质。
9.已知连续型随机变量X 的分布特性,分别用分布函数)(x F X 和概率密度函数)(x f X 表示概率}{21x X x P ≤<。
10. 随机变量X 的特征函数)(μX C 是如何定义的?写出由)(μX C 计算k阶矩)(k X E 的公式。
11.设X 1,X 2,…,Xn 为相互独立的随机变量,其特征函数分别为C 1(μ),C 2(μ),…,Cn(μ),设∑==n i i X Y 1,则C Y (μ)=?12. 对于一般的复随机变量,其数学期望、方差、协方差各是实数还是复数?13. 写出随机过程X(t)的n 维分布函数定义式。
14. 简述随机过程宽平稳性与严平稳性的区别。
15. 平稳过程与各态历经过程有何关系?16. 设平稳随机过程X(t)的自相关函数为R X (τ),X(t)依均方意义连续的条件是?17. 已知平稳随机过程X(t)、Y(t)的相关时间分别为X τ和Y τ,若X τ>Y τ,说明X(t) 与Y(t)的起伏程度那个较大?18. 两个随机过程广义联合平稳的条件是什么?19. 平稳随机过程)(t X 的功率谱密度)(ωX G 的物理意义是什么?)(ωX G 与物理谱密度有何关系?20. 白噪声的功率谱密度和自相关函数有何特点? 21. 简述维纳-辛钦定理并写出其表达式。
22. 何为线性系统?23. 写出希尔伯特变换器的频率响应、幅频响应和相频响应表达式。
24. 写出窄带过程的准正弦表达式和莱斯表达式。
随机信号分析习题二设正弦波随机过程为其中为常数;为均匀分布在内

随机信号分析习题二:1. 设正弦波随机过程为0()cos X t A w t =其中0w 为常数;A 为均匀分布在[0,1]内的随机变量,即1,01()0,others A a f a ≤≤⎧=⎨⎩(1) 试求00030,,,44t w w w πππ=时,()X t 的一维概率密度; (2) 试求02t w π=时,()X t 的一维概率密度。
2. 若随机过程()X t 为(),X t At t =-∞<<+∞式中,A 为在区间[0,1]上均匀分布的随机变量,求[()]E X t 及12(,)X R t t 。
3. 设随机振幅信号为0()sin X t V w t =其中0w 为常数;V 是标准正态随机变量。
求该随机信号的均值、方差、相关函数和协方差函数。
4. 设随机相位信号0()cos()X t a w t φ=+式中a 、0w 皆为常数,φ为均匀分布在[0,2]π上的随机变量。
求该随机信号的均值、方差、相关函数和协方差函数。
5. 设()sin(),X t A wt t θ=+-∞<<+∞,()sin(),Y t B wt t θφ=++-∞<<+∞,其中 A ,B ,w ,φ为实常数,~[0,2]U θπ,试求(,)XY R s t 。
6. 数学期望为()5sin X m t t =、相关函数为2210.5()12(,)3t t X R t t e --=的随机信号()X t 输入 微分电路,该电路输出随机信号()()Y t X t =。
求()Y t 的均值和相关函数。
7. 设随机信号3()cos2tX t Ve t =,其中V 是均值为5、方差为1的随机变量。
现设新的随机信号0()()tY t X d λλ=⎰。
试求()Y t 的均值、相关函数、协方差函数和方差。
8. 利用重复抛掷硬币的实验定义一个随机过程cos ,()2,t X t t π⎧=⎨⎩出现正面出现反面设“出现正面”和“出现反面”的概率都为1/2。
随机信号分析中文版答案

1≤ y ≤ 6
1 b−a
+∞ −∞
X 1 ⋅⋅⋅ X n 相互独立
φ X (ω ) = ∫
i
f X ( xi )e jω xi dxi
=∫
b
a
1 jω xi 1 1 jωb e dxi = (e − e jω a ) b−a b − a jω
(b+ a ) ⎛ (b − a )ω ⎞ jω 2 = Sa ⎜ ⎟e 2 ⎝ ⎠
π
2
−2+
π2
8
2 2 2 ∴ D [ x] = σ X =E⎡ ⎣x ⎤ ⎦ − E [ x] 2 =σy =
π
2
−2+
π2
8
−
π2
16
=
π2
16
+
π
2
−2
(4)
Rxy = E [ xy ]
π 1 π 2 2 xy sin ( x + y ) dxdy 2 ∫0 ∫0 π π ⎤ 1 π ⎡ = ∫ 2 x ⎢ − y cos ( x + y ) 02 + sin ( x + y ) 02 ⎥ dx 2 0 ⎣ ⎦
5
《随机信号分析》 课后习题答案
武汉理工大学信息工程学院
cx1x 2 = rx1x 2 − mx1mx 2 cx1x 2 ⎞ ⎛10 2 ⎞ ⎛c cx ( x1, x 2) = ⎜ x1x1 ⎟=⎜ ⎟ ⎝ cx 2 x1 cx 2 x 2 ⎠ ⎝ 2 10 ⎠
1 − f x ( x1 , x2 ) = e 192π
1.8 解: C XY = E[( x − mx )( y − m y )] = E[ XY ] − mx m y = m11 − mx m y
《现代数字信号处理》第2章习题答案

∞
∞
1 1− z
1 2 −1
+
1 3 1 −1 = ⋅ 1 1 −1 1− 2 z 4 (1 − 2 z )(1 − 1 2 z)
−1 1 (1 − 1 3 1 3 1 2 z ) (1 − 2 z ) = ⋅ ⋅ ⋅ = ⋅ −1 1 −1 1 1 −1 1 1 4 (1 − 2 z )(1 − 2 z ) (1 − 3 z ) (1 − 3 z ) 4 (1 − 3 z )(1 − 1 3 z )
1 1− ∑ a (k ) z
k =1 2 v p
−k
2 2 , Px ( z ) =H ( z ) H * (1/ z * ) σ w =σw
1 1− ∑ a (k ) e
k =1 p
2
− jkω
(b) Pz ( z ) = Px ( z ) + σ
2.4 设给定一个线性移不变系统,其系统函数为 H ( z ) = (1 −
σ ∑⎢ ⎣
i =1
N
⎡
2 x
−
2 2 1 2⎤ σx + σx ⎥ N N ⎦
=
N −1 2 σx N
(b) E
{(σ
2
x
− E {σ x }
2
)}
2
⎧⎛ 2 N − 1 2 ⎞ 2 ⎪ ⎫ ⎧ N − 1 2 2 ( N − 1) 2 4 ⎫ ⎪ ˆx − = E ⎨⎜ σ σ x ⎟ ⎬ = E ⎨σ x4 − 2 σ xσ x + σx ⎬ 2 N N N ⎝ ⎠ ⎩ ⎭ ⎪ ⎪ ⎩ ⎭
{ }
N
( N − 1) 2 4 σx N2
− x)
(I)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本章要点: 1、随机过程的概念 可理解为依赖于时间t的一族随机变量或 随机试验得到的一族时间t的函数。 2、随机过程的概率分布
p X ( x1 , x2 ,..., xn ; t1 , t 2 ,...,t n ) FX ( x1 , x2 ,..., xn ; t1 , t 2 ,...,t n ) x1x2 ...xn
2
3、随机过程的数字特征
数学期望
m X (t ) E[ X (t )] x p X ( x; t )dx
2 X 2
(t ) E[ X (t )] x 2 p X ( x ; t )dx 均方值
2 X (t ) D[ X (t )] E[{X (t ) m(t )}2 ] 方差
同理可得:
问题
FX ( x;2) P X (2) x
1 3 2 3
0, x 2 1 3, 2 x 5 FX ( x;6) P( X x,6) 2 3 , 5 x 7 1, x 7
1 3 ;x 3 3; 2 ;x 4 4; 3 6; 1 1; x 6 1 x FX ( x; 2) P X (2) x p( x)dx x 0 3
(2)解:由定义可知:
RX (t1, t2 ) E[ X (t1 ) X (t2 )];
由题知:
1
X (t1 )
1 1
2
sin t1
3
cos t1
X (t2 )
所以: R
X
sin t2
cos t2
(t1, t2 ) E[ X (t1 ) X (t2 )]; 1 (1 sin t1 sin t2 cos t1 cos t2 ); 3
(2)由自相关函数的定义: RX (t1 , t2 ) E[ X (t1 ) X (t2 )]
E[ A2 cos0t1 cos0t2 B2 sin 0t1 sin 0t2 ]
2[cos0t1 cos0t1 sin 0t1 sin 0t2 ]
E{[ A cos 0t1 B sin 0t1 ][ A cos 0t2 B sin 0t2 ]}
2.6
解:由图可得下表 ξ1 ξ2 4 7 ξ3 6 2
X(2) 3 X(6) 5 所以:
1 13 E[ X (2)] (3 4 6) ; 3 3
1 14 E[ X (6)] (5 7 2) ; 3 3 1 55 E[ X (2) X (6)] (3 5 4 7 6 2) ; 3 3
cos0 , 其中 t1 t2
2
2.10
解:由均值的定义:
E[ X (t )]
2 0
a a cos(0t ) p ( )d 2
2
0
cos( ot )d
由定义先求出均方值,就可以得到方差:
E[ X (t )] E[a cos (0t )] 2 1 cos(2 0 t 2 ) E[a ] 2 2 2 a a 2 cos(20t 2 )d 22 2 0 a 2
[ X (t2 ) f (t2 ) mX (t2 ) f (t2 )]}
CX (t1, t2 )
E{[ X (t1 ) mX (t1 )][ X (t2 ) mX (t2 )]}
2.9 解:(1)直接由定义可得:
E[ X (t )] E[ A cos(0t ) B sin(0t )] E[ A]cos(0t ) E[B]sin(0t ) 0
出现一个典型的错误:
182 E[ X (2) X (6)] E[ X (2)]E[ X (6)] ; 9
由定义可知:
FX ( x,2) P( X x,2);
显然在2这一时刻的可能取值为3,4,6; 可得:
0, x 3 1 3,3 x 4 P( X x, 2) 2 3 , 4 x 6 x6 1,
2.8 解:由定义出发:
E[Y (t )] E[ X (t ) f (t )];
E[ X (t )] E[ f (t )];
mX (t ) f (t )
由协方差的定义:
CY (t1, t2 ) E{[Y (t1 ) mY (t1 )][Y (t2 ) mY (t2 )]} E{[ X (t1 ) f (t1 ) mX (t1 ) f (t1 )]
2.11 解:
E[ X (t )] E[ A cos(0t )] E[ A]E[cos(0t )]
ada
0 1 2 0
1 cos(0t ) d 2
0
RX (t1, t2 ) E[ A cos(0t1 )cos(0t2 )]
2
2 2 2
0
所以:
2 2
a D[ X (t )] E[ X (t )] E[ X (t )] 2 RX (t1 , t2 ) E[ X (t1 ) X (t2 )]
2
E[a 2 cos(0t1 )cos(0t2 )] 2 a E[cos(0 (t1 t2 )) cos(0t1 0t2 2)] 2 2 a cos[ 0 (t1 t2 )] 0 2 2 a cos 其中 t1 t2 2
2.7 解:(1) 由题意可知
1 p(1 ) p ( 2 ) p (3 ) ; 3
所以 E[ X (t )] p(1 ) X (t ,1 ) p( 2 ) X (t , 2 ) p (3 ) X (t ,3 ) 1 (1 sin t cos t ) 3
x1 6
0
0
0
0
0 0
0
0 1/3
1/3
0 1/3
2/3
1/3 2/3
1
x2 7
问题
x2
x1
x2 2 2 x2 5
5 x2 7
x1 3
3 x1 4
4 x1 6
x1 6
0
0
0
0
0 0
0
1/9 2/9
1/3
2/9 4/9
2/3
1/3 2/3
1
x2 7
2.2
解: (1) 由于随机过程X(t)的样本具有确定的函 数形式( 为常数1,2,3),所以该随机过程 是确定性随机过程。 (2) 显然,任意时刻对应的随机变量是离散 随机变量,且具有相同的分布,所以概率密度 为:
p( x, t ) 0.6 ( x 1) 0.3 ( x 2) 0.1 ( x 3)
FX ( x1 , x2 ;2,6) P{ X (2) x1, X (6) x2}; P{( X (2) x1 X (6) x2 };
用表Байду номын сангаас来表示所求的联合分布:
x1
x2
x2 2 2 x2 5
5 x2 7
x1 3
3 x1 4
4 x1 6
互协方差函数
C XY (t1 , t 2 ) E[{X (t1 ) mX (t1 )}{Y (t 2 ) mY (t 2 )}]
两随机过程X(t)和Y(t)之间的统计独立、不相关和 正交概念 随机过程的特征函数 4、随机序列及其统计特性
重点及要求:
会计算随机信号的概率分布及各种数字特征; 对两随机过程X(t)和Y(t)之间的统计独立、不相关 和正交概念有明确认识;
0, x 3 1 3,3 x 4 P( X x, 2) 2 3 , 4 x 6 1, x 6
0, x 2 1 3, 2 x 5 P( X x, 6) 2 3 , 5 x 7 1, x 7
lim
t 0
RX (t , t t ) RX (t , t ) t
dRX (t ,t ) dt
证毕。
§1-2 逻辑代数基础
自相关函数
协方差函数
RX (t1 , t2 ) E[ X (t1 ) X (t2 )]
CX (t1 , t2 ) E[{X (t1 ) mX (t1 )}{X (t2 ) mX (t2 )}]
随机过程X(t)和Y(t)的互相关函数
RXY (t1, t2 ) E[ X (t1 )Y (t2 )]
E[ A2 ]E[cos(0t1 )cos(0t2 )] 1 cos 0 6
2.12 证明:
dX (t ) E[ X (t ) ] dt
X (t t ) X (t ) E[ X (t )lim ] t t 0
E[ X (t ) X (t t )] E[ X (t ) X (t )] lim t t 0
