随机信号分析2习题(供参考)
随机信号分析课后习题答案

1第一次作业:练习一之1、2、3题1.1 离散随机变量X 由0,1,2,3四个样本组成,相当于四元通信中的四个电平,四个样本的取值概率顺序为1/2,1/4,1/8,和1/8。
求随机变量的数学期望和方差。
解:875.087813812411210)(][41==⨯+⨯+⨯+⨯===∑=i i i x X P x X E81)873(81)872(41)871(21)870(])[(][2224122⨯-+⨯-+⨯-+⨯-=-=∑=i i i P X E x X D109.16471==1.2 设连续随机变量X 的概率分布函数为⎪⎩⎪⎨⎧≥<≤-+<=21201)](2πΑsin[0.500)(x x x x x F求(1)系数A ;(2)X 取值在(0.5,1)内的概率)15.0(<<x P 。
解:⎪⎩⎪⎨⎧<≤-π==其他0201)](2π[cos 2)()(x x A dx x dF x f 由1)(=⎰∞∞-dx x f得 2A 021)](2πAsin[1)]d (2π[cos 2=-=-π⎰∞∞-x x x A21A =35.042)]15.0(2[sin 21)]11(2[sin 21)5.0(F )1(F )15.0(==-π--π=-=<<x P1.3 试确定下列各式是否为连续随机变量的概率分布函数,如果是概率分布函数,求其概率密度。
(1)⎪⎩⎪⎨⎧<≥-=-000e 1)(2x x x F x (2)⎪⎩⎪⎨⎧≥<≤<=1110Α00)(2x x x x x F (3)0)]()([)(>--=a a x u x u a xx F (4)0)()()(>---=a a x u axa x u a x x F2解:(1)⎪⎩⎪⎨⎧<≥-=-000e 1)(2x x x F x 当0≥x 时,对于12x x ≥,有)()(12x F x F ≥,)(x F 是单调非减函数; 1)(0≤≤x F 成立;)()(x F x F =+也成立。
随机信号分析课后习题答案

随机信号分析课后习题答案随机信号分析课后习题答案随机信号分析是现代通信系统设计和信号处理领域中的重要基础知识。
通过对随机信号的分析,我们可以更好地理解和处理噪声、干扰等随机性因素对通信系统性能的影响。
下面是一些关于随机信号分析的课后习题及其答案,希望对大家的学习有所帮助。
1. 什么是随机信号?随机信号是在时间域上具有随机性质的信号。
与确定性信号不同,随机信号的每个样本值都是随机变量,其取值不是确定的。
随机信号可以用统计特性来描述,如均值、方差、功率谱密度等。
2. 什么是平稳随机信号?平稳随机信号是指在统计性质上不随时间变化的随机信号。
具体来说,平稳随机信号的均值和自相关函数不随时间变化。
平稳随机信号在实际应用中较为常见,因为它们具有一些方便的数学性质,可以简化信号处理的分析和设计。
3. 如何计算随机信号的均值?随机信号的均值可以通过对信号样本值的求平均来计算。
对于离散时间随机信号,均值可以表示为:E[x[n]] = (1/N) * Σ(x[n])其中,E[x[n]]表示信号x[n]的均值,N表示信号的样本数,Σ表示求和运算。
4. 如何计算随机信号的方差?随机信号的方差可以用均方差来表示。
对于离散时间随机信号,方差可以表示为:Var[x[n]] = E[(x[n] - E[x[n]])^2]其中,Var[x[n]]表示信号x[n]的方差,E[x[n]]表示信号的均值。
5. 什么是自相关函数?自相关函数是用来描述随机信号与其自身在不同时间延迟下的相似性的函数。
自相关函数可以用来分析信号的周期性、相关性等特性。
对于离散时间随机信号,自相关函数可以表示为:Rxx[m] = E[x[n] * x[n-m]]其中,Rxx[m]表示信号x[n]的自相关函数,E[ ]表示期望运算。
6. 如何计算随机信号的自相关函数?随机信号的自相关函数可以通过对信号样本值的乘积进行求平均来计算。
对于离散时间随机信号,自相关函数可以表示为:Rxx[m] = (1/N) * Σ(x[n] * x[n-m])其中,Rxx[m]表示信号x[n]的自相关函数,N表示信号的样本数,Σ表示求和运算。
随机信号分析(常建平,李林海)课后习题答案第二章习题讲解
A与 B独立 , f AB (a, b) f A (a) fB (b)
X (t) A Bt Y(t) A
A Y(t) X (t) Y (t)
B t
01 J1 1 1
t tt
1
xy 1
xy
f XY (x, y; t ) J f AB (a,b) t f AB ( y, t ) t f A ( y) f B ( t )
E X (t) E A cost XH cost EA XH
D X (t) E X 2 (t ) E2 X (t )
方法 2:
D X (t)
D Acost XH D Acost cos2 t DA cos2 t
12
D XH
公式: D aX+ bY a2 D X b2 D Y 2abC XY
RX (t1, t2 )=E Acost1 XH A cost2 XH
f X (x1;0)
1
x12 e 2,
2Байду номын сангаас
A
1
X (t)
~ N (0, )
t 30
2
4
f X ( x2; 3
)=
0
2 2
e
2
x2
2
,
X (t) t
=0,
f ( x3;2
)
0
20
( x3)
(离散型随机变量分布律 )
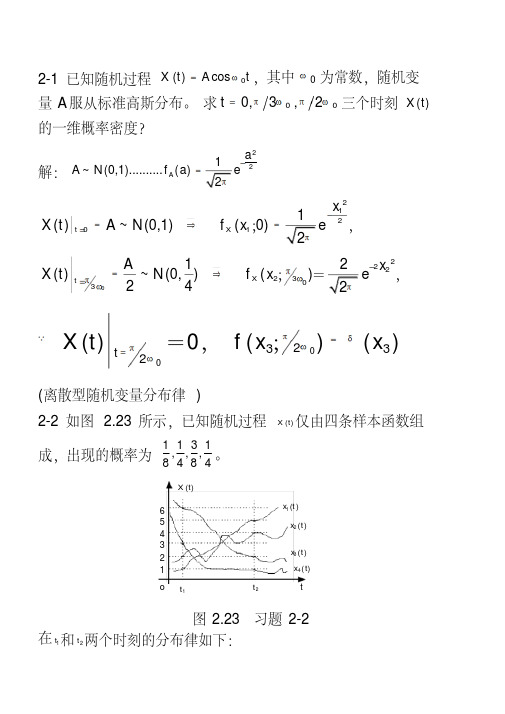
2-2 如图 2.23 所示,已知随机过程 X (t) 仅由四条样本函数组
成,出现的概率为
数 RX (t1, t2 ) ?②若已知随机变量相 A, B 互独立,
它们的概率密度分别为 f A (a) 和 f B (b) ,求 X (t) 的一
随机信号分析答案 哈工大

0 ≤ x <1 ,求 Y=5X+1 的概率密度函 其他
1.6 设随机变量 X 1 , X 2 ,⋅ ⋅ ⋅, X n 在[a , b] 上均匀分布,且互相独立。若 Y = ∑ X i ,求
i =1
n
(1)n=2 时,随机变量 Y 的概率密度。 (2)n=3 时,随机变量 Y 的概率密度。
⎧ 1 a≤ x≤b ⎪b − a ⎪ 解: f i ( xi ) = ⎨ i = 1,2,⋅ ⋅ ⋅, n ⎪0 其它 ⎪ ⎩ n=2 时, f Y ( y ) = f X 1 ( y ) ∗ f X 2 ( y )
-∞
⎧1 1.5 设随机变量 X 的概率密度为 f X ( x) = ⎨ ⎩0 数。 解:反函数 X = h(y) = (Y-1)/5 1≤y≤6 h′(y) = 1/5 fY (y) = fX (h(y))|h′(y)∣= 1 ×1/5 = 1/5 1≤ y ≤ 6 ⎧1 / 5 f Y ( y) = ⎨ 于是有 其他 ⎩ 0
⎧ X 1 = a1Y1 + b1Y2 ⎨ ⎩ X 2 = c1Y1 + d1Y2
( Y1 , Y2 )的联合概率密度为 证明:
⎧Y1 = aX 1 + bX 2 ⎨ ⎩Y2 = cX 1 + dX 2
f Y1Y2 ( y1 , y 2 ) =
1 f X X (a1 y1 + b1 y 2 , c1 y1 + d1 y 2 ) ad − bc 1 2
(4) F ( x) =
第二次作业:练习一之 4、5、6、7 题 1.4 随机变量 X 在[α,β]上均匀分布,求它的数学期望和方差。 解:因 X 在[α,β]上均匀分布 ⎧ 1 α≤下≤β ⎪ f ( x) = ⎨ β − α ⎪ 其他 ⎩0
北邮随机信号分析与处理第2章习题解答_2

不满足严格平稳。
思考:是否满足广义平稳?
3
2.17
随机过程由下述三个样本函数组成,且等概率发生:
X (t, e1 ) 1, X (t, e2 ) sin t, X (t, e3 ) cos t (1)计算均值 mX (t ) 和自相关函数 RX (t1 , t2 );
(2)该过程是否为平稳随机过程? 解: 1 1 1
ftp服务器地址
ftp://10.108.142.57
用户名和密码均为:sjxhfx
包括每次课的课件和部分习题解答
1
2.14
广义平稳随机过程 Y (t ) 的自相关矩阵如下,试确定矩阵中用 表示的元素。 2 1.3 0.4 2 1.2 0.8 RY 0.4 1.2 1.1 0.9 2 解:由自相关函数的性质
2
2.15
根据掷骰子试验,定义随机过程为
K X (t ) cos t ( K 1, 2,3, 4,5,6) 3 (1)求 X (1) 、X (2) 的概率密度; (2) X (t ) 是否为平稳随机过程?
解:
1/ 2, K 1,5 1/ 2, K 2, 4 K X (1) cos 1, K 3 3 1, K 6
E[ A(t1 ) A(t2 )cos t1 cos t2 ] E[ A(t1 ) B(t2 )cos t1 sin t2 ] E[ B(t1 ) A(t2 )sin t1 cos t2 ] E[ B(t1 ) B(t2 )sin t1 sin t2 ] RA (t1, t2 )cos t1 cos t2 RB (t1, t2 )sin t1 sin t2 R( )cos t1 cos t2 R( )sin t1 sin t2 R( )cos(t1 t2 ) R( )cos( )
随机信号习题2

一、填空题(20)1、 若)()()]()([2121t m t m t Y t X E Y X =,则随机过程()()X t Y t 与________(不相关、独立、正交);若联合平稳过程()()X t Y t 、的互功率谱密度XY S ()0ω=,则()()X t Y t 与_________(不相关、独立、正交);若(,;,)(,)(,)XY X Y f x t y t f x t f y t =,则()()X t Y t 、在同一时刻_______(不相关、独立、正交)。
2、 若随机过程()X t 的相关时间为1τ,()Y t 的相关时间为2τ,12ττ>,则()X t 比()Y t 的相关性要__强____,()X t 的起伏特性比()Y t 的要__小_____3、 两个高斯分布律的随机变量的卷积是___高斯_____分布律,它的均值和方差是原来两个高斯分布律的均值和方差的__代数和_____。
4、 白噪声通过理想低通系统后,功率谱密度变_窄__,相关性由_不相关___变为___相关_____。
二、简答题:(10)1、给出功率谱密度与相关函数的关系。
(5)2、给出狭义平稳随机过程和广义平稳随机过程的定义。
(5)三、考虑如图所示的系统,假定)()(t Y t X 、是统计独立的广义平稳随即过程。
求:(1)、根据)()(Y ττR R X 、,求)(Z τR ;(2)、根据)(G )(G Y ττ、X ,求)(G Z τ;四、已知)(t X 是0均值的高斯过程,求)()(2t X t Y =的自相关函数。
五、如图所示,若()X t 为平稳随机过程。
证明()Y t 的功率谱密度为: ()2()(1cos )Y X G G ωωωτ=+六、有限带宽的白噪声是具有如下常数功率谱密度函数的随机过程:00,0()()()220,X B B a G ωωωωω⎧≤-≤≤+⎪=⎨⎪⎩其它其中:0ω为中心频率,B 为带宽,a 为常数,求自相关函数()N R τ;七、设一随机过程()X t ,其中2[()],()()X E X t b R b b τδτ==+通过一物理可实现系统,其冲击响应为()()at h t e u t -=,求稳态输出()Y t 的自相关函数。
随机信号分析基础第二章习题

FX (x; 2) PX (2) x
x
p(x)dx
1
x
0
3
FX (x1, x2; 2, 6) P{X (2) x1, X (6) x2}; P{(X (2) x1 X (6) x2};
用表格来表示所求的联合分布:
x1
x2
x2 2
x1 3
0
3 x1 4 4 x1 6
CX (t1,t2 ) E[{X (t1) mX (t1)}{ X (t2 ) mX (t2 )}]
随机过程X(t)和Y(t)的互相关函数
RXY (t1,t2) E[X (t1)Y (t2)]
互协方差函数
CXY (t1,t2 ) E[{X (t1) mX (t1)}{Y (t2 ) mY (t2 )}]
RX (t1,t2) E[X (t1)X (t2)]
E[a2 cos(0t1 ) cos(0t2 )]
a2 2
E[cos(0
(t1
t2
))
cos(0t1
0t2
2)]
a2 2
cos[0 (t1
t2 )]
0
a2 cos
2
其中 t1 t2
2.11 解:
E[X (t)] E[Acos(0t )]
E{[X (t1) mX (t1)][X (t2) mX (t2)]}
CX (t1, t2 )
2.9 解:(1)直接由定义可得:
E[X (t)] E[Acos(0t) Bsin(0t)] E[A]cos(0t) E[B]sin(0t)
0
(2)由自相关函数的定义: RX (t1,t2) E[X (t1)X (t2)]
x,
2)
1 3
北邮随机信号分析与处理第2章习题解答_1

[ E ( X 2 ) E 2 ( X )] [ E ( XY ) E ( X ) E (Y )] t1 [ E ( XY ) E ( X ) E (Y )] t2 [ E (Y 2 ) E 2 (Y )] t1t2
mY (t ) E[ X (t ) (t )] E[ X (t )] (t ) mX (t ) (t )
协方差函数:
KY (t1 , t2 ) RY (t1, t2 ) mY (t1 )mY (t2 ) E{[( X (t1 ) (t1 )][ X (t2 ) (t2 )]} [mX (t1 ) (t1 )][mX (t2 ) (t2 )] E[ X (t1 ) X (t2 )] E[ X (t1 ) (t2 )] E[ X (t2 ) (t1 )] E[ (t1 ) (t2 )]
2 x1 x1 2 2 2 2 2 2 200 A0 x1 x3 50 A0 x12 x3
7
(0 x1 A0 , 250 x2 350, x1 x3 x1 )
2.5
X 3 的边缘概率分布为
x3
A0
350
250
f X1 X 2 X 3 ( x1 , x2 , x3 )dx2 dx1 2 x1
有
J1
1 a y
2 2
J2
1 a2 y2
于是
1 1 1 fY | A ( y | a ) 2 a 2 y 2 2
( y a)
1 a2 y2
1
a2 y2
9
2.5
由全概率公式
fY ( y ) f A (a ) fY | A ( y | a )dad f A (a) f ( ) fY | A ( y | a )dad
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.1 由下式定义的两电平二进制过程X(t)=A or – A,(n-1)T<t<nT 式中电平A 或-A 以等概率独立出现,T 为正常数,以及n=0,正负1,正负2,正负3……
(1)、画出一个样变函数的草图;(2)、它属于哪一类随机过程?
(3)、求一、二维概率密度函数。
(1)
(2) 所以是确定的。
(3)
2.2 设有下列离散随机过程:X (t )=C
C 为随机变量,可能取值为1,2,3,其出现的概率分别为0.6,0.3,0.1
(1) 是确定性随机过程?
(2 ) 求任意时刻X(t)的一维概密。
解:(1)是
(2) 1X(t)2,p(x,t)0.6(1)0.3(2)0.(3)3x x x δδδ⎧⎪==-+-+-⎨⎪⎩
2.3 已知随机过程X(t)为 00),t (Xcos )t (X ωω=是标准高斯随机变量是常熟X ,,求
X (t )的一维概率密度。
解:
发22x x cos(t)(,)(,)())cos(t)2cos (t)d x p x t F x t p dx ωωω'==- 2.4 利用投掷一枚硬币的实验定义随机过程为X(t)=cos πt,出现正面,2t ,出现反面,假设出现正面和反面的概论各位1/2,试确定X(t)的一维分布函数Fx(x;1/2), Fx(x;1),以及二维发布函数Fx(x1,x2;1/2,1).
解: x1 x2
X :(t=1/2) 0 1
Y (t=1) 1 2
2.5 随机过程X(t)由四条样本函数组成,如图题 2.6,出现的概论分别为p(§1)=1/8,p(§2)=1/4,p(§3)=3/8,p(§4)=1/4,求E[X(t1)],E[X(t2)],E[X(t1)X(t2)]及联合概率密度函数px(x1,x2;t1,t2)。
解:
2.6 随机过程X(t)由如题 2.6图所示的三条样本函数曲线组成,并以等概率出现,试求E[X(2)], E[X(6)], E[X(2)X(6)], Fx(x;2),Fx(x;6),Fx(x1,x2;2,6).
解:
()A or A A A k -=-=∑∞-∞=,;nT t h )t (X k k
X1 x2 x3
T1=2 3 4 6
E[X(2)]=3
13)643(31=++ E[X(6)]=314)752(31=++ E[X(2) X(6)]=155(3x54x76x2)33++= [])6x ()4x ()3x (3
1)x,2(f -+-+-=δδδ
2.7随机过程X(t)由三条样本函数构成,cost )3,t (X sint;)2,t (X ;1)1,t (X ===ξξξ ,并以等概率出现,求E (X(t)),和 R(t1,t2)
解:
2.8 已知随机过程X(t) 的均值为m(t), 协方差函数为C(t1,t2), 又知f(t)是确定的时间函
数,试求随机过程Y(t)=X(t)+f(t)的均值及协方差。
解:
2.9 随机过程X(t)为:)t (Acos )t (Acos )t (X 00ωω+= ,其中,0ω为常数,A,B 为两个相互独立的高斯变量,而且,E[A]=E[B]=0, 222]B [E ]A [E σ==, 试求X(t)的均值与自相关函数
解: 0)t (E[B]sin )t (E[A]cos )]t (Bcos )t (E[Acos )]t (E[X 0000=+=+=ωωωω
2.10 过程X(t)为:)t (acos )t (X 0Φ+=ω 式中a,0ω为常数,)2,0(~πΦ上均匀分布,
试求X(t)的均值、方差与自相关函数。
解:
2.11 随机过程X(t)为:)t (Acos )t (X 0Φ+=ω 式中0ω为常数,)2,0(~πΦ上均匀分布,
1a 0,
1)a (p <≤=,两个r.v.独立,试求X(t)的均值与自相关函数。
解:。
