第二章电光效应
电光效应

晶体的电光效应介质因电场作用而引起折射率变化的现象称为电光效应,介质折射率和电场的关系可表示为:+++=20bEaE n n (1)式中n 0是没有外加电场(E =0)时的折射率,a 和b 是常数,其中电场一次项引起的变化称为线性电光效应,由Pokels 于1893年发现,故也称为Pokels 效应;由电场的二次项引起的变化称为二次电光效应,由Kerr 在1875年发现,也称Kerr 效应,在无对称中心晶体中,一次效应比二次效应显著得多,所以通常讨论线性效应。
尽管电场引起折射率的变化很小,但可用干涉等方法精确地显示和测定,而且它有很短的响应时间,所以利用电光效应制成的电光器件在激光通信、激光测距、激光显示、高速摄影、信息处理等许多方面具有广泛的应用。
[实验目的]研究铌酸锂晶体的横向电光效应,观察锥光干涉图样,测量半波电压; 学习电光调制的原理和实验方法,掌握调试技能; 了解利用电光调制模拟音频光通信的一种实验方法;[实验原理]1. 晶体的电光效应按光的电磁理论,光在介质中传播的速度为210)(-==μεn c c ,ε为介电系数,是对称的二阶张量,即ji ij εε=,由此建立的D 和E 的关系为:j j i i E D ε= (3,2,1,=j i ) (2) 即:333232131332322212323132121111E E E D E E E D E E E D εεεεεεεεε++=++=++= 在各向同性的介质中,εεεε===332211,D 和E 成简单的线性关系,光在这类介质中以某一确定速度传播;但在各向异性的介质中,一般情况下各方向的折射率却不再相同,所以各偏振态的光传播速度也不同,将呈现双折射现象。
如果光在晶体中沿某方向传播时,各个方向的偏振光折射率都相等,则该方向称为晶体的光轴。
若晶体只含有一个这样的方向,则称为单轴晶体。
通常用折射率椭球来描述折射率与光的传播方向、振动方向的关系。
6-02电光、旋光效应

1 2
I0
sin2 (
no3V )
V V / 4
I线 性
交变输出光强
区
I
I0
I
电光晶体
N1
N2
0
V
V
/4
V
信 号
调制电信号
源
V
8
电光效应的应用
• 2.高速光闸
• 电光晶体以及具有电光效应的溶液对电场 的响应时间很短,~10-9s,在这一时间内可
以达到半波电压
• 打开或截止光路
,右旋θ,共转过2θ。
B
l
2
18
磁致旋光的应用
• 单通光闸:旋转方向与磁场方向有关
45
19
自动控制溶液浓度
转过角
转过 角
截止
光电探测器
浓度改变,
转过 角
导通 量糖术
20
光通信
• 使激光电矢量振动面偏转,再通过偏振片
对光强进行调制
(i)
I I (i)
交变信号源i
21
磁光克尔效应
• Magneto-optic Kerr effect (MOKE) • 被磁性介质反射的光,其偏振态发生变化 • 如果介质的磁性变化,对光的反射率也相应变化 • 依据介质磁矩相对于入射面的取向,分为三种
光的入射面
材料表面
y
x 极向MOKE 纵向MOKE 横向MOKE
z
nR nL 右旋
14
菲涅耳复合棱镜
• 将左旋石英和右旋石英三棱镜光轴平行依 次组合,做成复合棱镜
• 右旋晶体中,nR < nL ;左旋晶体中nL<nR
电光效应
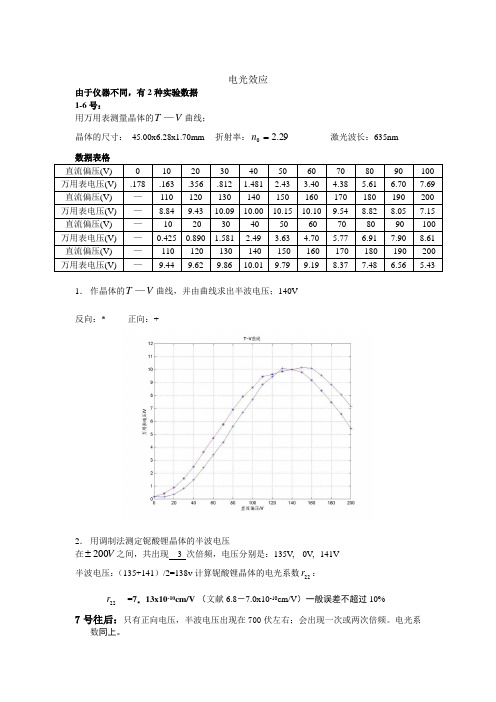
电光效应由于仪器不同,有2种实验数据 1-6号:用万用表测量晶体的V T —曲线;晶体的尺寸: 45.00x6.28x1.70mm 折射率:29.20=n 激光波长:635nm 数据表格 直流偏压(V) 0 10 20 30 40 50 60 70 80 90 100 万用表电压(V) .178 .163 .356 .812 1.481 2.43 3.40 4.38 5.61 6.70 7.69 直流偏压(V) — 110 120 130 140 150 160 170 180 190 200 万用表电压(V) — 8.84 9.43 10.09 10.00 10.15 10.109.54 8.82 8.05 7.15 直流偏压(V) — -10 -20 -30 -40 -50 -60 -70 -80 -90 -100 万用表电压(V) — 0.425 0.890 1.5812.493.634.705.776.917.908.61 直流偏压(V) — -110 -120 -130 -140 -150 -160 -170 -180 -190 -200 万用表电压(V)—9.449.629.8610.01 9.799.198.377.486.565.431. 作晶体的V T —曲线,并由曲线求出半波电压;140V反向:*正向:+2. 用调制法测定铌酸锂晶体的半波电压在V 200±之间,共出现 3 次倍频,电压分别是:135V, 0V , 141V 半波电压:(135+141)/2=138v 计算铌酸锂晶体的电光系数22r :22r =7.13x10-10cm/V (文献6.8-7.0x10-10cm/V )一般误差不超过10%7号往后:只有正向电压,半波电压出现在700伏左右;会出现一次或两次倍频。
电光系数同上。
注意作图要求:坐标纸、铅笔作图,数据点是否清晰标出,轴上的分度,变量名称、单位是否标出,是否有图名思考题及参考答案1. 本实验没有会聚透镜,为什么能看到锥光干涉?如何根据锥光干涉图调整光路? 没有会聚透镜时,需要用毛玻璃屏,经过毛玻璃屏漫反射产生各种不同方向的光。
电光效应

电光效应
泡克尔斯效应引起的相位差: 泡克尔斯效应引起的相位差:
∆ϕ p =
其中
2π
λ
3 no rV
—— 线性电光效应
no—o 光在晶体中的折射率; 光在晶体中的折射率; V —电压; 电压; r — 电光常数。 电光常数。
• 优点 :响应时间短,外加电压低,克尔效应的 响应时间短,外加电压低, 十分之一。 十分之一。 • 应用 : 电光开关、电光调制器。 电光开关、电光调制器。 如军用固体激光测距机。 如军用固体激光测距机。
电光效应
泡克尔斯效应(1893年 (2) 泡克尔斯效应(1893年)
P1 K K′ P2 ′
·
电光晶体
·
泡克尔斯盒
+ 。 。-
• 不加电场→ P2 无透射光 不加电场→ • 加电场→晶体变双轴晶体→原光轴方向附 加电场→晶体变双轴晶体→
加了双折射效应→ 有透射光。 加了双折射效应→ P2 有透射光。
电光效应
3. 磁致双折射效应
在外磁场作用下, 在外磁场作用下,某些非晶体也会显示出双 折射性质, 人为磁致双折射效应。 折射性质,称人为磁致双折射效应。 佛克脱效应: 佛克脱效应:发生于蒸汽中 科顿-穆顿效应:发生于液体中 科顿-穆顿效应:
ne − no = cλ0H
λo—光在真空中的波长; 光在真空中的波长; 光在真空中的波长 H—磁场强度; 磁场强度; C— 常数。 常数。
F ne − no = k S
光弹性效应
人为双折射产生的e光与 光与o光的位相差为 经人为双折射产生的 光与 光的位相差为
k⋅d ⋅2 π F ne − no + π = ∆ϕ = ⋅ +π λ λ S F 不同→ 不同→ 各处 不同→各处 ∆ϕ 不同→出现干涉条纹 S F 变→ ∆ϕ →干涉情况变。 变 干涉情况变。 S
电光效应
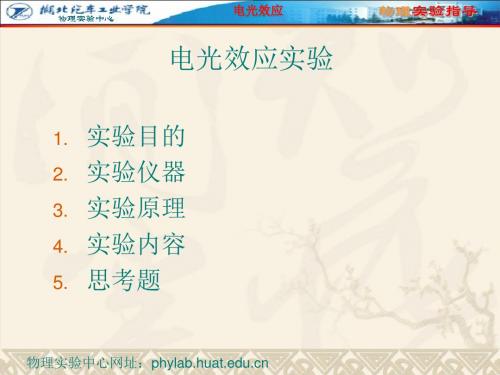
1. 一次电光效应和晶体的折射率椭球
在主轴坐标中,折射率椭球及其方程为
x2 y 2 z 2 2 2 1 2 nx ny nz
式中nx、ny、nz为椭球三个主轴方向上的折射 率,称为主折射率
折射率椭球
对于单轴晶体(如本实验所用的LN晶体)有nx = ny = no, nz = ne,于是
4
1 [1 cos( U m sin t )] 2 2 U
2U
1 [1 sin( U m sin t )] 2 U
U 1 [1 ( m )sin t ] 2 U
即
T sin t
调制器输出的信号和调制信号虽 然振幅不同,但是两者的频率却 是相同的,输出信号不失真,为 线性调制
输出信号仍是“倍频”失真的信号
直流偏压U0在0伏附近或在 U 附近变化时, 由于工作点不在线性工作区,输出波形将失真 当 U 0 U 2 ,Um> U 时,调制器的工作点虽然选定 在线性工作区的中心,但不满足小信号调制的要求,工作 点虽然选定在了线性区,输出波形仍然是失真的。
物理实验中心网址:
性电光效应
物理实验中心网址:
电光效应
物理实验指导
2. LN晶体的横向电光调制
横向电光调制器如下图所示:
起偏器的偏振方向平行于电光晶体的x轴,检偏器的偏振方向平行于y轴,因 此入射光经起偏器后变为振动方向平行于x轴的线偏振光,它在晶体的感应轴 x′和y′上的投影的振幅和相位均相等,将位于晶体表面(z=0)的光波设为
电光效应
物理实验指导
三、实验原理
电光效应:对晶体外加电场产生的人为双折射的现象。 电光效应分为: 一次电光效应(普克尔斯效应):介质折射率变化正比于电场强度 二次电光效应(克尔效应):介质折射率变化正比于电场强度的平方
耦合波导理论

第二章线性电光效应的耦合波理论 2001年,She 等人提出一种全新的理论,它从麦克斯韦方程出发,考虑二阶非线性极化强度(也就是只考虑线性电光效应),忽略其余高阶极化强度,推出关于线性电光效应的耦合波方程,得到在电场作用下的晶体中光的两个独立电场分量的解析解。
这种方法,可运用于研究光在任意一个方向的电场作用下沿任意方向传播的各种线性电光效应的情况,并且不单可以用于研究光的振幅调制,也可以容易去解决光的相位调制问题。
另外对于给定的一个晶体(点群),能根据需要利用该理论进行优化设计。
这全新的耦合波理论相对折射率椭球理论来说,它的物理图象清晰,得到的结果是解析解,不用再作任何数学变换。
我们不单可以方便地进行优化设计,而且也可用于电光调制器等电光器件性能的分析。
它的出现拓展电光材料的选择范围和优化调制器的调制方式,从而引起了电光效应研究领域内新一轮的探索。
2.1 理论推导波在介质中传播时,能够通过介质内的非线性极化而相互作用将导致形形色色的非线性光学现象,如高次谐波、参量转换、受激散射等等。
电光效应就是其中的一种非线性光学现象。
电(波)与光(波)的互作用,实质上又可以看作是几个处于不同波段的电磁波在非线性介质中的波耦合过程,因此可以象非线性光学那样,通过求解耦合波方程来获得电光作用的有关知识。
对于普克尔效应,是入射波为光+)(ω电波)(m ω产生一个输出光波)(m ωω+的三波耦合过程。
对于电光效应,它涉及到的是光与物质的相互作用,光是由麦克斯韦方程或场方程描述,物质体系是由光学布洛方程描述。
于是我们采用类似非线性光学方法,首先给出相应的非线性极化强度,把电场所感生的附加极化矢量当成一个微扰量P ∆,再将它视为新的极化光源引入麦克斯韦波动方程,通过整理最后可得到相应的耦合波方程。
线性电光效应耦合波理论就是以麦克斯韦波动方程为基础和出发点推导出来的。
我们可以由麦克斯韦方程组和物质方程推导出:220222)()]([)(t t P t c t E t E NLS ∂∂-=∂⋅∂+⨯∇⨯∇με (2-1) 根据矢量运算规则,E E E 2)(∇-⋅∇∇=⨯∇⨯∇ (2-2)这样可得:2202222)()]([)()]([t t P t c t E t E t E NLS ∂∂-=∂⋅∂+∇-⋅∇∇με (2-3) ε 为介质的相对介电张量,0μ为真空中的磁导率,c 为真空中的光速,E (t )为介质中的总电场强度,)(t P NLS 为只与电场强度E(t)有关的介质非线性极化强度,暂不考虑旋光效应。
高等光学-光在各向异性介质中的传播2-电光效应
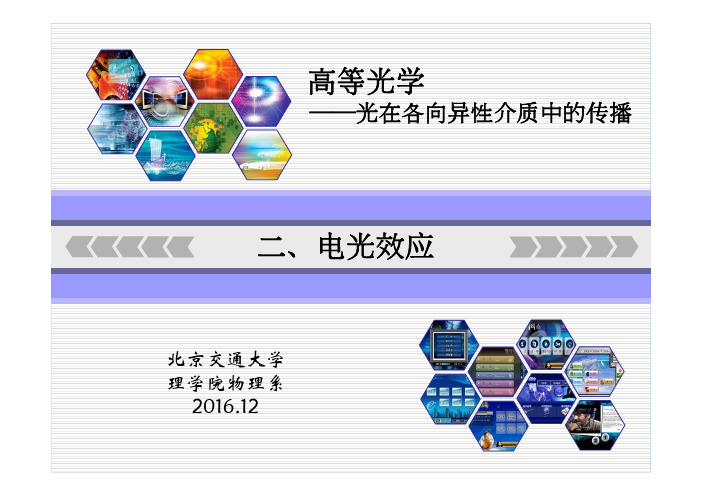
1二、主要内容电光效应:由电场引起的折射率变化; 磁光效应:由磁场引起的折射率变化; 弹光效应:由应力引起的折射率变化。
—>外界的各种因素引起晶体介电系数ε变化—>引起折射率n变化—>改变光的传播性质感应双折射:rr n με=++221E n ε()2312n n bE aE ++=二次电光效应/克尔效应(KDP(磷酸二氢钾)晶体外形图●光轴方向:x3轴;●四次旋转-反演对称轴:●二次旋转对称轴:KDP晶体外形图KDP晶体的线性电光张量:外加电场E 后,KDP晶体的折射率椭球方程为222222++n z n y n x eo oKDP晶体外形图由偏振光干涉理论:()hUdn d n n oe o λγπλπ32+-=纵向泡克尔斯效应横向泡克尔斯效应()hUdn d n n oe o λγπλπ32+-=光波传播方向与外电场方向垂直,无需透明电极有关,可提高d/h 来降低半波电压;存在自然双折射引起的相位差,易受温度影响。
-光波x’1x’1x’3DV yz yx zV通过检偏器输出的光强I与通过起偏器输入的光强I0之比I/I0为:δI光束通过玻璃光楔后的偏转若光线沿x 2′轴方向入射,振动方向为x 1′轴方向,则根据前面的分析可知:光在下面棱镜中的折射率为:在上面棱镜中,由于电场与该棱镜的x 3方向相反,所以折射率为:因此,上下光的折射率之差为:光束穿过偏振器后的偏转角为:式中,h 为x 3方向晶体宽度,l 为光线传播方向晶体的长度。
3633'121E n n n o o γ+=↓3633'121E n n n o o γ-=↑3633'1'1E n n n n o γ-=-=∆↓↑36333633U n Dhl E n D l o o γγθ==41The end。
光电效应

3、当入射光的频率大于极限频率时,光电流 强度与入射光的强度有关。
从光电管阴极射出的光电子具有一定的动能,
为了测量光电子的动能,可以在光电管的两个电
极上加上反向电压,如图所示,用于阻止光电子
到达阳极。
第二章 波粒二象性 第一节 光电效应
实验
一、光电效应
❖ 1.什么是光电效应? 物体在光的照射下发射电子的现象,
称为光电效应。发射出来的电子称为光电 子。
疑问:光电子的发射与什么因素有 关呢?为了研究这个问题,我们来 认识一种光学器件。
光电管
1.光电管就是利用光电效应把光信号转变 成电信号的一种传感器。
巩固练习
1、在演示光电效应的实验中,原来不带电 的一块锌板与灵敏验电器相连,用弧光灯照 射锌板时,验电器指针张开一个角度,如图 所示,这时 ( B ) A.锌板带正电,指针带负电 B.锌板带正电,指针带正电 C.锌板带负电,指针带正电 D.锌板带负电,指针带负电
2、若用绿光照射某种金属板不能发生光电效 应,则下列哪一种方法可能使该金属发生光 电效应( )
❖ 4.光电流强度的决定因素:当入射光频率ν>ν0 时,光电流随入射光强度的增大而增大.
A.光电子的动能随照射光频率的增大而增大 B.光电子的初速度与照射光的频率成正比 C.光电子的最大初动能与照射光的频率成正比 D.光电子的最大初动能随照射光频率的增大而增大
6、用绿光照射一光电管能产生光电效应,欲使光电 子从阴极逸出时的最大初动能增大应( )
A.改用红光照射
B.增大绿光的强度
D
C.增大光电管上的加速电压
探究光电流的大小
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 从电的角度来看,物质系统是正、负电荷 (或偶极子)束缚在一 起组成的。
•施加外电场必然会引起内部束缚电荷分布及电性 质的变化,从而导致物质光学特性的变化。这种 电致光学性质的变化统称为广义电光效应。 •其光性质的变化包括光的频率、振幅、相位、偏 振状态、传播方向等的变化。利用电场来控制光 的变化,无疑有广泛的科学技术价值。 效应与电场成正比的称为线性电光效应,与电场 平方成正比的称为平方(或非线性)电光效应。
3.光波导中电光改向与调制 • 如图2-7所示;
•在光波导层的表面制作叉 指形电极,加上电压后波 导层内的折射率将呈周期 性变化,好似一个“光 栅”。如果光以θ角入射, 在 2θ 方向上将得衍射光线, 衍射光的强度 I 随电压 V 变 化。 2 (BV) • I=I sin •式中B是与波导层折射率 O 及电光系数有关的系数。
1、氢原子的线性斯塔克效应 在外电场中原子光谱 线的分裂,归因于原子能 级的简并。
•主量子数 n 一定的能级,含有 若干角量子数l和磁量子数 m 不同的量子态。无外场时这 些量子态具有近似相同的能 量, •施加外电场以后,简并被部 分地或全部地解除。 •简并解除后,不同组合量子态 将具有不同的能量。一个简并 能级便分裂为多个能级。
•氢原子第一激发态的行为好象一个偶极矩的行为3ea0 的 电偶极子的行为,它相对外场E有三种取向:
•一种是平行外场,一种是反平行外场场,还有一体是垂 直外场取向,
•对应的附加能量是-3 e a0 E, 3 e a0 E和 0
•因 此 , 在 外 电 场 中 , n = 2 的 能 级 分 裂 成 三 个 级 。 对n=3的能级,会作类似分裂。由于能级的分裂, n =3和n =2能级之间的跃迁谱线,将由一条谱线分裂为 多条谱线。可能的跃迁如图2-2所示。
1、氢原子的线性斯塔克效应 •氢原子的第一激发态(n= 2)就是四度简并的,标 明 这 四 个 量 子 态 的 波 函 数 可 记 为 ψ2,0,0 , ψ2,1,0 , ψ2,1,1,ψ2,1,-1。施加外电场后,组合量子态为
•Ψ1=1/2( ψ2,0,0-ψ2,1,0);
•Ψ2=1/2( ψ2,0,0+ψ2,1,0)
第2节 泡克尔斯效应
•1893年德国物理学家泡克尔斯发现 •原本具有双折射的晶体,当加上直流或低频电压时,晶体的 双折射特性会发生变化,后来人们称它为泡克尔场效应。
•泡克尔斯广泛地研究了这个效应,确认电压诱 发的这双析射效应正比于所加电压或电场的一 次方,故又称它为线性电光效应。 •线性电光效应仅在无中心对称的晶体中存在,在 32 种晶体对称性中,有 20 种显示泡克尔斯效应, 有泡克尔斯效应的晶体同样也具有压电效应。
• 两个互相垂直的光振动的位相差为π。式中V λ/2称为半波电压。它是使二者之间产生λ/2 的光程差或π的相位差所加的电压。这时KD P出射的仍然是线偏振光,但偏振方向正好平 行偏振器P2的偏振化方向,从KDP出来的 为椭圆偏振光,对应不同的电压,从P2出射 的光强为 • I = I 0 sin2Δφ/ 2 = I 0 sin2 [π/ 2 • V/Vλ/2] (2-3) • 这就是利用泡克尔斯效应进行电光强度或振 幅调制和光开关的原理。
不加外电场,对单轴晶体,光 轴沿Z方向,当光沿Z轴方向 传播不会发生双折射;相应于 主折射率轴分别为n0、ne(n0 为对寻常光O光, ne对非常光 e光的折射率),沿X、Y轴的 主折射率没有差别, 若沿Z轴方向加电场E,这时晶体不再是单轴晶体,而成为双 轴晶体,X、Y轴也不再是主轴,Xˊ、Yˊ轴却成为主轴。当光 振动平行于Xˊ轴,相应的主折射率变成nxˊ,光传播的速度为 υzˊ;当光振动平行于Yˊ轴,相应的主折射率变成nyˊ,光传 播的速度为υz″;光振动沿不同方位有不同折射率和传播速度。 电场改变了主轴,并使两个主轴折射率有了差异。
类似地,由 ψ2,1,1, ψ2,1,-1的线性组合可得两个组合 量子态。后两个组合量子态能量位移为零, ψ1的能量位移为3ea0E,ψ2的能量位移为一3ea0E , 其中a0为玻尔半径,e为电子电量,E为外电场强度。
1、氢原子的线性斯塔克效应
•这种能量位移量,很象一个偶极子与外电场下 之间的相互作用能。
• 斯塔克效应的观察不如后面将要叙述 的塞曼效应那么容易。因为原子的内电场 很强。以氢原子基态为例,玻尔轨道附近 的电场高达5X109 V/cm,106 V/cm的外电 场(已不易产生)较之内电场也只算得是 一个微拢。因此,在原子物理学中斯塔克 效应远不如塞曼效应那样引人注意和感兴 趣。但近些年随着里德堡原子的发现和产 生这种原子技术的提高,斯塔克效应的价 值又开始受到重视。
3、里德堡原子和斯塔克效应
对于原子,存在大量激发态,一个原子中如果有一个电子处于主 量子数n很大的高激发态,便称为里德堡(Rydberg)原子。 •里德堡原子特性奇特,它的原子半径约为基态原子半径的105倍,庞 大的尺度,可以包容另一原子于其中;它也是长寿命的,它极易受外 场影响,相当弱的电场就会引起里德堡原子的强烈畸变,也可被磁场 挤压变形。 •里德堡原子的存在,开辟了原子物理研究的新领域,即研究经典力学 和量子力学交界的地带。这对于理解量子现象是很有意义的。 •里德堡原子的研究还对激光同位素分离、等离子体诊断、射电天文等, 有令人感兴趣的技术和科学价值。激光同位素分离的原理是基于同位 素核质量的差异会引起谱线产生位移和差异,利用激光对某同位素进 行选择性光电离,便可达到分离同位素的目的。测定灼热星体周围存 在的里德堡原子发射谱线的强度和宽度,可估算星体温度,谱线的位 置可提供有关星体距离和速度的信息。 •当原子处于高激发态成为里德堡原子后,和氢原子一样,在外电场中 会有显著的线性斯塔克效应。里德堡原子由斯塔克效应引起的能级的 总劈裂宽度近似与 n2成正比。(ΔE≈3/2 n2E)因此,里德堡原子产生 线性斯塔克效应的电场低得多,
•但是,如图2-6所示,只要将电光调制器加上正反馈,将输出 光的一部分由光探测器接收变成电信号并放大,用这放大的 电信号去控制加在电光晶体上的电压,正反馈产生的非线性 使装置具有如图2-5(b)所示的双稳特性,这便成了一 个光学双稳器。 • 光学双稳器可用来作为二进制光逻辑部件,也可作为光控 开关,对光脉冲进行限幅和整形,在光通信和光计算中有重 要的应用。
前述电光强度调制器是用加 在电光晶体上的调制电压去控制 光的输出,也就是用加在电光晶 体上的电压改变互相垂直的光振 动分量通过晶体产生的相位差, 达到调制输出光强的目的。在调 制电压一定的情况下,输出光强 与输入光强呈线性关系。
放大器 Ii ⊙
光电探测器
It
P1 偏振片 P 2 偏振片
图2-6 光学双稳装
泡克尔斯效应折射率与电压关系
• 纵向光电效应:(E电场//Z主轴,光//E)引起主折射率的变化
• n= n´y-n´x=n0363E ( 63为光电系数) • 偏振方向沿x´ ,y´的两列光波,沿z方向传播距离L,
电场引起的光程差nL,相位差2 nL / 0即(V=EL) • =2n0363EL / 0 = 2n0363V/ 0(2-1) •横向光电效应: (E电场Z主轴)引起主折射率的变化
第3节电光克尔效应 •
第一个电光效应是苏格兰物理 学家克尔( John Kerr )在 1875 年 发现的。他发现
•某些各向同性的透明物质处在电 场E中变成了双折射物质,这现 象被称为电光科尔效应。
•如 图 2 - 8 所 示 , 有 各 向 同 性 物 质 •电光克尔效应与泡克尔斯效应的差别 (如液体),在与透射光垂直的方向上 是:这效应中折射率变差与电场强度 施加高电压,各向同性物质便出现各向 的平方成正比,是二次电光效应,所 用材料不是压电晶体,而是原本无双 异性特征。这时,它很象一个单轴晶体, 折射的各向同性物质;泡克尔斯效应 光轴与所加电场方向一致。 是一次电光效应,是改变原本有双折 •对平行和垂直电场的光振动,物质显 射的晶体的双折射特性。 现的折射率(光速)不同,分别为ne •液体中的电光克尔效应,可归因于电 和no,它们的差为: 场使具有各向异性的分子趋于沿电场方 2 •Δ n=ne-no=Kλ 0E 向取向排列所致。在这里,单个分子的 •式中,K 称为克尔常数,λ 0是光在真 各向异性是重要的。对于固体,情况相 当复杂,但总的效果是要造成各向异性。 空的波长。
•n= n´y-nz=n0363E / 2 •沿x´传播距离为d,对应y´ 、z偏振相位差为:
• = 2 nd = n0363Ed/ 0 • = n0363 ( d / L ) V / 0 (2-2) •泡克尔斯效应提供了用电场控制光传播和光强度的方法
1.电光调制器
•电光晶体( KDP) 两端做涂层透明 电极,通过它对 kDP 施加电场。无 外加电场 V=0时,入射光通过偏振 片 P1 ,线偏振光通过它时无双折 射,,遇光轴与偏振器 P1 光轴(偏 振化方向)垂直的偏振器 P2 ,出射 光为零。 •当在光传播方向(KDP光轴方向) 施加电压V后,kDP的主轴便由X、 Y轴变到X ′Y′轴。偏振方向沿X 轴 的线偏振光的振幅A将向X ′Y′ 轴分 解为Ax′Ay′,成为两列偏振方向垂 直的线偏振光。 •它们在KDP中传播具有不同的速度, 在 KDP 出口处的相位差由式( 2 一 1 ) 决定。在出口处是同频率的两个互 相垂直的光振动的叠加,当电压 •V=V / 2 = 0 / 2n0363
2、二阶斯塔克效应
•按量子力学分析,一个原子具有永久偶极矩的 条件是未被外场拢动时能级是简并的,且含有相 反宇称的量子态,氢原子属这种情形。 •对于无永久偶极矩的原子,外加电场会使原子 正负电荷中心分离引起极化,产生附加诱导偶极 矩,这偶极矩正比于外电场E , •即P=E, 为原子静电极化率, • 与所有量子数有关,对每种电子组态 都是不 同的。这诱导偶极矩又处于外电场中,与外电场 相互作用的附加能量ΔE=1/2 E2。对不同量子 态,有不同 和不同能量位移,致使产生不同能 级分裂和谱线分裂。
