您的位置：360文档中心› 浙江省杭州市锦绣育才教育集团2019-2020学年第二学期八年级入学测试(PDF版,无答案)

浙江省杭州市锦绣育才教育集团2019-2020学年第二学期八年级入学测试(PDF版,无答案)

合集下载

浙江省杭州市拱墅区锦绣育才中学2019--2020学年八年级9月月考科学试题

浙江省杭州市拱墅区锦绣育才中学2019--2020学年八年级9月月考科学试题
B．b密度计排开的液体的液体重力较大
C．a密度计底部受到的液体压强较大
D．两烧杯底部所受液体压强相等
20．将一底面积为0.01m2的长方体木块用细线栓在一个空容器的底部，然后向容器中缓慢加水直到木块上表面与液面相平，如图甲所示，在此整个过程中，木块底部受到水的压强随容器中水的深度的变化如图乙所示，则下列说法不正确的是（）
A．26.7克B．30克C．31.6克D．35克
16．小船和密度为0.5g/m3的木块一起漂浮在水中,将木块从船中取出放入水中后,你将观察到的现象是
A．船身上浮一些,水面下降B．船身上浮一些,水面不变
C．船身下降一些,水面上升D．船身下降一些,水面不变
17．20℃时,甲、乙两烧杯硝酸钾饱和溶液的质量分别为500克和600克,在下列条件下析出晶体质量相同的是( )
浙江省杭州市拱墅区锦绣育才中学2019--2020学年八年级9月月考科学试题
学校:___________姓名：___________班级：___________考号：___________
一、选择题
1．在下列四个选项中，水循环最活跃的是（）
A．地表裸露的沙漠地区
B．森林覆盖良好的水库区
C．长江、黄河发源的地区
11．如图是港珠澳大桥海底隧道一施工现场。起重船“振华30”将长方形沉管放入水至全部浸没的过程中，“振华30”主船体所受浮力的变化图像是
A． B．
C． D．
12．在70℃时,73克氯化铵饱和溶液中含有氯化铵23克,则70℃时氯化铵溶解度S的计算式错误的是( )
A．S/100=23/（73-23）B．S/（100+S）=23/73
A．20℃时，甲、乙两杯都蒸发掉100g水B．甲杯蒸发掉50g水，乙杯蒸发掉60g

浙江杭州拱墅锦绣育才2019-2020学年中考数学模拟调研测试题

浙江杭州拱墅锦绣育才2019-2020学年中考数学模拟调研测试题

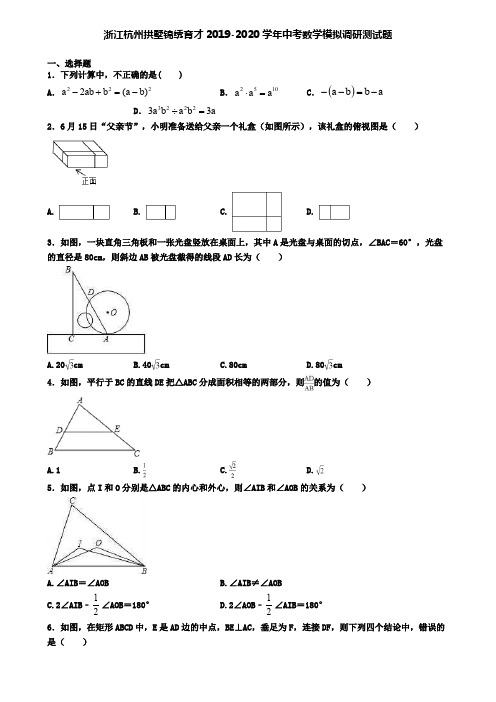
浙江杭州拱墅锦绣育才2019-2020学年中考数学模拟调研测试题一、选择题1．下列计算中，不正确的是( )A ．222a 2ab b (a b)-+=-B ．2510a a a ⋅=C ．()a b b a --=-D ．32223a b a b 3a ÷=2．6月15日“父亲节”，小明准备送给父亲一个礼盒（如图所示），该礼盒的俯视图是（ ）A. B. C. D.3．如图，一块直角三角板和一张光盘竖放在桌面上，其中A 是光盘与桌面的切点，∠BAC ＝60°，光盘的直径是80cm ，则斜边AB 被光盘截得的线段AD 长为（ ）A.20cmB.40cmC.80cmD.80cm4．如图，平行于BC 的直线DE 把△ABC 分成面积相等的两部分，则的值为（ ）A.1B.C.D.5．如图，点I 和O 分别是△ABC 的内心和外心，则∠AIB 和∠AOB 的关系为（ ）A.∠AIB ＝∠AOBB.∠AIB≠∠AOBC.2∠AIB ﹣12∠AOB ＝180°D.2∠AOB ﹣12∠AIB ＝180° 6．如图，在矩形ABCD 中，E 是AD 边的中点，BE ⊥AC ，垂足为F ，连接DF ，则下列四个结论中，错误的是（ ）A.△AEF ～△CABB.CF=2AFC.DF=DCD.tan ∠CAD=34 7．如图，抛物线y ＝ax 2+bx+c 的对称轴是x ＝13，小亮通过观察得出了下面四个结论：①c ＜0，②a ﹣b+c ＞0，③2a ﹣3b ＝0，④5b ﹣2c ＜0．其中正确的有（ ）A ．1个B ．2个C ．3个D ．4个8．如图，在△ABC 中，BC ＝4，BC 边上的中线AD ＝2，AB+AC ＝，则S △ABC 等于（ ）A B ．2 C ．D ．29．下列计算正确的是（ ）A.﹣a 4b÷a 2b ＝﹣a 2bB.（a ﹣b ）2＝a 2﹣b 2C.（﹣a ）2•a 4＝a 6D.1133a a-= 10．如图，在△ABC 中，∠C=50°，∠B=35°，分别以点A ，B 为圆心，大于12AB 的长为半径画弧，两弧相交于点M ，N ，直线MN 交BC 于点D ，连接AD ．则∠DAC 的度数为（ ）A ．85°B ．70°C ．60°D ．25°11．下列方程中，有实数根的是( )A 1=0B ．11x x +=C ．2x 4+3＝0D ．111x =-- 12．下列计算正确的是（ ）A ．a 3+a 4＝a 7B ．a 4•a 5＝a 9C ．4m •5m ＝9mD ．a 3+a 3＝2a 6二、填空题13．在△ABC 中，BC=a ．作BC 边的三等分点C 1，使得CC 1：BC 1=1：2，过点C 1作AC 的平行线交AB 于点A 1，过点A 1作BC 的平行线交AC 于点D 1，作BC 1边的三等分点C 2，使得C 1C 2：BC 2=1：2，过点C 2作AC 的平行线交AB于点A2，过点A2作BC的平行线交A1C1于点D2；如此进行下去，则线段A n D n的长度为______________.14．一组数据3，4，x，5，7的平均数是5，则这组数据的中位数是_____．15．在一个不透明的布袋中有除颜色外其它都相同的红、黄、蓝球共200个，某位同学经过多次摸球试验后发现，其中摸到红色球和蓝色球的频率稳定在35%和55%，则口袋中可能有黄球________个．16．已知扇形的圆心角为60°，半径为2，则扇形的弧长为________（结果保留π）．17．在x2+（________）+4=0的括号中添加一个关于x的一次项．．．，使方程有两个相等的实数根.18．在平面直角坐标系xOy中，点A，B的坐标分别为（m，3），（m+2，3），直线y＝3x+b与线段AB 有公共点，则b的取值范围为_____．（用含m的代数式表示）三、解答题19．某网店经营一种品牌水果，其进价为10元/千克，保鲜期为25天，每天销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示.(1)求y与x的函数关系式；(2)当该品牌水果定价为多少元时，每天销售所获得的利润最大？(3)若该网店一次性购进该品牌水果3000千克，根据(2)中每天获得最大利润的方式进行销售，发现在保鲜期内不能及时销售完毕，于是决定在保鲜期的最后5天一次性降价销售，求最后5天每千克至少降价多少元才能全部售完？20．如图，在平面直角坐标系xOy中，将直线y＝x向右平移2个单位后与双曲线y＝ax（x＞0）有唯一公共点A，交另一双曲线y＝kx（x＞0）于B．（1）求直线AB的解析式和a的值；（2）若x轴平分△AOB的面积，求k的值．21．解一元二次方程（1）（x﹣1）2＝4（2）x2﹣4x+1＝022．在△ABC中，AC＝4，BC＝2，点D在射线AB上，在构成的图形中，△ACD为等腰三角形，且存在两个互为相似的三角形，则CD的长是_____．23．实施新课程改革后，学生的自主学习、合作交流能力有很大提高，张老师为了了解所教班级学生自主学习、合作交流的具体情况，对本班部分学生进行了为期半个月的跟踪调查，并将调查结果分成四类，A：特别好；B：好；C：一般；D：较差；并将调查结果绘制成以下两幅不完整的统计图，请你根据统计图解答下列问题：（1）本次调查中C类女生有名，D类男生有名；将上面的条形统计图补充完整；（2）计算扇形统计图中D所占的圆心角是；（3）为了共同进步，张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习，请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.24．如图是在写字台上放置一本数学书和一个折叠式台灯时的截面示意图，已知数学书AB长25cm，台灯上半节DE长40cm，下半节CD长50cm．当台灯灯泡E恰好在数学书AB的中点O的正上方时，台灯上、下半节的夹角即∠EDC＝105°，下半节CD与写字台FG的夹角即∠DCG＝75°，求BC的长．(书的厚度和台灯底座的宽度、高度都忽略不计，F，A，O，B，C，G在同一条直线上，参考数据：0.1)25．问题再现：数形结合是解决数学问题的一种重要的思想方法，借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性，从而可以帮助我们快速解题．初中数学里的一些代数公式，很多都可以通过表示几何图形面积的方法进行直观推导和解释．例如：利用图形的几何意义推证完全平方公式．将一个边长为a的正方形的边长增加b，形成两个矩形和两个正方形，如图1，这个图形的面积可以表示成：（a+b）2或a2+2ab+b2∴（a+b）2＝a2+2ab+b2这就验证了两数和的完全平方公式．问题提出：如何利用图形几何意义的方法推证：13+23＝32 如图2，A表示1个1×1的正方形，即：1×1×1＝13，B 表示1个2×2的正方形，C与D恰好可以拼成1个2×2的正方形，因此：B、C、D就可以表示2个2×2的正方形，即：2×2×2＝23，而A、B、C、D恰好可以拼成一个（1+2）×（1+2）的大正方形，由此可得：13+23＝（1+2）2＝32尝试解决：请你类比上述推导过程，利用图形几何意义方法推证：13+23+33＝（要求自己构造图形并写出推证过程）类比归纳：请用上面的表示几何图形面积的方法探究：13+23+33+…+n3＝（要求直接写出结论，不必写出解题过程）实际应用：图3是由棱长为1的小正方体搭成的大正方体，图中大小正方体一共有多少个？为了正确数出大小正方体的总个数，我们可以分类统计，即分别数出棱长是1，2，3和4的正方体的个数，再求总和．例如：棱长是1的正方体有：4×4×4＝43个，棱长是2的正方体有：3×3×3＝33个，棱长是3的正方体有：2×2×2＝23个，棱长是4的正方体有：1×1×l＝13个，然后利用（3）类比归纳的结论，可得：＝图4是由棱长为1的小正方体成的大正方体，图中大小正方体一共有个．逆向应用：如果由棱长为1的小正方体搭成的大正方体中，通过上面的方式数出的大小正方体一共有44100个，那么棱长为1的小正方体一共有个．【参考答案】***一、选择题13．123nna-14．5 15．2016．2 3π17．4x±（只写一个即可）18．﹣3﹣3m≤b≤3﹣3m ．三、解答题19．（1）10300y x =-+；（2）该品牌水果定价为20元时，每天销售所获得的利润最大；（3）最后5天每千克至少降价10元才能全部售完.【解析】【分析】（1）依据题意利用待定系数法可得出每天的销售量y （千克）与销售单价x （元/千克）之间函数关系：y=-10x+300，（2）根据销售利润=销售量×（售价-进价），列出平均每天的销售利润w （元）与销售价x （元/千克）之间的函数关系式进行求解即可；（3）根据题意列出不等式[]20100510(20)3003000m ⨯+--+≥进行求解即可.【详解】 （1）设y kx b =+，将10,200（）和15,150（）代入y kx b =+得：20010,15015,k b k b =+⎧⎨=+⎩解得10,300k b =-⎧⎨=⎩， ∴10300y x =-+；（2）设每天销售所获得的利润为W ,则(10)(10300)W x x =--+2104003000x x =-+-21020)1000x =--+（，∵10＜x ≤30，∴当20x =时，W 取最大值1000，答：该品牌水果定价为20元时，每天销售所获得的利润最大.（3）将20x =代入10300y x =-+，得100y =，设最后5天每千克一次性降价m 元，依题意得：[]20100510(20)3003000m ⨯+--+≥，解得10m ≥，所以最后5天每千克至少降价10元才能全部售完.【点睛】本题考查了二次函数在实际生活中的应用．最大销售利润的问题常利用函数的增减性来解答，我们首先要吃透题意，确定变量，建立函数模型，然后结合实际选择最优方案．其中要注意应该在自变量的取值范围内求最大值（或最小值）20．（1）y ＝x ﹣2，a ＝﹣1；（2）k ＝3．【解析】【分析】（1）根据平移的性质求出一次函数的解析式，根据无交点求出a 的值， （2）解方程组12y x y x ⎧=⎪⎨⎪=-⎩可求出A 的坐标是（1，﹣1），由x 轴平分△AOB 的面积，可知B 的纵坐标是1，代入一次函数解析式可求出B 的坐标是（3，1），即可求出答案．【详解】（1）直线y ＝x 向右平移2个单位后的解析式是y ＝x ﹣2，即直线AB 的解析式为y ＝x ﹣2，得：x ﹣2＝a x，则x 2﹣2x ﹣a ＝0， △＝4+4a ＝0，解得：a ＝﹣1，（2）由（1）可得方程组12y x y x ⎧=⎪⎨⎪=-⎩，解得：11x y =⎧⎨=-⎩， A 的坐标是（1，﹣1），∵x 轴平分△AOB 的面积，∴B 的纵坐标是1，在y ＝x ﹣2中，令y ＝1，解得：x ＝3，则B 的坐标是（3，1），代入y ＝k x可得：k ＝3． 【点睛】本题考查了一次函数和反比例函数的交点问题，根的判别式，平移的性质，三角形的面积的应用，及待定系数法求反比例函数解析式，题目是一道比较好的题目，难度适中．21．（1）x 1＝3或x 2＝﹣1（2）x 1＝x 2＝2【解析】【分析】（1）运用直接开平方法解方程即可；（2）先利用配方法得到（x ﹣1）2＝9，然后利用直接开平方法解方程；【详解】解：（1）x ﹣1＝±2，∴x ﹣1＝2或x ﹣1＝﹣2，解得：x 1＝3或x 2＝﹣1；（2）x 2﹣4x ＝﹣1，x 2﹣4x+4＝3，（x ﹣2）2＝3，x ﹣2所以x 1＝x 2＝2【点睛】本题考查了解一元二次方程，熟练掌握解一元二次方程的方法是解题的关键．．22或2 【解析】【分析】分两种情形：①如图1中，当点D 在线段AB 上，DC=AD ，且△BCD ∽△BAC 时，设CD=x ，BD=y ．②如图2中，当点D 在AB 的延长线上时，AC=AD=4，△DCB ∽DAC ．设CD=x ，BD=y ，分别构建方程组求解．【详解】①如图1中，当点D 在线段AB 上，DC ＝AD ，且△BCD ∽△BAC 时，设CD ＝x ，BD ＝y ，则有：BC CD BD AB AC BC==，∴224y xx y==+，解得：x y∴CD．②如图2中，当点D在AB的延长线上时，AC＝AD＝4，△DCB∽DAC．设CD＝x，BD＝y，则：CD BC DB DA AC DC==，∴244x yx ==，解得x＝2，y＝1，∴CD＝2，综上所述，满足条件的CD或2．【点睛】本题考查了相似三角形的性质，根据相似三角形的性质得到方程组是解题的关键，学会用分类讨论的思想思考问题．23．（1）2；1；（2）36°；（3）P（一男一女）=12.【解析】【分析】(1)由扇形统计图可知,特别好的占总数的15%,人数有条形图可知3人,所以调查的样本容量是:3÷15%,即可得出C类女生和D类男生人数（2）用D的人数除以总人数再乘360°即可得到D的圆心角;（3）根据被调査的A类和D类学生男女生人数列表即可得出答案【详解】（1）3÷15%=20,20×25%=5.女生:5-3=21-25%-50%-15%=10%20×10%=2,男生:2-1=1故答案为:,2,1（2）从图中得到D 的人数为2人，总人数为20，236020⨯°=36° （3）画出树状图（或列表）∴共有6种等可能结果，其中一男一女的有3种，故P （一男一女）=3162= 【点睛】 此题考查条形统计图，扇形统计图，列表法，解题关键在于看懂图中数据24．BC 的长约为9.1cm ．【解析】【分析】过点D 作DM ⊥FG 于M ，DN ⊥EO 于N ，则四边形DMON 是矩形，解直角三角形求出CM 和DN 的长度，结合矩形的知识求出OM 的长，最后根据BC ＝OM ﹣CM ﹣BO 求出答案．【详解】如图，过点D 作DM ⊥FG 于M ，DN ⊥EO 于N ，在Rt △CDM 中，∵CD ＝50，∠DCM ＝75°， ∴CM CD ＝cos ∠DCM ， ∴50CM ＝cos70°≈0.26， 解得，CM≈13．∵DN ∥FG ，∴∠CDN ＝∠DCG ＝75°，在Rt △DEN 中，∵∠EDN ＝∠CDE ﹣∠CDN ＝105°﹣75°＝30°，DE ＝40， ∴DN DE ＝cos ∠EDN ，∴40DN ＝cos30°＝2，解得，DN＝≈34.6．∵∠DNO＝∠NOM＝∠DMO＝90°，∴四边形DNOM是矩形，∴OM＝DN≈34.6，∴BC＝OM﹣CM﹣BO≈34.6﹣13﹣12.5＝9.1(cm)．答：BC的长约为9.1cm．【点睛】本题考查解直角三角形、等腰直角三角形的性质、锐角三角函数，解答本题的关键是明确题意，找出所求问题需要的条件，利用锐角三角函数解答．25．（1）（1+2+3）2；（2）（1+2+3+…+n）2；（3）13+23+33+43，（1+2+3+4）2，100个；（4）8000．【解析】【分析】根据规律可以利用相同的方法进行探究推证，由于是探究13+23+33＝？肯定构成大正方形有9个基本图形（3个正方形6个长方形）组成，如图所示可以推证．实际应用：根据规律求大正方体中含有多少个正方体，可以转化为13+23+33+…+n3＝（1+2+3+…+n）2来求得．逆向应用：可将总个数看成m2，然后再写成＝（1+2+3+…+n）2得出大正方形每条边上有几个棱长为1的小正方体，进而计算出棱长为1的小正方体的个数．【详解】解：如图，A表示1个1×1的正方形，即1×1×1＝13；B表示1个2×2的正方形，C与D恰好可以拼成1个2×2的正方形，因此B、C、D就可以拼成2个2×2的正方形，即：2×2×2＝23；G与H、E与F和可以拼成3个3×3的正方形，即：3×3×3＝33；而整个图形恰好可以拼成一个（1+2+3）×（1+2+3）的大正方形，因此可得：13+23+33＝（1+2+3）2＝62．故答案为：（1+2+3）2或62．根据规律可得：13+23+33+…+n3＝（1+2+3+…+n）2．依据规律得：13+23+33+43＝（1+2+3+4）2＝102＝100．故答案为：13+23+33+43＝（1+2+3+4）2 100∵44100＝2102＝（1+2+3+…+n）2∴n＝20∴20×20×20＝8000故答案为8000．【点睛】此题是用几何直观推导13+23+33+…+n3的计算过程，通过几何图形之间的数量关系做出几何解释，得出规律，然后应用解决问题．采用归纳推理，由易到难，逐步得出结论．。

2024届杭州市锦绣育才教育科技集团数学八下期末复习检测试题含解析

2024届杭州市锦绣育才教育科技集团数学八下期末复习检测试题含解析

2024届杭州市锦绣育才教育科技集团数学八下期末复习检测试题考生须知：1．全卷分选择题和非选择题两部分，全部在答题纸上作答。

选择题必须用2B 铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。

2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。

3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

一、选择题(每小题3分,共30分)1．不等式组21241x x x x ＞＜-⎧⎨+-⎩的解集为（ ）A ．x ＞13B ．x ＞1C ．13＜x ＜1 D ．空集2．已知点(2,3)-在反比例函数(0)ky k x =≠的图象上，则下列点也在该函数图象上的是（ ）A ．(1,5)B ．(1,5)-C ．(3,2)D ．(2,3)-3．方程211x x =-的解是（ ）A ．x ＝3B ．x ＝2C ．x ＝1D ．x ＝﹣14．如图，图象（折线OEFPMN ）描述了某汽车在行驶过程中速度与时间的函数关系，下列说法中错误的是（ ）A ．第3分时汽车的速度是40千米/时B ．第12分时汽车的速度是0千米/时C ．从第3分到第6分，汽车行驶了120千米D ．从第9分到第12分，汽车的速度从60千米/时减少到0千米/时5．如图，在平行四边形ABCD 中，DE 平分∠ADC 交BC 于E ，AF ⊥DE ，垂足为F ，已知∠DAF ＝50°，则∠B ＝（）A ．50°B ．40°C ．80°D ．100°6．等腰三角形的腰长为5cm ,底边长为6cm ,则该三角形的面积是（ ）A ．16321y x =+B ．224cmC ．3232(2)131y =⨯-+=-≠D ．212cm7．下列多项式中，能用平方差公式因式分解的是（ ）A ．22m n -+B ．222a ab b -+C ．22m n +D ．22a b --8．随着电子制造技术的不断进步，电子元件的尺寸大幅度缩小，在芯片上某种电子元件大约只有0.0000007（毫米2），数据0.0000007用科学记数法表示为（ ）A ．6710-⨯B ．60.710-⨯C ．7710-⨯D ．87010-⨯9．如图所示，DE 是△ABC 的中位线，点F 在DE 上，且∠AFB ＝90°，若AB ＝5，BC ＝8，则EF 的长为（ ）A ．32B ．4C ．52D ．110．如图，点M 是正方形ABCD 边CD 上一点，连接AM ，作DE ⊥AM 于点E ，作BF ⊥AM 于点F ，连接BE . 若AF =1，四边形ABED 的面积为6，则B F 的长为（ ）A ．2B ．3C ．10D ．13二、填空题(每小题3分,共24分)11． 如图，在平面直角坐标系中，四边形AOBC 是菱形．若点A 的坐标是（6，8），则点C 的坐标是_____．12．计算：2221()-＝_____．13．中美贸易战以来，强国需更多的中国制造，中芯国际扛起中国芯片大旗，目前我国能制造芯片的最小工艺水平已经达到7纳米，居世界前列，已知1纳米=0.000000001米，用料学记数法将7纳米表示为______米.14．请你写出一个一次函数，使它经过二、三、四象限_____．15．勾股定理，是几何学中一颗光彩夺目的明珠，被称为“几何学的基石”．中国是发现和研究勾股定理最古老的国家之一．中国古代数学家称直角三角形为勾股形，较短的直角边称为勾，另一直角边称为股，斜边称为弦，所以勾股定理也称为勾股弦定理．三国时期吴国赵爽创制了“勾股圆方图”（如图）证明了勾股定理．在这幅“勾股圆方图”中，大正方形ABCD是由4个全等的直角三角形再加上中间的那个小正方形EFGH组成的．若小正方形的边长是1，每个直角三角形的短的直角边长是3，则大正方形ABCD的面积是_____．16．关于x的方程21111x mx x-=+++无解，则m的值为________.17．若一直角三角形的两直角边长为3，1，则斜边长为_____．18．如图，已知点A是第一象限内横坐标为3的一个定点，AC⊥x轴于点M，交直线y＝﹣x于点N．若点P是线段ON上的一个动点，∠APB＝30°，BA⊥PA，则点P在线段ON上运动时，A点不变，B点随之运动．求当点P从点O运动到点N时，点B运动的路径长是_____．三、解答题(共66分)19．（10分）如图，在等腰直角三角形ABC中，∠ACB=90°，BE⊥CE于E,AD⊥CE于D,AD=5cm，DE=3cm．（1）求证△CBE≌△ACD（2）求线段BE的长20．（6分）阅读材料：分解因式：x2+2x-3解：原式=x 2+2x+1-4=（x+1）2-4=（x+1+2）（x+1-2）=（x+3）（x-1）此种方法抓住了二次项和一次项的特点，然后加一项，使这三项成为完全平方式，我们把这种分解因式的方法叫配方法．请仔细体会配方法的特点，然后尝试用配方法解决下列问题：（1）分解因式x 2-2x-3=_______；a 2-4ab-5b 2=_______；（2）无论m 取何值，代数式m 2+6m+13总有一个最小值，请你尝试用配方法求出它的最小值；21．（6分）某商店购进一批小家电，单价40元，第一周以每个52元的价格售出180个，商店为了适当增加销量，第二周决定降价销售。

杭州市2019-2020学年八年级第二学期期末学业质量监测数学试题含解析

杭州市2019-2020学年八年级第二学期期末学业质量监测数学试题含解析

杭州市2019-2020学年八年级第二学期期末学业质量监测数学试题一、选择题（每题只有一个答案正确）1．已知锐角三角形的边长是2，3，x ，那么第三边x 的取值范围是（ ） A ．1＜x ＜5B ．513x <<C ．135x <<D ．515x <<2．△ABC 与△DEF 的相似比为，则△ABC 与△DEF 的面积比为（ ）A ．B ．C ．D ．3．为了解某校计算机考试情况，抽取了50名学生的计算机考试成绩进行统计，统计结果如表所示，则50名学生计算机考试成绩的众数、中位数分别为（ ） 考试分数（分） 20 16 12 8 人数 24 18 53A ．20，16B ．l6，20C ．20，l2D ．16，l24．将点P （2，1）沿x 轴方向向左平移3个单位，再沿y 轴方向向上平移2个单位，所得的点的坐标是（ ） A ．（1，1）B ．（-1，3）C ．（5，1）D ．（5，3）5．如图，有一个平行四边形ABCD 和一个正方形CEFG ，其中点E 在边AD 上.若40ECD ∠=︒，25AEF ︒∠=,则B 的度数为（ ）A ．55ºB ．60ºC ．65ºD ．75º6．将两个全等的直角三角形纸片构成如图的四个图形，其中属于中心对称图形的是（ ）A ．B ．C ．D ．7．如图，点A ，B ，C ，D 在一次函数2y x m =-+的图象上，它们的横坐标分别是-1，0，3，7，分别过这些点作x 轴、y 轴的垂线，得到三个矩形，那么这三个矩形的周长和为（ ）A ．614m -B ．52C ．48D ．872m -8．在平面直角坐标系xOy 中，线段AB 的两个端点坐标分别为A(-1，-1)，B(1，2)，平移线段AB 得到线段A’B’（点A 与A’对应），已知A’的坐标为(3，-1)，则点B’的坐标为( ) A ．(4，2)B ．(5，2)C ．(6，2)D ．(5，3)9．下列图案中，既是轴对称图形又是中心对称图形的是( )A ．B ．C ．D ．10．如图，四边形ABCD 中，//AD BC ，90ABC DCB ∠+∠=︒，且2BC AD =，以AB ，BC ，CD 为边向外作正方形，其面积分别为1S ，2S ，3S ．若14S =，264S =，则3S 的值为( )A ．8B ．12C ．24D ．60二、填空题11．每本书的厚度为0.62cm ，把这些书摞在一起总厚度h （单位：cm ）随书的本数n 的变化而变化，请写出h 关于n 的函数解析式_____．12．如果关于x 的方程2420x x m -+=有实数根，则m 的取值范围是_______________． 13．直线y=x+1与y=-x+7分别与x 轴交于A 、B 两点，两直线相交于点C ，则△ABC 的面积为___． 14．对甲、乙两台机床生产的同一种零件进行抽样检测（抽查的零件个数相同），其平均数、方差的计算结果是：机床甲：15x =甲，20.03s =甲；机床乙：15x =乙，20.06s =乙．由此可知：____（填甲或乙）机床性能较好．15．一元二次方程 22310x x --=的一次项系数为_________．16．通过测量一棵树的树围(树干的周长)可以计算出它的树龄．通常规定以树干离地面1.5 m 的地方作为测量部位．某树栽种时的树围为5 cm ，以后树围每年增长3 cm.假设这棵数生长x 年其树围才能超过2.4 m ．列满足x 的不等关系：__________________. 17．若30a b ab +-=，则11a b+=____． 三、解答题18．某校为了丰富学生的课外体育活动，购买了排球和跳绳，已知排球的单价是跳绳的单价的3倍，购买跳绳共花费了750元，购买排球共花费900元，购买跳绳的数量比购买排球的数量多30个，求跳绳的单价．19．（6分）已知：关于x 的方程240x x m ++=有两个不相等的实数根． （1）求m 的取值范围；（2）若m 为正整数，且该方程的根都是整数，求m 的值．20．（6分）随着车辆的增加，交通违规的现象越来越严重，交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理（速度在30﹣40含起点值30，不含终点值40），得到其频数及频率如表： 数据段 频数 频率 30﹣40 10 0.05 40﹣50 36 c 50﹣60 a 0.39 60﹣70 b d 70﹣80 20 0.10 总计2001（1）表中a 、b 、c 、d 分别为：a ＝ ； b ＝ ； c ＝ ； d ＝ （2）补全频数分布直方图；（3）如果汽车时速不低于60千米即为违章，则违章车辆共有多少辆？21．（6分）如图，△ABC 中，∠ACB ＝90°，D 是AB 中点，过点B 作直线CD 的垂线，垂足为E ，求证：∠EBC＝∠A．22．（8分）阅读下列题目的解题过程：已知a、b、c为△ABC的三边，且满足a2c2﹣b2c2=a4﹣b4，试判断△ABC的形状．解：∵a2c2﹣b2c2=a4﹣b4（A）∴c2（a2﹣b2）=（a2+b2）（a2﹣b2）（B）∴c2=a2+b2（C）∴△ABC是直角三角形问：（1）上述解题过程，从哪一步开始出现错误？请写出该步的代号：；（2）错误的原因为：；（3）本题正确的结论为：．23．（8分）如图，一次函数y＝﹣12x+4的图象与x轴y轴分别交于点A、点B，与正比例函数y＝32x的图象交于点C，将点C向右平移1个单位，再向下平移6个单位得点D．（1）求△OAB的周长；（2）求经过D点的反比例函数的解析式；24．（10分）甲、乙两车间同时开始加工—批服装．从开始加工到加工完这批服装甲车间工作了9小时，乙车间在中途停工一段时间维修设备，然后按停工前的工作效率继续加工，直到与甲车间同时完成这批服装的加工任务为止．设甲、乙两车间各自加工服装的数量为y(件)．甲车间加工的时间为x（时），y与x 之间的函数图象如图所示．（1）甲车间每小时加工服装件数为件；这批服装的总件数为件；（2）求乙车间维修设备后，乙车间加工服装数量y与x之间的函数关系式；（3）求甲、乙两车间共同加工完1140件服装时甲车间所用的时间．25．（10分）随着移动终端设备的升级换代，手机已经成为我们生活中不可缺少的一部分，为了解中学生在假期使用手机的情况（选项：A．和同学亲友聊天；B．学习；C．购物；D．游戏；E．其它），端午节后某中学在全校范围内随机抽取了若干名学生进行调查，得到图表（部分信息未给出）：根据以上信息解答下列问题：（1）这次被调查的学生有多少人？（2）求表中m，n，p的值，并补全条形统计图．（3）若该中学约有800名学生，估计全校学生中利用手机购物或玩游戏的共有多少人？并根据以上调查结果，就中学生如何合理使用手机给出你的一条建议．参考答案一、选择题（每题只有一个答案正确）1．B【解析】【分析】由三角形三条边的关系得1＜x＜5，由于该三角形是锐角三角形，再结合勾股定理求出由锐角三角形变为直角三角形的临界值.【详解】首先要能组成三角形，由三角形三条边的关系得1＜x＜5；下面求该三角形为直角三角形的边长情况（此为临界情况）：当3为斜边时，由勾股定理，22+x2=32，解得x=5.当x 为斜边时，由勾股定理，22+32=x2，解得x=13，综上可知，当5＜x＜13时，原三角形为锐角三角形．故选B．【点睛】本题考查了三角形三条边的关系和勾股定理，解题的是由勾股定理求出x的临界值，再结合三角形三条边的关系求出x的取值范围.2．D【解析】【分析】直接根据相似三角形的性质即可得出结论．【详解】解：∵△ABC∽△DEF，且△ABC与△DEF相似比为1：4，∴△ABC与△DEF的面积比=（）2=1：16，故答案为：D【点睛】本题考查的是相似三角形的性质，熟知相似三角形的面积的比等于相似比的平方是解答此题的关键．3．A【解析】【分析】找中位数要把数据按从小到大的顺序排列，位于最中间的一个数（或两个数的平均数）为中位数，众数是一组数据中出现次数最多的数据，注意众数可以不止一个．【详解】解：在这一组数据中20是出现次数最多的，故众数是20；将这组数据从大到小的顺序排列后，处于中间位置的数是1，1，那么这组数据的中位数1． 故选：A ． 【点睛】本题为统计题，考查众数与中位数的意义，中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数．众数是一组数据中出现次数最多的数． 4．B 【解析】 【分析】根据平移的方法：横坐标，右移加，左移减；纵坐标，上移加，下移减，即可得结论． 【详解】解：将点P （2，1）沿x 轴方向向左平移3个单位，再沿y 轴方向向上平移2个单位，所得的点的坐标是（-1，3）． 故选：B ． 【点睛】本题考查了坐标与图形变化-平移，解决本题的关键是，在平面直角坐标系内，把一个图形各个点的横坐标都加上（或减去）一个整数a ，相应的新图形就是把原图形向右（或向左）平移a 个单位长度；如果把它各个点的纵坐标都加（或减去）一个整数a ，相应的新图形就是把原图形向上（或向下）平移a 个单位长度．（即：横坐标，右移加，左移减；纵坐标，上移加，下移减．） 5．D 【解析】 【分析】首先根据180AEF FEC DEC ︒∠+∠+∠=,结合已知可得DEC ∠的度数,进而计算D B ∠=∠的度数. 【详解】解：根据平角的性质可得180AEF FEC DEC ︒∠+∠+∠= 25AEF ︒∠=又四边形CEFG 为正方形90FEC ︒∴∠=∴ 65DEC ︒∠=在三角形DEC 中180DEC ECD D ︒∠+∠+∠=40ECD ∠=︒75D ︒∴∠=四边形ABCD 为平行四边形75B D ︒∴∠=∠=故选D. 【点睛】本题主要考查平角的性质和三角形的内角定理，这些是基本知识，必须熟练掌握. 6．C ． 【解析】试题分析：A 、不是中心对称图形，故此选项错误； B 、不是中心对称图形，故此选项错误； C 、是中心对称图形，故此选项正确； D 、不是中心对称图形，故此选项错误． 故选C ．考点：中心对称图形． 7．C 【解析】 【分析】根据一次函数的图像与直角坐标系坐标特点即可求解. 【详解】由题意可得()1,2A m -+，()7,14D m -+.∴()()2712214C m m =--++--+⎡⎤⎡⎤⎣⎦⎣⎦总163248=+=. 故选C. 【点睛】此题主要考查一次函数的图像，解题的关键是熟知直角坐标系的特点. 8．B 【解析】试题解析：根据A 点的坐标及对应点的坐标可得线段AB 向右平移4个单位，然后可得B′点的坐标． ∵A （﹣1，﹣1）平移后得到点A′的坐标为（3，﹣1），∴向右平移4个单位，∴B （1，2）的对应点坐标为（1+4，2），即（5，2）． 故选B ． 9．B【解析】 【分析】根据轴对称图形与中心对称图形的概念求解． 【详解】A 、是轴对称图形，不是中心对称图形，故此选项错误；B 、是轴对称图形，也是中心对称图形，故此选项正确；C 、不是轴对称图形，是中心对称图形，故此选项错误；D 、不是轴对称图形，是中心对称图形，故此选项错误． 故选B ． 【点睛】考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合． 10．B 【解析】 【分析】过A 作//AE CD 交BC 于E ，则AEB DCB ∠=∠，依据四边形AECD 是平行四边形，即可得出CE AD =，AE CD =，再根据勾股定理，即可得到222BE AB AE =+，进而得到3S 的值．【详解】如图，过A 作AE //CD 交BC 于E ，则AEB DCB ∠∠=，AD //BC ，∴四边形AECD 是平行四边形，CE AD ∴=，AE CD =，ABC DCB 90∠∠+=︒，AEB ABC 90∠∠∴+=︒， BAE 90∠∴=︒，222BE AB AE ∴=+，BC 2AD =， BC 2BE ∴=，2221BC AB CD 4∴=+，即31644S 4⨯=+， 3S 12∴=，故选B ． 【点睛】本题考查了平行四边形的判定与性质，勾股定理，正确添加辅助线，熟练掌握和灵活运用相关知识是解题的关键. 二、填空题 11．h=0.62n 【解析】 【分析】依据这些书摞在一起总厚度h （cm ）与书的本数n 成正比，即可得到函数解析式. 【详解】每本书的厚度为0.62cm ，∴这些书摞在一起总厚度h （cm ）与书的本数n 的函数解析式为0.62h n =.故答案为：0.62h n =. 【点睛】本题主要考查了根据实际问题确定一次函数的解析式，找到所求量的等量关系是解决问题的关键. 12．2m ≤ 【解析】分析：根据方程的系数结合根的判别式,即可得出△=16-8m≥0,解之即可得出m 的取值范围. 详解：∵关于x 的方程2420x x m -+=有实数根, ∴△=(-4)²-4×2m=16-8m≥0, 解得:m≤2 故答案为:m≤2点睛：本题考查了根的判别式,根的判别式大于0,方程有两个不相等的实数根;根的判别式等于0,方程有两个相等的实数根;根的判别式小于0,方程没有实数根. 13．16 【解析】 【详解】在y=x+1中，令y=0，得x+1=0，解得x=−1，∴点A 的坐标为(−1,0)，在y=−x+7中，令y=0，得−x+7=0，解得x=7，∴点B 的坐标为(7,0)，联立两直线解析式得17y x y x =+⎧⎨=-+⎩， 解得34x y =⎧⎨=⎩， ∴点C 的坐标为(3,4)；即点C 的纵坐标为4∵AB=7−(−1)=8，∴S △ABC =12×8×4=16. 故答案为16.14．甲【解析】试题解析：∵S 2甲＜S 2乙，∴甲机床的性能较好．点睛：方差反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．15．3-【解析】【分析】一元二次方程经过整理都可化成一般形式ax²+bx+c=0（a≠0）．其中ax²叫作二次项，a 是二次项系数；bx 叫作一次项，b 是一次项系数；c 叫作常数项．【详解】解：一元二次方程 22310x x --=的一次项系数为-1．故答案为：3-．【点睛】本题考查的知识点是一元二次方程的一般形式，是基础题目，易于理解掌握．16．5＋3x ＞240【解析】【分析】因为树栽种时的树围为5cm ，以后树围每年增长约3cm ，x 年后树围将达到（5+3x ）cm ．不等关系：x 年其树围才能超过2.4m ．【详解】根据题意，得5+3x>240.故答案为：5+3x>240.【点睛】本题主要考查由实际问题抽象出一元一次不等式，抓住关键词语，弄清不等关系，才能把文字语言的不等关系转化为用数学符号表示的不等式．17．1【解析】【分析】由a+b-1ab=0得a+b 11333a b ab ab a b ab ab+=+===，. 【详解】解：由a+b-1ab=0得a+b=1ab ， 113a b ab a b ab ab++===1， 故答案为1．【点睛】本题考查了分式的化简求值，熟练运用分式的混合运算法则是解题的关键.三、解答题18．1元【解析】【分析】首先设跳绳的单价为x 元，则排球的单价为3x 元，根据题意可得等量关系：750元购进的跳绳个数﹣900元购进的排球个数=30，依此列出方程，再解方程可得答案．【详解】解：设跳绳的单价为x 元，则排球的单价为3x 元，依题意得：750900303x x-=，解方程，得x=1． 经检验：x=1是原方程的根，且符合题意．答：跳绳的单价是1元．【点睛】此题主要考查了分式方程的应用，关键是正确理解题意，找出题目中的等量关系，列出方程． 19．（1）4m <；（2）m 的值为1．【解析】【分析】（1）根据题意得出△＞0，代入求出即可；（2）求出m=1，2或1，代入后求出方程的解，即可得出答案．【详解】解：（1）∵关于x 的方程240x x m ++=有两个不相等的实数根，∴△=2440m ->．∴4m <；（2）∵4m <且m 为正整数，∴m 可取1、2、1．当m=1时，2410x x ++=的根不是整数，不符合题意；当m=2时，2420x x ++=的根不是整数，不符合题意；当m=1时，2430x x ++=，根为11x =-，23x =-，符合题意．∴m 的值为1．【点睛】本题考查根的判别式和解一元二次方程，能根据题意求出m 的值和m 的范围是解题的关键．20．（1）78；1；0.18；0.28；（2）见解析；（3）违章车辆共有76（辆）．【解析】【分析】（1）根据第一组的频数是10，对应的频率是0.05即可求得整理的车辆总数，然后根据百分比的意义求解； （2）根据（1）的结果即可补全直方图；（3）求得最后两组的和即可．【详解】（1）整理的车辆总数是：10÷0.05=200（辆），则a=200×0.39=78，c 36200==0.18； d=1﹣0.18﹣0.39﹣0.10=0.28，b=200×0.28=1．故答案为：78；1；0.18；0.28；（2）如图：；（3）违章车辆共有1+20=76（辆）．【点睛】本题考查了读频数分布直方图的能力和利用统计图获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．21．详见解析【解析】【分析】由直角三角形斜边中线等于斜边的一半可得CD＝BD，从而可得∠DCB＝∠ABC，再根据直角三角形两锐角互余通过推导即可得出答案.【详解】∵∠ACB＝90°，∴∠A+∠ABC＝90°，又∵D是AB中点，∴CD＝BD，∴∠DCB＝∠ABC，又∵∠E＝90°，∴∠ECB+∠EBC＝90°，∴∠EBC＝∠A．【点睛】本题考查了直角三角形斜边中线的性质，直角三角形两锐角互余，等腰三角形的性质，熟练掌握和灵活运用相关性质是解题的关键.22．（1）C；（2）没有考虑a=b的情况；（3）△ABC是等腰三角形或直角三角形．【解析】【分析】（1）根据题目中的书写步骤可以解答本题；（2）根据题目中B到C可知没有考虑a=b的情况；（3）根据题意可以写出正确的结论．【详解】（1）由题目中的解答步骤可得，错误步骤的代号为：C，故答案为：C；（2）错误的原因为：没有考虑a=b的情况，故答案为：没有考虑a=b的情况；（3）本题正确的结论为：△ABC是等腰三角形或直角三角形，故答案为：△ABC是等腰三角形或直角三角形．【点睛】本题考查因式分解的应用、勾股定理的逆定理，解答本题的关键是明确题意，写出相应的结论，注意考虑问题要全面．23．（1）2）y=-9x【解析】【分析】（1）根据题意可求A，B坐标，勾股定理可求AB长度，即可求△OAB的周长．（2）把两个函数关系式联立成方程组求解，即为C点坐标，通过平移可求D点坐标，用待定系数法可求反比例函数解析式．【详解】（1）∵一次函数y＝﹣12x+4的图象与x轴y轴分别交于点A、点B，∴A（8，0），B（0，4）∴OA＝8，OB＝4在Rr△AOB中，AB＝∴△OAB的周长＝（2）∵14232y xy x⎧=-+⎪⎪⎨⎪=⎪⎩,∴23 xy=⎧⎨=⎩∴C点坐标为（2，3）∵将点C向右平移1个单位，再向下平移6个单位得点D．∴D（3，﹣3）设过D点的反比例函数解析式y＝k x ,∴k＝3×（﹣3）＝﹣9∴反比例函数解析式y＝9 x -.【点睛】本题考查了反比例函数与一次函数的交点问题，把两个函数关系式联立成方程组求解，若方程组有解则两者有交点，方程组无解，则两者无交点．24．（1）90，1300；（2）70140y x =-；（3）1．【解析】【分析】（1）由图像可得点()9,810,()9,490可得答案；（2）由图可知乙车间每小时加工服装：140÷2=70件，求解维修设备后坐标为()4,140,再把（4，140）、（9，490）代入乙车间的函数关系式y=kx+b ，从而可得答案；（3）根据加工的服装总件数=工作效率×工作时间，求出甲车间加工服装数量y 与x 之间的函数关系式，将甲、乙两关系式相加令其等于1140，求出x 值，可得答案．【详解】解：（1）由图像可得点()9,810, 可得甲9小时加工了810件服装， 所以：甲车间每小时加工服装件数为810909=件， 由图像可得点()9,490，可得乙加工的总数为490件，所以这批服装共有8104901300+=件．故答案为：90,1300.（2）由图可知乙车间每小时加工服装：140÷2=70件，所以：乙车间共需要：490÷70=7小时，维修设备时间：9-7=2小时，∴ 维修设备后坐标为()4,140,设乙车间的函数关系式为：y=kx+b ，代入点（4，140）、（9，490）,得：41409490k b k b +=⎧⎨+=⎩解得，14070b k =-⎧⎨=⎩所以：y=70x ﹣140；（3）设甲车间1,y mx =代入点（9，110）得：则9m=110，解得：m=90，所以：190,y x由y + y1= 1140得：70x﹣140+90x=1140解得：x=1答：甲、乙两车间共同加工完1140件服装时甲车间所用时间是1小时．【点睛】本题考查了一次函数的应用以及解一元一次方程，解题的关键是：（1）根据数量关系，列式计算；（2）根据数量关系，找出乙车间维修设备后，乙车间加工服装数量y与x之间的函数关系式；（3）根据数量关系，找出甲车间加工服装数量y与x之间的函数关系式．25．（1）这次被调查的学生有50人；（2）m=0.2，n=10，p=20，见解析；（3）全校学生中利用手机购物或玩游戏的共有400人，可利用手机学习．【解析】【分析】（1）根据C的人数除以C所占的百分比，可得答案；（2）根据人数比抽查人数，所占的百分比乘以抽查人数，可得答案；（3）根据样本估计总体，可得答案．【详解】（1）从C可看出5÷0.1=50人，答：这次被调查的学生有50人；（2）m==0.2，n=0.2×50=10，p=0.4×50=20，，（3）800×（0.1+0.4）=800×0.5=400人，答：全校学生中利用手机购物或玩游戏的共有400人，可利用手机学习．【点睛】本题考查的是条形统计图的综合运用．读懂统计图，从统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据．。

2023-2024学年浙江省杭州市拱墅区锦绣育才教育集团八年级(下)期末数学试卷(含答案)

2023-2024学年浙江省杭州市拱墅区锦绣育才教育集团八年级(下)期末数学试卷(含答案)

2023-2024学年浙江省杭州市拱墅区锦绣育才教育集团八年级（下）期末数学试卷一、选择题：本题共10小题，每小题3分，共30分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.如所示图形中，既是中心对称图形又是轴对称图形的是( )A. B.C. D.2.下列方程中，一定是关于x 的一元二次方程是( )A. 2ax 2+x +1=0 B. 1x +x =0C. xy +x =0D. x 2+x =03.下列计算正确的是( )A.(−2)2=−2B. 4 2−22=2C. 3−2=1D. 4÷ 2=24.若用反证法证明命题“在△ABC 中，若AC >AB ，则∠B >∠C ”，则应假设( )A. ∠B >∠CB. ∠B ≤∠CC. AC >∠ABD. AC ≤AB5.下列一元二次方程中，有两个不相等的实数根的是( )A. x 2−2x +3=0B. x 2+6x +9=0C. 4x 2=3x +2D. 3x 2−x +2=06.小浙同学将一组数据准确地代入方差公式：S 2=(6−−x )2+(5−−x )2+(5−−x )2+(4−−x )24，下列对这组数据的描述正确的是( )A. 样本容量是4B. 众数是4C. 平均数是4D. 中位数是47.若反比例函数y =kx 的图象经过点A(x 1,y 1)，则下列结论中不正确的是( )A. 图象一定不经过(1,0) B. 图象一定经过(−y 1,−x 1)C. 图象一定经过(x 1+1,y 1−1)D. 图象一定经过(−x 1,−y 1)8.如图，∠BAC 的平分线交△ABC 的中位线DE 于点F ，若AC =10，AB =6，则EF 的长为( )A. 1B. 2C. 3D. 49.二次函数y=ax2+ax+c2+1(a,c为常数，且a≠0)的图象可能是( )A. B. C. D.10.如图，在矩形ABCD中，点E在BC的延长线上，点F在CD的延长线上，AD平分∠EAF，若要知道△AEF的面积，则需要知道( )A. CE的长B. 矩形ABCD的面积C. △ADF的面积D. ∠EAF的度数二、填空题：本题共6小题，每小题3分，共18分。

初中数学浙江省杭州市锦绣八年级下期中考模拟试数学考试题含答案.docx

初中数学浙江省杭州市锦绣八年级下期中考模拟试数学考试题含答案.docx

xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题（每空xx 分，共xx分）试题1:以下四个汽车标志中，是中心对称图形的为（）A． B． C． D．试题2:下列运算正确的是（）A. B.C. D.试题3:如图是某学校全体教职工年龄的频数分布直方图（每组年龄包含最小值，不包含最大值），根据图形提供的信息，评卷人得分下列说法中错误的是( )A.该学校教职工总人数是50人B.这一组年龄在40≤＜42小组的教职工人数占该学校全体(第3题)教职工总人数的20%C.教职工年龄的中位数一定落在40≤＜42这一组D.教职工年龄的众数一定在38≤＜40这一组试题4:如果式子化简的结果为，则的取值范围是（）A. B. C. D.试题5:如图，在ABCD中，∠A=70°，将ABCD折叠，使点D、C分别落在点F、E处（点F、E都在AB所在的直线上），折痕为MN，则∠AMF等于（）A．70° B．40° C．30° D．20°试题6:(第5题)已知四边形ABCD中，AC与BD交于点O，如果只给出条件“AB∥CD”，那么可以判定四边形ABCD是平行四边形的是（）①再加上条件“BC=AD”，则四边形ABCD一定是平行四边形．②再加上条件“∠BAD=∠BCD”，则四边形ABCD一定是平行四边形．③再加上条件“AO=CO”，则四边形ABCD一定是平行四边形．④再加上条件“∠DBA=∠CAB”，则四边形ABCD一定是平行四边形．A.①②B.①③④C.②③D.②③④试题7:为执行“均衡教育”政策，某县2014年投入教育经费2500万元，预计到2016年底三年累计投入1.2亿元．若每年投入教育经费的年平均增长百分率为，则下列方程正确的是（）A.B.C.D.试题8:用反证法证明命题“四边形中至少有一个角是钝角或直角”，应先假设（）A.四边形中没有一个角是钝角或直角B.四边形中至多有一个钝角或直角C.四边形中没有一个角是锐角D.四边形中没有一个角是钝角试题9:如图，△ABC中，AB=4，AC=3，AD、AE分别是其角平分线和中线，过点C作CG⊥AD于F，交AB于G，连接EF，则线段EF的长为（）A. B.1 C. D.7试题10:对于实数、，定义一种运算“”为：，有下列命题：①；②方程的根为：，；③不等式组的解集为：；其中正确的是( )A.①②③B.①③C.①②D.②③试题11:化简计算：，.试题12:若一个多边形的每个内角都是140°，则这个多边形是边形．试题13:若有意义，则的取值范围是___________________.试题14:已知一组数据，，……，的平均数为2,方差为，那么另一组数据，，……，的平均数为_______,方差为_______.试题15:由10块相同的小长方形地砖拼成面积为1.6m2的长方形ABCD(如图)，则长方形ABCD的周长为____________.试题16:在平行四边形ABCD中，BC上的高为4，AB＝5 ，AC=，则平行四边形ABCD的周长等于_____________.试题17:某学校抽查了某班级某月5天的用电量，数据如下表（单位：度）：度数9 10 11天数 3 1 1（1）求这5天用电量的平均数；（2）求这5天用电量的众数、中位数；（3）学校共有36个班级，若该月按22天计，试估计该校该月的总用电量. 试题18:计算：试题19:①；试题20:②试题21:（1）化简下列各式：，，，= ，…（2）通过观察，归纳写出能反映这个规律的一般结论，并证明．试题22:某租赁公司拥有汽车100辆．据统计，每辆车的月租金为4000元时，可全部租出．每辆车的月租金每增加100元，未租出的车将增加1辆．租出的车每辆每月的维护费为500元，未租出的车每辆每月只需维护费100元．（1）当每辆车的月租金为4600元时，能租出多少辆？并计算此时租赁公司的月收益（租金收入扣除维护费）是多少万元？（2）规定每辆车月租金不能超过7200元，当每辆车的月租金定为多少元时，租赁公司的月收益（租金收入扣除维护费）可达到40.4万元？试题23:如图，在平行四边形AB CD中，∠DAB=60°，点E、F分别在CD、AB的延长线上，且AE=AD，CF=CB．（1）求证：四边形AFCE是平行四边形；（2）若去掉已知条件的“∠DAB=60°，上述的结论还成立吗？若成立，请写出证明过程；若不成立，请说明理由．（第21题）试题24:如图，∠ABM为直角，点C为线段BA的中点，点D是射线BM上的一个动点（不与点B 重合），连接AD，作BE ⊥AD，垂足为E，连接CE，过点E作EF⊥CE，交BD于F．（1）求证：BF=FD；（2）点D在运动过程中能否使得四边形ACFE为平行四边形？如不能，请说明理由；如能，求出此时∠A的度数．（第22题）试题25:如果方程的两个根是，，那么，，请根据以上结论，解决下列问题：（1）若，，求方程的两根。

2020年浙江省杭州市拱墅区锦绣育才教育集团中考数学二模试卷

2020年浙江省杭州市拱墅区锦绣育才教育集团中考数学二模试卷

2020年浙江省杭州市拱墅区锦绣育才教育集团中考数学⼆模试卷2020年浙江省杭州市拱墅区锦绣育才教育集团中考数学⼆模试卷⼀.选择题（共10⼩题）1．﹣3的相反数是（）A．﹣3B．3C．D．2．已知⊙O的半径为5，若PO＝4，则点P与⊙O的位置关系是（）A．点P在⊙O内B．点P在⊙O上C．点P在⊙O外D．⽆法判断3．已知，则的值为（）A．B．C．D．4．将⼆次函数y＝5x2的图象先向右平移2个单位，再向下平移3个单位，得到的函数图象的解析式为（）A．y＝5（x+2）2+3B．y＝5（x﹣2）2+3C．y＝5（x+2）2﹣3D．y＝5（x﹣2）2﹣35．在⼀个不透明的盒⼦中装有8个⽩球，若⼲个黄球，它们除颜⾊不同外，其余均相同，若从中随机摸出⼀个球为⽩球的概率是，则黄球的个数为（）A．16B．12C．8D．46．如图，AD∥BE∥CF，点B，E分别在AC，DF上，DE＝2，EF＝AB＝3，则BC长为（）A．B．2C．D．47．如图，点A、B、C、P在⊙O上，CD⊥OA，CE⊥OB，垂⾜分别为D，E，∠DCE＝40°，则∠P的度数为（）A．70°B．60°C．40°D．35°8．已知抛物线y＝ax2+bx+c与反⽐例函数y＝的图象在第⼀象限有⼀个公共点，其横坐标为1，则⼀次函数y＝bx+ac的图象可能是（）A．B．C．D．9．如图，在矩形ABCD中，AB＝5，AD＝3，动点P满⾜S△P AB＝S矩形ABCD，则点P到A、B两点距离之和P A+PB 的最⼩值为（）A．B．C．5D．10．已知⼆次函数y＝（x﹣h）2+1（h为常数），在⾃变量x的值满⾜1≤x≤3的情况下，与其对应的函数值y的最⼩值为5，则h 的值为（）A．1或﹣5B．﹣1或5C．1或﹣3D．1或3⼆.填空题（共6⼩题）11．若sinα＝cos60°，则锐⾓α＝．12．已知点P是线段AB的黄⾦分割点，P A＞PB，AB＝2cm，那么P A＝cm．13．分解因式：12m2n2﹣12m2n+3m2＝．14．扇形的圆⼼⾓为150°，弧长为20π，则扇形的⾯积为（可保留π）．15．如图，半径为5的⊙A中，弦BC，ED所对的圆⼼⾓分别是∠BAC，∠EAD．已知DE＝6，∠BAC+∠EAD＝180°，则弦BC的弦⼼距等于．16．如图，在矩形纸⽚ABCD中，AB＝6，BC＝10，点E在CD上，将△BCE沿BE折叠，点C恰落在边AD上的点F处；点G在AF上，将△ABG沿BG折叠，点A恰落在线段BF上的点H处，有下列结论：①∠EBG＝45°；②△DEF∽△ABG；③S△ABG＝S△FGH；④AG+DF＝FG．其中正确的是．（填写正确结论的序号）三、解答题（共7⼩题）17．先化简，再求值：，其中a＝3．18．某校七、⼋年级各有10名同学参加市级数学竞赛，各参赛选⼿的成绩如下（单位：分）：七年级：89，92，92，92，93，95，95，96，98，98⼋年级：88，93，93，93，94，94，95，95，97，98整理得到如下统计表年级最⾼分平均分中位数众数⽅差七年级9894a m7.6⼋年级98n9493 6.6根据以上信息，完成下列问题（1）填空：a＝；m＝；n＝；（2）两个年级中，年级成绩更稳定；（3）七年级两名最⾼分选⼿分别记为：A1，A2，⼋年级第⼀、第⼆名选⼿分别记为B1，B2，现从这四⼈中，任意选取两⼈参加市级经验交流，请⽤树状图法或列表法求出这两⼈分别来⾃不同年级的概率．19．如图，甲、⼄两座建筑物的⽔平距离BC为78m．从甲的顶部A处测得⼄的顶部D处的俯⾓为48°，测得底部C处的俯⾓为58°，求甲、⼄建筑物的⾼度AB和DC．（结果取整数，参考数据：tan48°≈1.1，tan58°≈1.60）20．甲、⼄两车同时从A地出发，匀速开往B地，甲车⾏驶到B地后⽴即沿原路线以原速度返回A地，到达A地后停⽌运动：当甲车到达A地时，⼄车恰好到达B地，并停⽌运动．已知甲车的速度为150km/h，设甲车出发xh后，甲、⼄两车之间的距离为ykm，图中的折线OMNQ表⽰了整个运动过程中y与x之间的函数关系．（1）A、B两地的距离是km，⼄车的速度是km/h；（2）指出点M的实际意义，并求线段MN所表⽰的y与x之间的函数表达式；（3）当两车相距50km时，直接写出x的值．21．如图，AD是△ABC的外接圆⊙O的直径，点P在BC延长线上，且满⾜∠P AC＝∠B．（1）求证：P A是⊙O的切线；（2）弦CE⊥AD交AB于点F，若AF?AB＝12，求AC的长．22．已知在同⼀平⾯直⾓坐标系中有函数y1＝ax2﹣2ax+b，y2＝﹣ax+b，其中ab≠0．（1）求证：函数y2的图象经过函数y1的图象的顶点；（2）设函数y2的图象与x轴的交点为M，若点M关于y轴的对称点M'在函数y1图象上，求a，b满⾜的关系式；（3）当﹣1＜x＜1时，⽐较y1与y2的⼤⼩．23．已知正⽅形ABCD，点M为边AB的中点．（1）如图1，点G为线段CM上的⼀点，且∠AGB＝90°，延长AG、BG分别与边BC、CD交于点E、F．①求证：BE＝CF；②求证：BE2＝BC?CE．（2）如图2，在边BC上取⼀点E，满⾜BE2＝BC?CE，连接AE交CM于点G，连接BG并延长交CD于点F，求tan∠CBF的值．2020年浙江省杭州市拱墅区锦绣育才教育集团中考数学⼆模试卷参考答案与试题解析⼀.选择题（共10⼩题）1．【解答】解：﹣3的相反数是3．故选：B．2．【解答】解：∵⊙O的半径为5，若PO＝4，∴4＜5，∴点P与⊙O的位置关系是点P在⊙O内，故选：A．3．【解答】解：由，可得：2y＝5（x﹣2y），解得：5x＝12y，所以的值为，故选：D．4．【解答】解：由“左加右减”的原则可知，将⼆次函数y＝5x2的图象先向右平移2个单位所得函数的解析式为：y＝5（x﹣2）2；由“上加下减”的原则可知，将⼆次函数y＝5（x﹣2）2的图象先向下平移3个单位所得函数的解析式为：y＝5（x﹣2）2﹣3．故选：D．5．【解答】解：设黄球的个数为x个，根据题意得：＝，解得：x＝4．故选：D．6．【解答】解：∵AD∥BE∥CF，∴＝，∵DE＝2，EF＝AB＝3，∴＝，∴BC＝，7．【解答】解：∵CD⊥OA，CE⊥OB，垂⾜分别为D，E，∠DCE＝40°，∴∠DOE＝180°﹣40°＝140°，∴∠P＝∠DOE＝70°．故选：A．8．【解答】解：∵抛物线y＝ax2+bx+c与反⽐例函数y＝的图象在第⼀象限有⼀个公共点，∴b＞0，∵交点横坐标为1，∴a+b+c＝b，∴a+c＝0，∴ac＜0，∴⼀次函数y＝bx+ac的图象经过第⼀、三、四象限．故选：B．9．【解答】解：设△ABP中AB边上的⾼是h．∵S△P AB＝S矩形ABCD，∴AB?h＝AB?AD，∴h＝AD＝2，∴动点P在与AB平⾏且与AB的距离是2的直线l上，如图，作A关于直线l的对称点E，连接AE，连接BE，则BE的长就是所求的最短距离．在Rt△ABE中，∵AB＝5，AE＝2+2＝4，∴BE＝＝＝，即P A+PB的最⼩值为．故选：D．10．【解答】解：∵当x＞h时，y随x的增⼤⽽增⼤，当x＜h时，y随x的增⼤⽽减⼩，∴①若h＜1≤x≤3，x＝1时，y取得最⼩值5，可得：（1﹣h）2+1＝5，解得：h＝﹣1或h＝3（舍）；②若1≤x≤3＜h，当x＝3时，y取得最⼩值5，可得：（3﹣h）2+1＝5，解得：h＝5或h＝1（舍）；③若1≤h≤3时，当x＝h时，y取得最⼩值为1，不是5，∴此种情况不符合题意，舍去．综上，h的值为﹣1或5，故选：B．⼆.填空题（共6⼩题）11．【解答】解：∵sinα＝cos60°＝×＝，故答案为：45°．12．【解答】解：由于P为线段AB＝2的黄⾦分割点，且AP是较长线段；则AP＝2×＝（﹣1）cm．故答案为：（﹣1）cm．13．【解答】解：12m2n2﹣12m2n+3m2＝3m2（4n2﹣4n+1）＝3m2（2n﹣1）2．故答案为：3m2（2n﹣1）2．14．【解答】解：∵20π＝，∴r＝24，∴扇形的⾯积＝20π×24÷2＝240π，故答案为240π．15．【解答】解：作AH⊥BC于H，作直径CF，连结BF，如图，∵∠BAC+∠EAD＝180°，⽽∠BAC+∠BAF＝180°，∴∠DAE＝∠BAF，∴＝，∴DE＝BF＝6，∵AH⊥BC，∴CH＝BH，⽽CA＝AF，∴AH为△CBF的中位线，∴AH＝BF＝3．故答案为：3．16．【解答】解：∵根据折叠得出∠BAG＝∠FBG，∠CBE＝∠FBE，⼜∵四边形ABCD是矩形，∴∠BAC＝90°，∴∠EBG＝，∴①正确；∵四边形ABCD是矩形，∴AB＝DC＝6，BC＝AD＝10，∠A＝∠C＝∠D＝90°，∴根据折叠得∠BFE＝∠C＝90°，∴∠ABG+∠BGA＝90°，∠EFD+∠BF A＝90°，∵∠BGA＞∠BF A，∴∠BAG≠∠EFD，∵∠GHB＝∠A＝90°，∠EFB＝∠C＝90°，∴∠GHB＝∠EFB，∴GH∥EF，∴∠EFD＝∠HGF，根据已知不能推出∠AGB＝∠HGF，∴∠AGB≠∠EFD，即△DEF和△ABG不全等，∴②错误；∵根据折叠得：AB＝BH＝6，BC＝BF＝10，∴由勾股定理得：AF＝＝8，∴DF＝10﹣8＝2，HF＝10﹣6＝4，设AG＝HG＝x，在Rt△FGH中，由勾股定理得：GH2+HF2＝GF2，即x2+42＝（8﹣x）2，解得：x＝3，即AG＝HG＝3，∴S△ABG＝＝＝9，S△FHG＝＝＝6，∴③错误；∵AG+DF＝3+2＝5，GF＝10﹣3﹣2＝5，∴④正确；故答案为：①④．三、解答题（共7⼩题）17．【解答】解：原式＝÷＝?＝，当a＝3时，原式＝＝．18．【解答】解：（1）a＝94；m＝92，n＝（88+93+93+93+94+94+95+95+97+98）＝94；（2）七年级和⼋年级的平均数相同，但⼋年级的⽅差较⼩，所以⼋年级的成绩稳定；故答案为94，92，94；⼋；（3）列表得：A1A2B1B2⼄甲A1（A1，A2）（A1，B1）（A1，B2）A2（A2，A1）（A2，B1）（A2，B2）B1（B1，A1）（B1，A2）（B1，B2）B2（B2，A1）（B2，A2）（B2，B1）共有12种等可能的结果，这两⼈分别来⾃不同年级的有8种情况，∴P（这两⼈分别来⾃不同年级的概率）＝＝．19．【解答】解：作DE⊥AB于E，则四边形EBCD为矩形，∴DE＝BC＝78m，BE＝CD，由题意得，∠ADE＝48°，∠ACB＝58°，在Rt△ADE中，tan∠ADE＝，则AE＝DE?tan∠ADE≈78×1.1＝85.8，在Rt△ACB中，tan∠ACB＝，则AB＝BC?tan∠ACB≈78×1.60＝124.8≈125，则CD＝BE＝AB﹣AE＝39，答：甲建筑物的⾼度AB约为125m，⼄建筑物的⾼度DC约为39m．20．【解答】解：（1）由图象可得，A、B两地的距离是150×4＝600（km），⼄车的速度为：（600×2﹣150×5）÷5＝90（km/h），故答案为：600，90；（2）（150﹣90）×4＝60×4＝240（km），点M的实际意义是，在两车⾏驶4⼩时时，甲车到达B地，此时甲⼄两车的距离是240km；设线段MN所表⽰的y与x之间的函数表达式为y＝kx+b，，得，即线段MN所表⽰的y与x之间的函数表达式为y＝﹣240x+960；（3）当0≤x≤4时，（150﹣90）x＝50，解得x＝；当4＜x≤5时，（150+90）x+50＝600×2，解得，x＝；当x＞5时，（150+90）x﹣50＝600×2，解得，x＝；由上可得，当两车相距50km时，x的值是或或．21．【解答】（1）∵AD是⊙O的直径∴∠ACD＝90°；∴∠CAD+∠D＝90°∵∠P AC＝∠PBA，∠D＝∠PBA，∴∠CAD+∠P AC＝90°，∴∠P AD＝90°，∴P A⊥AD，∵点A在⊙O上，∴P A是⊙O的切线（2）∵CF⊥AD，∴∠ACF+∠CAD＝90°，∵∠CAD+∠D＝90°，∴∠D＝∠ACF，∴∠B＝∠ACF，∵∠BAC＝∠CAF，∴△ABC∽△ACF，∴，∴AC2＝AF?AB∵AF?AB＝12，∴AC2＝12，∴AC＝2．22．【解答】解：（1）证明：∵y1＝ax2﹣2ax+b＝a（x﹣1）2﹣a+b，∴函数y1的顶点为（1，﹣a+b），把x＝1代⼊y2＝﹣ax+b得，y＝﹣a+b，∴函数y2的图象经过函数y1的图象的顶点；（2）设函数y2的图象与x轴的交点M（m，0），则点M关于y轴的对称点M'（﹣m，0），由题意可知，解得b＝﹣a；（3）∵y1＝ax2﹣2ax+b，y2＝﹣ax+b，∴y1﹣y2＝ax（x﹣1）．∵﹣1＜x＜1，∴当﹣1＜x＜0，x（x﹣1）＞0．当0＜x＜1，x（x﹣1）＜0，当x＝0，x（x﹣1）＝0，∴y1＝y2；当a＞0且﹣1＜x＜0时，ax（x﹣1）＞0，y1＞y2；当a＞0且0＜x＜1时，ax（x﹣1）＜0，y1＜y2；当a＜0且﹣1＜x＜0时，ax（x﹣1）＜0，y1＜y2；当a＜0且0＜x＜1时，ax（x﹣1）＞0，y1＞y2．23．【解答】解：（1）①∵四边形ABCD是正⽅形，∴AB＝BC，∠ABC＝∠BCF＝90°，∴∠ABG+∠CBF＝90°，∵∠AGB＝90°，∴∠ABG+∠BAG＝90°，∴∠BAG＝∠CBF，∵AB＝BC，∠ABE＝∠BCF＝90°，∴△ABE≌△BCF，∴BE＝CF，②∵∠AGB＝90°，点M为AB的中点，∴MG＝MA＝MB，∴∠GAM＝∠AGM，⼜∵∠CGE＝∠AGM，∠GAM＝∠CBG，∴∠CGE＝∠CBG，⼜∠ECG＝∠GCB，∴△CGE∽△CBG，∴＝，即CG2＝BC?CE，由∠CFG＝∠GBM＝∠BGM＝∠CGF得CF＝CG，由①知BE＝CF，∴BE＝CG，∴BE2＝BC?CE；（2）延长AE、DC交于点N，∵四边形ABCD是正⽅形，∴AB∥CD，∴∠N＝∠EAB，⼜∵∠CEN＝∠BEA，∴△CEN∽△BEA，∴＝，即BE?CN＝AB?CE，∵AB＝BC，BE2＝BC?CE，∴CN＝BE，∵AB∥DN，∴＝＝，∵AM＝MB，∴FC＝CN＝BE，不妨设正⽅形的边长为1，BE＝x，由BE2＝BC?CE可得x2＝1?（1﹣x），解得：x1＝，x2＝（舍），∴＝，则tan∠CBF＝＝＝．。

2019-2020学年杭州市锦绣育才教育科技集团 2020 年中考模拟考试(一)

2019-2020学年杭州市锦绣育才教育科技集团 2020 年中考模拟考试(一)

2019-2020学年杭州市锦绣育才教育科技集团2020 年中考模拟考试（一）第二部分阅读理解(共两节，满分 40 分)第一节(共 15 小题，每小题 2 分，满分 30 分)阅读下列短文，从毎题所给的四个选项(A、B、C 和 D)中选出最佳选项。

AHe was a poet known for the nostalgia（乡愁）he describes in his poems. On December 14th, 2017, that famous Chinese poet passed away. He spent his whole life writing. “ The reason why I stick to writing till today comes down to my passion for the Chinese language,” he once said in a 2015 interview with People’s Daily. He then added that this passion was strengthened by his love for his mother and his motherland. Now, let’s a ppreciate the poem Nostalgia.1. What’s the best word for the “__ _____” in the poem?A. Indoors.B. Inside.C. Outdoors.D. Side.2. The poem is mainly developed by the change of _________.A. timeB. activitiesC. placesD. characters3. What can we learn from the poem Nostalgia?A. The poet’s mother moved to Shanghai.B. The poet made a lot of money from writing.C. The poet lived with his mother on the riverside.D. The poet missed his family and homeland a lot.【答案】BADBThe average American child spends three to five hours a day watching TV. In 1961, the average child began to watch television at age three; however, today it is nine months. Yet, most parents think that television has bad influence on their children. For example, in the early 1970s, my parents believed that my bad eyesight was the result of sitting too close to the screen, and they therefore made my stay at least six feet from it. Today, most people have no such worry, but many new ridiculous (荒谬的)sayings have appeared:• TV makes kids stupid. Many children watch more educational programs when they are pre-schoolers. When they grow up, they can read more books and have much better ideas to solve difficult problems than other children.• TV makes kids violent.The real story is not so simple. Hundreds of studies show that watching violence on TV makes children more aggressive (好斗的). But a study of over 5,000 children also finds that some positive programs make children kinder. The problem is that kids are increasingly watching shows with violence instead of those suitable for their age.• Sitting around watching TV makes kids overweight. An experiment finds that when children watch less television, they do lose extra weight; however, reducing their television time does not make them more active. The real problem lies in snacking. A widespread habit for kids, and junk-food advertisements.•TV helps kids get to sleep. The opposite is true. The more television children watch, the more likely they are to have irregular sleep and nap patterns. Allowing kids to watch television is part of the problem, not the solution.1.Which one is the advantage of educational TV programs?A. They will make children solve difficult problems better than others.B. They will improve children’s ability to get along with others.C. They are likely to make children more aggressive.D. They will make sure of children’s success in the future.2.What influence does watching TV have on a child’s sleep?A. Children are likely to sleep deeper after watching TV.B. Children’s sleep time will be greatly reduced.C. It will make children form a bad habit of sleeping.D. Children will go to sleep more easily.3.What is the purpose of this text?A. To increase people’s knowledge of watching TV.B. To warn parents of the disadvantages of watching TV.C. To explain the bad influences that watching TV has on children.D. To correct parents’ wrong ideas of television’s effect on children.【答案】ACDCThis is a tale of two friends --- one is blind, the other has no arms. On their own, the two are “disabled”. But together, they are a powerful team that has changed part of their village in North China’s Hebei Province into a rich, green forest. Meet 53-year-old Jia Haixia and Jia Wenqi!Their story began in 2000, when Haixia, who was already blind in his right eye, lost his left one after an illness. Wenqi lost his arms in an accident when he was just three. Neither could find a job, so the two decided to team up. They rented some poor land and began to plant trees. In return, the local officials paid them a small fee. Haixia and Wenqi never imagined that they would end up creating an environmental paradise. Their forest now has over 10,000 trees, hundreds of birds and many other wild animals. In addition, it saves the village from river flooding during the rainy season. When the friends work together, they focus on their strengths not their disabilities. Their day begins at 7 a.m. when the sightless Haixia carries Wenqi across the river to get to their work-site. Since they cannot afford to buy young trees to plant, the two use branches from existing trees. Haixia climbs to the tree-top and with Wenqi’s direction, selects the perfect branch. He then digs a hole and carefully plants it. Finally Wenqi waters the area.Neither Haixia nor Wenqi cares about money. Together, they already have everything they need --- a perfect pair of eyes, two strong hands, and the best friendship in the world!1. Why did Haixia and Wenqi start working together?A. Haixia needed someone to help him.B.They both needed a way to make money.C. They wanted to improve the environment.D .They were required to do so by local officials.2. Haixia and Wenqi’s forest has helped the village by______ .A. stopping floods in the rainy seasonB.increasing the number of touristsC. making the villagers richerD .providing more farmland3. Why do Haixia and Wenqi plant tree branchesA. They are easy to get.C.They do not cost money.C. They can grow very quickly.D.They are preferred by animals.4. In paragraph 5, when Wenqi says “We stand on our own feet, so the fruits of our work taste sweeter”, he means that “______”.A. they hope to make the forest even betterC.the fruits from their trees are very sweetC. they are proud not to depend on othersD.they are able to do any difficult work5. What can we learn from this story?A.Never give up and you will succeed.B.We should help the disabled to work.C. Try your best when facing difficulties.D .We can achieve more with teamwork.【答案】Ｂ；Ａ；Ｂ；Ｃ；ＤDMany objects in the universe are invisible( 看不见的), but they send radio waves. The radio telescope thus appeared, and it is considered one of the greatest inventions in the twentieth century. Reber built the world's first radio telescope in 1937. Ryle and Hewish developed radio telescope systems for the location of weak radio sources, and they shared the Nobel Prize for Physics in 1974.A radio telescope is usually made up of:◆One or more antennas to collect theradio waves. Most antennas aremade in the shape of a dish tocollect and reflect the radio wavesto the sub-reflector, in the sameway as a curved mirror focusesvisible light to one point.◆ A receiver and amplifier to receivethe radio waves from the sub-reflector, and make these weakradio waves strong enough to berecorded and turned into electronicsignals. To make an amplifiersensitive enough, it is usuallycooled to, very low temperatures (e.g. as low as -270℃）.◆ A recorder to keep a record of the electronic signals. Most radio telescopes today keepthe signals to the computer's memory disk for astronomers to analyze later.Radio wavelengths are much longer than those of visible light, and the radio waves from deep space are always weak. To catch these waves, radio telescopes usually have huge antennas.The sizes of most antennas in use today are around 50 to 300 metres in diameter. The antenna of FAST in Guizhou, China, the latest and largest radio telescope in the world, is 500 metres in diameter, as large as the size of 30 football fields.To avoid interferences, and keep the telescopes sensitive, radio telescopes are built in places where there are no human radio waves or electronic signals. For example, FAST is 5 kilometres away from the closest village and 25 kilometers away from the nearest town.Radio telescopes create pictures of the sky, not in visible light, but in radio waves. This is extremely useful, because there are objects that can't be seen, objects that we wouldn't even know without radio telescopes.1. Radio telescopes help collect ____________ from the universe.A. lightB. objectsC. radio wavesD. visible signals2．Most antennas of radio telescopes are made in the shape of a dish to ____________.A.make the antennas strong enoughB.increase the number of radio wavesC.turn radio waves into electronic signalsD.focus radio waves on the sub-reflector3. The underlined word "interferences" in the passage refers to __________________.A.the noises made by villagers and animalsB.the sounds from the radios and televisionsC.the people who go to Guizhou to watch FAST workD.the radio waves and electronic signals from humans4. What have we done with the help of radio telescopes?A.We have received pictures of deep space.B.We have discovered unknown lives in the universe.C. We have found some unknown objects in the universe.D. We have turned the radio waves from space into light.【答案】BDDC第二节（共5小题，每小题2分，满分10分）下面文章中有五处（第1-5题）需要添加句子，请从以下选项（A、B、C、D、和E）中选出符合上下文的句子。

2020年人教部编版浙江锦绣教育八年级(下)期中检测试题及答案解析

2020年人教部编版浙江锦绣教育八年级(下)期中检测试题及答案解析

浙江锦绣﹒育才教育集团第二学期其中检测卷初二英语（问卷）考生须知：1、本试卷满分120分，考试时间100分钟。

2、答题前，请在答题卡上写好学校、班级、姓名、考场号和座位号。

3、必须在答题纸的对应答题位置上答题，写在其他位置上无效。

4、做听力时，先将答案写在试题卷上，录音结束后，再将答案填涂在答题卡上。

第II卷笔试部分（95分）四、单项选择（每小题1分，共10分）从A、B、C、D四个选项中，选出可以填在空白处的最佳选项。

16.I am reading _____ story. It is _____ exciting story.A.the, aB.a, anC.the, anD./, the17.Kids won’t go to school. They will study _____ home _____ computers.A.in, inB.at, onC.at, byD. At, from18.I _____ to bed until my grandmother came back home.A.didn’t goB.wentC.had goneD.have gone19.I don’t like living ______. I will feel ______.A.lonely, lonelyB.lonely, aloneC.alone, aloneD.alone, lonely20._____ he _____ his homework when you visited him last night?A.Is, doingB.was, doingC.Does, doD.did, do21.-I’m sorry,Miss Green. I _____ my schoolbag on the school bus.-Please do and ______. You should be careful next time.A.fogot, get back itB.fogot, get it backC.left, get it backD.left, get back it22.-When will the plane _____?- In about ten minutes.A.put outB.take awayC.take offD.run away23.His parents don’t allow him _____ out with his friends after school.A.hungB.to hangC.hangingD.hangs24.Sally asked ____________ .A.how can she get to the zoo.B.how she can get to the zoo.C.how she could get to the zooD.Where was the zoo.25.-Oh, my god! I really don’t know ______ next.-What’s wrong? Can I help you?A.what to doB.how to doC.how do itD.so that五、完形填空（共15小题，每小题1分，满分15分）阅读下列短文，从短文后各题所给的四个选项A、B、C和D中，选出可以填入空白处的最佳选项。

浙江省杭州锦绣育才教育集团2023-2024学年八年级下学期3月月考英语试题(原卷版)

浙江省杭州锦绣育才教育集团2023-2024学年八年级下学期3月月考英语试题(原卷版)

锦绣育才教育集团2023学年第二学期三月月评八年级英语问卷（人教版）第I卷第一部分听力（共两节，满分20分）第一节（共5小题，每小题1分，满分5分）听下面5段小对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项。

每段对话仅读一遍。

1. What's the matter with Tom?A. He has a fever.B. He has a headache.C. He has a sore back.2. What should the boy do first?A. Wach TV.B. Clean the room.C. Do the homework.3. What chores does the boy like doing?A. CookingB. Cleaning the car.C. Sweeping the floor.4. What's Miss Liu's advice?A. To be a teacher.B. To work in a shopping center.C. To work as a tour guide.5. What does the man sometimes do in his free time?A. He watches TV.B. He hangs out.C. He stays at home.第二节（共10小题，第6-10题，每小题1分，第11-15题，每小题2分，满分15分）听下面3段对话或独白，每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项。

每段对话或独白读两遍。

听下面段对话，回答第6至第7两个小题。

6. What's wrong with the woman?A. She has a cold.B. She has a toothache.C. She has a cough.7. What does the doctor ask her to do?A Stay in hospital..B. Take a rest.C. Take some medicine.听下面一段对话，回答第8至第10三个小题。

2024届浙江杭州拱墅锦绣育才八下英语期末学业质量监测模拟试题含答案

2024届浙江杭州拱墅锦绣育才八下英语期末学业质量监测模拟试题含答案

2024届浙江杭州拱墅锦绣育才八下英语期末学业质量监测模拟试题满分120分，时间90分钟一、完形填空(10分)1、阅读下面的短文，掌握其大意，然后从短文后所给的A、B、C三个选项中，选出可以填入空白处的最佳选项。

“The next class is geography. I’m ____1____ with it. Let’s cut the class and go for a walk!” Grace said to Karen.In fact, Karen liked geography. She had no idea what she ____2____ do. “If I ____3____ Grace’s invitation, she will be angry with me,” she thought. “But if I go with her, I ____4____ catch the class.” It was difficult for her to say no to Grace. Then Karen remembered Mom’s words, “Reme mber who you are. And ____5____ do the right thing.”“I’m sorry, Grace,” Karen said. She finally made the right ____6____ . And she ____7____ Grace to take the class, too. “We have lots of time for a ____8____ after school, don’t we? We’d better take the c lass, ____9____ we will probably fail the final exam. I don’t want the teacher to call our parents.”Finally, the two girls sat in the geography classroom and listened to the teacher ____10____ .Did you ever have the experience like Karen? What did you do?1. A. glad B. bored C. sad2. A. must B. need C. should3. A. refuse B. accept C. choose4. A. will B. won’t C. can5. A. always B. hardly C. never6. A. decision B. plan C. invitation7. A. expected B. sent C. advised8. A. walk B. game C. meeting9. A. though B. if C. or10. A. beautifully B. carefully C. comfortably二、阅读理解（40分）2、Classic Chinese cartoons bring joy to most of us. Last month, three classic Chinese cartoons came out in the cinemas again. Let’s see how old artists put Chinese culture and art into the cartoons to make them classic.The Legend of Sealed Book tells the story of the boy Dansheng. He practices great tricks（魔法）from the book to help people. The film uses face painting from the Peking Opera. It helps to show the characters’ per sonalities（特征）. Lovely Dansheng looks like wawasheng, roles for kids in Peking Opera. A bad person in the story looks like a fool, with a large white part in the center of his face.Little Tadpole Looking for Mummy is China’s first ink（墨水）wash cartoon. Artists drew all the animals, plants and rocks with ink and brushes. They learned from the great artist Qi Baishi. Though it’s only about 15 minutes long, it took lots of work. Artists drew everything by hand. One second of the cartoon needed 24 pictures! Fifty-nine years later, the 2020 cartoon series Fog Hills of Five Elements also uses this style.Pigsy Eats Watermelon is China’s first paper cutting cartoon. This 15-minute cartoon came out in 1958. Artists cut Zhu Bajie out of colored paper. Then they moved its body parts and let it eat the watermelon. Making a paper cutting cartoon was not easy. The characters’ moves were not easy either. After a lot of work, they tried again and again and finallymade it!1. What may a bad character look like in The Legend of Sealed Book?A. B. C. D.2. These three cartoons are mixed with some traditional art forms, EXCEPT ________.A. paper cuttingB. shadow puppet playC. Peking OperaD. ink wash painting3. Which of the following statements is TRUE?A. The Legend of Sealed Book tells children how to draw face painting.B. Qi Baishi drew Little Tadpole Looking for Mummy in the form of ink wash.C. Over 20 thousand pictures were drawn to make Little Tadpole Looking for Mummy.D. Pigsy Eats Watermelon came out later than Little Tadpole Looking for Mummy.4. The writer introduces the three classic Chinese cartoons through ________.A. explaining different Chinese culture and artB. teaching how to paint classic Chinese cartoonsC. reminding people about the best characters in historyD. showing how difficult people made cartoons in the past3、What will you do if you feel angry, sad or lonely? You might want to eat something. But if there is a vending machine (自动贩卖机) in the street, you can tell it how you are feeling and it will give you something. These things may make you feel better. It sounds wonderful.In fact, there is a vending machine like this in Sydney. It has no potato chips (薯片) or chocolate, but there is something interesting in it, such as maps, notes and pencils. These things may help you improve your mental health. Each little packet (数据包) costs 2 Australian dollars (about 10 yuan). The packets have different names. Like “friendship”, “imagination” and so on, you can choose one that can cheer you up.For example, if you have problems with your friends, you can choose the “friendship” packet. There is a piece of paper in it. And you can find 10 everyday activities written on the paper. These activities can help you get on well with old friends or make new ones. If you always feel tired, you can choose the “imagination” packet. In it, there is a special pen and some notes. Yo u can draw something interesting with them. In this way you can feel relaxed.In order to help people with mental health problems, two Australian artists made the machine. They hope this machine could make more people think about mental health problems and help them solve the problems.1. What may you want to do if you feel sad according to Paragraph 1?A. To write on paper.B. To eat something.C. To sleep at home.D. To talk with friends.2. What CAN’T you find in the packets?A. Chips.B. Maps.C. Notes.D. Pencils.3. What does the underline word mental in Paragraph 2 mean?A. PhysicalB. Head.C. Mind.D. Hobby.4. Which of the following is true?A. You should spend 2 Yuan buying a packet from the machine.B. There are only 3 kinds of packets in the vending machine.C. There is a special pencil in the “friendship” packet.D. The vending machine is helpful to tired people.5. What is the best title of this passage?A. People’s Health Problems.B. Some Useful Packets.C. A New V ending Machine.D. Two Australian Artists.4、Do you know about ChatGPT? ChatGPT is an AI chat app that provides a human-like response（反应）to questions. It’s morethan just a fancy chatbot（聊天机器人）. Here are some surprising things you can do with ChatGPT.Make Conversations about Your Favorite TopicYou can start a conversation with ChatGPT on any topic that you want to discuss or learn. You can talk about movies, hobbies, science, or even about ChatGPT itself.Find Answers to Homework with ChatGPTAnother one of ChatGPT’s advantages is that it can help you solve your homework. Whether you’re in school, or at the university, ChatGPT can help you with your homework easily.Solve Math QuestionsIf you’re working on a math problem and you’re looking for the answer, ChatGPT can help. What’s more, it eve n shows its work and steps, so you can understand how to solve the problem yourself.Tell JokesNot just homework, you can also use ChatGPT for fun. One of the most common ways is to ask ChatGPT to tell jokes. If you prefer, you can also give a topic and ChatGPT will answer with jokes on that topic.SongwritingYou can use ChatGPT to create(创作) lyrics for a song. You should choose a theme（主题）or topic, and tell it the story you want.These are the cool things you can do with ChatGPT. In short, you can ask ChatGPT anything and it will answer you.1. According to the passage, how many things can ChatGPT do?A. 4B. 5C. 6D. 72. What does the underlined word “lyrics” mean?A. 歌词B. 台词C. 风格D. 诗歌3. How does the writer start this passage?A. By showing an example.B. By giving numbers.C. By telling a story.D. By asking a question.4. What of the following shows the structure （结构）of the passage?A. B. C. D.5. The passage is probably from ________.A. A cook book.B. A novel.C. A sports magazine.D. A science newspaper.5、1. If you need to take the first kind of medicine, when should you take the seventh pill?A. After 6 hours.B. After 8 hours.C. After 12 hours.D. After 24 hours.2. Who should not take the second kind of medicine?A. People with a headache.B. People with a stomachache.C. People with a toothache.D. People with a cold.3. Which kind of medicine is for people with a toothache?A. The first kind of medicine.B. The second kind of medicine.C. The third kind of medicine.D. The fourth kind of medicine.4. How many pills of the fourth medicine should an 8-year-old girl take in a day?A. 2.B. 4.C. 8.D. 16.三、补全对话（10分）6、请通读下面对话，根据对话内容，从下面的选项中选出能填入空白处的最佳选项，并将答题卡上对应题目所选的选项涂黑。

2019-2020学年浙江省杭州育才中学八年级(下)开学英语试卷(附答案详解)

2019-2020学年浙江省杭州育才中学八年级(下)开学英语试卷(附答案详解)

2019-2020学年浙江省杭州育才中学八年级（下）开学英语试卷一、完形填空（本大题共15小题，共15.0分）When I was a little girl,my father loved to play catch with me.I wasn't very good at it, (1) we would play anyway.He was (2) telling me "Keep your eye on the ball" as I would not be able to catch even the (3) of throws.As I got older,we didn't play catch as much.If I had a（n）(4) and would go to my father to (5) his advice,he would try to (6) with me and say "Keep your eye on the ball".We would both laugh (7) usually that advice was not useful to problems,but he would try to make me (8) . My father became (9)in 1995 when I was 23.There weren't more conversations,as he suffered from a stroke（中风）.He could not (10)，only mouth words,which were sometimes (11) to understand.I seemed to be pretty good at reading his lips after a while,even better than his nurses who were (12) him there.During one of our last conversations,I was telling him about a problem I was having with my boyfriend.(13)，I could read his lips,"Keep our eyes on the ball."We both smiled.That was the last time I saw my father (14) he passed away.Sometimes,all these years later,when I get in trouble,I just tell myself " (15) your eyes on the ball".1. A. and B. but C. so D. or2. A. hardly B. never C. sometimes D. always3. A. hardest B. easiest C. fastest D. biggest4. A. illness B. surprise C. problem D. lesson5. A. pay for B. ask for C. send for D. look for6. A. joke B. sing C. compete D. think7. A. because B. unless C. if D. when8. A. worry B. smile C. study D. stop9. A. ill B. busier C. wealthy D. healthier10. A. speak B. move C. see D. hear11. A. interesting B. boring C. simple D. difficult12. A. waiting for B. looking throughC. worrying aboutD. caring for13. A. Once again B. All in all C. Anyway D. On one hand14. A. after B. before C. until D. as15. A. Leave B. Hold C. Put D. Keep二、阅读理解（本大题共15小题，共30.0分）A16.David love sports and has a holiday from May 7 to May 15.Which activity will he takepart in？______A. Hiking in the mountains.B. Fishing in the countryside.C. Watching plants at night.D. Swimming in the sea.17.Sam wants to go to the countryside with his wife,his five-year-old daughter andseven-year-old son.How much should they pay？______A. ＄25.B. ＄55.C. ＄110.D. ＄160.18.Which of the following is NOT true？______A. If you go hiking in the mountains,you may see some animals.B. Anyone is welcome to go to the valley full of adventures.C. If you want to know more information about the adventure in the valley,make a call.D. You will see beautiful gardens and different birds during the trip to the countryside.BEveryone likes to feel that he or she is special.But many of us grow up believing that we're not special at all.We wish that we could be better at sports or more attractive.We wish that we had nicer clothes or more money.Like the Scarecrow（稻草人），the Tin Man,or the Cowardly Lion from The Wizard of Oz（绿野仙踪），we believe we're not good enough just as we are.In the movie ，the Scarecrow wishes that he had a brain（大脑）.The Tin Man wishes she had a heart,and the Lion wants courage.In the end,each of them realizes that he already has what he needs.Most parents want us to be the best we can be.They sometimes try to encourage us to do better by comparing us to others.They mean well,but the message we often get is that we're not good enough.We begin to believe that the only way we can be special is by being better thansomeone else,but we are often disappointed.There will always be someone out there who is better than we are at something There are plenty of people around who may not be as smart as we are but who are better at sports.Or they may not be as good-looking,but they have more money.It is impossible for us to be better than everyone else all the time.Like the Scarecrow,the Tin Man,and the Cowardly Lion,we all want what we believe will make us better people.What we don't realize is that often we already have inside us the very things that we seek.Parents sometimes forget to tell us that we are special ，and that we are good enough just as we are.Maybe no one told them that when they were growing up,or maybe they just forgot.Either way,it's up to us to remind them from time to time that each of us,in our own way,is special.19.What do most parents want us to do？______A. To be the best people.B. To be good at sports.C. To be good-looking.D. To be nice to others.20.What can we learn from the passage？______A. All the parents can be special.B. We should always try to be the best.C. The richer you are,the better you are.D. We are all good enough.21.Who might write the passage？______A. An expert.B. A teacher.C. A teenager.D. A parent.22.What is the best title for the passage？______A. The Wizard of Oz.B. Be yourself.C. How to get on with others.D. Believing or not believing.CIt was Day 1 of our vacation on Cortes,a beautiful quiet island. "iPhone,iPhone,iPhone," my son kept moaning（呻吟）.In front of him was a big window of facing the blue ocean.And a cool gentle wind was coming in from the door.Clearly,he saw and felt none of it.Back at home,I'd soon give up and hand the phone over to him after five minutes of listening to this kind of moaning.But not here.Before we left,I had told my 10-year-old son the rule--no e-mails,no Facebook,no video games,and no iPhone.We came here to get away from them all.Here we were on our first day and already,he couldn't stand it._____ I walked down the grass road to the beach and looked out to the sea.My 6-year-old daughter and my husband were drawing on pieces of wood.They were doing just fine.On Day 2，we spent the whole morning digging for shells（贝壳）.This time,my son joined us.He collected shellfish and other sea treasures.When we got back to our little wood house.I gave my son a book,and put him on the lovely garden chair.It was almost dinner when he looked up.The next few days passed in peace.On Day 6，my son was lying beside me on the beach,watching the sun going down.He was playing with the sand.And there was something shining in his eyes.I realized how time slowed down for both of us.It was exactly what I wanted.Finally,we were able to sit quietly without thinking about screens,phone calls and e-mails.A week away from all the electronics and life is good.23.What is the special rule for the writer's vacation？______A. They couldn't use their electronics.B. They must keep quiet and stay in the house.C. The had to spend their vacation on an island.D. They should collect as many shells as possible.24.Which of the following can be put in "_______" in Paragraph 4？______A. I felt really tired and went to bed.B. I closed the door and stayed with him.C. I just walked outside to leave him alone.D. I gave him iPhone and let him stay inside.25.The change of the son's feelings can be described as ______ .A. angry→surprised→proudB. excited→peaceful→boredC. worried→angry→hopefulD. bored→peaceful→pleased26.The best title for the passage can be ______ .A. A Terrible Life on the IslandB. A Special iPhone for My SonC. A Fight between Mother and SonD. A Vacation Away from ElectronicsDAre you nearsighted （近视的）？Do you wear glasses？Many of you may say"yes".In fact China's young people have the highest rate （率）of nearsightedness in thewold,according to a report from the World Heath Organization.More than 70 percent of middle school students in China are nearsighted.In August,a plan to solve this problem was introduced.It aims to cut down the rate of nearsightedness for middle school students to less than 6 o percent by 2030.Schools across the country are taking action to meet this goal.Luoyang Experimental School in Henan started with its desks.It has designed special desks which nave a board above the desktop.The board stops students from lowering their heads too close to their desktops.More than 400 students have used them so far.More students will use them son.similarly,the High School Affiliated to Renmin University Chaoyang Branch Schools now providing desks and chairs according to students' heights.Studies have shown that proper desk height can prevent（预防）nearsightedness.Spending more time outside can also reduce nearsightedness.Yucai Middle School attached to Chengdu No.7 High School makes sure that its students play outside for at least 80 minutes every day. "We have a PE class and a 20-minute break in the morning and afternoon to do exercise,"said Sun Zihan,14.Staring at screens can also hurt our eyes.Beijing 101 Middle School has a solution to this problem.In its classrooms,there are special boxes for storing students' cell phones."We have to hand in our cell phones every morning and get them back after school,"said Huang Jiameng,15.27.How many way are mentioned to prevent nearsightedness in this passage？______A. Two.B. Three.C. Four.D. Five.28.The board above the desktop was designed to ______ .A. make the students see it clearly in classB. make the teachers work hardC. protect the students' eyes in classD. encourage the students to take part in all kinds of activities29.How long do the students in Chengdu No.7 High School play outside at least every day？______A. For 20 minutes.B. For 40 minutes.C. For 60 minutes.D. For 80 minutes.30.What's the best title of the passage？______A. Spending more time outsideB. Taking action to save our sightC. What makes us nearsightedD. A kind of special desk三、信息匹配（本大题共5小题，共10.0分）As we all know,nobody lives alone and we all need others help and opinions.If you treat others well,you will win their respect and get on well with them.That will make the world become better and more beautiful.(1) show your smile to them and that will make the relationship between each other much better.(2) And in other words,say it in a tactful（有分寸的）way.Try not to use any words that make others feel uncomfortable.we may have different ideas towards the same person or thing.we also have the right to show our feeling If we say that in a polite way,it will bring a good result.(3) You should start with"Could I or"May I" .These expressions will tell others you are a polite person and they will accept you or your opinions more easily.(4) You should rot confine（限制）yourself to your comfortable lifestyle,but rise to the occasion （时机）to help others.(5) Try to be polite when communicating with others and leave good impressions on them.31. A. A B. B C. C D. D E.E F. F32. A. A B. B C. C D. D E.E F. F33. A. A B. B C. C D. D E.E F. F34. A. A B. B C. C D. D E.E F. F35. A. A B. B C. C D. D E.E F. F四、阅读填空（本大题共1小题，共10.0分）36.It snowed heavily last Sunday in Beijing.Several people are talking about theirexperiences that day.Speaker 1：My name is Andy.When the snowstorm began,I (1) （climb）the Great Wall with my family.There were some other (2) （tour），too. (3) snow looked beautiful and we couldn't stop taking photos.But slowly it was getting heavier and heavier.And I nearly fell down (4) the ground was kind of slippery.Speaker 2I'm Mona.I was having a walk with my friend Li Dong when the snow flakes startedfalling.Like other people,we were happy at first.Then we started (5) （run）around and playing with snow.As it was snowing (6) （hard），the road got slipperier and one or two old people fell down.Then we begin to help them to get up.Of course,we were glad (7) （hear）thanks from them.Speaker 3：I'm Lily!I went to have my piano lessons that day.After class,I waited for the bus to come(8) lots of passengers around.When the bus finally came,people rushed to the door of thebus at the same time.So it was very difficult for me to get on it.Another bus came twenty(9) （minute）later,but it ran very (10) （slow）because the road was slippery.(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)五、单词拼写-单句（本大题共10小题，共10.0分）37.My back really h ______ now because I did so much housework this morning.38.Aron Rolston,a mountain climber,is used to t ______ risks.39.It's hard to i ______ the difficulties the doctors had at the beginning of the epidemic inWuhan.40.In order to help her daughter d ______ independence,the mother sent the girl to a boardingschool （寄宿学校）.41.She kept herself busy in reading i ______ of wasting time during the holiday.42.The sun was r ______ up when I got up in the morning.43.If something e ______ you,it makes you feel very happy.44.The soldiers fought bravely and finally s ______ in beating off （击退）the enemy.45.--Please look at the s______"No smoking" over there.-Sorry,I didn't see it.46.We b ______ some books from the library last week．六、书面表达（本大题共1小题，共15.0分）47.假如你是李峰，请你对你的笔友Emily的邮件进行回复，词数80左右。

2019-2020锦绣育才集团2020年中考模拟卷(二)

2019-2020锦绣育才集团2020年中考模拟卷(二)

2019-2020学年浙江省杭州市锦绣育才教育集团2020年中考模拟考试（二）阅读理解（共两节，满分40 分）第一节（共15小题，每小题2分，满分30分）阅读下列短文，从每题所给的四个选项（A.B.C.D）中选出最佳选项A1.With help from a Mr. H, you can___________ .A. stop using batteriesB. finish your homework on timeC. remember your teachers’ instructionsD. get your room tidied on your way home2.A PENGO W ATCH CONTROL can help you to __________.A. repair your TVB. Ask parents or teachers for helpC. be a James BandD. know what the weather is like3.Where would you be most likely to find the two texts?A. On a notice board.B. In a science fiction.C. On a teenage website.D. In a geographical magazine【答案】BDCBIf you stay in space for a long time, will your body change? Mark Kelly and Scott Kelly from the United States will show you the answer. Mark and Scott are twins. They are both retired NASA(美国国家航天航空局) astronauts. From 2015 to 2016, Scott spent 340 days at the international space station, while Mark stayed on the earth. People took measures of both men before, during and after the flight. They were helping with a NASA project which studies how long-term space travel influences the human body. The full results of the study will come out in a year or two. But scientists are sharing some findings in the journal Nature.A change in appearance was easy to see. Scott, when he returned to the Earth, was 5cm taller before. Another change was that Scott’s eyesight declined after he came back. He found he couldn’t see clearly. He also found that he couldn’t move his legs so easily like before. Scientist found that after coming back to the earth, he took a little longer to understand things and make decisions.There were also changes that were much harder to see. As someone ages, his telomeres(端粒) get shorter and become less effective to stop DNA from getting damaged. But during Scott’s stay in space, his telomeres got longer while Mark’s kept getting shorter.Further tests on the twins are still going on. NASA plans to send people to Mars in the 2030s, and the twins’ research could help them prepare for those space trips.1. Which of the following is NOT true about Scott?A. He is from the United States.B. He has a twin brother.C. He was once a NASA astronaut.D. He has never been to space before.2. We can know that scientists did the research between the twins in order to ____.A. study how twin brothers act differently in lifeB. learn more about the twins’ daily lifeC. study how long-term space travel influences the human bodyD. decide if Mars is suitable for humans to live on3. What does the underlined word “declined” mean in Chinese?A. 控制B. 漂浮C. 提高D. 下降4. What didn’t Scott experience while he returned to the earth?A. He could walk faster than before.B. He grew taller than before.C. He couldn’t understand others as well as before.D. His telomeres became longer.5. The last paragraph mainly tells us ____.A. the full results of the twins’ researchB. the purpose of the twins’ researchC. the fun of space travelD. the success of the twins’ research【答案】DCDABCIn choosing a friend, one should be very careful. A good friend can help you study. You can have fun together and make each other happy. Sometimes you will meet fair-weather friends. They will be with you as long as you have money or luck, but when you are down, they will run away. How do I know when I have found a good friend? I look for certain qualities (品质) of character, especially understanding, honesty and reliability (可靠).Above all else, I look for understanding in a friend. A good friend tries to understand how another person is feeling. He is not quick to judge. Instead, he tries to learn from others. He puts himself in the other person's place, and he tries to think of ways to be helpful. He is also a good listener.At the same time, however, a good friend is honest. He does not look for faults (过错) in others. He notices their good points. In short, a friend will try to understand me and accept me.Another quality of a friend is reliability. I can always depend on (信赖) a good friend. If he tells me he will meet me somewhere at a certain time, I can be sure that he will be there. If I need a favor, he will do his best to help me. If I am in trouble, he will not run away from me.There is a fourth quality that makes a friend special. A special friend is someone with whom we can have fun. We should enjoy our lives, and we would enjoy our friendship. That is why I especially like friends who are fun to be with. A good friend likes the same things I like. We share experience (经验) and learn from each other. A good friend has a good sense of humor (幽默), too. He likes tolaugh with me. That is how we share in the joy of being friends. And I know that he is looking for the same quality in me.When I meet someone who is reliable, honest, and understanding, I know I've found a friend!1. Which of the following qualities the writer thinks is the most important in choosing a friend?A. a sense of humor.B. honesty.C. understanding.D. reliability.2. If you have fair-weather friends, ______.A. you can be sure that you get real friendsB. you will be refused when you get into troubleC. they will give you all that they have when you need helpD. you will become rich3. Good friends need to ______.A. look for faults in othersB. be helped with moneyC. understand each other's feelingsD. have money or luck4. This passage mainly discuss ______.A. the qualities of a friendB. where to choose friendsC. how to get along with friendsD. the importance of having a friend【答案】CBCADOne of the latest trend（趋势）in American Childcare is Chinese au pairs. Au Pair in Stamford, for example, has got increasing numbers of request for Chinese au pairs from aero to around 4,000 since 2004. And that’s true all across the country.“I thought it would be useful for him to learn Chinese at an early age” Joseph Stocke, the managing director of a company, says of his 2-year old son. “I would at least like to give him the chance to use the language in the future,” After only six months of being cared by 25-year-old woman from China, the boy can already understand basic Chinese daily expressions, his dad says.Li Drake, a Chinese native raising two children in Minnesota with an American husband, had another reason for looking for an au pair from China. She didn’t want her children to miss out on their roots.” Because I am Chinese, my husband and I wanted the children to keep exposed to(接触) the language and culture（文化）.” she says.“Staying with a native speaker is better for children than simply sitting in a classroom,” says Suzann e Flynn, a professor in language education of Children.” But parents must understand that just one year with au pair is unlikely to produce wonders. Complete mastery demands continued learning until the age of 10 or 12.” The popularity of au pairs from China has been strengthened by the increasing numbers of American parents who want their children who want their children to learn Chinese. It is expected that American demand for au pairs will continue to rise in the next few years.1. What does that term “au pair” in the text mean?A. A mother raising her children on her ownB. A child learning a foreign language at homeC. A professor in language education of childrenD. A young foreign woman taking care of children.2. Li Drake has her children study Chinese because she wants them ______.A. to live in China some dayB. to speak the language at homeC. to catch up wit other childrenD. to learn about the Chinese culture3. What can we infer from the text?A. Learning Chinese is becoming popular in AmericaB. Educated woman do better in looking after childrenC. Chinese au pairs need to improve their English Skills.D. Children can learn a foreign language well in six months.【答案】DDA第二节（共五小题，每小题2分，满分10分）下面文章中有五处需要添加小标题，请从以下选项（ABCDEF）中选出符合各段意思的小标题，选项中有一项是多余选项。

2020年人教部编版浙江锦绣教育八年级(下)英语期中检测试题及答案解析

2020年人教部编版浙江锦绣教育八年级(下)英语期中检测试题及答案解析

II 笔试部分（95分钟）三、单项选择（每题1分，共10分）从A 、B 、C 、D 四个选项中选出最佳选项。

16. Which group of the following words has the different pronounciations on their underlined parts?A. short, fish, EnglishB. about, around, sofaC. sofa, coat, newD. what, when, white 17. run in the hallways. A. Not B. Can ’t C. NoD. Don ’t18. ---Who the piano?---My sister, when she time. A. plays, has B. is playing, has C. plays, is having D. played, has 19. --- does it take to get to school?---It takes about one hour. A. How B. How many C. How far D. How long 20. As a reporter, I can meet different people. That ’s exciting.. A. kind of; kind of B. kinds of; kind of C. kind of; kinds of D. kinds of; kinds of21. is interesting.A. Taking the trainB. Take the trainC. By a trainD. By train 22. Who wants to the art club?A. take inB. joinC. join inD. take part in 23. Look at the boy in red. He always playing with his brothers.A. has funB. is having funC. is funD. is funny 24. ---What are you doing, Peter?--- . I am just watching a boring TV show.A. OkB. NothingC. Not muchD. Something great 25. ---Would you like a cup of tea?--- .A. I ’d loveB. Yes, please.C. No, I wouldn ’tD. Sorry四、完形填空 （每小题1分，共10分）通读下面短文，掌握其大意，然后在各题所给的四个选项（A 、B 、C 、D ）中选出最佳选项。

锦绣育才教育集团2019年中考模拟考试(二)

锦绣育才教育集团2019年中考模拟考试(二)

锦绣育才教育集团2019年中考模拟考试(二)阅读理解AAs the number of private cars is increasing rapidly,it has caused lots of presure to the traffic.Traffic accidents are terrible words we modern people have got used to using or hearing.It’s reported that many people died from traffic accidents each year.Traffic accidents have become one of the most dangerous killers for modern people in the past few years.What are the main causes of traffic accidents?The following charts may tell you.Luckily,road safety has got much more attention and many rules have been made to cut down the traffic accidents.Everyone who drives a car should take road safety seriously.They should know how dangerous it is when driving their cars at a very fast speed or after drinking too much or some other behaviors like that.They have to stick to the traffic laws.It might be the best way solve the problem.What’s more,some other things can be done to cut down the accident.Not long ago,the action called“Go to work by bike”was arising in Paris.This action has received a good result.We can follow the example and choose bicycle riding,the simple and healthy way instead of cars when we go out.Maybe when one day we find out that riding a bike is an interesting sport,we will get away from the trouble of getting into heavy traffic.1.The main factors in car accidents are____.A.driver factorsB.vehicle factorsC.road factorsD.drunk driving1.The best way to cut down the traffic accident is to____.A.slow down when driving.e seat beltsC.drive cars when we are not tiredD.stick to the traffic laws2.The author wrote this passage to____.A.call on people to pay attention to road safetyB.tell people to drink less when drivingC.tell people how many people die from traffic accidentsD.ask people to go out only by bike every day3.We can probably find a passage from a____.A.science magazineB.news reportC.novelD.tour guide【参考答案】ADABBUncle Harold is a changed man.For years he has bored Aunt Grace with his expressions of regret at missing opportunities,particularly bargains he has failed to take advantage of.When he wanted to buy something,he would think of the buying over and over again.He would find it hard to make up his mind.“You remember that old chest,”he would say to her.“I wish I’d bought it.It would have been worth twice as much.”Aunt Crace’s usual answer was a sign,though it was never clear whether she was arguing with her husband’s sense of loss,or whether she was silently saying,“I wish you would stop going on what might have been.”However,Uncle Harold clearly suffered a change of heart last month.He returned from a furniture sale where he had bought nearly everything in sight.“I realized,”he told Aunt Grace “how often I have regretted not receiving a bargain when I saw one.So now I’ve taken a bold step.”He showed her a Victorian sofa,a rocking chair,a stuffed bird in a glass case,a damaged coffee table,and three vases.She signed.For the past weeks,Uncle Harold has been moving around the house speaking to himself,“I wish I’d never seen that sofa”,“If only I hadn’t bought that coffee table”,and “had I known that terrible bird was going to be watching me...”Perhaps he isn’t a changed man,after all.Certainlly Aunt Grace signed as much as ever.1.By saying “Uncle Harold is a changed man,”the author means that ____.A.Uncle Harold is quite different from what he was B.Uncle Harold often regrets at missing chances C.Uncle Harold always bores Aunt Grace D.Uncle Harold has changed in his look2.The passage tells us that Uncle Harold did not buy ____.A.a rocking chair B.a coffee table C.an old chest D.a sofa3.Uncle Harold felt ____when he said,“had I known that terrible bird was going to be watching me...”A.sorry B.angry C.happy D.surprised4.What does the underlined word “bold”in the passage mean in Chinese?A.明显的.B.无私的.C.大胆的.D.厚颜无耻的.【参考答案】ACBCCHere is an experiment to see how ants can organize some clever teamwork.1.First,you need some ants.You may have to wait until the summer to find2.When you have found an ant,put a thin slice of fruit in front of it.It may3.Check the fruit later after an hour.Have other ants being attracted to it.If4.When there are lots ofants,move the fruit to a new position,a little to thethem on paths around your home.eat some of it or carry bitsaway.so,what are they doing?side.What do the ants do?What’s going on?You can see one of the best examples of insect teemwork by watching ants.If one ant finds food,it will lead others there to eat it too.They follow each other by making long trails.The ants go back and forth collecting food to take it back to their nest.When you move the fruit,the ants wil still find it.But instead of making a new direct route(路线)to the food,they will follow each other through their old trail route.1.What will happen if one ant finds food?A.The ant will eat all the food.B.The ant will watch other antsC.The ants will lead others to the food.D.The ant will wait until others come.2.If the fruit is moved to a new position,the ants will____.A.fail to find itB.give up looking fot itC.make a new direct route to itD.get to it through the old trail route3.Which is the correct order to do this experiment?a.Move the fruit to a new position.b.Find an ant.c.Check the fruit an hour later.d.Put a thin slice of fruit in front of the antA.a-b-c-dB.b-d-c-aC.d-b-c-aD.c-a-d-b4.What can we learn from this experiment?A.The experiment is done successfully in the lab.B.Ants do the experiment to show their team spirit.C.Careful watching does little help in this experiment.D.We can find out some facts by doing small experiments.【参考答案】CDBDDThe Silk Road is the name of different roads that long ago connected Europe,Africa amd Asia.People reached these different places along these roads.Scientists believe people began to travel the Silk Road about3000years ago.By the time the Chinese silk trade became important in the world,the Silk Road covered almost6500 kilometers.It spread from Rome to China,which is from the West to the Far East.Traders Travelling along the Silk Road carried silk,of course.They also carried and traded spices(香料),cloth, valuable stones and gold.There is a famous old story along the old road.It is said that Roman soldiers travelled through central Asia. They started to live somewhere near the ancient Chinese village of Liqian.Some of thesse Romans married local Chinese women and the story of blue-eyed villages of China was started.During its busiest period,the Silk Road allowed people from many different cultures and countries to meet each other and mix.The Silk Road allowed the sharing of valuable goods and new ideas.These included people and trading goods from the Mediterranean,Persian,Magyar,American,Bactrian,Indian and Chinese areas.All these peoples travelled the Silk Road,and they shared goods,stories,languages,and cultures.In modern times,the old Silk Road routes are still used,but now they are crossed by trains instead of camels and horses.There is even a Silk Route Museum in Jiuquan in China.It has over35,000objects from all along the Silk Road.In this way,China protects the history of many countries and peoples.1.Traders carried all kinds of goods along the Silk Road.Which of the following is not mentioned in the passage?A.Silk.B.Cloth.C.Gold.D.Tea.2.What can we infer(推断)from the passage?A.Valuable things could not be sold along the Silk Road.B.The Silk Road allowed people from different countries to mix.C.Ancient Chinese along the Silk Road may be able to speak different languages.D.The objects in the museum in Jiuquan in China are from all along the Silk Road.3.Which part of a magazine can this passage come from?A.History and Geography.B.Sports World.C.Man and Animals.D.Popular Science.【参考答案】DCA任务型阅读下面文章中有五处（第1-5题）需要添加句子，请从以下选项（A、B、C、D、E和F）中选出符合上下文的句子。

2020-2021学年浙江省杭州市拱墅区锦绣育才教育集团八年级(下)月考试卷(3月份)(附答案详解)

2020-2021学年浙江省杭州市拱墅区锦绣育才教育集团八年级(下)月考试卷(3月份)(附答案详解)

2020-2021学年浙江省杭州市拱墅区锦绣育才教育集团八年级（下）月考试卷（3月份）一、完形填空（本大题共15小题，共15.0分）I lived in Missouri,near a river called the Jacks Fork.Before I was born,my grandparents decided to help（1）______ the river clean.So,they started a（2）______ called Stream Team 713.I like its another（3）______ better the Jacks Fork River Rats.The club makes sure the water is clean and（4）______ for fish and people.And now I'm old enough to help（5）______ the river.Picking up（6）______ is like a treasure hunt（寻宝）.My friends and I find plastic bags,（7）______ bottles and cans,paper and other things.But there used to be（8）______ more trash here.One weekend my grandparents picked up six tons of trash.That was as（9）______ as an elephant.The trash is（10）______ for the river or the animals and plants that live there.So the Jacks Fork River Rats asks people who are relaxing on the river to（11）______ trash with them instead of throwing it into the river.My favorite thing is to（12）______ water bugs!The bugs like to stay at the bottom of the river.Some bugs don't care（13）______ dirty the water is,but some bugs can only live there if the water is clean.（14）______ we find lots of bugs that need clean water,we will know the river is clean enough for fish and people.We（15）______ taking care of the river.We help make sure it's clean and safe place.1. A. keep B. give C. avoid D. continue2. A. music B. note C. club D. school3. A. plan B. shape C. name D. picture4. A. thirsty B. healthy C. hungry D. full5. A. get into B. take after C. run along D. care for6. A. fruit B. trash C. flowers D. snacks7. A. empty B. full C. difficult D. famous8. A. ever B. none C. hardly D. even9. A. big B. strong C. heavy D. tall10. A. different B. bad C. good D. necessary11. A. meet B. pass C. take D. offer12. A. look after B. put up C. take off D. look for13. A. how B. what C. why D. when14. A. Unless B. if C. Before D. Though15. A. hate B. improve C. enjoy D. reply二、阅读理解（本大题共15小题，共30.0分）A16.What might May often do in the past？______A. Playing with Sam.B. Staying alone in her bedroom.C. Talking with her dad.D. Helping her mom with the chores.17.Which subject may Zhu Le be good at？______A. English.B. Chinese.C. Math.D. History.18.What can we know from the information？______A. Joe often gives some old things away to poor kids.B. There are at least four people in May's family.C. Wang Zi needs a great job to develop his skills.D. Zhu Le is from a poor family,but loves to study.BAlmost all children expect their parents to give them more pocket money.But most of the time,their parents just give them a certain amount（数量）.And the amount of money that children get from their parents is different from family to family.The frequency（频率）of getting money is different,too.Some children get pocket money every month.Do you know why？First of all,parents expect children to choose between the spending and the saving.Then children should understand what their parents expect them to buy with their pocketually,some children spend all of the money soon after they get it.Experts usually advise parents not to offer more money until it is the right time.By doing this，children will learn to spend money well.In order to encourage children to do the housework,some parents pay children for doingthat.However,some experts don't agree because helping at home is a normal part of family life. Pocket money can give children a chance to experience three things.They can spend it by giving it to a good course.They can spend by buying things they want.They can save it for future use.Saving money helps children understand that money never comes easily.Saving money can also open the door to a better future for children.19.When parents give pocket money to their children, ______ .A. they usually give it twice a weekB. they usually give them a certain amountC. they usually give it in the same wayD. they usually give it every two months20.What does the underlined word "this" refer to？______A. Spending pocket money at the right time.B. Making a good plan for spending pocket money.C. Making a choice between the spending and the saving.D. Giving more pocket money to children at the right time.21.What can we learn from the passage？______A. Almost all children get pocket money every week.B. Experts think parents should give children pocket money at a certain time.C. Children can have more money if they have a habit of saving money.D. Some experts don't agree that parents should give children money for doinghousework.22.Where can we probably read this passage？______A. In a diary.B. In a magazine.C. In a notice.D. In a dictionary.CIt was Day 1 of our vacation on Cortes,a beautiful quiet island. "iPhone,iPhone,iPhone,"my son kept moaning（呻吟）.In front of him was a big window facing the blue ocean.And a cool gentle wind was coming in from the door.Clearly,he saw and felt none of it.Back at home,I'd soon give up and hand the phone over to him after five minutes of listening to this kind of moaning.But not here.Before we left,I had told my 10-year-old son the rule-no emails,no social media,no video games,and no iPhone.We came here to get away from them all.Here we were on our first day and already,he couldn't stand it..I walked down the grass road to the beach and looked out to the sea.My 6-year-old daughter and my husband were drawing on pieces of wood.They were doing just fine.On Day 2，we spent the whole morning digging for shells（贝壳）.This time,my son joined us.He collected shellfish and other sea treasures.When we got back to our little wood house,I gave my son a book,and put him on the lovely garden chair.It was almost dinner when he looked up.The next few days passed in peace.On Day 6，my son was lying beside me on the beach,watching the sun going down.He was playing with the sand.And there was something shining in his eyes.I realized how time slowed down for both of us.It was exactly what I wanted.Finally,we were able to sit quietly without thinking about screens,phone calls and e-mail.A week's life away from all the electronics is good.23.What is the special rule for the writer's vacation？______A. They couldn't use their electronics.B. They must keep quiet and stay in the house.C. They had to spend their vacation on an island.D. They should collect as many shells as possible.24.Which of the following can be put in " ______ " in Paragraph 4？A. I felt really tired and went to bed.B. I closed the door and stayed with him.C. I just walked outside to leave him alone.D. I gave him his iPhone and let him stay inside.25.The change of the son's feelings can be described as ______ .A. angry→ surprised→ proudB. excited→ peaceful→ boredC. worried→ angry→ hopefulD. bored→ peaceful→ pleased26.The best title for the passage can be ______ .A. A Terrible Life on the IslandB. A Special iPhone for My SonC. A Fight between Mother and SonD. A Vacation Away from ElectronicsDParents may be surprised at how fast their kids grow up,but a study finds that U.S teenagers are developing more slowly than those in the past.Scientists at San Diego State University have worked on a study of over 8 million U.S kids aged 13-19 for 40 years.The findings show that today's teenagers are less responsible（负责任的）and that most of them don't have a part-time job. "The whole development has slowed down.Today's 18-year-olds are more like 15-year-olds in the past," said Professor Jean Twenge. "Teenagers are taking fewer risk than those in the past."Scientists have also found that more teenagers spend longer time living with their parents instead of renting（租）their own room or apartment.So is that slower development "good" or "bad"？It may depend on how you look at it,the scientists said."The upside of slower development is that teenagers aren't growing up before they are ready,"said Professor Twenge."But the downside is that they go to college and into the workplace without as much experience with independence." Today's students may be smart and creative,but they often have trouble with planning,time management （管理）and problem-solving,added ProfessorTwenge.One of the reasons for these changes is that today's teenagers would like to spend much time online.They keep on watching videos or playing games on the Internet instead of spending more time with their family and friends in person.Another one is that parents have become much more child-centric.In fact,parents had better let their children do everything by themselves.They should try their best to make their children become independent as soon as possible.27.What can we know from the first two paragraphs？______A. The study lasted for about 20 years.B. Teenagers now are more hard-workingC. Teenagers in the past took more risks.D. Today's teenagers don't like slow life.28.Why do today's teenagers grow up slowly？______a.Their parents do too many things for them.b.It's difficult for them to get a part-time job.c.They dislike living in the real world.d.They spend too much time onlineA. abB. bcC. bdD. ad29.Which of the following shows the right structure of the passage？______A. ①；②；③④B. ①②；③④C. ①；②③；④D. ①②；③；④30.Which is the best title for the passage？______A. Study on Teenagers in the Past.B. Slow Development of U.S Teenagers.C. U.S.Teenagers' Personal Development.D. Different ideas about Today's Teenagers.三、信息匹配（本大题共5小题，共5.0分）Everyone has parents.But not all of you can get on well with your parent.Well,how to solve this problem？Here is some useful advice.（1）______Parents bring you to the world and care about you all the time.They really do their most and best for you,so you should try not to make them sad or angry and be polite to them.（2）______You may choose whatever you can do.For example,doing the dishes,taking out the rubbish or cleaning the room.In fact,when you help them at home,you'll learn how to look after yourself in the future（3）______Have a talk with them about their work when they come back.Try to make them happy when they are sad in life.Remind warmer clothes on cold days.（4）______In some ways,most parents wish their kids can be top at school and get a better future.You should try to learn hard and get on well with classmates and teachers so that they don't have to worry about you.（5）______Don't always think of online games in your free time.If possible,you can stay with your parents.When shopping,buy something for your parents.On weekends,take a short trip with them.For parents and you,staying with each other is great.A.Care for parents.B.Sleep with parents sometimes.C.Spend some time with parents.D.Learn to respect （尊敬）parents.E.Try to be best at school.F.Help to do some housework.31. A. A B. B C. C D. D E.E F. F32. A. A B. B C. C D. D E.E F. F33. A. A B. B C. C D. D E.E F. F34. A. A B. B C. C D. D E.E F. F35. A. A B. B C. C D. D E.E F. F四、单词拼写/单词释义（本大题共1小题，共10.0分）36.Hi Clair,I'm so excited.Guess what--- it's my Dad's（1）______ （forty ）birthday next month.So he's taking（2）______ （we）all to London for a weekend!Cool,eh？We're flying over on Thursday evening.As soon as we arrive,we're going on a tour of the city.They say London is（3）______ （real）beautiful at night,and I' m really looking forward to seeing all those famous places.On Friday we're going to the Tate Modern （the art gallery near the river Thames），then to the Design Museum.It's not far from our hotel,so we're（4）______ （plan）to walk there.In the afternoon,we're going on the London Eye.In fact,the London Eye is so tall（5）______ we can see it from all directions during our trip!I can't wait（6）______ （see）the Houses of Parliament from up there!Saturday is for shopping--- there' s no doubt about that!We're going to Portobello Road（7）______ （one）.Then in the afternoon,we're visiting Harrods ---（8）______ （famous）shop in London!Dad's not very happy about it,（9）______ I'm sure he'll enjoy it when we're there.On Sunday morning,we're going to Hyde Park,and we're flying home in the afternoon It's one of my（10）______ （dream）---and it's happening!Hope everything's OK with you.Love,Cynthia五、单词拼写-单句（本大题共10小题，共10.0分）37.The house is in a m ______ after the party.Let's help clean it up.38.My brother makes a d ______ to be a teacher when he grows up.39.We can't solve the problem by o ______ and let's ask the teacher for help.40.– Shall we climb mountains tomorrow,Dad？– It d ______ on the weather.If it rains,we will put off the plan.41.As a helper,the dog can guide the b ______ to the places they would like to go to.42.My sister t ______ down her schoolbag and went to her bedroom.43. A car h ______ a tall tree,but luckily,the driver didn't hurt himself badly.44.Would you mind o ______ the door for me？My hands are full of things and I can't do itmyself.45.Mr.Green is no longer the o ______ of the house.He sold it last year.46.You see,I'm only able to have a "dog helper" because of your k ______ .六、书面表达（本大题共1小题，共15.0分）47.你的笔友city想了解你在上周志愿者活动。

2020杭州市育才教育集团习得课程八年级下册检测试卷(无答案)

2020杭州市育才教育集团习得课程八年级下册检测试卷(无答案)

考生须知：锦绣育才教育集团寒假习得课程——阶段性检测初二科学（问卷）1. 本试卷满分为 120 分，考试时间为 60 分钟。

2. 答题前，在答题纸上写姓名和准考证号。

3. 必须在答题纸的对应位置上答题，写在其它地方无效。

答题方式详见答题纸上的说明。

4. 考试结束后，试题和答题纸一并上交。

5.以下相对原子质量，C-12, Ca-40，O-16 ,H-1一、选择题（本大题共 60 分，每小题 3 分，每小题只有一个正确选项） 1、下列各组元素中，元素符号的小写字母相同的一组是 （ ）A ．钠、镁、铝B ．氮、氖、汞C ．镁、银、汞D ．锰、铜、钠2、若将条形磁铁据成许多小段，则每一段的两端（）A.将是两个北极B. 将是一个北极和一个南极C. 将是两个南极D.无极性3、为了判断一根铁棒是否具有磁性、小明进行了如下四个实验，根据实验现象不能确定该 铁棒具有磁性的是（ ）A ．悬挂的铁棒，静止时刚好指向南北B ．将铁棒一端靠近小磁针，相互排斥C ．将铁棒一端靠近大头针，大头针被吸引D ．将铁棒悬挂起来，用一个条形磁铁去靠近，相互排斥 4、关于磁场，下列说法中正确的是（ ）A ．磁体周围的磁感线从磁体N 极发出，回到磁体S 极B ．磁极间的相互作用不都是通过磁场发生的C. 磁感线是磁场中真实存在的一些曲线D. 地磁北极在地理北极附近，地磁南极在地理南极附近，与地球两极并不完全重合5、淳安特色其中之一是杭州最大的负氧离子库”。

空气中氧分子得到电子就能形成负氧离子（如 O 22-），O 22-与 O 2 不相同的是（ ）A. 质子数B ．电子数C ．含氧原子个数D ．相对原子质量之和6、某石灰石样品，测得含钙元素的质量分数为36%（杂质中不含有钙元素），则含碳酸钙的 质量分数为（ ） A ．36% B ．95% C ．90% D ．40%7、由氮氧两种元素组成的气体中，氮与氧的质量之比为 7：8，则该气体不可能是（ ） A ．NO 2、N 2O B ．N 2O 、N 2 C ．NO 2、N 2 D ．NO 2、N 2O 、N 2 8、高压输电线落在地面上时，人不能走近，其原因是（ ） A ．要把人吸过去 B ．要把人弹开来C ．输电线和人体之间会发生放电现象 D ．存在跨步电压9、作为相对原子质量标准的碳-12可以写成12C 。

2024届杭州市锦绣育才教育科技集团物理八年级第二学期期末学业水平测试模拟试题含解析

2024届杭州市锦绣育才教育科技集团物理八年级第二学期期末学业水平测试模拟试题含解析

2024届杭州市锦绣育才教育科技集团物理八年级第二学期期末学业水平测试模拟试题注意事项1．考试结束后，请将本试卷和答题卡一并交回．2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．一、选择题1．掷实心球是某市的中考体育加试项目之一．掷出去的实心球从a处出手后，在空中的运动轨迹如图所示，球最终停在水平地面e点处(不计空气阻力)则实心球( )A．在各点处都有内能，在a处重力势能最小、d处动能为零B．在b处受到了推力和重力的作用C．在a、b、c三处时具有的机械能相等D．在d处由于受到惯性的作用，能继续运动到e处2．如图所示，C是水平地面，A、B是两个长方体物块，F是作用在物块B上沿水平方向的力，大小为200N，物块A和B以相同的速度做匀速直线运动。

由此可知，关于A、B间摩擦力F1和B、C间摩擦力F2的分析中，正确的是A．F1=0N F2=200N B．F1=0N F2=0NC．F1=200N F2=0N D．F1=200N F2=200N3．两手分别拿着两个体积相同的小木块和石块浸没在水中，同时松手，小木块上浮，石块下沉。

比较松手时两者所受的浮力A．木块受的浮力大B．石块受的浮力大C．两者受的浮力一样大D．条件不足，无法比较4．一艘轮船空载时排水量为1000t，满载时排水量为5000t，下列说法不正确的是A．轮船自身质量为1×106kgB．装载的货物的最大质量为4×106kgC．满载时，受到的浮力为5×107 ND．如果排开液体的密度为1.0×103kg/m3，满载时排开液体的体积为5×104m35．如图所示是小球从高处下落到水平地面不断弹起的过程中，每隔相等时间曝光一次所得到的照片，小球在1、2位置的高度一样，下面說法正确的是A．小球运动时先后经过1、3、2三个位置B．小球在1位置的动能、机械能比2位置都小C．小球在1、2位置的重力势能相同，且机械能大小也相同D．小球在1、2位置的动能相同，且机械能大小相同6．如图所示，关于光现象的说法中，正确的是（）A．平面镜成正立等大的虚像B．放大镜成倒立放大的实像C．人在阳光下的影子是由于光的折射形成的 D．看见勺子在水面处“折断”是光的反射现象7．下列关于压强的说法不正确的是（）A．用吸管能把饮料吸入嘴里,是因为嘴内气压大于外界的大气压B．用高压锅煮食物熟得快,是因为锅内气压大液体沸点高C．三峡电站大坝利用液体压强规律设计成“上窄下宽D．气体和液体一样具有流动性,所以对各个方向都有压强8．（2016·威海卷）图中甲、乙、丙、丁四根弹簧完全相同，甲、乙左端固定在墙上，图中所示的力F均为水平方向，大小相等，丙、丁所受的力均在一条直线上，四根弹簧在力的作用下均处于静止状态，其长度分别是L甲、L乙、L丙、L丁．下列选项正确的是（）A．L甲＜L丙L乙＞L丁B．L甲= L丙L乙= L丁C．L甲＜L丙L乙= L丁D．L甲= L丙L乙＞L丁9．随着新国标《电动自行车安全技术规范》的出台，交警部门规定，从2019年4月15日起，电动自行车最高车速不得超过25km/h，并要求驾乘人员佩戴安全头盔。

2020-2021学年浙江省杭州市拱墅区锦绣育才教育集团八年级(下)月考数学试卷(3月份)

2020-2021学年浙江省杭州市拱墅区锦绣育才教育集团八年级(下)月考数学试卷(3月份)

2020-2021学年浙江省杭州市拱墅区锦绣育才教育集团八年级（下）月考数学试卷（3月份）（考试时间：120分钟满分：120分）一．选择题（没小题3分，共30分）1．下列图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．2．下列计算正确的是（）A．﹣＝B．+＝C．＝×D．÷＝43．如图，将▱ABCD的一边BC延长至点E，若∠A＝110°，则∠1等于（）A．110°B．35°C．70°D．55°4．若代数式有意义，则实数x的取值范围是（）A．x＞0 B．x≥0 C．x＞0且x≠2 D．x≥0且x≠25．去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵，每棵产量的平均数（单位：千克）及方差S2（单位：千克2）如下表所示．今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植，应选的品种是（）甲乙丙丁24 24 23 20S2 1.9 2.1 2 1.9A．甲B．乙C．丙D．丁6．若关于x的一元二次方程（m﹣1）x2+2x﹣2＝0有两个不相等的实数根，则实数m的取值范围是（）A．m＜B．m＞C．m＞且m≠1 D．m≠17．如图，平行四边形ABCD中，E，F是对角线BD上的两点，如果添加一个条件使四边形AECF是平行四边形，则添加的条件不能是（）A．AE＝CF B．BE＝FD C．BF＝DE D．∠1＝∠28．如果方程x2﹣x﹣2＝0的两个根为α，β，那么α2+β﹣2αβ的值为（）A．7 B．6 C．﹣2 D．09．如图，若▱AFPE、▱BGPF、▱EPHD的面积分别为15、6、25，则阴影部分的面积是（）A．20 B．15.5 C．23 D．2510．如图，在平行四边形ABCD中，AD＝2，AB＝，∠B是锐角，AE⊥BC于点E，F是AB的中点，连接DF、EF．若∠EFD＝90°，则AE长为（）A．2 B．C．D．二．填空题（每小题3分，共24分）11．用反证法证明“若|a|＜2，则a2＜4”是真命题，第一步应先假设．12．在抗击新型冠状病毒疫情期间，某校学生主动发起为武汉加油捐款活动，为了了解学生捐款金额（单位：元），随机调查了该校的部分学生，根据调查结果，绘制出如图的统计图．统计的这组学生捐款数据的众数是，中位数是．13．若一个多边形截去一个角后，形成的另一个多边形的内角和是1620°，则原来的多边形的边数是．14．如图，AB＝AC，四边形AEDF是平行四边形，△CFD和△DEB的周长分别为5和10，则△ABC的周长是．15．如图，已知△ABC中，点M是BC边上的中点，AN平分∠BAC，BN⊥AN于点N，若AB＝8，MN＝2，则AC 的长为．16．如果关于x的一元二次方程ax2+bx+c＝0有两个实数根，且其中一个根为另外一个根的2倍，则称这样的方程为“倍根方程”，以下关于倍根方程的说法，正确的有（填序号）①方程x2﹣x﹣2＝0是倍根方程；②若（x﹣2）（mx+n）＝0是倍根方程：则4m2+5mn+n2＝0；③若p，q满足pq＝2，则关于x的方程px2+3x+q＝0是倍根方程；④若方程以ax2+bx+c＝0是倍根方程，则必有2b2＝9ac．三．解答题（共66分）17．计算和解方程：（1）+﹣+．（2）（﹣）（+）+（﹣2）2．（3）5x+2＝3x2．（4）（2x﹣1）2＝（3x﹣4）2．18．某学校抽查了某班级某月5天的用电量，数据如下表（单位：度）：度数9 10 11天数 3 1 1（1）求这5天的用电量的平均数；（2）求这5天用电量的众数、中位数；（3）学校共有36个班级，若该月按22天计，试估计该校该月的总用电量．19．如图，在▱ABCD中，点E，F在对角线AC上，且AE＝CF．求证：（1）DE＝BF；（2）四边形DEBF是平行四边形．20．已知关于x的方程x2﹣（m+1）x+2（m﹣1）＝0（1）求证：无论m取何值时，方程总有实数根；（2）若等腰三角形一边长为4，另两边恰好是此方程的根，求此三角形的另两边长．21．如图，四边形ABCD是平行四边形，∠BAD的角平分线AE交CD于点F，交BC的延长线于点E．（1）求证：BE＝CD；（2）若BF恰好平分∠ABE，连接AC、DE，求证：四边形ACED是平行四边形．22．如图，平行四边形ABCD中，AB＝8cm，BC＝6cm，∠A＝45°，点P从点A沿AB边向点B移动，点Q从点B沿BC边向点C移动，P、Q同时出发，速度都是1cm/s，当一点先达到终点，另一点也停止运动．（1）P、Q移动几秒时，△PBQ为等腰三角形；（2）设S△PBQ＝y，请写出y（cm2）与点P、Q的移动时间x（s）之间的函数关系式，并写出x的取值范围；（3）能否使S△PBQ＝？若不能请说明理由，若能，也说明理由．23．如图，平行四边形ABCD，AD＝AC，AD⊥AC．（1）如图1，点E在AD延长线上，CE∥BD，求证：点D为AE中点；（2）如图2，点E在AB中点，F是AC延长线上一点，且ED⊥EF，求证：ED＝EF；（3）在（2）的条件下，若DC的延长线与FB交于点P，试判断四边形ACPE是否为平行四边形？并证明你的结论（先补全图形再解答）．。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

锦绣育才教育集团2019学年第二学期入学测试
初二数学
一、选择题
1.下列等式一定正确的是（
）A.81=±9 B.-()3²3-= C.a ²a = D.-3
³3-3=2.在平行四边形ABCD 中，∠A:∠B=7:2,则∠C 的度数是（）A.70° B.280° C.140° D.105°
3.若1<x <4，则()²x-||x-14+的值为（）
A.2x -5
B.3
C.5-2x
D.-34.以下是某九年级10名同学参加学校演讲比赛的统计表，则这组数据的众数和中位数分别为（）
成绩/分80859095
人数/人1342
A.85，87.5
B.85，85
C.85，90
D.90，90 5.双十一期间，某超市以优惠价销售A 、B 、C 、D 、E 五种礼盒，单价分别为90元、80元、70元、60元、50元天销售情况如图所示，则当天礼盒的平均售价为（）A.65元 B.66.5元C.70元 D.75元6.冠状病毒具有人传人的特性，调查发现，1人感染后如果不隔离，那么经过两轮将会有25人感染，若设1人平均一轮平均感染x 人，依题意可列方程式（）
A.1+x =25
B.1+x ²=25
C.(1+x )²=25
D.1+(1+x )²=25
7.若关于x 的一元二次方程()02212=+x-x m-有两个不相等的实数根，则实数m 的取值范围是（）
A.m<21
B.m>21
C.m>21且m ≠1
D.m ≠18.如图，在平行四边形ABCD 中，AB 垂直AC ，若AB=8，AC=12，则BD 的长是（）A.22 B.20 C.18 D.169.如图，在矩形ABCD 中，点E 在AB 上，点F 在CD 上，且BE=2AE ，DF=2CF ，点G 、H 是对角线AC 的三等分点，若四边形EGFH 的面积为1，则矩形ABCD 的面积为（）
A.9
B.12
C.18
D.610.如图，在菱形ABCD 中，点E ，F 分别是边AB 和BC 的中点，EP 垂直CD 于点P ，若∠FPC=56°，则∠A=（）
A.98°
B.105°
C.112°
D.119°
第8题第9题第10题
二，填空题
11.用反证法证明a>b 时，应先假设____，
12.若x ，y 都是实数，且833y +-+-=x x ，则x +3y 的立方根为____，
13.如果样本数据3，6，a ，4，2的平均数为4，则这个样本的方差为____，
14.若a 的方程x ²-3x +1=0，计算：a ²-3a+1
²a 3a +=____，15.如图，已知正方形ABCD 的边长为4，点E ，F 分别在AD ，DC 上，AE=DF=1，BE 与AF 相交于点G ，点H 为BF 中点，连接GH ，则GH 的长为____,
16.如图，矩形ABCD 中，BC>AB ，对角线AC ，BD 相交于O 点，且AC=5，过B 点作BE 垂直AC 于E 点，若BE=2，则AD 的长度等于____.
第15题
第16题三，解答题
17.计算（6分）
（1）()()22322+-（2）()
²233112--+18.解方程（8分）
（1）x ²-7x +2=0(2)4(x -1)²=9(x -5)²
19.（8分）为弘扬泰山文化，我市某校举行“泰山诗文大赛”活动，初学、高中部根据初赛成绩，各选出5名选手组成小学代表队和初中代表队参加决赛，两个队各选出5名选手的决赛成绩如下：
（1）根据视图填写图表
平均数（分）中位数（分）众数（分）
小学部85
初中部85100
（2）结合两队的平均数和中位数，分析哪个队决赛成绩较好：
20.（10分）已知：关于x的方程2x2+k x−1=0
(1)求证：方程有两个不相等的实数根；
(2)若方程的一个根是−1，求另一个根及k值。

21.（10分）把一张边长为20cm的正方形硬纸板，进行适当的裁剪，折成一个长方体盒子（纸板的厚度忽略不计）．若在正方形硬纸板的四角各剪掉一个同样大小的正方形，将剩余部分折成一个无盖的长方体盒子．
（1）要使折成的长方体盒子的底面积为121cm2，那么剪掉的正方形的边长为多少？
（2）折成的一个长方体盒子，侧面积能否达到192cm2，如果能，求此时剪掉的正方体的边长，如果没有请说明理由。

22.如图，在▱ABCD中，点E，F是直线BD上的两点，DE=BF.
(1)求证：四边形AFCE是平行四边形。

(2)若BD⊥AD，AB=13
2，AD=4，四边形AFCE是矩形，求DE的长。

(3)在(2)的条件下，求矩形AFCE的周长
23.如图，在菱形ABCD中，AE⊥BC于点E
(1)若∠BAE=30°，AE=4，求菱形ABCD的周长。

(2)作AF⊥CD于点F,连结EF,BD,求证：EF∥BD.
(3)设AE与对角线BD相交于点G,若CE=3,BE=6,四边形CDGE和△AGD的面积分别是S1和S2,求S1−S2的值。

相关文档
最新文档