数值线性代数二版徐树方高立张平文上机习题第三章实验报告
数值代数上机实验报告

数值代数上机实验报告试验项目名称:平方根法与改进平方根法实验内容:先用你熟悉的计算机语言将平方根法和改进平方根法编写成通用的子程序,然后用你编写的程序求解对称正定方程组Ax=b,其中,A=[101 10 1…1 10 11 10]100*100b随机生成,比较计算结果,评论方法优劣。
实验要求:平方根法与改进的平方根的解法步骤;存储单元,变量名称说明;系数矩阵与右端项的生成;结果分析。
实验报告姓名:罗胜利班级:信息与计算科学0802 学号:u200810087 实验一、平方根法与改进平方根法先用你所熟悉的计算机语言将平方根法和改进的平方根法编成通用的子程序,然后用你编写的程序求解对称正定方程组AX=b,其中系数矩阵为40阶Hilbert矩阵,即系数矩阵A的第i行第j列元素为=,向量b的第i个分量为=.平方根法函数程序如下:function [x,b]=pingfanggenfa(A,b)n=size(A);n=n(1);x=A^-1*b; %矩阵求解disp('Matlab自带解即为x');for k=1:nA(k,k)=sqrt(A(k,k));A(k+1:n,k)=A(k+1:n,k)/A(k,k);for j=k+1:n;A(j:n,j)=A(j:n,j)-A(j:n,k)*A(j,k);endend %Cholesky分解for j=1:n-1b(j)=b(j)/A(j,j);b(j+1:n)=b(j+1:n)-b(j)*A(j+1:n,j);endb(n)=b(n)/A(n,n); %前代法A=A';for j=n:-1:2b(j)=b(j)/A(j,j);b(1:j-1)=b(1:j-1)-b(j)*A(1:j-1,j);endb(1)=b(1)/A(1,1); %回代法disp('平方根法的解即为b');endfunction [x]=ave(A,b,n) %用改进平方根法求解Ax=b L=zeros(n,n); %L为n*n矩阵D=diag(n,0); %D为n*n的主对角矩阵S=L*D;for i=1:n %L的主对角元素均为1L(i,i)=1;for i=1:nfor j=1:n %验证A是否为对称正定矩阵if (eig(A)<=0)|(A(i,j)~=A(j,i)) %A的特征值小于0或A非对称时,输出wrong disp('wrong');break;endendendD(1,1)=A(1,1); %将A分解使得A=LDL Tfor i=2:nfor j=1:i-1S(i,j)=A(i,j)-sum(S(i,1:j-1)*L(j,1:j-1)');L(i,1:i-1)=S(i,1:i-1)/D(1:i-1,1:i-1);endD(i,i)=A(i,i)-sum(S(i,1:i-1)*L(i,1:i-1)');endy=zeros(n,1); % x,y为n*1阶矩阵x=zeros(n,1);for i=1:ny(i)=(b(i)-sum(L(i,1:i-1)*D(1:i-1,1:i-1)*y(1:i-1)))/D(i,i); %通过LDy=b解得y的值endfor i=n:-1:1x(i)=y(i)-sum(L(i+1:n,i)'*x(i+1:n)); %通过L T x=y解得x的值改进平方根法函数程序如下:function b=gaijinpinfanggenfa(A,b)n=size(A);n=n(1);v=zeros(n,1);for j=1:nfor i=1:j-1v(i)=A(j,i)*A(i,i);endA(j,j)=A(j,j)-A(j,1:j-1)*v(1:j-1);A(j+1:n,j)=(A(j+1:n,j)-A(j+1:n,1:j-1)*v(1:j-1))/A(j,j);end %LDL'分解B=diag(A);D=zeros(n);for i=1:nD(i,i)=B(i);A(i,i)=1;EndA=tril(A); %得到L和Dfor j=1:n-1b(j)=b(j)/A(j,j);b(j+1:n)=b(j+1:n)-b(j)*A(j+1:n,j);endb(n)=b(n)/A(n,n); %前代法A=D*(A');for j=n:-1:2b(j)=b(j)/A(j,j);b(1:j-1)=b(1:j-1)-b(j)*A(1:j-1,j);endb(1)=b(1)/A(1,1); %回代法disp('改进平方根法解得的解即为b');end调用函数解题:clear;clc;n=input('请输入矩阵维数:');b=zeros(n,1);A=zeros(n);for i=1:nfor j=1:nA(i,j)=1/(i+j-1);b(i)=b(i)+1/(i+j-1);endend %生成hilbert矩阵[x,b]=pingfanggenfa(A,b) b=gaijinpinfanggenfa(A,b)运行结果:请输入矩阵维数:40Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 6.570692e-020. > In pingfanggenfa at 4In qiujie at 10Matlab自带解即为x平方根法的解即为bx =1.60358.96850.85621.01950.9375-50.2500-3.0000-16.000024.0000-49.5000-30.000039.000022.0000-64.0000-12.00002.000010.2500-10.5000-1.0000-10.875083.000046.0000-98.0000-69.000068.000021.0000-50.7188-8.7500-8.0000 112.0000 6.0000 -68.7500 22.000044.0000 -28.0000 8.0000 -44.000012.0000b =1.0e+007 *0.0000-0.00000.0001-0.0004-0.00140.0424-0.29801.1419-2.73354.2539-4.30182.7733-1.19890.5406-0.36880.32850.4621-0.25130.05650.0000-0.00510.0071-0.0027-0.0031-0.00190.00090.0002-0.0002-0.00060.00040.0001-0.00020.00010.0000-0.00000.0000-0.0000-0.0000改进平方根法解得的解即为bb =1.0e+024 *0.0000-0.00000.0001-0.0012-0.0954 0.4208 -1.2101 2.0624 -1.0394 -3.3343 6.2567 -0.2463 -7.45942.80303.6990 0.7277 -1.7484 -0.4854 -3.6010 0.2532 5.1862 1.4410 0.8738 -4.5654 1.0422 4.0920 -2.7764 -2.2148 -0.8953 0.3665 4.8967 1.0416 0.1281-1.1902-2.83348.4610-3.6008实验二、利用QR分解解线性方程组:利用QR分解解线性方程组Ax=b,其中A=[16 4 8 4;4 10 8 4;8 8 12 10;4 4 10 12];b=[32 26 38 30];求解程序如下:定义house函数:function [v,B]=house(x)n=length(x);y=norm(x,inf);x=x/y;Q=x(2:n)'*x(2:n);v(1)=1;v(2:n)=x(2:n);if n==1B=0;elsea=sqrt(x(1)^2+Q);if x(1)<=0v(1)=x(1)-a;elsev(1)=-Q/(x(1)+a);endB=2*v(1)^2/(Q+v(1)^2);endend进行QR分解:clear;clc;A=[16 4 8 4;4 10 8 4;8 8 12 10;4 4 10 12]; b=[32 26 38 30];b=b';x=size(A);m=x(1);n=x(2);d=zeros(n,1);for j=1:n[v,B]=house(A(j:m,j));A(j:m,j:n)=(eye(m-j+1)-B*(v')*v)*A(j:m,j:n); d(j)=B;if j<m< p="">A(j+1:m,j)=v(2:m-j+1);endend %QR分解R=triu(A); %得到R D=A;I=eye(m,n);Q=I;for i=1:nD(i,i)=1;endH=tril(D);M=H';for i=1:nN=I-d(i)*H(1:m,i)*M(i,1:m);Q=Q*N;end %得到Qb=(Q')*b; %Q是正交阵for j=n:-1:2b(j)=b(j)/R(j,j);b(1:j-1)=b(1:j-1)-b(j)*R(1:j-1,j);endb(1)=b(1)/R(1,1); %回带法运行结果如下:R =18.7617 9.8072 15.7769 11.08640 9.9909 9.3358 7.53410 0 5.9945 9.80130 0 0 -0.5126Q =0.8528 -0.4368 -0.2297 -0.17090.2132 0.7916 -0.4594 -0.34170.4264 0.3822 0.2844 0.76890.2132 0.1911 0.8095 -0.5126b=1.000000000000001.000000000000010.9999999999999881.00000000000001实验三、Newton下山法解非线性方程组:3x-cos(yz)-=0,-81+sinz+1.06=0,exp(-xy)+20z+=0;要求满足数值解=满足或.定义所求方程组的函数:Newtonfun.mfunction F = Newtonfun(X)F(1,1)=3*X(1)-cos(X(2)*X(3))-1/2;F(2,1)=X(1)^2-81*(X(2)+0.1)^2+sin(X(3))+1.06;F(3,1)=exp(-X(1)*X(2))+20*X(3)+(10*pi-3)/3;End向量求导:Xiangliangqiudao.mfunction J=xiangliangqiudao()syms x y zX=[x,y,z];F=[3*X(1)-cos(X(2)*X(3))-1/2;X(1)^2-81*(X(2)+0.1)^2+sin(X(3))+1.06;exp(-X(1)*X(2))+20*X(3)+(10*pi-3)/3];J=jacobian(F,[x y z]);End代值函数:Jacobi.mfunction F=Jacobi(x)F=[ 3,x(3)*sin(x(2)*x(3)), x(2)*sin(x(2)*x(3));2*x(1), -162*x(2)-81/5,cos(x(3));-x(2)/exp(x(1)*x(2)),-x(1)/exp(x(1)*x(2)),20];End方程组求解:format long; %数据表示为双精度型X1=[0,0,0]';eps=10^(-8);k=1;i=1;X2=X1-Jacobi(X1)^(-1)*Newtonfun(X1);while (norm(subs(X2-X1,pi,3.1415926),2)>=eps)&&(norm(Newtonfun(X1),2)>=eps) if norm(Newtonfun(X2),2)<="" p="">X1=X2;B=inv(Jacobi(X2));C=Newtonfun(X2);X2=X2-B*C;i=i+1;elsev=1/(2^k); %引入下山因子X1=X2;B=inv(Jacobi(X2));C=Newtonfun(X2);X2=X2-v*B*C;k=k+1;endendj=i+k-1 %迭代次数X=X2 %输出结果运行结果如下:j =5X =0.500000000000000 -0.000000000000000 -0.523598775598299</m<>。
数值线性代数第二版徐树方高立张平文上机习题第一章实验报告(供参考)

上机习题1.先用你所熟悉的的计算机语言将不选主元和列主元Gauss 消去法编写成通用的子程序;然后用你编写的程序求解84阶方程组;最后将你的计算结果与方程的精确解进行比较,并就此谈谈你对Gauss 消去法的看法。
Sol :(1)先用matlab 将不选主元和列主元Gauss 消去法编写成通用的子程序,得到P U L ,,: 不选主元Gauss 消去法:[])(,A GaussLA U L =得到U L ,满足LU A =列主元Gauss 消去法:[])(,,A GaussCol P U L =得到P U L ,,满足LU PA =(2)用前代法解()Pb or b Ly =,得y用回代法解y Ux =,得x求解程序为()P U L b A Gauss x ,,,,=(P 可缺省,缺省时默认为单位矩阵)(3)计算脚本为ex1_1代码%算法(计算三角分解:Gauss 消去法)function [L,U]=GaussLA(A)n=length(A);for k=1:n-1A(k+1:n,k)=A(k+1:n,k)/A(k,k);A(k+1:n,k+1:n)=A(k+1:n,k+1:n)-A(k+1:n,k)*A(k,k+1:n);endU=triu(A);L=tril(A);L=L-diag(diag(L))+diag(ones(1,n));end%算法计算列主元三角分解:列主元Gauss消去法)function [L,U,P]=GaussCol(A)n=length(A);for k=1:n-1[s,t]=max(abs(A(k:n,k)));p=t+k-1;temp=A(k,1:n);A(k,1:n)=A(p,1:n);A(p,1:n)=temp;u(k)=p;if A(k,k)~=0A(k+1:n,k)=A(k+1:n,k)/A(k,k);A(k+1:n,k+1:n)=A(k+1:n,k+1:n)-A(k+1:n,k)*A(k,k+1:n); elsebreak;endendL=tril(A);U=triu(A);L=L-diag(diag(L))+diag(ones(1,n));P=eye(n);for i=1:n-1temp=P(i,:);P(i,:)=P(u(i),:);P(u(i),:)=temp;endend%高斯消去法解线性方程组function x=Gauss(A,b,L,U,P)if nargin<5P=eye(length(A));endn=length(A);b=P*b;for j=1:n-1b(j)=b(j)/L(j,j);b(j+1:n)=b(j+1:n)-b(j)*L(j+1:n,j); endb(n)=b(n)/L(n,n);y=b;for j=n:-1:2y(j)=y(j)/U(j,j);y(1:j-1)=y(1:j-1)-y(j)*U(1:j-1,j);endy(1)=y(1)/U(1,1);x=y;endex1_1clc;clear;%第一题A=6*eye(84)+diag(8*ones(1,83),-1)+diag(ones(1,83),1);b=[7;15*ones(82,1);14];%不选主元Gauss消去法[L,U]=GaussLA(A);x1_1=Gauss(A,b,L,U);%列主元Gauss消去法[L,U,P]=GaussCol(A);x1_2=Gauss(A,b,L,U,P);%解的比较subplot(1,3,1);plot(1:84,x1_1,'o-');title('Gauss');subplot(1,3,2);plot(1:84,x1_2,'.-');title('PGauss');subplot(1,3,3);plot(1:84,ones(1,84),'*-');title('精确解');结果为(其中Gauss表示不选主元的Gauss消去法,PGauss表示列主元Gauss 消去法,精确解为[]'⨯8411,,1 ):-6-4-202468Gauss050100PGauss 00.20.40.60.811.21.41.61.82精确解由图,显然列主元消去法与精确解更为接近,不选主元的Gauss 消去法误差比列主元消去法大,且不如列主元消去法稳定。
2021年数值线性代数第二版徐树方高立张平文上机习题实验报告2

第四章上机习题1考虑两点边值问题⎪⎩⎪⎨⎧==<<=+.1)1(,0)0(10 ,22y y a a dx dy dx y d ε 轻易知道它正确解为ax e e ay x +---=--)1(111εε为了把微分方程离散化, 把[0,1]区间n 等分, 令h=1/n,1,,1,-==n i ih x i得到差分方程,21211a hy y h y y y i i i i i =-++-++-ε简化为 ,)2()(211ah y y h y h i i i =++-+-+εεε从而离散化后得到线性方程组系数矩阵为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+-++-++-++-=)2()2()2()2(h h h h h h h A εεεεεεεεεε 对,100,2/1,1===n a ε分别用Jacobi 迭代法, G-S 迭代法和SOR 迭代法求线性方程组解, 要求有4位有效数字, 然后比较与正确解得误差。
对,0001.0,01.0,1.0===εεε考虑一样问题。
解 (1)给出算法:为解b Ax =, 令U L D A --=, 其中][ij a A =, ),,,(2211nn a a a diag D = ,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡------=-00001,21323121n n n n a a a a a a L,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡------=-0000,122311312 n n n n a a a a a a U 利用Jacobi 迭代法, G-S 迭代法, SOR 迭代法解线性方程组, 均能够下步骤求解: step1给定初始向量x0=(0,0,...,0), 最大迭代次数N, 精度要求c, 令k=1 step2令x=B*x0+gstep3若||x-x0||2<c, 算法停止, 输出解和迭代次数k, 不然, 转step4step4若k>=N,算法停止, 迭代失败, 不然, 令x0=x, 转step2在Jacobi 迭代法中, B=D -1*(L+U),g=D -1*b在G-S 迭代法中, B=D -1*(L+U),g=D -1*b在SOR 迭代法中, B=(D-w*L)-1*[(1-w)*D+w*U],g=w*(D-w*L)-1*b另外, 在SOR 迭代法中, 上面算法step1中要给定松弛因子w, 其中0<w<2 为计算结果, 要求w=0.5。
概率论与数理统计(茆诗松)第二版课后第三章习题参考解答

1
(1)(X1, X2, X3)的联合分布列; (2)(X1, X2)的联合分布列. 解: (1) P{( X 1 , X 2 , X 3 ) = (0, 0, 0)} =
⎛ 50 ⎞⎛ 30 ⎞⎛ 20 ⎜ ⎜ i ⎟ ⎟⎜ ⎜ j⎟ ⎟⎜ ⎜ ⎝ ⎠ ⎝ ⎠⎝ 5 − i − 且 P{ X = i, Y = j} = ⎛100 ⎞ ⎜ ⎜ 5 ⎟ ⎟ ⎝ ⎠
故 (X, Y ) 的联合分布列为
⎞ ⎟ j⎟ ⎠ , i = 0, 1, 2, 3, 4, 5; j = 0, L , 5 − i ,
i =1, 2 的分布列如下,且满足 P{X1X2 = 0} = 1,试求 P{X1 = X2}.
4. 设随机变量 Xi ,
Xi P
−1 0 1 0.25 0.5 0.25
解:因 P{X1 X2 = 0} = 1,有 P{X1 X2 ≠ 0} = 0, 即 P{X1 = −1, X2 = −1} = P{X1 = −1, X2 = 1} = P{X1 = 1, X2 = −1} = P{X1 = 1, X2 = 1} = 0,分布列为
故 (X, Y ) 的联合分布列为
Y X 0 1 2 3 4 5
0 0.00032 0.004 0.02 0.05 0.0625 0.03125
1 0.0024 0.024 0.09
2 0.054 0.135
3 0.054 0.0675 0 0 0
4 0.0081 0.02025 0 0 0 0
5 0.00243 0 0 0 0 0
《数值计算方法》上机实验报告

《数值计算方法》上机实验报告华北电力大学实验名称数值il•算方法》上机实验课程名称数值计算方法专业班级:电力实08学生姓名:李超然学号:200801001008 成绩: 指导教师:郝育黔老师实验日期:2010年04月华北电力大学实验报告数值计算方法上机实验报吿一.各算法的算法原理及计算机程序框图1、牛顿法求解非线性方程*对于非线性方程,若已知根的一个近似值,将在处展开成一阶xxfx ()0, fx ()xkk泰勒公式"f 0 / 2 八八,fxfxfxxxxx 0 0 0 0 0 kkkk2!忽略高次项,有,fxfxfxxx 0 ()()(),,, kkk右端是直线方程,用这个直线方程来近似非线性方程。
将非线性方程的**根代入,即fx ()0, X ,* fxfxxx 0 0 0 0, ,, kkkfx 0 fx 0 0,解出fX 0 *k XX,, k' fx 0 k水将右端取为,则是比更接近于的近似值,即xxxxk, Ik, Ikfx ()k 八XX, Ikk* fx()k这就是牛顿迭代公式。
,2,计算机程序框图:,见,,3,输入变量、输出变量说明:X输入变量:迭代初值,迭代精度,迭代最大次数,\0输出变量:当前迭代次数,当前迭代值xkl,4,具体算例及求解结果:2/16华北电力大学实验报吿开始读入l>k/fx()0?,0fx 0 Oxx,,01* fx ()0XX,,,?10kk, ,1,kN, ?xx, 10输出迭代输出X输出奇异标志1失败标志,3,输入变量、输出变量说明: 结束例:导出计算的牛顿迭代公式,并il •算。
(课本P39例2-16) 115cc (0), 求解结果:10. 75000010.72383710. 72380510. 7238052、列主元素消去法求解线性方程组,1,算法原理:高斯消去法是利用现行方程组初等变换中的一种变换,即用一个不为零的数乘 -个 方程后加只另一个方程,使方程组变成同解的上三角方程组,然后再自下而上 对上三角3/16华北电力大学实验报告方程组求解。
数值代数上机实验报告

数值代数课程设计实验报告姓名: 班级: 学号: 实验日期:一、实验名称 代数的数值解法 二、实验环境 MATLAB7.0实验一、平方根法与改进平方根法一、实验要求:用熟悉的计算机语言将不选主元和列主元Gasuss 消元法编写成通用的子程序,然后用编写的程序求解下列方程组⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--⨯14151515157681681681681681612321n n n n n x x x x x x 用所编的程序分别求解40、84、120阶方程组的解。
二、算法描述及实验步骤GAuss 程序如下:(1)求A 的三角分解:LU A =;(2)求解b y =L 得y ; (3)求解y x =U 得x ;列主元Gasuss 消元法程序如下: 1求A 的列主元分解:LU PA =;2求解b y P L =得y ; 3求解y x =U 得x ;三、调试过程及实验结果:%----------------方程系数---------------->> A1=Sanduijiaozhen(8,6,1,40); >> A2=Sanduijiaozhen(8,6,1,84); >> A3=Sanduijiaozhen(8,6,1,120); >> b1(1)=7;b2(1)=7;b3(1)=7;>> for i=2:39b1(i)=15;end>> b1(40)=14;>> for i=2:83b2(i)=15;end>> b2(40)=14;>> for i=2:119b1(i)=15;end>> b3(120)=14;%----------------方程解---------------->> x11=GAuss(A1,b1')>> x12=GAuss Zhu(A1,b1')>> x21=GAuss(A2,b2')>> x22=GAuss Zhu(A3,b3')>> x31=GAuss(A3,b3')>> x32=GAuss Zhu(A3,b3')运行结果:(n=40)GAuss消元法的解即为x11 =1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.0000列主元GAuss消元法的解即为x12 =1 1 1 1 1 1 1 1 1 1 111111111111111111111111111111六、源程序:function A=Sanduijiaozhen(a,b,c,n)%生成n阶以a,b,c为元素的三对角阵A=diag(b*ones(1,n),0)+diag(c*ones(1,n-1),1)+diag(a*ones(1,n-1),-1);function x=GAuss(A,b)n=length(b);x=b;%-------分解---------------for i=1:n-1for j=i+1:nmi=A(j,i)/A(i,i);b(j)=b(j)-mi*b(i);for k=i:nA(j,k)=A(j,k)-mi*A(i,k);endAB=[A,b];endend%-----------回代------------------x(n)=b(n)/A(n,n);for i=n-1:-1:1s=0;for j=i+1:ns=s+A(i,j)*x(j);endx(i)=(b(i)-s)/A(i,i);endfunction x=GAussZhu(A,b)n=length(b);x=b;%----------------------选主元---------------------for k=1:n-1a_max=0;for i=k:nif abs(A(i,k))>a_maxa_max=abs(A(i,k));r=i;endendif r>kfor j=k:nz=A(k,j);A(k,j)=A(r,j);A(r,j)=z;endz=b(k);b(k)=b(r);b(r)=z;end%--------------消元-----------------for i=k+1:nm=A(i,k)/A(k,k);for j=k:nA(i,j)=A(i,j)-m*A(k,j);endb(i)=b(i)-m*b(k);endendif abs(A(n,n))==0return;endAbZhu=[A,b];%----------------回代-----------------------x(n)=b(n)/A(n,n);for i=n-1:-1:1for j=i+1:nb(i)=b(i)-A(i,j)*x(j);endx(i)=b(i)/A(i,i);end实验二、平方根法与改进平方根法一、实验要求:用计算机语言将平方根法和改进的平方根法编成通用的子程序,然后用编写的程序求解对称正定方程组100阶方程组AX=b,二、算法描述及实验步骤:平方根法函数程序如下:1、求A 的Cholesky 分解:L L A T=;2、求解b y =L 得y ;3、求解y x =TL 得x ; 改进平方根法函数程序如下:1、求A 的Cholesky 分解:T=LDL A ; 2、求解b y =L 得y ; 3、求解y x =TDL 得x ;三、调试过程及实验结果:clear;clc;%----------------方程系数---------------->> A=Sanduijiaozhen(1,10,1,100); >> b(1)=11; >> for i=2:99 b(i)=12; end>> b(100)=11;>> x1=Cholesky(A,b') >> x2=GJCholesky(A,b')运行结果:平方根法的解即为 x1 =1.0000 1.00001.0000 1.00001.0000 1.00001.0000 1.00001.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.0000改进平方根法解得的解即为x2 =1.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.0000 1.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00000.99991.00090.99081.09080.1010四、源程序:function x=Cholesky(A,b)n=size(A);n=n(1);% x=A^-1*b;% disp('Matlab自带解即为x');%-----------------Cholesky分解-------------------for k=1:nA(k,k)=sqrt(A(k,k));A(k+1:n,k)=A(k+1:n,k)/A(k,k);for j=k+1:n;A(j:n,j)=A(j:n,j)-A(j:n,k)*A(j,k);endend%------------------前代法求解Ly=b----------------------------for j=1:n-1b(j)=b(j)/A(j,j);b(j+1:n)=b(j+1:n)-b(j)*A(j+1:n,j);endb(n)=b(n)/A(n,n);%-----------------回代法求解L'x=y-----------------------------A=A';for j=n:-1:2b(j)=b(j)/A(j,j);b(1:j-1)=b(1:j-1)-b(j)*A(1:j-1,j);endb(1)=b(1)/A(1,1);disp('平方根法的解即为');function b=GJCholesky(A,b)n=size(A);n=n(1);v=zeros(n,1);%----------------------LDL'分解-----------------------------for j=1:nfor i=1:j-1v(i)=A(j,i)*A(i,i);endA(j,j)=A(j,j)-A(j,1:j-1)*v(1:j-1);A(j+1:n,j)=(A(j+1:n,j)-A(j+1:n,1:j-1)*v(1:j-1))/A(j,j);endB=diag(A);D=zeros(n);for i=1:nD(i,i)=B(i);A(i,i)=1;end%-------------------前代法---------------------------A=tril(A); %得到L和Dfor j=1:n-1b(j)=b(j)/A(j,j);b(j+1:n)=b(j+1:n)-b(j)*A(j+1:n,j);endb(n)=b(n)/A(n,n);%-----------------回代法-----------------------------A=D*(A');for j=n:-1:2b(j)=b(j)/A(j,j);b(1:j-1)=b(1:j-1)-b(j)*A(1:j-1,j);endb(1)=b(1)/A(1,1);disp('改进平方根法解得的解即为');实验三、二次多项式拟合一、实验要求:用计算机语言编制利用QR分解求解线性最小二乘问题的通用子程序,用编写的程序求解一个二次多项式使在残向量的范数最小的意义下拟合下面的数据t-1 -0.75 -0.5 0 0.25 0.5 0.75iy 1.00 0.8125 0.75 1.00 1.3125 1.75 2.3125i二、算法描述及实验步骤:QR分解求解程序如下:1、求A 的QR 分解;2、计算b c 11T =Q ;3、求解上三角方程1c x =R 得x ;三、调试过程及实验结果:>> t=[-1 -0.75 -0.5 0 0.25 0.5 0.75];>> y=[ 1.00 0.8125 0.75 1.00 1.3125 1.75 2.3125]; >> plot(t,y,'r*');>> legend('实验数据(ti,yi)'); >> xlabel('t'), ylabel('y');>> title('二次多项式拟合的数据点(ti,yi)的散点图');运行后屏幕显示数据的散点图(略).(3)编写下列MATLAB 程序计算)(x f 在),(i i y x 处的函数值,即输入程序 >> syms a b c>> t=[-1 -0.75 -0.5 0 0.25 0.5 0.75]; >> fi=a.*t.^2+ b.*t+c%运行后屏幕显示关于 ,,a b c 的线性方程组fi =[a-b+c,9/16*a-3/4*b+c,1/4*a-1/2*b+c,c,1/16*a+1/4*b+c,1/4*a+1/2*b+c,9/16*a+3/4*b +c]编写构造残向量2范数的MATLAB 程序>> y=[ 1.00 0.8125 0.75 1.00 1.3125 1.75 2.3125]; >> y=[ 1.00 0.8125 0.75 1.00 1.3125 1.75 2.3125]; >> fy=fi-y; fy2=fy.^2; J=sum(fy.^2); 运行后屏幕显示误差平方和如下 J=(a-b+c-1)^2+(9/16*a-3/4*b+c-13/16)^2+(1/4*a-1/2*b+c-3/4)^2+(c-1)^2+(1/16*a+1/4*b+c-21/16)^2+(1/4*a+1/2*b+c-7/4)^2+(9/16*a+3/4*b+c-37/16)^2为求,,a b c 使J 达到最小,只需利用极值的必要条件0J a ∂=∂,0J b ∂=∂,0J c∂=∂,得到关于,,a b c 的线性方程组,这可以由下面的MATLAB 程序完成,即输入程序 >> Ja1=diff(J,a); Ja2=diff(J,b); Ja3=diff(J,c);>> Ja11=simple(Ja1), Ja21=simple(Ja2), Ja31=simple(Ja3) 运行后屏幕显示J 分别对,,a b c 的偏导数如下 Ja11 =451/128*a-63/32*b+43/8*c-887/128 Ja21 =-63/32*a+43/8*b-3/2*c-61/32Ja31 =43/8*a-3/2*b+14*c-143/8解线性方程组112131000Ja Ja Ja ===,,,输入下列程序 >> A=[451/128, -63/32, -3/2 ;-63/32,43/8,-3/2;43/8,-3/2,14]; >> B=[887/128,61/32,143/8]; >> C=B/A, f=poly2sym(C)运行后屏幕显示拟合函数f 及其系数C 如下 C =0.3081 0.8587 1.4018 f =924/2999*x^2+10301/11996*x+4204/2999 故所求的拟合曲线为2()0.30810.8581 1.4018f x x x =++四、源程序:>> t=[-1 -0.75 -0.5 0 0.25 0.5 0.75];>> y=[ 1.00 0.8125 0.75 1.00 1.3125 1.75 2.3125]; >> plot(t,y,'r*');>> legend('实验数据(ti,yi)'); >> xlabel('t'), ylabel('y');>> title('二次多项式拟合的数据点(ti,yi)的散点图'); >> syms a b c>> t=[-1 -0.75 -0.5 0 0.25 0.5 0.75]; >> fi=a.*t.^2+ b.*t+c fi =[ a-b+c, 9/16*a-3/4*b+c, 1/4*a-1/2*b+c, c, 1/16*a+1/4*b+c, 1/4*a+1/2*b+c, 9/16*a+3/4*b+c]>> y=[ 1.00 0.8125 0.75 1.00 1.3125 1.75 2.3125]; >> y=[ 1.00 0.8125 0.75 1.00 1.3125 1.75 2.3125]; >> fy=fi-y; fy2=fy.^2; J=sum(fy.^2) J =(a-b+c-1)^2+(9/16*a-3/4*b+c-13/16)^2+(1/4*a-1/2*b+c-3/4)^2+(c-1)^2+(1/16*a+1/4*b+c-21/16)^2+(1/4*a+1/2*b+c-7/4)^2+(9/16*a+3/4*b+c-37/16)^2>> Ja1=diff(J,a); Ja2=diff(J,b); Ja3=diff(J,c);>> Ja11=simple(Ja1), Ja21=simple(Ja2), Ja31=simple(Ja3)Ja11 =451/128*a-63/32*b+43/8*c-887/128Ja21 =-63/32*a+43/8*b-3/2*c-61/32Ja31 =43/8*a-3/2*b+14*c-143/8>> A=[451/128, -63/32, -3/2 ;-63/32,43/8,-3/2;43/8,-3/2,14]; >> B=[887/128,61/32,143/8];>> C=B/A, f=poly2sym(C)C =0.3081 0.8587 1.4018f =924/2999*x^2+10301/11996*x+4204/2999>>。
徐树芳-数值线性代数-答案完全版精选全文完整版

数值线性代数习题解答习题11.求下三角阵的逆矩阵的详细算法。
[解] 设下三角矩阵L的逆矩阵为T我们可以使用待定法,求出矩阵T的各列向量。
为此我们将T按列分块如下:注意到我们只需运用算法1·1·1,逐一求解方程便可求得[注意]考虑到内存空间的节省,我们可以置结果矩阵T的初始状态为单位矩阵。
这样,我们便得到如下具体的算法:算法(求解下三角矩阵L的逆矩阵T,前代法)2.设为两个上三角矩阵,而且线性方程组是非奇异的,试给出一种运算量为的算法,求解该方程组。
[解]因,故为求解线性方程组,可先求得上三角矩阵T的逆矩阵,依照上题的思想我们很容易得到计算的算法。
于是对该问题我们有如下解题的步骤:(1)计算上三角矩阵T的逆矩阵,算法如下:算法1(求解上三角矩阵的逆矩阵,回代法。
该算法的的运算量为)(2)计算上三角矩阵。
运算量大约为.(3)用回代法求解方程组:.运算量为;(4)用回代法求解方程组:运算量为。
算法总运算量大约为:3.证明:如果是一个Gauss变换,则也是一个Gauss变换。
[解]按Gauss变换矩阵的定义,易知矩阵是Gauss变换。
下面我们只需证明它是Gauss变换的逆矩阵。
事实上注意到,则显然有从而有4.确定一个Gauss变换L,使[解] 比较比较向量和可以发现Gauss变换L应具有功能:使向量的第二行加上第一行的2倍;使向量的第三行加上第一行的2倍。
于是Gauss变换如下5.证明:如果有三角分解,并且是非奇异的,那么定理1·1·2中的L和U都是唯一的。
[证明]设,其中都是单位下三角阵,都是上三角阵。
因为A非奇异的,于是注意到,单位下三角阵的逆仍是单位下三角阵,两个单位下三角阵的乘积仍是单位下三角阵;上三角阵的逆仍是上三角阵,两个上三角阵的乘积仍是上三角阵。
因此,上述等将是一个单位下三角阵与一个上三角阵相等,故此,它们都必是单位矩阵。
即,从而即A的LU分解是唯一的。
(完整word版)数值线性代数第二版徐树方高立张平文上机习题第四章实验报告
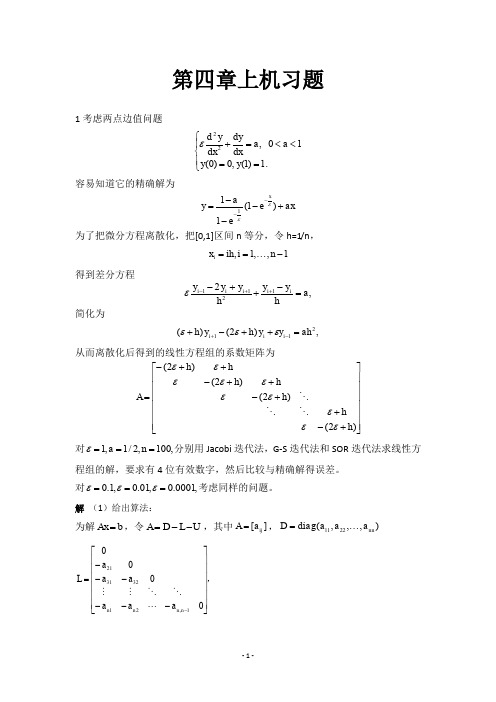
第四章上机习题1考虑两点边值问题⎪⎩⎪⎨⎧==<<=+.1)1(,0)0(10 ,22y y a a dx dy dx y d ε 容易知道它的精确解为ax e e ay x +---=--)1(111εε为了把微分方程离散化,把[0,1]区间n 等分,令h=1/n ,1,,1,-==n i ih x i得到差分方程,21211a hy y h y y y i i i i i =-++-++-ε简化为 ,)2()(211ah y y h y h i i i =++-+-+εεε从而离散化后得到的线性方程组的系数矩阵为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+-++-++-++-=)2()2()2()2(h h h h h h h A εεεεεεεεεε 对,100,2/1,1===n a ε分别用Jacobi 迭代法,G-S 迭代法和SOR 迭代法求线性方程组的解,要求有4位有效数字,然后比较与精确解得误差。
对,0001.0,01.0,1.0===εεε考虑同样的问题。
解 (1)给出算法:为解b Ax =,令U L D A --=,其中][ij a A =,),,,(2211nn a a a diag D = ,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡------=-00001,21323121n n n n a a a a a a L,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡------=-0000,122311312 n n n n a a a a a a U 利用Jacobi 迭代法,G-S 迭代法,SOR 迭代法解线性方程组,均可以下步骤求解: step1给定初始向量x0=(0,0,...,0),最大迭代次数N ,精度要求c ,令k=1 step2令x=B*x0+gstep3若||x-x0||2<c ,算法停止,输出解和迭代次数k ,否则,转step4 step4若k>=N,算法停止,迭代失败,否则,令x0=x ,转step2在Jacobi 迭代法中,B=D -1*(L+U),g=D -1*b在G-S 迭代法中,B=D -1*(L+U),g=D -1*b在SOR 迭代法中,B=(D-w*L)-1*[(1-w)*D+w*U],g=w*(D-w*L)-1*b另外,在SOR 迭代法中,上面算法step1中要给定松弛因子w ,其中0<w<2 为计算结果,规定w=0.5。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
- 1 -第三章上机习题用你所熟悉的的计算机语言编制利用QR 分解求解线性方程组和线性最小二乘问题的通用子程序,并用你编制的子程序完成下面的计算任务: (1)求解第一章上机习题中的三个线性方程组,并将所得的计算结果与前面的结果相比较,说明各方法的优劣;(2)求一个二次多项式+bt+c y=at 2,使得在残向量的2范数下最小的意义下拟合表3.2中的数据;(3)在房产估价的线性模型111122110x a x a x a x y ++++=中,1121,,,a a a 分别表示税、浴室数目、占地面积、车库数目、房屋数目、居室数目、房龄、建筑类型、户型及壁炉数目,y 代表房屋价格。
现根据表3.3和表3.4给出的28组数据,求出模型中参数的最小二乘结果。
(表3.3和表3.4见课本P99-100) 解 分析:(1)计算一个Householder 变换H :由于TTvv I ww I H β-=-=2,则计算一个Householder 变换H 等价于计算相应的v 、β。
其中)/(2,||||12v v e x x v T=-=β。
在实际计算中,为避免出现两个相近的数出现的情形,当01>x 时,令212221||||)(-x x x x v n +++= ;为便于储存,将v 规格化为1/v v v =,相应的,β变为)/(221v v v T=β 为防止溢出现象,用∞||||/x x 代替 (2)QR 分解:利用Householder 变换逐步将n m A n m ≥⨯,转化为上三角矩阵A H H H n n 11 -=Λ,则有⎥⎦⎤⎢⎣⎡=0R Q A ,其中n H H H Q 21=,:),:1(n R Λ=。
在实际计算中,从n j :1=,若m j <,依次计算)),:((j m j A x =对应的)1()1()~(+-⨯+-k m k m j H即对应的j v ,j β,将)1:2(+-j m v j 储存到),:1(j m j A +,j β储存到)(j d ,迭代结束后再次计算Q ,有⎥⎥⎦⎤⎢⎢⎣⎡=-~001j j j H I H ,n H H H Q 21=(m n =时1-21n H H H Q =) (3)求解线性方程组b Ax =或最小二乘问题的步骤为i 计算A 的QR 分解;ii 计算b Q c T11=,其中):1(:,1n Q Q = iii 利用回代法求解上三角方程组1c Rx =(4)对第一章第一个线性方程组,由于R 的结果最后一行为零,故使用前代法时不计最后一行,而用运行结果计算84x 。
运算matlab 程序为1 计算Householder 变换 [v,belta]=house(x) function [v,belta]=house(x) n=length(x);x=x/norm(x,inf);sigma=x(2:n)'*x(2:n); v=zeros(n,1); v(2:n,1)=x(2:n); if sigma==0 belta=0; elsealpha=sqrt(x(1)^2+sigma); if x(1)<=0v(1)=x(1)-alpha; elsev(1)=-sigma/(x(1)+alpha); endbelta=2*v(1)^2/(sigma+v(1)^2); v=v/v(1,1); end end2计算A的QR分解[Q,R]=QRfenjie(A)function [Q,R]=QRfenjie(A)[m,n]=size(A);Q=eye(m);for j=1:nif j<m[v,belta]=house(A(j:m,j));H=eye(m-j+1)-belta*v*v';A(j:m,j:n)=H*A(j:m,j:n);d(j)=belta;A(j+1:m,j)=v(2:m-j+1);endendR=triu(A(1:n,:));for j=1:nif j<mH=eye(m);temp=[1;A(j+1:m,j)];H(j:m,j:m)=H(j:m,j:m)-d(j)*temp*temp';Q=Q*H;endendend3 解下三角形方程组的前代法x=qiandaifa(L,b)function x=qiandaifa(L,b)n=length(b);for j=1:n-1b(j)=b(j)/L(j,j);b(j+1:n)=b(j+1:n)-b(j)*L(j+1:n,j);endb(n)=b(n)/L(n,n);x=b;end4 求解第一章上机习题中的三个线性方程组ex3_1clear;clc;%第一题A=6*eye(84)+diag(8*ones(1,83),-1)+diag(ones(1,83),1); b=[7;15*ones(82,1);14];n=length(A);%QR分解[Q,R]=QRfenjie(A);c=Q'*b;x1=huidaifa(R(1:n-1,1:n-1),c(1:n-1));x1(n)=c(n)-R(n,1:n-1)*x1;%不选主元Gauss消去法[L,U]=GaussLA(A);x1_1=Gauss(A,b,L,U);%列主元Gauss消去法[L,U,P]=GaussCol(A);x1_2=Gauss(A,b,L,U,P);%解的比较figure(1);subplot(1,3,1);plot(1:n,x1);title('QR分解');subplot(1,3,2);plot(1:84,x1_1);title('Gauss');subplot(1,3,3);plot(1:84,x1_2);title('PGauss');%第二题第一问A=10*eye(100)+diag(ones(1,99),-1)+diag(ones(1,99),1); b=round(100*rand(100,1));n=length(A);%QR分解tic;[Q,R]=QRfenjie(A);c=Q'*b;x2=huidaifa(R,c);toc;%不选主元Gauss消去法tic;[L,U]=GaussLA(A);x2_1=Gauss(A,b,L,U);toc;%列主元Gauss消去法tic;[L,U,P]=GaussCol(A);x2_2=Gauss(A,b,L,U,P);toc;%平方根法tic;L=Cholesky(A);x2_3=Gauss(A,b,L,L');toc;%改进的平方根法tic;[L,D]=LDLt(A);x2_4=Gauss(A,b,L,D*L');toc;%解的比较figure(2);subplot(1,5,1);plot(1:n,x2);title('QR分解');subplot(1,5,2);plot(1:n,x2_1);title('Gauss');subplot(1,5,3);plot(1:n,x2_2);title('PGauss');subplot(1,5,4);plot(1:n,x2_3);title('平方根法'); subplot(1,5,5);plot(1:n,x2_4);title('改进的平方根法'); %第二题第二问A=hilb(40);b=sum(A);b=b';n=length(A);[Q,R]=QRfenjie(A);c=Q'*b;x3=huidaifa(R,c);%不选主元Gauss消去法[L,U]=GaussLA(A);x3_1=Gauss(A,b,L,U);%列主元Gauss消去法[L,U,P]=GaussCol(A);x3_2=Gauss(A,b,L,U,P);%平方根法L=Cholesky(A);x3_3=Gauss(A,b,L,L');%改进的平方根法[L,D]=LDLt(A);x3_4=Gauss(A,b,L,D*L');%解的比较figure(3);subplot(1,5,1);plot(1:n,x3);title('QR分解');subplot(1,5,2);plot(1:n,x3_1);title('Gauss');subplot(1,5,3);plot(1:n,x3_2);title('PGauss');subplot(1,5,4);plot(1:n,x3_3);title('平方根法');subplot(1,5,5);plot(1:n,x3_4);title('改进的平方根法');5 求解二次多项式ex3_2clear;clc;t=[-1 -0.75 -0.5 0 0.25 0.5 0.75];y=[1 0.8125 0.75 1 1.3125 1.75 2.3125];A=ones(7,3);A(:,1)=t'.^2;A(:,2)=t';[Q,R]=QRfenjie(A);Q1=Q(:,1:3);c=Q1'*y';x=huidaifa(R,c)6 求解房产估价的线性模型ex3_3clear;clc;A=xlsread('E:\temporary\专业课\数值代数\cha3_3_4.xls','A2:L29'); y=xlsread('E:\temporary\专业课\数值代数\cha3_3_4.xls','M2:M29'); [Q,R]=QRfenjie(A);Q1=Q(:,1:12); c=Q1'*y;x=huidaifa(R,c); x=x'计算结果为(1)第一章上机习题中的三个线性方程组结果对比图依次为0.20.40.60.811.21.41.61.8QR 分解-6-4-22468Gauss05010011111111PGauss050100-20246810QR 分解050100-202468Gauss050100-20246810PGauss050100-20246810平方根法050100-2246810改进的平方根法02040-2000-1500-1000-50005001000150020002500QR 分解02040-200-150-100-5050100150200Gauss2040-300-200-1000100200300400PGauss2040-5-4-3-2-10123457平方根法02040-80-60-40-200204060改进的平方根法以第二个线性方程组为例,比较各方法的运行速度。
