茹科夫斯基转椅演示角动量守恒
角动量守恒 教学ppt课件

i
12
M外 Mi外 ri Fi
i
i
----各质点所受外力矩的矢量 和称为质点系所受合外力矩
M内 Mi内 (ri fij ) 0
i
i
ji
----各质点所受内力矩 的矢量和
(证明如下:)
Fi
m2
m1
mi
fij ri
f ji m j
0
rj
13
内力总是成对出现的,所以内力矩也是成对出
:质量线密度
线积分
对质量面分布的刚体: dm dS
:质量面密度
对质量体分布的刚体:dm dV
:质量体密度
面积分
体积分 26
计算转动惯量 I 的三条有用的定理:
(1)叠加定理:对同一转轴 I 有可叠加性
I Ii
I mr mr mr
m2
I
r1
m1
r2 r3
m3
转轴
(2)平行轴定理: I Ic md 2
常矢量
7
若 M 0 ,则 L 常矢量
M 0
的条件是
— 质点角动量守恒定律
F 0
或 F 过固定点:有心力
(如行星受的万有引力)
角动量守恒定律是物理学的基本定
律之一,它不仅适用于宏观体系,也 适用于微观体系,而且在高速低速范 围均适用。
8
角动量守恒定律可导出行星运动的开
普勒第二定律:
L
(书P79页例3.1)
i
与内力矩无关 v
守恒条件 M i 0 i
20
§3.3 定轴转动刚体的角动量 转动惯量 一、定轴转动刚体的角动量
把刚体看作非常多质元构成 的质点系,第i个质元对原点o
z v vvi
茹科夫斯基转椅演示角动量守恒

茹科夫斯基转椅演示角动量守恒
茹科夫斯基转椅演示角动量守恒
【实验原理】: 绕定轴转动的刚体,当对转轴的合外力矩为零时,刚体对转轴的角动量守恒,即J与w的乘积不变。
刚体的转动惯量J 一般为常量,J不变使得w不变,即刚体在不受合外力矩时将维持匀角速度转动。
但是,假若转动物体是一种可发生形变的固体,并可以改变它对转轴的转动惯量,则物体的角速度就会产生相应的变化:当J增大时w就减小,J减小时w就增大,从而保持乘积Jw不变。
茹可夫斯基转椅实验中,因为人的双臂并不产生对转轴的外力矩,忽略转轴的摩擦,系统的角动量应保持守恒,人和凳的转速随着人手臂的伸缩而改变。
【应用前景】:跳芭蕾舞的时候,运动员在转动的过程之中,会收缩双手,来实现减少转动惯量,则角速度变大,转动得越快。
跳水运动中,运动员在在完成动作时,会将身体蜷缩成球形,目的也是减小转动惯量,加快转动速度,更好地完成动作。
宇宙飞船在空间中运行的时候,通过深处或受其两根杆来改变转动惯量,从而改变转动的速度。
体操运动员在完成空翻动作的时候,也是尽量蜷缩身体,是转动惯量减小,加快转速。
跳远的时候,起跳之后由于力会产生一个转动惯量,如果不向后摆手来抵消这个转动惯量,运动员就会向前翻转。
智慧树答案无处不在的物理现象(哈尔滨工程大学)知到课后答案章节测试2022年

绪论1.物体的转动惯量与它旋转的速度答案:没有关系2.如果一个物理所受的合外力为零,则它的角动量守恒。
答案:错3.当花样滑冰运动员做旋转动作时,会收拢手臂,这样做的目的是答案:减小转动惯量4.绕固定轴旋转物体的角动量与角速度答案:成正比5.在茹科夫斯基凳演示实验中,伸开双臂可以使旋转速度变快答案:错6.库伦发现了电荷之间的相互作用?答案:对7.钕铁硼磁铁是一种强磁铁?答案:对8.磁场线是真实存在的?答案:错9.自制的纸质音响,可以用纯铜丝来代替漆包线?答案:错10.超声波比其他声波传播的速度快?答案:错11.利用双耳效应可以判断声源方位?答案:对12.“震耳欲聋”是说声音的响度高?答案:对13.用超声波洗涤仪器,说明声波能够传递能量?答案:对第一章1.在透镜成像过程中,从物点发出、到达像点的光线中,靠近光轴的光线由于所走的路径较短,光程小。
答案:错2.基于费马原理,光线可以沿着光纤传输到很远的距离。
答案:对3.海面上的海市蜃楼是由于()答案:海面温度低,空气密度大,折射率高4.当光照到肥皂泡时,肥皂泡出现了多变的颜色,这些颜色是由于答案:不同颜色的光在肥皂泡上发生了干涉现象5.光的偏振现象是说明光是一种纵波。
答案:错6.课程中的“光尺”指的是()答案:利用光学方法进行测量7.利用光衍射方法,可以测量很细物体(如头发丝)的直径。
答案:对8.精确测量月地距离是利用光学成像方法。
答案:错9.测量月地距离需要利用激光很好的方向性。
答案:对10.根据大爆炸理论,离我们越远的星系离开我们的运动速度越快,发出的光谱线红移越明显。
答案:对第二章1.理想黑体是指完全不发光的物体。
答案:错2.太阳是个非常好的黑体。
答案:对3.理想黑体是指答案:吸收率为100%的物体4.黑体辐射谱线的峰值波长与黑体温度之间答案:成反比5.碳纳米管可以制成非常理想的黑体。
答案:对6.光镊通常是由平行激光束构成答案:错7.关于光镊下列说法正确的是:()答案:光镊是单光束梯度力势阱的形象称呼8.处于光场中的物体受到的光散射力来自于:()答案:光子动量改变9.光纤光镊可以不依赖于生物显微镜。
无滑动滚动

一、刚体的定轴转动定律
dLz d Mz Jz Jz dt dt
Mz :外力矩沿z轴分量的代数和
Lz : 刚体沿z轴的角动量
z
ri mi
O
Lz Jz
Jz : 刚体对z轴的转动惯量
Jz mi ri , Jz r 2dm
2 i
dLz d Mz Jz Jz dt dt
关于瞬转轴列转动定理重解:
mgR sin J p
J p JC mR mgR sin 2 JC mR
2
简单多了!
25
五、进动(旋进,Precession) 高速自转的物体,其自转轴绕另一个轴缓慢 转动的现象。 【演示实验】车轮进动 M L
M L M L sin
三、刚体转动的功和能 合外力矩对一个绕固定轴转动的刚体所做的 功,等于它的转动动能的增加 1 1 2 W E k 2 E k 1 J 2 J12 2 2
力矩的功: W M d
1 2
不太大刚体的重力势能:E p mghC
机械能守恒定律:只有保守力做功时
Ek E p 常数
Mp Jp
J p : 关于过p点转轴的转动惯量
证明:
无滑动滚动:vpt vC , apt aC a p aC apt apn a a a C C pn ac C a pn
按切、法向分解:a p a pt a pn
( F mg) t mvC 0
l C F
vC 0
F mg t m
质心以vC0的初速做上抛运动。
(2)在上抛过程中棒的转动 绕过质心转轴,列转动定理:
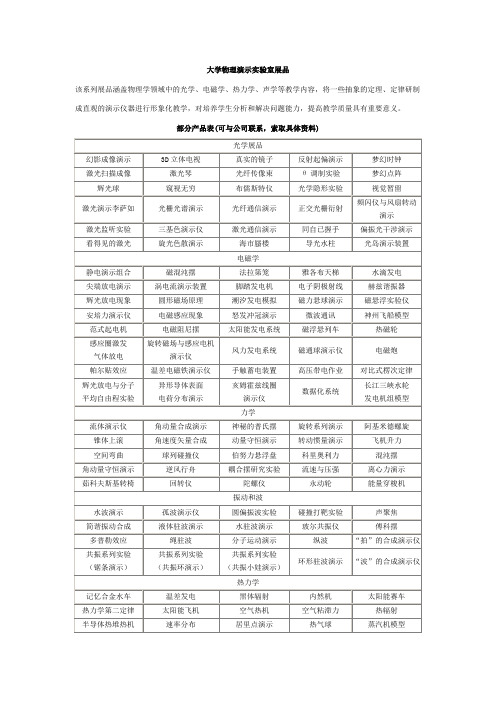
大学物理演示实验室展品
共振系列实验
(共振环演示)
共振系列实验
(共振小娃演示)
环形驻波演示
“波”的合成演示仪
热力学
记忆合金水车
温差发电
黑体辐射
内然机
太阳能赛车
热力学第二定律
太阳能飞机
空气热机
空气粘滞力
热辐射
半导体热堆热机
速率分布
居里点演示
热气球
蒸汽机模型
其他
三球仪
莫比乌斯球
回顾与展望
系列展板
光栅立体画
互补色图像
电磁炮
帕尔贴效应
温差电磁铁演示仪
手触蓄电装置
高压带电作业
对比式楞次定律
辉光放电与分子
平均自由程实验
异形导体表面
电荷分布演示
亥姆霍兹线圈
演示仪
数据化系统
长江三峡水轮
发电机组模型
力学
流体演示仪
角动量合成演示
神秘的普氏摆
旋转系列演示
阿基米德螺旋
锥体上滚
角速度矢量合成
动量守恒演示
转动惯量演示
飞机升力
空间弯曲
球列碰撞仪
伯努力悬浮盘
科里奥利力
混沌摆
角动量守恒演示
逆风行舟
耦合摆研究实验
流速与压强
离心力演示
茹科夫斯基转椅
回转仪
陀螺仪
永动轮
能量穿梭机
振动和波
水波演示
孤波演示仪
圆偏振波实验
碰撞打靶实验
声聚焦
简谐振动合成
液体驻波演示
水驻波演示
玻尔共振仪
傅科摆
多普勒效应
绳驻波
分子运动演示
纵波
“拍”的合成演示仪
深圳大学-角动量守恒定律实验报告

深圳大学实验报告课程名称:大学物理实验(三)
实验名称:验证角动量守恒定律及误差分析
学院:物理科学与技术学院
组号25 指导教师:
报告人:学号:
实验地点科技楼B109 实验时间:2014.06.03
实验报告提交时间:
2.1.3、在空载情况下,承物台在质量不同的砝码作用下的角速度图像如图3:
2.1.4、经修正过后的角加速度的真实值如下表一所示:
表一:不同情况下的角加速度β
砝码m(g) g(m/s 2) 滑轮r(mm) mgr(kg*m 2/s 2) 负载
β1(kg/m2) 空载
β2(kg/m2) 40 9.8 14.5 0.005684 0.2598 0.4265 50 9.8 14.5 0.007105 0.3420 0.5558 60 9.8 14.5 0.008526 0.4265 0.6827 图2 负载时不同砝码质量下角速度
图3 空载时不同砝码质量下角速度
从图6中可以整理出如表二所示的数据:
表二:合外力矩为零,将圆环落在转动的盘上的角速度变化情况
序号 1 2 3 4 5
空载转动惯量J
=0.0109kg
·m2角速度ω
(rad/s)
27.58 27.14 26.1 25.42 24.82
角速度ω
1
(rad/s)
18.06 17.68 16.89 16.56 16.07
图6 角速度变化情况。
大学物理 2.1 刚体的定轴转动和平面平行运动

对轴的力矩的计算:
把外力分解成转动平面内的 分力和垂直于转动平面的分力。
垂直分力与转轴平行,对O点力矩垂直于转轴,则对 转轴力矩为零。
外力对转轴的力矩,就是转动平面内的分力对 该转轴的力矩
M z rf sin rf hf
【思考】如何确定正、负号?
证明:重力对过质心轴的合力矩等于零
刚体各个质元所受重力对任意
2.1.1 刚体的定轴转动
平动:刚体中任意两个质点的连线在运动
刚体的运动
中始终保持平行。 转动
刚体平动的运动特点:刚体平动时各个质元的运动情况 完全相同,可以用刚体质心的运动来表达刚体的平动。
vi ri
ai ri
转 轴:在某一惯性参考系中固定不变的质点集合。 转动平面:垂直于转轴的平面。
刚体转动的运动特点:除转轴上的质元之外,刚体各个质 元都在转动平面内做圆周运动。
把刚体想象地分割成许多质元,刚体就可以看成是由 这些质元组成的质点系。在整个运动和受力过程中,这 种质点系中任何两个质点之间的距离都保持不变。
刚体的运动规律,可通过把牛顿运动定律应用到这种 特殊的质点系上得到。
2.1 刚体的定轴转动和平面平行运 动
2.1.1 刚体的定轴转动 2.1.2 刚体定轴转动定理 转动惯量 力矩 2.1.3 刚体的平面平行运动
例如:圆柱体、球等轴对称刚体在平面上的滚动,等 等。
平面平行运动可分解成:质心运动和绕垂直于运动平 面的过质心轴的转动。
质心运动服从质心运动定理;刚体绕过质心轴的转动 定理与定轴转动定理的形式相同
MC IC
证明:质心运动定理
如果过质心轴没有加速度,相对刚体质心静止的参
考系是惯性系,MC=IC 显然成立。
一点O的合力矩
物理演示与探索实验室 仪器使用说明

物理演示与探索实验室仪器使用说明目录茹科夫斯基凳 (5)角动量守恒转台 ......................................... 错误!未定义书签。
两用陀螺进动演示 (6)大型玻璃杯共振演示 (7)惯性系中运动规律演示 (9)立式对比滚柱转动惯量 (10)超弹性碰撞 (11)旋飞球演示角动量守恒 (12)定向陀螺 (13)直升飞机演示角动量守恒 (14)大型蛇形摆 (15)声波可见 (16)飞机升力 (17)气体压强模拟 (18)弦驻波演示 (19)伯努力悬浮球 (20)大型弹簧纵驻波 (21)黑体辐射与吸收 (22)黑体模型 (23)磁阻尼摆 (24)电磁驱动 (25)神奇的跳环 (26)RC电路时间常数演示 (27)手触电池 (28)亥姆霍兹线圈演示 (29)通电线圈间相互作用力演示 (30)涡流热效应演示 (32)偏振光干涉演示 (33)动态窥视无穷 (34)反射光栅变换画 (35)便携式绿激光干涉演示 (36)便携式绿激光衍射演示 (37)便携式光的偏振现象演示 (38)基于同轴光路的光学干涉系统................. 错误!未定义书签。
静电跳球 (39)静电摆球 (40)静电滚筒 (41)静电风轮 (42)电风吹烛 (43)避雷针演示 (44)平行板电场演示 (45)电磁炮 (46)雅格布天梯 (47)实验名称...................................................... 错误!未定义书签。
茹科夫斯基凳操作方法:1.操作者坐在凳上系好安全带,手持哑铃,两臂收缩在胸前;2.其他人推动转椅,使转椅转动起来,然后操作者伸开双臂,可看到操作者和凳的转速显著变慢;3.操作者再度收缩两臂,系统转速变快。
原理:质点系绕定轴转动时,当质点系所受到的对转轴的合外力矩为零时,质点系对转轴的总角动量守恒,即∑J iωi=恒量,说明内力矩不影响质点系的总角动量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
茹科夫斯基转椅演示角动量守恒
【实验原理】: 绕定轴转动的刚体,当对转轴的合外力矩为零时,刚体对转轴的角动量守恒,即J与w的乘积不变。
刚体的转动惯量J 一般为常量,J不变使得w不变,即刚体在不受合外力矩时将维持匀角速度转动。
但是,假若转动物体是一种可发生形变的固体,并可以改变它对转轴的转动惯量,则物体的角速度就会产生相应的变化:当J增大时w就减小,J减小时w就增大,从而保持乘积Jw不变。
茹可夫斯基转椅实验中,因为人的双臂并不产生对转轴的外力矩,忽略转轴的摩擦,系统的角动量应保持守恒,人和凳的转速随着人手臂的伸缩而改变。
【应用前景】:跳芭蕾舞的时候,运动员在转动的过程之中,会收缩双手,来实现减少转动惯量,则角速度变大,转动得越快。
跳水运动中,运动员在在完成动作时,会将身体蜷缩成球形,目的也是减小转动惯量,加快转动速度,更好地完成动作。
宇宙飞船在空间中运行的时候,通过深处或受其两根杆来改变转动惯量,从而改变转动的速度。
体操运动员在完成空翻动作的时候,也是尽量蜷缩身体,是转动惯量减小,加快转速。
跳远的时候,起跳之后由于力会产生一个转动惯量,如果不向后摆手来抵消这个转动惯量,运动员就会向前翻转。
