高考数学专题复习立体几何练习题
高考数学复习-精选立体几何大题30题

立体几何大题2.如图,已知正四棱柱ABCD—A1B1C1D1的底面边长为3,侧棱长为4,连结A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E。
(Ⅰ)求证:D1B⊥平面AEC;(Ⅱ)求三棱锥B—AEC的体积;(Ⅲ)求二面角B—AE—C的正弦.3.如图,正三棱柱ABC—A1B1C1的底面边长为1,点M在BC上,△AMC1是以M为直角顶点的等腰直角三角形.(I)求证:点M为BC的中点;(Ⅱ)求点B到平面AMC1的距离;(Ⅲ)求二面角M—AC1—B的正切值.AB CA1B1C1M第3题图4.如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1,F是CD的中点.(Ⅰ)求证:AF∥平面BCE;(Ⅱ)求多面体ABCDE的体积;(Ⅲ)求二面角C-BE-D 的正切值.5.已知:ABCD是矩形,设PA=a,PA⊥平面ABCD.M、N分别是AB、PC的中点.(Ⅰ)求证:MN⊥AB;(Ⅱ)若PD=AB,且平面MND⊥平面PCD,求二面角P—CD—A的大小;(Ⅲ)在(Ⅱ)的条件下,求三棱锥D—AMN的体积..6.如图,正方体ABCD —A 1B 1C 1D 1中,P 、M 、N 分别为棱DD 1、AB 、BC 的中点。
(I )求二面角B 1—MN —B 的正切值; (II )证明:PB ⊥平面MNB 1;(III )画出一个正方体表面展开图,使其满足 “有4个正方形面相连成一个长方形”的条件, 并求出展开图中P 、B 两点间的距离。
(III )PB132,符合条件的正方体表面展开图可以是以下6种之一:AB CD P A 1B 1C 1D 1第6题图MN7.如图,四棱锥P—ABCD的底面是正方形,PA⊥底面ABCD,PA=AD=2,点M、N 分别在棱PD、PC上,且PC⊥平面AMN.(Ⅰ)求证:AM⊥PD;(Ⅱ)求二面角P—AM—N的大小;(Ⅲ)求直线CD与平面AMN所成角的大小....8.如图,在直三棱柱ABC—A1B1C1中,∠ACB=90°. BC=CC1=a,AC=2a. (I)求证:AB1⊥BC1;(II)求二面角B—AB1—C的大小;(III)求点A1到平面AB1C的距离.9.在长方体ABCD-A1B1C1D1中,已知AB=BC=2,BB1=3,连接BC1,过B1作B1E⊥BC1交CC1于点E(Ⅰ)求证:AC1⊥平面B1D1E;(Ⅱ)求三棱锥C1-B1D1E1的体积;(Ⅲ)求二面角E-B1D1-C1的平面角大小10.在矩形ABCD中,AB=4,BC=3,E为DC的中点,沿AE将△AED折起,使二面角D-AE-B为60 .(Ⅰ)求DE与平面AC所成角的大小;(Ⅱ)求二面角D-EC-B的大小.答案:如图1,过点D作DM⊥AE于M,延长DM与BC交于N,在翻折过程中DM⊥AE,MN⊥AE保持不变,翻折后,如图2,∠DMN为二面角D-AE-B的平面角,∠DMN=60 ,AE⊥平面DMN,又因为AE⊂平面AC,则AC⊥平面DMN.(Ⅰ)在平面DMN内,作DO⊥MN于O,∵平面AC⊥平面DMN,∴DO⊥平面AC.连结OE,DO⊥OE,∠DEO为DE与平面AC所成的角.如图1,在直角三角形ADE中,AD=3,DE=2,,1323DEADAE2222=+=+=.134AEDEME,136AEDEADDM2===⋅=如图2,在直角三角形DOM中,,133360sinDMDO=︒⋅=在直角三角形DOE中,13233DEDODEOsin==∠,则.26393arcsinDEO=∠∴DE与平面AC所成的角为.26393arcsin(Ⅱ)如图2,在平面AC内,作OF⊥EC于F,连结DF,ADBCEA BCED第10题∵DO ⊥平面AC ,∴DF ⊥EC ,∴∠DFO 为二面角D -EC -B 的平面角. 如图1,作OF ⊥DC 于F ,则Rt △EMD ∽Rt △OFD ,,DEEMDO OF = ∴.DEEMDO OF ⋅=如图2,在Rt △DOM 中,OM =DMcos ∠DMO =DM·cos60 =133.如图1,.1318OF ,139MO DM DO ==+= 在Rt △DFO 中,,213OF DO DFO tg ==∠ ∴二面角D -EC -B 的大小为213arctg .11.直三棱柱ABC -A 1B 1C 1中,AC =CB =AA 1=2,∠ACB =90°,E 是BB 1的中点,D ∈AB ,∠A 1DE =90°.(Ⅰ)求证:CD ⊥平面ABB 1A 1; (Ⅱ)求二面角D -A 1C -A 的大小.分平面,平面平面,平面,平面知,平面-由直三棱柱,分的中点是),,(,即,有①、②由②,又①,)(,∥),,(,),,(),,(),,(则分,),,(,可设,),,(,),,(又),,(,),,(则坐标系如图,为原点,建立空间直角以2..2..0111.10902022202202221220020002.1202021111111111111⋅⋅⋅⋅⋅⋅⋅⋅⊥∴=⋂⊂⊥⊥∴=⋅⋅⋅⋅⋅⋅⋅⋅⋅∴===∴=⋅∴︒=∠=+∴=+-∴-=-=∴--=--=⋅⋅⋅⋅⋅⋅⋅⋅∈→-→--→-→-→-→-→--→-A ABB CD AB A ABB ABC ABC CD A ABB ABC C B A ABC AB CD CB AC AB D D n m mn ED D A DE A n m n m AB AD AB n m AD n m D A n m ED n m D AB D B A E A C(Ⅱ)解:分的大小为--二面角>,<分),,(的法向量,故可取平面平面显然),,(可取,可得令,即,且则有,),,(的法向量为设平面),,(,),,(3.33arccos.33131||||cos 4.010.111.11.0.022000.20201112121212111111111⋅⋅⋅⋅⋅⋅⋅⋅⋅∴=⋅=⋅∴⋅⋅⋅⋅⋅⋅⋅⋅⋅=⊥-=∴==-==+∴⎩⎨⎧=+=+=⋅=⋅===→→→→→→→-→→-→→→--→-A C A D n n nn n n n CA A CA A CB n z y x z x z x y x CA n CD n z y x n C DA CA CD12.如图,已知斜三棱柱ABC —A 1B 1C 1中,∠BCA=90°,AC=BC=a ,点A 1在底面ABC 上的射影恰为AC 的中点D ,BA 1⊥AC 1。
2023届高考数学总复习《立体几何》附答案解析

(2)若点 N 为 BC 的中点,求四面体 A'MNB 的体积.
【解答】证明:(1)连接 BD,设 BD∩EC=F,连接 MF,
由题意可得四边形 BCDE 为正方形,则 F 为 BD 的中点,
∴MF 为△A′BD 的中位线,可得 MF∥A′B,
又 A′B⊄平面 EMC,MF⊂平面 EMC,
∴A'B∥平面 EMC;
2023 年高考:立体几何复习题及答案
1.如图,已知直角梯形 ABCD,BC∥AD,BC=CD=2,AD=4,∠BCD=90°,点 E 为 AD 的中点,现将三角形 ABE 沿 BE 折叠,得到四棱锥 A'﹣BCDE,其中∠A'ED=120°, 点 M 为 A'D 的中点.
(1)求证:A'B∥平面 EMC;
第2页共3页
∵BE⊂平面 BEF,∴平面 BEF⊥平面 AMD, 结合题意分析知,点 F 在线段 AD 上,连接 MF, 过 A 作 AH⊥MF,交 MF 的延长线于点 H,
则结合已知条件得
,解得 AH ,
设 Dt ,
第3页共3页
【解答】解:(1)证明:由题意知 PC2+AC2=PA2,∴PC⊥AC, 同理,PC⊥BC,又 AC∩BC=C,∴PC⊥平面 ABC, ∵D,E 分别是 AC,PA 的中点,∴DE∥PC, ∴DE⊥平面 ABC, 又 DE⊂平面 BDE,∴平面 BDE⊥平面 ABC. (2)在△BDE 中,DE⊥BD,BD=2 ,DE=2,∴BE=4, 如图,过 A 作 AM⊥BE 于 M,连接 MD, 在△ABE 中,AB=BE=4,AE=2 ,解得 AM ,ME=1, ∵DM⊂平面 BDE,∴AC⊥DM, 在 Rt△ADM 中,AM ,AD=2,∴DM , ∴DM2+EM2=DE2,∴MD⊥BE, ∵AM∩MD=M,∴BE⊥平面 AMD,
高考数学立体几何专题复习(含答案)
的中点.
(Ⅰ)证明: PA / / 平面 EDB ; (Ⅱ)求三棱锥 A BDP 的体积.
试卷第 2 页,总 2 页
参考答案
1、【答案】(1)详见解析;(2) . 试题分析(:1)过 B 作 CD 的垂线交 CD 于 F,则
6、如图所示,在直三棱柱 ABC-A1B1C1 中,AC=3,BC=4,AB=5,AA1=4,点 D 是 AB 的中点. (1)求证:AC1∥平面 CDB1; (2)求异面直线 AC1 与 B1C 所成角的余弦值.
7、如图所示,在三棱锥 A BOC 中,OA 底面 BOC ,OAB OAC 300 , AB AC 2 , BC 2 ,
高考数学—立体几何专题复习
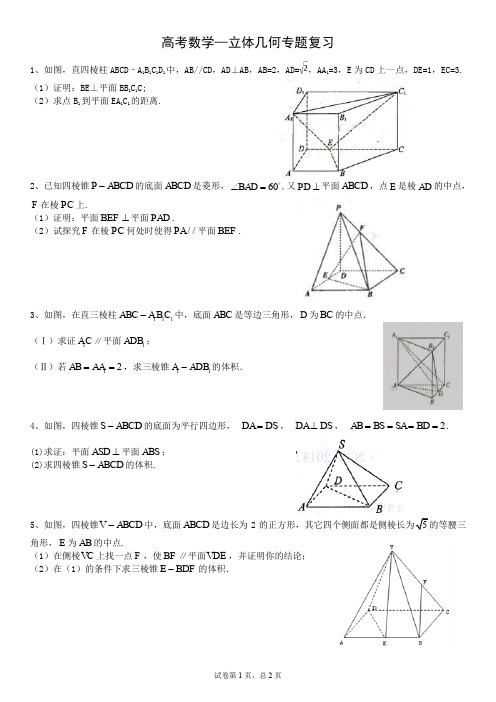
1、如图,直四棱柱 ABCD–A1B1C1D1 中,AB//CD,AD⊥AB,AB=2,AD= ,AA1=3,E 为 CD 上一点,DE=1,EC=3. (1)证明:BE⊥平面 BB1C1C; (2)求点 B1 到平面 EA1C1 的距离.
2、已知四棱锥 P ABCD 的底面 ABCD 是菱形, BAD 60 ,又 PD 平面 ABCD ,点 E 是棱 AD 的中点, F 在棱 PC 上. (1)证明:平面 BEF 平面 PAD . (2)试探究 F 在棱 PC 何处时使得 PA / / 平面 BEF .
答案第 1 页,总 6 页
试题解析:
(1)证明:
PD EB
平面ABCD 平面ABCD
PD
EB
,
又底面 ABCD 是 A 60 的菱形,且点 E 是棱 AD 的中点,所以 EB AD ,
高三立体几何专题练习(含答案)

立体几何专题练习卷一、填空题(本大题满分56分,每小题4分) 1.正方体DC B A ABCD 111-的棱长为a ,则异面直线1AB 与1BC 所成的角的大小是__________.2.已知某铅球的表面积是2484cm π,则该铅球的体积是___________2cm .3.若圆锥的侧面积为20π,且母线与底面所成的角为4arccos5,则该圆锥的体积为___________.4.在长方体1111ABCD A B C D -中,若12,1,3AB BC AA ===,则1BC 与平面11BB D D 所成的角θ可用反三角函数值表示为θ=____________.5.若取地球的半径为6371米,球面上两点A 位于东经O12127',北纬O 318',B 位于东经O12127',北纬O 255',则A B 、两点的球面距离为_____________千米(结果精确到1千米).6.已知圆锥的母线长为5cm ,侧面积为π15 2cm ,则此圆锥的体积为__________3cm .7.若圆锥的底面半径和高都是2,则圆锥的侧面积是_____________. 8.如图,是一个无盖正方体盒子的表面展开图,A B C 、、为其上的三个点,则在正方体盒子中,ABC ∠=____________.9.一个圆柱形容器的轴截面尺寸如右图所示,容器内有一个实心的球,球的直径恰等于圆柱的高.现用水将该容器注满,然后取出该球(假设球的密度大于水且操作过程中水量损失不计),则球取出后,容器中水面的高度为__________cm. (精确到0.1cm )10.如图,用铁皮制作一个无盖的圆锥形容器,已知该圆锥的母线与底面所在平面的夹角为45︒,容器的高为10cm .制作该容器需要铁皮面积为__________cm2.(衔接部分忽略不计,结果保留整第9题数)11.如图,圆锥的侧面展开图恰好是一个半圆,则该圆锥的母线与底面所成的角的大小是__________ .12.如右下图,ABC ∆中, 90=∠C ,30=∠A ,1=BC .在三角形内挖去半圆(圆心O 在边AC 上,半圆与BC 、AB 相切于点C 、M ,与AC 交于N ),则图中阴影部分绕直线AC 旋转一周所得旋转体的体积为__________ .13.如图所示,以圆柱的下底面为底面,并以圆柱的上底面圆心为顶点作圆锥, 则该圆锥与圆柱等底等高。
立体几何 高考数学大题热点50题训练学生版

2023 立体几何大题热点50 题一.解答题(共50 小题)1.(2023•新城区校级模拟)如图,在三棱柱 ABC −A ′B ′C ′中, AB ⊥BC ,平面 ABC ⊥平面 ABB ′A ′,2AB BC BB '===,BB ' 在BA 上的投影为1.(1)证明:BC CC ⊥'.(2)求二面角B AC B '--的余弦值.2.(2023•温州模拟)已知三棱锥D ABC -中,BCD ∆是边长为3的正三角形,AB AC AD ==,AD 与平面BCD 所成角的余弦值为33.(1)求证:AD BC ⊥;(2)求二面角D AC B --的平面角的正弦值.3.(2023•抚顺模拟)如图,四棱锥S ABCD -的底面是正方形,点P ,Q 在侧棱SD 上,E 是侧棱SC 的中点.(1)若SQ QP PD ==,证明://BE 平面PAC ;(2P AC D --的大小.①SD ⊥平面PAC ;②P 为SD 的中点.4.(2023•九江二模)如图,在三棱柱111ABC A B C -中,AC ⊥平面11AA B B ,13ABB π∠=,1AB =,12AC AA ==,D 为棱1BB 的中点.(1)求证:AD ⊥平面11A C D ;(2)在棱BC 上是否存在异于点B 的一点E ,使得DE 与平面11A C D 所成的角为6π?若存在,求出BE BC的值若存在,请说明理由.5.(2023•太原模拟)如图,四棱锥P ABCD -中,//AB CD ,AB AD ⊥,且24AB AD CD ===,2PA =,60PAB ∠=︒,直线PA 与平面ABCD 的所成角为30︒,E ,F 分别是BC 和PD 的中点.(1)证明://EF 平面PAB ;(2)求平面PAB 与平面PAD夹角的余弦值.6.(2023•江苏模拟)在三棱柱111ABC A B C -中,平面11A B BA ⊥平面ABC ,侧面11A B BA 为菱形,13ABB π∠=,1AB AC ⊥,2AB AC ==,E 是AC 的中点.(1)求证:1A B ⊥平面1AB C ;(2)点P 在线段1A E 上(异于点1A ,)E ,AP 与平面1A BE 所成角为4π,求1EP EA 的值.7.(2023•浙江模拟)如图,四面体ABCD 中,90BAD BAC CAD ∠=∠=∠=︒,AC AD =,AB 与面BCD 的所成角为45︒.(1)若四面体ABCD 的体积为223,求AC 的长;(2)设点M 在面BCD 中,45ABM ∠=︒,30ACM ∠=︒,过M 作CD 的平行线,分别交BC 、BD 于点H 、F ,求面AFH 与面ACD 所成夹角的余弦值.8.(2023•贵州模拟)如图甲,在四边形PBCD 中,//PD BC ,2PB BC CD AD PA =====,将ABP ∆沿AB 折起得图乙,点M 是PD 上的点.(1)若M 为PD 的中点,证明:PC ⊥平面ABM ;(2)若PC =,试确定M 的位置,使二面角M AB C --的正弦值等于.9.(2022秋•滨江区校级期末)如图①,在等腰梯形ABCD 中,//AB CD ,222AB AD CD ===,将ADC ∆沿AC 折起,使得AD BC ⊥,如图②.(1)求直线BD 与平面ADC 所成的角;(2)在线段BD 上是否存在点E ,使得二面角E AC D --的平面角的大小为4π?若存在,指出点E 的位置;若不存在,请说明理由.10.(2023•桃城区校级一模)如图所示,A ,B ,C ,D 四点共面,其中90BAD ADC ∠=∠=︒,12AB AD =,点P ,Q 在平面ABCD 的同侧,且PA ⊥平面ABCD ,CQ ⊥平面ABCD .(1)若直线l ⊂平面PAB ,求证://l 平面CDQ ;(2)若//PQ AC ,45ABP DAC ∠=∠=︒,平面BPQ ⋂平面CDQ m =,求锐二面角B m C --的余弦值.11.(2023•榆林二模)如图,在四棱锥P ABCD -中,BD PC ⊥,60ABC ∠=︒,四边形ABCD 是菱形,PB ==,E 是棱PD 上的动点,且PE PD λ=.(1)证明:PA ⊥平面ABCD .(2)是否存在实数λ,使得平面PAB 与平面ACE ?若存在,求出λ的值;若不存在,请说明理由.12.(2023•大英县校级模拟)在三棱锥P ABC -中,ABC ∆是边长为4的等边三角形,平面PAB ⊥平面ABC ,PA PB ==M 为棱BC 的中点,点N 在棱PC 上且满PN PC λ=,已知使得异面直线MN 与AC 所成角的余弦值为12的λ有两个不同的值1λ,212()λλλ<.(1)求1λ,2λ的值;(2)当12λλ=时,求二面角N AM C --的余弦值.13.(2023•贵州模拟)如图甲,已知四边形ABCD 是直角梯形,E ,F 分别为线段AD ,BC 上的点,且满足,AB =2EF =4CD =4,AB ⊥BC ,,将四边形CDEF 沿EF 翻折,使得C ,D 分别到C 1,D 1的位置,并且,如图乙(1)求证:ED 1⊥BC 1;(2)求平面AD 1E 与平面BC 1F 所成的二面角的余弦值.14.(2023•南充模拟)在四棱锥P ABCD -中,底面ABCD 是边长为2的菱形,60ABC ∠=︒,PB PD =,PA AC ⊥.(1)证明:BD ⊥平面PAC ;(2)PA =,是否存在常数[0λ∈,1],满足CM CP λ= ,且直线AM 与平面PBC 所成角的正弦值为144?若存在,求出点M 的位置;若不存在,请说明理由.15.(2023•兰州模拟)如图所示的五边形SBADC 中ABCD 是矩形,2BC AB =,SB SC =,沿BC 折叠成四棱锥S ABCD -,点M 是BC 的中点,2SM =.(1)在四棱锥S ABCD -中,可以满足条件①SA =②5cos 5SBM ∠=;③6sin 3SAM ∠=,请从中任选两个作为补充条件,证明:侧面SBC ⊥底面ABCD ;(注:若选择不同的组合分别解答,则按第一个解答计分.)(2)在(1)的条件下求直线SC 与平面SAD 所成角的正弦值.16.(2023•开封二模)如图1,在直角梯形ABCD 中,//AB CD ,90BAD ∠=︒,12AD CD AB ===E 为AC 的中点,将ACD ∆沿AC 折起(如图2),在图2所示的几何体D ABC -中:(1)若AD BC ⊥,求证:DE ⊥平面ABC ;(2)若BD 与平面ACD 所成的角为60︒,求二面角D AC B --的余弦值.17.(2022秋•天津期末)在如图所示的几何体中,四边形ABCD 是菱形,ADNM 是矩形,ND ⊥平面ABCD ,3DAB π∠=,2AD =,1AM =,E 为AB 的中点.(1)求证://AN 平面MEC ;(2)求平面EMC 与平面BMC 夹角的余弦值.(3)在线段AM 上是否存在点P ,使直线PE 与平面MBC 所成的角为3π?若存在,求出PE 的长;若不存在,请说明理由.18.(2023•丰台区一模)如图,在四棱锥P ABCD -中,底面是边长为2的菱形,AC 交BD 于点O ,60BAD ∠=︒,PB PD =.点E 是棱PA 的中点,连接OE ,OP .(1)求证://OE 平面PCD ;(2)若平面PAC 与平面PCD 的夹角的余弦值为155,再从条件①,条件②这两个条件中选择一个作为已知,求线段OP 的长.条件①:平面PBD ⊥平面ABCD ;条件②:PB AC ⊥.注:如果选择条件①和条件②分别解答,按第一个解答计分.19.(2023•包头一模)如图,已知矩形ABCD 是圆柱的轴截面,P 是CD 的中点,直线BP 与下底面所成角的正切值为13,矩形ABCD 的面积为12,MN 为圆柱的一条母线(不与AB ,CD 重合).(1)证明:BN MP ⊥;(2)当三棱锥B MNP -的体积最大时,求二面角N BM P --的正弦值.20.(2023•兴庆区校级一模)如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,AD CD ⊥,//AD BC ,2PA AD CD ===,3BC =.E 为PD 的中点,点F 在PC 上,且在13PF PC =.(Ⅰ)求证:平面PCD ⊥平面PAD ;(Ⅱ)求二面角F AE P --的余弦值;(Ⅲ)设点G 在PB 上,且23PG PB =.判断直线AG 是否在平面AEF 内,说明理由.21.(2023•南宁模拟)如图1,平面图形ABCD 是一个直角梯形,其中//AB CD ,90ABC ∠=︒,2BC DC ==,6AB =,E 是AB 上一点,且2AE EB =.将AED ∆沿着ED 折起使得平面AED ⊥平面DEBC ,连接AB 、AC ,M 、N 分别是AD 、AC 的中点,如图2.(1)证明:在图2中E 、M 、N 、B 四点共面,且平面ADC ⊥平面AED ;(2)在图2中,若G 是线段AE 上一个动点,当直线CG 与平面BDG 所成角的正弦值取得最大值时,求GE 的长.22.(2023•石景山区一模)如图,在四棱锥P ABCD -中,底面ABCD 是边长为2的正方形,侧面PAD 为等腰直角三角形,且2PAD π∠=,点F 为棱PC 上的点,平面ADF 与棱PB 交于点E .(Ⅰ)求证://EF AD ;(Ⅱ)从条件①、条件②、条件③这三个条件中选择两个作为已知,求平面PCD 与平面ADFE 所成锐二面角的大小.条件①:AE =条件②:平面PAD ⊥平面ABCD ;条件③:PB FD ⊥.注:如果选择的条件不符合要求,第(Ⅱ)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.23.(2023•安康二模)如图,在斜三棱柱111ABC A B C -中,O 为AB 中点,1A O ⊥底面ABC ,14A O =,AC BC =,26AB OC ==,G ,E 分别在线段AC ,1BC 上,且112AG BE GC C E ==.(1)求证://GE 面11AA B B ;(2)记面1B GE ⋂面ABC l =,求二面角1B l B --的余弦值.24.(2022秋•郴州期末)如图2,在平行四边形ABCD 中,2AB =,BC =30ABC ∠=︒.将DAC ∆沿AC 翻折,使点D 到达点P 位置(如图3),且平面PAC ⊥平面PBC .(1)求证:平面PAC ⊥平面ABC ;(2)设Q 是线段PB 上一点,满足PQ mPB = ,试问:是否存在一个实数m ,使得平面QAC 与平面PAB 的,若存在,求出m的值;若不存在,请说明理由.25.(2023•新疆模拟)如图,在平面四边形ABCD中,1,AB AD BC CD ====,且BC CD ⊥,以BD 为折痕把ABD ∆和CBD ∆向上折起,使点A 到达点E 的位置,点C 到达点F 的位置,且平面FBD 和平面EBD 不重合.(1)求证:EF BD ⊥;(2)若点G 为ABD ∆的重心(三条中线的交点),EG ⊥平面ABD ,求直线BD 与平面ABE 所成角的余弦值.26.(2022秋•驻马店期末)如图,在多面体ABCDEF 中,四边形ABCD 是平行四边形,四边形ACEF 是矩形,22BC AB AF ==,60ABC ∠=︒,AF BC ⊥,H 是棱AD 的中点,P 是棱EF 上的动点.(1)证明:AB ⊥平面ACEF ;(2)求平面PBH 与平面CDE 所成锐二面角的余弦值的最大值.27.(2023•烟台一模)如图,在四棱棱V ABCD -中,底面ABCD 为菱形,2AB =,60BAD ∠=︒,VBC ∆为等边三角形.(1)求证:BC VD ⊥;(2)若二面角A BC V --的大小为60︒,求直线VA 与平面VBC 所成角的正弦值.28.(2023•咸阳校级模拟)已知直四棱柱1111ABCD A B C D -中,底面ABCD 为梯形,//AB CD ,5AB =,6AD =,2CD =,E ,H 分别是11B C ,1AA 上的点,且111113,3,,34B E BC AH AA DH AB F ===⊥为AB 上的点.(1)证明:EF DH ⊥;(2)当3AF =时,求平面DEF 与平面11AA D D 所成的二面角的正弦值.29.(2023•焦作二模)如图1,在ABC ∆中,AB AC =,23BAC π∠=,E 为BC 的中点,F 为AB 上一点,且EF AB ⊥.现将BEF ∆沿EF 翻折到△B EF ',如图2.(1)证明:EF AB '⊥.(2)已知二面角B EF A '--为3π,在棱AC 上是否存在点M ,使得直线BC 与平面B MF '所成角的正弦值M 的位置;若不存在,请说明理由.30.(2023•龙岩模拟)三棱柱111ABC A B C -中,AB AC ⊥,2AB AC ==,侧面11A ACC ,为矩形,123A AB π∠=,三棱锥1C ABC -的体积为233.(1)求侧棱1AA 的长;(2)侧棱1CC 上是否存在点E ,使得直线AE 与平面1A BC 所成角的正弦值为5?若存在,求出线段1C E 的长;若不存在,请说明理由.31.(2023•沙坪坝区校级模拟)如图,在三棱锥P ABC -中,PA PB =,2AB BC ==,90APB ABC ∠=∠=︒,平面PAB ⊥平面ABC ,点E 是线段PA 上的动点.(1)证明:平面APC ⊥平面PBC ;(2)若点Q 在线段BC 上,23BQ =,且异面直线EQ 与PB 成30︒角,求平面EBC 和平面ABC 夹角的余弦值.32.(2023•湖北模拟)如图,在斜三棱柱111ABC A B C -中,底面ABC ∆是边长为2的正三角形,侧面11BCC B 为菱形,已知160BB C ∠=︒,1AB a =.(1)当a =时,求三棱柱111ABC A B C -的体积;(2)设点P 为侧棱1BB 上一动点,当3a =时,求直线1PC 与平面11ACC A 所成角的正弦值的取值范围.33.(2023•平湖市模拟)如图在三棱柱111ABC A B C -中,D 为AC 的中点,2AB BC ==,111AA B B BC ∠=∠.(1)证明:1BB AC ⊥;(2)若1BB BC ⊥,且满足:_____,(待选条件).从下面给出的①②③中选择两个填入待选条件,求二面角11B B D C --的正弦值.①三棱柱111ABC A B C -的体积为②直线1AB 与平面11BCC B 所成的角的正弦值为;③二面角1A BB C --的大小为60︒;注:若选择不同的组合分别解答,则按第一个解答计分.34.(2022秋•西山区期末)如图,在四棱锥P ABCD -中,底面ABCD 是平行四边形,23ADC π∠=,24PD DC BC ===,点E 是线段AD 的中点,点F 在线段AP 上且满足AF AP λ= ,PD ⊥面ABCD .(Ⅰ)当13λ=时,证明://PC 平面BFE ;(Ⅱ)当λ为何值时,平面BFE 与平面PBD所成的二面角的正弦值最小?35.(2023•宛城区校级开学)四棱柱1111ABCD A B C D -中,底面ABCD 为正方形,1AA ⊥面ABCD ,点M ,N ,Q 分别为棱1DD ,AD ,1BB 的中点.(1)求证:平面//MNQ 平面1BC D ;(2)若12AA AB =,棱11A B 上存在点P ,使得二面角P MN Q --的余弦值为132163,求111A P A B的值.36.(2023•南开区校级模拟)如图,已知梯形ABCD 中,//AD BC ,90DAB ∠=︒,22AB BC AD ===,四边形EDCF 为矩形,2DE =,平面EDCF ⊥平面ABCD .(1)求证://DF 平面ABE ;(2)求平面ABE 与平面BEF 的夹角的余弦值;(3)若点P 在线段EF 上,且直线AP 与平面BEF 所成角的正弦值为1414,求线段AP 的长.37.(2023春•荔湾区月考)如图,把边长为ABCD 沿对角线AC 折成直二面角,F 是BC的中点,O 是原正方形ABCD 的中心,动点E 在线段AD (包含端点A ,)D 上.(1)若E 为AD 的中点,求直线AB 到平面EOF 的距离;(2)在线段AD 上是否存在点E ,使得平面EOF 与平面ABC 的夹角的余弦值为13,若存在,求出DE EA的值;若不存在,请说明理由.38.(2023•九龙坡区校级开学)如图,在梯形ABCD 中,//AB CD ,23BCD π∠=,四边形ACFE 为矩形,且CF ⊥平面ABCD ,1AD CD BC CF ====.(1)求证:平面EFD ⊥平面BCF ;(2)点M 在线段EF 上运动,当点M 在什么位置时,平面MAB 与平面FCB 所成锐二面角的余弦值为34.39.(2023•石家庄模拟)如图,四棱锥S ABCD -中,底面ABCD 为矩形且垂直于侧面SAB ,O 为AB 的中点,2SA SB AB ===,AD =.(Ⅰ)证明:BD ⊥平面SOC ;(Ⅱ)侧棱SD 上是否存在点E ,使得平面ABE 与平面SCD 夹角的余弦值为15,若存在,求SE SD的值;若不存在,说明理由.40.(2023•高州市一模)如图,四棱柱1111ABCD A B C D -的底面ABCD 为直角梯形,90DAB ADC ∠=∠=︒,1AB AD ==,2CD =,1BD CD ⊥.点M 为1CD 的中点,且12CD BM =.(1)证明:平面BDM ⊥平面1BCD ;(2)若钝二面角B DM C --的余弦值为,当1BD BD >时,求1BD 的长.41.(2023•邵阳一模)如图所示,在多面体ABCDEF 中,底面ABCD 为直角梯形,//AD BC ,AB BC ⊥,侧面ABEF 为菱形,平面ABEF ⊥平面ABCD ,M 为棱BE 的中点.(1)若DE 上有一点N 满足//MN 平面ABCD ,确定点N 的位置并证明;(2)若12AB BC AD ==,60EBA ∠=︒,求平面MAD 与平面EFD 所成二面角的正弦值.42.(2023•重庆二模)如图,在四棱锥P ABCD -中,侧棱PD ⊥矩形ABCD ,且PD CD =,过棱PC 的中点E ,作EF PB ⊥交PB 于点F ,连接DE ,DF ,BD ,BE .(1)证明:PB DF ⊥;(2)若1PD =,平面DEF 与平面ABCD 所成二面角的大小为3π,求P DEF V -的值.43.(2023•武威模拟)如图,在四棱锥P ABCD -中,四边形ABCD 是直角梯形,AD AB ⊥,//AB CD ,22PB CD AB AD ===,PD =,PC DE ⊥,E 是棱PB 的中点.(1)证明:PD ⊥平面ABCD ;(2)若AF AB λ= ,求平面DEF 与平面PAD 所成的锐二面角的余弦值的最大值.44.(2023•舞钢市开学)如图所示,在四棱锥A BCDE -中,ABC ∆是等边三角形,//CD BE ,BD CD ⊥,记平面ACD 与平面ABE 的交线为l .(1)证明://l CD .(2)若2AD BE ===,DE =Q 为l 上一点,求BC 与平面QBD 所成角的正弦值的最大值.45.(2023•新城区校级一模)如图,三棱柱111ABC A B C -的底面ABC 是正三角形,侧面11ACC A 是菱形,平面11ACC A ⊥平面ABC ,E ,F 分别是棱11A C ,BC 的中点.(1)证明://EF 平面11ABB A ;(2)若112,60,2AC ACC C G GC =∠=︒= ,求直线11B C 与平面EFG 所成角的正弦值.46.(2023•安徽开学)如图,四棱锥P ABCD -的底面ABCD 为正方形,二面角P AB D --为直二面角,PAB PBA ∠=∠,点M 为棱AD 的中点.(1)求证:PD MC ⊥;(2)若PA AB =,点N 是线段BD 上靠近B 的三等分点,求直线PA 与平面PMN 所成角的正弦值.47.(2023•湖北模拟)如图,在四棱锥S ABCD -中,底面ABCD 是直角梯形,//AD BC ,AB BC ⊥,SA ⊥平面ABCD ,22SA AB BC AD ====.(1)求C 到平面SBD 的距离;(2)求平面SAB 与平面SCD 的夹角的正弦值.48.(2023•河南模拟)如图,在四棱锥M ﹣ABCD 中,底面ABCD 是平行四边形,AB =4,AD =2,MC =2,∠ADC =45°,点M 在底面ABCD 上的射影为CD 的中点O ,E 为线段AD 上的点(含端点).(1)若E 为线段AD 的中点,证明:平面MOE ⊥平面MAD ;(2)若3AE =DE ,求二面角D ﹣ME ﹣O 的余弦值.49.(2023•梅州一模)如图,在边长为4的正三角形ABC 中,E 为边AB 的中点,过E 作ED AC ⊥于D .把ADE ∆沿DE 翻折至△1A DE 的位置,连接1A C 、1A B .(1)F 为边1A C 的一点,若12CF FA = ,求证://BF 平面1A DE ;(2)当四面体1C EBA -的体积取得最大值时,求平面1A DE 与平面1A BC 的夹角的余弦值.50.(2023•新乡模拟)如图,已知圆锥P ABC -,AB 是底面圆O 的直径,且长为4,C 是圆O 上异于A ,B 的一点,PA =P AC B --与二面角P BC A --的大小分别为α与β.(1)求2211tan tan αβ+的值;(2)若tan βα=,求二面角A PC B --的余弦值.。
高三数学立体几何专项练习题及答案

高三数学立体几何专项练习题及答案一、选择题1. 下列哪个几何体的所有面都是三角形?A. 正方体B. 圆柱体C. 正六面体D. 球体答案:C2. 一个有8个面的多面体,其中6个面是正方形,另外2个面是等边三角形,它的名字是?A. 正八面体B. 正十二面体C. 正二十面体D. 正二十四面体答案:C3. 空间中任意一点到四个角落连线的垂直距离相等的四棱锥称为?A. 正四棱锥B. 圆锥台C. 四棱锥D. 无法确定答案:C4. 任意多面体的面数与顶点数、棱数的关系是?A. 面数 + 顶点数 = 棱数 + 2B. 面数 + 棱数 = 顶点数 + 2C. 顶点数 + 棱数 = 面数 + 2D. 顶点数 + 面数 = 棱数 + 2答案:A5. 求下列多面体的棱数:(1)正六面体(2)正八面体(3)正十二面体答案:(1)正六面体的棱数为 12(2)正八面体的棱数为 24(3)正十二面体的棱数为 30二、填空题1. 下列说法正确的是:一棱锥没有底面时,它的底面是一个______。
答案:点2. 铅垂线是指从一个多面体的一个顶点到与它相对的棱上所作的垂线,它与该棱垂足的连线相交于该多面体的______上。
答案:中点3. 对正八面体,下列说法不正确的是:_____条对角线与_____两两垂直。
答案:六,相邻面三、计算题1. 一个棱锥的底面是一个边长为6cm的正三角形,其高为8cm。
求棱锥体积。
解答:底面积 S = (1/2) ×底边长 ×高 = (1/2) × 6 × 8 = 24 cm²棱锥体积 V = (1/3) × S ×高 = (1/3) × 24 × 8 = 64 cm³所以,棱锥的体积为64 cm³。
2. 一个正四棱锥的底面是一个边长为10cm的正方形,其高为12cm。
求四棱锥的体积。
解答:底面积 S = 边长² = 10² = 100 cm²四棱锥体积 V = (1/3) × S ×高 = (1/3) × 100 × 12 = 400 cm³所以,四棱锥的体积为400 cm³。
2023年高考数学总复习《立体几何》附答案解析
所以 z1=0,
,故可取
, ,,
于是 < , >
,
设所成锐二面角为θ,所以 sinθ
,
所以平面 PAD 和平面 PBE 所成锐二面角的正弦值为 .
第3页共3页
第1页共3页
∴CF CC1 AA1 , ∵∠BAC=90°,
∴CD
,
在 Rt△FCD 中,tan∠FDC 맨
,
故直线 DF 与平面 ABC 所成角的正切值为 .
2.如图所示,四棱锥 P﹣ABCD 的底面 ABCD 是边长为 1 的菱形,∠BCD=60°,E 是 CD 的中点,PA⊥底面 ABCD,PA=2. (1)证明:平面 PBE⊥平面 PAB; (2)求平面 PAD 和平面 PBE 所成二面角(锐角)的正弦值.
【解答】(1)证明:如图所示,连接 BD,由 ABCD 是菱形且∠BCD=60°, 知△ABC 是等边三角形. ∵E 是 CD 的中点, ∴BE⊥CD,又 AB∥CD, ∴AB⊥BE,∴BE⊥平面 PAB, 又 BE⊂平面 PBE, ∴平面 PBE⊥平面 PAB. (2)解:在平面 ABCD 内,过点 A 作 AB 的垂线,如图所示,以 A 为原点建立空间直角
【解答】(1)证明:连接 DG、FG, 由直三棱柱的性质知,BB1∥CC1,且 BB1=CC1, ∵B1E=2EB,C1F=2FC, ∴EB∥FC,且 EB=FC, ∴四边形 BCFE 为平行四边形, ∴EF∥BC,EF=BC, ∵BD=2DA,CG=2GA, ∴GD∥BC,且 GD BC, ∴EF∥GD,且 GD EF, ∴四边形 DEFG 为梯形,即 D、E、F、G 四点共面, ∴点 G 在平面 EFD 内. (2)解:由直三棱柱的性质知,CC1⊥平面 ABC, ∵F 为 CC1 上一点, ∴点 F 在平面 ABC 上的投影为点 C, 连接 CD,则∠FDC 即为直线 DF 与平面 ABC 所成角. ∵点 D 在棱 AB 上,且 BD=2DA, ∴AD AB , ∵C1F=2FC,
(word完整版)高三数学立体几何经典例题
厦门一中立体几何专题一、选择题(10 X 5' =50 ')1•如图,设0是正三棱锥 P-ABC 底面三角形 ABC 的中心, 过0的动平面与P-ABC 的三条侧棱或其延长线的交点分别记 为 Q 、R 、S ,则-11 1( )PQ PR PSA. 有最大值而无最小值B. 有最小值而无最大值C. 既有最大值又有最小值,且最大值与最小值不等D. 是一个与平面QRS 位置无关的常量2•在正n 棱锥中,相邻两侧面所成的二面角的取值范围是 (A., B., C. 0,D.nn2n的面积的取值范围是()若B €a ,C €3 ,则厶ABC 的周长的最小值是( )B.2 .75.如图,正四面体 A-BCD 中,E 在棱AB 上,F 在棱CD 上,使得詈 Cy =入(0<入<+m ),记f (入)=a x+ 3入,其中a 入表示EF 与AC 所成的角,3入表示EF 与BD 所成的角,贝U( )A. f (入)在(0,+ g )单调增加B. f (入)在(0,+ g )单调减少C. f (入)在(0,1)单调增加,在(1,+ g )单调减少D. f (入)在(0,+ g )为常数合是 ()A. 一条直线B. —个平面C.两条平行直线D.两个平面7.正四棱锥底面积为 Q ,侧面积为S ,则它的体积为 ()A. 1 Q (S2Q 2)B. 1 Q (S2Q 2)6 •3 'C. 1 -Q(S2Q 2)23•正三棱锥P-ABC 的底面边长为 2a,点E 、F 、G 、H 分别是 PA 、PB 、BC 、AC 的中点,则四边形 EFGHA.(0,+ g )B.C.D. ^a 2, 24.已知二面角a -a-3为60°,点A 在此二面角内,且点A 到平面a 、3的距离分别是AE=4, AF=2,6.直线a //平面3,直线a 到平面3的距离为 1,则到直线a 的距离与平面3的距离都等于7的点的集第5题图D.f QS第1题图8. 已知球O的半径为R, A、B是球面上任意两点,则弦长|AB|的取值范围为()B.(0,2R]C. ( 0,2R )D. : R,2R ]9•已知平面aQ 平面B =l,m 是平面a 内的一条直线,则在平面B 内A. .—定存在直线与直线 m 平行,也一定存在直线与直线B. —定存在直线与直线 m 平行,但不一定存在直线与直线C. 不一定存在直线与直线 m 平行,但一定存在直线与直 线m 垂直D. 不一定存在直线与直线 m 平行,也不一定存在直线与 直线m 垂直10. 如图为一个简单多面体的表面展开图(沿图中虚线折11. ______________________________________________________________________ 边长为a 的等边三角形内任一点到三边距离之和为定值,这个定值为 __________________________ ;推广到空间,棱长为a 的正四面体内任一点到各面距离之和为 ______________12. 在厶ABC 中,AB=9, AC=15,/ BAC=120°,其所在平面外一点 P 到A 、B 、C 三个顶点的距离都是14,贝U P 点到直线 BC 的距离为 _____________ . 13. 已知将给定的两个全等的正三棱锥的底面粘在一起, 恰得到一个所有二面角都相等的六面体, 并且该六面体的最短棱的长为 2,则最远的两顶点间的距离是 _______________ .14. ___________________________________________________________________ 有120个等球密布在正四面体 A-BCD 内,问此正四面体的底部放有 ___________________________ 个球. 三、解答题(4X 10' +14' =54')15. 定直线11丄平面a ,垂足为M ,动直线12在平面a 内过定点 N ,但不过定点 M.MN=a 为定值,在11、12上分别有动线段 AB=b,CD = c.b 、c 为定值.问在什么情况下四面体 ABCD 的体积最大?最大值是多少?AC 的中点,求:(1) PM 与FQ 所成的角; (2) P 点到平面 EFB 的距离; (3 )异面直线PM 与FQ 的距离.16.如图所示,已知四边形 ABCD 、EADM 和MDCF 都是边长为 a 的正方形,点 P 、Q 分别是ED 和A. : 0,2 R ] m 垂直A.6B.7C.8D.9、填空题 (4X 4 ' =16')叠即可还原),则这个多面体的顶点数为 (第16题图连结人丘‘将厶DAE 沿AE 折起到△ D 1AE 的位置,使得/(1)试用基向量 AB , AE , AD 1表示向量OD 117.如图,在梯形 ABCD 中,AB // CD ,/ ADC = 90° ,3AD=DC=3,AB=2,E 是 CD 上一点,满足 DE = 1 ,D 1AB = 60° ,设AC 与BE 的交点为O.(2) 求异面直线OD i与AE所成的角.(3) 判断平面D i AE与平面ABCE是否垂直,并说明理由第17题图18. 如图,在斜棱柱ABC —A i B i C i中,底面为正三角形,侧棱长等于底面边长,且侧棱与底面所成的角为60°顶点B i在底面ABC上的射影O恰好是AB的中点.(i)求证:B i C± C i A;(2 )求二面角C i-AB-C的大小.第i8题图i9.如图所示,在三棱锥P-ABC中,PA=PB=PC , BC=2a,AC=a,AB=、3 a,点P到平面ABC的距离为 | a.(i )求二面角P-AC-B的大小;(2)求点B到平面FAC的距离.第i9题图立体几何练习参考答案一、选择题 1.D 设正三棱锥P-ABC 中,各棱之间的夹角为a,棱与底面夹角为B ,h 为点S 到平面PQR 的距离,1 11则 V S -PQR = 3S ^PQR • h= — ( — PQ • PR • sin a ) • PS • sin B ,另一方面,记 O 到各平面的距离为 d,则有33 211 1 dV S -PQR =V O -PQR +V O -PRS +V O -PQS =S ^PQR °d+ S ^PRS ,d+S^PQS -d=3333a + d • - -PQ -PS-sin a •故有 PQ -PR -PS-sin B =d(PQ -PR+PR -PS+PQ -PS),即旦—-PQ -PR -sin a +— •丄 PS ・PR ・sin2321 1 _ sinPR PS d3 2 PQ 常量.2.B 设正n 棱锥的高为h,相邻两侧面所成二面角为B .当h f 0时,正n 棱锥的极限为正n 边形,这时 相邻两侧面所成二面角为平面角,即二面角Qfn.当h fg 时,正n 棱锥的极限为正n 棱柱,这时相邻两侧面所成二面角为正n 边形的内角,nEFGH 为矩形,当 P f 底面△ ABC 的中心O 时,矩形EFGH f 矩形E i F i GH.3a=_Aa 23 34. C 如图,I a 丄AE,a 丄AF,「. a 丄平面 AEF.设a 交平面 AEF 于点G ,则/ EGF 是二面角a -a-3的平面角,/ EGF=60° ,/ EAF=120。
2023届高考数学总复习:立体几何复习题附答案
a,
在 Rt△FCM 中,tan∠FCM .
,
∴sin∠FCM ,
故直线 CF 与平面 ACDE 所成角的正弦值为 . 2.如图,在三棱柱 ABC﹣A1B1C1 中,BC⊥平面 AA1C1C,D 是 AA1 的中点,△ACD 是边长
为 1 的等边三角形. (1)证明:CD⊥B1D; (2)若 BC ,求二面角 B﹣C1D﹣B1 的大小.
,令
由(1)知,平面 B1C1D 的一个法向量为
,得
,, ,
, ,,
故 th< , >
,
所以二面角 B﹣C1D﹣B1 的大小为 30°.
第3页共3页
在直角梯形 AEFB 中,有 AF EF,BF
쳌
∴AF2+BF2=AB2,即 AF⊥BF.
∵BC∩BF=B,BC、BF⊂平面 BCF,
∴AF⊥平面 BCF.
EF,AB=2EF,
(2)解:∵AE⊥平面 ABC,AE⊂平面 ACDE,∴平面 ACDE⊥平面 ABC,
又平面 ABC∥平面 DEF,∴平面 ACDE⊥平面 DEF.
【解答】解:(1)证明:因为△ACD 是边长为 1 的等边三角形,所以∠ADC=60°,∠ DA1C1=120° 因为 D 是 AA1 的中点,所以 AD=A1D=A1C1=1,即△A1C1D 是等腰三角形, 则∠A1DC1=30°,故∠CDC1=90°,即 CD⊥C1D, 因为 BC⊥平面 AA1C1C,BC∥B1C1,所以 B1C1⊥平面 AA1C1C, 因为 CD⊂平面 AA1C1C,所以 B1C1⊥CD, 因为 B1C1∩C1D=C1,B1C1⊂平面 B1C1D,C1D⊂平面 B1C1D,所以 CD⊥平面 B1C1D, 因为 B1D⊂平面 B1C1D,所以 CD⊥B1D;
专题立体几何(2012-2021)高考数学真题
专题11 立体几何 【2021年】 1.(2021年全国高考乙卷数学(文)试题)在正方体1111ABCD A B C D -中,P 为11B D 的中点,则直线PB 与1AD 所成的角为( )A .π2B .π3C .π4D .π62.(2021年全国高考甲卷数学(理)试题)2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为8848.86(单位:m ),三角高程测量法是珠峰高程测量方法之一.如图是三角高程测量法的一个示意图,现有A ,B ,C 三点,且A ,B ,C 在同一水平面上的投影,,A B C '''满足45AC B ∠'''=︒,60A B C ''∠'=︒.由C 点测得B 点的仰角为15︒,BB '与CC '的差为100;由B 点测得A 点的仰角为45︒,则A ,C 两点到水平面A B C '''的高度差AA CC ''-约为(3 1.732≈)( )A .346B .373C .446D .4733.(2021年全国高考甲卷数学(理)试题)已如A ,B ,C 是半径为1的球O 的球面上的三个点,且,1AC BC AC BC ⊥==,则三棱锥O ABC -的体积为( )A .212B .312C .24D .344.(2021年全国新高考Ⅰ卷数学试题)已知圆锥的底面半径为2,其侧面展开图为一个半圆,则该圆锥的母线长为( )A .2B .22C .4D .42二、填空题5.(2021年全国高考甲卷数学(文)试题)已知一个圆锥的底面半径为6,其体积为30π则该圆锥的侧面积为________.三、解答题6.(2021年全国高考乙卷数学(文)试题)如图,四棱锥P ABCD -的底面是矩形,PD ⊥底面ABCD ,M 为BC 的中点,且PB AM ⊥.(1)证明:平面PAM ⊥平面PBD ;(2)若1PD DC ==,求四棱锥P ABCD -的体积.8.(2021年全国高考甲卷数学(文)试题)已知直三棱柱111ABC A B C -中,侧面11AA B B 为正方形,2AB BC ==,E ,F 分别为AC 和1CC 的中点,11BF A B ⊥.(1)求三棱锥F EBC -的体积;(2)已知D 为棱11A B 上的点,证明:BF DE ⊥.10.(2021年全国新高考Ⅰ卷数学试题)如图,在三棱锥A BCD -中,平面ABD ⊥平面BCD ,AB AD =,O 为BD 的中点.(1)证明:OA CD ⊥;(2)若OCD 是边长为1的等边三角形,点E 在棱AD 上,2DE EA =,且二面角E BC D --的大小为45︒,求三棱锥A BCD -的体积.【2012年——2020年】1.(2020年全国统一高考数学试卷(文科)(新课标Ⅰ))埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )A .514-B .512-C .514+ D .512+ 2.(2020年全国统一高考数学试卷(文科)(新课标Ⅰ))已知,,A B C 为球O 的球面上的三个点,Ⅰ1O 为ABC 的外接圆,若Ⅰ1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为( )A .64πB .48πC .36πD .32π3.(2020年全国统一高考数学试卷(文科)(新课标Ⅰ))已知ⅠABC 是面积为934的等边三角形,且其顶点都在球O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为( )A .3B .32C .1D .324.(2019年全国统一高考数学试卷(理科)(新课标Ⅰ))已知三棱锥P -ABC 的四个顶点在球O 的球面上,P A =PB =PC ,ⅠABC 是边长为2的正三角形,E ,F 分别是P A ,AB 的中点,ⅠCEF =90°,则球O 的体积为 A .86π B .46π C .26π D .6π5.(2019年全国统一高考数学试卷(理科)(新课标Ⅰ))设α,β为两个平面,则αⅠβ的充要条件是 A .α内有无数条直线与β平行B .α内有两条相交直线与β平行C .α,β平行于同一条直线D .α,β垂直于同一平面6.(2019年全国统一高考数学试卷(文科)(新课标Ⅰ))如图,点N 为正方形ABCD 的中心,ECD ∆为正三角形,平面ECD ⊥平面,ABCD M 是线段ED 的中点,则A .BM EN =,且直线,BM EN 是相交直线B .BM EN ≠,且直线,BM EN 是相交直线C .BM EN =,且直线,BM EN 是异面直线D .BM EN ≠,且直线,BM EN 是异面直线7.(2018年全国普通高等学校招生统一考试文科数学(新课标I 卷))已知圆柱的上、下底面的中心分别为1O ,2O ,过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为A .122πB .12πC .82πD .10π8.(2018年全国普通高等学校招生统一考试文科数学(新课标I 卷))在长方体1111ABCD A B C D -中,2AB BC ==,1AC 与平面11BB C C 所成的角为30,则该长方体的体积为A .8B .62C .82D .839.(2018年全国普通高等学校招生统一考试理数(全国卷II ))在长方体1111ABCD A B C D -中,1AB BC ==,13AA =1AD 与1DB 所成角的余弦值为A .15B .56C 5D .2210.(2018年全国卷Ⅰ理数高考试题)设A B C D ,,,是同一个半径为4的球的球面上四点,ABC 为等边三角形且其面积为3D ABC -体积的最大值为A .123B .183C .243D .311.(2017年全国普通高等学校招生统一考试)如图,在下列四个正方体中,A 、B 为正方体的两个顶点,M 、N 、Q 为所在棱的中点,则在这四个正方体中,直线AB 与平面 MNQ 不平行的是( ) A . B . C . D . 12.(2017年全国普通高等学校招生统一考试文科数学(新课标3卷))已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为A .πB .3π4C .π2D .π413.(2016年全国普通高等学校招生统一考试文科数学(新课标1))平面α过正方体ABCD—A 1B 1C 1D 1的顶点A ,,ABCD m α⋂=平面,11ABB A n α⋂=平面,则m ,n 所成角的正弦值为 A .32 B .22 C .33 D .1314.(2016年全国普通高等学校招生统一考试文科数学(全国2卷))体积为8的正方体的顶点都在同一球面上,则该球面的表面积为A .12πB .323πC .8πD .4π15.(2016年全国普通高等学校招生统一考试)在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球,若AB BC ⊥,6AB =,8BC =,13AA =,则该球体积V 的最大值是A .4πB .92πC .6πD .323π 16.(2015年全国普通高等学校招生统一考试理科数学(新课标Ⅰ带解析))(2015新课标全国I 理科)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有A .14斛B .22斛C .36斛D .66斛17.(2013年全国普通高等学校招生统一考试理科数学(新课标1卷))如图,有一个水平放置的透明无盖的正方体容器,容器高8cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm ,如果不计容器的厚度,则球的体积为A .5003πcm 3B .8663πcm 3C .13723πcm 3D .10003πcm 3 18.(2013年全国普通高等学校招生统一考试))已知三棱锥S ABC -的所有顶点都在球O 的球面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此棱锥的体积为A .26 B 3 C .23 D .22二、填空题19.(2020年全国统一高考数学试卷(理科)(新课标Ⅰ))如图,在三棱锥P –ABC 的平面展开图中,AC =1,3AB AD ==,AB ⅠAC ,AB ⅠAD ,ⅠCAE =30°,则cosⅠFCB =______________.20.(2020年全国统一高考数学试卷(文科)(新课标Ⅰ))设有下列四个命题:p 1:两两相交且不过同一点的三条直线必在同一平面内.p 2:过空间中任意三点有且仅有一个平面.p 3:若空间两条直线不相交,则这两条直线平行.p 4:若直线l ⊂平面α,直线m Ⅰ平面α,则m Ⅰl .则下述命题中所有真命题的序号是__________.Ⅰ14p p ∧Ⅰ12p p ∧Ⅰ23p p ⌝∨Ⅰ34p p ⌝∨⌝21.(2019年全国统一高考数学试卷(文科)(新课标Ⅰ))已知ⅠACB=90°,P 为平面ABC 外一点,PC =2,点P 到ⅠACB 两边AC ,BC 的距离均为3,那么P 到平面ABC 的距离为___________.22.(2019年全国统一高考数学试卷(文科)(新课标Ⅰ))学生到工厂劳动实践,利用3D 打印技术制作模型.如图,该模型为长方体1111ABCD A B C D -挖去四棱锥O EFGH -后所得的几何体,其中O 为长方体的中心,,,,E F G H 分别为所在棱的中点,16cm 4cm AB =BC =, AA =,3D 打印所用原料密度为30.9/g cm ,不考虑打印损耗,制作该模型所需原料的质量为___________g .23.(2018年全国普通高等学校招生统一考试文数(全国卷II))已知圆锥的顶点为S,母线SA,SB互相垂直,SA与圆锥底面所成角为30,若SAB的面积为8,则该圆锥的体积为__________.24.(2018年全国普通高等学校招生统一考试)已知三棱锥S ABC-的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA AC=,SB BC=,三棱锥S ABC-的体积为9,则球O的表面积为______.25.(2017年全国普通高等学校招生统一考试理科数学(新课标1卷))如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O.D,E,F为圆O上的点,ⅠDBC,ⅠECA,ⅠF AB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起ⅠDBC,ⅠECA,ⅠF AB,使得D,E,F重合,得到三棱锥.当ⅠABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为______.26.(2017年全国普通高等学校招生统一考试)长方体的长,宽,高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为__________.27.(2016年全国普通高等学校招生统一考试)a,b为空间中两条互相垂直的直线,等腰直角三角形ABC 的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:Ⅰ当直线AB与a成60°角时,AB与b成30°角;Ⅰ当直线AB与a成60°角时,AB与b成60°角;Ⅰ直线AB与a所成角的最小值为45°;Ⅰ直线AB与a所成角的最大值为60°.其中正确的是________.(填写所有正确结论的编号)28.(2013年全国普通高等学校招生统一考试文科数学(新课标1卷带解析))已知H是球O的直径AB上一点, :1:2AH HB=,AB⊥平面α,H为垂足, α截球O所得截面的面积为π,则球O的表面积为_______.三、双空题29.(2019年全国统一高考数学试卷(理科)(新课标Ⅰ))中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.四、解答题30.(2020年全国统一高考数学试卷(文科)(新课标Ⅰ))如图,D为圆锥的顶点,O是圆锥底面的圆心,ABC是底面的内接正三角形,P为DO上一点,ⅠAPC=90°.(1)证明:平面P ABⅠ平面P AC;(2)设DO23π,求三棱锥P−ABC的体积.32.(2020年全国统一高考数学试卷(文科)(新课标Ⅰ))如图,已知三棱柱ABC –A 1B 1C 1的底面是正三角形,侧面BB 1C 1C 是矩形,M ,N 分别为BC ,B 1C 1的中点,P 为AM 上一点.过B 1C 1和P 的平面交AB 于E ,交AC 于F .(1)证明:AA 1//MN ,且平面A 1AMN Ⅰ平面EB 1C 1F ;(2)设O 为ⅠA 1B 1C 1的中心,若AO =AB =6,AO //平面EB 1C 1F ,且ⅠMPN =π3,求四棱锥B –EB 1C 1F 的体积.34.(2020年全国统一高考数学试卷(文科)(新课标Ⅰ))如图,在长方体1111ABCD A B C D -中,点E ,F 分别在棱1DD ,1BB 上,且12DE ED =,12BF FB =.证明:(1)当AB BC =时,EF AC ⊥;(2)点1C 在平面AEF 内.36.(2019年全国统一高考数学试卷(文科)(新课标Ⅰ))如图,直四棱柱ABCD–A 1B 1C 1D 1的底面是菱形,AA 1=4,AB =2,ⅠBAD =60°,E ,M ,N 分别是BC ,BB 1,A 1D 的中点.(1)证明:MN Ⅰ平面C 1DE ;(2)求点C 到平面C 1DE 的距离.38.(2019年全国统一高考数学试卷(文科)(新课标Ⅰ))如图,长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⅠEC 1.(1)证明:BE Ⅰ平面EB 1C 1;(2)若AE =A 1E ,AB =3,求四棱锥11E BB C C -的体积.40.(2019年全国统一高考数学试卷(文科)(新课标Ⅰ))图1是由矩形,ADEB Rt ABC ∆和菱形BFGC组成的一个平面图形,其中1,2AB BE BF ===, 60FBC ∠=,将其沿,AB BC 折起使得BE 与BF 重合,连结DG ,如图2.(1)证明图2中的,,,A C G D 四点共面,且平面ABC ⊥平面BCGE ;(2)求图2中的四边形ACGD 的面积.42.(2018年全国普通高等学校招生统一考试文科数学(新课标I 卷))如图,在平行四边形ABCM 中,3AB AC ==,90ACM ∠=︒,以AC 为折痕将ⅠACM 折起,使点M 到达点D 的位置,且AB DA ⊥. (1)证明:平面ACD ⊥平面ABC ;(2)Q 为线段AD 上一点,P 为线段BC 上一点,且23BP DQ DA ==,求三棱锥Q ABP -的体积.44.(2018年全国普通高等学校招生统一考试文数(全国卷II ))如图,在三棱锥P ABC -中,22AB BC ==4PA PB PC AC ====,O 为AC 的中点.(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且2MC MB =,求点C 到平面POM 的距离.46.(2018年全国卷Ⅰ文数高考试题)如图,矩形ABCD 所在平面与半圆弧CD 所在平面垂直,M 是CD 上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC ;(2)在线段AM 上是否存在点P ,使得MC ∥平面PBD ?说明理由.49.(2017年全国普通高等学校招生统一考试文科数学(新课标2卷))四棱锥P ABCD -中,侧面PAD 为等边三角形且垂直于底面ABCD ,01,90.2AB BC AD BAD ABC ==∠=∠= (1)证明:直线//BC 平面PAD ; (2)若ⅠPCD 面积为7,求四棱锥P ABCD -的体积.51.(2017年全国普通高等学校招生统一考试文科数学(新课标3))如图,四面体ABCD 中,ⅠABC 是正三角形,AD =CD .(1)证明:AC ⅠBD ;(2)已知ⅠACD 是直角三角形,AB =BD .若E 为棱BD 上与D 不重合的点,且AE ⅠEC ,求四面体ABCE与四面体ACDE 的体积比.53.(2016年全国普通高等学校招生统一考试)如图,已知正三棱锥P -ABC 的侧面是直角三角形,PA=6,顶点P 在平面ABC 内的正投影为点D ,D 在平面PAB 内的正投影为点E ,连结PE 并延长交AB 于点G.(Ⅰ)证明:G 是AB 的中点;(Ⅰ)在图中作出点E 在平面PAC 内的正投影F (说明作法及理由),并求四面体PDEF 的体积.55.(2016年全国普通高等学校招生统一考试文科数学(新课标2卷))如图,菱形ABCD 的对角线AC 与BD 交于点O ,点,E F 分别在,AD CD 上,,AE CF EF =交BD 于点H ,将DEF ∆沿EF 折起到D EF ∆'的位置.(Ⅰ)证明:AC HD ⊥';(Ⅰ)若55,6,,224AB AC AE OD ==='=D ABCFE '-的体积.57.(2016年全国普通高等学校招生统一考试数学)如图,四棱锥P ABC -中,PA ⊥平面ABCD ,AD BC ∥,3AB AD AC ===,4PABC ,M 为线段AD 上一点,2AM MD =,N 为PC 的中点.(I )证明MN ∥平面PAB ;(II )求四面体N BCM -的体积.59.(2015年全国普通高等学校招生统一考试文科数学(新课标Ⅰ)如图四边形ABCD 为菱形,G 为AC 与BD 交点,BE ABCD ⊥平面,(I )证明:平面AEC ⊥平面BED ; (II )若120ABC ∠=,,AE EC ⊥ 三棱锥E ACD -6,求该三棱锥的侧面积.61.(2015年全国普通高等学校招生统一考试文科数学(新课标Ⅰ))如图,长方体1111ABCD A B C D -中,116,10,8AB BC AA ===,点,E F 分别在1111,A B D C 上,114A E D F ==,过点,E F 的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法与理由);(2)求平面α把该长方体分成的两部分体积的比值.63.(2014年全国普通高等学校招生统一考试文科数学(新课标Ⅰ))如图,三棱柱中,侧面为菱形,的中点为,且平面.(1)证明:(2)若,求三棱柱的高.65.(2013年全国普通高等学校招生统一考试文科数学(新课标1卷))如图,三棱柱111ABC A B C -中,CA CB =,1AB AA =,160BAA ∠=.(1)证明:; (2)若,,求三棱柱111ABC A B C -的体积.68.(2012年全国普通高等学校招生统一考试文科数学(课标卷))如图,三棱柱111ABC A B C -中,侧棱垂直底面,ⅠACB=90°,AC=BC=12AA 1,D 是棱AA 1的中点.(I) 证明:平面BDC Ⅰ平面1BDC(Ⅰ)平面1BDC 分此棱柱为两部分,求这两部分体积的比.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何测试卷
班级 姓名 学号
一、选择题:
1.一个圆锥的侧面积是其底面积的2倍,则该圆锥的母线与底面所成的角为( ) (A )30 (B )45 (C )60 (D )75 2.两个完全相同的长方体的长、宽、高分别为5 cm 、4cm 、3cm ,把它们重叠在一起组成一个新长方体,在这些新长方体中,最长的对角线的长度是 ( ) (A )cm 77 (B )cm 27 (C )cm 55 (D )cm 210 3.等边三角形ABC 的边长为4,M 、N 分别为AB 、AC 的中点,沿MN 将AMN ∆折起,使得面AMN 与面MNCB 所成的二面角为30 ,则四棱锥A —MNCB 的体积为( ) (A )
2
3
(B )23 (C )3 (D )3
4.若二面角βα--l 为120 ,直线m α⊥,则β所在平面内的直线与m 所成角的取值范围是 ( )
(A )(]
90,0 (B )[
]
60
,30 (C )[]
90,60 (D )[]
90,30
5.关于直线a 、b 、l 及平面M 、N ,下列命题中正确的是 ( ) (A )若a // M,b // M,则a // b (B )若a // M,b ⊥a,则b ⊥ M (C )若a ,,M b M ⊂⊂且l b l a ⊥⊥,则M l ⊥ (D )若,//,N a M a ⊥则N M ⊥ 6.棱长为a 的正方体中,连接相邻的中心,以这些线段为棱的八面体的体积为( )
(A )33a (B )43a (C )63a (D )12
3
a
7.一个四面体的所有棱长都为2,四个顶点在同一球面上,则此球的表面积为( ) (A )3π (B )4π (C )π33 (D )6π 8. 已知圆锥的底面半径为R ,高为3R ,它的所有内接圆柱中,全面积的最大值是( ) (A )22
R π (B )
249R π (C )238R π (D )22
5
R π 9.在下列条件中,可判断平面α与β平行的是 ( ) (A )βα、都垂直于平面γ (B )α内存在不共线的三点到β的距离相等
(C )l 、m 是内两条直线,且l //β
β//,m
D )l 、m 是两条异面直线,且ββαα//,//,//,//m l m l
10.在正三棱柱ABC —A 1B 1C 1中,若AB=2BB 1,则AB 1与C 1B 所成的角的大小为 (A )60 (B )90 (C )105 (D )75 二、填空题:
11.将长度为1的铁丝分成两段,分别围成一个正方形和一个圆形。
要使它们的面积之和最小,正方形的周长应为:________________________
12.已知某球体的体积与其表面积的数值相等,则此球体的半径为:_________________ 13.在正四棱锥P —ABCD 中,若侧面与底面所成二面角的大小为60 ,则异面直线PA 与BC 所成角的正弦值为:_____________________ 14.把半径为3cm ,中心角为π3
2
的扇形卷成一个圆锥形容器这个容器的容积为: _________________ 三、解答题:
15.已知三棱柱ABC —A 1B 1C 1,如图所示中底面边长和侧棱长均为a ,侧面A 1ACC 1⊥底面ABC ,A 1B=
a 26。
(1) 求异面直线AC 与BC 1所成角的余弦值; (2) 求证:A 1B ⊥面AB 1C
16.如图,点P 为斜三棱柱ABC —A 1B 1C 1的侧棱BB 1上一点,PM ⊥BB 1交AA 1于点M ;PN ⊥BB 1交CC 1于点N 。
求证:CC ⊥1MN (2)在任意三角形DEF 中有余弦定理DE DFE EF DF EF DF cos 22
2
2
⋅-+=。
拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角的关系式,并予以证明。
A
B
C
A
B
C 1
17.如图ABCD —1111D C B A 是正四棱柱,侧棱长为1,底面边长为2,E 是棱BC 的中点。
(1) 求三棱锥D 1—DBC 的体积; (2) 证明BD 1 // 平面C 1DE
(3) 求面C 1DE 与面CDE 所成二面角的正切值。
18.如图,正三棱柱ABC--111C B A 中,D 是BC 的中点,AB=a.
(1) 求证:111C B D A
(2) 求点D 到平面ACC 1的距离;
(3) 判断A 1B 与平面ADC 1的位置关系,并证明你的结
论
A
B
C D
E
A
B 1
D 1
C
A
B
C
C 1
B 1
A 1
O
19.如图四棱锥P---ABCD 的底面是边长为a 的正方形,PB ⊥面ABCD 。
(1) 若面PAD 与面ABCD 所成的二面角为
60 ,求这个四棱锥的体积;
(2) 证明:无论四棱锥的高怎样变化,面PAD
与面PCD 所成的二面角恒大于90
20.在棱长为a 的正方体OABC--1111C B A O 中,E 、F 分别是棱AB 、BC 上的动点,且AE=BF 。
(1) 求证:E C F A 11⊥;
(2) 当三棱锥B 1—BEF 的体积取得最大值时,求二面角B 1-EF-B 的大小。
P
C
D
A
B
(注:文档可能无法思考全面,请浏览后下载,供参考。
可复制、编制,期待你的好评与关注)。
