第二章不可计算性
第二章--计算流体力学的基本知识
第二章计算流体力学的基本知识流体流动现象大量存在于自然界及多种工程领域中，所有这些工程都受质量守恒、动量守恒和能量守恒等基本物理定律的支配。
这章将首先介绍流体动力学的发展和流体力学中几个重要守恒定律及其数学表达式，最后介绍几种常用的商业软件。
2.1计算流体力学简介2.1.1计算流体力学的发展流体力学的基本方程组非常复杂，在考虑粘性作用时更是如此，如果不靠计算机，就只能对比较简单的情形或简化后的欧拉方程或N-S方程进行计算。
20世纪30～40年代，对于复杂而又特别重要的流体力学问题，曾组织过人力用几个月甚至几年的时间做数值计算，比如圆锥做超声速飞行时周围的无粘流场就从1943年一直算到1947年。
数学的发展，计算机的不断进步，以及流体力学各种计算方法的发明，使许多原来无法用理论分析求解的复杂流体力学问题有了求得数值解的可能性，这又促进了流体力学计算方法的发展，并形成了"计算流体力学"。
从20世纪60年代起，在飞行器和其他涉及流体运动的课题中，经常采用电子计算机做数值模拟，这可以和物理实验相辅相成。
数值模拟和实验模拟相互配合，使科学技术的研究和工程设计的速度加快，并节省开支。
数值计算方法最近发展很快，其重要性与日俱增。
自然界存在着大量复杂的流动现象，随着人类认识的深入，人们开始利用流动规律来改造自然界。
最典型的例子是人类利用空气对运动中的机翼产生升力的机理发明了飞机。
航空技术的发展强烈推动了流体力学的迅速发展。
流体运动的规律由一组控制方程描述。
计算机没有发明前，流体力学家们在对方程经过大量简化后能够得到一些线形问题解读解。
但实际的流动问题大都是复杂的强非线形问题，无法求得精确的解读解。
计算机的出现以及计算技术的迅速发展使人们直接求解控制方程组的梦想逐步得到实现，从而催生了计算流体力学这门交叉学科。
计算流体力学是一门用数值计算方法直接求解流动主控方程(Euler或Navier-Stokes方程)以发现各种流动现象规律的学科。
第二章大学物理实验基础知识
有效位数取决于仪器和被测量量本身的大小，仪器精度决定 存疑数字的位置（一般为仪器最小刻度的下一位），被测量量 的大小决定可靠数字的个数。
0 mm 10 20 30 40
L=14.6(mm)
第二章 大学物理实验基础知识
使用不同精度的测量仪器，得到的测量数据，其有效数字的 有效位数则不同，有效位数越多，说明测量结果越精确。
第二章 大学物理实验基础知识
过失误差 由于测量者在测量过程中粗心大意所发生的错误 或失误而造成的一种误差，只要认真、细心操作， 完全可以避免这种误差。
第二章 大学物理实验基础知识
§2.3测量结果的有效数字
对某一物理量测量时，由仪器中读取的准确数字称为可靠数 字，估读的欠准确数字称为存疑数字，可靠数字和存疑数字统 称为测量结果的有效数字，有效数字的个数叫有效位数。 有效数字一般都是由几位可靠数字和1—2位存疑数字构成。
用模拟法测绘静电场 气垫导轨上的实验 三棱镜折射率的测量 透镜焦距的测量
有效数字的读取和计算 光栅衍射实验
密立根油滴实验 测量及其结果表达式
实验基础理论知识 电学元件伏安特性的研究、
电位差计的使用 灵敏电流计的研究、
数据处理方法
自组装直流单臂电桥 基本实验方法 自组望远镜
基础性实验
综合性实验
实验项目 设计性实验
掌握测量误差的基本知识， 具有正确处理实验数据的 处理实验数据的常 用方法 基本能力
基本
要求
掌握基本物理量的测量方法。 了解和学会常用的物理实验方法。 掌握实验室常用仪器的性能。 掌握常用的实验操作技术 。
第二章 大学物理实验基础知识
§2.1 测量
测量
将待测量量与同类计量标准单位相比较的过程。 测量结果 由测量所得到的赋予被测量的值，具有单位和量纲 测量可分为直接测量和间接测量。 测量也可分为单次测量和多次测量。
第二章保险法四大基本原则
最大诚信原则理论依据 之经
济学分析
• 保险所涉及信息的性质与一般民商活动所 涉及信息的性质不同。
• 信息可分为“生产性事实”、“再分配性 事实”和“危害性事实”三类信息
最大诚信原则理论依据
分析
之经济学
• “生产性事实”是可以增加财富的信息
对生产性信息本身或获取途径必 然要在技能和知识方面进行经济投资，通 过该信息交易而带来的财富就是对该投资 的补偿。
➢瑕痴担保义务+法律有权要求人们所说的不 会对他人产生误导
诚信原则与最大诚信原则
• 一般民商活动：要求不向对方作出错误的 意思表示——诚信原则
• 特殊商事活动：要求当事人必须主动地、 充分地披露重要事实——最大诚信原则
最大诚信原则理论依据 之经
济学分析
• 保险的特殊性——射幸行为
• 不确定性向确定性的转化面临有关风险资 料的信息不对称问题，从而影响到保险公 司准确预测危险和损失。
故，对作为“危害性事实”的信 息，当事人应负揭示或披露义务。
从社会观点来看，这种保护性费用是一种 浪费，无效率，不应激励。
故，对作为“再分配性事实”的信息，当 事人应负揭示或披露义务。
最大诚信原则理论依据
分析
之经济学
• “危害性事实”指如果不揭示和披露就将引 起对某人的财产或人身伤害的信息。
此类信息如果不披露，将造成对 另一方当事人的财产损害或人身的伤害， 是对财富的无效率破坏。
事权利和履行民事义务，不欺诈、恪守信 用，善意地进行民事活动。
• 诚信原则不仅涉及当事人之间利益关系还 涉及当事人与社会间的利益关系
• ——帝王条款
诚信原则与最大诚信原则 ——诚信原则的要求
中科大算法第二章近似算法--黄刘生(调整后适合打印版)
NP-完全性理论
Karp的贡献
理查德·卡普（Richard Karp ， 1935- ） 1972 年论文 ”Reducibility among Combinatorial Problems” 发 展和加强了由库克提出的“NP完全性”理论。 尤其是库 克仅证明了命题演算的可满足问题是NP完全的，而卡普则证明了从 组合优化中引出的大多数经典问题(背包问题、覆盖问题、匹配问 题、分区问题、路径问题、调度问题等)都是NP完全问题。只要证 明其中任一个问题是属于P类的，就可解决计算复杂性理论中最大 的一个难题，即P=?NP。
SAT∈P当且仅当P=NP
Cook 于1961 年获 Michigan 大学学士学位， 1962 和 1966年分获哈佛 大学硕士与博士学位。 1966-1970 ，他在 UC Berkeley 担任助教授； 1970年加盟多伦多大学，现为该校CS 和数学系教授，他的论文开启 了NP完备性的研究，令该领域于之后的十年成为计算机科学中最活 跃和重要的研究。因其在计算复杂性理论方面的贡献，尤其是在奠 定NP完全性理论基础上的突出贡献而荣获1982年度的图灵奖。
9
P、NP及NPC类问题
NP=？P
∵确定型图灵机是非确定型图灵机的特例，∴P⊆NP 是否有NP⊆P？即是否NP=P？
美国麻省的Clay数学研究所于2000年5月24日在巴黎法兰西学院宣 布：对七个“千年数学难题”中的每一个均悬赏 100 万美元，而 问题NP=？P位列其首:
1.P问题对NP问题 2.霍奇猜想 3. 庞加莱猜想 (2002.11-2003.7 ，俄罗斯数学家佩雷尔曼在 3 篇 论文预印本中证明了几何化猜想，2006被授予菲尔兹奖) 4.黎曼假设 5.杨－米尔斯存在性和质量缺口 6.纳维叶－斯托克斯方程的存在性与光滑性 7.贝赫和斯维讷通－戴尔猜想
第二章财务管理之时间价值和风险价值
递延年金现值的计算
例15 某企业向银行借入一笔款项，银行贷款
的年利息率为8%，银行规定前10年不用还本 付息，但从第11年至第20年每年年末偿还本息 1000元，问这笔款项的现值应为多少？
思路一
P=A*[（P/A，i，n+m）- （P/A，i，m）]
A ＝ 150× （ A/F ， 8% ， 3 ） =150/3.2462=46.21万元
（三）普通年金现值的计算
P A(1 i)1 A(1 i)2 A(1 i)(n1) A(1 i)n 1 (1 i)n
P A i
P A(P / A,i, n)
举例：普通年金现值计算
例9：某企业未来5年每年年末等额从银 行取1万元，为职工发奖金，年利率3%， 现在应该存入多少金额以保证未来5年每 年末从银行等额提出1万元？
=1000*1.08*14.487
=15 645
例13 某企业租用一设备，在10年中每年年 初要支付租金5 000元，年利息率为8%， 问这些租金的现值是多少？
思路一
P=A*[（F/A，i，n-1）+1] =1000* [（F/A，8%,9）+1 ] =1000*（6.247+1） =36 235元
风险是“一定时期内”的风险。
与风险相联系的另一个概念是不确定性。严格说 来，风险和不确定性有区别。
风险可能给投资人带来超出预期的收益，也可能 带来超出预期的损失。
财务管理中的风险按形成的原因一般可分为经营 风险和财务风险两大类。
二、风险程度的衡量——概率分析法
确定概率分布 计算期望值 计算标准离差
25
第二章建筑围护结构的传热原理及计算分析
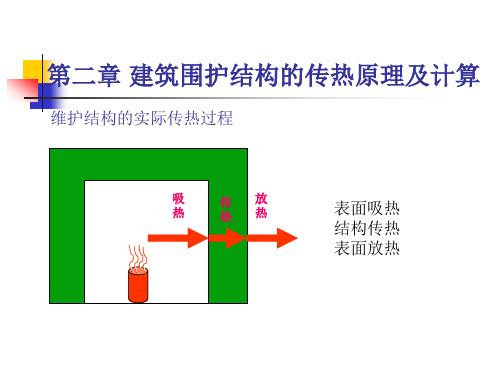
d2
i q(
1
d1
2
d2
)
………… 多层壁内第j层与第j+1层之间接触面温度：
j 1 i q(
1
d1
2
d2
dj
j
)
第二章 建筑围护结构的传热原理及计算
1.2 对流换热
层流边界层：由于摩擦力作用，在紧贴固体壁面处有一平行于固体壁 面流动的流体薄层称为层流边界层。
第二章 建筑围护结构的传热原理及计算
q1
1
d1
( i 2 )
q2
2
d2
( 2 3 )
q3
3
d3
( 3 e )
对于多层复合壁体而言，由于每一层都是由单一材料组成的，在壁体两 侧稳定温度场的作用下，流经各层材料的热流强度都是相等的： q=q1=q2=q3 由上面四式可得：
第二章 建筑围护结构的传热原理及计 算
q
d
(i e )
i e
d
i e
R
我们将上式中的R=d/λ 称为热阻，单位m2*K/W。热阻是热流通过壁体 时受到的阻力，反映了壁体抵抗热流通过的能力。 说明： 1）在同样的温差条件下，热阻越大，通过壁体的热量就越少，如 果要增加热阻，可以加大平壁的厚度d，或者选用导热系数小的材料 2）导热系数λ 它反映了壁体材料的导热能力，当材料层单位厚度 内的温差为1摄氏度时，在单位时间内通过1m2表面积的热量 3）影响材料导热系数的因素：
第二章 建筑围护结构的传热原理及计算
1.3.4 辐射换热计算
以上仅是对单一物体热辐射能力的讨论，由于通常情况下自然
信息技术导论知识点
第一章计算科学简介1．简述计算科学的概念⑴是描述和变换信息的算法过程。
⑵包括其理论分析、设计，效率分析、实现和应用系统的研究。
⑶计算科学的基本问题就是：什么能（有效地）自动进行，什么不能（有效地）自动进行。
2．计算科学涵盖了：计算机科学、计算机技术、计算机工程。
3．计算机科学研究的课题是：计算机程序能做什么和不能做什么（可计算性）；如何使程序更高效的执行特定任务（算法和复杂性理论）；程序如何存取不同类型的数据（数据结构和数据库）；程序如何显得更具有智能（人工智能）；人类如何与程序沟通（人机互动和人机界面）。
4．计算机技术的内容非常广泛，可粗分为：计算机系统技术；计算机器件技术；计算机部件技术；计算机组装技术等。
5．计算科学的主要内容主要分为14个领域：离散结构程序设计基础算法与复杂性体系结构操作系统网络计算程序设计语言人－机交互图形学和可视化计算智能系统信息管理软件工程社会和职业问题科学计算离散结构•主要内容：集合论、数理逻辑、近似代数、图论和组合数学等。
程序设计基础•内容包括：程序设计结构、算法、问题求解和数据结构等。
•基本问题主要包括：对给定的问题进行程序设计、编码、测试和调试。
算法与复杂性•主要包括：算法的复杂度分析、典型的算法策略、分布式算法、并行算法、可计算理论、P类和NP类问题、自动机理论、密码算法、以及几何算法等。
•基本的问题：对于给定的问题类，最好的算法是什么？算法的复杂度如何？算法的性能如何？操作系统•主要内容：操作系统的逻辑结构、并发处理、资源分配与调度、存储管理、设备管理、文件系统等。
•基本问题：在计算机系统操作的每一个级别上，可见的对象和允许进行的操作是什么？等等。
程序设计语言•主要内容：程序设计模式、虚拟机、类型系统、执行控制模型、语言翻译系统、程序设计语言的语义学、基于语言的并行构件等。
•基本问题：语言表示的虚拟机的可能组织结构是什么？语言如何定义机器？机器如何定义语言？什么样的表示法可以有效地用于描述计算机应该做什么？软件工程•主要内容：软件过程、软件需求与规格说明、软件设计、软件验证、软件演化、软件项目管理、软件开发工具与环境、基于构件的计算、形式化方法、软件可靠性、专用系统开发等。
第二章 资产评估的基本方法
计算方法： 1、用资产生产能力来计算经济性贬值
经 济 性 贬 值 [ 1 （ 现实生产能力 X ） ] 被 估 资 产 重 置 成 本 原设计生产能力
X称为生产能力指数，X一般取值0.4～0.9 例2-9：评估资产为某专用生产线，重置成本为20万元，设计日生产能力2000 只。因市场出现可替代产品，现时及今后趋势每日只能生产1200只。如取X=0.6， 则： 1200 0.6 经济性贬值 [1 （ ） ] 200000 52760 （元） 2000 2、利用年收益损失额现值来计算经济性贬值： 经济性贬值=年收益损失额×（1－所得税率）×年金现值系数
截 至 评 估 日 时 资 产 累实 际 利 用 时 间 计 资产利用率 100% 截 至 评 估 日 时 资 产 累法 定 利 用 时 间 计
资产利用率<1，表示开工不足，资产实际已使用年限小 于名义使用年限； 资产利用率=1，表示资产满负荷运转，资产实际已使用 年限等于名义使用年限； 资产利用率>1，表示资产超负荷运转，资产实际已使用 年限比名义已使用年限长。
2、用超额投资成本（视为功能性贬值）估算： 功能性贬值 =复原重置成本－更新重置成本
（四）经济性贬值及其估算 ———指由外部环境变化引起的资产由于利用率降低或 收益额减少而引起的贬值。 哪些情况下不需要计算经济性贬值： （1）资产使用基本正常时；（不存在外在因素造成资产 利用率下降或收益减少） （2）对不能直接计算收益的单台、单件资产进行评估。
三、市场法的优缺点 1、优点： ①能客观反映资产目前的市场情况，其评估的参数、 指标直接从市场获得。 ②评估值更能反映市场现实价格，评估结果易于被各 方理解和接受。 2、缺点： ①需要有公开活跃的市场作为基础。 ②不适合用于评估专用机器设备、大部分的无形资产以 及受到地区、环境等严格限制的一些资产。 四、市场法适用的资产业务： 单项资产的买卖。如买卖设备、原材料、房屋等，用 单项生产要素作为投资参股、合作经营等。 在课征财产税和遗产税时，有时也以现行市价为基础。
大学化学：第二章 化学反应的基本原理
§2-1 §2-2 §2-3 §2-4
熵与熵变 吉布斯函数变 反应限度与化学平衡 化学反应速率
§2-1 熵与熵变
一、过程的可逆与不可逆性一、过程的可逆与不可逆性 从自然界中观察到的过二程、(变熵化与)都熵是增不加可原逆理的。 ➢热由高温物体传给低温三物、体熵，值直及至熵温变差的为计零算； ➢气体从高压扩散到低压，直至压差为零； ➢正电荷从高电位迁移到低电位，直至电位差为零； ➢不同种组分的相互混合、扩散(推动力?)；
▪ 对于化学反应，反应物质是可逆的，且变化在无 限接平衡状态下进行时，为热力学可逆过程。
▪ 可逆过程的逆过程发生后，体系及环境都得以复 原，不留下任何变化的痕迹(包括物质的和能量的)。
二、熵与熵增加原理
1、熵与熵变 对于简单、熟悉的过程，可用诸如ΔT、 Δ p、 ΔE
等作为自发过程方向与限度的判据(推动力)； 对于复杂的物理化学过程，用什么函数来判断? 已知很多放热反应是自发的，那么放热则自发？
放热并非一定自发
二、熵与熵增加原理
1、熵与熵变
S qr 定温可逆过程: S qr
T
T
对定温的任意过程: S q 不可逆 (2-1-1)
T 可逆
封闭系统的定温过程中，系统的熵变不可能小于
过程的热温商。
即封闭系统的定温可逆过程中，熵变等值于过程 热温商，不可逆中，系统的熵变大于过的热温商；
S是一个状态函数（广度性质），但宏观抽象。
生的熵变。食物（蛋白质、淀粉等）的熵小于排泄 物的熵。
“新陈代谢的最基本内容是：有机体成功地使自 身放出他活着时不得不产生的全部熵。”
3
三、熵值及熵变的计算
1、物质的规定熵与标准摩尔熵 ➢由热三律指出：规定，纯物质完美晶体，S0K＝0 ➢物质的标准摩尔熵：Sθm(B,T)为单位物质的量的纯 物质标准条件下的规定熵。单位“J·K-1·mol-1”。
材料力学性能——第二章
一、缺口效应
（一）缺口试样在弹性状态下的应力分布（厚板）
理论应力集中系数
Kt max
与薄板相比， 厚板在垂直于板厚方向的收缩变形受到 约束，即：
z 0
z
1 E
[ z
(
x
y )]
z ( x y )
y＞ z＞ x
材料力学性能
一、缺口效应
（二）缺口试样在塑性状态下的应力分布（厚板）
一、应力状态软性系数α
(1)较硬的应力状态试验，主要用于塑性金属材料力学性能的测定。 (2)较软的应力状态试验，主要用于脆性金属材料力学性能的测定。
材料力学性能
第二节 压缩
一、压缩试验的特点
(1) 单向压缩试验的应力状态软性系数α=2，所以 主要用于拉伸时呈脆性的金属材料力学性能的测定。
(2) 拉伸时塑性很好的材料，在压缩时只发生压缩 变形而不断裂。
原因：
切应力：引起金属材料产生塑性变形以及韧性断裂。 正应力：引起金属材料产生脆性断裂。
反之亦然
1
材料力学性能
第一节 应力状态软性系数
材料在受到载荷作用时(单向拉伸)， max s
max k
产生屈服 产生断裂
在复杂的应力状态下（用三个主应力表示成σ1、σ2、 σ3 ）
最大切应力理论： max
一、缺口效应 定义
在静载荷作用下，由于缺口的存在，而使其尖端出现应力、应变集中； 并改变了缺口前方的应力状态，由原来的单向应力状态变为两向或三向 应力状态； 并使塑性材料的强度增加，塑性降低。
材料力学性能
一、缺口效应
（一）缺口试样在弹性状态下的应力分布（薄板）
在拉应力σ的作用下，缺口的存在使 横截面上的应力分布不均匀： 轴向应力σy分布：σy在缺口根部最大， 随着距离x↑ ，σy ↓ ，所以在缺口根部 产生了应力集中的现象。 横向应力σx分布：缺口根部可自由变形， σx=0，远离x轴，变形阻力增大， σx↑， 达到一定距离后，由于σy↓导致σx ↓。
第二章：热力学第二定律(物理化学)
精选可编辑ppt
31
克劳修斯不等式的意义
克劳修斯不等式引进的不等号，在热力学上可以
作为变化方向与限度的判据。
dS Q T
dSiso 0
“>” 号为不可逆过程 “=” 号为可逆过程
“>” 号为自发过程 “=” 号为处于平衡状态
I < 20% 1度电/1000g煤
高煤耗、高污染（S、N氧化物、粉尘和热污染）
精选可编辑ppt
16
火力发电厂的能量利用
400℃
550℃
ThTC67330055%
Th
673
I < 40% 1度电/500g煤
ThTC82330063%
Th
823
精选可编辑ppt
17
火力发电厂的改造利用
精选可编辑ppt
十九世纪，汤姆荪（Thomsom）和贝塞罗特（Berthlot） 就曾经企图用△H的符号作为化学反应方向的判据。他们认 为自发化学反应的方向总是与放热的方向一致，而吸热反应 是不能自动进行的。虽然这能符合一部分反应，但后来人们 发现有不少吸热反应也能自动进行，如众所周知的水煤气反 应就是一例。这就宣告了此结论的失败。可见，要判断化学 反应的方向，必须另外寻找新的判据。
精选可编辑ppt
4
2.2 自发变化不可逆症结
T1高温热源 Q1
M
W
Q2
T2低温热源
精选可编辑ppt
5
2.3 热力学第二定律（The Second Law of Thermodynamics)
开尔文(Kelvin) ：“不可能从单一热源取出热使之完全 变为功，而不发生其它的变化。”
第二章计算理论与计算模型
➢ 由于计算与算法联系在一起，因此，可计 算性理论又称算法理论。
10
计算理论 计算模型
2.2 计算理论
1.可计算理论的发展
可计算理论起源于对数学基础问题的研究。从20世纪30年 代开始，为了讨论所有问题是否都有求解的算法，数学家和逻 辑学家从不同角度提出了几种不同的算法概念精确化定义。
为什么学习算法：①算法是计算机的灵魂；②算法是数学机 械化的一部分，能够帮助我们解决复杂的计算问题；③算法作为 一种思想，能锻炼我们的思维，使思维变得更清晰、更有逻辑。
6
计算理论 计算模型
2.2 计算理论
Hale Waihona Puke 计算理论：关于计算和计算机械的数学理论， 它研究计算的过程与功效。
计算理论主要包括算法、算法学、计算复杂 性理论、可计算性理论、自动机理论和形式语言 理论等等。
5
计算理论 计算模型
2.1 计算的几种视角
算法：为解决一个特定的问题所采取确定的有限步骤。 计算机用于解决数值计算，如科学计算中的数值积分、解线 性方程等计算方法，就是数值计算的算法。 计算机用于解决非数值计算，如用于管理、文字处理、图像 图形等的排序、分类和查找，就是非数值计算的算法。
算法的组成：操作、数据。 这些操作包括加、减、乘、除和判断等，并按顺序、分支、 循环等控制结构所规定的次序执行。 数据是指操作对象和操作结果，包括布尔值、字符、整数和 实数等；以及向量、记录、集合、树和图以及声音等。
➢ 图灵给出的可计算性定义：能够在图灵机上 执行的过程（通常又称算法的过程）。
➢ 图灵之所以能取得成功，是他采用了算法思 维来研究计算的过程，从而揭示可计算性的 概念。
初一数学第二章知识点总结
初一数学第二章知识点总结一、有理数的基本概念1. 有理数的定义：有理数是可以表示为两个整数的比的数，形式为a/b，其中a和b 是整数，且b≠0。
2. 有理数的分类：- 正有理数：大于0的有理数。
- 负有理数：小于0的有理数。
- 零：既不是正数也不是负数的有理数。
3. 有理数的性质：- 封闭性：加法、减法、乘法和除法（除数不为零）在有理数集内封闭。
- 加法和乘法的交换律、结合律。
- 减法和除法的逆元存在性。
二、有理数的运算1. 加法运算：- 同号相加：取相同的符号，绝对值相加。
- 异号相加：取绝对值较大的数的符号，绝对值相减。
- 任何数与零相加等于原数。
2. 减法运算：- 减去一个数等于加上这个数的相反数。
3. 乘法运算：- 同号得正，异号得负，绝对值相乘。
- 任何数与零相乘等于零。
4. 除法运算：- 除以一个不等于零的数等于乘以这个数的倒数。
- 零除以任何非零数等于零。
5. 混合运算：- 先乘除后加减。
- 同级运算从左到右进行。
三、绝对值与有理数比较1. 绝对值：- 绝对值表示一个数距离零的距离，用符号“| |”表示。
- 一个正数的绝对值是它本身，一个负数的绝对值是它的相反数，零的绝对值是零。
2. 有理数的比较：- 正数大于零，负数小于零。
- 两个负数比较大小，绝对值大的反而小。
四、有理数的简化1. 简化的概念：- 简化是有理数分数形式的最简表示，即分子和分母没有公因数。
2. 简化的方法：- 找出分子和分母的最大公因数，然后分子分母都除以这个数。
五、分数的加减乘除1. 分数的加法：- 需要找到公共分母，然后按照同分母分数的加法规则进行计算。
2. 分数的减法：- 同样需要找到公共分母，然后按照同分母分数的减法规则进行计算。
3. 分数的乘法：- 分子乘分子，分母乘分母。
4. 分数的除法：- 分子乘分母的倒数。
六、小数与有理数的互化1. 小数转化为有理数：- 根据小数点后的位数，将小数乘以10的相应次方，转化为分数形式。
第二章 第二节 技术的本质和特征
第二章科学、技术、工程的内涵及本质特征第二节技术的本质和特征一、技术的内涵“技术”一词源于古希腊语(techne)，意指“技能”、“技艺”等。
在我国古代，技术泛指“百工”。
即各种手工业者和手工业行业的总称。
《考工记·总序》：“国有六职，百工与居一焉。
”春秋战国时，出现了私人手工业者，故《论语·子张》中有“百工居肆，以成其事”。
鲁班是春秋末期鲁国著名的科学家，被古人称为“机械之圣人”，“百工之首”。
近代以来，技术对自然科学理论的应用导致了技术的理论化趋向，从而在技术的构成要素中，技能、经验等主观性因素不再占主导地位，“技术”一词也从最初的techne 转变成technology，其后缀—ology有“学问”、“学说”之意。
马克思从实践的角度，从人类社会发展演变的物质过程，揭示了技术的深刻内涵：技术是人类为满足自身的需要，在实践活动中根据实践经验或科学原理所创造或发明的各种手段和方式方法的总和。
它体现在两个方面：一是技术活动；二是技术成果。
技术揭示出人对自然的能动关系和实践关系，是人的本质力量的展现，属于直接生产力。
科学和技术的区别：第一，技术和科学在本质上都反映了人对自然的能动关系，都属于生产力范畴，但它们与自然的关系不同，科学是人对自然能动关系的知识形态，是人对自然的理论关系，属于间接生产力或一般生产力；技术则是人对自然能动关系的现实形态，是人对自然的实践关系，属于直接生产力。
第二，二者的可预见性程度不同，科学的具体的发展途径如何，哪一项突破在什么时间在哪个实验室出现，一般来说是不可预见的，而技术是以对自然界的认识为根据，利用已有的认识来改造自然，为人类服务。
由于技术有了科学的根据，就有了明确的目标和实现目标的手段，并根据人们的需要和现实的可能，包括人力、资金和技术条件进行规划，因此总体来说技术是可预见的。
第三，科学的任务是解决“是什么、为什么”的问题，技术的任务是解决“做什么、怎么做”的问题。
遗传算法第二章实用详解
遗传算法遗传算法实用流程在第一章概念之后，第二章就是具体是实用。
实用采用回答的方式来解析遗传算法。
一、编码和产生初始化群体方式有哪些？答：遗传算法（Genetic Algorithm，GA）是一种模拟自然选择和遗传机制的优化算法，常用于解决搜索和优化问题。
在遗传算法中，编码和产生初始化群体是两个关键步骤，它们决定了问题的表示形式以及初始解的生成方式。
下面简单介绍一些常见的编码和初始化群体方式：1. 编码方式：-二进制编码(Binary Encoding)：将问题的每个变量转换为二进制串。
例如，要优化一个有4个变量的问题，每个变量的取值范围是[0, 10]，可以用4个16位的二进制串来表示一个解：1010010110111001。
在计算适应度函数时，需要将二进制串转换回对应的实际值。
-实数编码(Real-Valued Encoding)：直接使用实数表示问题的变量。
例如，要优化一个有2个变量的问题，变量1的取值范围是[0, 5]，变量2的取值范围是[-10, 10]，一个解可以是(3.2, -5.7)。
适应度函数会直接使用实数值进行评估。
-整数编码(Integer Encoding)：将问题的变量转换为整数值。
例如，要优化一个有3个变量的问题，变量1的取值范围是[1, 100]，变量2的取值范围是[0, 50]，变量3的取值范围是[10, 20]，一个解可以是(50, 25, 15)。
2. 初始化群体方式：-随机初始化(Random Initialization)：随机生成一组解作为初始群体。
在二进制编码中，可以随机生成一串0和1组成的二进制串。
在实数编码和整数编码中，可以随机生成变量的实数值或整数值。
-均匀初始化(Uniform Initialization)：根据变量的取值范围，均匀地生成初始解。
在实数编码和整数编码中，可以根据变量范围使用均匀分布来生成初始解。
-根据问题特点初始化(Special Initialization)：有时候根据问题的特点，可以使用一些启发式方法来生成初始解。
财务管理学第二章重难点
2-1.［识记］简述时间价值的概念及表现形式？一、时间价值是指一定量的资本在不同时点上的价值量的差额.时间价值来源于资本进入社会再生产过程后的价值增值，是资本在使用中产生的，是资本所有者让渡资本使用权而参与社会财富分配的一种形式。
时间价值有相对数和绝对数两种表示方式.实际工作中，可以用通货膨胀率很低时的政府债券利率来表示时间价值。
一般情况下，时间价值通常用相对数表示。
二、时间价值的表现形式1、现值（1）未来某一时点的一定量资本折合到现在的价值。
(2)现在的本金。
通常记作“P”.2、终值又称将来值,是现在一定量的资本在未来某一时点的价值,即未来的本利和。
通常记作“F”。
2-2[应用]如何计算单利终值与现值？例1：某人于20X5年1月1日存入中国建设银行10000元人民币，存期5年，存款年利率为5％，到期本息一次性支付。
求到期单利终值与利息是多少？例2：某人3年后将为其子女支付留学费用300000元人民币，20X5年3月5日，他将款项一次性存入中国银行，存款年利季4。
5％，则此人应存款的额数是多少？时间价值一般用利率来表示。
利息的计算通常包含单利和福利两种形式。
单利是只对本金计算利息。
即资本无论期限长短，各期的利息都是相同的，本金所派生的利息不再加入本金计算利息。
(1）单利终值单利重视是指一定量的资本在若干期以后包括本金和单利利息在内的未来价值。
单利终值的计算公式为：F=P+P n r=P(1+n r)单利利息的计算公式为：I=P n r式中：P是现值（本金）;F是终值(本利和）；I是利率；r是利率；n是计算利息的期数。
在例1中：单利终值=10000（1+5）=12500（元）利息=p=2500（元）(2)单利现值单利现值是指未来某一时点取得或付出的一笔款项，按一定折现率计算的现在的价值。
单利现值的计算公式为：P=F/(1+n）现值的计算与终值的计算是互逆的,由终值计算现值的过程为折现，这时的利率称为折现率，相应的计算期数称为折现期数。
线性代数习题参考答案
第一章行列式§1 行列式的概念1．填空(1) 排列6427531的逆序数为，该排列为排列。
(2) i= ，j= 时，排列1274i56j9为偶排列。
(3) n阶行列式由项的代数和组成，其中每一项为行列式中位于不同行不同列的n个元素的乘积，若将每一项的各元素所在行标按自然顺序排列，那么列标构成一个n元排列。
若该排列为奇排列，则该项的符号为号；若为偶排列，该项的符号为号。
(4) 在6阶行列式中，含152332445166a a a a a a的项的符号为，含324314516625a a a a a a的项的符号为。
2．用行列式的定义计算下列行列式的值(1)112223323300 0aa aa a…解：该行列式的3!项展开式中，有项不为零，它们分别为，所以行列式的值为。
(2)12,121,21,11, 12,100000nn nn n n n n n n n n nnaa aa a aa a a a------解：该行列式展开式中唯一不可能为0的项是，而它的逆序数是，故行列式值为。
3．证明：在全部n元排列中，奇排列数与偶排列数相等。
证明：n元排列共有!n个，设其中奇排列数有1n个，偶排列数为2n个。
对于任意奇排列，交换其任意两个元的位置，就变成偶排列，故一个奇排列与许多偶排列对应，所以有1n 2n ，同理得2n 1n ，所以1n 2n 。
4． 若一个n 阶行列式中等于0的元素个数比n n -2多，则此行列式为0，为什么 5． ~6．n 阶行列式中，若负项的个数为偶数，则n 至少为多少（提示：利用3题的结果）7． 利用对角线法则计算下列三阶行列式（1）201141183---^（2）222111ab c a b c§2 行列式的性质1．利用行列式的性质计算系列行列式。
(1) 2141 3121 1232 5062-》(2)100 110 011 001abcd ---(3)ab ac ae bd cd de bf cf ef ---?2． 证明下列恒等式(1) ()33ax by ay bzaz bx x y z D ay bzaz bx ax by a b yz x az bx ax by ay bzzxy+++=+++=++++ （提示：将行列式按第一列分解为两个行列式之和，再利用性质证明）】(2)()()()()()()()()()()()()22222222222222221231230123123a a a a b b b b cc c cd d d d ++++++=++++++*(3)1111221100001000001n n n n n n n x x x a x a x a x a a a a x a ------=++++-+(提示：从最后一列起，后列的x 倍加到前一列)3． 已知四阶行列式D 的第三行元素分别为：1,0,2,4-；第四行元素的对应的余子式依次是2，10，a ，4，求a 的值。
灾害管理学习题
第一章绪论一、判断题1、当代灾害不仅数量急剧增加，还呈现出由普遍现象变成个别孤立事件的趋势。
（F）P142、全球灾害形势呈现出灾害致灾因子不确定性有可能增加的发展特点。
（T）P143、全球灾害形势呈现出灾害承灾体的暴露性和脆弱性渐进减弱的特点。
（F）P144、全球灾害风险呈现出空间上不断扩大和强度上增加的趋势。
（T）P145、只有围绕减灾所进行的管理或对灾害进行的管理，才是灾害管理。
（T）P176、灾害管理既是政府行为，又是社会群体行为，它贯穿于减灾系统工程的全过程，是社会减灾行动系统的中枢。
（T）P187、灾害管理是管理的一种特殊类型，是减灾活动中的管理，是对减灾的管理。
（T）P188、危机是指灾害事件的发生概率，灾害则是指事关组织、个人生死存亡的突发性事件。
（F）P209、现代减灾管理是研究灾害形成发展规律和灾害控制技术的应用管理科学。
（T）P2110、灾害管理就是由风险管理和危机管理组成的。
（T）P2111、风险管理是危机管理的技术和信息支撑。
（T）P2112、从灾害危机管理向灾害综合风险管理转变势在必行，是全面提高中国防灾减灾能力的客观需要。
（T）P2513、与风险管理相比，风险治理主要强调风险管理主体的多元性、社会因素和心理因素、风险利益相关者和公众的参与性、风险沟通等方面的作用。
（T）P4014、灾害风险管理强调的是，在灾害发生前着手进行准备、预测、减轻和早期报警工作，对可能出现的灾害进行预先处理。
（T）P4215、综合灾害风险管理集中于灾害风险和灾体脆弱性分析，不强调多层面、多元化和多学科参与合作的全面整合的灾害管理模式。
（F）P4216、综合灾害管理的目标是通过对各种自然灾害风险的识别、评价、控制和处置，以最低成本获得最大保障。
（T）P43二、多项选择题1、灾害风险结构包括：（ABC）P43A.风险因子B.承灾体C.承灾体易损性D.危险源E.风险预估2、综合灾害风险管理是一门新型交叉学科体系，可进一步分为（ABC）二级学科。
第二章的第二节多侧电源网络相间短路的方向性电流保护
第⼆章的第⼆节多侧电源⽹络相间短路的⽅向性电流保护第⼆节多侧电源⽹络相间短路的⽅向性电流保护⼀、⽅向性电流保护的⼯作原理实际的电⼒系统是由很多电源组成的复杂⽹络，此时，采⽤第⼀节中介绍的三段式电流保护不能满⾜选择性的要求。
图2－13 双侧电源⽹络接线及保护动作⽅向的规定（a ）1d 点短路时的电流分布；（b ）2d 点短路时的电流分布；（c ）各保护动作⽅向的规定；例如在图2—13所⽰的双侧电源⽹络接线中，每条线路的两侧均需装设断路器和保护装置。
因为当线路上发⽣短路故障时，线路两侧分别流过各侧电源提供的短路电流，如果只在线路的⼀侧装设断路器和保护装置，实际上并不能真正切除故障。
假设保护1、2、3、4的电流速断仍按第⼀节中的整定原则，其起动电流依据电源1E 单独存在情况下整定；保护5、6、7、8的电流速断依据电源∏E 单独存在情况下整定。
在图2-13（a ）中1d 点发⽣短路时，按照选择性的要求应该由距故障点最近的保护2和6动作切除故障。
然⽽，由电源∏E 供给的短路电流1d I ''也将通过保护1，如果1d I ''⼤于保护1电流速断的起动电流1.dz I '，则保护1的电流速断就要误动作。
因此，可以得出这样的结论：在双侧或多侧电源的复杂⽹络中，采⽤电流速断不能满⾜选择性的要求。
那么，此类⽹络中能否采⽤定时限过电流保护呢？结论也是否定的。
因为当1d 点短路时，要求25t t >；但是，当2d 点短路时，⼜要求52t t >。
这两个要求是不可能同时得到满⾜的。
对误动作的保护进⾏分析可知，误动作的原因是由对侧电源供给的短路电流引起的；此时误动作保护的实际短路功率⽅向是由线路流向母线的。
因此，为了消除双侧电源或多侧电源中三段式电流保护的⽆选择动作，需要在可能误动作的保护上增设⼀个功率⽅向闭锁元件。
该元件当短路功率⽅向由母线流向线路时动作，开放电流保护；⽽当短路功率⽅向由线路流向母线时不动作，闭锁电流保护。
2 计算理论与计算模型
22
• 转换函数的另一种表示: 状态
a b c d
(b,1,R) (b,1,R) (c,1,R) (a,0,S)停机
23
[例]做一个以1的个数表示数值的加法运算，在磁带上的数据是： 0011101100 , 就是3+2的意思。 输出结果为0011111000。
•
当前状态-读入-查表-改变状态-写出
36
时间复杂度= (n+1)+ n(n+1)+n2+ n2(n+1)+n3=2n3+3n2+2n+1
算法时间复杂度
• 时间复杂度的表示
–一般情况下，算法中基本操作重复执行的次 数是问题规模n的某个函数，用T(n)表示。
• T(n)=2n3+3n2+2n+1
37
–若有某个辅助函数f(n)，使得当n趋近于无 穷大时，T(n)/f(n)的极限值为不等于零的 常数，则称f(n)是T(n)的渐近函数。 –记作T(n)=O(f(n))，称O(f(n)) 为算法的渐 进时间复杂度，简称时间复杂度。
• 问题的规模与计算复杂性
– 问题的规模，即一个问题的大小。 – 给定一个算法以后，计算大小为n的问题 所需要的时间、空间就可以表示为 n的函 数。
29
问题规模
30
【例】有两个算法A1和A2求解同一问题，时间消耗分别是： T1(n)=100n2，T2(n)=5n3 （1）当输入量n＜20时，有T1(n)＞T2(n)，后者花费的时间较少。 （2）随着问题规模n的增大，两个算法的时间开销之比 100n2/5n3=20/n亦随着增小。即当问题规模较大时，算法A1比算 法A2要有效得多。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
华中科技大学计算机科学与技术学院 jrc@
§5 Gödel不完备性定理
• 每一个形式系统都可以写成一台图灵机。 • 形式系统不过是一种产生定理的机械程序 ，或者说数学家在一个形式系统中进行演 算的过程就是一台图灵机的运行过程。 • 有了图灵机概念以后人们开始期望造出能 证明所有数学定理的机器。 • 但是，既然形式系统就等价于图灵机，那 么图灵机的局限就是形式系统的局限。
华中科技大学计算机科学与技术学院 jrc@
§３ 停机问题的不可解性
引理2 K是r.e.集，但不是可计算集。 证 可构造一台机器(图灵机)M接受集合K： M：对任意输入x∈N，（1）将x解码为 图灵机Tx；（2）模拟Tx以x为输入的 运行。 故K是r.e.集。 因为可计算集的补集一定是可计算集， 可计算集一定是r.e.集，但K的补集不 是r.e.集，故K不是可计算集。
华中科技大学计算机科学与技术学院 jrc@
§３ 停机问题的不可解性
因为A*与N是可以建立一一对应的，可以认为图 灵机的输入都是N中的非负整数。 定义 N的子集K={i|i∈wi}={i|ϕi(i)↓} θ= K = {i | i ∉ wi } = {i | ϕi (i ) ↑} 引理1 θ不是r.e.集。 证 用反证法。假设θ是r.e.集，则存在常数p使得 θ =wp，则p∈wp当且仅当p∈θ当且仅当 p ∉ wp ， 矛盾
第二章 不可计算性
华中科技大学计算机科学与技术学院 jrc@
§１ 胜奕机之不存在性
假设存在一个计算机系统A，它下国际象棋能 击败任何对手。 于是存在一个被另一个人掌握的与A同样的计 算机系统B，它下国际象棋能击败任何对手。 现在让A与B下国际象棋。有如下三种可能： i>Ａ击败B；ii>下成平局；iii>B击败Ａ； 在任何情况下与假设矛盾。 因此，根本不存在胜奕机。
华中科技大学计算机科学与技术学院 jrc@
§5 Gödel不完备性定理
哥德尔的不完备性定理在给出图灵机概 念之后就有了如下几种等价说法： （1）没有定理证明机器（或机器程序） 能够证明所有的数学真理。 （2）数学是算法不可完全的。 （3）数学是机器程序不可穷尽的。 （4）停机问题不可解，因此本质上，计 算机的能力是有局限的。
华中科技大学计算机科学与技术学院 jrc@
§２ 不可计算函数的存在性
考虑从N到N的全函数，即映射f：N→N。 引理 记 NN={f| f：N→N}，则NN与N之间不存 在一一对应的关系。 定理 NN中至少有一个函数不是可计算的。 引理 记 2N={A| A⊆N}，则2N与N之间不存在 一一对应的关系。 定理 2N中至少有一个集合不是r.e.集。
华中科技大学计算机科学与技术学院 jrc@
§5 Gödel不完备性定理
2002年美国《时代周刊》 列出“20世纪震撼人类思 想界的四大伟人”: 爱因斯坦（Albert Einstein） 图灵（Alnes）
华中科技大学计算机科学与技术学院 jrc@
§３ 停机问题的不可解性
证法2 假设有程序实现H(x,y)的计算，则存在如下程序： θ (x) { If H(x,x)==1 then while(1){x=x;};//死循环 } 由Church-Turing论题，存在一台图灵机Tz与程序θ功 能完全一样，则H(z,z)=1当且仅当θ(z)永不停机当且 仅当Tz(z)永不停机当且仅当H(z,z)=0，矛盾 因此假设是错的，即没有程序实现H(x,y)的计算。
华中科技大学计算机科学与技术学院 jrc@
§5 Gödel不完备性定理
1930年获得博士学位之后，哥德尔开始沿着 希尔伯特方案的路线着手解决希尔伯特第 二问题。 哥德尔最初是想寻此方案首先建立算术理论 的一致性，然后再建立相对于算术而言更 复杂的实数理论的一致性，但出乎意外的 是，他得到了与希尔伯特预期完全相反的 结果。
华中科技大学计算机科学与技术学院 jrc@
§5 Gödel不完备性定理
1997年曾任美国数学会主席的斯梅尔 （S.Smale）效仿数学家希尔伯特向全世界 数学家提出了21世纪需要解决的24个数学 问题，其中的第18个问题是，“人类智能 的极限和人工智能的极限是什么”？并且 指出，这个问题与哥德尔不完全性定理有 关。 哥德尔定理说出了对于形式系统的局限，但 是定理并没有给出人类理性的界限。 人脑是不是计算机？“人心”是不是计算机？ 图灵机的计算模型是否可以超越？
华中科技大学计算机科学与技术学院 jrc@
§5 Gödel不完备性定理
哥德尔实际上证明了：任何丰富到足以展开初 等数论的形式系统，至少会遗漏一个数学真 理，数学形式系统不能囊括所有的数学真理。 那么，能不能添加更强的公理扩充原有的系统 以穷尽所有的数学真理呢？ 哥德尔定理的回答：不行！因为，新扩充的系 统也还是一台新的图灵机，还会有新的数学 真命题在其中不可证，…… 继续扩充，情形 依然如此。
Kurt Gödel, 1906－1978
华中科技大学计算机科学与技术学院 jrc@
§5 Gödel不完备性定理
1900年巴黎数学家会议上，希尔伯特遵从 “世界上没有不可知”，“人类理性提出 的问题人类理性一定能够回答”的哲学信 念，提出23个数学问题，其中的第二个问 题就是建立整个数学的一致性（即无矛盾 性或称协调性）。 1920年代希尔伯特本人曾提出了一个使用有 穷方法建立实数和分析的一致性的方案， 称为希尔伯特元数学方案。
华中科技大学计算机科学与技术学院 jrc@
§5 Gödel不完备性定理
在一个形式系统中，各种陈述都表示成有穷长度的 符号串。 系统的形成规则指明什么样的符号串是合法的公式： 一些符号串被当作公理。系统中还包括一系列推理 规则。 一个证明就是从公理出发，对公式按推理规则进行 变形而形成的有穷长的公式序列。序列中的每一 个公式，要么是公理，要么是由在前的公式依照 推理规则形成的公式，而且系统中每一个定理都 是这样经过有穷步骤得到的结果。
jrc@
§5 Gödel不完备性定理
一阶逻辑（又称谓词逻辑）的所有公理和规则， 加上Peano给出的自然数系统的五条公理。这 就形成了皮亚诺算术系统(Peano’s Arithmetic system)。 该系统中用如下符号来表示自然数。 数： 0 1 2 3 …… 符号：0 S0 SS0 SSS0 …… 这里的S表示后继者。 “6是偶数”表示成“∃e(SS0·e) ＝SSSSSS0”
华中科技大学计算机科学与技术学院 jrc@
§4 不可解性的直观理解
1。仿照图灵机编码方法，试给C语言程序编码，从 而证明C语言所写的程序集是r.e.集。 2。试证明不可能用C语言写一个程序A，它能判断任 意一个C语言写的程序X，当输入为Y时是否能最终 正常退出。 3。试证明不可能用C语言写一个程序A，它能判断任 意一个C语言写的程序X，当输入为Y时是否会格式 化系统盘。 4。试证明不可能用C语言写一个程序，用它来判断 任何一个C语言写的程序是否有死循环漏洞。或判 断是否会做任何恶意的事情。
华中科技大学计算机科学与技术学院 jrc@
§5 Gödel不完备性定理
计算机科学研究受到的启发： 模拟人类智能，超越图灵机概念，探讨以自然 为基础的生物计算、量子计算等新的计算模 式，实施一种“算法+自然机制”的方法论策 略。 对于能够归为传统算法解决的问题，依然使用 算法手段解决，不能归为传统算法解决的问 题，借助自然的生物、化学、物理的机制解 决，并期望借助这种“半人工”手段制造出 堪与人脑匹敌的所谓“半人工智能”来。如: 拟物拟人算法、人工神经网络、遗传进化算法、 模拟淬火算法、蚁群算法
华中科技大学计算机科学与技术学院 jrc@
§5 Gödel不完备性定理
皮亚诺（Peano,1858-1932）公理 关于自然数的 五条公理。用非形式化的方法叙述如下： ①0是自然数； ②每一个确定的自然数a，都有一个确定的后 继数a ' ， a ' 也是自然数； ③如果b、c都是自然数a的后继数，那么b = c； ④0不是任何自然数的后继数； ⑤任意关于自然数的命题，如果证明了它对自 然数0是对的，又假定它对自然数n为真时，可 以证明它对n' 也真，那么，命题对所有自然数 都真。 华中科技大学计算机科学与技术学院
华中科技大学计算机科学与技术学院 jrc@
§３ 停机问题的不可解性
定义 停机函数H: N×N →{0,1}
1, 若ϕ x ( y ) ↓; H ( x, y ) = 否则 0, 定理 H(x,y)不是可计算函数。即停机问题不 可计算。 证法1 χK(x)=1 当且仅当x∈K当且仅当H(x,x)=1. 若H(x,y)可计算，则K的特征函数χK也可计算, 与K不是可计算集矛盾。
华中科技大学计算机科学与技术学院 jrc@
§5 Gödel不完备性定理
定理(Gödel) 初等数论的真命题中至少有一个不可能 从皮亚诺算术系统中得到证明。 证：设命题为假，即初等数论中的任一真命题皆可 从皮亚诺算术系统中得到证明。对于任一给定的 自然数i， ϕi(i)↓与ϕi(i)↑这两个命题都是初等数论 中的命题，且恰有一个真，另一个为假。于是用 枚举出皮亚诺算术系统中的全部真命题的方法， 可以判定问题ϕi(i)↓?是否为真。 我们可以构造一台图灵机，模拟以上枚举算 法。如此则可用一台Turing机判定“ϕi(i)↓ ？”问 题。即K是可计算集，矛盾。