第五章圆轴的扭转
材料力学扭转第5节 圆轴扭转时的变形
BA
T1l1 GI P1
180
0.8110
CB
T2l2 GI P 2
180
0.9810
CA CB BA 0.9810 (0.8110 ) 0.17 0
例4-4 如图,已知ABC轴结构尺寸为 lAB 1.6m, lBC 1.4m。材料切变模量 G 80GPa,轴上作用有外 力矩 M A 900 N·m,M B 1500 N·m,M C 600 N·m,试
求截面C的相对截面A的转角。
解: 1)用截面法求
各段扭矩
1
2
AB 段:
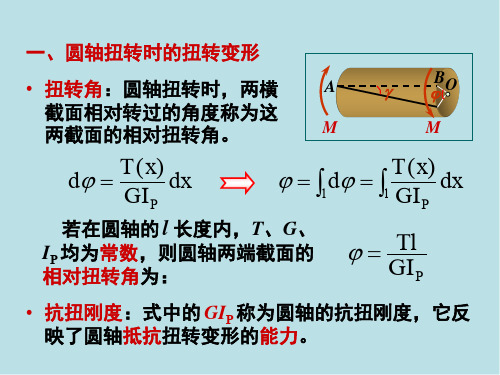
一、圆轴扭转时的扭转变形
• 扭转角:圆轴扭转时,两横
A
BO
截面相对转过的角度称为这
两截面的相对扭转角。
M
M
d
T (x) GIP
dx
l d
T (x)
l GIP
dx
若在圆轴的 l 长度内,T、G、
IP 均为常数,则圆轴两端截面的 相对扭转角为:
Tl
GIP
• 抗扭刚度:式中的 GIP 称为圆轴的抗扭刚度,它反 映了圆轴抵抗扭转变形的能力。
T1 MA 900 N m
BC 段:
T
600Nm
T2 M c 600 N m
画出扭矩图如图所示
900Nm
AB 截面 极惯性矩
I P1
d14
32
BC 截面 极惯性矩
2)C 截面相对于 A 截面的转角
IP2
d
4AB 段: BC 段:
材料力学 第五章扭转变形.强度、刚度条件(6,7,8)汇总
( 4)
例题 6-6
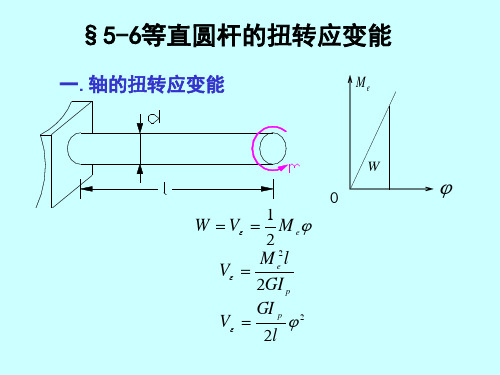
5. 实心铜杆横截面上任意点的切应力为 Ta Ga M e 0 ra ρa I pa Ga I pa Gb I pb 空心钢杆横截面上任意 点的切应力为
b
Tb Gb M e I pb Ga I pa Gb I pb
2
1 dV (dxdydz ) 2 dV dW v dV dxdydz 1 v 2
一、密圈螺旋弹簧
——螺旋角
F
O
d
d ——簧丝横截面的直径 D ——弹簧圈的平均直径
O D
密圈螺旋弹簧 ——螺旋角<5°时的圆柱形弹簧
§4.5
密圈螺旋弹簧的计算
O F
例题 6-6
Me Tb Ta
解: 1. 实心铜杆和空心钢杆横截面上的扭矩分别为Ta 和Tb(图b),但只有一个独立平衡方程 Ta+Tb= Me (1) 故为一次超静定问题。
例题 6-6
Me Tb Ta
2. 位移相容条件为实心杆和空心杆的B截面相对 于A截面的扭转角相等。在图b中都用表示(设 A端固定)。 Ba Bb ( 2)
a
b
ra
ra
a rb
切应力沿半径的变化 情况如图c所示。
ra
rb
(c)
§5-8非圆截面等直杆扭转的概念
圆截面杆扭转时的应力和变形公式,均建立在平 面假设 的基础上。对于非圆截面杆,受扭时横截面不 再保持为平面,杆的横截面已由原来的平面变成了曲 面。这一现象称为截面翘曲。因此,圆轴扭转时的应 力、变形公式对非圆截面杆均不适用。
(2)
圆 轴扭转时的变形和刚度计算

a<[
]
60MP
a
可见强度满足要求。
目录
扭转\圆轴扭转时的变形和刚度计算
4)刚度校核。轴的单位长度最大扭转角为
=
max
Tmax GIp
180=
2.86103 N m
π 80109 P a 6.44106
m4
180 3.14
=0.318 / m 1.1 / m
可见刚度也满足要求。
目录
扭转\圆轴扭转时的变形和刚度计算
【例3.6】 一钢制传动圆轴。材料的切变模量G=79×103MPa,
许用切应力[τ]= 88.2 MPa,单位长度许用扭转角 0.5 /m,承受
的扭矩为T = 39.6 kN·m。试根据强度条件和刚度条件设计圆轴的直 径D。
【解】 1)按强度条件设计圆轴的直径。由强度条件
=Tmax W max
床的加工精度;机器的传动轴如有过大的扭转变形,将使机器在运
转时产生较大振动。因此,必须对轴的扭转变形加以限制,即使其
满足刚度条件:
=Tmax max GIp
式中:[ ]——单位长度许用扭转角,单位为rad/m,其数值是由轴
上荷载的性质及轴的工作条件等因素决定的,可从有关设计手册中
查到。在工程实际中,[ ]的单位通常为 /m ,因而刚度条件变为
Gπ2[ ]
3 21 8 0 3 9.6 1 03
79109 2 0.5 m 0.156m 156mm
故取D=160mm,显然轴能同时满足强度条件和刚度条件。
目录
力学
该轴的强度和刚度。
目录
扭转\圆轴扭转时的变形和刚度计算
【解】 1)计算外力偶矩。
M eA
9549
圆 轴 的 扭 转

4.71kN.m
x
T
此时轴的扭矩图如下
可见轴内的最大扭矩值比原来减小了。
注释:若将A轮与B轮相互调换,则轴的左右两段内的扭矩分别是
C
A
B
MA
MB
1
MC
2
[例1]已知:一传动轴, n =300r/min,主动轮输入 P1=500kW,从动轮输出 P2=150kW,P3=150kW,P4=200kW,试绘制扭矩图。
C
B
A
MB
MA
1
MC
2
T1
1
MA
T2
2
MC
(b) 扭矩。在集中力偶MA与MB之间和MB与MC之间的圆轴内,扭矩是常量,分别 假设为正的扭矩T1和T2。
由截面法
由结果可知扭矩的符号都为正。
C
B
A
MB
MA
1
MC
2
(c) 扭矩图:扭矩数值最大值发生在AB段。
2.32kN.m
7.03kN.m
x
T
(+)
(b) 扭矩。用截面法求出AC段和CB段内的扭矩
(c) 变形谐调条件。圆轴的两端固定,所以A、B截面的相对转角等于零。
(d) 分别算出A、C截面和C、
A
B
MB
(e) 补充方程。把上二式代入到变形谐调条件中去就得到补充方程。
(f) 解方程组。联立补充方程和平衡方程解得
a
c
d
dx
b
dy
´
´
t
z
剪应变:
直角的改变量
式中:G是材料的一个弹性常数,称为剪切弹性模量,因 无量纲,故G的量纲与 相同,不同材料的G值可通过实验确定,钢材的G值约为80GPa。
材料力学-扭转1ppt课件

横截面上 —
max
T IP
max
IP
T
max
T WP
Ip—截面的极惯性矩,单位:m4 , mm 4
WP
Ip
max
WP —抗扭截面模量,单位:m3, mm3.
整个圆轴上——等直杆:
max
Tm a x WP
三、公式的使用条件: 1、等直的圆轴, 2、弹性范围内工作。
30
四、圆截面的极惯性矩 Ip 和抗扭截面系数Wp
d
dx
d / dx-扭转角变化率
二)物理关系:
弹性范围内 max P
G → G
G
d
dx
方向垂直于半径。
28
三)静力关系:
T A dA
T A dA
G d 2dA dx A
I p
2dA
A
Ip
横截面对形心的极惯性矩
T
GI p
d
dxp
29
二、圆轴中τmax的确定
结论:
横截面上 0, 0 0 0
根据对称性可知剪应力沿圆周均匀分布;
t D, 可认为剪应力沿壁厚均匀分布,
且方向垂直于其半径方向。
t
D
20
3、剪应力的计算公式:
T
AdA.r0
2 0
r0
2td
r02t2
d
T
2r0 2t
薄壁圆筒横截面上的剪应力计算式
21
二、关于剪应力的若干重要性质
例题: 1、一传动轴作200r/min的匀速转动,轴上装有五个轮子。 主动轮2输入的功率为60kW,从动轮1、3、4、5依次输出的 功率为18kW、12kW、22kW和8kW。试作出该轴的扭矩图。
[理学]化工设备机械基础习题解答
![[理学]化工设备机械基础习题解答](https://img.taocdn.com/s3/m/58cfdb32ff00bed5b9f31d39.png)
目录化工设备机械基础课后习题解答 .............................. 错误!未定义书签。
EXERCISE EXPLANATION AND DESIGNING OF THE BASIC OF CHEMICAL EQUIPMENT AND MECHANISM .. 错误!未定义书签。
第一章刚体的受力分析及其平衡规律 .. (2)第一部分例题及其解析 (2)第二部分习题及其解答 (10)第二章金属的力学性能 (18)第一部分例题及其解析 (18)第二部分习题及其解答 (19)第三章受拉(压)构件的强度计算与受剪切构件的实用计算 (22)第一部分例题及其解析 (22)第二部分习题及其解答 (24)第四章直梁的弯曲 (27)第一部分例题及其解析 (27)第二部分习题及其解答 (35)第五章圆轴的扭转 (39)第一部分例题及其解析 (39)第二部分习题及其解答 (43)第六章压力容器与化工设备常用材料 (46)第一部分习题及其解析 (46)第七章压力容器中的薄膜应力、弯曲应力、与二次应力 (48)第一部分习题及其解析 (48)第八章内压容器 (52)第一部分例题及其解析 (52)O(c)CAB(a )第二部分 习题及其解答 (55)第九章 外压容器与压杆的稳定计算 (60)第一部分 例题及其解析 .................................................................................................................. 60 第二部分 习题及其解答 .. (67)第一章 刚体的受力分析及其平衡规律第一部分 例题及其解析1.下图(a)是一个三角支架,它由两根杆和三个销钉组成,销钉A 、C 将杆与墙 连接,销钉B 则将两杆连接在一起。
当AB 杆中央 置一重物时,试确定AB 杆两端的约束反力力线方 位(杆的自身质量不计)。
轴的扭转刚度计算

Hypermesh求解
长度单位全部为毫米(mm) 最大应变为1.936e-4mm 扭转角度=最大应变/(r/2)=3.872e-5rad=2.219deg 扭转刚度 Kt=T/扭转角度=4.507 Nm/deg
计算结果对比
公式计算 直径/mm 长度/mm 扭矩/N
剪切模量 Ip
扭转角度/rad 扭转角度/deg 刚度/N/deg
10
300
0.01 8.00E+10 9.82E-10
3.82E-05
2.19E-03 4.57E+00
hypermes量 2.10E+11
扭转角度/rad 扭转角度/deg 刚度/N/deg 0.00003872 0.00221849 4.5075758
轴的扭转刚度计算方法
张志军
扭转变形计算公式:
扭转角(φ):圆轴扭转时两横截面相对转过的角度。
G—剪切弹性模量
几种材料特性举例:
公式求解:
已知:直径为10mm,长度为300mm,受到扭矩为 0.01Nm,求扭转刚度?
首先将长度单位化为米(m) Ip=π*d^4/32=9.82e-10 扭转角度=T*l/(G*Ip)=3.82e-5 rad=2.19e-3 deg 扭转刚度Kt=T/扭转角度=4.57 Nm/deg
机械基础——轴的扭转变形和计算(教学教案)
ab图14—17汽车传动轴轴的扭转变形和计算章节名称 轴的扭转变形和计算授课形式讲授课时2班级中专0101教学目的 掌握外力偶矩、转速和功率三者的关系,会计算轴的扭矩,知道圆轴扭转时 横截面上的应力分布规律。
教学重点 会计算轴的扭矩,知道圆轴扭转时 横截面上的应力分布规律。
教学难点 会计算轴的扭矩辅助手段课外作业课后体会机械中的轴类零件往往承受扭转,它 的受力特点是:在垂直于轴线的两个平面内受一对大小相等、方向相反的力偶作用,轴的各横截面都绕其轴线作相对转动,这种变形称为扭转变形。
一、圆轴扭转时横截面上内力的计算图14—18截面法求扭矩l 、外力偶矩:为了求出圆轴扭转时截面上的内力,必须先计算出轴上的外力偶矩,作用在轴上的外力偶矩往往不是直接给出的,而是根据给定的轴的传递功率和轴的转速算出来的,功率、转速和外力偶矩三者间的关系是:M =9550 P /n式中:P ——轴传递的功率(千瓦, KW) n ——轴的转速(转/分, r / min) M ——作用在轴上的外力偶矩(牛顿米,Nm)2、扭转时横截面上的内力——扭矩圆轴在外力偶矩的作用下,横截面上产生内力。
求内力的方法仍用截面法。
右图表示装有四个皮带轮的传动轴,在四个带轮上分别作用有主动力偶矩 M 1和从动力偶矩M 2、M 3、M 4,外力偶矩分别为 M 1=110Nm ,M 2=60Nm ,M 3=20Nm , M 4=30Nm 。
若计算 AB 段内任一截面上的内力,可假想沿该段内的任一截面1—1将轴截开,取左边部分为研究对象。
如图所示。
为了保证该段的平衡,必须以内力偶矩 Mn 1代替另一部分对被研究部分的作用, Mn 1称为扭矩。
扭矩的正负有如下规定:使右手拇指与截面法线的方向一致,若截面上的扭矩的转向与其它四指的转向相同,则扭矩取正号:反之取负号。
应用截面法时,一般都先假设截面上的扭矩为正。
扭矩的大小用平衡方程Σm=0求得,即AB 段内: Σm=0, M 1十Mn 1=0Mn 1=一M 1=一l10 Nm (设反)图14—19圆轴扭转变形图14—20圆轴的横截 面上剪应力的分布规律BC 段内: Σm =0 M 1—M 2+Mn 2=0 得 Mn 2=—50 Nm (设反) CD 段内: Σm =0 M 1—M 2—M 3十Mn 3=0 得 Mn 3=—30 Nm (设反) 为了清楚地看出各截面上的扭矩变化情况,以便确定危险截面,通常把扭矩随截面位置的变化绘成图形,称为扭矩图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结论:取圆轴直 径d=44mm。
32 M T max 180 0 4 32 477 .5 10 3 180 0 d4 43.2mm 2 3 2 3 G 80 10 1 10
33
作 业
P96 第27、28题
34
35
MT
MT R J MT W
书上有错 因
W 令 :
J R
称为抗扭截面模量
R
MT J
21
三、极惯性矩和抗扭截面模量
1、实心圆轴
dA 2d
J dA 2
2 A d /2 0
d
3
d
J R
4
32
0.1d
4
(902 852 )
4
687 m m2
实心轴的横截面面积为
A实
D12
4
532
4
2210m m2
在两轴长度相等,材料相同情况下,两轴重量之比 等于横截面面积之比,即
687 0.31 W实 A实 2210 W空 A空
27
687 0.31 W实 A实 2210
距离圆心为ρ处的 E点切应变(横截 面上任一点E切应 变):
HH ' HH ' g tang EH 17 dx
在微段中取出一个扇形体放大后的图
DD' DD' g tang AD dx
HH ' HH ' g tang EH dx
g HH ' ' g DD R
4
W
d
3
16
0.2d
3
22
2、空心圆轴
J
D 32
4
பைடு நூலகம்
d
4
0.1D 1
4 4
d D
3 4
W
D 16D
4
d4
D3
1 0.2 D 1 16
4
o d D
23
5.4 扭转的强度条件
为了保证圆轴安全工作,要求最大切应力不超过材 料的许用切应力。
32
(2)按强度条件设计轴的直径
M T max 16M T max max 3 W d
d 3 16 M T max
3 16 477 . 5 10 3 39 .3mm 40
3、按刚度条件设计轴的直径
M T max 1800 32M T max 1800 4 GJ Gd
变形特点:任意两个横截面之间都发生绕轴线的相对 转动(轴表面纵线歪成螺旋线)。
B端相对于A端面的转角φ,称为扭转角。
4
5.2 扭转时的外力和内力
一、扭转时的外力偶矩计算
在工程实际中,外力偶矩往往不是直接给出,给出 的是轴所传递的功率 N 和轴的转速 n ,因此需要根 据N、n来计算外力偶矩。
传递功率N
转速n
5
5.2 扭转时的外力和内力
输入功率N n 转速n R P v
齿轮、传动链条和皮带的圆周力对轮心的力矩就是使轴发生扭转变形的外力偶矩
①若已知圆周力P和半径R,则外力偶矩
②若已知功率N(kW)和转速n(r/min),则
m PR
N 10 P v
3
P 2R n / 60 m2n / 60
MT
28
5.5 圆轴的扭转变形与刚度条件
一、圆轴的扭转变形 用两端面相对扭转角表示
j R g l
G g
j
l
GR
MT R 又 J
MT l j G J
29
工程上常用单位长度扭转角表示扭转变形大小。
MT l G J
Pa(N/m2)
m
MT
正
右手螺 旋法则
m
MT
负
8
求扭矩的快捷方法
mB 1 mC mA 2 3 mD
B
1
C
2 A
3
D
MT 1 mB
M T 2 mB mC MT 3 mB mC mA
扭矩的大小等于截面任何一侧所有外力偶矩的代 数和。外力偶矩正负号规定同扭矩。 9
书上的一个问题
m1 mC m2 mC mA
j
N· m 单位:rad/m m4
工程上中规定的单位长度许用扭转角[θ]常以°/m为 单位,故上式可改写成
M T 180 G J
0
/m
GJρ—抗扭刚度
30
二、扭转的刚度条件
M 180 G J
要求精密度高、运转稳定的轴: [θ]=0.250~0.500/m
二、横截面上切应力的计算公式
静力关系 各微面积上微内力对中心之矩的总和应等于截面扭矩
M T dA
A
dA
R
MT
o
2
R
A
dA
MT
20
MT
R
A
dA
2
2
dA
令: J dA
A
o
称为截面的极惯性矩,与截 面尺寸有关的几何量。
MT MT 1527 .8 16103 max 52.2MPa 3 W D 85 3 4 (1 ) 90 1 <[τ ] 16 90 25 故该传动轴强度足够。
【例5-3】若上例中的传动轴采用实心轴,其它条件 不变,现要求它与原来的空心轴强度相同(即最大切 应力相同),试确定其直径,并比较空心轴与实心轴 的重量。 解:(1)确定实心轴的直径D1 因要求与上例空心轴强度相同,故实心轴的最大切 应力也应为52.2MPa。即
横截面上各点无轴向变形,故横截面上没有正应力。
横截面绕轴线发生了旋转式的相对错动,矩形变为
平行四边形,故横截面上有切应力存在。 各横截面半径不变,所以切应力方向与半径垂直。
16
变形几何关系 根据几何关系, 圆周表面任一点 A 的切应变:
在受扭圆轴中取一个微段dx来分析。注意dφ、ABCD
DD' DD' g tang AD dx
N m 9550 , N.m n 6
二、扭转时横截面上的内力
求出所有外力偶矩后,即可用截面法求横截面上 的内力。 m m
x
m
MT
m 0 MT m 0
MT m
取右段,MT方向相反7
作用在横截面上的内 力偶 MT 称为扭矩。
扭矩的正负号规定 为使取左侧和右侧得到的同一截面的扭矩,不仅数值 相等,且符号相同,对扭矩的正负号规定如下。
NA m A 9550 3.82 kN m n
mB 0.96kN m mC 1.27kN m
mD 1.59kN m
M T 1 0.96kN m
Mt1 Mt2 Mt3
M T 2 3.82 0.96 2.86kN m
M T 3 1.59kN m
扭矩一定要按 正向假设
10
外力偶矩的正负号同扭矩,右手,离开截面为正。
m
MT
正
m MT
右手螺 旋法则
负
11
【 例 5 - 1 】 主 动 轮 N A =12 0 kW , 从 动 轮 N B = 3 0 kW , NC=40kW,ND=50kW,转速n=300r/min,求截面1-1、 1-2、1-3的扭矩。 解:
要求一般的轴:
[θ] =0.500~1.00/m
要求精密度低的轴:[θ] =1.00~3.00/m
31
【例5-4】传动轴主动轮C输入外力偶矩mC=955N.m, 从动轮A、B、D分别输出 mA=159.2N.m, mB=318.3N m, mD=477.5N.m,已知材料切变弹性模量G=80×103 MPa,许用切应力[τ]=40MPa,单位长度许用扭转角[θ] =1º /m。设计轴的直径。 解:(1)计算扭矩,画扭矩图; AB段:MT1= - 159.2N.m, BC段:MT2=-477.5N.m, CD段:MT3= 477.5N.m。 MTmax= 477.5N.m
14
5.3 扭转时横截面上的应力
一、应力分布规律
①变形后圆周线的形状、大小都没有改变,两相邻圆 周线之间的距离也没有改变。 ②纵向线仍为直线,都倾斜了同一个角度γ,原来矩形 变成了平行四边形。
15
平面假设 圆轴扭转变形后各个横截面仍为 平面,而且其大小、形状以及相 邻两截面之间的距离保持不变, 横截面半径不变。 推断结论
W空
A空
可见在相同的外力偶矩情况下,强度相等的空心轴 的重量仅为实心轴的31%,即选用空心轴要比实心 轴更省材料。
解释 从截面应力分布可见,实心轴圆 周上τmax≈[τ]时,中间部分切应 力与[τ]相差甚远,中间材料大 部分没有充分利用。若把中间部 分材料向边缘移,成为空心截面, 就会增大Wρ,提高强度。
第5章 圆轴的扭转
5.1 圆轴扭转的实例与概念 5.2 扭转时的外力和内力 5.3 扭转时横截面上的应力
5.4 扭转的强度条件
5.5 圆轴的扭转变形与刚度条件
1
5.1 扭转变形的实例与概念
2
传动轴
3
Mn A'
A
g
Mn
B j
x
B'
扭转角φ
切应变γ
受力特点:圆截面杆受到一对大小相等、方向相反的 外力偶作用,力偶作用面垂直圆杆轴线。
