建筑力学第六章圆轴扭转
合集下载
工程力学 第6章扭转

max
M n max Wn
式中:
max — —横截面圆周处的最大 剪应力。
M n max — —横截面上的最大扭矩 。 Wn — —抗扭截面系数 (m m3 ),只与截面形状和大小有 关的几何量。
抗扭截面系数计算公式: Wn
对于直径为D的实心圆截面: Wn
I R
0.2 D 3
A
2 dA
2 4 令: dA I — —极惯性矩( mm ) A
得:
Mn I
剪 应 力 分 布 图
结论:(1)圆轴扭转时其横截面上只有剪应力而无正应力。 (2)圆轴扭转时横截面上任一点的剪应力与该点到 圆心的距离成正比,与半径垂直。
三.圆轴扭转强度计算
3.圆轴扭转的强度条件:
D 3
16
D D 3 对于内外径比为 的空心圆截面: Wn 1 4 0.2 D 3 1 4 d 16
三.圆轴扭转强度计算
4.强度条件的应用
(1)校核轴的扭转强度。
(2)确定圆轴的直径。 (3)确定轴所能传递的功率或转速。
解:(1)求A、B、C点的剪应力
截面上的扭矩: M n M e 4 106 N mm
一.扭转的概念
1.扭转变形 受力特点——两外力偶作用面与杆件轴线垂直。 变形特点——杆件相邻两横截面绕轴线发生相对转动。
2.在工程中,作用在圆轴上的外力偶矩通常根据轴所传递的 功率和轴来的转速来计算。 外力偶矩的计算公式:
N (kW ) m 9549 n(r / min)
式中: m——外力偶矩(牛米) N——轴传递的功率(千瓦) n——轴的转速为(转/分)
工程力学:第六章 扭转

9.55
150 300
4.78 (kN m)
m4
9.55
P4 n
9.55
200 300
6.37
(kN m)
n D
m2 1 m3 2 m1 3 m4
n A 1 B 2 C 3D
②求扭矩(扭矩按正方向假设)
m 0 , T1 m2 0, T1 m2 4.78kN m m 0; T2 m1 m2 0
例 已知:一传动轴转数 n =300r/min,主动轮输入功率
P1=500kW,从动轮输出功率 P2=150kW,P3=150kW, P4=200kW,试绘制扭矩图。
解:①计算外力偶矩
m2
m3
m1
m4
m1
9.55
P1 n
9.55
500 300
15.9(kN m)
A
BC
m2
m3
9.55
P2 n
T2 m2 m3 (4.78 4.78) 9.56kN m
m 0 , T3 m4 0, T3 m4 6.37kN m
③绘制扭矩图 m2
m3
m1
m4
n
A
B
C
D
6.37kN.m
扭矩图
–
–
4.78kN.m
9.56kN.m
T 9.56 kN m, BC段为危险截面。 max
6.3 圆轴扭转时的应力及强度条件
第6章 扭转
6.1 扭转的概念 6.2 圆轴扭转时的内力 6.3 圆轴扭转时的应力及强度条件 6.4 圆轴扭转时的变形及刚度条件
6.1 扭转的概念
汽车传动轴
汽车方向盘
看到图片后大家再仔细想想我们日常生活中还有哪些属于 扭转变形?拧衣服
建筑力学_剪切与扭转

同样强度下,空心轴使用材料仅为实心轴的三分之一,故空心轴
较实心轴合理。
实际挤压面
有效挤压面
对圆截面杆:
Abs d t
d
挤压力
bs
Fbs Abs
t
Fbs
Abs=td
①挤压面为平面,计算挤压面就是该面 ②挤压面为弧面,取受力面对半径的投 影面
计算挤压面
Fs 切应力强度条件: A
挤压强度条件:
F bs bs Abs
胶缝
As 0.03 0.01 3104 m2
FS 5 103 6 u 16 . 7 10 Pa 16.7MPa 4 As 3 10
已知: 插销材料为20钢,[] =30MPa,直 d=20mm, t = 8mm, 1.5t =12 mm, P =15kN。 求:校核插销的剪切强度.
Tmax [ ] Wp
Tmax Wp [ ]
Tmax Wp [ ]
T=1.98kN· m,[]=100MPa,试校核轴的强度。
例 某汽车主传动轴钢管外径 D=76mm ,壁厚 t=2.5mm ,传递扭矩
扭转
解:计算截面参数: D 4 4 4 4 I ( 1 ) 77 . 1 10 m m p 32 W I p 20.3 103 m m3 p D/2 由强度条件:
变形特点:任意两个横截面都绕杆轴线作相对转动。 以扭转变形为主的杆称为轴。 扭转角(j):任意两截面绕轴线转动而发生的角位 移。
剪应变( ):直角的改变量。 受扭转变形杆件通常为轴类零件,其横截面大都是圆形的。
材料力学主要研究圆轴扭转问题。
汽车传动轴
传动轴
齿轮传动轴
较实心轴合理。
实际挤压面
有效挤压面
对圆截面杆:
Abs d t
d
挤压力
bs
Fbs Abs
t
Fbs
Abs=td
①挤压面为平面,计算挤压面就是该面 ②挤压面为弧面,取受力面对半径的投 影面
计算挤压面
Fs 切应力强度条件: A
挤压强度条件:
F bs bs Abs
胶缝
As 0.03 0.01 3104 m2
FS 5 103 6 u 16 . 7 10 Pa 16.7MPa 4 As 3 10
已知: 插销材料为20钢,[] =30MPa,直 d=20mm, t = 8mm, 1.5t =12 mm, P =15kN。 求:校核插销的剪切强度.
Tmax [ ] Wp
Tmax Wp [ ]
Tmax Wp [ ]
T=1.98kN· m,[]=100MPa,试校核轴的强度。
例 某汽车主传动轴钢管外径 D=76mm ,壁厚 t=2.5mm ,传递扭矩
扭转
解:计算截面参数: D 4 4 4 4 I ( 1 ) 77 . 1 10 m m p 32 W I p 20.3 103 m m3 p D/2 由强度条件:
变形特点:任意两个横截面都绕杆轴线作相对转动。 以扭转变形为主的杆称为轴。 扭转角(j):任意两截面绕轴线转动而发生的角位 移。
剪应变( ):直角的改变量。 受扭转变形杆件通常为轴类零件,其横截面大都是圆形的。
材料力学主要研究圆轴扭转问题。
汽车传动轴
传动轴
齿轮传动轴
建筑力学 第6章 扭转

2、计算过程中列出物理单位的目的是给同学作 分析示范的,真正计算其切应力时,不必在中 间过程内加注物理单位,只需在计算结果后加 注切应力的物理单位帕(Pa)或兆帕(MPa)。
【 150(a例k)所N6-·示3m】、,一M请实2确=心定4圆0该k轴轴N直·的m径许、为可M13应0=0力3m0值mk,[Nτ]·。受m三,个其外转力向偶如M图16=解:本题受扭情况同上题,其轴的扭矩图如图6—5(b)所示。 其应力许可值可由公式6-8计算:
(a)
)
(b
(c)
(d) 图6-5
解:1、用m-m截取轴的左侧一段如图65(b)所示,
由 T1+10=0 有 T1=-10(kN·m);
2、用n-n截取轴的左侧一段如图6-5(c)所 示,
由 T2+10-40=0 有 T2=30(kN·m);
3、将计算的扭矩值画于轴线上,如图65(d)。
6.2 圆轴扭转时的截面应力分布
(a)
(b) 图6-8
解:根据本题条件,可绘出其轴的扭矩图,如图6—8(b)所示。 其最大应力值出现在到横截面外沿的圆周上,其切应力值的计 算可用公式(6-6)解出:
由公式(6-8),有
可见,该轴的强度符合要求。
max
Tmax Wp
30103 (N) 1000(mm) 0.2 1003 (mm)3
4)
,其中, d D
IP的单位长度是四次方,常用mm4。
最大切应力τmax在圆周处
max
T m ax
Ip
T R Ip
令 Wp=IP/R,称为抗扭截面系数,有
max
Mn Wp
直径为D的圆截面的计算公式为
解:本题受扭情况同上题,其轴的扭矩图如图6—5(b)所示。 其轴的外径可通过公式(6-10)计算:
【 150(a例k)所N6-·示3m】、,一M请实2确=心定4圆0该k轴轴N直·的m径许、为可M13应0=0力3m0值mk,[Nτ]·。受m三,个其外转力向偶如M图16=解:本题受扭情况同上题,其轴的扭矩图如图6—5(b)所示。 其应力许可值可由公式6-8计算:
(a)
)
(b
(c)
(d) 图6-5
解:1、用m-m截取轴的左侧一段如图65(b)所示,
由 T1+10=0 有 T1=-10(kN·m);
2、用n-n截取轴的左侧一段如图6-5(c)所 示,
由 T2+10-40=0 有 T2=30(kN·m);
3、将计算的扭矩值画于轴线上,如图65(d)。
6.2 圆轴扭转时的截面应力分布
(a)
(b) 图6-8
解:根据本题条件,可绘出其轴的扭矩图,如图6—8(b)所示。 其最大应力值出现在到横截面外沿的圆周上,其切应力值的计 算可用公式(6-6)解出:
由公式(6-8),有
可见,该轴的强度符合要求。
max
Tmax Wp
30103 (N) 1000(mm) 0.2 1003 (mm)3
4)
,其中, d D
IP的单位长度是四次方,常用mm4。
最大切应力τmax在圆周处
max
T m ax
Ip
T R Ip
令 Wp=IP/R,称为抗扭截面系数,有
max
Mn Wp
直径为D的圆截面的计算公式为
解:本题受扭情况同上题,其轴的扭矩图如图6—5(b)所示。 其轴的外径可通过公式(6-10)计算:
扭转—扭转轴的应力及强度计算(建筑力学)
1.5 10 6
MPa 51.4MPa
4
WP
2.92 10
扭转
(2) 求空心轴的内径
因为要求实心轴和空心轴的扭转强度相同,故两轴的最
大切应力相等,即
'max max 51.4MPa
max
Tmax
Tmax
WP
D23 1 4 16
6
16Tmax
16
变形的能力。单位GPa,其数值可由试验测得。
切应变的其单位是 弧度(rad)
扭转
二、圆轴扭转时横截面上的应力
从几何关系、物理关系和静力学关系这三个方面来分析圆
轴受扭时横截面上的应力。
1. 几何变形方面
取一圆轴进行扭转试验
试验现象表明,圆轴表面上各点的变形与薄壁圆筒扭转
时的变形一样。
扭转
由观察到的现象,对圆轴内部的变形可做如下假设:扭转
截面(危险截面) 边缘点处。因此,强度条件也可写成 maxFra bibliotekTmax
[ ]
W
圆轴强度条件可以解决圆轴扭转时的三类强度问题,即
进行扭转强度校核、圆轴截面尺寸设计及确定许用荷载。
扭转
例9-6 一实心圆轴,承受的最大扭矩Tmax=1.5kN•m,轴
的直径d1=53mm。求:(1)该轴横截面上的最大切应力。
扭转
第四节 圆轴扭转的强度计算
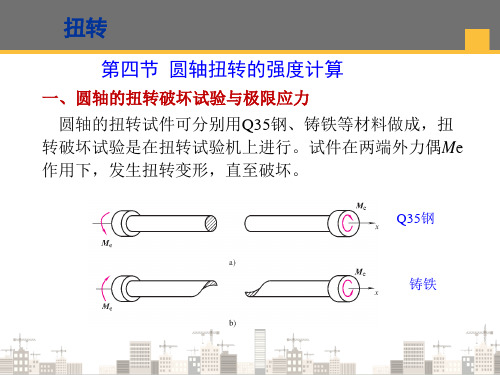
一、圆轴的扭转破坏试验与极限应力
圆轴的扭转试件可分别用Q35钢、铸铁等材料做成,扭
转破坏试验是在扭转试验机上进行。试件在两端外力偶Me
作用下,发生扭转变形,直至破坏。
Q35钢
铸铁
MPa 51.4MPa
4
WP
2.92 10
扭转
(2) 求空心轴的内径
因为要求实心轴和空心轴的扭转强度相同,故两轴的最
大切应力相等,即
'max max 51.4MPa
max
Tmax
Tmax
WP
D23 1 4 16
6
16Tmax
16
变形的能力。单位GPa,其数值可由试验测得。
切应变的其单位是 弧度(rad)
扭转
二、圆轴扭转时横截面上的应力
从几何关系、物理关系和静力学关系这三个方面来分析圆
轴受扭时横截面上的应力。
1. 几何变形方面
取一圆轴进行扭转试验
试验现象表明,圆轴表面上各点的变形与薄壁圆筒扭转
时的变形一样。
扭转
由观察到的现象,对圆轴内部的变形可做如下假设:扭转
截面(危险截面) 边缘点处。因此,强度条件也可写成 maxFra bibliotekTmax
[ ]
W
圆轴强度条件可以解决圆轴扭转时的三类强度问题,即
进行扭转强度校核、圆轴截面尺寸设计及确定许用荷载。
扭转
例9-6 一实心圆轴,承受的最大扭矩Tmax=1.5kN•m,轴
的直径d1=53mm。求:(1)该轴横截面上的最大切应力。
扭转
第四节 圆轴扭转的强度计算
一、圆轴的扭转破坏试验与极限应力
圆轴的扭转试件可分别用Q35钢、铸铁等材料做成,扭
转破坏试验是在扭转试验机上进行。试件在两端外力偶Me
作用下,发生扭转变形,直至破坏。
Q35钢
铸铁
工程力学(静力学与材料力学)-6-圆轴扭转

dz
,这就是剪应力成对定理(
pairing principle of shear
stresses)。
第6章 圆轴扭转
剪应力互等定理 剪切胡克定律
School of Life and Environmental Science
剪切胡克定律
当在弹性范围内加载时,剪 应力与剪应变成正比:
G
剪切胡克定律
G
O
School of Life and Environmental Science
第6章 圆轴扭转
圆轴扭转时横截面上的剪应力分析与强度设 计
G
d
dx
G G d
dx
School of Life and Environmental Science
dx GIP
IP
2dA
A
式中 GIP—扭转刚度; IP—横截面的极惯性矩。
School of Life and Environmental Science
第6章 圆轴扭转
圆轴扭转时横截面上的剪应力分析与强度设 计
[N m]
School of Life and Environmental Science
第6章 圆轴扭转
外加扭力矩、扭矩与扭矩图
外加扭力矩Me确定后,应用截面法可以确定横截面上的 内力——扭矩,圆轴两端受外加扭力矩Me作用时,横截面上 将产生分布剪应力,这些剪应力将组成对横截面中心的合力矩, 称为扭矩(twist moment),用Mx表示。
这种线性关系称为剪切胡克定律。
比例常数G称为材料的切变模量。
O
第6章 圆轴扭转
建筑力学第六章扭转课件

作业
P112:6-3
第四节 等直圆杆扭转时的应力.强度条件
强度条件 max [ ]
强度计算的三类问题:
(1)、强度校核
Tmax [ ]
Wp
(2)、截面设计
Wp
Tm a x
[ ]
(3)、确定许用荷载 Tmax [ ]Wp
第四节 等直圆杆扭转时的应力.强度条件
例6-5. P=7.5kW,n=100r/min,许用切应力[τ]=40MPa,空心圆
第二节 转动轴的外力偶矩·扭矩及扭矩图
例6-1. 图示圆轴中,各轮上的转矩分 别
为mA =4kN·m,mB =10kN·m, mC =6kN ·m,试求1-1截面和2-2截面上 的扭
矩,并画扭矩图。
第二节 转动轴的外力偶矩·扭矩及扭矩图
例6-2. 一圆轴如图所 示,
已知其转速为n =300转/
分,主动轮A输入的功率
解:圆轴受扭时,里、外层之间无相对滑动,这表明 二者形成一 个整体,同时产生扭转变形。根据平面假 定,二者组成的组合截 面,在轴受扭后依然保持平 面,即其直径保持为直线,但要相当 于原来的位置转过一角度。
因此,在里、外层交界处二者具有相同的切应变。 由于内层 (实心轴)材料的剪切弹性模量大于外层(圆环截面)的剪切弹
D2 3 40106 (1 0.54 ) 45.99mm
第四节 等直圆杆扭转时的应力.强度条件
例6-5. 一内径d=100mm的空心圆轴如图示,已知圆轴受扭矩 T=5kN·m,许用切应力[τ]=80MPa,试确定空心圆轴的壁厚。
因不知道壁厚,所以不知道是不是薄壁圆筒。分别按薄壁圆筒 和空心圆轴设计
第二节 转动轴的外力偶矩·扭矩及扭矩图
外加力偶矩与功率和转速的关系
工程力学第6章 扭转

T 2 A0
6.2.2 切应力互等定理
从薄壁圆筒中包括横截 面取出一个单元体
将(d)图投影到铅垂坐标平面,得到一个平面单元
根据力偶平衡理论
y
(dydz )dx ( dxdz)dy
dy
dz
在相互垂直的两个平面 上,切应力必成对出现, 两切应力的数值相等, 方向均垂直于该平面的 x 交线,且同时指向或背 离其交线。
对于各向同性材料,在弹性变形范围内,切变 模量G 、弹性模量E 和泊松比之间有下列关系:
G
E (1 ) 2
6-3 实心圆轴扭转时的应力和强度条件
6.3.1 、 扭转剪应力在横截面上的分布规律
Ⅰ. 横截面上的应力 表面 变形 情况 推断 横截面 的变形 情况 横截面 上应变 应力-应变关系
两互相垂直截面上在其相交处的剪应力 成对存在,且数值相等、符号相反,这称为 剪应力互等定理。
例题 3
试根据切应力互等定理,判断图中所示的各 单元体上的切应力是否正确。
10 kN
30 kN 50 kN
10 kN
20 kN
50 kN 30 kN
20 kN
30 kN
6.2.3 剪切胡克定律(Hooke’s law in shear) Me Me
n
主轴
主动轮 叶片
本章研究杆件发生除扭转变形外,其它变形可忽略的 情况,并且以圆截面(实心圆截面或空心圆截面)杆为主要
研究对象。此外,所研究的问题限于杆在线弹性范围内工
作的情况。
6-1 概述
1. 扭转的概念 4种基本变形(轴向拉压、剪切、扭转、弯曲)之一 特点: 圆截面轴(实心、空心)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Mn Mn
6.1.2 扭 转 轴 的 内 力— 扭 矩
Mn
外荷载:作用平面垂直于杆件轴线的力偶 内荷载:作用在横截面上的内力偶—扭矩 扭矩的大小:等于截面任意一侧的所有横截 面外力偶矩的代数和.
M n 左或右侧 mi
6.1.2 扭 转 轴 的 内 力— 扭 矩
扭矩的正负号:按右手螺旋法则确定,当拇 指方向与截面外法线方向一致时为正, 反之为负。 单位:N· m 或 kN· m
图6-12
6.3.3 工 程 实 例 计 算
6.3.3 工 程 实 例 计 算
6.3.3 工 程 实 例 计 算
【例6-5】挖掘机的传动轴如图6-13所示,转数n=300 r/min 主动轮A的输入功率PkA=500 kW,三个从动轮的输出功率
,
PkB=PkC=150kW,PkD=200kW,若[τ]=60 MPa,G=80 GPa,[θ]
M n3 M eD 3.82kN m
(3)画扭矩图
内力图要求
1. 标明内力性质 2. 正确画出内力沿杆轴分布规律 3. 标明特殊截面的内力数值 4. 标明正负号 5. 注明单位(只在内力标志后面写一个亦可) 作扭矩图步骤 1. 计算各段扭矩 2. 作扭矩图
6.1.3 扭 矩 图
1.圆轴扭转变形的几何特点
扭转角:圆轴扭转时,两横截面间绕轴线相对转过的角
GI P
单位长度的扭转角
M nl GI p
的单位为 rad 称为截面抗扭刚度
6.2.3 圆 轴 扭 转 时 的 变 形
Mn l GI p
M n 180 GI P
【例6-2】图6-11(a)所示为阶梯轴,AB段直径d1=120 mm,l1=400 mm,BC段直径d2=100 mm,l2=350 mm。扭转力偶矩为 mA=22kN·m,mB=36 kN·m,mC=14 kN·m,已知材料的剪切弹性模量 G=80 GPa,试求AC轴最大切应力,并求C点处的截面相对于A点处截 面的扭转角。 6.2.3 圆 轴 扭 转 时 的 变 形
3.应力分布特点
(1)由横截面刚性绕轴线旋转,产生了剪应变。说明 横截面上必然存在剪应力。 (2)由各圆周线的形状、大小和间距不变,说明 横截面上的剪应力必然垂直半径,且无正应力。 (3)由横截面上任意点的剪应变 与该点到圆心的距离
6.2.1 圆 轴 扭 转 时 的 应 力
成正比。横截面上任意一点处的剪应力与该点到
当 ρ = ρmax
max
式中
Mn Wn
Ip
Wn
max
称抗扭截面模量,单位:m3.
6.2.1 圆 轴 扭 转 时 的 应 力
Ip
D
4
32
Wn
D 3
16
Ip
D
4
32
1
4
Wn
D 3
16
1
4
d D
6.2.2 极 惯 性 矩 IP 和 抗 扭 截 面 模 量 Wn 的 确 定
6.1.2 扭 转 轴 的 内 力— 扭 矩
当作用在轴上的外力偶多于两个时,轴
上各横截面的扭矩值往往不同,为将扭矩沿
轴的变化情况表示出来,可画图象。 以横轴表示横截面的位置,以纵轴表示 相应截面的扭矩,得出的图象叫扭矩图。
6.1.3 扭 矩 图
【例6-1】图6-5(a)所示的传动轴,n=300 r/min,主动轮A输入
图6-11
6.2.3 圆 轴 扭 转 时 的 变 形
6.2.3 圆 轴 扭 转 时 的 变 形
max
M n max Wn
6.3.1 圆 轴 扭 转 强 度 条 件
max
M n max GI p
或
max
M n max 180 GI p
若已知轴的转速为n(r/min),带轮输入的功率为 P(kW),注意两者的单位.则因1kW = 1000N*m/s,输 入P(kW)就相当于每秒钟输入 W = P*1000N*m 的功.输入的功是经由带轮以力偶矩m作用于轴上 来完成的,因轴的转速为n,轴在1s的时间内转过角 度为2π*n/60,则力偶矩在1s时间内完成作功W = 2π*n/60*M(M为力偶矩) 由作功相等,有 W = P*1000N*m = 2π*n/60*M 得 M = 1000*60*P/(2π*n) = 9549P/n = 9550P/n(unit:N*m)
6.1
6.2 6.3
扭矩与扭矩图
扭转轴横截面上的应力与变形
圆轴扭转的强度条件和刚度条件及应用
学习目标
(1)理解并掌握圆轴的受力、变形特点。 (2)能够计算指定截面的扭矩值并画出扭矩图。 (3)能够应用公式求解不同点的应力和变形计算。 (4)能够熟练应用强度条件和刚度条件求解各种实际问题。
扭转变形是由大小相等、转向相反、作用面垂直于轴线的 两个力偶作用而产生的。如图6-1(a)所示的齿轮轴传动装置,其 圆轴工作时因两端受到力偶作用而发生扭转变形。扭转变形的 特点是杆轴上任意两个横截面绕轴线作相对转动,产生相对扭转 角,如图6-1(b)所示。
(1)圆周线的形状、大小、间距不变;绕轴线发 生了相对转动。 (2)纵线间距不变,转过一个相同角度γ—剪应 变。
6.2.1 圆 轴 扭 转 时 的 应 力
2.平面假设
横截面在扭转变形后仍保持为平面,且形状、 大小、间距都不变,半径仍为直线。各横截面就 象刚性平面一样绕轴线转过一定 的角度。据此假 设,横截面上没有正应力,只有剪应力,其方向 与所在半径垂直,指向扭矩的转向。 6.2.1 圆 轴 扭 转 时 的 应 力
机械结构中的轴工作时受到的外力偶矩通常不会直接给出, 但可利用给出的功率和转速确定,即
Pk M e 9549 N m n
Pk 表示功率,单位为千瓦( kW)
n
表示转速,单位为每分钟的转数( r
min)
M e 表示外力矩,单位为牛顿· 米( N m)
6.1.1 外 力 偶 矩 的 计 算
M eD
PKD 120 9549 ( N m) 9549 3.82kN m n 300
6.1.3 扭 矩 图
(2)截面上的扭矩计算
M n1 (左 或 右 侧 ) mi M eB 2.87kN m
M n 2 M eB M eC 5.73kN m
圆心的距离成正比。所有跟圆心等距离的各点, 其剪应力数值相等,在周边的剪应力最大,圆心 处有最小值,是零。
6.2.1 圆 轴 扭 转 时 的 应 力
4.应力计算
Mn
称极惯性矩
单位:m4.
6.2.1 圆 轴 扭 转 时 的 应 力
最大剪应力
图6-1
日常生活中,经常可接触到受扭构件,如扭紧螺钉 的螺丝刀、开门时扭动的钥匙等。如图6-2所示的房 屋中钢筋混凝土雨篷梁、现浇框架边梁等,也是典型 的受扭构件。
图6-1
受力特点:杆件两端受到两个在垂直于轴线平面 的大小相等,转向相反的力偶作用;
变形特点:各横截面绕轴线转过不同角度, 产生相对扭转角 。 轴(shaft) :以扭转变形为主的杆件,如圆轴。
功率PkA=300 kW,其他各轮的输出功率分别PkB=PkC=90kW,PkD=120
kW,试画出扭矩图。
6.1.3 扭 矩 图
(1)外力矩的计算
M eA 9549 PKA 300 ( N m) 9549 9.5kN m n 300
M eB M eC 9549
PKB 90 ( N m) 9549 2.87kN m n 300
=0.5°/m。试设计轴径。
6.3.3 工 程 实 例 计 算
6.3.3 工 程 实 例 计 算
6.3.3 工 程 实 例 计 算
若已知轴的转速为n(r/min),带轮输入的功率为 P(kW),注意两者的单位.则因1kW = 1000N*m/s,输 入P(kW)就相当于每秒钟输入 W = P*1000N*m 的功.输入的功是经由带轮以力偶矩m作用于轴上 来完成的,因轴的转速为n,轴在1s的时间内转过角 度为2π*n/60,则力偶矩在1s时间内完成作功W = 2π*n/60*M(M为力偶矩) 由作功相等,有 W = P*1000N*m = 2π*n/60*M 得 M = 1000*60*P/(2π*n) = 9549P/n = 9550P/n(unit:N*m)
6.3.2 圆 轴 扭 转 刚 度 条 件
【例6-3】卷扬机的传动轴直径为d=40 mm,转动功率P=30 kW,
转速n=1 400 r/min,轴的材料为45号钢,G=80 GPa,[τ]=40 MPa,[θ]=2°/m,试校核该轴的强度和刚度。
6.3.3 工 程 实 例 计 算
【例6-4】某运输设备的传动轴如图6-12所示,由45号钢的无缝 钢管制成。其外径D=90 mm,内径d=85 mm,工作时的最大扭矩 Mn=1.5 kN·m,已知许用切应力[τ]=60 MPa。试校核该轴的 强度,并求在最大切应力相同情况下的实心轴直径,比较空心轴 与实心轴的重量。
