二年级数学奥数知识点手写笔记
小学二年级奥数知识点第二讲数数与计数

小学二年级奥数知识点第二讲数数与计数第二讲数数与计数从数数与计数中,可以发现重要的算术运算定律.例1 数一数,下面图形中有多少个点?解:方法1:从上到下一行一行地数,见下图.点的总数是:5+5+5+5=5×4.方法2:从左至右一列一列地数,见下图.点的总数是:4+4+4+4+4=4×5.因为不论人们怎样数,点数的多少都是一定的,不会因为数数的方法不同而变化.所以应有下列等式成立:5×4=4×5从这个等式中,我们不难发现这样的事实:两个数相乘,乘数和被乘数互相交换,积不变.这就是乘法交换律.正因为这样,在两个数相乘时,以后我们也可以不再区分哪个是乘数,哪个是被乘数,把两个数都叫做“因数”,因此,乘法交换律也可以换个说法:两个数相乘,交换因数的位置,积不变.如果用字母a、b表示两个因数,那么乘法交换律可以表示成下面的形式:a×b=b×a.方法3:分成两块数,见右图.前一块4行,每行3个点,共3×4个点.后一块4行,每行2个点,共2×4个点.两块的总点数=3×4+2×4.因为不论人们怎样数,原图中总的点数的多少都是一定的,不会因为数数的方法不同而变化.所以应有下列等式成立:3×4+2×4=5×4.仔细观察图和等式,不难发现其中三个数的关系:3+2=5所以上面的等式可以写成:3×4+2×4=(3+2)×4也可以把这个等式调过头来写成:(3+2)×4=3×4+2×4.这就是乘法对加法的分配律.如果用字母a、b、c代表三个数,那么乘法对加法的分配律可以表示成下面的形式:(a+b)×c=a×c+b×c分配律的意思是说:两个数相加之和再乘以第三数的积等于第一个数与第三个数的积加上第二个数与第三个数的积之和.进一步再看,分配律是否也适用于括号中是减法运算的情况呢?请看下面的例子:计算(3-2)×4和3×4-2×4.解:(3-2)×4=1×4=43×4-2×4=12-8=4.两式的计算结果都是4,从而可知:(3-2)×4=3×4-2×4这就是说,这个分配律也适用于一个数与另一个数的差与第三个数相乘的情况.如果用字母a、b、c(假设a>b)表示三个数,那么上述事实可以表示如下:(a-b)×c=a×c-b×c.正因为这个分配律对括号中的“+”和“-”号都成立,于是,通常人们就简称它为乘法分配律.例2 数一数,下左图中的大长方体是由多少个小长方体组成的?解:方法1:从上至下一层一层地数,见上右图.第一层4×2个第二层4×2个第三层4×2个三层小长方体的总个数(4×2)×3个.方法2:从左至右一排一排地数,见下图.第一排2×3个第二排2×3个第三排2×3个第四排2×3个四排小长方体的总个数为(2×3)×4.若把括号中的2×3看成是一个因数,就可以运用乘法交换律,写成下面的形式:4×(2×3).因为不论人们怎样数,原图中小长方体的总个数是一定的,不会因为数数的方法不同而变化.把两种方法连起来看,应有下列等式成立:(4×2)×3=4×(2×3).这就是说在三个数相乘的运算中,改变相乘的顺序,所得的积相同.或是说,三个数相乘,先把前两个数相乘再乘以第三个数,或者先把后两个数相乘,再去乘第一个数,积不变,这就是乘法结合律.如果用字母a、b、c表示三个数,那么乘法结合律可以表示如下:(a×b)×c=a×(b×c).巧妙地运用乘法交换律、分配律和结合律,可使得运算变得简洁、迅速.从数数与计数中,还可以发现巧妙的计算公式.例3 数一数,下图中有多少个点?解:方法1:从上至下一层一层地数,见下图.总点数=1+2+3+4+5+6+7+8+9=45.方法2:补上一个同样的三角形点群(但要上下颠倒放置)和原有的那个三角形点群共同拼成一个长方形点群,则显然有下式成立(见下图):三角形点数=长方形点数÷2因三角形点数=1+2+3+4+5+6+7+8+9而长方形点数=10×9=(1+9)×9代入上面的文字公式可得:1+2+3+4+5+6+7+8+9=(1+9)×9÷2=45.进一步把两种方法联系起来看:方法1是老老实实地直接数数.方法2可以叫做“拼补法”.经拼补后,三角形点群变成了长方形点群,而长方形点群的点数就可以用乘法算式计算出来了.即1+2+3+4+5+6+7+8+9=(1+9)×9÷2.这样从算法方面讲,拼补法的作用是把一个较复杂的连加算式变成了一个较简单的乘除算式了.这种方法在700多年前的中国的古算书上就出现了.再进一步,若脱离开图形(点群)的背景,纯粹从数的方面找规律,不难发现下述事实:这个等式的左边就是从1开始的连续自然数相加之和,第一个数1又叫首项,最后一个数9叫末项,共有9个数又可以说成共有9项,这样,等式的含义就可以用下面的语言来表述:从1开始的连续自然数前几项的和等于首项加末项之和乘以项数的积的一半.或是写成下面的文字式:和=(首项+末项)×项数÷2这个文字式通常又叫做等差数列求和公式.例4 数一数,下图中有多少个点解:方法1:从上至下一层一层地数,见下图:总点数=2+3+4+5+6=20.方法2:补上一个同样的梯形点群,但要上下颠倒放置,和原图一起拼成一个长方形点群如下图所示:由图可见,有下列等式成立:梯形点数=长方形点数÷2.因为梯形点数=2+3+4+5+6而长方形点数=8×5=(2+6)×5代入上面的文字式,可得:2+3+4+5+6=(2+6)×5÷2与例1类似,我们用拼补法得到了一个计算梯形点群总点数的较为简单的公式.再进一步,若脱离开图形(点群)的背景纯粹从数的方面找找规律,不难发现下述事实:这个等式的左边就是一个等差数列的求和式,它的首项是2,末项是6,公差是1,项数是5.这样这个等式的含义就可以用下面的语言来表述:等差数列前几项的和等于首项加末项之和乘以项数的积的一半.写成下面较简化的文字式:和=(首项+末项)×项数÷2这就是等差数列的求和公式.例5 数一数,下图中有多少个小三角形?解:方法1:从上至下一层一层地数,见下图.小三角形总数=1+3+5+7=16个.方法2:补上一个同样的图形,但要上下颠倒放置、和原来的一起拼成一个大平行四边形如下图所示.显然平行四边形包含的小三角形个数等于原图中的大三角形所包含的小三角形个数的两倍,即下式成立.大三角形中所含=平行四边形所含÷2平行四边形所含=8×4=(1+7)×4(个)大三角形中所含=1+3+5+7=16代入上述文字式:1+3+5+7=(1+7)×4÷2这样,我们就得到了一个公式:小三角形个数=(第一层的数+最末层的数)×层数÷2脱离开图形的背景,纯粹从数的方面进行考察,找找规律,不难发现下述事实:等式左边就表示一个等差数列的前几项的和,它的首项是1,末项是7,公差是2,项数是4.这样这个等式的含义也就可以用下面的语言来表述:等差数列前几项的和等于首项加末项之和乘以项数之积的一半.写成较简单的文字式:和=(首项+末项)×项数÷2.。
小学奥数知识总结
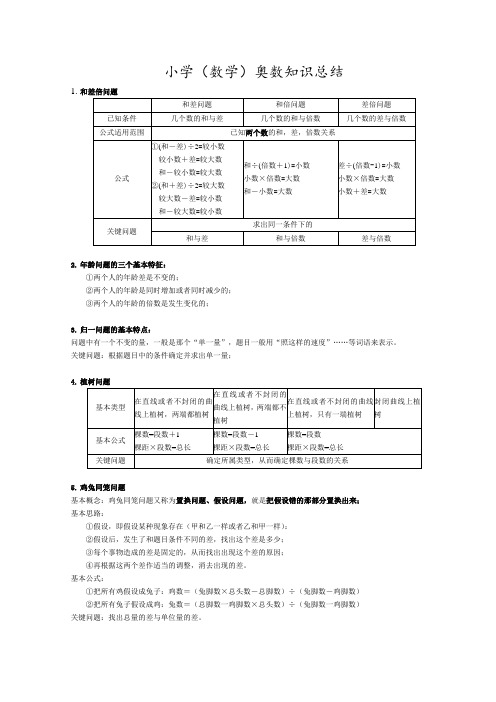
小学(数学)奥数知识总结1.和差倍问题和差问题和倍问题差倍问题已知条件几个数的和与差几个数的和与倍数几个数的差与倍数公式适用范围已知两个数的和,差,倍数关系公式①(和-差)÷2=较小数较小数+差=较大数和-较小数=较大数②(和+差)÷2=较大数较大数-差=较小数和-较大数=较小数和÷(倍数+1)=小数小数×倍数=大数和-小数=大数差÷(倍数-1)=小数小数×倍数=大数小数+差=大数关键问题求出同一条件下的和与差和与倍数差与倍数2.年龄问题的三个基本特征:①两个人的年龄差是不变的;②两个人的年龄是同时增加或者同时减少的;③两个人的年龄的倍数是发生变化的;3.归一问题的基本特点:问题中有一个不变的量,一般是那个“单一量”,题目一般用“照这样的速度”……等词语来表示。
关键问题:根据题目中的条件确定并求出单一量;4.植树问题基本类型在直线或者不封闭的曲线上植树,两端都植树在直线或者不封闭的曲线上植树,两端都不植树在直线或者不封闭的曲线上植树,只有一端植树封闭曲线上植树基本公式棵数=段数+1棵距×段数=总长棵数=段数-1棵距×段数=总长棵数=段数棵距×段数=总长关键问题确定所属类型,从而确定棵数与段数的关系5.鸡兔同笼问题基本概念:鸡兔同笼问题又称为置换问题、假设问题,就是把假设错的那部分置换出来;基本思路:①假设,即假设某种现象存在(甲和乙一样或者乙和甲一样):②假设后,发生了和题目条件不同的差,找出这个差是多少;③每个事物造成的差是固定的,从而找出出现这个差的原因;④再根据这两个差作适当的调整,消去出现的差。
基本公式:①把所有鸡假设成兔子:鸡数=(兔脚数×总头数-总脚数)÷(兔脚数-鸡脚数)②把所有兔子假设成鸡:兔数=(总脚数一鸡脚数×总头数)÷(兔脚数一鸡脚数)关键问题:找出总量的差与单位量的差。
小学奥数知识点汇总,所有奥数知识点都在这啦!

⼩学奥数知识点汇总,所有奥数知识点都在这啦!今天分享的这篇⽂章包括⼩升初常考的题⽬类型,有⼯程问题、⾏程问题、质数合数问题等。
快收藏吧!1、年龄问题的三⼤特征①两个⼈的年龄差是不变的;②两个⼈的年龄是同时增加或者同时减少的;③两个⼈的年龄的倍数是发⽣变化的;2、植树问题总结:基本类型:在直线或者不封闭的曲线上植树,两端都植树在直线或者不封闭的曲线上植树,两端都不植树在直线或者不封闭的曲线上植树,只有⼀端植树。
3、鸡兔同笼问题基本概念:鸡兔同笼问题⼜称为置换问题、假设问题,就是把假设错的那部分置换出来;基本思路:①设,即假设某种现象存在(甲和⼄⼀样或者⼄和甲⼀样):②假设后,发⽣了和题⽬条件不同的差,找出这个差是多少;③每个事物造成的差是固定的,从⽽找出出现这个差的原因;④再根据这两个差作适当的调整,消去出现的差。
基本公式:①把所有鸡假设成兔⼦:鸡数=(兔脚数×总头数-总脚数)÷(兔脚数-鸡脚数)②把所有兔⼦假设成鸡:兔数=(总脚数⼀鸡脚数×总头数)÷(兔脚数⼀鸡脚数)关键问题:找出总量的差与单位量的差。
4、盈亏问题盈亏问题基本概念:⼀定量的对象,按照某种标准分组,产⽣⼀种结果:按照另⼀种标准分组,⼜产⽣⼀种结果,由于分组的标准不同,造成结果的差异,由它们的关系求对象分组的组数或对象的总量.基本思路:先将两种分配⽅案进⾏⽐较,分析由于标准的差异造成结果的变化,根据这个关系求出参加分配的总份数,然后根据题意求出对象的总量.基本题型:①⼀次有余数,另⼀次不⾜;①⼀次有余数,另⼀次不⾜;基本公式:总份数=(余数+不⾜数)÷两次每份数的差②当两次都有余数;基本公式:总份数=(较⼤余数⼀较⼩余数)÷两次每份数的差③当两次都不⾜;基本公式:总份数=(较⼤不⾜数⼀较⼩不⾜数)÷两次每份数的差基本特点:对象总量和总的组数是不变的。
关键问题:确定对象总量和总的组数。
二年级奥数知识点-第四讲·一笔画

图a
故直接判断该图不能一笔画 注意:在判定前首要先判定是否为“连通图”,节省做题时间
步骤 1:判定是连通图吗?——是
步骤 2:数一数图中奇点个数有几个?
图b
如图 b 所示,奇点个数为 4 个,超过 2 个,
故图 b 不能一笔画
奇点个数超过 2 个的连通图形不能一笔画成!!!
步骤 1:判定是连通图吗?——是
E D
G
A
F
C
B
杭州学而思二年级奥数知识点“每周一讲” 李莹
例题解析
例 1【解析】学会什么是“奇点”,什么是“偶点”。
奇点:与奇数条线连接的点
偶点:与偶数条线连接的点
图中从每个点出发的线数分别为:
AGB
A: 2 条(偶) B:2 条(偶) C: 2 条(偶)
从 A 点出发有 两条线路可以 走,即与 A 点相 连的线有 2 条
杭州学而思二年级奥数知识点“每周一讲” 李莹
第四讲 一笔画
知识点拨 一、基本功(一笔画的相关概念)
1、一笔画要求: 在一个平面内 ⑴笔不离开纸;⑵每条线只画一次,不重复。 2、奇点:与奇数条线连接的点 3、偶点:与偶数条线连接的点 注意: (1) 在数“与点连接的线”的多少时我们可记为“从该点出发的线”,这样不容 易出错。如下图中从 A点出发的线应该是 2 条,A 是偶点。
条路线;或者从奇点 D 开始,走到奇点 F 不重复走完商场的每条路线
注意:奇点个数为 2 时,必须从一个奇点开始到另一个奇点结束,才可以完成一笔画 B
D
G C
拓展练习
1、图是某一儿童乐园的平面图,在 A,B,C,D 四个点上选两个准备设出入口,应设在哪 里才能不重复地走遍每条路?
二年级春季数学奥数班第1讲 一笔画

一笔画月日姓名【知识要点】1.概念:一笔画是指笔不离开纸,而且每条线都只画一次不准重复而画成的图形。
2.分类:图中的点可分两大类:(1)双数点:从这点出发的线的数目是双数的,叫双数点。
(2)单数点:从这点出发的线的数目是单数的,叫单数点。
3.规律:一个图形能否一笔画成,关键在于图中单数点的多少。
(1)凡是图形中没有单数点的一定可以一笔画成。
(2)凡是图形中只有两个单数点,一定可以一笔画成,画时必须从一个单数点为起点,最后以另一单数点为终点。
(3)凡是图形中单数点的个数多于两个时,此图肯定是不能一笔画成。
【典型例题】例1.判断下面图形中哪些点是单数点,哪些点是双数点。
例2.下列图形中各有几个单数点?能一笔画成吗?(1)(2)(3)(4)例3.如图,能不能一笔画成?如果能,应该怎样画?例4.将下图去掉最少的线改成一笔画图形。
随堂小测姓名成绩1.判断下面图形哪些是单数点,哪些是双数点。
2. 下列图形中各有几个单数点?能一笔画成吗?3. 一个邮递员投递信件要走的街道如下左图,为节约时间,他想自己设计一条线路,可以不重复的走遍每一条街道,你能帮帮他吗?4. 一只蚂蚁要想不重复的爬遍每一条线路,应从哪里出发,到哪里结束?(3)AC E(1)(2)(3)(4)5. 将下图加上最少的线改成一笔画的图形。
【知识拓展】1.为迎接2008年奥运会在北京召开,你能一笔画出奥运会的五环图案吗?2.你能用一笔画成4条线段把下图的9朵小花都连起来吗?课后作业姓名成绩1.判断下面图形中哪些点是单数点哪些点是双数点。
2.判断下面图形能不能一笔画成。
(1)(2)B3.下图能否一笔画成?如果能,应怎样画?4.如图,是一个公园的平面图,请你设计好入口、出口,并给出一种游玩路线,要求走遍每一条路且不重复。
5.如图,是一个名画展厅的平面图,要使参观者不重复地走遍每一条画廊,问:出口、入口应设在哪里?家长签名:【课外知识链接】七桥问题著名古典数学问题之一。
二年级奥数知识要点整理汇总及典型练习题

二年级奥数知识要点整理汇总及典型练习题目录1.二年级奥数.几何1.1.二年级奥数.几何.巧求周长1.2.二年级奥数.几何.数形结合1.3.二年级奥数.几何.一笔画问题1.4.二年级奥数.几何.找规律2.二年级奥数.计算2.3.二年级奥数.计算.等式加减2.4.二年级奥数.计算.巧填算式2.5.二年级奥数.计算.竖式谜2.6.二年级奥数.计算.数阵图2.7.二年级奥数.计算.算得快的奥妙3.二年级奥数.应用题3.1.二年级奥数.应用题.倍数问题3.2.二年级奥数.应用题.倒推法3.3.二年级奥数.应用题.对号入座3.4.二年级奥数.应用题.和差问题3.5.二年级奥数.应用题.间隔与分段3.6.二年级奥数.应用题.两步应用题3.7.二年级奥数.应用题.平均数4.二年级奥数.杂题4.1.二年级奥数.杂题.操作与应用4.2.二年级奥数.杂题.等量代换4.3.二年级奥数.杂题.逻辑推理4.4.二年级奥数.杂题.时间与日期4.5.二年级奥数.杂题.数字游戏4.6.二年级奥数.杂题.重重叠叠4.7.二年级奥数.杂题.最大与最小几何专题把下面图形的边框勾成蓝色.封闭图形一周的长度,就是这个图形的周长.让学生更直观的来认识什么是图形的周长,然后让学生把图形的周长画一画,更能加深对“周长”这个抽象概念的理解.怎样才能知道图形的周长是多少?怎样来求呢?这节课我们就先从简单的长方形和正方形的周长开始研究吧!【例1】小精灵来到篮球场打球,发现篮球场是一个长方形的,他和小朋友量了量,这个篮球场长28米,宽15米.这个篮球场的周长是多少米?【例2】打完球小精灵累的满头大汗,这时小白兔送上来了一个手帕为他擦擦汗.这个手帕是正方形的,量了量每条边的长是2分米,这个正方形手帕的周长是多少?知识框架巧求周长例题精讲【例3】比一比,赛一赛.下面图形的周长,看谁算得快【例4】Hello Kitty去商场买回来一面镜子.她要沿镜子的四边做一个铝合金的边框,请你帮助算一算,大约需要多少米长的铝合金材料?【例5】明明用一根长30分米的黑线,给自己的照片镶了一条黑边,这个长方形相框的宽是6分米,你知道这个相框的长是多少分米?【例6】小明家有一个正方形的花坛,这个正方形的花坛边长是 6米,在这个正方形花坛的四周围上栏杆,栏杆长多少米?【例7】红红用一根28厘米的铁丝,围成了一个正方形,这个正方形的边长是多少?【例8】两个大小相同的正方形,拼成一个长方形后,周长比原来两个正方形周长的和减少了 4厘米,原来一个正方形的周长是多少厘米?【例9】如下图,你能求出这些图形的周长吗?【例10】求下图的周长【随练1】一个模型,如图,外形是两个重叠的正方形,正方形的边长是2分米,两个正方形重叠的相交点是正方形边的中点.求这个模型的周长是多少分米?课堂检测【随练2】如下图是一个长宽分别为60 厘米和50厘米的长方形.甲、乙两只小蚂蚁同时从A 出发,以同样的速度分别沿图中虚线爬行到达B点,问:哪只蚂蚁先到达?两只蚂蚁共爬行了多少路程?【作业1】求下面图形的周长.【作业2】一个长方形的周长是50 厘米,宽是10厘米,长是多少厘米?【作业3】用一根长44 厘米的绳子围成一个正方形,这个正方形的边长是多少?家庭作业【作业4】下图是一个游乐场的平面图,你跟根据已知条件,求出这个游乐场的周长是多少?【作业5】求下面图形的周长.【作业6】一个长12分米,宽5分米的长方形,如图在它的两个角上各减去一个小长方形,现在这个新的图形的周长是多少?【作业7】计算下面各图的周长.(单位:厘米)【作业8】下图的周长是多少厘米?形和数的密切关系,在古代就被人们注意到了.古希腊人发现的形数就是非常有趣的例子.最初的数和最简的图相对应.1 和·(点)2 和(线:两点连成一条直线)3 和(平面:三点确定一个平面)4 和(立体:不在同一平面上的四个点构成一个四面体)这是古希腊人的观点,他们说一切几何图形都是由数产生的.【例11】我国在春秋战国时代就有了“洛图”(见下图).图中也是用“圆点”表示数,而且还区分了偶数和奇数,偶数用实心点表示,奇数用空心点表示.你能把这张图用自然数写出来吗?【例12】古希腊数学家毕达哥拉斯发现了“形数”的奥秘.比如他把l,3,6,10,15,…叫做三角形数.因为用圆点按这些数可以堆垒成三角形,见下图.请写出第100个三角形数。
小学奥数知识点及公式总汇(必背)

⼩学奥数知识点及公式总汇(必背)⼩学奥数知识点及公式总汇(必背)1.和差倍问题 22.年龄问题的三个基本特征:3.归⼀问题的基本特点:4.植树问题5.鸡兔同笼问题6.盈亏问题 37.⽜吃草问题8.周期循环与数表规律9.平均数10.抽屉原理 411.定义新运算12.数列求和13.⼆进制及其应⽤ 514.加法乘法原理和⼏何计数15.质数与合数 616.约数与倍数17.数的整除 718.余数及其应⽤19.余数、同余与周期20.分数与百分数的应⽤ 821.分数⼤⼩的⽐较 922.分数拆分23.完全平⽅数24.⽐和⽐例 1025.综合⾏程26.⼯程问题27.逻辑推理 1128.⼏何⾯积29.⽴体图形30.时钟问题—快慢表问题 1231.时钟问题—钟⾯追及32.浓度与配⽐33.经济问题 1333.经济问题34.简单⽅程35.不定⽅程36.循环⼩数 14和差倍问题和差问题和倍问题差倍问题已知条件⼏个数的和与差⼏个数的和与倍数⼏个数的差与倍数公式适⽤范围已知两个数的和,差,倍数关系公式①(和-差)÷2=较⼩数较⼩数+差=较⼤数和-较⼩数=较⼤数②(和+差)÷2=较⼤数较⼤数-差=较⼩数和-较⼤数=较⼩数和÷(倍数+1)=⼩数⼩数×倍数=⼤数和-⼩数=⼤数差÷(倍数-1)=⼩数和-⼩数=⼤数差÷(倍数-1)=⼩数⼩数×倍数=⼤数⼩数+差=⼤数关键问题求出同⼀条件下的和与差和与倍数差与倍数 2.年龄问题的三个基本特征:①两个⼈的年龄差是不变的;②两个⼈的年龄是同时增加或者同时减少的;③两个⼈的年龄的倍数是发⽣变化的;3.归⼀问题的基本特点:问题中有⼀个不变的量,⼀般是那个“单⼀量”,题⽬⼀般⽤“照这样的速度”……等词语来表⽰。
关键问题:根据题⽬中的条件确定并求出单⼀量;4.植树问题基本类型在直线或者不封闭的曲线上植树,两端都植树在直线或者不封闭的曲线上植树,两端都不植树在直线或者不封闭的曲线上植树,只有⼀端植树封闭曲线上植树基本公式棵数=段数+1棵距×段数=总长棵数=段数-1棵距×段数=总长棵数=段数棵距×段数=总长关键问题确定所属类型,从⽽确定棵数与段数的关系 5.鸡兔同笼问题基本概念:鸡兔同笼问题⼜称为置换问题、假设问题,就是把假设错的那部分置换出来;基本思路:①假设,即假设某种现象存在(甲和⼄⼀样或者⼄和甲⼀样):②假设后,发⽣了和题⽬条件不同的差,找出这个差是多少;③每个事物造成的差是固定的,从⽽找出出现这个差的原因;④再根据这两个差作适当的调整,消去出现的差。
小学数学奥数知识点顺口溜

小学数学奥数知识点顺口溜一、整数四则运算正负结合简便记,两正相加更强力,同号相减均正数,异号相减看绝对。
乘法中符号不变化,同号正,异号负,除法中同正同负,同号正,异号负,除法进位有窍门,除整除,余继续。
二、分数的加减法分母相同简单了,分子相加就好。
分母不同不用愁,先通分再相加。
异分共分添加法,先找最小公倍数。
公倍数除分母得,分子相加乘倍数。
三、分数的乘除法分数乘法简单了,分子分母分别乘。
分数除法记窍门,倒数乘就没烦恼。
倒数就是分子分母调,再乘除法就好。
四、小数的四则运算小数加减先对齐,按位相加减就对。
小数乘法省工夫,先不算小数点位置。
两小数位数相加,小数点一起往后移。
小数点后有几位,结果小数点后就是。
五、比例与百分数比例问题要注意,等比例关系很重要。
百分数是百分之几,百分比不可忽视。
百分数转小数很简单,除以一百就是了。
小数转百分数说易行,乘以一百处理好。
六、几何图形平行线没有交,对应角相等。
三角形有分类,等边等腰直角。
正方形四边等,对角线相等长。
矩形对角线平分,长和宽用好。
梯形上底下底和高,求面积公式别忘。
圆的直径和周长,半径和面积要懂。
几何题多动脑,观察要细致思考。
七、解方程方程两边同时加减,使方程保持平衡。
方程两边同时乘除,等式依然成立。
解方程要记住,变量消失是最好。
去括号合并同类项,一元方程变一步。
分式方程有窍门,先去分母再求解。
方程题要动脑,试几个答案再求证。
总结:小学数学奥数知识点,顺口溜记牢牢。
整数分数小数运算,四则运算要规范。
比例百分数记心间,几何图形要观察。
解方程灵活应用,数学奥数轻松学习。
