旋转椭圆有5种方法
高中数学复习指导:生成椭圆的五种平面几何条件

x2 y 2 + = 1 上. a 2 b2
5.利用两直线的交点生成椭圆: 利用两直线的交点生成椭圆:
y −0 y −0 b2 y −b y +b b2 ⋅ = − 2 ,或 ⋅ =− 2 x−a x+a a x −0 x −0 a 2 2 2 2 2 2 2 x y y x y a −x (1) 把 2 + 2 = 1 变形为 2 = 1 − 2 , 2 = , a b b a b a2
椭圆方程: 椭圆方程:
y2 b2 y −0 y −0 b2 = ⋅ = − 在 x ≠ ±a 的条件下,又可变为 2 ,即 , a − x 2 a2 x−a x+a a2 b2 这表明椭圆上的点 ( x, y) 与长轴端点连线的斜率之比为定值 − 2 . a b2 即当我们过定点 (a,0) 、 ( −a,0) 作两条直线,其斜率之积为 − 2 时, a 2 2 x y 交点 M 在椭圆 2 + 2 = 1 上. a b 2 2 x y x2 y2 x2 b 2 − y 2 (2)把 2 + 2 = 1 变形为 2 = 1 − 2 , 2 = ,在 x ≠ 0 的条件下, a b a b a b2 b2 b 2 − y 2 y −b y +b b2 = ⋅ = − 又可变为 2 ,即 , a x2 x −0 x −0 a2 b2 这表明椭圆上的点 ( x, y ) 与短轴端点连线的斜率之比为定值 − 2 . a
生成椭圆的五种平面几何条件
我们以焦点在 x 轴上的椭圆为例探究其产生的主要的平面几何条件: 1.由两定点生成椭圆( : 由两定点生成椭圆(椭圆的定义) 椭圆的定义)
பைடு நூலகம்
( x + c)2 + y 2 + ( x − c)2 + y 2 = 2a ( 2a > 2c > 0 ) . 椭圆方程: 椭圆方程
【参考借鉴】尺规作图五点定椭圆的方法.docx
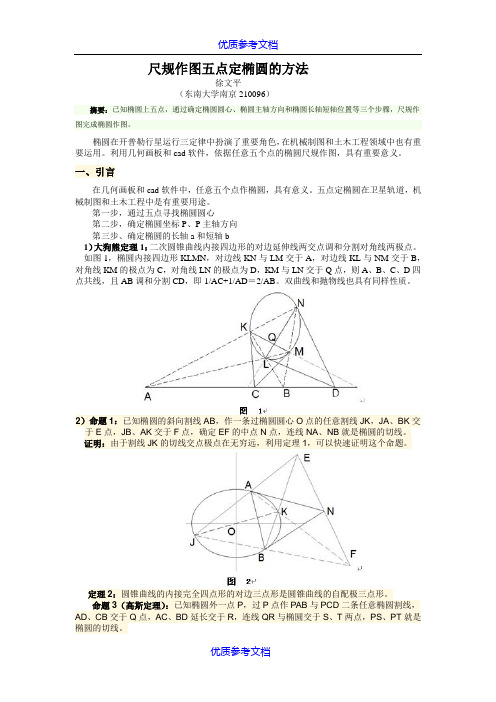
尺规作图五点定椭圆的方法徐文平(东南大学南京210096)摘要:已知椭圆上五点,通过确定椭圆圆心、椭圆主轴方向和椭圆长轴短轴位置等三个步骤,尺规作图完成椭圆作图。
椭圆在开普勒行星运行三定律中扮演了重要角色,在机械制图和土木工程领域中也有重要运用。
利用几何画板和cad软件,依据任意五个点的椭圆尺规作图,具有重要意义。
一、引言在几何画板和cad软件中,任意五个点作椭圆,具有意义。
五点定椭圆在卫星轨道,机械制图和土木工程中是有重要用途。
第一步,通过五点寻找椭圆圆心第二步,确定椭圆坐标P、P主轴方向第三步、确定椭圆的长轴a和短轴b1)大狗熊定理1:二次圆锥曲线内接四边形的对边延伸线两交点调和分割对角线两极点。
如图1,椭圆内接四边形KLMN,对边线KN与LM交于A,对边线KL与NM交于B,对角线KM的极点为C,对角线LN的极点为D,KM与LN交于Q点,则A、B、C、D四点共线,且AB调和分割CD,即1/AC+1/AD=2/AB。
双曲线和抛物线也具有同样性质。
2)命题1:已知椭圆的斜向割线AB,作一条过椭圆圆心O点的任意割线JK,JA、BK交于E点,JB、AK交于F点,确定EF的中点N点,连线NA、NB就是椭圆的切线。
证明:由于割线JK的切线交点极点在无穷远,利用定理1,可以快速证明这个命题。
定理2:圆锥曲线的内接完全四点形的对边三点形是圆锥曲线的自配极三点形。
命题3(高斯定理):已知椭圆外一点P,过P点作PAB与PCD二条任意椭圆割线,AD、CB交于Q点,AC、BD延长交于R,连线QR与椭圆交于S、T两点,PS、PT就是椭圆的切线。
图3二、通过五点寻找椭圆圆心原理:通过已知五点,作椭圆切线,获得割线的极点,将割线的极点和割线中点连接并延伸,必定通过椭圆的圆心。
图4问题1:只有五点,没有坐标轴和原点,椭圆斜的,割线PQ的切线极点如何办?切线方法:帕斯卡定理(五点+一个切点二次)做切线,或者如图5方法作切线。
犀牛命令详解

曲线命令 Curve --------------------------指令: _Line直线起点 ( 法线(N) 指定角度(A) 与工作平面垂直(V) 四点(F) 等角线(B) 垂直(P) 正切(T) 延伸(E) 两侧(O) ):直线终点 ( 两侧(B) ):指令: _Polyline多重直线起点:多重直线的下一点 ( 复原(U) ):多重直线的下一点。
操作完毕请按 Enter 键 ( 复原(U) ):多重直线的下一点。
操作完毕请按 Enter 键 ( 封闭(C) 复原(U) ):指令: _Rectangle矩形的第一角 ( 三点(P) 垂直(V) 中心点(C) 圆角(R) ):其他角或长度:指令: _Polygon内接多边形中心点 ( 边数(N)=5 外切(C) 边缘(E) 星形(S) 垂直(V) 环绕曲线(A) ):多边形的角 ( 边数(N)=5 ):指令: _Curve曲线起点 ( 阶数(D)=3 ):下一点 ( 阶数(D)=3 复原(U) ):下一点。
操作完毕请按 Enter 键 ( 阶数(D)=3 复原(U) ):下一点。
操作完毕请按 Enter 键 ( 阶数(D)=3 封闭(C) 尖锐封闭(S)=否复原(U) ):指令: _Circle圆心 ( 可塑形的(D) 垂直(V) 直径(I) 三点(P) 正切(T) 环绕曲线(A) ):半径 <10.296> ( 直径(D) ):指令: _Arc圆弧中心点 ( 可塑形的(D) 起点(S) 正切(T) 延伸(E) ):圆弧起点:终点或角度:指令: _Ellipse椭圆中心点 ( 垂直(V) 角(C) 直径(D) 从焦点(F) 环绕曲线(A) ):第一轴终点 ( 角(C) ):第二轴终点:指令: _Parabola抛物线焦点 ( 顶点(V) 标示焦点(M)=否一半(H)=否 ):抛物线 ( 标示焦点(M)=否一半(H)=否 ):抛物线终点 ( 标示焦点(M)=否一半(H)=否 ):焦点到顶点的距离 = 14.1394,长度 = 22.5428指令: _Conic圆锥线起点 ( 正切(T) 垂直(P) ):圆锥线终点 ( 顶点(A) 正切(T) 垂直(P) ):顶点:曲率点或 Rho:指令: _Helix轴的起点 ( 垂直(V) 环绕曲线(A) ):轴的终点:半径和起点 <1.000> ( 直径(D) 模式(M)=圈数圈数(T)=10 螺距(P)=1 反向扭转(R)=否 ):指令: _Spiral轴的起点 ( 平坦(F) 垂直(V) 环绕曲线(A) ):轴的终点:第一半径和起点 <1.000> ( 直径(D) 模式(M)=圈数圈数(T)=10 螺距(P)=1.4 反向扭转(R)=否 ): 第二半径 <0> ( 直径(D) 模式(M)=圈数圈数(T)=10 螺距(P)=1.4 反向扭转(R)=否 ):指令: _Extend选取边界物件或输入延伸长度。
椭圆方程的几种常见求法

椭圆方程的几种常见求法对于求椭圆方程的问题,通常有以下常见方法:一、定义法例1 已知两圆C1:,C2:,动圆在圆C1内部且和圆C1 相内切,和圆C2相外切,求动圆圆心的轨迹方程.分析:动圆满足的条件为:①与圆C1相内切;②与圆C2相外切.依据两圆相切的充要条件建立关系式.解:设动圆圆心M(,),半径为,如图所示,由题意动圆M内切于圆C1,∴,圆M外切于圆C2 ,∴,∴,∴动圆圆心M的轨迹是以C1、C2为焦点的椭圆,且,,故所求轨迹方程为:.评注:利用圆锥曲线的定义解题,是解决轨迹问题的基本方法之一.此题先根据平面几何知识,列出外切的条件,内切的条件,可发现利用动圆的半径过度,恰好符合椭圆的定义.从而转化问题形式,抓住本质,充分利用椭圆的定义是解题的关键.二、待定系数法例2已知椭圆的中心在原点,以坐标轴为对称轴,且经过两点,求该椭圆的方程.分析:已知两点,椭圆标准方程的形式不确定,我们可以设椭圆方程的一般形式:=1(,进行求解,避免讨论。
解:设所求的椭圆方程为=1(.∵椭圆经过两点,∴解得,故所求的椭圆标准方程为.评注:求椭圆标准方程,可以根据焦点位置设出椭圆标准方程,用待定系数法求出的值:若焦点位置不确定,可利用椭圆一般形式简化解题过程.三、直接法例3设动直线垂直于轴,且交椭圆于A、B两点,P是上线段AB外一点,且满足,求点P的轨迹方程.分析:如何利用点P的坐标与椭圆上A,B两点坐标的关系,是求点P的轨迹的关键,因直线垂直于轴,所以P、A、B三点的横坐标相同,由A、B在椭圆上,所以A、B两点的纵坐标互为相反数,因此,紧紧抓住等式即可求解.解:设P(,),A(,),B(,),由题意:==,+=0∴,,∵P在椭圆外,∴-与-同号,∴=(-)(-)=∵,即为所求.评注:求轨迹方程,首先要找出动点与已知点之间的关系,建立一个等式,用坐标代换.四、相关点法例4的底边BC=16,AC和AB两边上的中线长之和为30,求此三角形重心G和定点A的轨迹方程.分析:由题意可知G到B、C两点的距离之和为定值,故可用定义法求解,A点和G点的关系式好建立,故可用相关点法去求.解(1)以BC边所在直线为轴,BC边的中点为坐标原点建立直角坐标系,设G(,),由,知G点的轨迹是以B、C为焦点,长轴长为20的椭圆且除去轴上的两顶点,方程为.(2)设A(,),G(,则由(1)知G的轨迹方程是∵G为的重心∴代入得:其轨迹是中心为原点,焦点在轴上的椭圆,除去长轴上的两个端点.评注:本题的两问是分别利用定义法和相关点法求解的,要注意各自的特点,另要注意轨迹与轨迹方程的不同.。
生成椭圆的五种平面几何条件

生成椭圆的五种平面几何条件我们以焦点在x 轴上的椭圆为例探究其产生的主要的平面几何条件:1.由两定点生成椭圆(椭圆的定义):椭圆方程2a (220a c >>).若动点(,)M x y 到定点1(,0)F c -、2(,0)F c 距离之和为定值2a ,其中220a c >>, 则动点M 的轨迹是椭圆.根据这个定义,椭圆方程为:2a (220a c >>). 可以进一步导出椭圆的标准方程为22221x y a b+=,其中222b a c =-. 2.由一定点与定直线生成椭圆(推导标准方程过程中的副产品):c a x c=- (0a c >>). 根据椭圆的定义可知椭圆上的点(,)M x y 满足方程:2a ,将左边的一个根式移到右边并两边平方可得2a cx -=c a x c=-(,)x y 与2(,0)F c 的距离, 2a x c -表示(,)x y 与直线2a x c=的距离, 因此当点(,)M x y 满足椭圆到定点2(,0)F c 与到定直线2a x c =距离之比为定值c a时, 得到点(,)M x y 的轨迹方程为22221x y a b+=. 3.用一个圆生成椭圆:椭圆方程:22()()1xy a b+=(a b ≠) 把22221x y a b +=变形为22()()1x y a b+=,设椭圆上任意一点00(,)M x y , 则2200()()1x y a b +=,令0x x a =,0y y b=,则221x y +=, 注意到0x ax =,0y by =,即把圆221x y +=上的点的横坐标变为原来的a 倍, 同时纵坐标变为原来的b 倍,其中a b ≠,则得椭圆22221x y a b+=. 4.利用两个圆生成椭圆:椭圆方程: cos ,sin .x a y b θθ=⎧⎨=⎩把22221x y a b +=变形为22()()1x y a b+=, 联想22cos sin 1θθ+=,于是利用三角换元cos x a θ=,sin y bθ=, 即cos x a θ=,sin y b θ=,其中cos x a θ=可以看作圆222x y a +=上点的横坐标,sin y b θ=可以看作圆222x y b +=上点的横坐标,于是以两个同心圆为基础可以作出椭圆,作法如下:如图1,作射线OA 交圆222x y a +=于A ,交圆222x y b +=于B ,过A 作AN x ⊥轴于N ,过B 作BM AN ⊥轴于M ,则M 的坐标为(cos ,sin )a b θθ,显然M 在椭圆22221x y a b+=上. 5.利用两直线的交点生成椭圆:椭圆方程: 2200y y b x a x a a --⋅=--+,或2200y b y b b x x a-+⋅=--- (1) 把22221x y a b +=变形为22221y x b a =-,22222y a x b a -=,在x a ≠±的条件下,又可变为22222y b a x a =-,即2200y y b x a x a a --⋅=--+, 这表明椭圆上的点(,)x y 与长轴端点连线的斜率之比为定值22b a-. 即当我们过定点(,0)a 、(,0)a -作两条直线,其斜率之积为22b a-时, 交点M 在椭圆22221x y a b+=上. (2)把22221x y a b +=变形为22221x y a b =-,22222x b y a b -=,在0x ≠的条件下, 又可变为22222b b y a x-=,即2200y b y b b x x a -+⋅=---, 这表明椭圆上的点(,)x y 与短轴端点连线的斜率之比为定值22b a -. 即当我们过定点(0,)b 、(0,)b -作两条直线, 其斜率之积为22b a -时,交点M 在椭圆22221x y a b+=上.。
椭圆的五种画法及各种弦的制作(很不错的几何画板教程).
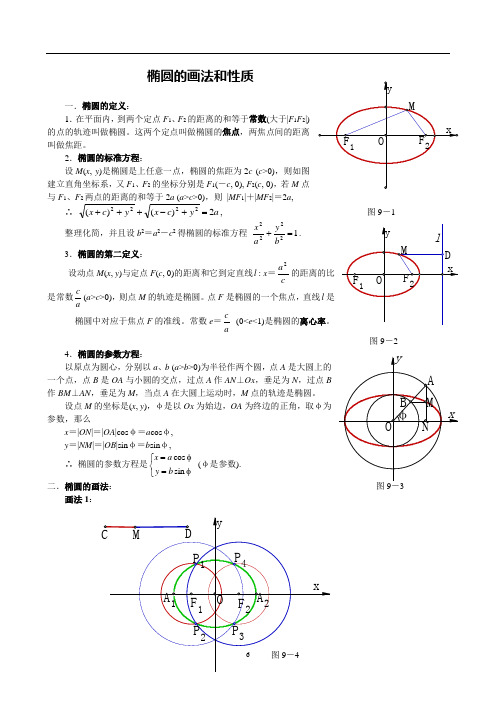
椭圆的画法和性质一.椭圆的定义: 1.在平面内,到两个定点F 1、F 2的距离的和等于常数(大于|F 1F 2|)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点间的距离叫做焦距。
2.椭圆的标准方程:设M (x , y )是椭圆是上任意一点,椭圆的焦距为2c (c >0),则如图建立直角坐标系,又F 1、F 2的坐标分别是F 1(-c , 0), F 2(c , 0),若M 点与F 1、F 2两点的距离的和等于2a (a >c >0),则 |MF 1|+|MF 2|=2a ,∴a y c x y c x 2)()(2222=+-+++, 图9-1整理化简,并且设b 2=a 2-c 2得椭圆的标准方程12222=+b y a x . 3.椭圆的第二定义:设动点M (x , y )与定点F (c , 0)的距离和它到定直线l : x =ca2的距离的比是常数ac(a >c >0),则点M 的轨迹是椭圆。
点F 是椭圆的一个焦点,直线l 是椭圆中对应于焦点F 的准线。
常数e =ac(0<e <1)是椭圆的离心率。
图9-24.椭圆的参数方程:以原点为圆心,分别以a 、b (a >b >0)为半径作两个圆,点A 是大圆上的一个点,点B 是OA 与小圆的交点,过点A 作AN ⊥Ox ,垂足为N ,过点B 作BM ⊥AN ,垂足为M ,当点A 在大圆上运动时,M 点的轨迹是椭圆。
设点M 的坐标是(x , y ),φ是以Ox 为始边,OA 为终边的正角,取φ为参数,那么x =|ON |=|OA |cos φ=a cos φ,y =|NM |=|OB |sin φ=b sin φ,∴ 椭圆的参数方程是⎩⎨⎧φ=φ=sin cos b y a x (φ是参数).二.椭圆的画法:画法1:1.在x 轴上取两点F 1、F 2,使|OF 1|=|OF 2|,用它们作为两个焦点; 2.在图形外作一条线段CD ,使|CD |=2a ,(|CD |>|F 1F 2|); 3.以O 为中心,在x 轴上取两点A 1、A 2,使|A 1A 2|=|CD |;4.在CD 上分别取C '、D ',使|CC '|=|A 1F 1|=|DD '|;作线段C 'D ',并用“作图”菜单中的“对象上的点”功能在C 'D '上作点M ;5.分别以F 1、F 2为圆心,用|CM |、|MD |为半径作圆,两圆相交于P 1、P 2两点;同样方法分别以F 1、F 2为圆心,用|DM |、|CD |为半径作圆,两圆相交于P 3、P 4两点;并将这四个点定义为“追踪点”;6.依次选中点M 、点P 1 (或点M 、点P 2),用“作图”菜单中的“轨迹”功能,作出椭圆。
椭圆题型总结 课件高二上学期数学人教A版(2019)选择性必修第一册

∙ 2 = 2 ∙tanΘ
(2π),即
Θ∈(0,
2
),令P由点A向点B运动,则△F 1 PF 2 的边
F 1 F 2 不变,但边F 1 F 2 上的高在逐渐增大,故 S逐渐增大,
从而tanΘ逐渐变大,由Θ∈(0,
提示:确定动点满足条件→建立等式→判断是否符合椭圆定义
→求方程→验证
如图所示,以线段BC所在直线为x轴,线段BC的垂直平分线
为y轴,建立平面直角坐标系,设A(x,y),由题意得,知B(-
3,0),C(3,0),
|AB|+|BC|+|AC|=16,又|BC|=6,所以|AB|+|AC|=10,
因为|AB|+|AC|>|BC|,
3.1椭圆
题型总结
题型一:求椭圆的标准方程
● 定义法:例1:如图,已知椭圆C的中心为原点O,F(-2 5, 0)为C的左焦点,P为C上一点,若
)
|OP|=|OF|,且|PF|=4,则椭圆C的方程为(
2
A.
25
2
C.
30
+
2
5
+
2
10
2
36
=1
.
=1
2
D.
45
+
+
2
16
2
25
=1
=1
=(|PF1|+|PF2|)2-2∙|PF1|∙|PF2|-2∙|PF1|∙|PF2|∙cos2Θ=4a22∙|PF1|∙|PF2|∙(1+cos2Θ)=4c2
22
所以|PF1|∙|PF2|=
,
1+cos2Θ
光的横波性与五种偏振态解读

结论:
(1)圆偏振光可以分解为两个互相垂直 的振幅相等、相位差为 / 2 的线偏振光。 (2)可以由这两束线偏振光来代替 这束圆偏振光。
4)圆偏振光的总光强:
I A A 2A
2 x 2 y
2
5)左旋圆偏振光与右旋圆偏振光
(1)定义: 迎着光线传播方向观看, 若振动矢量 E 顺时针旋转就称为 右旋圆偏振光,此时: / 2 若振动矢量 E 逆时针旋转就称为 左旋圆偏振光,此时: / 2
I0
自然光
P
I
1 旋转偏振片P一周,出射光强均为: I I0 2
若入射的自然光强为:I 0
3)试证明自然光通过偏振片后 出射光强为入射光强的一半。
自然光由无数条非相干的线偏振光组成 数密度: 单位夹角内包 含的 线偏振光的条数 ( ) 0 角内包含的线偏振 光的条数:
A
注意:
(1)只适用于线偏振光 (2)马吕斯定律公式上的 三角函数项是平方项。
5)起偏器和检偏器
起偏器:任何偏振态的光通过后透射 光都变为线偏振光的器件。 检偏器:检查入射光偏振态的器件 线偏振射光通过此器件后光 强变为零。 偏振片既是起偏器,又是检偏器。
6)一束线偏振光可以分解为两束 互相垂直的线偏振光
若振动矢量 E 顺时针旋转就称为 右旋椭圆偏振光, 若振动矢量 E 逆时针旋转就称为
左旋椭圆偏振光。
6)各种相位差对应的椭圆偏振态图
(1)当坐标系为如图所示时 (2)参量方程为:
Ex Ax cos(t )
Ey Ay cos( t )
y
x
(3)就有如下的各种相位差对应的椭圆偏振态图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
旋转椭圆有5种方法。
1:使用圆锥曲线,此方法是唯一能直接在草绘中画出斜置椭圆的办法。
画4条首尾相接的圆锥曲线,rho值均为sqrt(2)-1,交点均与长短轴成90度。
绘制出椭圆。
如图:
图有点乱。
2:旋转参照。
在草绘之前,先建好一个有角度的基准平面,以此基准平面作为草绘参照。
在草绘中直接绘出正交椭圆,完成后即为有与基准平面角
度一样的斜椭圆。
如图:
[ 此帖被醋男李果在2009-04-30 09:35重新编辑
]
顶端
Posted: 2009-04-28 22:18 |
3 楼
醋男李果
级别: 工程师
精华: 0
发帖: 895
威望: 2 点
小 中 大 引用 推荐 编辑 只看 复制
3:旋转复制。
先草绘一个正交椭圆,退出草绘。
然后复制,再选
择性复制,选择旋转放置。
如图:
9 7 0机械币贡献值: 0点注册时间: 2 0 0 8 -1 1 -0 8 最后登录: 2 0
1
-1 0 -2 8
4:使用方程。
这个方法只限于曲线。
笛卡尔方程如下:x=A*cos(t*360+T)
y=b*sin(t*360) z=0 A,B为长轴短轴,T为旋转角度。
5:先绘制一正交椭圆,再应用“旋转”变换。
此法完成后,原来的正交椭圆消失,不再显示。
修改角度应修改“扭曲”特例,修改长短轴应修改
正交椭圆。
此方法只适用于4.0野火版。
如图:
[ 此帖被醋男李果在2009-04-30 09:33重新编辑 ]
.。
