06 测验常模及分数的合成
合集下载
心理学测量笔记连载第四章:测验的常模和分数的解释

4、 常模样本:
找来代表常模总体的样本,就是常模样本。常模样本必须具备常模总体的基本特征。
5、 常模样本的容量:
总体的数目。一般情况,最小样本为30 ~ 100个。要是全国性的常模,一般地要求有2000 ~ 3000人为宜。
3、 常模团体:
做心理测验,得到的测验分数需要做出有意义的解释,因而参考标准不可缺少。导出分数是由原始分数转换而来,而原始分数由被试完成测验后得到,因此,许多被试构成的人群就是构成参照标准的被试团体,也叫参照团体,或叫常模团体。
常模团体是由具有某些共同特征的人所组成的一个群体,或者是该群体的一个样本。
心理学测量笔记连载第四章:测验的常模和分数的解释
1、 导出分数:
原始分数的意义需有参照意义标2、 准才能体现出来,在心理测验中,这种标准是由原始分数构成的分布转换而来的分数,就叫导出分数。导出分数具有一定的参照点和单位。
2、 常见的导出分数分:
常模参照分数、内容参照分数、结果参照分数。
人们常常会忽略常模的时间性。常模分数和常模均会随时间的变化而改变,因此常模必须经常修订。
9、 常模的表示方法:
6、 取样
就是:从目标总体中选择有代表性的样本。一般地有两类取样方法:随机抽样和非随机抽样。具体说有:简单随机抽样、系统抽样、分组抽样、分层抽样。
7、 常模分数:
就是施测常模样本被试后,将被试的原始分数按一定规则转换出来的导出分数。
8、 常模分数构成的分布是:
通常所说的常模。它是解释心理测验分数的基础。
找来代表常模总体的样本,就是常模样本。常模样本必须具备常模总体的基本特征。
5、 常模样本的容量:
总体的数目。一般情况,最小样本为30 ~ 100个。要是全国性的常模,一般地要求有2000 ~ 3000人为宜。
3、 常模团体:
做心理测验,得到的测验分数需要做出有意义的解释,因而参考标准不可缺少。导出分数是由原始分数转换而来,而原始分数由被试完成测验后得到,因此,许多被试构成的人群就是构成参照标准的被试团体,也叫参照团体,或叫常模团体。
常模团体是由具有某些共同特征的人所组成的一个群体,或者是该群体的一个样本。
心理学测量笔记连载第四章:测验的常模和分数的解释
1、 导出分数:
原始分数的意义需有参照意义标2、 准才能体现出来,在心理测验中,这种标准是由原始分数构成的分布转换而来的分数,就叫导出分数。导出分数具有一定的参照点和单位。
2、 常见的导出分数分:
常模参照分数、内容参照分数、结果参照分数。
人们常常会忽略常模的时间性。常模分数和常模均会随时间的变化而改变,因此常模必须经常修订。
9、 常模的表示方法:
6、 取样
就是:从目标总体中选择有代表性的样本。一般地有两类取样方法:随机抽样和非随机抽样。具体说有:简单随机抽样、系统抽样、分组抽样、分层抽样。
7、 常模分数:
就是施测常模样本被试后,将被试的原始分数按一定规则转换出来的导出分数。
8、 常模分数构成的分布是:
通常所说的常模。它是解释心理测验分数的基础。
第六章-常模与测验分数的解释

多重划分(连续栅栏)
几个预测源都很重要,并且所测特质之 间不能互相补偿时需要给每个预测源都 确定一个标准,将个体成绩划分为合格 与不合格两类。(咨询师考试)
测验分数解释
解释分类
常模参照 测验
测验 分类
标准参照 测验
测验分数解释模型
高德曼三维模型 资料来源 资料处理方法 解释测验分数
一、心理年龄
按照儿童心理发展的程度锁定的年龄 20世纪初,比奈提出了将一个儿童的行为与各 年龄的水平的一般儿童比较以测量心理成长的 设想。在1908年修订的比奈-西蒙量表中开始 用年龄做单位来度量智力。 要将原始分数变成年龄分数必须有年龄常模。 怎样制作年龄常模呢? 选择一标准化样组作为常模团体,对常模团体 进行测验,得到原始分数,求出每个年龄组的 平均分数,这一平均分数就是原始分数,这个 年龄组的年龄就是这个原始分数对应的智力年 龄。
评价: 1.能充分利用总体已知信息,提高样本 的代表性。 2.花费小。
back
(四)整群抽样 聚类抽样 先将总体分为若干个群体,随机抽取一些群体, 然后以这些群内所有个体构成样本 优点:便于实施,节省费用 缺点:样本分布面不广,样本对整体的代表性 相对较差,抽样误差往往大于简单随机抽样。 back
年龄量表的基本要素是:1.一套可区分 不同年龄组的题目2.一个由各个年龄的 被试所组成的代表性样本(即常模团体) 3.一个表明答对哪些题或得多少分可归 入哪个年龄的对照表(即常模表)
年龄量表的评价: 优点:1.容易理解。 缺点: 1. 一个测验题目归入哪个年龄组的标准 不易确定。 2. 年龄量表的单位不是等距的,只表示 一个人心理发展的绝对水平,不能表示 心理发展的相对水平。 3. 获得相同的年龄分数并不表明具有相 同的心理水平。
分数合成与解释

标准化样组的规模要有适当的大小 标准化样组是一定时空的产物
3.2 常用的概率抽样方法
表选 择被试作为样本。保证每个人都有相同的机会进入样本。
等距抽样
以被试的某些与所测特征无关的特性(如电话号码、学号)将被 试按照一定的顺序排列,研究者确定一个随机的起始点,如果从 总体中抽取1/K的被试,那么列表中第K个就成为样本成员。
单位加权:各个变量直接相加合成分数 XC=X1+X2+X3…+Xn 非等量加权,合成后,变异较大的变量将在
预测和作决定时起较大作用。 案例:为什么教科院的分数线这么高?
研究生入学考试:专业课、外语、政治
等量加权 要对各个变量作等量加权,可将所有分数转 换成标准分数(Z),然后相加。 ZC=Z1+Z2+Z3+…+Zn 在特殊情况下使用:
分数合成与解释
打起精神!!! 不许瞌睡!!!
主要内容
分数合成 分数解释 常模化样组 组内常模 发展性常模
1、分数的合成
分数合成的层次 分数合成的方法
1.1 分数合成的层次
项目的组合
Xa= ∑ Xai
分量表的组合 案例:以SCL-90 为例 测验的组合 案例:高考、研究生入学考试
分数解释:应注意的问题
从遗传特征、测验前经验和测验情境三个方 面解释测验分数
解释测验分数时,要寻求常模资料、信效度 资料
测验分数是对真实分数的最佳区间估计。
分数解释:如何向当事人报告分数
使用当事人理解的语言 保证当事人知道测验目的 明确解释常模团体 认识到“分数”是最佳估计 使当事人知道如何运用他的分数 注意测验分数给当事人带来的心理影响 让当事人积极参与分数解释
1.2 分数合成的方法
3.2 常用的概率抽样方法
表选 择被试作为样本。保证每个人都有相同的机会进入样本。
等距抽样
以被试的某些与所测特征无关的特性(如电话号码、学号)将被 试按照一定的顺序排列,研究者确定一个随机的起始点,如果从 总体中抽取1/K的被试,那么列表中第K个就成为样本成员。
单位加权:各个变量直接相加合成分数 XC=X1+X2+X3…+Xn 非等量加权,合成后,变异较大的变量将在
预测和作决定时起较大作用。 案例:为什么教科院的分数线这么高?
研究生入学考试:专业课、外语、政治
等量加权 要对各个变量作等量加权,可将所有分数转 换成标准分数(Z),然后相加。 ZC=Z1+Z2+Z3+…+Zn 在特殊情况下使用:
分数合成与解释
打起精神!!! 不许瞌睡!!!
主要内容
分数合成 分数解释 常模化样组 组内常模 发展性常模
1、分数的合成
分数合成的层次 分数合成的方法
1.1 分数合成的层次
项目的组合
Xa= ∑ Xai
分量表的组合 案例:以SCL-90 为例 测验的组合 案例:高考、研究生入学考试
分数解释:应注意的问题
从遗传特征、测验前经验和测验情境三个方 面解释测验分数
解释测验分数时,要寻求常模资料、信效度 资料
测验分数是对真实分数的最佳区间估计。
分数解释:如何向当事人报告分数
使用当事人理解的语言 保证当事人知道测验目的 明确解释常模团体 认识到“分数”是最佳估计 使当事人知道如何运用他的分数 注意测验分数给当事人带来的心理影响 让当事人积极参与分数解释
1.2 分数合成的方法
06测验分数的意义与解释

内容参照又称范围参照,领域参照。
指衡量被试对指定范围中的知识或技能
掌握如何。 主要适用范围:成就测验,资格测验。
1.掌握分数(mastery score)
标准九(stanine)
标准化九级分制 标准九=5+2Z,即平均数为5,标准差为2
标准九分 9 8 7 6 5 4 本段面积(%) 4 7 12 17 20 17 累加面积(%) 100 96 89 77 60 40 段中值与平均 数的距离() >2.0 1.5 1.0 0.5 0 0.5
返回
3.顺序量表(ordinal scales)
用于鉴别儿童在具体行为机能的发展中所达到的阶段。 盖塞尔发展程序表:按月份显示儿童在运动、适应性、 语言、社会性等方面的大致发展水平。
4周
不能控制 头部,仰 卧姿势左 右不对称
16周
颈可竖直, 头微摇动, 仰卧姿势左 右对称
28周
40周
52周
扶起独坐, 可独坐,爬 身体前倾 行,扶着物 件站立
返回
常态化的标准分数
大多数常模参照测验的编制者都假设测验对 象总体的水平呈正态分布,但在实践中获取 的样组测验分数并非都呈正态分布。 为了更好地解释被试个体分数在团体中的相 对位置,能对各分测验的分数进行综合,测 验编制者常常把测验分数转换为正态分布的 标准分数。
常模原始分数的正态性检验
正态性检验
标准九的分布特点
返回
正态Z分数与标准十的转换方法
正态Z分数 z<-2.0 -2.0≤Z<-1.5 -1.5≤Z<-1.0 -1.0≤Z<-0.5 -0.5≤Z<0.0 0.0 ≤Z<0.5 0.5≤Z<1.0 1.0≤Z<1.5 1.5≤Z<2.0 Z≥2.0 合计 标准等级 总体中的百分比 1 2.3% 2 4.4% 3 9.2% 4 15.0% 5 19.1% 6 19.1% 7 15.0% 8 9.2% 9 4.4% 10 2.3% 100% —
指衡量被试对指定范围中的知识或技能
掌握如何。 主要适用范围:成就测验,资格测验。
1.掌握分数(mastery score)
标准九(stanine)
标准化九级分制 标准九=5+2Z,即平均数为5,标准差为2
标准九分 9 8 7 6 5 4 本段面积(%) 4 7 12 17 20 17 累加面积(%) 100 96 89 77 60 40 段中值与平均 数的距离() >2.0 1.5 1.0 0.5 0 0.5
返回
3.顺序量表(ordinal scales)
用于鉴别儿童在具体行为机能的发展中所达到的阶段。 盖塞尔发展程序表:按月份显示儿童在运动、适应性、 语言、社会性等方面的大致发展水平。
4周
不能控制 头部,仰 卧姿势左 右不对称
16周
颈可竖直, 头微摇动, 仰卧姿势左 右对称
28周
40周
52周
扶起独坐, 可独坐,爬 身体前倾 行,扶着物 件站立
返回
常态化的标准分数
大多数常模参照测验的编制者都假设测验对 象总体的水平呈正态分布,但在实践中获取 的样组测验分数并非都呈正态分布。 为了更好地解释被试个体分数在团体中的相 对位置,能对各分测验的分数进行综合,测 验编制者常常把测验分数转换为正态分布的 标准分数。
常模原始分数的正态性检验
正态性检验
标准九的分布特点
返回
正态Z分数与标准十的转换方法
正态Z分数 z<-2.0 -2.0≤Z<-1.5 -1.5≤Z<-1.0 -1.0≤Z<-0.5 -0.5≤Z<0.0 0.0 ≤Z<0.5 0.5≤Z<1.0 1.0≤Z<1.5 1.5≤Z<2.0 Z≥2.0 合计 标准等级 总体中的百分比 1 2.3% 2 4.4% 3 9.2% 4 15.0% 5 19.1% 6 19.1% 7 15.0% 8 9.2% 9 4.4% 10 2.3% 100% —
心理测量学测验常模

第14页
标准九分
9 8 7 6 5 4 3 2 1
本段变积
4% 7% 12% 17% 20% 17% 12% 7% 4%
累加变积
100% 96 89 77 60 40 23 11 4
心理测量学测验常模
第15页
心理测量学测验常模
第16页
第二节 分数合成
一、分数合成意义 (一)种类 1.项目标组合 2.分测验或量表组合 3.测验或预测源组合
心理测量学测验常模
心理测量学测验常模
第1页
第一节 分数转换
一、基础概念
1.原始分数 被试在接收测验后,依据测验记分标准,对照被试反
应所计算出测验分数 2.导出分数 在原始分数转换基础上,按照一定规则,经过统计处
理后取得含有一定参考点和单位,且能够相互比较分 数。 3.分数转换 按某种规则将原始分数转化为导出分数过程。
(2)过程:联立方程 (3)输出: ①回归方程式(各个预测源加权量) ②复相关系数R
R2:决定系数,表示效标中变异数可由预测源来解释百分比
心理测量学测验常模
第24页
3.预测源确实定
首先选取最正确预测源 直到渐近效度不再增加 普通2-4个 条件:线性关系、连续性资料、同时取得
心理测量学测验常模
第25页
(四)多重划分
1.条件:预测源间不具互偿性
2.含义:在各个特质上都确定一个标准,从 而把成绩划分为合格与不合格两类。在一 个测验上合格了,不能确保总要求一定能 合格。只有每个测验都合格时,总要求才 算合格。
心理测量学测验常模
第26页
3.过程:连续栅栏
最有效预测源前置 其它原因:比较简单、花费少前置
心理测量学测验常模
第六章-测验常模

10
9
30~ 21 64 40.76
25~ 16 43 27.39
20~ 11 27 17.20
15~ 9 16 10.19
10பைடு நூலகம் 7 7 4.46
合计 157
三、原则分数(standard score) (一)定义及特征
• 又叫基分数或Z分数,是以原则差为单位表达原始分数 在团队中所处位置旳相对位置量数。
5. 原始分数转换成Z分数后,只需要看Z分数旳数 值和正负号,就能够立即明确该原始分数旳相对 地位。(可见,Z分数比使用平均分和原始分数体 现了更多信息。)
(二)性质
1.一组原始数据所相应旳Z分数旳和为0,则Z分数 旳平均数也为0。
2.一组数据所相应旳Z分数旳原则差为1。
(三)优点
1.可比性。不同性质旳分数转换为原则分数(均值为0, 原则差=1),就把它们放在了同一背景(Z分数), 这么具有可比性。
瑞文原则推理测验智力水平分级原则
• 测验原则分数等于或超出同年龄常模组旳95 一级 %,为高水平智力。 二级 • 测验原则分数在75%-95%之间,智力水平
良好。 三级 • 测验原则分数在25%-75%之间,为中档水
平智力。 四级 • 测验原则分数在5%-25%之间,智力水平
中下。 五级 • 测验原则分数低于5%,为智力缺陷。
四、原则分数旳变式 • T分数:T=10Z+50( 平均数是50,原则差为10。)
• Δ=13+4Z • Z’=A·Z+B
五、原则九分数 • 其量表是9级分数量表(1-9)。 • 以1为间距,它是以5为平均数,以2为原则差旳一
种分数量表。P100
第二节 分数合成
一、种类:3种 • 1、将基本测验项目构成一种测验或分测验; • 2、由几种分测验上旳得分构成测验总分数; • 3、由几种测验旳得分组合,取得合成预测。 二、分数合成旳措施 • 1、临床诊疗——直觉合成 • 2、加权求和合成 • 3、多重回归 • 4、多重划分
第七章测验的常模

分数转换
分数合成 常模编制
第一节分数转换
原始分数与导出分数
百分等级分数 标准分数
一、原始分数与导出分数
被试在接受测验后,根据测验的记分标准,对 照被试的反应所计算出的分数称作原始分数。 导出分数就是在原始分数的基础上,按照一定 的规则,经过统计处理后获得的具有一定参照 点和单位,且可以相互比较的分数。
某团体共100人,试问第15名的百分等级是多 少?
若团体人数分别为50人,40人,20人时,其
百分等级是多少?
若团体人数为200,500,1000呢?
100 15 50 P 100 85.5 15 100 10015 50 P 100 71 15 50 P 63.75, P 27.5 15 15
葛塞尔(1947)婴儿 早期行为发展顺序量表
婴幼儿智力发展量表
葛塞尔发展量表(1940,4周~5岁) 麦利尔-帕尔默量表(1岁半~6岁) 卡特尔婴幼儿评定量表(1973,3天~4周) 贝利婴儿发展是表(1933,1969,2~30月) 麦卡锡儿童能力量表(1972,2岁半~8岁半) 考夫曼儿童成套评估测验(1983,2.5~12.5) 丹佛发展筛选测验(1967,初生~6岁) 中国0~3岁小儿精神检查表(茅于燕) 中国3~6岁儿童发展量表(1985,张厚粲)
二、分数合成的方法
(一)临床诊断——直觉合成 根据主观经验,直觉地将各种因素加权,而获得结论 或预测的方法叫做临床诊断。 优点: 1、具有高度的综合性。 2、具有灵活针对性,能就特定个人作具体的结论。 缺点: 1、主观加权易受决策者的偏见影响,不够客观。 2、缺乏精确的数量分析,没有精确的数量指标。
心理测验常模与测验分数的解释
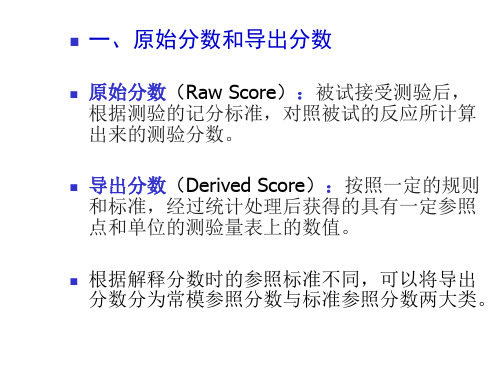
PR为百分等级,R为排名顺序的序号,N为 被试总人数。
例2:某被试在一次有50人参加的测验中得 80分,排名第9,则该生成绩的百分等级为 多少?
例1:下表是某班智力测验的分数分布,请计 算原始分数为40~45的百分等级。
分组区间 55~60
50~55 45~50 40~45 35~40 30~35 25~30 20~25
2.剖析图(Profiles) 剖析图是将一套测验中几个分测验分数在一张图上呈
现出来,以便更直观地比较被试在几个分测验上的表 现,并对其在整个测验上的表现得出一个整体的印象。 如,韦氏儿童智力测验剖析图(见word文档)或P131 图7-3 一些著名的人格测验,如MMPI、16PF等都在测验手册 上说明剖析图的制作方法。
线性转换标准分数的性质:
1. 标准分数的分布的平均数为0,标准差为1;
2.Z分数有正负之分,正表示大于平均数,负 表示小于平均数。表示离开平均数多少个标准 差。
3.是等距量表,能进行四则运算。
4. 其分布形状与原始分数相同,结果没有丝 毫失真。
5.假如原始分数的分布为常态,则Z分数的范 围大致是-3~3。
前所编制的常模可能不再适合,因此常模必须 定期地修订,并尽可能采用新近的常模。 6.要将一般常模和特殊常模结合起来
常用的具体抽取方式有抽签法和随机数字法。
1.抽签:把总体中的每一个个体编上号并作出签,充 分混合后从中随机抽取一部分,这部分签所对应的个 体就组成一个样本。
2.随机数字表
用随机数字表来抽取数字。
3.美国大学入学考试委员会使用的标准分数: CEEB分数:
CEEB 500100Z
20- 12
32
26
0.26 -0.64
例2:某被试在一次有50人参加的测验中得 80分,排名第9,则该生成绩的百分等级为 多少?
例1:下表是某班智力测验的分数分布,请计 算原始分数为40~45的百分等级。
分组区间 55~60
50~55 45~50 40~45 35~40 30~35 25~30 20~25
2.剖析图(Profiles) 剖析图是将一套测验中几个分测验分数在一张图上呈
现出来,以便更直观地比较被试在几个分测验上的表 现,并对其在整个测验上的表现得出一个整体的印象。 如,韦氏儿童智力测验剖析图(见word文档)或P131 图7-3 一些著名的人格测验,如MMPI、16PF等都在测验手册 上说明剖析图的制作方法。
线性转换标准分数的性质:
1. 标准分数的分布的平均数为0,标准差为1;
2.Z分数有正负之分,正表示大于平均数,负 表示小于平均数。表示离开平均数多少个标准 差。
3.是等距量表,能进行四则运算。
4. 其分布形状与原始分数相同,结果没有丝 毫失真。
5.假如原始分数的分布为常态,则Z分数的范 围大致是-3~3。
前所编制的常模可能不再适合,因此常模必须 定期地修订,并尽可能采用新近的常模。 6.要将一般常模和特殊常模结合起来
常用的具体抽取方式有抽签法和随机数字法。
1.抽签:把总体中的每一个个体编上号并作出签,充 分混合后从中随机抽取一部分,这部分签所对应的个 体就组成一个样本。
2.随机数字表
用随机数字表来抽取数字。
3.美国大学入学考试委员会使用的标准分数: CEEB分数:
CEEB 500100Z
20- 12
32
26
0.26 -0.64
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
常模的分类
• 导出分数是从原始分数转换而来的具有一定参 照点和单位的测验量表上的数值。 达到目的的方法: • (1)已经达到的发展水平; • (2)在某一特殊团体中的相对位置。
• 根据参照的是已达到的发展水平还是某团体中 的相对位置,常模就可ቤተ መጻሕፍቲ ባይዱ分为发展常模和团体内 常模两大类型。 • 发展常模有年龄常模、年级常模和顺序常模等; • 团体内常模有百分等级常模与标准分数常模等。
第六章 测验常模与分数的合成
一、原始分数与导出分数
• 被试在接受测验后,根据测验的记分 标准,对照被试的反应所计算出的分 数称作原始分数。 • 导出分数就是在原始分数的基础上, 按照一定的规则,经过统计处理后获 得的具有一定参照点和单位,且可以 相互比较的分数。
– 目的:指示个体在标准化样组中的 位置;提供了一些可比较的量度,使对 个体的不同测验中的作业情况的比较成 为可能。
• 未分组数据计算百分等级 分数的步骤:
– 已知某个原始数据。 – 计算所有数据项中,小于 或等于该分数的个数,记 为i。 – PR=(i/N)×100
例:某公司12名职员的月薪发下, 求2440对应的百分等级分数。
2210,2225,2350,2380,2380, 2390,2420,2440,2450,2550, 2630,2825。
(60 59.5) 4 152 5 PR 100 157 =97 98 (42 39.5) 4 5 100 157
PR
=70
建立百分等级常模的方法和步骤
• 第一,根据测验所应测验的对象,科学地 选择一个有充分代表性的被试样组(标准 化常模样组)。 • 第二,按照标准化施测程序,把测验施测 于该被试样组,取得实测数据。 • 第三,编制实测数据次数分布表。应计算 出每个分数区间的实有分数的次数,以及 由低向高的累积次数、相对次数和累积相 对次数,形成一个完整的次数分布表。 • 第四,计算测验原始分数所对应的百分等 级, • 第五,编制百分等级分数常模表。
标准分数
• Z分数的转化
–T分数:T=50+10Z –离差智商:IQ=100+15Z –CEEB分数:CEEB=500+100Z
五、发展性常模
• 1、年龄常模——智龄
– 1908年修订的比奈-西蒙量表中开始使用智龄来度量 智力,此后通过翻译和修订的斯比量表,智龄大为 盛行。但当时比奈却使用智力水平(mental level) 一词。 – 在年龄量表中,如比奈量表及其修订版中,题目被 划入各个年龄水平。智龄的计算通常要计算一个基 本年龄,即全部被通过的最高的一组题目所代表的 年龄。在所有更高年龄水平上通过的题目,用月份 计算,加在基础年龄上。 – 困难在于如何将题目分到不同的年龄组。(4岁组 77%,6岁组70.8%,14岁组为55.6%)
二、常模的概念
• 一个与被试同类的团体在相同行为上 的分数结构模式。(黄光扬) • 所谓常模即指标准化样本的测验作业 情况,一般把用作比较的团体叫做常 模团体,常模团体的一般平均分数叫 做常模。(金瑜) • 常模是根据标准化样本的测验分数经 过统计处理而建立起来的具有参照点 和单位的测验量表。(戴海琦)
常模资料呈现的方法
• 1、转化表(常模表) • 简单转化表 • 复杂转化表
测验量表剖析图
• 剖析图是把一套测验中几个分测验分数用 图表(或图形)表示出来。 • 从剖析图上可以很直观、全面 地看出被试在各个分测验中的表现及其相 对应的位置。
七、分数的合成
分数合成的用途:将几个分数或几个预测源组合 起来以获得一个合成分数或作出总的预测. 分数合成的类型:
发展性常模
• 年级当量
– 注意:
• 首先,年级常模仅仅适用于各个年 级都开设的共同科目。 • 年级当量的解释比较困难。 • 年级常模不能被误认为是成绩标准。
发展性常模
• 顺序量表
– 20世纪中期,瑞士儿童心理学家皮亚杰 提出认知发展阶段。 – 有人把皮亚杰在研究中所彩的一些作业 和问题组成了标准化量表,用来研究儿 童在每一发展阶段的特性,以提供儿童 实际能做什么的信息。在这种量表上, 分数可以用相近的年龄水平来表示,同 时还能对儿童的物为作质的描述。
i 8 8 PR 100 66.67 12
PR一般为整数,66.67究竟该为66百分等级, 还是67百分等级?
百分等级
• 分组数据计算百 分等级分数的方 法:
( x L )f Fb i 100 PR N PR : x对应的百分等级分数 L : x所在组的精确下限 Fb : 小于L的累积次数 f : x所在组的次数 i : 组距 N : 总次数
六、其他导出分数常模
• 1、标准九分数与标准十分数 • 标准九分数和标准十分数就是将原始分数转换而成的分数, 划分成九或十个区段。 • 若原始分数服从正态分布,标准九分数是以0.5个标准差 为单位,将正态曲线下的横轴分为九段,最高一段为9分, 最低一段为1分,最中间一段为5分,除分布的两端(9分、 1分)外,每段均有0.5个标准差宽,这样就可将z分数划 分成九部分。
组 别 65-69 60-64 55-59 50-54 45-49 40-44 35-39 30-34 23-29 20-24 15-19 10-14 合 计
f 1 4 6 8 16 24 34 21 16 11 9 7 157
累积次数 157 156 152 146 138 122 98 64 43 27 16 7
四、团体内常模
• 团体内常模也称作组内常模,通常 是根据标准化被试样组的测验分数、 经过统计处理而建立起来的、具有 参照点和单位的测验量表。
• 可根据标准化被试样组的成绩来评 价被试水平。团体内常模的分数有 一个统一而清楚地定义好的数量关 系,能运用大多数统计分析技术, 所以更易为人们所接受。
百分等级
•标准十分数也是以个0.5标准差为单位,将 正态曲线下的横轴分为十段的标准分数系统; 其最高一段为10分,最低一段为1分,最中 间两段各为5分和6分,除分布的两端(1分、 10分)外,每段均有0.5个标准差宽。
几种导出分数间的相互关系
全国常模与特殊常模
• 根据样本的大小和来源,通常有全国常模、 区域常模和特殊常模。
发展性常模
• 3、比率智商
MA IQ 100 CA IQ为智力商数,简称智商;MA为智龄;CA为实龄。
比较: 离差IQ=100+15Z
4、商数
教育商数 优点:不受智力发展的年 成就商数 龄关系限制;
发展性常模
• 发展量表的优点: – 以年龄或年级当量作为单位来报告分数易于被人 理解 – 可以与同等团体做直接比较 – 为个人内比较与纵向比较提供了基础 • 发展量表的缺点: – 只适用于所测的特质随年龄或年级发生系统变化 的情况,因此仅适用于年纪小的儿童,对成人不 适用。 – 由于人的行为发展受教育与经济的影响,因此发 展量表只适用于典型环境下成长的儿童。 – 发展量表的单位不相等。 – 获得同样的年龄或年级当量分数,并不一定具有 相同的智力或学业水平。如:两个不同年龄的小 孩同得智龄8岁。
接 受 (+)
高
拒绝(-) 接受(+)
• 连续栅栏
测 验
B
拒 绝 (+)
拒绝(-)
拒绝(-)
低
低
拒绝(-)
高 接受(+)
测验 A 两个预测源的多重分段模式
• 完形记分:
• 将各个变量看做一个整体,不是孤立地看每个 反应结果,而是看总的反应模式.
• 轮廓分析:
• 考虑被试在各个测验或量表上所得分数的轮廓, 而不是将各个变量做简单的线性组合.
• 2、加权求和法 • 采用加权的方法对分数进行合成的条件是: 各个测验所测的特质间有代偿作用,分数 是连续资料并且能够同时获得。 ---单位加权 ---等量加权 ---差异加权
• 3、多重回归法 • 使用条件:同时采用几个预测源来预测一个 效标,并且这些预测源变量之间又具有互偿 性.
• 4、多重划分法 • 综合分段
三、编制常模的步骤
• 1、确定测验将用于哪一个群体。
– – – – – – 群体构成的界限必须明确 常模团体必须是所测群体的一个代表性样本 取样的过程必须明确且有详尽的描述 样本大小要适当 常模团体必须是近时的 注意一般常模与特殊常模的结合
• 2、对常模团体进行施测,获得团体成员的 测验分数及分数分布。 • 3、确定常模分数类型,制作常模分数转换 表,即常模表,同时给出抽取常模团体的 书面说明,以及常模分数的解释指南等。
标准分数
• 一般Z分数
例:学生甲期末考试,数学成绩92分,语文成绩83分。全班数学 平均分90分,标准差15分;语文平均分75分,标准差8分。问学生 甲的数学、语文成绩的优劣如何?
解 : Z数
92 90 0.13 15 83 75 Z语 1 8 Z语 Z 数 甲生的语文成绩优于数学成绩
• • •
项目的合成 分测验或量表的组合 测验或预测源的组合
分数合成中的问题
• 1、分数合成的方法 • 2、分数组合的最佳形式 • 3、分数组合所需的测验分数的种类和数量
分数合成的方法
• 1、临床诊断 • 临床诊断是一种根据直觉的经验,主 观地将各种因素加权而获得结论或预 测的方法。这就好比临床医生,把各 种化验、检验所获得的资料与实际观 察所得的结果结合起来,根据经验做 出诊断一样。
发展性常模
• 2、年级当量
– 教育成就测验上的分数经常可用年级当量来解 释。例,某学生的成就为:拼写相当于7年级, 阅读相当于8年级,数学相当于5年级。 – 年级常模可以从计算各年级学生在某份测验上 的平均原始分数而得。各年级之间的年级当量, 可以采用内插法而得,也可通过在一学年中的 各时期直接测量而得到。 – 年级当量可以用年级月数来表示。年级当量通 常用两位数表示,第一位为年,第二位为月。 如,4.0表示四年级开始的水平,4.5表示四年 级学年中期的水平。
