一题多解之五种方法解一道经典数学题
初中数学9种常考压轴题+5种策略整理,预习、复习必看内容

九种题型01、线段、角的计算与证明中考的解答题一般分为两至三部分。
第一部分基本上都是一些简单题或者中档题,目的在于考察基础。
第二部分往往就是开始拉分的中难题了。
对这些题轻松掌握的意义不仅在于获得分数,更重要的是对整个做题过程中士气、军心的影响。
线段与角的计算和证明,一般来说难度不会很大,只要找到关键“题眼”,后面的路子自己就“通”了。
02、图形位置关系初中数学中,图形位置关系主要包括点、线、三角形、矩形、正方形以及圆这几类图形之间的关系。
在中考中会包含在函数、坐标系以及几何问题中,但是主要还是通过圆与其他图形的关系来考察,这其中最重要的就是圆与三角形的各种问题。
03、动态几何从历年中考来看,动态问题经常作为压轴题目出现,得分率也是最低的。
动态问题一般分为两类,一类是代数综合方面,在坐标系中有动点、动直线,一般是利用多种函数交叉求解。
另一类是几何综合题,在梯形、矩形、三角形中设立动点、线以及整体平移翻转,对考生的综合分析能力进行考察。
04、一元二次方程与二次函数在这一类问题中,尤以涉及到的动态几何问题最为艰难。
几何问题的难点在于想象、构造,有时候一条辅助线没有想到,整道题就卡壳了。
相较于几何综合题,代数综合题不需要太多巧妙的方法,但是对考生的计算能力以及代数功底有较高的要求。
中考数学中,代数问题往往是以一元二次方程与二次函数为主体,多种其他知识点辅助的形式出现的。
一元二次方程与二次函数问题中,纯粹的一元二次方程解法通常会以简单解答题的方式进行考察。
但是在后面的中难档大题中,通常会与根的判别式、整数根和抛物线等知识点相结合。
05、多种函数交叉综合初中数学所涉及的函数是一次函数、反比例函数以及二次函数。
这类题目本身并不会太难,很少作为压轴题出现,一般都是作为一道中档次题目来考察考生对一次函数以及反比例函数的掌握程度。
因此在中考中面对这类问题,一定要做到避免失分。
06、列方程(组)解应用题在中考中,有一类题目说难不难、说不难又难,有的时候三两下就有了思路,有的时候苦思冥想很久也没有想法,这就是列方程或方程组解应用题。
初中数学-12345模型

初中数学——模型12345数学解题五境界第一个境界:正确解题.很多同学以为如果一道题目做错,订正一下,知道哪里错了,怎么做,就行了,其实这只是最低境界.第二个境界:一题多解.我们要养成的良好习惯是,不要满足于用一种做法和思路解题.一道题目做完之后想一想还有没有其它方法,哪种方法更简单.对于最后的结果,是不是可以有其它的合理解释.第三个境界:多题一解.完成一道题目的分析后,尝试推而广之,或把其中的数字换成字母,或把一些条件做一些改变,从这道题目延伸出去,探究与此相关的一类题目.第四个境界:发现定理.到了这个境界,可以自己发现一些结论或定理、规律。
这些结论、定理规律都是解题的有用工具。
解题高手都有自己的定理库.第五个境界:自己编题.解题的最高境界是能够编题。
不是所有的老师都具备编题的能力。
解题高手拿到一道题目,会知道出题者的意图,会发现出题者的陷阱。
即便出题者粗心出现了一个错误,他也能够很快地纠正纠偏.刘俊勇:如果没有真正消化吸收为自己的东西,过一段时间就忘却了,真正弄清楚更重要,远胜于蜻蜓点水式浏览一遍.一方面重视技巧,尤其是考试技巧学习技巧,另一方面回归数学本质,回归教育意义当我们听到一个技巧的时候,除了拿来使用之外,还需要去体会专家在思考、总结过程的数学思考,这个我觉得更加重要和有意义。
因为专家的本意也正是立足于思想的交流,而不是一招一式的传递,在本地方的一些小型的培训中,我注意到活动中最最怕的就是坐在下面的教师一直把自己当成听众、容器,同时,相当一部教师的都有简单的拿来主义和简单的怀疑主义倾向,这个也特别可怕数学是思维的体操,没有绝技想拿冠军是不可能的。
以教材为主对大部分学生适用,但在我们这光靠教材的知识点,中考想考满分概率为零。
学灵魂在于积累、创新、规纳而不是照搬的模仿和接受,要有自己的数学大格局,适合自己的就是最好的!版块一引入问题1.如图1-1,在3×3 的网格中标出了∠1 和∠2,则∠1+∠2=图1-1 图1-22.如图1-2,在△ABC 中,∠BAC=45°,AD 是BC 边上的高,BD=3,DC=2,则AD 的长为.版块二“1 2 3”+“4 5”的来源一般化结论:若α+β= 45︒则有tanα=a - 1,a + 1tanβ=1(a>1),a当 a =3时,则得到tanα=2tan β=1(了解)2 3 5当a=2 时,则得到tanα=1tan β=1(重要)2 3当a =5时,则得到tanα=2tan β=3(了解);2 5 7当a = 4 时,则得到tanα=1tan β=3(次重要)4 55510【例 1】(济南市中考题)如图2-1, ∠AOB 是放置在正方形网络中的一个角,则cos ∠AOB 的值是 .图 2-1【例 2】(2015 湖北十堰)如图 2-2,正方形 ABCD的边长为 6,点 E ,F 分别在 AB ,AD 上,若 CE = 3 ,且∠ECF =45°,则 CF 的长为( )A . 2B . 3C .5103图 2-2倍角与半角构造D .10 53当出现等腰三角形或翻折的背景问题时,解决策略“ 顶角⇔ 底角⇔ 顶角”解题依据“ 90︒ 1 - 顶角=底角”. 2如图,在等腰三角形 ABC 中,AB =AC . ⑴若 tan ∠BCA = 2 ,则 tan ∠BAC =.⑵若 tan ∠BAC = 4,则 tan ∠ABC =.3【例3】如图2-3,已知正方形ABCD 中,E 为BC 上一点.将正方形折叠起来,使点A 和点E 重合,折痕为MN.若tan ∠AEN =1,DC+CE=10.3⑴求△ANE 的面积;⑵求sin ∠ENB 的值.图2-3【例4】如图2-4,已知正方形ABCD 的边长为,对角线AC、BD 交于点O,点E 在BC 上,且CE=2BE,过B 点作BF ⊥AE 于点F,连接OF,则线段OF 的长度为。
一题多解之五种方法解一道经典数学题
O BCD①A 一题多解之五种方法解一道经典数学题江苏海安紫石中学 黄本华一题多解是我们学习数学的特好方法!通过一题多解,我们可以多角度、多方位地去思考解题的方案,这样不仅能加强知识间的联系,同时也增添新颖性和趣味性,优化我们的思维结构,提升我们的思维能力。
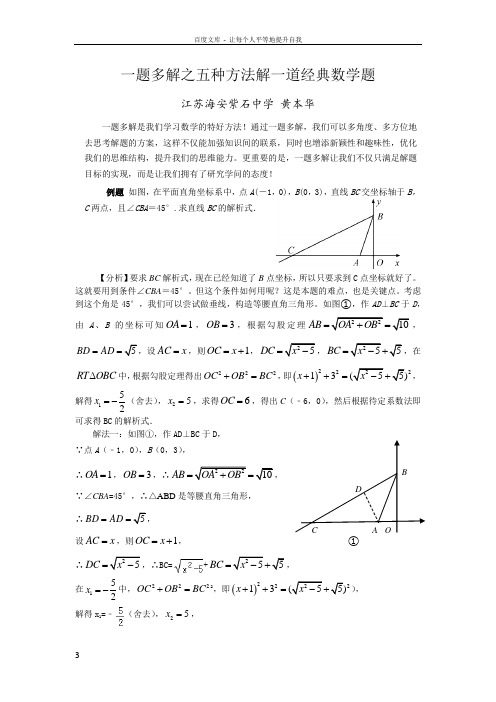
更重要的是,一题多解让我们不仅只满足解题目标的实现,而是让我们拥有了研究学问的态度!例题 如图,在平面直角坐标系中,点A (-1,0),B (0,3),直线BC 交坐标轴于B ,C 两点,且∠CBA =45°.求直线BC 的解析式.【分析】要求BC 解析式,现在已经知道了B 点坐标,所以只要求到C 点坐标就好了。
这就要用到条件∠CBA =45°。
但这个条件如何用呢?这是本题的难点,也是关键点。
考虑到这个角是45°,我们可以尝试做垂线,构造等腰直角三角形。
如图①,作AD ⊥BC 于D ,由A 、B 的坐标可知1OA =,3OB =,根据勾股定理2210AB OA OB =+=,5BD AD ==AC x =,则1OC x =+,25DC x =-255BC x =-,在RT OBC ∆中,根据勾股定理得出222OC OB BC +=,即()222213(55)x x ++=-,解得152x =-(舍去),25x =,求得6OC =,得出C (﹣6,0),然后根据待定系数法即可求得BC 的解析式.解法一:如图①,作AD ⊥BC 于D , ∵点A (﹣1,0),B (0,3),∴1OA =,3OB =,∴2210AB OA OB =+=, ∵∠CBA =45°,∴△ABD 是等腰直角三角形, ∴5BD AD ==设AC x =,则1OC x =+, ∴25DC x =-,∴BC=+255BC x =-+,在152x =-中,222OC OB BC +=2,即()222213(55)x x ++=-), 解得x 1=﹣(舍去),25x =,②③∴5AC =,6OC =,∴C (﹣6,0), 设直线BC 的解析式为3y kx =+, 解得12k =,∴直线BC 的解析式为132y x =+. 【点评】虽然这种解法思路比较清晰,但是用勾股定理得出的方程比较复杂,解方程很繁,很费时,很累。
数学解题之一题多解与多题一解

摘要本文意在明确一题多解和多题一解与学生思维能力发展之间的关系,从而使教师在数学解题教学过程中更加重视解题方法对学生思维能力的培养。
本文通过两种典型例题即一题多解型和多题一解型的讲解,阐述了通过不同的例题可以达到对学生思维能力的训练培养的目的。
通过一题多解,可以开阔学生思路、发散学生思维,让学生学会多角度分析和解决问题;通过多题一解,能够加深学生的思维深度,分析事物时学会由表及里,抓住事物的本质,找出事物间内在的联系。
与此同时,对一题多解和多题一解的运用,要注意相互结合,灵活运用,不可只求一技,失之偏颇。
关键词:一题多解多题一解思维能力AbstractA multi solution with multi-title, a solution is a commonly used method in the teaching of mathematical problem solving. To a given problem, can mathematical knowledge has been an organic gathering of students'divergent thinking is a good opportunity for its exercise; a solution of the multi-title, students can digest the knowledge, but also training the students of the Idea.In this paper, two typical example that is a question to the multi-solution and multi-title solution-based explanation on the purpose of training the training of the students' thinking abilities can be achieved through different examples. To a given problem, you can broaden the horizons of the students 'thinking, divergent thinking of the students, for students to learn multi-angle analysis and problem solving; a solution more than the question, can enhance students' depth of thinking, learn to analyze things from outside to inside, to seize the the nature of things, find things intrinsically linked.This article is intended relationship between the development of the ability to clear a given problem and a solution of the multi-title, with students thinking, so that teachers pay more attention to the culture of problem-solving approach to students' thinking ability in mathematical problem solving teaching process.Key words:Multiple solutions for one question A solutions of the multi-title Thinking ability数学解题过程中一题多解与多题一解对学生思维能力的培养引言现代心理学认为,数学是人类思维的体操,在培养人的聪明才智方面起着巨大的作用。
鸡兔同笼问题五种基本公式和例题讲解。

鸡兔同笼问题五种基本公式和例题讲解。
鸡兔同笼问题五种基本公式和例题讲解鸡兔问题是一种经典的数学问题,下面介绍五种基本公式及例题讲解。
公式1:已知总头数和总脚数,求鸡、兔各多少:兔数 = (总脚数-每只鸡的脚数×总头数)÷(每只兔的脚数-每只鸡的脚数)鸡数 = 总头数 - 兔数或者是鸡数 = (每只兔脚数×总头数-总脚数)÷(每只兔脚数-每只鸡脚数)兔数 = 总头数 - 鸡数例如,“有鸡、兔共36只,它们共有脚100只,鸡、兔各是多少只?”XXX:(100-2×36)÷(4-2)=14(只)兔,36-14=22(只)鸡。
解二:(4×36-100)÷(4-2)=22(只)鸡,36-22=14(只)兔。
公式2:已知总头数和鸡兔脚数的差数,当鸡的总脚数比兔的总脚数多时,可用公式兔数 = (每只鸡脚数×总头数-脚数之差)÷(每只鸡的脚数+每只兔的脚数)鸡数 = 总头数 - 兔数或者是鸡数 = (每只兔脚数×总头数+鸡兔脚数之差)÷(每只鸡的脚数+每只兔的脚数)兔数 = 总头数 - 鸡数公式3:已知总数与鸡兔脚数的差数,当兔的总脚数比鸡的总脚数多时,可用公式。
兔数 = (每只鸡的脚数×总头数+鸡兔脚数之差)÷(每只鸡的脚数+每只兔的脚数)鸡数 = 总头数 - 兔数或者是鸡数 = (每只兔的脚数×总头数-鸡兔脚数之差)÷(每只鸡的脚数+每只兔的脚数)兔数 = 总头数 - 鸡数公式4:得失问题(鸡兔问题的推广题)的解法,可以用下面的公式:不合格品数= (1只合格品得分数×产品总数-实得总分数)÷(每只合格品得分数+每只不合格品扣分数)或者是不合格品数 = 总产品数-(每只不合格品扣分数×总产品数+实得总分数)÷(每只合格品得分数+每只不合格品扣分数)例如,“灯泡厂生产灯泡的工人,按得分的多少给工资。
各阶段数学解题技巧方法总结

各阶段数学解题技巧方法总结小学数学解题方法1、实物演示法利用身边的实物来演示数学题目的条件和问题,及条件与条件,条件与问题之间的关系,在此基础上进行分析思考、寻求解决问题的方法。
这种方法可以使数学内容形象化,数量关系具体化。
比如:数学中的相遇问题。
通过实物演示不仅能够解决“同时、相向而行、相遇”等术语,而且为学生指明了思维方向。
再如,在一个圆形(方形)水塘周围栽树问题,如果能进行一个实际操作,效果要好得多。
二年级数学教材中,“三个小朋友见面握手,每两人握一次,共要握几次手”与“用三张不同的数字卡片摆成两位数,共可以摆成多少个两位数”。
像这样的有关排列、组合的知识,在小学教学中,如果实物演示的方法,是很难达到预期的教学目标的。
特别是一些数学概念,如果没有实物演示,小学生就不能真正掌握。
长方形的面积、长方体的认识、圆柱的体积等的学习,都依赖于实物演示作思维的基础。
所以,小学数学教师应尽可能多地制作一些数学教(学)具,而且这些教(学)具用过后要好好保存,可以重复使用。
这样可以有效地提高课堂教学效率,提升学生的学习成绩。
2、图示法借助直观图形来确定思考方向,寻找思路,求得解决问题的方法。
图示法直观可靠,便于分析数形关系,不受逻辑推导限制,思路灵活开阔,但图示依赖于人们对表象加工整理的可靠性上,一旦图示与实际情况不相符,易使在此基础上的联想、想象出现谬误或走入误区,最后导致错误的结果。
比如有的数学教师爱徒手画数学图形,难免造成不准确,使学生产生误解。
在课堂教学当中,要多用图示的方法来解决问题。
有的题目,图画出来了,结果也就出来的;有的题,图画好了,题意学生也就明白了;有的题,画图则可以帮助分析题意、启迪思路,作为其他解法的辅助手段。
例1:把一根木头锯成3段需要24分钟,锯成6段需要多少分钟(图略)思维方法是:图示法。
思维方向是:锯几次,每次用几分钟。
思路是:锯3段锯了几次,每次用几分钟,锯6段锯了几次,需要多少分钟。
初中数学-12345模型 (1)

初中数学-12345模型 (1)初中数学——模型12345数学解题五境界第一个境界:正确解题.很多同学以为如一道题目做错,订正一下,知道哪里错了,怎么做,就行了,其实这只是最低境界.第二个境界:一题多解.我们要养成良好习惯是,不要满足于用一种做法和思路解题.一道题目做完之后想一想还有没有其它方法,哪种方法更简单.对于最后的结果,是不是可以有其它的合理解释.第三个境界:多题一解.完成一道题目的分析后,尝试推而广之,或把其中的数字换成字母,或把一些条件做一些改变,从这道题目延伸出去,探究与此相关的一类题目.第四个境界:发现定理.到了这个境界,可以自己发现一些结论或定理、规律。
这些结论、定理规律都是解题的有用工具。
解题高手都有自己的定理库.第五个境界:自己编题.解题的最高境界是能够编题。
不是所有的老师都具备编题的能力。
解题高手拿到一道题目,会知道出题者的意图,会发现出题者的陷阱。
即便出题者粗心出现了一个错误,他也能够很快地纠正纠偏.刘俊勇:如没有真正消化吸收为自己的东西,过一段时间就忘却了,真正弄清楚更重要,远胜于蜻蜓点水式浏览一遍.一方面重视技巧,尤其是考试技巧学习技巧,另一方面回归数学本质,回归教育意义当我们听到一个技巧的时候,除拿来使用之外,还需要去体会专家在思考、总结过程的数学思考,这个我觉得更加重要和有意义。
因为专家的本意也正是立足于思想的交流,而不是一招一式的传递,在本地方的一些小型的培训中,我注意到活动中最最怕的就是坐在下面的教师一直把自己当成听众、容器,同时,相当一部教师的都有简单的拿来主义和简单的怀疑主义倾向,这个也特别可怕数学是思维的体操,没有绝技想拿冠军是不可能的。
以教材为主对大部分学生适用,但在我们这光靠教材的知识点,中考想考满分概率为零。
学灵魂在于积累、创新、规纳而不是照搬的模仿和接受,要有自己的数学大格局,适合自己的就是最好的!版块一引入问题1.如图1-1,在3×3 的网格中标出了∠1 和∠2,则∠1+∠2=图1-1 图1-22.如图1-2,在△ABC 中,∠BAC=45°,AD 是BC 边上的高,BD=3,DC=2,则AD 的长为.版块二“1 2 3”+“4 5”的来源一般化结论:若α+β= 45︒则有tanα=a - 1,a + 1tanβ=1(a>1),a当 a =3时,则得到tanα=2tan β=1(了解)2 3 5当a=2 时,则得到tanα=1tan β=1(重要)2 3当a =5时,则得到tanα=2tan β=3(了解);2 5 7当a = 4 时,则得到tanα=1tan β=3(次重要)4 555 10【例 1】(济南市中考题)如图 2-1, ∠AOB 是放置在正方形网络中的一个角,则cos ∠AOB 的值是 .图 2-1【例 2】(2015 湖北十堰)如图 2-2所示,正方形 ABCD 的边长为 6,点 E ,F 分别在 AB ,AD 上,若 CE = 3, 且∠ECF =45°,则 CF 的长为( )A . 2B . 3C .5103图 2-2倍角与半角构造D .10 53当出现等腰三角形或翻折的背景问题时,解决策略“ 顶角⇔ 底角⇔ 顶角”解题依据“ 90︒ 1 - 顶角=底角”. 2如图所示,在等腰三角形 ABC 中,AB =AC . ⑴若 tan ∠BCA = 2 ,则 tan ∠BAC =.⑵若 tan ∠BAC = 4,则 tan ∠ABC =.3【例3】如图2-3所示,已知正方形ABCD 中,E 为BC 上一点.将正方形折叠起来,使点A 和点E 重合,折痕为MN.若tan ∠AEN =1,DC+CE =10.3⑴求△ANE 的面积;⑵求sin ∠ENB 的值.图2-3【例4】如图2-4,已知正方形ABCD 的边长为,对角线AC、BD 交于点O,点E 在BC 上,且CE=2BE,过B 点作BF ⊥AE 于点F,连接OF,则线段OF 的长度为。
小学数学五大模型练习题

小学数学五大模型练习题在小学数学教学中,五大模型是教师经常使用的一种教学方法。
它包括了常见的五种问题解决模型,即归纳模型、演绎模型、类比模型、建模模型和解决问题的启发模型。
通过学习和练习这些模型,学生可以提高对数学问题的分析和解决能力。
本文将针对小学数学五大模型进行一系列练习题的介绍和解析。
一、归纳模型归纳模型强调观察事物,找出其中的规律,由此推广到更一般的情况。
下面是一道归纳模型的练习题:练习题1:阿明用2元钱买了4个苹果,那么他用8元钱可以买几个苹果?解析:观察题目中的数据,可以发现钱和苹果的数量存在一定的倍数关系。
根据归纳模型的思路,我们可以得出苹果数量是钱数的2倍的规律。
因此,阿明用8元钱可以买8个苹果。
二、演绎模型演绎模型强调从已知条件出发,进行推理和演绎,得出问题的结论。
下面是一道演绎模型的练习题:练习题2:有一个数,它是3的倍数,它加上4得到的和还是3的倍数,那么这个数是多少?解析:根据演绎模型的思路,我们从已知条件出发进行推理。
设这个数为x,根据题目条件,得到以下两个等式:1)x是3的倍数:x = 3n (n为自然数)2)x加上4得到的和是3的倍数:(x + 4) = 3m (m为自然数)将第一个等式代入第二个等式,得到 3n + 4 = 3m。
整理等式,得到3n + 1 = 3m。
由于3n是3的倍数,所以3n + 1不可能是3的倍数。
因此,不存在满足条件的数。
三、类比模型类比模型强调将问题与已经熟悉的情境进行类比,找到相似之处,利用已有的知识解决问题。
下面是一道类比模型的练习题:练习题3:班级里有30个男生和18个女生,请问男生人数是女生人数的几倍?解析:根据类比模型的思路,我们可以用一个已知的情境进行类比:小明抓了30只蚂蚁和18只蜘蛛,请问蚂蚁的数量是蜘蛛数量的几倍?从直观上来看,蚂蚁和蜘蛛数量的比例应该与男生和女生的比例相同。
因此,男生人数是女生人数的 $\frac{30}{18}$ 倍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
O B
C
D
①
A 一题多解之五种方法解一道经典数学题
江苏海安紫石中学 黄本华
一题多解是我们学习数学的特好方法!通过一题多解,我们可以多角度、多方位地去思考解题的方案,这样不仅能加强知识间的联系,同时也增添新颖性和趣味性,优化我们的思维结构,提升我们的思维能力。
更重要的是,一题多解让我们不仅只满足解题目标的实现,而是让我们拥有了研究学问的态度!
例题 如图,在平面直角坐标系中,点A (-1,0),B (0,3),直线BC 交坐标轴于B ,
C 两点,且∠CBA =45°.求直线BC 的解析式.
【分析】要求BC 解析式,现在已经知道了B 点坐标,所以只要求到C 点坐标就好了。
这就要用到条件∠CBA =45°。
但这个条件如何用呢?这是本题的难点,也是关键点。
考虑到这个角是45°,我们可以尝试做垂线,构造等腰直角三角形。
如图①,作AD ⊥BC 于D ,由A 、B 的坐标可知1OA =,3OB =,根据勾股定理2
2
10AB OA OB =+=,
5BD AD ==AC x =,则1OC x =+,25DC x =-255BC x =-,在
RT OBC ∆中,
根据勾股定理得出222OC OB BC +=,即()2
222
13(55)x x ++=-,解得15
2
x =-
(舍去),25x =,求得6OC =,得出C (﹣6,0),然后根据待定系数法即可求得BC 的解析式.
解法一:如图①,作AD ⊥BC 于D , ∵点A (﹣1,0),B (0,3),
∴1OA =,3OB =,∴2
2
10AB OA OB =+=, ∵∠CBA =45°,∴△ABD 是等腰直角三角形, ∴5BD AD ==
设AC x =,则1OC x =+, ∴25DC x =-,∴BC=+255BC x =
-+,
在152
x =-
中,222OC OB BC +=2
,即()222213(55)x x ++=-), 解得x 1=﹣
(舍去),25x =,
∴5AC =,6OC =,∴C (﹣6,0), 设直线BC 的解析式为3y kx =+,
2
②
③
解得12k =
,∴直线BC 的解析式为1
32
y x =+. 【点评】虽然这种解法思路比较清晰,但是用勾股定理得出的方程比较复杂,解方程很繁,很费时,很累。
当我们作AD BC ⊥时,我们应该想到求出D 点坐标不也可以吗?根据
ABD ∆是等腰直角三角形,我们很容易构造K 型全等形AED DFB ∆≅∆,如图②,从而求
出D 点坐标。
解法二:作AD ⊥BC 于D ,DE OC ⊥于E
BF DE ⊥于F ,如图②
易证AED DFB ∆≅∆,设AE x =, 则DE =1FB x =+,1FD OA ==
113x ∴++=,∴1x =,(2,2)D ∴-
设直线BC 的解析式为3y kx =+,
232k -+=,解得12
k =
∴∴直线BC 的解析式为1
32
y x =
+. 【点评】比较方法一和方法二,方法二计算量显然比解法一要少很多了。
进一步探索:我们如果如图③构造等腰直角三角形和K 型全等型ADE BOA ∆≅∆,是不是更容易求出点的坐标呢?我们会惊喜地发现D 点坐标几乎不用计算,就可以求出。
解法三:AD AB ⊥交BC 于D ,DE OC ⊥于E 易证:ADE BOA ∆≅∆,
==1DE OA ∴, =3AE OB =,
设直线BC 的解析式为3y kx =+,
∴431k -+=,∴1
2
k =
∴∴直线BC 的解析式为1
32
y x =+.
【点评】显然,解法三又比前两种解法简便多了。
但是我们不容易想到解法三的原因是:过点A 只习惯作BC 的垂线,而不习惯作AB 的垂线。
因此,我们只有通过一题多解的训练,才能拓展我们的思维,克服定势思维。
继续探究:如果我们过C 点作AB 的垂线,构造等腰BCD ∆,如图④,可以做吗? 容易发现ADC
AOB ∆
∆,则::::1:3AD DC AC AO BO AB ==,
这样也容易求出C 点的坐标。
解法四:如图④,作CD AB ⊥于D , 易证:ADC AOB ∆∆
则::::1:3AD DC AC AO BO AB ==
3
⑤
设:AD x =,则3DC DB x ==
310x x -=102
x =
105AC x ∴==,6OC ∴=,
设直线BC 的解析式为y=kx+3
∴630k -+=,解得12
k =
∴直线BC 的解析式为y=
x+3.
【点评】这种解法也是不错的哦!
换个思路分析一下:要求直线BC 的解析式,并不一定要再求一个点的坐标,只要求出比例系数k 就行了。
即求出
BO
OC
的值即可。
因此,只要我们掌握公式tan tan tan()1tan tan αβ
αβαβ
++=
-,
那么,辅助线都不用作,就能轻易做出。
解法五:
tan 45tan tan tan(45)1tan 45tan ABO CBO ABO ABO ︒+∠∠=︒+∠=-︒∠1
1321
13
+
=
=- 即2CO BO =,∴12
BO k CO == ∴直线BC 的解析式为y=
x+3.
【点评】哇!多记一个公式,解法这么简单!原来知识丰富,解题方法也就丰富啊! 通过过这道题的解法研究,我们可以发现,这道题把一次函数与等腰直角三角形,勾股定理,方程,全等三角形,相似三角形,三角函数等知识都联系起来了,所以一题多解训练,才能真正发挥例题的功能,不仅能复习或巩固更多的知识,也发散了我们的思维,拓展了我们的思路。
如果我们经常的对一些题目尝试一题多解,何愁数学不拔尖呢?。
