第十章双样讲义本假设检验及区间估计
区间估计和假设检验

在回归分析中,区间估计可以用来估计未知参数的取值范围,从 而更好地理解参数对结果的影响。
假设检验的应用场景
检验假设是否成立
在科学研究或实际应用中,我们经常需要通过假设检验来检验某个 假设是否成立,以做出决策或得出结论。
诊断准确性评估
在医学诊断中,假设检验常用于评估诊断方法的准确性,例如比较 新方法与金标准之间的差异。
非参数检验的优点是不受总体分布限制,适用于更广泛的情况。常见的非参数检验包括秩和检验、符 号检验等。
假设检验的步骤
选择合适的统计方法
根据假设和数据类型选择合适 的统计方法进行检验。
确定临界值
根据统计量的分布情况,确定 临界值。
提出假设
根据研究问题和数据情况,提 出一个或多个假设。
计算统计量
根据选择的统计方法计算相应 的统计量。
区间估计和假设检验
目录
• 区间估计 • 假设检验 • 区间估计与假设检验的联系 • 应用场景 • 案例分析
01
区间估计
定义
区间估计
基于样本数据,对未知参数或总体分布特征 给出可能的取值范围。
参数估计
基于样本数据,对总体参数进行估计,如均 值、方差等。
非参数估计
基于样本数据,对总体分布特征进行估计, 如分位数、中位数等。
结果具有互补性
03
区间估计和假设检验的结果可以相互补充,帮助我们更全面地
了解总体的情况。
区别
1 2 3
目的不同
区间估计的目的是估计一个参数的取值范围,而 假设检验的目的是检验一个关于总体参数的假设 是否成立。
侧重点不同
区间估计更侧重于估计总体参数的可能取值范围 ,而假设检验更侧重于对总体参数的假设进行接 受或拒绝的决策。
第十章双样本假设检验及区间估计

不用均值差检验,而是求出每一对观察数据的差,直接进行一对一的比较。如果
采用“前测”“后测”两个总体无差异的零假设,也就是等于假定实验刺激无效。
于是,问题就转化为每对观察数据差的均值μd =0 的单样本假设检验了。求每
一对观察值的差,直接进行一对一的比较。
设配对样本的样本单位前测与后测的观察数据分别
是 X 0i 与 X 1i,其差记作 di
p1 q1 n1
p2 q2
n2
[例]有一个大学生的随机样本,按照性格“外向”和“内向”,把他们分成 两类。结果发现,新生中有 73%属于“外向”类,四年级学生中有 58%属于“外 向”类。样本中新生有 171 名,四年级学生有 117 名。试问,在 0.01 水平上, 两类学生有无显著性差异?
第二节 两总体小样本假设检验
女按对婚后生活的态度分为“满意”和“不满意”两组。从满意组中随机抽取
600 名妇女,其平均婚龄为 8.5 年,标准差为 2.3 年;从不满意组抽出 500 名妇
女,其平均婚龄为 9.2 年,标准差 2.8 年。试问在 0.05 显著性水平上两组是否
存在显著性差异?
样本
人数
均值
标准差
满意组
600
8.5
与对单总体小样本假设检验一样,我们对两总体小样本假设检只讨论总体满
足正态分布的情况。
1. 小样本均值差假设检验
(1)
当
2 1
和
2 2
已知时,小样本均值差检验,与上一节所述
大样本总体均值差检验完全相同,这里不再赘述。
(2)
2 1
和
2 2
未知,但假定它们相等时, 关键是要解决
( X1 X 2 )
的算式。
区间估计与假设检验

但是,我们的兴趣不仅要得到 ,还要利用它对真值 做出推断。或者说,我们的目的不仅是要得到样本回归函数, 还要用它来推测总体回归函数。
2021/8/5
6
尽管有了高斯-马尔可夫定理,但由于OLS法不对ui的概 率性质做任何假定,仍难以从SRF去推断PRF。
对这一不足,在回归分析中,人们常常假定ui遵从正态分 布。在第4章中讨论的经典线性回归模型的假定中增加ui 的正 态性假定,就得到了所谓的
与点估计相对照,在区间估计中,我们提供真θ将落入其间的 一个可能值域。
例如,如果变量X是正态分布的,则样本均值 X 也是正态分
布的,且其均值=μ,方差=σ2/n。即估计量 X 的抽样或概率
分布是
。因此我们可以构造区间:
并这样的区间约有95%的概率包含真μ,那么我们正在构造着
μ的一个区间估计。注意上面所给的区间依据于一个样本变到
2021/8/5
8
性质:对两个正态分布变量来说,零协方差或零相关就意 味着两个变量互相独立。 因此,在正态性假定下,ui 和uj 协方差为零不仅意味着它 们不相关,而且它们是独立分布的。可写成:
NID表示正态且独立分布(normally and independently distributed)。
区间估计与假设检验
◆ 经典正太线性回归模型
◆ 统计学预备知识 ◆ 区间估计基本概念 ◆回归系数β1和β2的置信区间 ◆σ2的置信区间
2021/8/5
2
一、经典正太线性回归模型
所谓统计推断的经典理论由两个分支构成,即估计和假设检 验。
前面讨论了双变量线性回归模型的参数估计问题。用OLS方 法,估计参数β1 ,β2 ,σ2 。在经典线性回归模型的假定下, 可以证明 、 和 这些参数的估计量满足线性性、无偏 性和最小方差(BLUE)。
高等数学与工程数学课件第十章数理统计基础.ppt

的平均直径为15.25 mm? ( 0.05) 解 提出原假设: 0 15.25,
由于方差已知,故选统计量
U X 0 ~ N (0,1) n
由P{|U | } P{U } P{U } 1 () () 2 2 () 0.05 .
由P{ 2
2}
2
0.025, 2
~
2 (15),查表得2
27.5,
由P{ 2
1}
1
2
0.975, 2
~
2 (15),查表得1
6.26.
故 2的95%的置信区间为
15
0.00244,15 27.5
0.00244 6.26
即 [0.0013,0.0058] .
二、假设检验的方法
假设检验的一般步骤如下: (1) 提出原假设 H0,明确所要检验的对象, (2) 构造合适的统计量 , (3) 求出临界值,确定拒绝域,
6
9.05.
S2 1 6 5 i1
2
Xi X
1 0.052 0.252 0.052 0.252 0.152 0.152
5
0.035.
返回
4、解: X N u, 2 且已知 2
选取统计量
U
X
n
该统计量服从标准正态分布,即:U N 0,1.
ห้องสมุดไป่ตู้
返回
机变量
X1,X
,
2
,X n 的函数称为样本函数,若样本函
数不含未知参数且是连续的,我们称之为统计量.(不含
未知参数的样本函数叫统计量.)
区间估计与假设检验的联系与区别讲义资料

区间估计与假设检验的联系与区别讲义资料
区间估计与假设检验是统计推断的两种常见方法。
它们虽然都属于推断统计,但也有明显的不同之处。
区间估计的主要目的是估计总体参数的值,也可以称作参数估计。
根据样本信息,我们可以得出一个可能的参数值范围,也就是置信区间,从而得到一个可靠的估计区间。
估计是不断变化的,每一次统计分析给出的参数估计值都可能有所变化,从而慢慢趋近真实值。
假设检验即“判断”,是统计学中比较常用的检验方法,目的是确定两个总体之间的差异是由随机因素造成的,还是由特定的因素(如环境因素)造成的。
假设检验涉及两个立场:备择假设和原假设。
假设检验的结果由抽样分布决定,不同的抽样分布对应不同的结论,比如有抽样分布下假设检验结果可能是拒绝备择假设,也可能是接受备择假设。
从概念上讲,区间估计技术计算的是一个参数的值的估计,而假设检验是用于检查参数的方法,它只检验两个总体是否具有显著的性质差异,而不会真正测量它们的差异。
总的来说,区间估计通过单组数据范围尽可能准确地估计参数的取值范围,而假设检验则是针对任何特定统计主题,利用数据样本来检验其是否与假设相符。
两者都具有自己的优点和不足,可以结合使用来为抽样荟萃而得出结论,从而更准确地了解样本的真实情况。
第十章双变量回归与相关

(9-3) (9-4)
式中 lXY 为 X 与 Y 的离均差积和:
l
XY
(X
X
)(Y
Y
)
XY
(
X
)( n
Y
)
(9 5)
除了图中所示两变量呈直线关系外,一 般还假定每个 X 对应Y 的总体为正态分布, 各个正态分布的总体方差相等且各次观测 相互独立。这样,公式(9-1)中的 Yˆ 实际上 是 X 所对应 Y 的总体均数 Y|X 的一个样本估 计值,称为回归方程的预测值(predicted value), 而 a 、 b 分别为 和 的样本估计。
(Y Y ) 2 (Yˆ Y ) 2 (Y Yˆ ) 2
数理统计可证明:
å (Yˆ - Y )(Y - Yˆ ) = 0
上式用符号表示为
SS总 SS回 SS残
(9-6)
式中
SS总 即 (Y Y)2 , 为 Y 的 离 均 差 平 方
和,表示未考虑 X 与Y 的回归关系时Y 的 总变异。
离 Y Yˆ 。
➢ 求解a、b实际上就是“合理 地”找到一条能最好地代表
数据点分布趋势的直线。
最小二乘法(least sum of squares)原则:即保证各实 测点至直线的纵向距离的 平方和最小。
(X,Y)
b lXY lXX
( X X )(Y Y ) (X X )2
a Y bX
5.列出回归方程(回归直线绘制见图 9-1)
Yˆ 1.6617 0.1392X
此直线必然通过点( , )X且与Y 纵坐标轴相交于 截距 a 。如果散点图没有过坐标系原点,可在 自变量实测范围内远端取易于读数的 X 值代入 回归方程得到一个点的坐标,连接此点与点 ( , )也可X绘Y出回归直线。
假设检验和区间估计
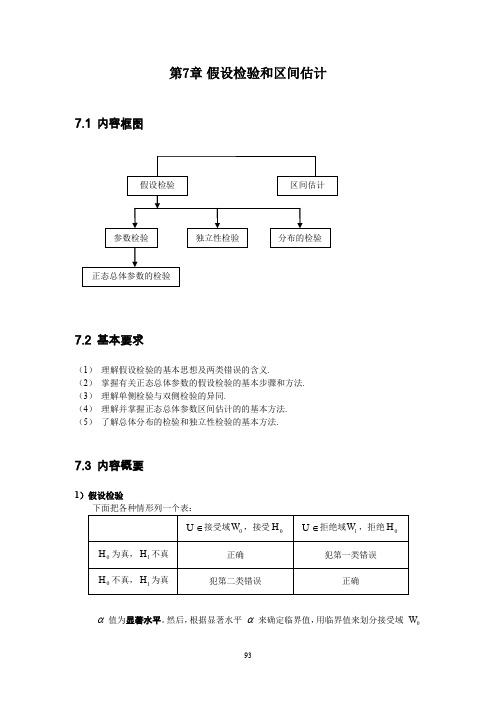
第7章 假设检验和区间估计7.1 内容框图7.2 基本要求(1) 理解假设检验的基本思想及两类错误的含义.(2) 掌握有关正态总体参数的假设检验的基本步骤和方法. (3) 理解单侧检验与双侧检验的异同.(4) 理解并掌握正态总体参数区间估计的的基本方法. (5) 了解总体分布的检验和独立性检验的基本方法.7.3 内容概要1)假设检验下面把各种情形列一个表:∈U 接受域0W ,接受0H∈U 拒绝域1W ,拒绝0H0H 为真,1H 不真 正确 犯第一类错误0H 不真,1H 为真犯第二类错误正确α值为显著水平。
然后,根据显著水平 α来确定临界值,用临界值来划分接受域 0W 假设检验 区间估计参数检验 分布的检验正态总体参数的检验独立性检验和拒绝域 1W 。
这样的检验,称为显著性检验。
假设检验的一般步骤是: (1)提出原假设 0H ;(2)选取合适的检验统计量 U ,从样本求出 U 的值;(3)对于给定的显著水平α,查 U 的分布表,求出临界值,用它划分接受域 0W 和拒绝域 1W ,使得当 0H 为真时,有 α=∈}{1W U P ;(4)若 U 的值落在拒绝域 1W 中,就拒绝 0H ,若 U 的值落在接受域 0W 中,就接受 0H 。
假设检验的理论依据是所谓的小概率事件原理,即一个概率很小的事件在一次试验中几乎是不可能发生的.要检验一个根据实际问题提出的原假设0H 是否成立,如果已知在0H 成立时,某个事件发生的可能性很小,而试验的结果却是这个事件发生了,那么根据小概率事件原理,我们就可以认为所提出的这个假设0H 是不成立的,即拒绝0H ;反之,则接受0H .这里的原假设0H 可以根据实际问题提出,事件是否发生可根据试验观测值判断,因此假设检验的关键问题就是要确定在0H 成立时,发生可能性很小的某个事件.我们知道,正态分布有个3σ原则,即ξ若服从正态分布,那么ξ的取值会大多集中在其均值附近,落入两侧的可能性很小.事实上,当ξ服从t 分布,2x 分布,F 分布时,其取值落入两侧的可能性也都相对很小.因此,我们要确定0H 成立时一个发生可能性很小的事件,只需根据样本构造出服从正态分布,t 分布,2x 分布或F 分布的随机变量(统计量)就可以了. 根据上述分析,正态总体参数的假设检验可概括为如下步骤。
假设检验和区间估计

第7章假设检验和区间估计7.1 内容框图7.2 基本要求(1)理解假设检验的基本思想及两类错误的含义.(2)掌握有关正态总体参数的假设检验的基本步骤和方法.(3)理解单侧检验与双侧检验的异同.(4)理解并掌握正态总体参数区间估计的的基本方法.(5)了解总体分布的检验和独立性检验的基本方法.7.3 内容概要1)假设检验α值为显著水平。
然后,根据显著水平α来确定临界值,用临界值来划分接受域W和拒绝域 1W 。
这样的检验,称为显著性检验。
假设检验的一般步骤是: (1)提出原假设 0H ;(2)选取合适的检验统计量 U ,从样本求出 U 的值;(3)对于给定的显著水平α,查 U 的分布表,求出临界值,用它划分接受域 0W 和拒绝域 1W ,使得当 0H 为真时,有 α=∈}{1W U P ;(4)若 U 的值落在拒绝域 1W 中,就拒绝 0H ,若 U 的值落在接受域 0W 中,就接受 0H 。
假设检验的理论依据是所谓的小概率事件原理,即一个概率很小的事件在一次试验中几乎是不可能发生的.要检验一个根据实际问题提出的原假设0H 是否成立,如果已知在0H 成立时,某个事件发生的可能性很小,而试验的结果却是这个事件发生了,那么根据小概率事件原理,我们就可以认为所提出的这个假设0H 是不成立的,即拒绝0H ;反之,则接受0H .这里的原假设0H 可以根据实际问题提出,事件是否发生可根据试验观测值判断,因此假设检验的关键问题就是要确定在0H 成立时,发生可能性很小的某个事件.我们知道,正态分布有个3σ原则,即ξ若服从正态分布,那么ξ的取值会大多集中在其均值附近,落入两侧的可能性很小.事实上,当ξ服从t 分布,2x 分布,F 分布时,其取值落入两侧的可能性也都相对很小.因此,我们要确定0H 成立时一个发生可能性很小的事件,只需根据样本构造出服从正态分布,t 分布,2x 分布或F 分布的随机变量(统计量)就可以了. 根据上述分析,正态总体参数的假设检验可概括为如下步骤。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
H1:12D0
(3)否定域:单侧 t(n1n22) 双侧 t/2(n1n22)
(4)检验统计量
t
X1
X2
D 0
(5)比较判定
(X1X2)
(X1 X2) D0 n1S12 n2S22 n1 n2
一年级 73% (171)
27%
01.03.2021
8
[解] 据题意
新生组的抽样结果为:
p1
=0.73,
q2
=0.27,n1=171
四年级学生组的抽样结果为:
p2
=0.58,
q2
=0.42,n2=117
H0:p1―p2=D0=0
H1:p1―p2=D0≠0
计算检验统计量 p X n 1 1 n X 2217 0 1 .7 17 3 1 111 1 0 .7 7 5 80 .669
[解] 据题意,
“不满意”组的抽样结果为:X 1
“满意”组的抽样结果为:X 2 H0:μ1―μ2=D0=0
=9.2年, S1=2.8年, n1=500; =8.5 年,S2=2.3 年, n2=600。
H1: μ1―μ2 ≠0
计算检验统计量
ZX1X2D0 9.28.5 4.47
2 1
22
2.82 2.32
n1 n2
500600
确定否定域,
因为α=0.05,因而有 Zα/2=1.96<4.47 因此否定零假设,即可以认为在0.05显著性水平上,婚龄对妇女婚
后生活的态度是有影响的。同时我们看到,由于样本计算值Z=4.47 远大
于单侧 Z0.05 的临界值1. 65,因此本题接受μ1―μ2 >0 的备择假设,即可 以认为妇女婚龄长容易对婚后生活产生“不满意”。
(2)备择假设:
单侧
H1:12D0
或 H1:12D0
双侧
H1:12D0
(3)否定域:单侧 Z
双侧 Z / 2
(4)检验统计量 (5)比较判定
Z
X1
X2
D 0
12
2 2
n1 n2
01.03.2021
3
[例]为了比较已婚妇女对婚后生活的态度是否因婚
龄而有所差别,将已婚妇女按对婚后生活的态度分为 “满
01.03.2021
5
2.大样本成数差检验
(1)零假设: (2)备择假设:H0:p1p2D0
单侧
双侧
H1:p1p2D0
或 H1:p1p2D0
H1:p1p2D0
(3)否定域:单侧 Z
双侧 Z / 2
(4)检验统计量
Z(p1p2)D0 (p1p2)D0
(p1p2)
p1q1 p2q2 n1 n2
其中:
布就是
N(1
2,n112
22
n2
)
。与单样本的情况相同,在大样本的
情况下(两个样本的容量都超过50),这个定理可以推广应用于任何具
有均值μ1和μ2以及方差
2和
1
2 2
的两个总体。当n1和n2逐渐变大
时,(X1 X2) 的抽样分布像前面那样将接近正态分布。
01.03.2021
2
1.大样本均值差检验
(1)零假设: H0:12D0
意”和“不满意”两组。从满意组中随机抽取600名妇女,
其平均婚龄为8.5年,标准差为2.3年;从不满意组抽出
500名妇女,其平均婚龄为9.2年,标准差2.8年。试问在
0.05显著性水平上两组是否存在显著性差异?
样本
人数
均值
标准差
满意组
600
8.5
2.3
不满意组
500
9.2
2.8
01.03.2021
4
度,所以全部自由度的数目就成为
S
( X1X 2 )
n1 n2 n1n2
01(.0n31.2+02n12―2)。 于是有
11
这样,对小样本正态总体, 1 2 和 2 2 未知,但σ1=σ2 ,
其均值差的检验步骤如下:
(1)零假设: H0:12D0
(2)备择假设:
单侧
双侧
H1:12D0
或 H1:12D0
(5“外向”和
“内向”,把他们分成两类。结果发现,新生中有73% 属
于“外向”类,四年级学生中有58%属于“外向”类。 样本
中新生有171名,四年级学生有117名。试问,在0.01水平 上,两类学生有无显著外性向差异? 内向
四年级 58% (117)
42%
第十章双样本假设检验及区间估
精品jin
第一节 两总体大样本假设检验
为了把单样本检验推广到能够比较两个样本的均值的检验,必须 再一次运用中心极限定理。下面是一条由中心极限定理推广而来的重
要定理:如果从 N(2,22) 和 N(1,12) 两个总体中分别抽取容量为
n1和n2 的独立随机样本,那么两个样本的均值差 (X1 X2) 的抽样分
p1
X1 n1
p2
X2 n2
为总体1的 样本成数
为总体2的 样本成数。
01.03.2021
6
当p1和p2未知,须用样本成数
p1
和
p2
进行估算时,分以下两
种情况讨论:
① 若零假设中两总体成数的关系为 p1 p2 ,这时两总体可看作成数
P 相同的总体,它 们的点估计值为
p
X1X2 n1n2
n1
p1n2 p2 n1n2
( X1 X 2 )
11 n1n2
( X1X2 )
n1 n2
n1n2
现又因为σ未知,所以要用它的
无偏估计量
S
替代它。由于两个样
本的方差基于不同的样本容量,因而
可以用加权的方法求出σ的无偏估计
S
n1S12 n2S22
n1 n2 2
量,得
注意,上式的分母上减2,是因为
根据 X 1 和 X 2 计算S1和S2时,分别损 失了一个自由度,一共损失了两个自由
Z p1p2
0.7 30.58 2.66
pq
n1n2 n1n2
0.660 9.33 1171 117 171117
确定否定域
因为α=0.01,因而有 Zα/2=Z0.005=2.58<2.66 因而否定零假设,即可以认为在0.01显著性水平上,两类学生在
性01.0格3.2上021是有差异的。
9
第二节 两总体小样本假设检验
与对单总体小样本假设检验一样,我们对两
总体小样本假设检只讨论总体满足正态分布的情
况。
1. 小样本均值差假设检验
(1)
当
2 1
和
2 2
已知时,小样本均值差
检验,与上一节所述大样本总体均值差检验完全
相同,这里不再赘述。
01.03.2021
10
(2)
2 1
和
2 2
未知,但假定它们相等时,
关键是要解决
的算式。
此时上式中检验 统计量 Z 可简化为
Z (p1p2)0 p1p2
pq pq
n1
n2
pq
n1n2 n1n2
② 若零假设中两总体成数 p1 p2 ,那么它们的点估计值有
p1 p1
p2 p2
此时上式中 检验统计量Z为
01.03.2021
Z ( p1 p2 ) D0
p1 q1 p2 q2
n1
n2
