三角函数整理专题
第3篇三角函数专题

sin θ<0, ① cos θ>0,
y 轴负半轴, 由 cos θ>0 判断 θ 在第一或第四象限或 x 轴正半 轴,故 θ 在第四象限.
sin θ>0, ② cos θ<0,
此时,由 sin θ>0 判断 θ 在第一或第二象限或
y 轴正半轴, 由 cos θ<0 判断 θ 在第二或第三象限或 x 轴负半 轴,故 θ 在第二象限. 所以角 θ 是第二或第四象限角. (2)因为点 P(sin θcos θ,2cos θ)位于第三象限, 所以 sin θcos θ<0,2cos
答案 A
考点梳理
1.同角三角函数的基本关系
2 2 (1)平方关系: sin α+cos α=1 sin α (2)商数关系: cos α=tan α .
.
2.三角函数的诱导公式 公式一:sin(α+2kπ)=sin α,cos(α+2kπ)=cos α ,tan(α +2kπ)=tan α,其中 k∈Z.
(
B. - Biblioteka D. - ).3 2 3 2
3 1 ,- 2 2 3 1 , 2 2
1 C. -2,-
解析
设 α=∠POQ,由三角函数定义可知,Q 点的坐标(x,
y)满足 x=cos α,y=sin α, 1 3 ∴x=-2,y= 2 , → 3 1 ∴OQ=- , . 2 2
4.(2013· 潍坊质检)已知角 α 的终边经过点 P(m,-3),且 4 cos α=- ,则 m 等于 5 11 A.- 4 C.-4 11 B. 4 D.4 ( ).
m 4 解析 由题意可知,cos α= 2 =- ,m<0,解得 m= 5 m +9 -4,故选 C.
(精心整理)高中数学三角函数专题(重要知识点和经典方法大合集)
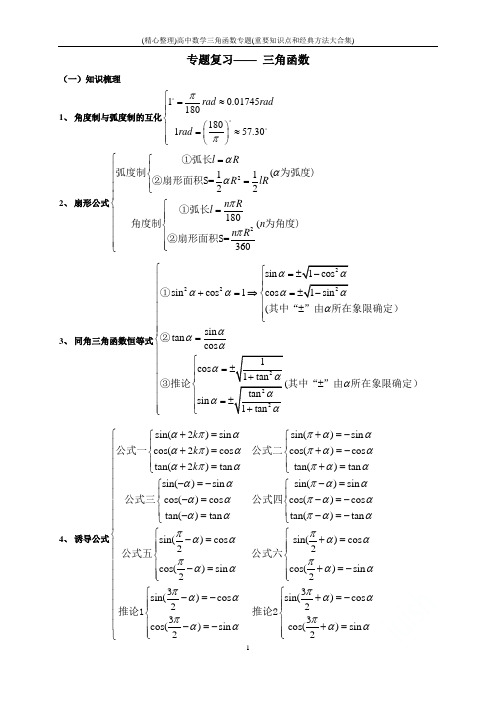
专题复习—— 三角函数(一)知识梳理1、 角度制与弧度制的互化10.01745180180157.30rad rad rad ππ⎧=≈⎪⎪⎨⎛⎫⎪=≈ ⎪⎪⎝⎭⎩2、 扇形公式22(11=22180(=360l R R lR n R l n n R αααππ⎧=⎧⎪⎪⎨⎪=⎪⎪⎩⎪⎨⎧=⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩⎩①弧长弧度制为弧度)②扇形面积S ①弧长角度制为角度)②扇形面积S3、 同角三角函数恒等式22sin sin cos 1cos (sin tan cos cos sin ααααααααααα⎧⎧=⎪⎪⎪⎪+=⇒=⎨⎪⎪⎪±⎪⎩⎪⎪⎪=⎨⎪⎪⎧=⎪⎪⎪⎪±⎨⎪⎪⎪=⎪⎪⎩⎩①其中“”由所在象限确定)②③推论其中“”由所在象限确定)4、 诱导公式sin(2)sin sin()sin cos(2)cos cos()cos tan(2)tan tan()tan sin()sin sin()sin cos()cos cos()cos tan()tan tan()tan s k k k απαπαααπαπαααπαπααααπααααπααααπαα+=+=-⎧⎧⎪⎪+=+=-⎨⎨⎪⎪+=+=⎩⎩-=--=⎧⎧⎪⎪-=-=-⎨⎨⎪⎪-=-=-⎩⎩公式一公式二公式三公式四公式五in()cos sin()cos 22cos()sin cos()sin 2233sin()cos sin()cos 2233cos()sin cos()sin 22ππααααππααααππααααππαααα⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎧⎨-=+=⎪⎪⎪⎪⎪⎪⎨⎨⎪⎪⎪-=+=-⎪⎪⎪⎩⎩⎪⎧⎧⎪-=-+=-⎪⎪⎪⎪⎪⎨⎨⎪⎪⎪⎪-=-+=⎪⎪⎩⎩⎩公式六推论1推论25、差(和)角公式cos()cos cos sin sincos()cos cos sin sinsin()sin cos cos sinsin()sin cos cos sintan tantan()1tan tantan tantan()1tan tanαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβ⎧-=+⎪+=-⎪⎪-=-⎪⎪+=+⎨-⎪-=⎪+⎪+⎪+=⎪-⎩余余正正号相反正余余正号相同6、二倍角公式(倍角公式)22222221sin22sin cos sin cos sin22cos2cos sin1cos2cos212sin sin21cos2 cos22cos1cos22tantan21tanαααααααααααααααααααα⎧⎪=⇒=⎪⎪=-⎪⎪-⎪=-⇒=⎨⎪+⎪=-⇒=⎪⎪⎪=⎪-⎩7、正弦定理及推论2(sin sin sin2sin,2sin,2sinsin,sin,sin222::sin:sin:sinsin sin sin,,sin sin sina b cR R ABCA B Ca R Ab R Bc R Ca b cA B CR R Ra b c A B Ca A a Ab Bb Bc C c C⎧===∆⎪⎪===⎪⎪⎪===⎨⎪⎪=⎪⎪===⎪⎩①为外接圆的半径)②③④⑤8、余弦定理及推论222 222222 222222 2222cos cos22cos cos22cos cos2b c a a b c bc A Abca c bb ac ac B Baca b c c a b ab C Cab⎧+-=+-⇒=⎪⎪+-⎪=+-⇒=⎨⎪⎪+-=+-⇒=⎪⎩9、三角形面积公式1(21()(2111=sin sin sin222S ah aS r a b c r ABCS ab C ac B bc A⎧=⎪⎪⎪=++∆⎨⎪⎪==⎪⎩为底,h为高)为内切圆的半径)10、求最小正周期的公式sin()2= cos()tan()= y A x kTy A x ky A x k Tωϕπωϕωπωϕω⎧=++⎪=++⎪⎨⎪=++⎪⎩最小正周期为的最小正周期为11、正弦函数y=sinx[]maxmin111+2,2,22(2)3+2,2,.222()1;2(3)2() 1.2(4)((5)y sinRk k k Zk k k Zx k k Z yx k k Z yk k Z kxππππππππππππππ-⎧⎡⎤-+∈⎪⎢⎥⎪⎣⎦⎨⎡⎤⎪+∈⎢⎥⎪⎣⎦⎩⎧+∈=⎪⎪⎨⎪+∈=-⎪⎩∈≠=()定义域:,值域:,在单调递增;单调性在单调递减当且仅当=时,最值当且仅当=-时,周期性:周期为2且0),最小正周期为2.奇偶性:,;(6)2.Rx k k Zk k Zπππ⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧+∈⎪⎪⎨⎪⎪∈⎪⎩⎩为上的奇函数.①为轴对称图形,对称轴为=对称性②为中心对称图形,对称中心为(,0),12、余弦函数y=cosx[][][]maxmin111+2,2,(2)2,2,.2()1;(3)2() 1.(4)((5)y cos,(6)Rk k k Zk k k Zx k k Z yx k k Z yk k Z kx Rx k kππππππππππππ-⎧-∈⎪⎨+∈⎪⎩∈=⎧⎨+∈=-⎩∈≠=()定义域:,值域:,在单调递增;单调性在单调递减当且仅当=时,最值当且仅当=时,周期性:周期为2且0),最小正周期为2.奇偶性:为上的偶函数.①为轴对称图形,对称轴为=对称性;+.2Zk k Zππ⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪∈⎧⎪⎪⎪⎨∈⎪⎪⎩⎩②为中心对称图形,对称中心为(,0),13、正切函数y=tanx1|,,22-+,),.22(3)(0.(4)y tan(5),0),.2x x k k Z Rk k k Zk k Z kxkk Zπππππππππ⎧⎧⎫≠+∈⎪⎨⎬⎩⎭⎪⎪+∈⎪⎪⎪∈≠⎨⎪=⎪⎪⎧⎪⎪⎨⎪∈⎪⎪⎩⎩()定义域:值域:()单调性:在开区间(单调递增周期性:周期为且),最小正周期为奇偶性:为奇函数.①不是轴对称图形;对称性②是中心对称图形,对称中心为(14、简谐运动sin()y A xωϕ=+[)2=1(0,0,0,)2xA xTπωωωπωϕϕ⎧⎪⎪⎪⎪⎪=>>∈+∞⎨⎪⎪⎪⎪⎪⎩①振幅:A②周期:T③频率:f=其中④相位:x+⑤初相:=0时的相位2222sin cos)(tan)0)sin cos)(tan)ba xb x a b xaa aa xb x a b xbωωωϕϕωωωϕϕ⎧+=++=⎪⎪⎨>⎪+=+-=⎪⎩①其中15、三角恒等变换之辅助角公式(其中②其中辅助角公式的证明如下:证明:asin xω+bcos xω22a b+22a b+sin xω22a b+cos xω),①22a b+=cosϕ22a b+=sinϕ,则asin xω+bcos xω22a b+xωcosϕ+cos xωsinϕ)22a b+xω+ϕ) (其中tanϕ=ba)② 22a a b+=sin ϕ22b a b+ϕ,则asin x ω+bcos x ω22a b +x ωsin ϕ+cos x ωcos ϕ) 22a b +x ω-ϕ),(其中tan ϕ=a b) 注:其中ϕ的大小可以由sin ϕ、cos ϕ的符号确定ϕ的象限,再由tan ϕ的值求出;或由tan ϕ=ba和(a,b)所在的象限来确定. 例:化简32cos 2y x x =+.法一:逆用差(和)角公式3132cos 22(2cos 2)2(sin 2cos cos 2sin )2sin(2)2666y x x x x x x x πππ=+=+=+=+法二:应用辅助角公式32cos 22sin(2)6y x x x π=+=+ (其中3tan 363πϕϕ==⇒=)(二)考点剖析考点一:正、余弦定理,三角形面积公式的应用 例1: 在△ABC 中,C =2B ,AB AC =43. (1)求cos B ;(2)若BC =3,求S △ABC . 解:(1)由C =2B 和正弦定理得sin C =2sin B cos B =2·AC AB sin C ·cos B ∴cos B =AB 2AC =23 (2)设AC =3x ,则AB =4x . 由余弦定理得(3x )2=(4x )2+32-2×4x ×3cos B ,即9x 2=`16x 2+9-16x ∴7x 2-16x +9=0 解得x =1或x =97当x =1时,AC =3,AB =4 ∴S △ABC =12BA ×BC ×sin B =12×4×3×53=2 5.当x =97时,AC =277,AB =367 ∴S △ABC =12BA ×BC ×sin B =12×367×3×53=1875.考点二:利用正、余弦定理判断三角形的形状例2:在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且2a sin A =(2b +c )sin B +(2c +b )sin C . (1)求角A 的大小;(2)若sin B +sin C =1,试判断△ABC 的形状.解:(1) 2a sin A =(2b +c )sin B +(2c +b )sin C由正弦定理得2a 2=(2b +c )b +(2c +b )c ,即a 2=b 2+c 2+bc ① 由余弦定理得a 2=b 2+c 2-2bc cos A12cos cos 2bc A bc A ∴-=⇒=- 又0A π<< 23A π∴=. (2)由①得sin 2A =sin 2B +sin 2C +sin B sin C 又sin B +sin C =1 ∴sin B =sin C =12又0,022B C ππ<<<<∴B =C ∴△ABC 是等腰三角形.考点三:三角恒等变换之辅助角公式:sin cos )(tan )ba xb x x aωωωϕϕ+=+=其中例3:已知函数2()2sin cos 2cos f x x x x =+,x R ∈(1) 求f(x)的最小正周期及最大值; (2) 求函数f(x)的单调递增区间; (3) 若0,2x π⎡⎤∈⎢⎥⎣⎦,求函数f(x)的值域 .解:2()2sin cos 2cos f x x x x =+sin 2cos21x x =++)14x π=++(1) f(x)的最小正周期为22T ππ==,最大值为max ()1f x =. (2) 由222,242k x k k Z πππππ-+≤+≤+∈得3,88k x k k πππππ-+≤≤+∈∴函数f(x)的单调递增区间为3,,88k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦(3)02x π≤≤52444x πππ∴≤+≤sin(2)14x π≤+≤ 0)114x π∴≤++≤即0()1f x ≤≤∴函数f(x)的值域为1⎡⎤⎣⎦即时训练:已知函数22(sin cos )y x x x =++x R ∈(1) 求函数f(x)的最小正周期、最小值及单调递减区间; (2) 当02x π<<时,求函数f(x)的值域.【高考地位】三角函数式的化简和求值是高考考查的重点内容之一. 掌握化简和求值问题的解题规律和一些常用技巧,以优化我们的解题效果,做到事半功倍. 这也是解决三角函数问题的前提和出发点. 在高考中常以选择题、填空题出现,其试题难度考查不大.【方法点评】方法一 切割化弦使用情景:一般三角求值类型解题模板:第一步 利用同角三角函数的基本关系sin tan cos θθθ=,将题设中的切化成弦的形式; 第二步 计算出正弦与余弦之间的关系; 第三步 结合三角恒等变换可得所求结果.例1已知1tan()2πα+=,则sin cos 2sin cos αααα-+=( ) A .41 B .21 C .41- D .21- 【答案】C 【解析】试题分析:21tan =α,将原式上下同时除以αcos ,即411tan 21tan cos sin 2cos sin -=+-=+-αααααα,故选C.考点:同角三角函数基本关系学*科网 【变式演练1】已知2)tan(-=-απ,则=+αα2cos 2cos 1( )A .3 B. 52C.25- D.3- 【答案】C 【解析】考点:诱导公式,同角间的三角函数关系,二倍角公式.方法二 统一配凑使用情景:一类特殊三角求值类型解题模板:第一步 观察已知条件中的角和所求的角之间的联系;第二步 利用合理地拆角,结合两角和(或差)的正弦(或余弦)公式将所求的三角函数值转化为已知条件中的三角函数值;第三步 利用三角恒等变换即可得出所求结果.例2已知,31tan ,71tan ==βα则=+)2tan(βα 【答案】1 【解析】 试题分析:212tan 3tan ,tan 231tan 4ββββ===-,()13tan tan 274tan 21131tan tan 2174αβαβαβ++∴+===--⨯考点:两角和的正切公式.方法三 公式活用例3 下列式子结果为3的是( ) ①tan25tan353tan25tan35︒+︒+︒︒; ②()2sin35cos25cos35cos65︒︒+︒︒; ③1tan151tan15+︒-︒;④2tan61tan6ππ-.A. ①②B. ③C. ①②③D. ②③④ 【答案】C【高考再现】1.(2018年全国卷Ⅲ文)若,则A .B .C .D .【答案】B 【解析】 分析:由公式可得.详解:,故答案为B.点睛:本题主要考查二倍角公式,属于基础题.2. 【2016高考新课标3理数】若3tan 4α= ,则2cos 2sin 2αα+=( ) (A)6425 (B) 4825 (C) 1 (D)1625【答案】A 【解析】试题分析:由3tan 4α=,得34sin ,cos 55αα==或34sin ,cos 55αα=-=-,所以2161264cos 2sin 24252525αα+=+⨯=,故选A .考点:1、同角三角函数间的基本关系;2、倍角公式.【方法点拨】三角函数求值:①“给角求值”将非特殊角向特殊角转化,通过相消或相约消去非特殊角,进而求出三角函数值;②“给值求值”关键是目标明确,建立已知和所求之间的联系.4.【2017山东,文4】已知3cos 4x =,则cos2x = A.14- B.14 C.18- D.18【答案】D 【解析】【考点】二倍角公式【名师点睛】(1)三角函数式的化简与求值要遵循“三看”原则,一看角,二看名,三看式子结构与特征.(2)三角函数式化简与求值要注意观察条件中角之间的联系(和、差、倍、互余、互补等),寻找式子和三角函数公式之间的共同点.6. 【2015高考福建,文6】若5sin13α=-,且α为第四象限角,则tanα的值等于()A.125B.125-C.512D.512-【答案】D【考点定位】同角三角函数基本关系式.【名师点睛】本题考查同角三角函数基本关系式,在sinα、cosα、tanα三个值之间,知其中的一个可以求剩余两个,但是要注意判断角α的象限,从而决定正负符号的取舍,属于基础题.6.(2018年全国卷II文)已知,则__________.【答案】.【解析】分析:利用两角差的正切公式展开,解方程可得.详解:,解方程得.学科*网点睛:本题主要考查学生对于两角和差公式的掌握情况,属于简单题型,解决此类问题的核心是要公式记忆准确,特殊角的三角函数值运算准确.7.【2018年全国普通高等学校招生统一考试数学(江苏卷)】已知为锐角,,.(1)求的值;(2)求的值.【答案】(1);(2)【解析】分析:先根据同角三角函数关系得,再根据二倍角余弦公式得结果;(2)先根据二倍角正切公式得,再利用两角差的正切公式得结果.详解:解:(1)因为,,所以.因为,所以,因此,.点睛:应用三角公式解决问题的三个变换角度(1)变角:目的是沟通题设条件与结论中所涉及的角,其手法通常是“配凑”.(2)变名:通过变换函数名称达到减少函数种类的目的,其手法通常有“切化弦”、“升幂与降幂”等. (3)变式:根据式子的结构特征进行变形,使其更贴近某个公式或某个期待的目标,其手法通常有:“常值代换”、“逆用变用公式”、“通分约分”、“分解与组合”、“配方与平方”等. 学#科网【反馈练习】1.【山东省济南市2018届高三第一次模拟考试数学(文)试题】若72sin 410A π⎛⎫+=⎪⎝⎭, ,4A ππ⎛⎫∈ ⎪⎝⎭,则sin A 的值为( )A .35 B . 45 C . 35或45 D . 34【答案】B 【解析】5,,,4424A A πππππ⎛⎫⎛⎫∈∴+∈⎪ ⎪⎝⎭⎝⎭,所以cos 04A π⎛⎫+< ⎪⎝⎭,且22cos 1sin 4410A A ππ⎛⎫⎛⎫+=--+=- ⎪ ⎪⎝⎭⎝⎭, 所以4sin sin sin cos cos sin 4444445A A A A ππππππ⎡⎤⎛⎫⎛⎫⎛⎫=+-=+-+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,选B. 点睛:本题主要考查同角三角函数基本关系式、两角差的正弦公式等,属于易错题.解答本题的关键是拆角,将sin A 拆成sin 44A ππ⎡⎤⎛⎫+- ⎪⎢⎥⎝⎭⎣⎦.2.【山西省2018年高考考前适应性测试文科数学试题】已知tan 3α=,则sin21cos2αα=+( )A . 3-B . 13-C . 13D . 3 【答案】D 【解析】222sin cos 3122sin tan cos cos αααααα===+故选D3.【江西省上饶市2018届高三下学期第二次高考模拟数学(理)试题】000sin65sin35cos30cos35-=( ) A . 3-B . 12-C . 12D . 3【答案】C 【解析】由题得()00000000sin 3530sin35cos30cos35sin301sin30cos35cos352+-===,故选C. 4.【河南省濮阳市2018届高三第一次模拟考试数学(理)试题】设()0,90α∈︒︒,若()3sin 7525α︒+=-,则()()sin 15sin 75αα︒+⋅︒-= ( )A .110 B . 2 C . 110- D . 2-【答案】B【解析】()()sin 75cos 15αα-=+, 所以原式等于()()()1sin 15cos 15sin 3022ααα++=+ 而()()()()2sin 302sin 75245sin 752cos 7522αααα⎡⎤⎡⎤+=+-=+-+⎣⎦⎣⎦ , ()75275,255α+∈ ,又因为()sin 7520α+<,所以()752180,255α+∈,可求得()4cos 7525α+=- , 那么()()()22342sin 302sin 752cos 7525510ααα⎡⎤⎛⎫⎛⎫⎡⎤+=+-+=---= ⎪ ⎪⎢⎥⎣⎦⎝⎭⎝⎭⎣⎦,那么()12sin 3022α+=,故选B. 5.【安徽省宣城市2018届高三第二次调研测试数学理试题】已知3cos 5α=, 3,22παπ⎛⎫∈⎪⎝⎭,则cos 3πα⎛⎫-= ⎪⎝⎭__________.【答案】34310- 【解析】∵3cos 5α=, 3,22παπ⎛⎫∈⎪⎝⎭∴4sin 5α=- ∴3143343cos cos cos sin sin 333525πππααα-⎛⎫⎛⎫-=+=⨯+-⨯= ⎪⎪⎝⎭⎝⎭ 故答案为343-. 三角函数的图像和性质问题【高考地位】近几年高考降低了对三角变换的考查要求,而加强了对三角函数的图象与性质的考查,因为函数的性质是研究函数的一个重要内容,是学习高等数学和应用技术学科的基础,又是解决生产实际问题的工具,因此三角函数的性质是高考的重点和难点。
《三角函数》复习专题

《三角函数》复习专题一、重要知识点清理1.角的概念:(了解)正角:按 时针方向旋转形成的角叫做正角. 负角:按 时针方向旋转形成的角叫做负角. 零角:射线没有做任何旋转,我们称它形成一个零角. 2.象限角、象限界角(轴线角)把角置于直角坐标系中,使角的顶点与 重合,角的始边与 重合,角的终边(除端点外)的位置在第几象限,就称这个角是第几象限角。
角的终边在坐标轴上的角称为象限界角,它不属于任何象限.α是第二象限角可表示为: . α是第四象限角可表示为: . 3.终边相同的角:与α角终边相同的角的集合可以记做 . 4.弧度制的定义:(略)α= . 弧长公式:l = ; 扇形面积公式:S = = .5.角度与弧度的换算:180o = ; 1o = rad ;1ra d 6.任意角的三角函数的定义:7.三角函数的值在各象限的符号:8.作三角函数线平方关系:;商数关系: ; 公式(一):sin(2)k πα+= c o s (2)k πα+= t a n (2)k πα+= 公式(二):sin()πα+= c o s ()πα+= t a n ()πα+= 公式(三):sin()α-= c o s ()α-= t a n ()α-=公式(四):sin()πα-= c o s ()πα-= t a n ()πα-= 公式(五):sin(2)πα-= c o s (2)πα-= t a n (2)πα-= 公式(六):sin()2πα-= c o s ()2πα-= t a n ()2πα-=公式(七):sin()2πα+= c o s ()2πα+= t a n ()2πα+= 公式(八):3sin()2πα-= 3c o s ()2πα-= 3t a n ()2πα-=公式(九):3sin()2πα+= 3c o s ()2πα+= 3t a n ()2πα+= 九个诱导公式的简记口诀为: (注意公式的逆向变换,符号是关键)求值,化简的步骤为: 12.函数()y f x =为周期函数⇔存在 T ,使 恒成立; 13.函数2cos(2)13y x π=-++,的 定义域为 ;值域为 ;周期为 ;增区间 ;减区间为 ;对称轴方程为 ;对称中心为 ; 14.有关函数sin()y A x b ωϕ=++(0,0,,A b ωϕ>>为常数)的方法要点 ①求其对称轴、中心、最大值和最小值:正弦型函数sin()y A x ωϕ=+的对称中心是其 点;对称轴经过其 点; ②求其单调区间方法:17.正弦、余弦、正切函数的图象和性质18.函数图象变换:①函数y =sin(x ±φ)( φ>0)的图象可由函数y=sin x 的图象向左(或右)平移 个单位而得到,称为 变换.这种变换的实质是:纵坐标,横坐标增加(或减少) 个单位. ②函数y =sin ωx (ω>0)的图象可由函数y =sin x 的图象沿x 轴伸长(ω<1)或缩短(ω>1)到原来的ω1倍而得到,称为 变换.这种变化的实质是:纵坐标 ,横坐标伸长(0<ω<1)或缩短(ω>1)到原来的 倍.③函数y =A sin x 的图象可由函数y =sin x 的图象沿y 轴伸长(A >1)或缩短(A <1)到原来的A 倍而得到的,称为 变换.这种变换的实质是:横坐标 ,纵坐标伸长(A >1)或缩小(0<A <1)到原来的 倍.19.综合变换:以函数y =3sin(2x -3π),x ∈R 为例.①按φ、ω、A 顺序变换:y =sin x →y=sin(x -3π)→y =sin(2x -3π)→y =3sin(2x -3π) 图象变换:②按ω、φ、A 顺序变换:y =sin x →y =sin2x →y =sin(2x -3π)→y =3sin(2x -3π)图象变换:y =sin(x -3π)y =sin(2x -3π)y =3sin(2x -3π)y =sin(2x -3πy =3sin(2x -3π)用流程图来表示:。
三角函数专题复习

三角函数专题复习一、任意角和弧度制例1.下列各角中,终边相同的角是 ( )A.23π和240B.5π−和314 C.79π−和299π D.3和3例2.已知扇形圆心角60α=,α所对的弧长6l π=,则该扇形面积与其内切圆面积的比值为__________.练习:1.将1665−化成2(02,Z)k k απαπ+<∈的形式是( )A .584ππ−− B .384ππ− C .5104ππ− D .3104ππ− 2.(多选)如图,A ,B 是单位圆上的两个质点,点B 的坐标为(1,0),60BOA ∠=︒,质点A 以1rad /s 的角速度按逆时针方向在单位圆上运动,质点B 以2rad /s 的角速度按顺时针方向在单位圆上运动,则( )A .1s 时,BOA ∠的弧度数为π33+B .πs 12时,扇形AOB 的弧长为7π12 C .πs 6时,扇形AOB 的面积为π3 D .5s 9时,A ,B 在单位圆上第一次相遇3.若角α与角β的终边关于y 轴对称,则α与β的关系是____ _______.4.如图,分别以等边三角形ABC 的三个顶点为圆心,以边长为半径画弧,得到的封闭图形是莱洛三角形,若2AB =,则莱洛三角形的面积(即阴影部分面积)为______.二、三角函数的概念例3. 若θ是第二象限角,则 ( ) A.sin θ2>0 B.cos θ2<0 C.tan θ2>0 D.以上均不对例4.已知111A B C △与222A B C △满足:12sin cos A A =,12sin cos B B =,12sin cos C C =,则( )A .111ABC △是钝角三角形,222A B C △是锐角三角形B .111A BC △是锐角三角形,222A B C △是钝角三角形C .两个三角形都是锐角三角形D .两个三角形都是钝角三角形例5. 已知函数()263x f x a−=+(0a >且1a ≠)的图象经过定点A ,且点A 在角θ的终边上,则sin cos sin cos θθθθ−=+______. 练习:5.有四个关于三角函数的命题:1:p x ∃∈R ,221sin cos 222x x +=;2:p x ∃、y ∈R ,sin()sin sin x y x y −=−; ()3π:sin cos 2πZ 2p x y x y k k =⇒+=+∈;4π:0,2p x ⎛⎫∀∈ ⎪⎝⎭,1cos tan sin x x x =. 其中真命题的是( )A .1p ,3pB .1p ,4pC .2p ,3pD .2p ,4p6.sin1cos 2tan 3⋅⋅的值( )A .大于0B .小于0C .等于0D .不确定7.已知sin α=,则sin 4α-cos 4α的值为 ( )A.-B. -C.D.8.,,A B C ∠∠∠是三角形的三个内角,下列选项能判断ABC 为等腰三角形的是( )A .()()sin sin ABC A B C +−=−+B .sincos 22A B C A B C +−−+= C .sin sin 22A B C A B C +−−+=D A 9.已知关于x 的方程4x 2-2(m+1)x+m=0,的两个根恰好是一个直角三角形的一个锐角的正弦、余弦,则实数m 的值为________.10.(1(2α是第三象限角.11.已知sin cos x x t +=,t ⎡∈⎣.(1)当12t =且x 是第四象限角时,求33sin cos x x −的值; (2)若关于x 的方程()sin cos sin cos 1x x a x x −++=有实数根,求a 的取值范围.三、诱导公式例6.若角α的终边经过点()()sin 780,cos 330P ︒−︒,则sin α=( ) AB .12 C.2 D .1例7.已知()()()()9π7πsin cos tan 2π22tan πsin πf αααααα⎛⎫⎛⎫−−− ⎪ ⎪⎝⎭⎝⎭=−+. (1)化简()f α;(2)若()π22f f αα⎛⎫+= ⎪⎝⎭,求()π2f f αα⎛⎫− ⎪⎝⎭的值.练习:12.已知n ∈Z ,化简()πsin π16n n ⎡⎤+−=⎢⎥⎣⎦______________. 13.已知2πtan(π)3α+=−. (1)求πsin(2022π)2sin 2π3cos cos(π)2αααα⎛⎫+−+ ⎪⎝⎭⎛⎫−−− ⎪⎝⎭的值; (2)若为α第四象限角,求sin cos αα+的值.14.已知角α的顶点在坐标原点,始边与x 轴非负半轴重合,终边经过函数()33x f x a −=−−(0a >且1a ≠)的定点M .(1)求sin 2cos +tan ααα−的值;(2)求()()()()3πsin πcos 2tan 3πcos 2πsin ααααα⎛⎫++− ⎪⎝⎭−+−+−的值.15.已知函数()()()sin πcos πf x x x =+−,且π04x <<. (1)若()14f x =,求πcos cos 2x x ⎛⎫++ ⎪⎝⎭的值; (2)若函数()g x 满足()()tan g x f x =,求14g ⎛⎫ ⎪⎝⎭的值.。
高三三角函数专题复习(题型全面)

三角函数考点(kǎo diǎn)1:三角函数(sānjiǎhánshù)的有关概念;考点(kǎo diǎn)2:三角(sānjiǎo)恒等变换;(两角和、差公式(gōngshì),倍角半角公式、诱导公式、同角的三角函数关系式)考点3:正弦函数、余弦函数、正切函数的图象和性质;(定义域、值域、最值;单调区间、最小正周期、对称轴对称中心)考点4:函数y=Asin(的图象与性质;(定义域、值域、最值;单调区间、最小正周期、对称轴对称中心、图像的变换)一、三角函数求值问题1. 三角函数的有关概念例1.若角的终边经过点,则= .练习1.已知角的终边上一点的坐标为(),则角 的最小正值为()A、 B、 C、 D、2、公式法:例2.设,若,则=()A. B. C. D.练习1.若,则等于()A.B.C.D.2.α是第四象限角,,则( ) A . B .C .D .3. 的值为 。
4.已知,且,则的值是 .3.化简求值例3.已知为第二(d ì èr)象限角,且,求的值练习(li ànx í):1。
已知,则的值为( )A .15-B .C .15D .2.已知. (I )求的值. (II )的值. 3.若,则的值为( )A. B.12-C.12D.4 化简= .4、配凑求值 例4.已知,sin()=-sin则os=____ .练习(li ànx í):1 设α∈(),β∈(0,),cos(α-4π)=,sin(+β)=,则sin(α+β)=_________2.已知sin α=53,α∈(,π),tan(π-β)= ,则tan(α-2β)=______3.求的值4.若,则= ( )A .B .C .D .方法(f āngf ǎ)技巧:1.三角函数恒等变形(bi àn x íng)的基本策略。
(1)常值代换:特别是用“1”的代换,如1=cos 2θ+sin 2θ=tanx ·cotx=tan45°等。
专题06知识点 三角函数的图像与性质

-
-3 2
-2
1
o
-1
2
3
2 2
7
3 2
5
4
2
x
y
y=tanx
y
y=cotx
3 -2
-
-2
o
2
3
x
2
-
-2
o
2
3 2 x
2
函数 y=sinx
y=cosx
定义 域
值域
R
R
[-1,1]x=2kπ+ [-1,1] 2
时 ymax=1
x=2kπ时
x=2kπ- 2
时 ymin=-1
ymax=1
0
2 3 5
3 2
6
4
3
2
3
4
6
2
3.弧长及扇形面积公式
弧长公式: l .r
扇形面积公式:S= 1 l.r 2
----是圆心角且为弧度制。 r-----是扇形半径
知识点二:诱导公式
1.常用的诱导公式
公式一: 设α为任意角,终边相同的角的同一三角函数的值相等:
sin(2kπ+α)=sinα cos(2kπ+α)=cosα tan(2kπ+α)=tanα cot(2kπ+α)=cotα 公式二: 设α为任意角,π+α的三角函数值与α的三角函数值之间的关 系: sin(π+α)=-sinα cos(π+α)=-cosα tan(π+α)=tanα cot(π+α)=cotα 公式三: 任意角α与 -α的三角函数值之间的关系: sin(-α)=-sinα cos(-α)=cosα tan(-α)=-tanα cot(-α)=-cotα 公式四: 利用公式二和公式三可以得到π-α与α的三角函数值之间的关 系: sin(π-α)=sinα cos(π-α)=-cosα tan(π-α)=-tanα cot(π-α)=-cotα
三角函数专题复习

三角函数专题复习(一)1. 三角函数(约16课时)(1)任意角、弧度制:了解任意角的概念和弧度制,能进行弧度与角度的互化。
(2)三角函数①借助单位圆理解任意角三角函数(正弦、余弦、正切)的定义。
②借助单位圆中的三角函数线推导出诱导公式(的正弦、余弦、正切),能画出的图象,了解三角函数的周期性。
③借助图象理解正弦函数、余弦函数在,正切函数在上的性质(如单调性、最大和最小值、图象与x轴交点等)。
④理解同角三角函数的基本关系式:⑤结合具体实例,了解的实际意义;能借助计算器或计算机画出的图象,观察参数A,ω,对函数图象变化的影响。
⑥会用三角函数解决一些简单实际问题,体会三角函数是描述周期变化现象的重要函数模型。
一、要点●疑点●考点1、任意角和弧度制:①、任意角:正角(按逆时针方向旋转形成的角)、负角(按顺时针方向旋转形成的角)、零角(没有作任何旋转的角);②、象限角:角的顶点与原点重合,角的始边与x轴的正半轴重合,那么角的终边落在第几象限,我们就说这个角是第几象限的角;【注意】:如果角的终边落在坐标轴上,就认为这个角不属于任何一个象限。
③、a:终边相同的角的集合:S={β︱β=α+k·360o,k∈Z};b:终边在x轴上的角的集合:S={β︱β=k•180o,k∈Z};c:终边在y轴上的角的集合:S={β︱β=90o+k·180o,k∈Z};d:终边在坐标轴上的角的集合:S={β︱β=k·90o,k∈Z};e:终边在直线y=x上的角的集合:S={β︱β=45o+k•180o,k∈Z}④、角度制与弧度制:用度作为单位来度量角的单位制叫着角度制;用实数作为单位来度量角的单位制叫着弧度制;把长度等于半径长的弧所对的圆心角叫着1弧度的角,用符号rad表示,读着弧度。
如果半径为r的圆的圆心角α所对的弧长为l,那么,角αα的正负由角α的终边的旋转方向决定。
角度制与弧度制的转化只要通过【注意】:今后用弧度制表示角时,“弧度”二字或“rad”通常略去不写,而只写该角所对应的弧度数。
(完整word版)三角函数专题讲义

三角函数专题一、核心知识点归纳:1、正弦函数、余弦函数和正切函数的图象与性质:sin y x =cos y x =tan y x =图象定义域 R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭值域[]1,1-[]1,1-R最值当22x k ππ=+()k ∈Z 时,max 1y =; 当22x k ππ=-()k ∈Z 时,min 1y =-. 当()2x k k π=∈Z 时,max 1y =;当2x k ππ=+()k ∈Z 时,min 1y =-.既无最大值也无最小值周期性 2π2ππ奇偶性奇函数 偶函数奇函数单调性在2,222k k ππππ⎡⎤-+⎢⎥⎣⎦()k ∈Z 上是增函数;在32,222k k ππππ⎡⎤++⎢⎥⎣⎦ ()k ∈Z 上是减函数.在[]()2,2k k k πππ-∈Z 上是增函数;在[]2,2k k πππ+ ()k ∈Z 上是减函数. 在,22k k ππππ⎛⎫-+ ⎪⎝⎭()k ∈Z 上是增函数.对称性对称中心()(),0k k π∈Z对称中心对称中心函 数 性 质2。
正、余弦定理:在ABC ∆中有: ①正弦定理:2sin sin sin a b cR A B C===(R 为ABC ∆外接圆半径) 2sin 2sin 2sin a R A b R B c R C =⎧⎪=⎨⎪=⎩⇒ sin 2sin 2sin 2a A Rb B Rc C R⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩注意变形应用 ②面积公式:111sin sin sin 222ABC S abs C ac B bc A ∆=== ③余弦定理: 2222222222cos 2cos 2cos a b c bc A b a c ac B c a b ab C ⎧=+-⎪=+-⎨⎪=+-⎩ ⇒ 222222222cos 2cos 2cos 2b c a A bc a c b B ac a b c C ab ⎧+-=⎪⎪+-⎪=⎨⎪⎪+-=⎪⎩二、方法总结:1.三角函数恒等变形的基本策略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题1:两角和与差公式的应用一、【学习目标】1、熟记两角和与差的正弦、余弦、正切公式;2、利用公式进行三角函数式的化简和求值。
二、两角和与差的正弦、余弦、正切公式:(1)cos()αβ-= ;(2)cos()αβ+= ; (3)sin()αβ+= ;(4)sin()αβ-= ; (5)tan()αβ+= ;(6)tan()αβ-= ;辅助角公式:sin cos )a x b x x ϕ++,其中cos ϕϕ==三、例1.求值:(1)sin 75 (2)7cos 12π(3)tan105(4)cos 20cos70sin 20sin 70- (5)sin119︒sin181︒-sin91︒sin29︒(6)001cos15sin1522+ (7)0022-例2. 已知A 、B 均为钝角且sin A B ==,求(1))cos(B A +;(2)A+B.例3. 已知324πβαπ<<<,12cos()13αβ-=,3sin()5αβ+=-.求sin 2α. 【同类变式】 1、求值:①1tan151tan15+︒-︒= ②sin 72cos 42cos72sin 42-=③=o 15sin ④=015tan 。
2、已知βα、均为锐角,55sin =α ,1010cos =β,求(1))sin(βα-;(2)βα-.3、已知βα,⎪⎭⎫ ⎝⎛∈ππ,43,)sin(βα+=,53-,13124sin =⎪⎭⎫ ⎝⎛-πβ求cos ⎪⎭⎫ ⎝⎛+4πα4、若tan(α+β)=25,tan(β-π4)=14,求tan(α+π4)的值。
【巩固提高】1、已知0<α<π2<β<π,cos α=35,sin(α+β)=-35,则cos β的值为________.2、已知sin α=55,sin(α-β)=-1010,α、β均为锐角,则β等于________. 3、已知cos 3()45πα-=,sin 512()413πβ+=-且β3(0,),(,)444πππα∈∈,求sin(α+β).4、已知α、β∈(,)22ππ-,且tan α,tan β是方程x 2的两个根,求α+β值。
5、已知函数()sin cos f x x x =+(1)求函数()f x 的周期、单调区间; (2)若[,]4x ππ∈-求函数()f x 的值域。
课题2:倍角公式与其他三角公式应用一、【学习目标】1、熟记二倍角的正弦、余弦、正切公式以及一些公式的变形;2、利用公式或变形形式进行三角函数式的化简和求值。
二、1、二倍角的正弦、余弦、正切公式: (1)sin 2α=(2)cos2α= = = (3)tan 2α= 2、公式的变形:降幂公式:2cos α= ,2sin α= ,=θθcos sin ,2tan α= 。
三、例1.求值:(1)15cos 15sin (2)8sin 8cos 22ππ- (3)5.22tan 15.22tan 22-(4)52sin cos 11212ππ- (5) 12cos 24cos 48cos 48sin 8ππππ例2. 已知4sin 5θ=,并且θ在第二象限,求θ2sin 、θ2cos 、θ2tan 的值。
例3.已知函数21()(2cos 1)sin 2cos 42f x x x x =-+,(1)求()f x 的最小正周期及最大值; (2)若(0,),4x π∈求函数()f x 的值域。
【同类变式】1、求值(1)2sin 2cos 44αα- (2)ααtan 11tan 11+--(3)θθ2cos cos 212-+ (4)35coscoscoscos 128812ππππ2、若已知23πθπ<<,且43tan =θ,求θ2sin 、θ2cos 、θ2tan 的值。
3、已知函数2()cos sin cos f x x x x =+(1)求()f x 的最小正周期及最小值;(2) 若(,),42ππα∈且3()8f πα+=,求cos α的值。
【巩固提高】1、若270°<α<360°,则α2cos 21212121++= 2、已知2sin cos 3x x +=,则sin 2x =________. 3、化简:(1)2+2cos8+21-sin8 (2)2cos 22cot()cos ()44xx x ππ+-4、已知α为锐角,且21tan =α,求ααααα2cos 2sin sin cos 2sin -的值.5、已知10,sin cos 25x x x π-<<+=. (1)求sin cos x x -的值.(2)求223sin 2sin cos cos 2222tan cot x x x x x x-++的值.课题3:倍角公式与其他三角公式应用(二)一、【学习目标】利用公式或变形形式进行三角函数式的化简和求值。
二、公式的变形:(1)tan tan αβ±=(2)降幂公式:2cos α= ,2sin α= ,=θθcos sin ,2tan α= 。
例1. 求函数22sin cos 2sin 1y x x x =-+的最值、周期和单调区间。
【同类变式】 1、求x x x y cos sin cos 32+= 的最值、周期和单调区间。
2、已知3sin ,1)4x m =(,2,cos )44x x n =(cos ,求()f x m n =•的最值和周期。
【巩固提高】1、已知函数()cos(2)2sin()sin()344f x x x x πππ=-+-+,(1)求函数()f x 的最小值; (2)求函数()f x 的零点;(3)求函数()f x 在区间[,]122ππ-上的值域。
2、已知函数2()sin cos 2f x x x x ωωω=⋅- (0)ω>的最小正周期为2π。
(1)求()f x 的表达式;(2)将函数()f x 的图像向右平移8π个单位后,再将得到的图像上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数()y g x =的图像,若关于x 的方程()0g x k +=在区间[0,]2π上有解,求实数k 的取值范围。
课题4:三角恒等变换(一)【学习目标】一、会利用和、差、倍、半角公式解决比较复杂的求值和化简问题。
二、1、半角公式:sin 2α= ;cos2α= ;tan2α= = = 。
2、倍角公式与其他三角公式应用时的基本思路:(1)“化异为同”“切化弦” “1的代换”是三角恒等变换的常用技巧。
“化异为同”是指“化异名为同名”“化异次为同次”“化异角为同角”。
(2)角的变换是三角变换的核心,如()βαβα=+-,2()()ααβαβ=++-,2()()βαβαβ=+--,22αα=⨯例1. 已知:0<α<π2<β<π,cos(β-π4)=13,sin(α+β)=45.(1)求sin2β的值;(2)求cos(α+π4)的值.例2. 求值:42212cos 2cos 22tan()sin ()44x x x x ππ-+-+例3. 求值: (1)1cos 20sin10(cot 5tan 5)2sin 20+︒-︒︒-︒︒(2)已知sin 11cos 2αα=+,求sin cos αα+【同类变式】1、已知0,22ππαβπ<<<<,且15tan,sin()2213ααβ=+=,(1)求cos α和cos β的值.(2)求tan 2αβ-的值.2、设3177cos(),45124x x πππ+=<<,求2sin 22sin 1tan x x x +-值3、求值:课题5:三角恒等变换(二)【学习目标】一、利用和、差、倍、半角公式解决三角恒等变换的综合问题二、1.三角恒等变换与三角函数性质的综合:三角函数的周期性、单调性、最值;2.三角恒等变换与向量的综合:向量的模、向量共线、垂直;三、例1、已知函数f (x )=-2sin ⎝⎛⎭⎫2x +π4+6sin x cos x -2cos 2x +1,x ∈R . ①求f (x )的最小正周期;②求f (x )在区间⎣⎡⎦⎤0,π2上的最大值和最小值.例2、设向量a =(3sin x ,sin x ),b =(cos x ,sin x ),x ∈⎣⎡⎦⎤0,π2. ①若|a |=|b |,求x 的值;②设函数f (x )=a ·b ,求f (x )的最大值.【同步训练】1、已知函数f (x )=(2cos 2x -1)sin 2x +12cos 4x .(1)求f (x )的最小正周期及最大值;(2)若α∈⎝⎛⎭⎫π2,π,且f (α)=22,求α的值.2、已知函数f (x )=sin(ωx +φ),其中ω>0,|φ|<π2,若a =(1,1),b =(cos φ,-sin φ),且a ⊥b ,又知函数f (x )的最小正周期为π. (1)求f (x )的解析式;(2)若将f (x )的图象向右平移π6个单位长度得到g (x )的图象,求g (x )的单调增区间.3、设函数2()2sin cos cos sin sin 2f x x x x ϕϕ=+- (0)ϕπ<<在x π=处取最小值。
(1)求ϕ的值;(2) 在△ABC 中,内角A 、B 、C 所对的边分别是a,b,c ,已知1,()a b f A ==C【巩固提升】1、若1cos cos sin sin3x y x y +=,则()cos 22x y -=________.2、设当x θ=时,函数()sin 2cos f x x x =-取得最大值,则cos θ=______.3、设f(x)=错误!未找到引用源。
sin3x+cos3x,若对任意实数x 都有|f(x)|≤a,则实数a 的取值范围是____ .4、设函数2()sin cos (0)f x x x x ωωωω=->,且()y f x =的图象的一个对称中心到最近的对称轴的距离为4π,(Ⅰ)求ω的值(Ⅱ)求()f x 在区间3[,]2ππ上的最大值和最小值。
课题6 三角恒等变换复习 知识点复习1、两角和与差的正弦、余弦和正切公式:⑴()cos αβ-= ;⑵()cos αβ+= ;⑶()sin αβ-= ;⑷()sin αβ+= ; ⑸()tan αβ-=⇒tan tan αβ-= ;()tan αβ+=⇒tan tan αβ+= .2、二倍角的正弦、余弦和正切公式:⑴sin2α= 1sin 2α⇒±= 。
⑵cos2α= = = 。
⇒降幂公式2cos α= ,2sin α= ,αα=sin cos .⑶tan 2α= .3、辅助角公式:sin cos a b θθ±= (其中0,0,a b >> )4、三角变换中对角的变形如:①α2是α的二倍;α4是α2的二倍;α是2α的二倍;2α是4α的二倍; ②2304560304515oooooo=-=-=;③ββαα-+=)(;④)4(24αππαπ--=+;⑤)4()4()()(2απαπβαβαα--+=-++=。
