离散系统的数学描述
离散时间系统的数学模型—差分方程
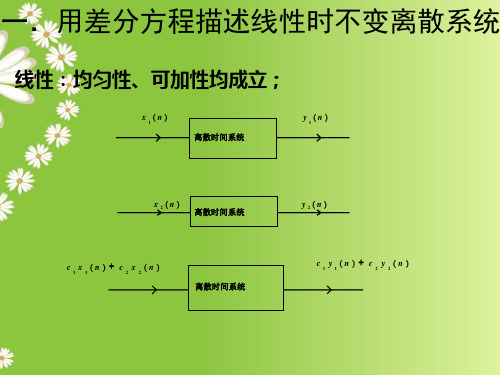
一．用差分方程描述线性时不变离散系统
线性：均匀性、可加性均成立；
x (n) 1
离散时间系统
y (n) 1
x 2 ( n ) 离散时间系统
c x (n ) + c x (n )
x1n+ x2n
x2 n
乘法器：
x1n x1n+ x2n
x2 n
x1 n
x1n x2 n
x2 n
系统框图
乘法器
xn
延时器
axn
a
yn
1
yn 1
E
xn a axn
yn
yn 1
z 1
五．差分方程的特点
(1)输出序列的第n个值不仅决定同一瞬间的输入样值， 而且还与前面输出值有关，每个输出值必须依次保留。
11
22
离散时间系统
y2 (n )
c y (n ) + c y (n )
11
22
时不变性
xn yn，xn N yn N 整个序列右移 N位
x(n)
y(n)
1 1 0 1 2 3 n
1
系统
1 o 1 2 3 4 n
x(n N )
y(n N )
1
1
系统
1 0 1 2 3
yt ynT yn
f t f nT f n
yn yn 1 ayn+ f n
T
yn 1 yn 1+ T f n
1 aT
1 aT
当前输出 前一个输出 输入
自动控制原理离散系统知识点总结
自动控制原理离散系统知识点总结自动控制原理中的离散系统是指在时间域和数值范围上都是离散的系统。
在离散系统中，信号是以离散时间点的形式传递和处理的。
本文将对自动控制原理离散系统的知识点进行总结，包括离散系统的概念、离散信号与离散系统的数学表示、离散系统的稳定性分析与设计等。
一、离散系统的概念与特点离散系统是指系统输入、输出和状态在时间上都是以离散的方式存在的系统。
与连续系统相比，离散系统具有以下特点：1. 离散时间：离散系统的输入、输出和状态是在离散时间点上采样得到的，而不是连续的时间信号。
2. 离散数值：离散系统的输入、输出和状态都是以离散数值的形式存在的，而不是连续的模拟数值。
二、离散信号与离散系统的数学表示离散信号是指在离散时间点上采样得到的信号。
离散系统可以通过离散信号的输入与输出之间的关系进行描述。
常见的离散系统数学表示方法有差分方程和离散时间传递函数。
1. 差分方程表示：差分方程是通过离散时间点上的输入信号和输出信号之间的关系来描述离散系统的。
差分方程可以是线性的或非线性的，可以是时不变的或时变的。
2. 离散时间传递函数表示：离散时间传递函数描述了离散系统输入与输出之间的关系，类似于连续时间传递函数。
离散时间传递函数可以通过Z变换得到。
三、离散系统的稳定性分析与设计离散系统的稳定性是指系统的输出在有限时间内收敛到有限范围内，而不是无限增长或震荡。
离散系统的稳定性分析与设计是自动控制原理中的重要内容。
1. 稳定性分析：离散系统的稳定性可以通过判断系统的极点位置来进行分析。
若系统的所有极点都位于单位圆内，则系统是稳定的；若存在至少一个极点位于单位圆外，则系统是不稳定的。
2. 稳定性设计：若离散系统不稳定，可以通过调整系统的参数或设计控制器来实现稳定性。
常见的稳定性设计方法包括PID控制器调整、根轨迹设计等。
四、离散系统的性能指标与优化离散系统的性能指标与优化是指通过调整控制器参数或控制策略，使离散系统的性能得到优化。
离散数学的主要内容
离散数学的主要内容离散数学是一门研究离散对象及其性质的数学学科。
它的主要内容包括集合论、图论、逻辑、代数系统等。
集合论是离散数学的基础，它研究的是集合以及集合之间的关系。
在集合论中，我们可以学习到集合的基本概念和运算、集合之间的关系、集合的基本定理等等。
集合论在计算机科学中有着广泛的应用，例如在数据库设计中，我们需要使用集合运算来实现数据的查询和处理。
图论是离散数学中的重要分支，它研究的是图及其性质。
在图论中，我们可以学习到图的基本概念、图的遍历算法、最短路径算法、最小生成树算法等等。
图论在计算机科学中有着广泛的应用，例如在计算机网络中，我们需要使用图论来设计网络拓扑结构和路由算法。
逻辑是离散数学中的另一个重要分支，它研究的是命题和命题之间的关系。
在逻辑中，我们可以学习到命题逻辑、谓词逻辑、命题的推理规则等等。
逻辑在计算机科学中有着广泛的应用，例如在人工智能领域中，我们需要使用逻辑来实现知识表示和推理。
代数系统是离散数学中的另一个重要分支，它研究的是数学对象之间的代数关系。
在代数系统中，我们可以学习到群论、环论、域论等等。
代数系统在计算机科学中有着广泛的应用，例如在密码学中，我们需要使用代数系统来设计加密算法和解密算法。
除此之外，离散数学还包括了排列组合、图论算法、离散概率论、离散优化等等内容。
这些内容在计算机科学中都有着广泛的应用，例如在算法设计中，我们需要使用排列组合来分析算法的时间复杂度和空间复杂度。
总的来说，离散数学是计算机科学中非常重要的数学基础学科，它涉及到了计算机科学中的许多重要问题和应用。
学好离散数学对于计算机科学专业的学生来说是非常重要的。
离散系统的数学模型
离散系统的数学模型
1.1 离散时间系统的数学模型
为激励信号,
为响应信号
离散时间系统 将激励序列转换为响应序列的系统，其 输入输出都是离散信号。在数学上，离 散系统的输入-输出关系可表示为
离散系统可以用差分方程来描述 差分方程 由输入序列、输出序列以及它们的差分所组
成的方程。 例如:
无反馈差分方程 某ຫໍສະໝຸດ 时刻的输出只与输入有关，而余 ，月利率为1%。写出结余 与净存款
的
关系式。
解： 当月的净存款
月末结余
月末利息
所以有
或
例5.3.2 试写出第k 节点电压 的数学模型。
解： 整理得
例5.3.3 假设离散时间系统的差分方程为 求其传输算子
解：算子方程为 即
所以
离散系统的模拟框图表示
差分方程的基本元算符号
例5.3.4 某离散系统的差分方程为
与该时刻之前的输出无关 。
有反馈差分方程 某一时刻的输出不仅与输入有关，还 与该时刻之前的输出有关。
系统的差分方程的一般形式 ：
前向差分方程
后向差分方程
差分算子 离散系统的传输算子
差分方程 算子方程
传输算子
系统的输入-输出模型
1.2离散时间系统数学模型的建立
例5.3.1 某一银行按月结余。设第 个月末的结
试用模拟框图表示此系统。 解：系统的差分方程可化为 框图来表示为
信号与系统
离散系统的数学模型
2326.4 离散系统的数学模型为研究离散系统的性能，需要建立离散系统的数学模型。
线性离散系统的数学模型有差分方程、脉冲传递函数和离散状态空间表达式三种。
本节主要介绍差分方程及其解法，脉冲传递函数的定义，以及求开环脉冲传递函数和闭环脉冲传递函数的方法。
有关离散状态空表达式及其求解，将在第8章介绍。
6.4.1 线性常系数差分方程及其解法对于线性定常离散系统，k 时刻的输出)(k c ，不但与k 时刻的输入)(k r 有关，而且与k 时刻以前的输入 ),2(),1(--k r k r 有关，同时还与k 时刻以前的输出 ),2(),1(--k c k c 有关。
这种关系一般可以用n 阶后向差分方程来描述，即∑∑==-+--=mj jni i j k r bi k c a k c 01)()()( (6-34)式中，i a ，i =1，2，…，n 和j b ，j ＝0，1，…，m 为常系数，n m ≤。
式(6-34)称为n 阶线性常系数差分方程。
线性定常离散系统也可以用n 阶前向差分方程来描述,即∑∑==-++-+-=+mj jni i j m k r bi n k c a n k c 01)()()( (6-35)工程上求解常系数差分方程通常采用迭代法和z 变换法。
1. 迭代法若已知差分方程式(6-34)或式(6-35)，并且给定输出序列的初值，则可以利用递推关系，在计算机上通过迭代一步一步地算出输出序列。
例6-10 已知二阶差分方程)2(6)1(5)()(---+=k c k c k r k c输入序列1)(=k r ，初始条件为1)1(,0)0(==c c ，试用迭代法求输出序列)(k c ， ,5,4,3,2,1,0=k 。
解 根据初始条件及递推关系，得0)0(=c 1)1(=c6)0(6)1(5)2()2(=-+=c c r c 25)1(6)2(5)3()3(=-+=c c r c 90)2(6)3(5)4()4(=-+=c c r c301)3(6)4(5)5()5(=-+=c c r c2. z 变换法233设差分方程如式(6-34)所示，对差分方程两端取z 变换，并利用z 变换的实数位移定理，得到以z 为变量的代数方程，然后对代数方程的解)(z C 取z 反变换，可求得输出序列)(k c 。
第3章-线性离散系统数学描述
根据线性系统叠加原理 ，已知 h * ( t )后，任意输入脉冲序列 u * ( t )， 可得系统输出为 y * ( t ) = u( 0 ) h * ( t ) + u (1) h * ( t − T ) + L + u( n ) h * ( t − nT ) + L y ( k ) = ∑ u ( j ) h( k − j ) =
z →1
i =0 i =1 m n
已知，用递推法求解。 例3 − 2 − 2 y ( k + 1) = ay ( k ) + bu( k ), 设 y ( 0 )、 u( k )已知，用递推法求解。 解： k = 0 k =1 M
k
y (1) = ay ( 0 ) + bu( 0 ) y ( 2 ) = ay (1) + bu(1) = a 2 y ( 0 ) + abu ( 0 ) + bu(1)
它的齐次方程为 y( k + n) + a1 y( k + n − 1) + L + a n y( k ) = 0
它的特征方程为 r n + a1 r n −1 + a 2 r n − 2 + L + a n = 0
个特征根： 有 n个特征根： 则方程通解为： （1）若解为 n个单根 r1 , r2 , L , rn , 则方程通解为： y ( k ) = c 1 r1k + c 2 r2k + L + c n rnk； 重根， （2）若解有 m 重根，则 m 重根的解的形式为 r k , kr k , k 2 r k， ， k m -1 r k的线性组合， 的线性组合， L 通解中的系数 c n由系统的初始条件确定 。
离散数学定义(必须背)
命题逻辑▪令狐采学▪(论域)定义：论域是一个数学系统，记为D。
它由三部分组成：•(1)一个非空对象集合S，每个对象也称为个体；•(2) 一个关于D的函数集合F；•(3)一个关于D的关系集合R。
▪（逻辑连接词）定义•设n>0,称为{0,1}n到{0,1}的函数为n元函数，真值函数也称为联结词。
•若n =0，则称为0元函数。
▪（命题合式公式）定义：•(1).常元0和1是合式公式；•(2).命题变元是合式公式；•(3).若Q,R是合式公式，则(Q)、(Q R) 、(Q R) 、(Q R) 、(Q R) 、(Q R)是合式公式；•(4).只有有限次应用(1)—(3)构成的公式是合式公式。
▪（生成公式）定义1.5 设S是联结词的集合。
由S生成的公式定义如下：•⑴若c是S中的0元联结词，则c是由S生成的公式。
•⑵原子公式是由S生成的公式。
•⑶若n≥1，F是S中的n元联结词，A1,…,An是由S生成的公式，则FA1…An是由S生成的公式。
▪（复杂度）公式A的复杂度表示为FC(A)•常元复杂度为0。
•命题变元复杂度为0，如果P是命题变元，则FC (P)=0。
•如果公式A=B，则FC (A)=FC(B)+1。
•如果公式A=B1 B2，或A=B1 B2，或A=B1B2，或A=B1 B2，或A=B1 B2，或则FC (A)=max{FC(B1), FC(B2)}+1。
▪命题合式公式语义•论域：研究对象的集合。
•解释：用论域的对象对应变元。
•结构：论域和解释称为结构。
•语义：符号指称的对象。
公式所指称对象。
合式公式的语义是其对应的逻辑真值。
▪（合式公式语义）设S是联结词的集合是{，，，，，}。
由S生成的合式公式Q在真值赋值v下的真值指派v(Q)定义如下：•⑴v(0)=0, v(1)=1。
•⑵若Q是命题变元p，则v(A)= pv。
•⑶若Q1,Q2是合式公式▪若Q= Q1，则v(Q)= v(Q1)▪若Q=Q1 Q2，则v(Q)=v(Q1)v(Q2)▪若Q=Q1∨Q2，则v(Q)=v(Q1)∨v(Q2)▪若Q=Q1Q2，则v(Q)=v(Q1)v(Q2)▪若Q=Q1 Q2，则v(Q)=v(Q1) v(Q2)▪若Q=Q1Q2，则v(Q)=v(Q1)v(Q2)▪（真值赋值）由S生成的公式Q在真值赋值v下的真值v(Q)定义如下：•⑴若Q是S中的0元联结词c，则v(Q)=c。
数学一数学二和数学三的数学离散数学介绍
数学一数学二和数学三的数学离散数学介绍数学一、数学二和数学三的数学离散数学介绍数学在我们的生活中扮演着重要的角色，它是一门独特而又智慧的学科，被广泛用于解决实际问题和推动科学的发展。
而数学学科又可以分为许多分支，其中离散数学是一个重要而有趣的领域。
本文将介绍数学一、数学二和数学三的离散数学的相关概念和知识。
一、离散数学的概述离散数学是数学中的一门学科，与连续数学形成鲜明对比。
连续数学关注于连续对象，如实数、连续函数等，而离散数学则主要研究离散对象，如整数、集合、图等。
离散数学的研究对象离散且有限，因此被广泛应用于计算机科学、信息技术等领域。
二、数学一中的离散数学数学一作为大学数学课程中的一门重要课程，也涉及到了离散数学的部分内容。
在数学一中，离散数学主要包括以下几个方面的内容：1. 集合论：集合论是离散数学的基础，它研究集合及其操作和关系。
在数学一中，我们学习了集合的基本概念、集合的表示方法、集合之间的关系和运算等内容。
2. 逻辑与命题：逻辑与命题是离散数学中的重要部分。
在数学一的学习中，我们研究了命题及其逻辑运算、命题的等值关系、命题的推理和证明等内容。
3. 代数系统：数学一中的离散数学还包括了代数系统的研究，其中包括了群、环、域等代数结构的概念和性质。
三、数学二中的离散数学在数学二中，离散数学的研究进一步深入，涉及到以下几个方面的内容：1. 图论：图论是离散数学中的一个重要分支，它研究了图及其性质、图的遍历和连通性、最短路径和最小生成树等问题。
在数学二中，我们学习了图的基本概念、图的表示方法和图的算法以及与图相关的应用问题。
2. 网络流与匹配理论：网络流与匹配理论是离散数学中涉及到实际问题的一部分。
在数学二中，我们学习了网络流与匹配理论的相关概念和算法，并应用于实际问题的求解中，如网络传输、最大匹配问题等。
四、数学三中的离散数学数学三作为数学专业学生的一门重要课程，较为深入地研究了离散数学的相关内容。
数学的动力系统分支
数学的动力系统分支动力系统是数学中一个重要的研究领域，它涉及到研究对象在时间上的演化规律，以及相应的数学模型和解析方法。
在这个广泛的领域中，有几个重要的分支，包括离散动力系统、连续动力系统、混沌理论等等。
1. 离散动力系统离散动力系统研究的是在离散时间点上的演化规律。
离散动力系统常常由递推关系或差分方程来描述。
其中，最经典的例子是著名的斐波那契数列。
斐波那契数列是由以下递推关系定义的：F(0) = 0, F(1) = 1,F(n) = F(n−1) + F(n−2), n ≥ 2.这个递推关系描述了每一项等于前两项之和，从而得到一系列的数列。
离散动力系统的研究不仅仅局限于数列，还包括其他各种递推关系和差分方程。
2. 连续动力系统与离散动力系统相对应的是连续动力系统。
连续动力系统研究的是在连续时间上的演化规律。
连续动力系统的数学模型常常是由微分方程来描述的，例如常见的一阶常微分方程：dy/dx = f(x, y).这个方程描述了函数y(x)在变量x变化的过程中的演化规律。
连续动力系统可以描述许多自然界中的现象，如弹簧振子、电路的响应等。
3. 混沌理论混沌理论是动力系统研究中一个非常重要的分支，它研究的是具有确定性而表现出不可预测行为的系统。
混沌系统的演化非常敏感，微小的变化可能导致完全不同的结果。
一个著名的混沌系统是洛伦兹系统。
这个系统由以下三个非线性微分方程组成：dx/dt = σ(y - x),dy/dt = x(ρ - z) - y,dz/dt = xy - βz.洛伦兹系统的解轨迹表现出奇妙的“蝴蝶效应”，即在相空间中形成复杂的混沌结构。
混沌系统的研究不仅仅限于数学领域，它对于理解自然界中的许多现象，如天气预报、流体力学等，都有着重要的应用。
总结：动力系统作为数学中一个重要的研究领域，涉及到研究对象在时间上的演化规律，以及相应的数学模型和解析方法。
离散动力系统研究的是离散时间点上的演化规律，常常由递推关系或差分方程来描述；连续动力系统研究的是连续时间上的演化规律，常常由微分方程来描述；混沌理论研究的是具有确定性而表现出不可预测行为的系统。
离散系统的基本概念
06
CATALOGUE
离散系统的发展趋势与展望
离散系统的新理论与方法
离散系统的新理论
随着科技的不断发展，离散系统的新理论也在不断涌现。例如，离散概率论、离散控制论、离散信息论等，这些 新理论为离散系统的发展提供了重要的理论支持。
离散系统的新方法
在实践中，人们不断探索新的方法来处理离散系统的问题。例如，离散数学、离散优化算法、离散模拟技术等， 这些新方法为离散系统的研究提供了更有效的工具。
状态转移图的绘制方法
根据状态方程，通过计算或模拟得到状态变量的时间序列解，并绘 制成图形。
状态转移图的应用
通过观察状态转移图，可以直观地了解系统动态行为和变化趋势。
04
CATALOGUE
离散系统的稳定性分析
线性离散系统的稳定性分析
定义
线性离散系统是指系统 的数学模型可以表示为 离散时间的线性方程组 ，如差分方程或离散时 间状态方程。
状态方程
1
状态方程是描述离散时间动态系统状态变化的基 本方程，通常表示为离散时间序列的递推关系。
2
状态方程通常由当前状态和输入量来预测下一个 状态，是离散系统分析的重要基础。
3
状态方程的解法包括递归法和矩阵法等，其中递 归法较为直观，而矩阵法适用于大规模系统。
转移矩阵
转移矩阵是描述离散系统状态转移关系的矩阵，其元素表示状态之间的转 移概率。
社会科学领域
在社会学、经济学、管理学等领域中，离散系统也有着广泛的应用。例如，在经济学中，离散模型被用 于描述经济活动中的离散事件；在社会学中，离散模型被用于描述社会结构和社会动态。
离散系统未来的研究方向
要点一
复杂离散系统的研究
随着科技的不断发展，复杂离散系统 的研究已经成为一个重要的研究方向 。例如，复杂网络、离散事件动态系 统等，都是复杂离散系统的研究重点 。
离散控制系统的数学模型
即
Y (z)
z2
z 3z
2
(z
z 1)( z
2)
利用反演积分法求出z反变换，得 y(k) 1 2k k 0,1, 2,
y(t) (1 2k ) (t kT ) k 0
1.2 脉冲传递函数
1.脉冲传递函数定义
在线性定常离散控制系统中，当初始条件为零时，系统离散输出信号的z
变换与离散输入信号的z变换之比，称为线性定常离散控制系统的脉冲传递函
R(z) 1 G1 (z)HG2(z)
自动控制原理
例1-13 试用z变换法求解下列二阶前向差分方程 y(k 2) 3y(k 1) 2y(k) 0
其中，初始条件为 y(0) 0, y(1) 1 。
解：对方程两端取z变换，得
z2Y (z) z2 y(0) zy(1) 3zY (z) 3zy(0) 2Y (z) 0
即 (z2 3z 2)Y (z) y(0)z2 ( y(1) 3y(0))z 代入初始条件，得 (z2 3z 2)Y (z) z
（2）串联环节之间无采样开关时
设开环离散系统如图1-18所示，在两个串联连续环节G1(s)和G2(s)之间没 有理想采样开关。此时系统的传递函数为 G(s) G1(s)G2 (s)
上式作为一个整体进行z变换，由脉冲传递函数定义得
G(z)
Y (z) R(z)
G1G2 (z)
图1-18 环节之间无理想采样开关的开环采样系统
自动控制原理
离散控制系统的数学模型
1.1 线性常系数差分方程
对于线性定常离散控制系统，一般可用n阶后向差分方程描述，即
n
m
y(k) ai y(k i) bir(k j)
i 1
j 1
《自动控制原理》离散系统的数学模型
K (t) L1[G(s)]
(7-55)
再将 K (t) 按采样周期离散化，得加权序列 K (nT ) ；最后将 K (nT ) 进
行 z 变换，按式(7-53)求出 G(z) 。这一过程比较复杂。其实，如果把 z 变
换表 7—2 中的时间函数 e(t) 看成 K (t) ，那么表中的 E(s) 就是 G(s) (见式 (７-55)，而 E(z) 则相当于 G(z) 。因此，根据 z 变换表 7—2，可以直接从 G(s) 得到 G(z) ，而不必逐步推导。
本章所研究的离散系统为线性定常离散系统。 注意 zx：离散系统有本质连续和本质离散两种情况
本质连续的离散系统：如液位 炉温采样控制系统中的被控对象 本质离散的离散系统：如计算机。系统直接进行离散计算 问题：如何建立离散系统的数学模型？ c(n) F[r(n)] F 的具体形式？ 分析：本质连续的离散系统的方框图， 能否 G(s)?G(z)=?
众所周知，利用传递函数研究线性连续系统的特性，有公认的方便 之处。对于线性连续系统，传递函数定义为在零初始条件下，输出量的 拉氏变换与输入量的拉氏变换之比。对于线性离散系统，定义类似。
设开环离散系统如图 7-22 所示，如果系统的初始条件为零，输入信号
为 r(t) ，采样后 r*(t) 的 z 变换函数为 R(z) ，系统连续部分的输出为 c(t) ，
微分方程的经典解法类似，差分方程的经典解法[EX]*也要求出齐次方程 的通解和非齐次方程的一个特解，非常不便。这里仅介绍工程上常用的 后两种解法。
(1)迭代法 又称递推法 若已知差分方程(7-49)或(7-50)，并且给定输入序列和输出序列的初 值，则可以利用递推关系可以一步一步地算出输出序列。 例 7-14 已知差分方程
7-4离散系统的数学模型
n
c(k ) 5c(k 1) 6c(k 2) r (k )； r (k ) 1(k )； c(0) 0, c(1) 1。
试用递推法计算输出序列c(k)，k = 0,1,2,…,10。
解 采用递推关系 c(k+2) = 1+5c(k+1) - 6c(k)； 得 c(0) 0；c(1) 1；
7-4 离散系统的数学模型
1. 离散系统的数学定义
2. 线性常系数差分方程及其解法
3. 脉冲传递函数 4. 组合环节的等效脉冲传递函数 5. 闭环系统的脉冲传递函数计算
6. Z变换的局限性及修正Z变换
离散系统的数学模型 与连续系统类似，单输入单输出线性时不变 离散系统数学模型有三大类：差分方程 ( 时域 ) 、 脉冲传递函数 ( 复数域 ) 和状态空间模型。本节重 点讨论差分方程及其解法、脉冲传递函数的基本 概念、开环和闭环脉冲传递函数的建立方法。 1. 离散系统的数学定义
k 1
2
z c(kT ) ( z 2)( z 3)
z k 1 ( z 1)( z 2) z 3
z 1
z ( z 1)( z 3)
k 1
z 2
0.5 2
k 1
0.5 3 ，k 0；
k 1
c(2) 6； c(3) 25； c(10) 86526；
┇
k
c(0) 1； c(1) 1 0.5 1.5；
lim c(k ) 1.0；
这两个示例表明，用递推法求解差分方程， 计算过于烦琐，不易得到c(k)的通项表达式。
(2) Z变换法(例7-17 )
离散数学公式
离散数学公式
离散数学是一门利用数学原理研究离散复杂系统的科学，是一门多维而全面的学科，其研究范围涵盖了计算机科学、逻辑学、概率论和组合数学等领域。
关系公式：若集合X和Y之间存在一对一的函数关系，则X到Y的映射关系可以用公式f：X→Y表示，其中•x∈X表示x是X集合中的一个元素，•f（x）∈Y表示f（x）是Y集合中的一个元素，•f：X→Y表示Y集合的每个元素都可以通过函数f映射回X集合中的一个元素。
函数关系公式：若集合X和Y之间存在可定义的函数关系，则可以用f：X→Y表示，其中•f：X→Y表示函数f把X集合中的元素映射到Y集合中，•f（x）表示x在X集合中的元素映射到Y集合中的元素。
算数逻辑公式：若集合X和Y之间存在逻辑关系，则可以用公式
x∈X⊃y∈Y表示，其中•x∈X表示x是X集合中的一个元素，•y∈Y表示y是Y集合中的一个元素，•x∈X⊃y∈Y表示若x属于X集合，则y属于Y集合。
离散数学的基本概念和运算
离散数学的基本概念和运算离散数学是数学的一个重要分支，它研究离散结构和离散对象之间的关系。
与连续数学不同，离散数学关注的是离散的、离散的事物，如整数、图形、逻辑、集合等。
在计算机科学、信息技术以及其他许多领域中，离散数学都担当着重要的角色。
本文将介绍离散数学的一些基本概念和运算，以帮助读者更好地理解和应用离散数学。
一、集合论集合论是离散数学的基石之一，它研究集合以及集合之间的关系和运算。
集合是指一组元素的事物的整体，元素可以是任何事物，比如数字、字母、人或其他对象。
常见的集合运算有并集、交集、差集和补集等。
并集表示两个或多个集合中的所有元素的集合，交集表示同时属于两个或多个集合的元素的集合，差集表示从一个集合中减去另一个集合的元素的集合，补集表示在给定参考集合中不属于某个特定集合的元素的集合。
二、逻辑逻辑是离散数学的另一个重要内容，它研究命题、逻辑运算和推理。
在离散数学中，命题是指能够判断真假的陈述句。
逻辑运算包括与、或、非、异或等。
与运算表示两个命题同时为真时结果为真，或运算表示两个命题中至少有一个为真时结果为真，非运算表示对命题的否定，异或运算表示两个命题中仅有一个为真时结果为真。
推理是利用逻辑规则从已知命题中得出新的结论的过程，常见的推理方法有直接证明、反证法和归纳法。
三、图论图论是离散数学中的一个重要分支，它研究由节点和边组成的图形结构。
图形是由节点（或顶点）和边组成的抽象化模型，节点表示某个对象，边表示节点之间的关系。
图论研究图形的性质、特征和算法。
常见的图形类型有无向图和有向图，无向图的边没有方向，有向图的边有方向。
图形的表示方法有邻接矩阵和邻接表等。
在计算机科学中，图论广泛应用于网络、路径规划、数据结构等领域。
四、代数系统代数系统是离散数学中的另一个重要概念，它研究运算规则和运算对象之间的关系。
代数系统包括集合、运算和运算规则。
常见的代数系统有代数结构、半群、群、环、域等。
代数结构是指由一组元素和一组运算构成的系统，运算可以是加法、乘法或其他操作。
离散数学中的语言公理系统描述
离散数学中的语言公理系统描述离散数学是一门研究离散对象的数学学科，它主要涉及离散结构的表示、分析和推理。
语言公理系统是离散数学中的一种重要工具，用于描述和分析形式语言的结构和性质。
本文将介绍语言公理系统的基本概念、符号表示以及相关的公理和规则。
一、语言公理系统简介语言公理系统是一种形式化的记号系统，用于描述和分析形式语言的结构和性质。
它由一个字母表（Alphabet）以及一组公理（Axioms）和推理规则（Inference Rules）组成。
通过这些公理和规则的运用，可以进行形式语言的推导和证明。
二、符号表示在语言公理系统中，我们需要明确标记和表示离散对象。
通常使用字母、数字和特殊符号等来表示各种概念和关系。
比如，用大写字母A、B、C等表示语言中的句子或公式，用小写字母a、b、c等表示语言中的原子命题或符号。
三、公理和规则语言公理系统通过一组公理和推理规则来表达和推导语言中的语句。
公理是一些基本的陈述或规则，它们被认为是不需要证明的，是系统的起点。
推理规则则用于由已知的语句推导出新的语句。
常见的公理包括：1. 自反律（Reflexivity）：对于任何句子A，有A=A。
2. 对称律（Symmetry）：对于任何句子A和B，如果A=B，则B=A。
3. 传递律（Transitivity）：对于任何句子A、B和C，如果A=B且B=C，则A=C。
常见的推理规则包括：1. 消去规则（Elimination Rule）：根据已有的语句，可以推导出它们的部分或完全消去形式。
2. 引入规则（Introduction Rule）：根据已有的语句，可以推导出它们的新的引入形式。
3. 等价规则（Equivalence Rule）：根据已有的等价语句，可以推导出新的等价语句。
四、语言公理系统的应用语言公理系统在离散数学的求解和证明过程中发挥着重要作用。
通过应用公理和规则，我们可以进行逻辑的推导和分析，判断语句的真假、推导结论的正确性。
离散系统贝尔曼方程
离散系统贝尔曼方程是一种描述离散系统动态特性的数学方程，它基于贝尔曼的优化算法，用于解决离散系统的最优控制问题。
下面是对离散系统贝尔曼方程的介绍：
贝尔曼方程的基本形式可以表示为：
dx/dt = f(x, u)
其中x 是状态变量，u 是控制变量，f 是状态和控制的函数。
在离散系统中，状态和控制的更新是基于过去的观测和当前的控制输入。
离散系统贝尔曼方程的形式为：
x[k+1] = x[k] + γ[k] * u[k] * (τ[k+1] -τ[k]) / τ[k]
其中x[k] 表示在时间k 的状态变量，γ[k] 表示在时间k 的奖励率，u[k] 表示在时间k 的控制输入，τ[k] 和τ[k+1] 分别表示时间和控制周期。
奖励率γ[k] 是系统的重要参数，它决定了系统对奖励的敏感度。
这个方程是基于贝尔曼的优化算法得到的，它基于最优控制理论，通过最大化长期期望回报来寻找最优控制序列。
这个方程可以用来解决离散系统的最优控制问题，例如机器人、交通控制系统、金融市场等领域的实际问题。
通过求解离散系统贝尔曼方程，可以得到最优控制序列，从而实现对系统的最优控制。
在实际应用中，需要根据具体系统的特性和约束条件来选择合适的控制策略和算法，并进行实验和验证。
总之，离散系统贝尔曼方程是一种重要的数学方程，它基于贝尔曼的优化算法，用于解决离散系统的最优控制问题。
通过求解这个方程，可以得到最优控制序列，实现对系统的最优控制。
在实际应用中，需要根据具体系统的特性和约束条件来选择合适的控制策略和算法，并进行实验和验证。
数学中的离散动力系统研究
数学中的离散动力系统研究在数学领域中，离散动力系统是指由一系列离散时间步骤组成的动力系统，其中状态变量在这些时间步骤中按照特定的动力学规律进行演化。
离散动力系统的研究对于深入理解自然界和社会现象的动态行为提供了理论基础。
本文将介绍离散动力系统的概念、性质以及在不同领域中的应用。
1. 离散动力系统的概念离散动力系统是一类由时间和状态变量所描述的动力学系统，其演化在离散的时间步骤中进行。
离散动力系统可以形式化地表示为一个映射函数：\[X_{n+1} = f(X_n)\]其中，\(X_n\) 表示在第 \(n\) 个时间步骤中的系统状态，\(X_{n+1}\) 是在下一个时间步骤中的状态，而 \(f\) 是系统的演化规律。
离散动力系统的演化可以通过迭代得到：\(X_1 = f(X_0), X_2 = f(X_1), \ldots\)。
2. 离散动力系统的性质离散动力系统具有一些重要性质，其中最基本的是：不变性、周期性和混沌性。
2.1 不变性在某些情况下，离散动力系统可能存在不动点，即满足 \(f(X) = X\) 的状态变量 \(X\)。
当系统处于不动点时，其状态不会随时间演化而改变。
2.2 周期性如果系统存在一个周期为 \(T\) 的状态轨迹，即在每隔 \(T\) 个时间步骤后系统进入相同的状态，那么该系统就具有周期性。
2.3 混沌性当离散动力系统状态的演化表现出高度敏感性和不可预测性时，我们称其为混沌现象。
混沌动力系统的特征包括：对初始条件极其敏感、演化规律具有确定性但无法准确预测、状态轨迹呈现出非周期性等。
3. 离散动力系统在自然科学中的应用离散动力系统在自然科学领域中有广泛的应用，包括物理学、生物学、化学等。
3.1 物理学离散动力系统在物理学中的应用涉及到许多领域，如天体力学、流体力学和量子力学等。
例如，天体力学中的三体问题可以通过离散动力系统进行建模和分析，研究天体的轨道演化及稳定性。
3.2 生物学生物学中的许多现象，如种群动力学、神经网络和生物节律等，都可以用离散动力系统来描述和解释。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
离散系统的数学描述
1. 状态空间描述法
状态空间描述离散系统使用ss 命令。
语法：
G=ss(a,b,c,d,Ts) %由a 、b 、c 、d 参数获得状态方程模型
说明：Ts 为采样周期，为标量，当采样周期未指明可以用-1表示。
【例6.2】用状态空间法建立离散系统。
a=[-1.5 -0.5;1 0];
b=[1;0];
c=[0 0.5];
d=0;
G=ss(a,b,c,d,0.1)
%采样周期为0.1s
a =
x1 x2
x1 -1.5 -0.5
x2 1 0
b =
u1 x1 1
x2 0
c =
x1 x2
y1 0 0.5
d =
u1
y1 0
Sampling time: 0.1
Discrete-time model.
2. 脉冲传递函数描述法
脉冲传递函数也可以用tf 命令实现。
语法：
G=tf(num,den,Ts) %由分子分母得出脉冲传递函数
说明：Ts 为采样周期，为标量，当采样周期未指明可以用-1表示，自变量用'z'表示。
【例6.2续】创建离散系统脉冲传递函数21120.5z 1.5z 10.5z 0.51.5z z 0.5z G(z)---+-=+-=。
num1=[0.5 0];
den=[1 -1.5 0.5];
G1=tf(num1,den,-1)
Transfer function:
0.5 z
-----------------
z^2 - 1.5 z + 0.5
Sampling time: unspecified
MATLAB中还可以用filt命令产生脉冲传递函数。
语法：
G=filt(num,den,Ts) %由分子分母得出脉冲传递函数
说明：Ts为采样周期，当采样周期未指明Ts可以省略，也可以用-1表示，自变量用'z-1'表示。
【例6.2续】使用filt命令产生脉冲传递函数。
num2=[0 0.5];
G2=filt(num2,den)
Transfer function:
0.5 z^-1
-----------------------
1 - 1.5 z^-1 + 0.5 z^-2
Sampling time: unspecified
程序说明：用filt命令生成的脉冲传递函数的自变量不是z而是z-1，因此分子应改为“[0 0.5]”。
3. 零极点增益描述法
离散系统的零极点增益用zpk命令实现。
语法：
G=zpk(z,p,k,Ts) %由零极点得出脉冲传递函数
【例6.2续】使用zpk命令产生零极点增益传递函数。
G3=zpk([0],[0.5 1],0.5,-1)
Zero/pole/gain:
0.5 z
-------------
(z-0.5) (z-1)
Sampling time: unspecified
语法：
G=ss(传递函数) %由传递函数转换获得
G=ss(零极点模型) %由零极点模型转换获得
【例 6.3】将单输入双输出的系统传递函数12s 5s 3s 52s s 23s (s)G 2321+++⎥⎦⎤⎢⎣⎡+++=
转换为状态空间描
述。
num=[0 3 2;
1 2 3];
den=[3 5 2 1];
G11=tf(num(1,:),den)
Transfer function:
3 s + 2
-----------------------
3 s^3 + 5 s^2 + 2 s + 1
G12=tf(num(2,:),den)
Transfer function:
s^2 + 2 s + 3
-----------------------
3 s^3 + 5 s^2 + 2 s + 1
G=ss([G11;G12])
a =
x1 x2 x3
x1 -1.667 -0.3333 -0.08333
x2 2 0 0
x3 0 2 0
b =
u1
x1 1
x2 0
x3 0
c =
x1 x2 x3
y1 0 0.5 0.1667
y2 0.3333 0.3333 0.25
d =
u1
y1 0
y2 0
Continuous-time model.
(2) 传递函数的获得
由tf命令实现将系统的状态空间法和零极点增益模型转换为传递函数。
语法：
G=tf(状态方程模型) %由状态空间转换
G=tf(零极点模型) %由零极点模型转换
【例6.3续】由状态空间描述转换为传递函数。
G1=tf(G)
Transfer function from input to output...
s + 0.6667
#1: -----------------------------------
s^3 + 1.667 s^2 + 0.6667 s + 0.3333
0.3333 s^2 + 0.6667 s + 1
#2: -----------------------------------
s^3 + 1.667 s^2 + 0.6667 s + 0.3333
(3) 零极点模型的获得
由zpk命令实现将状态空间法、传递函数转换为零极点模型。
语法：
G=zpk(状态方程模型) %由状态方程模型转换
G=zpk(传递函数) %由传递函数转换
【例6.3续】由传递函数和状态方程模型转换零极点模型。
G2=zpk(G) %由状态方程模型转换
Zero/pole/gain from input to output...
(s+0.6667)
#1: -----------------------------------
(s+1.356) (s^2 + 0.3103s + 0.2458)
0.33333 (s^2 + 2s + 3)
#2: -----------------------------------
(s+1.356) (s^2 + 0.3103s + 0.2458)
G2=zpk(G1); %由传递函数转换
2.模型参数的获取
语法：
[a,b,c,d]=ssdata(G) %获取状态空间参数
[a,b,c,d,e]=dssdata(G) %获取状态空间参数
[num,den]=tfdata(G) %获取传递函数参数
[z,p,k]=zpkdata(G) %获取零极点参数
【例6.3续】获取各模型的参数。
[a,b,c,d]=ssdata(G1) %获取状态方程参数
a =
-1.6667 -0.3333 -0.0833
2.0000 0 0
0 2.0000 0
b =
1
c =
0 0.5000 0.1667
0.3333 0.3333 0.2500
d =
3. 模型类型的检验
【例6.3续】检验模型的类型。
class(G)
%得出系统模型类型
ans =
ss
isa(G,'tf')
%检验系统模型类型
ans =
结构框图的模型表示
1. 串联结构
SISO 的串联结构是两个模块串联在一起，如图6.1所示。
实现串联结构传递函数的命令：
G=G1*G2
G=series(G1,G2)
2. 并联结构 SISO 的并联结构是两个模块并联在一起，
如图6.2所示。
实现并联结构传递函数的命令：
G=G1+G2
G=parallel(G1,G2)
3. 反馈结构
反馈结构是前向通道和反馈通道模块构成正反馈和负反馈，如图6.3所示。
图6.1 串联结构
图6.2 并联结构
实现反馈结构传递函数的命令：
G=feedback(G1,G2,Sign)
说明：Sign 用来表示正反馈或负反馈，Sign=-1或省略则表示为负反馈。
【例6.6】根据系统的结构框图求出整个系统的传递函数，结构框图如图6.4所示，其中1
2s s 1(s)G 21++=，1s 1(s)G 2+=，12s 1(s)G 3+=，s 1(s)G 4=。
G1=tf(1,[1 2 1])
Transfer function:
1
-------------
s^2 + 2 s + 1
G2=tf(1,[1 1]);
G3=tf(1,[2 1]);
G4=tf(1,[1 0]);
G12=G1+G2
%并联结构
Transfer function:
s^2 + 3 s + 2
---------------------
s^3 + 3 s^2 + 3 s + 1
G34=G3-G4
%并联结构
Transfer function:
图6.4结构框图
图6.3 反馈结构
-s - 1
---------
2 s^2 + s
G=feedback(G12,G34,-1) %反馈结构
Transfer function:
2 s^4 + 7 s^
3 + 7 s^2 + 2 s
------------------------------------- 2 s^5 + 7 s^4 + 8 s^3 + s^2 - 4 s - 2。