第三章扭转习题
材料力学扭转练习题

材料力学扭转练习题基本概念题一、选择题1. 图示传动轴,主动轮A的输入功率为PA =0 kW,从动轮B,C,D,E的输出功率分别为PB =0 kW,PC = kW,PD = 10 kW,PE = 1kW。
则轴上最大扭矩T。
A.BA段 B.AC段 C.CD段 D.DE段max出现在题1图2. 图示单元体的应力状态中属正确的纯剪切状态的是。
题2图3. 上题图示单元体的应力状态中属正确的是。
4. 下列关于剪应力互等定理的论述中正确的是。
A.剪应力互等定理是由平衡B.剪应力互等定理仅适用于纯剪切的情况C.剪应力互等定理适用于各种受力杆件D.剪应力互等定理仅适用于弹性范围E.剪应力互等定理与材料的性能无关5. 图示受扭圆轴,其横截面上的剪应力分布图正确的是。
-12-题5图6. 实心圆轴,两端受扭转外力偶作用。
直径为D时,设轴内的最大剪应力为?,若轴的直径改为D2,其它条件不变,则轴内的最大剪应力变为。
A.8? B.?C.16? D.?7. 受扭空心圆轴,在横截面积相等的条件下,下列承载能力最大的轴是。
A.??0 B.??0.5C.??0. D.??0.88. 扭转应力公式T?的适用范围是。
IpA.各种等截面直杆 B.实心或空心圆截面直杆C.矩形截面直杆 D.弹性变形 E.弹性非弹性范围 9. 直径为D的实心圆轴,最大的容许扭矩为T,若将轴的横截面积增加一倍,则其最大容许扭矩为。
A.2TB.2T C.22TD.4T10. 材料相同的两根圆轴,一根为实心,直径为D1;另一根为空心,内径为d2,外径为D2d2D??。
若两轴横截面上的扭矩T,和最大剪应力?max均相同,则两轴外径之比1 D2D2为。
A.1??B.1?? C.343D.411. 阶梯圆轴及其受力如图所示,其中AB段的最大剪应力?max1与BC段的最大剪应力?max2的关系是。
A.?max1??max2B.?max1?313?max2C.?max1??max2D.?ma x1??max248-13-题12图题13图12. 在图示的圆轴中,AB段的相对扭转角?1和BC段的相对扭转角?2的关系是。
材料力学第3 章 扭 转习题及答案

第 三 章 扭 转一、判断题1.杆件受扭时,横截面上的最大切应力发生在距截面形心最远处。
( × ) 2.薄壁圆管和空心圆管的扭转切应力公式完全一样。
( × ) 3.圆杆扭转变形实质上是剪切变形。
( √ ) 4.非圆截面杆不能应用圆截面杆扭转切应力公式,是因为非圆截面杆扭转时“平截面假设”不能成立。
( √ )5.材料相同的圆杆,它们的剪切强度条件和扭转强度条件中,许用应力的意义相同,数值相等。
( × ) 6.切应力互等定理,仅适用于纯剪切情况。
( × ) 7.受扭杆件的扭矩,仅与杆件受到的转矩(外力偶矩)有关,而与杆件的材料及其横截面的大小、形状无关。
( √ ) 8.受扭圆轴在横截面上和包含轴的纵向截面上均无正应力。
( √ ) 9.受扭圆轴的最大切应力只出现在横截面上。
( × ) 10. 因木材沿纤维方向的抗剪能力差,故若受扭木质圆杆的轴线与木材纤维方向平行,当扭矩达到某一极限值时,圆杆将沿轴线方向出现裂纹。
( √ )二、填空题1.一级减速箱中的齿轮直径大小不等,在满足相同的强度条件下,高速齿轮轴的直径要比低速齿轮轴的直径( 小 )。
2. 当实心圆轴的直径增加1培时,其抗扭强度增加到原来的( 8 )倍,抗扭刚度增加到原来的( 16 )倍。
3. 直径D=50mm 的圆轴,受扭矩T=2.15kn.m ,该圆轴横截面上距离圆心10mm 处的剪应力τ=(35.0 MPa ),最大剪应力τmax=(87.6 MPa )。
4. 一根空心轴的内外径分别为d ,D ,当D=2d 时,其抗扭截面模量为(33256153215D d ππ或)。
5. 直径和长度均相等的两根轴,在相同的扭矩作用下,而材料不同,它们的τmax 是( 相 )同的,扭转角φ是( 不 )同的。
6. 等截面圆轴扭转时的单位长度相对扭转角为θ,若圆轴直径增大一倍,则单位长度扭转角将变为(16θ)。
(仅供参考)第3章扭转作业参考解答
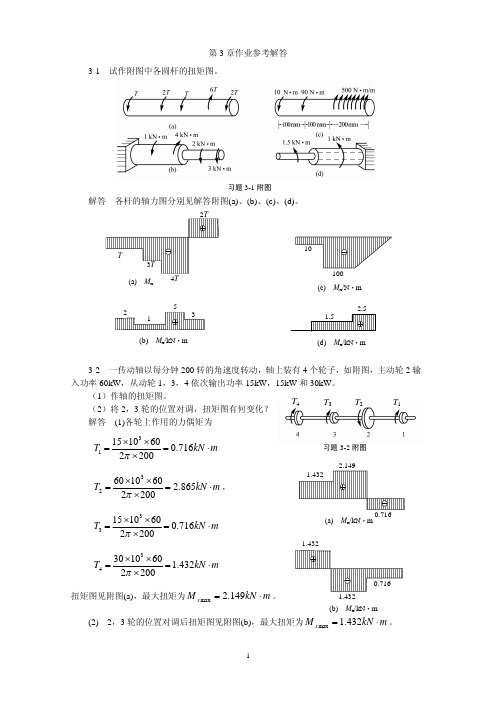
第3章作业参考解答3-1 试作附图中各圆杆的扭矩图。
习题3-1附图解答 各杆的轴力图分别见解答附图(a)、(b)、(c)、(d)。
3-2 一传动轴以每分钟200转的角速度转动,轴上装有4个轮子,如附图,主动轮2输入功率60kW ,从动轮1,3,4依次输出功率15kW ,15kW 和30kW 。
(1)作轴的扭矩图。
(2)将2,3轮的位置对调,扭矩图有何变化? 解答 (1)各轮上作用的力偶矩为m kN T ×=´´´=716.0200260101531pm kN T ×=´´´=865.2200260106032p ,m kN T ×=´´´=716.0200260101533pm kN T ×=´´´=432.1200260103034p扭矩图见附图(a),最大扭矩为m kN M x ×=149.2max 。
(2) 2,3轮的位置对调后扭矩图见附图(b),最大扭矩为m kN M x ×=432.1max 。
(a) M x(c) M x /N ·m(b)M x /kN ·m(d) M x /kN ·m习题3-2附图T 1T 2 T 3 T 4 (a)M x /kN ·m1.432(b) M x /kN ·m3-3 一直径d =60mm 的圆杆,其两端受T =2kN·m 的外力偶矩作用而发生扭转,如附图示。
设轴的切变模量G =80GPa 。
试求横截面上1,2,3点处的切应力和最大切应变,并在此三点处画出切应力的方向。
解答 1,2,3点处的切应力分别为MPaMPa W T p 4.313/22.4716/06.014.320000.031332===´===t t t t 切应力方向见附图(1)。
扭转典型习题解析

扭转典型习题解析1 一内径d =100mm 的空心圆轴如图示,已知圆轴受扭矩m kN 5⋅=T ,许用切应力][τ=80MPa ,试确定空心圆轴的壁厚。
解题分析:因为不知道壁厚,所以不能确定是不是薄壁圆管。
分别按薄壁圆管和空心圆轴设计。
解: 1、按薄壁圆管设计薄壁圆管扭转时,假设切应力沿壁厚均匀分布,设壁厚为δ,平均半径为2/0)(δ+=d R ,则扭转切应力为 δτ20π2R T=强度条件为][ττ≤,于是得][π22τδδTd =+)( ][π22223τδδδTd d =++ ()Pa1080πm N 1052m 10100m 1010026323233××⋅××=×+××+−−δδδ解得 mm 70.3m 1070.33=×=−δ 2、按空心圆轴设计强度条件为 ][pmax ττ≤=W T将δ216π44p +=−=d D d D DW );(代入得][π16][π][π164444=−−≤−τττd TD D d D DT,)(0Pa)108(m 1.0πm N 10516Pa 1080π64346=××−×⋅××−×××)(D D解得mm 107.7m 10107.73=×=−Dmm 85.32mm100mm 7.1072=−=−=d D δ 比较可知,两种设计的结果非常接近。
讨论: 当10/0R ≤δ时,即认为是薄壁圆管,可以直接使用薄壁管扭转公式。
2 图示受扭圆杆,沿平面ABCD 截取下半部分为研究对象,如图b 所示。
试问截面ABCD 上的切向内力所形成的力偶矩将由哪个力偶矩来平衡?解题分析:由切应力互等定理可知截面ABCD 上的切向内力分布及其大小。
该截面上切向内力形成一个垂直向上的力偶矩。
在图b 中,左右两个横截面上的水平切向内力分量形成垂直于截面ABCD 的竖直向下的力偶矩,正好与截面ABCD 上切向内力的合力偶矩平衡。
扭转习题解答
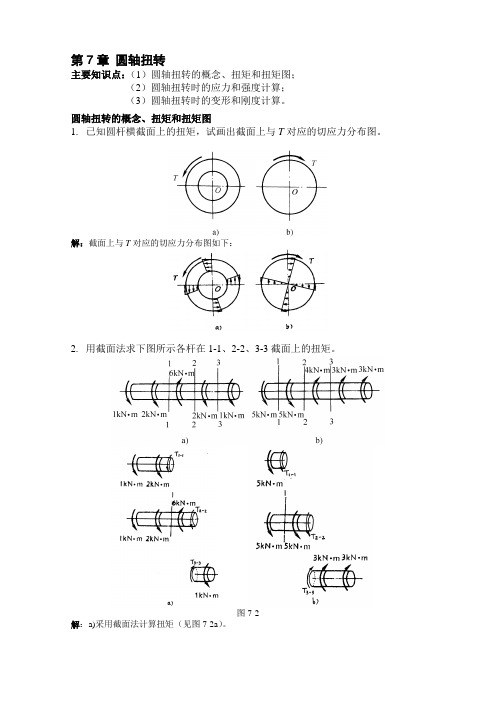
第7章圆轴扭转主要知识点:(1)圆轴扭转的概念、扭矩和扭矩图;(2)圆轴扭转时的应力和强度计算;(3)圆轴扭转时的变形和刚度计算。
圆轴扭转的概念、扭矩和扭矩图1.已知圆杆横截面上的扭矩,试画出截面上与T对应的切应力分布图。
解:截面上与T对应的切应力分布图如下:2.用截面法求下图所示各杆在1-1、2-2、3-3截面上的扭矩。
图7-2解:a)采用截面法计算扭矩(见图7-2a)。
取1-1截面左侧外力偶矩计算,可得m kN T ⋅-=-311。
取2-2截面左侧外力偶矩计算,由平衡方程062122=+⋅-+-T m kN )(,可得m kN T ⋅=-322。
取3-3截面右侧外力偶矩计算,可得m kN T ⋅=-133。
b) 采用截面法计算扭矩(见图7-2b )。
取1-1截面左侧外力偶矩计算,可得m kN T ⋅-=-511。
取2-2截面左侧外力偶矩计算,由平衡方程05522=+⋅+-T m kN )(,可得m kN T ⋅-=-1022。
取3-3截面右侧外力偶矩计算,由平衡方程03333=+⋅+-T m kN )(,可得m kN T ⋅-=-633。
3. 作下图各杆的扭矩图。
解:a)采用截面法计算扭矩(见图7-3a )。
取1-1截面左侧外力偶矩计算,可得m kN T ⋅=-411。
取2-2截面右侧外力偶矩计算,可得m kN T ⋅-=-222。
作出扭矩图。
a)b) 图7-3 b) 由力矩平衡方程可得e A M M 2-=(负号表示与图中假设方向相反)。
采用截面法计算扭矩(见图7-3b )。
取1-1截面左侧外力偶矩计算,可得e M T 211-=-。
取2-2截面右侧外力偶矩计算,可得e M T -=-22。
作出扭矩图。
圆轴扭转时的应力和强度计算4. 实心圆轴和空心轴通过牙嵌离合器而连接,如图所示。
已知轴的转速n =100r/min ,传递的功率P=7.5kW ,材料的许用应力][τ=40MP a ,试通过计算确定(1) 采用实心轴时,直径d 1和的大小;(2) 采用内外径比值为1/2的空心轴时,外径D 2的大小。
材料力学扭转练习题

材料力学扭转练习题基本概念题一、选择题1. 图示传动轴,主动轮A的输入功率为PA =0 kW,从动轮B,C,D,E的输出功率分别为PB =0 kW,PC = kW,PD = 10 kW,PE = 1kW。
则轴上最大扭矩T。
A.BA段 B.AC段 C.CD段 D.DE段max出现在题1图2. 图示单元体的应力状态中属正确的纯剪切状态的是。
题2图3. 上题图示单元体的应力状态中属正确的是。
4. 下列关于剪应力互等定理的论述中正确的是。
A.剪应力互等定理是由平衡B.剪应力互等定理仅适用于纯剪切的情况C.剪应力互等定理适用于各种受力杆件D.剪应力互等定理仅适用于弹性范围E.剪应力互等定理与材料的性能无关5. 图示受扭圆轴,其横截面上的剪应力分布图正确的是。
-12-题5图6. 实心圆轴,两端受扭转外力偶作用。
直径为D时,设轴内的最大剪应力为?,若轴的直径改为D2,其它条件不变,则轴内的最大剪应力变为。
A.8? B.?C.16? D.?7. 受扭空心圆轴,在横截面积相等的条件下,下列承载能力最大的轴是。
A.??0 B.??0.5C.??0. D.??0.88. 扭转应力公式T?的适用范围是。
IpA.各种等截面直杆 B.实心或空心圆截面直杆C.矩形截面直杆 D.弹性变形 E.弹性非弹性范围 9. 直径为D的实心圆轴,最大的容许扭矩为T,若将轴的横截面积增加一倍,则其最大容许扭矩为。
A.2TB.2T C.22TD.4T10. 材料相同的两根圆轴,一根为实心,直径为D1;另一根为空心,内径为d2,外径为D2d2D??。
若两轴横截面上的扭矩T,和最大剪应力?max均相同,则两轴外径之比1 D2D2为。
A.1??B.1?? C.343D.411. 阶梯圆轴及其受力如图所示,其中AB段的最大剪应力?max1与BC段的最大剪应力?max2的关系是。
A.?max1??max2B.?max1?313?max2C.?max1??max2D.?ma x1??max248-13-题12图题13图12. 在图示的圆轴中,AB段的相对扭转角?1和BC段的相对扭转角?2的关系是。
机械振动课后习题集和规范标准答案第三章习题集和标准答案
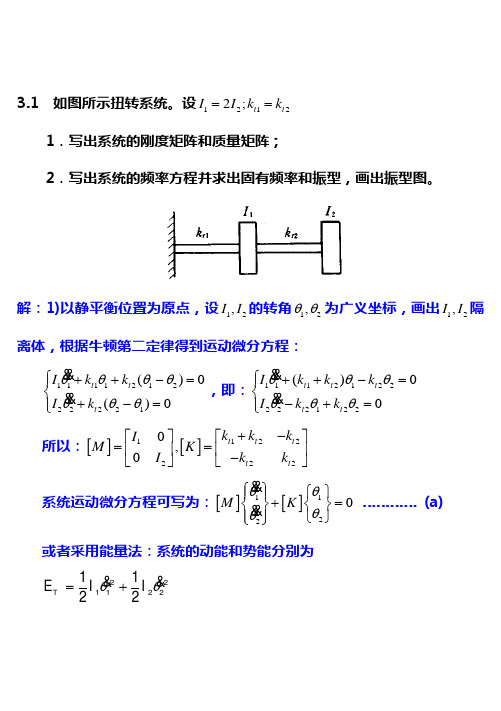
3.1 如图所示扭转系统。
设12122;t t I I k k ==1.写出系统的刚度矩阵和质量矩阵;2.写出系统的频率方程并求出固有频率和振型,画出振型图。
解:1)以静平衡位置为原点,设12,I I 的转角12,θθ为广义坐标,画出12,I I 隔离体,根据牛顿第二定律得到运动微分方程:111121222221()0()0t t t I k k I k θθθθθθθ⎧++-=⎪⎨+-=⎪⎩&&&&,即:1112122222122()00t t t t t I k k k I k k θθθθθθ⎧++-=⎪⎨-+=⎪⎩&&&&所以:[][]12212220,0t t t t t k k k IM K k k I +-⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦系统运动微分方程可写为:[][]11220M K θθθθ⎧⎫⎧⎫⎪⎪+=⎨⎬⎨⎬⎪⎪⎩⎭⎩⎭&&&& ………… (a)或者采用能量法:系统的动能和势能分别为θθ=+&&2211221122T E I Iθθθθθθθ=+-=++-222211212121221121111()()2222t t t t t t U k k k k k k 求偏导也可以得到[][],M K由于12122;t t I I k k ==,所以[][]212021,0111t M I K k -⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦2)设系统固有振动的解为: 1122cos u t u θωθ⎧⎫⎧⎫=⎨⎬⎨⎬⎩⎭⎩⎭,代入(a )可得:[][]122()0u K M u ω⎧⎫-=⎨⎬⎩⎭………… (b)得到频率方程:22121211222()0t t t t k I k k k I ωωω--==--V即:224222121()240t t I k I k ωωω=-+=V解得:211,222(22t k I ω±==所以:1ω=<2ω= ………… (c)将(c )代入(b )可得:112121211122(22220(22t t t t t t k k I k I u u k k k I I ⎡⎤±--⎢⎥⎧⎫⎢⎥=⎨⎬⎢⎥⎩⎭⎢⎥--⎢⎥⎣⎦g g g解得:11212u u =-;12222u u = 令21u =,得到系统的振型为:-0.70710.70713.2 求图所示系统的固有频率和振型。
《材料力学》第3章 扭转 习题解
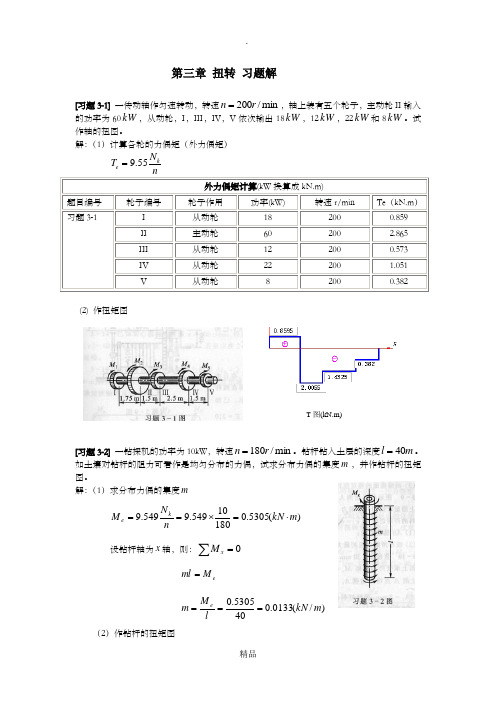
第三章扭转 习题解[习题3-1] 一传动轴作匀速转动,转速min /200r n =,轴上装有五个轮子,主动轮II 输入的功率为60kW ,从动轮,I ,III ,IV ,V 依次输出18kW ,12kW ,22kW 和8kW 。
试作轴的扭图。
解:(1)计算各轮的力偶矩(外力偶矩) nN T ke 55.9= 外力偶矩计算(kW 换算成kN.m)题目编号 轮子编号轮子作用 功率(kW) 转速r/minTe (kN.m ) 习题3-1I 从动轮 18 200 0.859 II 主动轮 60 200 2.865 III 从动轮 12 200 0.573 IV 从动轮 22 200 1.051 V从动轮82000.382(2) 作扭矩图[习题3-2] 一钻探机的功率为10kW ,转速min /180r n =。
钻杆钻入土层的深度m l 40=。
如土壤对钻杆的阻力可看作是均匀分布的力偶,试求分布力偶的集度m ,并作钻杆的扭矩图。
解:(1)求分布力偶的集度m)(5305.018010549.9549.9m kN n N M k e ⋅=⨯== 设钻杆轴为x 轴,则:0=∑xMe M ml =)/(0133.0405305.0m kN l M m e ===(2)作钻杆的扭矩图T 图(kN.m)x x lM mx x T e0133.0)(-=-=-=。
]40,0[∈x 0)0(=T ; )(5305.0)40(m kN M T e ⋅-==扭矩图如图所示。
[习题3-3] 圆轴的直径mm d 50=,转速为120r/min 。
若该轴横截面上的最大切应力等于60MPa ,试问所传递的功率为多大? 解:(1)计算圆形截面的抗扭截面模量:)(245445014159.3161161333mm d W p =⨯⨯==π (2)计算扭矩2max /60mm N W Tp==τ )(473.1147264024544/6032m kN mm N mm mm N T ⋅=⋅=⨯=(3)计算所传递的功率 )(473.1549.9m kN nN M T ke ⋅=== )(5.18549.9/120473.1kW N k =⨯=[习题3-4] 空心钢轴的外径mm D 100=,内径mm d 50=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
- 1 - 第三章 扭转习题
一、单项选择题
1、横截面都为圆的两个杆,直径分别为d 和D ,并且d=0.5D 。
两杆横截面上扭矩相等两杆横截面上的最大切应力之比maxD
maxd ττ为 A 、2倍, B 、4倍,
C 、8倍,
D 、16倍。
二、填空题
1、扭转变形时,公式p
Tl GI τ=中的 表示单位长度的扭转角,公式中的T 表示横截面上的 ;G 表示杆材料的 弹性模量;I P 表示杆横截面对形心的 ;GI P 表示杆的抗扭 。
2、截面为圆的杆扭转变形时,所受外力偶的作用面与杆的轴线 .
3、实心圆轴扭转时,横截面上的切应力分布是否均匀,横截面上离圆心愈远的点处切应力 ,圆心处的切应力为 ,圆周上切应力
4、两根实心圆轴的直径d 和长度L 都相同,而材料不同,在相同扭矩作用下,它们横截面上的最大切应力是否相同 ,单位长度的扭转角是否相同 。
5、剪切虎克定律的表达式
G τγ=,式中/miniportal/static/singer/index/hot_singer_0.html 的G 表示材料的
模量,式中的γ称为 。
6、根据切应力互等定理,单元体两互相垂直截面上在其相交处的切应力成对存在, 且 相等,而 现反。
三、计算题
1、如图所示圆轴,一端固定。
圆轴横截面的直径D=100mm ,所受的外力偶矩M 1=6kN•m, M 2=4kN•m 。
试求圆轴横截面上的最大扭矩和最大切应力。
答:圆轴横截面上的最大扭矩为 kN•m ;
圆轴横截面上的最大切应力为 Mpa 。
- 2 -
2、如图所示阶梯形圆轴,一端固定。
圆轴横截面的直径分别为50mm 和75mm ,所受的外力偶矩M C =1200 N•m ,M B =1800 N•m 。
试求BC 段横截面上的扭矩和该阶梯轴的最
大切应力。
答:BC 段横截面上的扭矩为 N•m ;
该阶梯轴的最大切应力为 Mpa 。
3、如图所示圆轴,一端固定。
圆轴横截面的直径d=100mm ,所受的外力偶矩M 1=7000
N•m M 2=5000 N•m 。
试求圆轴横截面上的最大
扭矩和最大切应力。
答:最大扭矩为 N •m 。
最大切应力为 Mpa 。
4、某传动轴为实心圆轴,轴内的最大扭矩
=1.5kN m T ,许用切应力[]=50MPa τ,试确定该轴的横截面直径。
5、圆轴AB 传递的功率为P = 7.5kW ,转速n = 360r/min 。
轴的AC 段为实心圆截面,CB 段为空心圆截面,如图所示。
已知D= 30mm 。
试计算AC 段横截面边缘处的切应力。
图 3.3.3 图3.3.5。
