统计学课后答案2
统计学徐国祥第二版课后题答案

第1章总论1.1 复习笔记一、统计学的产生和发展从统计学的产生和发展过程来看可以把统计学划分为3个时期统计学的萌芽期、统计学的近代期和统计学的现代期。
1统计学的萌芽期统计学的萌芽期始于17世纪中叶至18世纪中、末叶主要有国势学派和政治算术学派。
2统计学的近代期统计学的近代期始于18世纪末至19世纪末主要有数理统计学派和社会统计学派。
3统计学的现代期统计学的现代期为20世纪初到现在的数理统计时期发展有三个明显的趋势1随着数学的发展统计学依赖和吸收数学营养的程度越来越迅速2向其他学科领域渗透或者说以统计学为基础的边缘学科不断形成3随着应用的日益广泛和深入特别是借助电子计算机后统计学所发挥的功效越益增强。
二、统计学的研究对象和研究方法1统计的涵义“统计”一词具有统计学、统计工作和统计资料三种涵义。
1统计学是研究如何搜集资料、整理资料和进行数量分析、推断的一门方法论科学。
2统计工作即统计实践是对社会、经济以及自然现象的总体数量方面进行搜集、整理和分析的活动过程。
3统计资料即统计工作的成果是统计工作过程所取得的各项数字和有关情况的资料它反映现象的规模、水平、速度和比例关系等等以表明现象发展的特征。
三者之间的联系统计工作的好坏直接影响统计资料的数量和质量。
统计工作的发展需要统计理论的指导。
统计学来源于统计工作是统计工作经验的理论概括又用理论和方法指导统计工作推动统计工作的不断提高。
随着统计工作的进一步发展统计学不断地充实和提高两者是理论和实践的关系。
2统计学的研究对象统计学的研究对象是大量现象的数量其性质是一门适用于自然现象和社会现象的方法论学科。
3统计学的研究方法1大量观察法大量观察法是指对所研究的事物的全部或足够数量进行观察的方法。
它的数学依据是大数定律。
2综合指标法综合指标是从数量方面对现象总体的规模及其特征的概括说明。
综合指标法是运用各种综合指标对现象的数量关系进行对比分析的方法。
3统计推断法统计推断法是在一定置信程度下根据样本资料的特征对总体的特征作出估计和预测的方法。
统计学第五版课后习题答案(完整版)

统计学(第五版)课后习题答案(完整版)第一章思考题1.1什么是统计学统计学是关于数据的一门学科,它收集,处理,分析,解释来自各个领域的数据并从中得出结论。
1.2解释描述统计和推断统计描述统计;它研究的是数据收集,处理,汇总,图表描述,概括与分析等统计方法。
推断统计;它是研究如何利用样本数据来推断总体特征的统计方法。
1.3统计学的类型和不同类型的特点统计数据;按所采用的计量尺度不同分;(定性数据)分类数据:只能归于某一类别的非数字型数据,它是对事物进行分类的结果,数据表现为类别,用文字来表述;(定性数据)顺序数据:只能归于某一有序类别的非数字型数据。
它也是有类别的,但这些类别是有序的。
(定量数据)数值型数据:按数字尺度测量的观察值,其结果表现为具体的数值。
统计数据;按统计数据都收集方法分;观测数据:是通过调查或观测而收集到的数据,这类数据是在没有对事物人为控制的条件下得到的。
实验数据:在实验中控制实验对象而收集到的数据。
统计数据;按被描述的现象与实践的关系分;截面数据:在相同或相似的时间点收集到的数据,也叫静态数据。
时间序列数据:按时间顺序收集到的,用于描述现象随时间变化的情况,也叫动态数据。
1.4解释分类数据,顺序数据和数值型数据答案同1.31.5举例说明总体,样本,参数,统计量,变量这几个概念对一千灯泡进行寿命测试,那么这千个灯泡就是总体,从中抽取一百个进行检测,这一百个灯泡的集合就是样本,这一千个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是参数,这一百个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是统计量,变量就是说明现象某种特征的概念,比如说灯泡的寿命。
1.6变量的分类变量可以分为分类变量,顺序变量,数值型变量。
变量也可以分为随机变量和非随机变量。
经验变量和理论变量。
1.7举例说明离散型变量和连续性变量离散型变量,只能取有限个值,取值以整数位断开,比如“企业数”连续型变量,取之连续不断,不能一一列举,比如“温度”。
《统计学原理》课后习题答案

第一章练习题参考答案一.单项选择题1.B;2.A;3.B;4.C;5.D;6.A;7.C;8.C;9.C;10.A;11.C;12.C。
二.多项选择题1.ABDE;2.ACD;3.BCD;4.ACD;5.ACDE;6.ACE;7.AD;8.ABC;9.ACD;10.AD;11.BCDE;12.ABCDE;13.AC。
三.判断题1.×;2.×;3.×;4.×;5.√;6.×;7.×;8.√;9.×;10.√。
第二章练习题参考答案一.单项选择题1.C;2.C;3.D;4.B;5.D;6.D;7.B;8.D;9.B;10.B;11.A;12.C;13.D。
二.多项选择题1.CE;2.ACE;3.CE;4.BCD;5.ABCE;6.BC;7.BCD;8.ABD;9.ABD;10.ACDE;11.ABCE;12.ABE。
三.判断题1.×;2.√;3.×;4.×;5.×;6.×;7.√;8.×;9.×;10.×。
第三章练习题参考答案一.单项选择题1.B;2.C;3.C;4.C;5.D;6.B;7.B;8.B;9.D;10.B;11.A;12.B;13.D;14.A。
二.多项选择题1.AB;2.AC;3.AB;4.ABC;5.AB;6.ABD;7.ABC;8.ACE;9.BD;10.ABDE。
三.判断题1.√;2.×;3.×;4.×;5.√;6.×;7.√;8.√;9.×;10.×。
四.计算分析题1.解:(1)按职称编制的分配数列2.解:编制单项式变量数列3.解:(1)编制组距式变量数列。
(2直方图(略)第四章练习题参考答案一.单项选择题1.C;2.D;3.B;4.D;5.C;6.A;7.C;8.C;9.B;10.C;11.B;12.D;13.A;14.D;15.16.B;17.B;18.D;19.C;20.C;21.D;22.B;23.C;24.C;25.B。
统计学课后第二章习题答案

第2章练习题1、二手数据的特点是()A.采集数据的成本低,但搜集比较困难B. 采集数据的成本低,但搜集比较容易C.数据缺乏可靠性D.不适合自己研究的需要2、从含有N个元素的总体中,抽取n个元素作为样本,使得总体中的每一个元素都有相同的机会(概率)被抽中,这样的抽样方式称为()A.简单随机抽样B.分层抽样C.系统抽样D.整群抽样3、从总体中抽取一个元素后,把这个元素放回到总体中再抽取第二个元素,直至抽取n个元素为止,这样的抽样方法称为()A.重复抽样B.不重复抽样C.分层抽样D.整群抽样4、一个元素被抽中后不再放回总体,然后从所剩下的元素中抽取第二个元素,直至抽取n个元素为止,这样的抽样方法称为()A.不重复抽样B.重复抽样C.系统抽样D.多阶段抽样5、在抽样之前先将总体的元素划分为若干类,然后从各个类中抽取一定数量的元素组成一个样本,这样的抽样方式称为()A. 简单随机抽样B. 系统抽样C.分层抽样D.整群抽样6、先将总体各元素按某种顺序排列,并按某种规则确定一个随机起点,然后每隔一定的间隔抽取一个元素,直至抽取n个元素形成一个样本。
这样的抽样方式称为()A. 分层抽样B. 简单随机抽样C.系统抽样D.整群抽样7、先将总体划分为若干群,然后以群作为抽样单位从中抽取部分群,再对抽中的各个群中所包含的所有元素进行观察,这样的抽样方式称为()A. 系统抽样B. 多阶段抽样C.分层抽样D.整群抽样8、为了调查某校学生的购书费用支出,从男生中抽取60名学生调查,从女生中抽取40名学生调查,这种调查方是()A. 简单随机抽样B. 整群抽样C.系统抽样D.分层抽样9、为了调查某校学生的购书费用支出,从全校抽取4个班级的学生进行调查,这种调查方法是()A. 系统抽样B. 简单随机抽样C.分层抽样D.整群抽样10、为了调查某校学生的购书费用支出,将全校学生的名单按拼音顺序排列后,每隔50名学生抽取一名学生进行调查,这种调查方法是?()A.分层抽样B. 整群抽样C.系统抽样D.简单随机抽样11、为了了解女性对某种化妆品的购买意愿,调查者在街头随意拦截部分女性进行调查。
统计学课后习题答案(全)
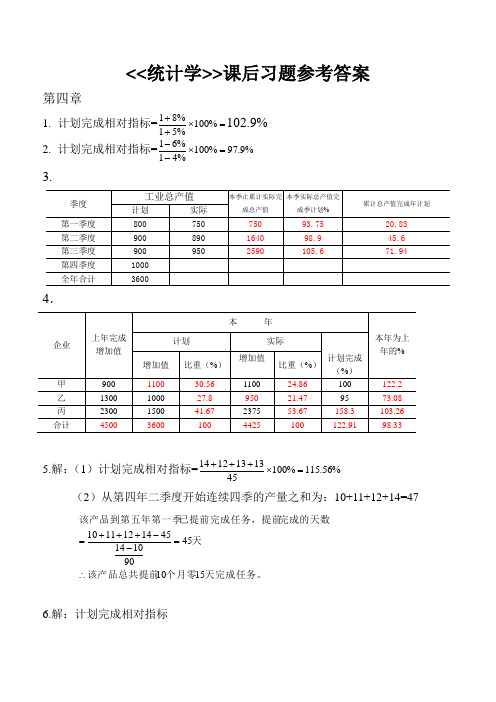
<<统计学>>课后习题参考答案第四章1. 计划完成相对指标==⨯++%100%51%81102.9% 2. 计划完成相对指标=%9.97%100%41%61=⨯--3.4.5.解:(1)计划完成相对指标=%56.115%1004513131214=⨯+++(2)从第四年二季度开始连续四季的产量之和为:10+11+12+14=47天完成任务。
个月零该产品总共提前天完成的天数已提前完成任务,提前该产品到第五年第一季1510459010144514121110∴=--+++=6.解:计划完成相对指标=%75.126%100%1.0102005354703252795402301564=⨯⨯⨯++++++(2)156+230+540+279+325+470=2000(万吨) 所以正好提前半年完成计划。
7.8.略第五章 平均指标与标志变异指标1.甲X =.309343332313029282726=++++++++乙X =44.319403836343230282520=++++++++ AD 甲=}22.29303430333032303130303029302830273026=-+-+-+-+-+-+-+-+-AD 乙=}06.594044.313844.313644.313444.313244.313044.312844.312544.3120=-+-+-+-+-+-+-+-+-R 甲=34-26=8 R 乙=40-20=20σ甲=9)3334()3033()3032()3031()3030()3029()3028()3027()3026(222222222-+-+-+-+-+-+-+-+-=2.58 σ乙=9)44.3140()44.3138()44.3136()44.3134()44.3132()44.3130()44.3128()44.3125()44.3120(222222222-+-+-+-+-+-+-+-+-=6.06V 甲=1003058.2⨯%=8.6% V 乙=%3.19%10044.3106.6=⨯所以甲组的平均产量代表性大一些. 2.解:计算过程如下表:甲X =.)(5.101780元= 乙X =(元)9708077600= 3.解:计算过程如下表:甲X =.4.119809550=(件) 乙X =8.120809660=(件) σ甲=06.98075.6568=(件) σ乙=81.10809355=(件) V 甲=1004.11906.9⨯%=7.58% V 乙=%94.8%1008.12081.10=⨯所以甲厂工人的平均产量的代表性要高些.4. 解:()()94.761018102457047.7610121871871870775121873595128518757653550=⨯-+==⨯-+--+==++++⨯+⨯+⨯+⨯+⨯=e M M X 5.解:(1)上期的平均计划完成程度为:()()第六章元解解度为下期的平均计划完成程tH V P X P P P P /3.2884102950943.5062900255.3212800604.43210943.506255.321604.432:.7%1.32%1009067.0291.0291.0%67.901%67.90%67.90%67.90%10030028300:.6%37.103%1031400%1011200%107810%110961400120081096:)2(%67.99%1001500100070080%951500%1001000%108700%1108044=⨯⎪⎭⎫ ⎝⎛++⨯++==⨯==-⨯====⨯-==++++++=⨯+++⨯+⨯+⨯+⨯σ1.()())(7.788%67.41500:2000%67.41500600:.6)(6.62126907106557306806702650600269071061527106556552655730620273068060026806706402670650:2)(7.62327107006907206806202680610271070062527006906452690720640272068062026806206002620680:)1(:.5%63.79%1002576462450243526206005802580:.4%85.105%100%113385%102350%97463%120485%105412%112410%98368%106350%105310%110324%102306%101303385350463485412410368350310324306303::.3872232122221030980329809002290010201210208402284067022670600.2104万吨年该县粮食产量为平均增长速度解元工人的月平均工资为乙工区上半年建筑安装元工人的月平均工资为甲工区上半年建筑安装解解度为全年月平均计划完成程解=+⨯=-==++++++⨯++⨯++⨯++⨯++⨯++⨯+=++++++⨯++⨯++⨯++⨯++⨯++⨯+=⨯++++++==⨯++++++++++++++++++++++=+++++⨯++⨯++⨯++⨯++⨯++⨯+=C a 7解:计算过程如下表:)(94.6653.444.45:1994:3.46025844.4594092万元年的地方财政支出额为则直线趋势方程为=⨯++=======∑∑∑bta y t tyb ny a二次曲线方程为:y = 0.0108x 2 + 4.1918x + 24.143(过程略) 指数曲线方程为:y = 26.996e 0.0978x8.解:计算过程如下表:9.解:(1)同季平均法求季节比率的过程如下表:(2)趋势剔除法测定的季节变动如下表:第七章 统计指数()()()()01001011111175000124000081138.44%5000012350008750002540000182138.03%500002535000181075000940000390.98%127500084000022750002540000425qqzpk q z q zq p k q pq z kq z p q k p q⨯+⨯===⨯+⨯⨯+⨯===⨯+⨯⨯+⨯===⨯+⨯⨯+⨯==∑∑∑∑∑∑∑∑111111110102.12%75000184000015602.108.8%1200360110%105%pp q p q k p q p q p p=⨯+⨯====+∑∑∑∑11111560.135.65%1150135.65%124.68%108.8%.120%1800115%90096%6003.114.27%330042003300111.38%114.27%.pqpq qpqpq p qp q k p qk k k q q p q p q k q p q pkk k======⨯+⨯+⨯=======∑∑∑∑∑∑ 110101001013200005.100%128%250000128%123.1%14%320000307692.3104%307692.325000057692.3320000307692.312307.pq pqq PpK K K p qp q K p q p qq p q =⨯====+===-=-=-=-=∑∑∑∑∑∑1解:K 零售量变动对零售额变动影响的绝对值为:(万元)零售物价变动对零售总额变动影响的绝对值为:p 1110010000107350000120%120%180000110%110%116%116%17.6%107.6%350000291666.67120%180000163636.36.110%1pq pq q q pq pq q q K q K q p q Kq p q K p q p q ==+===+==+==+========⨯=∑∑∑∑∑∑∑∑城1城农城农1农1城城城1农农农城城城(万元)6.解:已知p ,,p ,,K ,K p 则p K 0010111101001116%291666.67338333.33107.6%163636.36176072.72350000180000103.03%338333.33176072.723%q pp q p q p q q q k p q p q p q ⨯==⨯=⨯=++====++∴∑∑∑∑∑∑∑∑农农农11城农城农K p p 该地区城乡价格上涨了。
梁前德《统计学》(第二版)学习指导与习题训练答案:02第二章统计调查与整理习题答案

旗开得胜1第二章统计调查与整理习题答案、名词解释用规范性的语言解释统计学中的名词。
1. 统计调查:是按照统计工作任务的要求,运用科学的调查方法,有组织地搜集各项原始资料的工作过程。
2. 一次性调查:是不连续登记的调查,它是对事物每隔一段时期后在一定时点上的状 态进行登记。
其主要目的是获得事物在某一时点上的水平、状况的资料。
3. 统计整理:是对调查资料进行加工、汇总,使其系统化、条理化、科学化,以反映现象总体综合特征的工作过程。
根据统计研究的需要,按照一定的重要标志将总体划分为若干个性质不同的部分。
在统计分组的基础上,将总体所有的单位按组归类整理,并按一定顺序排列,形成总体中各单位在各组间的分布,称分布数列。
8.统计表:是把统计数据按照一定的结构和顺序,用表格显示的一种形式。
5.分组标志: 是将统计总体划分为几个性质不同部分的标准或依据。
6.复合分组:按两个或两个以上标志对总体进行分组。
4.统计分组:7.分布数列:旗开得胜二、填空题根据下面提示的内容,将适宜的名词、词组或短语填入相应的空格之中。
1.统计设计、统计整理、统计分析2.准确性3.每一个单位4.非全面调查5.调查单位6.报告单位、填报单位7.调查项目8.单一表、一览表9.调查期限10.绝对大比重、重点单位11.一次性12.随机原则、数量上13.普查、统计报表制度、抽样调查、重点调查2旗开得胜14.直接对个别典型单位进行调查、在分类的基础上、选择一部分典型单位调查15.全面调查、非全面调查3旗开得胜16. 重点单位、非全面调查17. 简单分组、分组体系18. 标志、层层19. 离散、组距式20. 反比21. 组中值、一般水平22. 同一个数值、不同数值23. 总标题、数字资料24. 调查表、分析表、分组表、复合表25. 几何图形、具体形象三、单项选择从各题给出的四个备选答案中,选择一个最佳答案,填入相应的括号中。
1. D2. D3. A4. B5. C6. B7. B8. B9. C 10. D11. D 12. A 13. A 14. C 15. B4旗开得胜16. C 17. D 18. C 19. A 20. C21. A 22. B 23. B 24. C 25. A26. D 27. A 28. C 29. B 30. C四、多项选择从各题给出的四个备选答案中,选择一个或多个正确的答案,填入相应的括号中。
统计学习题及答案(完整)2

统计学习题及答案(完整)2计量资料的统计描述一、最佳选择题1、描述一组偏态分布资料的变异度,以()指标较好。
A、全距B、标准差C、变异系数D、四分位数间距E、方差2.用均数和标准差可以全面描述()资料的特征。
A.正偏态分布B.负偏态分布C.正态分布D.对称分布E.对数正态分布3.各观察值均加(或减)同一数后()。
A.均数不变,标准差改变B.均数改变,标准差不变C.两者均不变D.两者均改变E.以上都不对4.比较身高和体重两组数据变异度大小宜采用()。
A.变异系数B.方差C.极差D.标准差E.四分位数间距5.偏态分布宜用()描述其分布的集中趋势。
A.算术均数B.标准差C.中位数D.四分位数间距E.方差6.各观察值同乘以一个不等于0的常数后,()不变。
A.算术均数B.标准差C.几何均数D.中位数E.变异系数7.()分布的资料,均数等于中位数。
A.对数正态B.正偏态C.负偏态D.偏态E.正态8.对数正态分布是一种()分布。
(说明:设X变量经Y=lgX变换后服从正态分布,问X变量属何种分布?)A.正态B.近似正态C.左偏态D.右偏态E.对称9.最小组段无下限或最大组段无上限的频数分布资料,可用()描述其集中趋势。
A.均数B.标准差C.中位数D.四分位数间距E.几何均数10.血清学滴度资料最常用来表示其平均水平的指标是()。
A.算术平均数B.中位数C.几何均数D.变异系数E.标准差二、简答题1、对于一组近似正态分布的资料,除样本含量n外,还可计算,S和,问各说明什么?2、试述正态分布、标准正态分布及对数正态分布的某单位1999年正常成年女子血清联系和区别。
甘油三酯(mmol/L)测量结果3、说明频数分布表的用途。
4、变异系数的用途是什么?组段频数5、试述正态分布的面积分布规律。
0.6~ 10.7~ 3 三、计算分析题0.8~ 9 1、根据1999年某地某单位的体检资料,116名正常0.9~ 13 成年女子的血清甘油三酯(mmol/L)测量结果如右表, 1.0~ 19 请据此资料: 1.1~ 25(1)描述集中趋势应选择何指标?并计算之。
统计学课后题及答案解析王文华

统计学课后题及答案解析王文华1 、什么是统计学?答:统计学是关于数据的科学,它所提供的是一套有关数据收集、处理、分析、解释并从数据中得出结论的方法,统计所研究的是来自各领域的数据。
数据收集即取得统计数据;数据处理是将数据用图表等形式展示出来;数据分析则是选择适当的统计方法研究数据,并从数据中提取有用信息进而得出结论。
2、解释描述统计和推断统计。
答:数据分析所用的方法可分为描述统计方法和推断统计方法。
(1)描述统计研究的是数据收集、处理、汇总、图表描述、概括与分析等统计方法。
(2)推断统计是研究如何利用样本数据来推断总体特征的统计方法。
比如,对产品的质量进行检验,往往是破坏性的,不可能对每个产品进行测量。
这就需要抽取部分个体即样本进行测量,然后根据获得的样本数据对所研究的总体特征进行推断,这就是推断统计要解决的问题。
3、统计数据可分为哪几种类型?不同类型的数据各有什么特点?答:统计数据是对现象进行测量的结果,可以从不同角度对统计数据进行分类:(1)按照所采用的计量尺度不同,可以将统计数据分为分类数据、顺序数据和数值型数据。
①在分类数据中,各类别之间是平等的并列关系,无法区分优劣或大小,各类别之间的顺序是可以改变的;②顺序数据也表现为类别,但这些类别之间是有顺序的;③数值型数据具有分类数据和顺序数据的特点,并且还可以进行加、减、乘、除运算。
(2)按照统计数据的收集方法,可以将其分为观测数据和实验数据。
①观测数据是通过调查或观测而收集到的数据,这类数据是在没有对事物进行人为控制的条件下得到的,有关社会经济现象的统计数据几乎都是观测数据;②实验数据是在实验中通过控制实验对象收集到的数据,自然科学领域的大多数数据都是实验数据。
(3)按照被描述的现象与时间的关系,可以将统计数据分为截面数据和时间序列数据。
①截面数据是在相同或近似相同的时间点上收集的数据,这类数据通常是在不同的空间上获得的,用于描述现象在某一时刻的变化情况;②时间序列数据是在不同时间上收集到的数据,这类数据是按时间顺序收集到的,用于描述现象随时间变化的情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A 150 B 200 C 100 D 250
3.从均值为200,标准差为50的总体中抽取容量为 100的简单随机样本,样本均值的标准差为
A 50
B 10 C 5
D 15
4.抽样分布是指( )
A 一个样本各观测值的分布 B 总体中各观测值的分布 C 样本统计量的分布 D 样本数量的分布
5. 从服从正态分布的无限总体中分别抽 取容量为4,16,36的样本,当样本容 量增大时,样本均值的标准差( )
A 保持不变
B 增加
C 减小
D 无法确定
6. 假设一总体服从均匀分布,从该总体中抽
取容量为36的样本,则样本均值的抽样分布
(
)
A 服从非正态分布 B 近似正态分布
C 服从均匀分布
D 服从t分布
7. 假设总体比例为0.55,从该总体中抽取 容量为100的样本,则样本比例的标准差 为( B ) A 0.01 B 0.05 C 0.06 D 0.55
在95%的置信水平下估计大学生平均 每 天 参 加 锻 炼 的 时 间 在 24.824 ~ 27.176 分钟之间。
解:总体的分布未知,总体方差也未知,但所抽
样本容量36为大样本,因此,求总体均值的 置信区间可用样本标准差代替总体标准差
置信区间为:
x Z
2
s4 0 1 .6 4 5 54 0 1 .3 7
1. 设X1,X2,…Xn是从某总体X中抽取的 一个样本,下面哪一个不是统计量( )
A.
_
X
1
n
Xi
n i1
C.
n
[Xi E(X )]2
i1
B.
S2 1
n
_
(Xi X)2
n i1
D. S2 1
n
_
(Xi X)2
n1i1
2.从均值为200,标准差为50的总体中抽取容量为 100的简单随机样本,样本均值的数学期望为
检验统计量: z xn 09 26 00 011 00 00 021.645
统计决策: 因为 Z Z ,Z值位于拒绝域,
所以应拒绝H0,检验表明这批灯泡的使用寿命
低于1000小时,批发商不应购买这批灯泡。
解: H0: μ≥1000小时 应购买灯泡 H1: μ<1000小时 拒绝购买灯泡
已知μ0 = 1000(小时),σ=200(小时),x 960(小时) n = 100,因为是大样本,故选择Z统计量
解:已知 n=200 ,p =0.7 , np =140>5,
n(1- p)=60>5,= 0.95,Z/2=1.96
pˆ Z 2
pˆ (1 pˆ ) n
0 . 7 1 . 96 0 . 7 (1 0 . 7 ) 200
0 .636 ,0 .764
我们可以95%的概率保证该企业职工由 于同管理人员不能融洽相处而离开的比 例在63.6%~76.4%之间
n
3 6
则投保人平均年龄在90%的置信度下的
置信区间为38.63岁-41.37岁。
解:因为总体近似服从正态分布,方差未知, 所抽样本为小样本,则总体均值的置信区间为
xt0.025(161)
s 322.131 8 324.26227.738
n
16
xt0.025(161)
s 322.131 8 324.26236.262
在置信度为95%水平下,金属棒的平均长度在 7.456~7.504厘米之间。
【例2】解:虽然总体分布未知,但总体方
差已知,样本量充分大, x=26, =6,
n=100, Z/2=1.96
x Z 2
n
,
x
Z
2
n
26 1.96
6 ,26 1.96 100
6 100
24.824,27.176
所 以 拒 绝 H0 , 新 员 工 的 月 平 均 销 售 额 与老员工相比有显著差异。
解: H0: μ≥1000小时 应购买灯泡 H1: μ<1000小时 拒绝购买灯泡
已知μ0 = 1000(小时),σ=200(小时),x 960(小时) n = 100,因为是大样本,故选择Z统计量
α=0.05,本题为左侧检验,因此zα= 1.645
解:已知=120(元),Z/2=1.96,E=20(元)
应抽取的样本容量为
n
Z
2
2
E2
2
(1 .96 ) 2 120 2 20 2
138 .2976 139
结论:应抽取139个顾客作为样本。
解 : 已 知 2=1800000 , =0.05 , Z/2=1.96,E=500
应抽取的样本容量为
n
Z
2
2
E2
2
(1 .96 ) 2 (1800000 500 2
)
27 .66 28
解: 已知E=0.05,=0.05,Z/2=1.96,当p未知时 用最大方差0.25代替
应抽取的样本容量为
n
Z
2
2
p (1
p)
E2
(1 .96 ) 2 ( 0 .5 )(1 0 .5 ) ( 0 .05 ) 2 Nhomakorabea 385
解: H0: μ= 15万元 没有明显差异 H1: μ 15万元 有显著差异
已知μ0 = 15万元,σ=2万元,x 12万元 n = 200,因为是大样本,故选择Z统计量 α=0.05,z0.025=1.96
检验统计量: Zx0121591.96 n 2 36
统计决策: 因为 Z Z/2 ,Z值位于拒绝域,
B t分布
C F分布
D c2分布
解:总体服从正态分布,方差已知,置信度为95% 则z0.025=1.96,
x Z 2 n 7 .4 8 1 .9 6 0 .2 0 5 6 7 .4 8 0 .0 2 4 7 .4 5 6
x Z 2 n 7 .4 8 1 .9 6 0 .2 0 5 6 7 .4 8 0 .0 2 4 7 .5 0 4
8. 假设总体比例为0.4,采取重复抽样的 方法从此总体中抽取一个容量为100的样 本,则样本比例的期望是( ) A 0.3 B 0.4 C 0.5 D 0.45
9. 大样本的样本比例的抽样分布服从( )
A 正态分布
B t分布
C F分布
D c2分布
10.大样本的样本均值之差的抽样分布服从
A 正态分布
n
16
因此,有95%的把握估计全部顾客平均年龄在 27.738至36.262之间。
【例5】解:已知n=100,zα/2 =1.96, p=42/100=0.42
p 1 p
0 .4 2 1 0 .4 2
p z /2
0 .4 2 1 .9 6 n
1 0 0
0.420.097
因此,该校找到工作的应届毕业生中女 同学的比例为0.323-0.517
