四川大学物理习题册第五章解答2共18页文档
四川大学大学物理学练习册上册习题答案

,m/s 6/(1):−==t x v ΔΔ解质点运动学(1)——答案一、选择题1.D2.B3.D4.D5.D 二、填空题 1. 23 m/s2. ()[]t t A t ωβωωωββsin 2cos e 22 +−−; ()ωπ/1221+n (n = 0, 1, 2,…) 3. 0.1 m/s 24. bt +0v ; 2402/)(b R bt ++v5. −g /2; ()g 3/322v 三、计算题1.2.3.(1)t A y tA x ωωsin cos 21==,消去t 得轨道方程为1222212=+A y A x (椭圆)(2)r j t A i t A dtvd j t A i t A dtrd 2221221sin cos a cos sin v ωωωωωωωωω−=−−==+−==a 与反向,故a 恒指向椭圆中心。
(3)当t=0时,x=A 1,y=0,质点位于ωπ2=t 时,2212sin,02cosA A y A x ====ππ。
质点位于图中的Q 点。
显然质点在椭圆形轨,910(2)2t t dx/dt v −==,/16(2)s v −=,1810t −=dt dv a /(3)=s2(2)m/26−=a vx 处的速度为解:设质点在dt dx dx dv dt dv a ⋅==dxdv v =x 263+=,)63(002dx x vdv v x∫∫+=)4(631/2x x v +=道上沿反时针方向运动。
在M 点,加速度a 的切向分量t a 如图所示。
可见在该点切向加速度t 的方向与速度v 的方向相反。
所以,质点在通过M 点速率减小。
4.5.所以质点的运动方程为:解:先求质点的位置,s 2=t 225220×+×=s )(m)(60在大圆=dt ds v /=,1020t +=m/s40(2)=v 时s 2=t dt dv a t /=m/s10=R va n/2=。
电路理论(四川大学)第五章习题答案

5.7 已知网络N只含LTI正电阻(图5-9),但不知 道电路的初始状态,当
时,电路响应为
U
iL t 1 3e
uS
t
t
2 c o s tU
t
A
t
为单位阶跃。
2 cos t 4
求(1)求同样初始状态下,当 u S t =0时的 i L t (2)求在同样初始状态下,当电源均为零值时的 i L t
d i1
2
t
2
dt
5
d i1 t dt
4 i1 t 1 2
t
2 4U
t
(1 )
1 1,
2 4
t
通解:
i1 h t k 1 e
k 2e
4 t
A
求特解: 特解响应为t>0以后,由(1)式有:
d i1 t
3 t L
iL 0
4 9 1 e
Lh
3 0
4
A
iL
4 9 13
A
t 0 A 自由响应: i t 9 e 强迫响应: i t 4 9 1 3 由三要素法有:i t i 0 e 3 t 4 e 3 t A LZP L
0
1
U(t)存在:
iL
1
t
iL t iL 0
iL e
t
iL
t
t 0
1 1 eΒιβλιοθήκη 1 1 2e A
四川大学大学物理第五章习题册解答 PPT
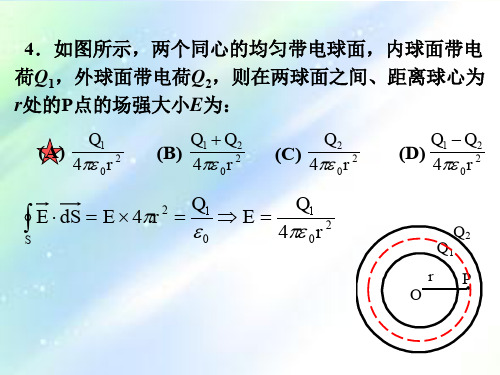
5.一无限长均匀带电圆柱体,半径为R,沿轴线方向的
线电荷密度为l,试分别以轴线和圆柱表面为电势零点,
求空z解间:的en 电 势E分dS布以Q.0轴线22为rr电hhEE势 零ll00Rr点RR22h22h
E E
lr 2 0R
l 2 0r
P
x
b
0dx
x
0 b
s 0
dx
s 0
bx
b
0 x
s 0
dx
s 0
x b
ห้องสมุดไป่ตู้
x
b
b x
0dx
0 b
s 0
dx
s 0
bx
b
s b 0
-b
o +b x
s b 0
8.一空气平板电容器,极板A、B的面积都是S,极板
Q1
4 0r 2
Q2 Q1
rP O
5.一个带负电荷的质点,在电场力作用下从A点经C 点运动到B点,其运动轨迹如图所示,已知质点运动的
速率是递减的,图中关于C点场强方向的四个图示中正 确的是:
A
E
B
C
B
C
B
E
A
A
E
C C
B D C
B
AE
d
Ft A
Fn
dt 0 at 0 运动轨迹为曲线,存在法向加速度
Q
0
E E
s 2 0
x
b, E
四川大学大学物理习题册答案05第五章静电场

qiq0 ri3
ri
q1
q2 q3
r1 r2
r3
F3
F2
q0
F1
由力的叠加原理得 q0所受合力
F Fi
i
第五章 真空中的静电场 矢量的基本性质:具有一定的大小和方向,加法遵从 平行四边形/三角形法则的量,具有空间平移不变性。
第五章 真空中的静电场
物理学研究具体问题时,常常在参考系上建立直角坐
(A)Q 2 2q (C)Q4q
(B)Q 2q (D)Q2q
F 0
q
2
4e 0a2
4e 0 2a
2
0
Q
Q 2 2q
Q
q
5 – 2 静电场 电场强度
第五章 真空中的静电场
5.2.1.1 静电场
实验证实了两静止电荷间存在相互作用的静电力, 但其相互作用是怎样实现的?
电荷
电场
电荷
场是一种特殊形态的物质,具有质量、能量、动 量等简单带电体系统的电场强度分布。
5 – 1 库仑定律
第五章 真空中的静电场
5.1.1.1 电荷的种类 经其他物体摩擦过的物体所具有的吸引
轻小物体的性质表明物体带了电。
物体所带电荷的多少称作电量,单位C。 实验表明,自然界中只存在两种电荷:
正电荷(如:丝绸摩擦过的玻璃棒所带电荷) 负电荷(如:毛皮摩擦过的硬橡胶棒所带电荷)
静电场的两个物理量:电场强度 E 和电势 j 的概念。 ( E 是矢量场,j 是标量场,二者均具有叠加性)
二、理解高斯定理的物理意义,会用点电荷电场强 度公式 + 场强叠加原理、 高斯定理求解特殊带电体系 的电场强度分布。
三、理解静电场的环路定理,会用电势的积分定义 式、点电荷的电势公式 + 电势叠加原理求解特殊带电 体系的电势分布。
高分子物理课件 - 四川大学 - 冉蓉 - 第五章 晶态高聚物

* 结晶高聚物最重要的证据为x射线衍射花样—— 同心环(德拜环)和衍射曲线。 * 非晶的x射线衍射花样——弥散环。 下图是等规立构的聚苯乙烯和无规立构的聚苯乙 烯的x射线衍射花样:
3、高聚物晶体中分子链的构象:
结晶过程中高聚物的密度↑ ,比容↓ ,分子链采 取位能最低的特定构象排入晶格。
1)、锯齿形构象:
4、分子量:
分子量小,结晶速率快
分子量大,结晶速率慢
5、压力、应力、溶剂、杂质
压力、应力↑
压力 应力
加速结晶
PE,Tm=137℃,一般当温度>Tm时,不结 晶,而在150MPa高压下,PE在160℃的温度 下可结晶。 应力使分子链朝某个方向排列,加速结晶—— 应力诱导结晶 NR,室温观察不到结晶,拉伸立刻产生结晶。
3)、不同高聚物的结晶速率不等: 结晶速率——体积收缩一半时对应的时间 (
t1/ 2 )的倒数。 t1/ 2 ——半结晶期
聚合物
聚异戊二烯
t1/ 2
0.42
秒
5 × 103
尼龙-66
二、 高聚物结晶的温度依耐性:
晶核形成 与低分子一样包括 晶体长大 结晶的温度范围 Tg~Tm 而实际的结晶温度范围是: Tg~T1 ( T1< Tm) 此即是结晶过冷的现象。
不同成核和生长类型的Avrami指数值
生长类型 三维生长 (球状晶体) 二维生长 (球状晶体) 一维生长 (球状晶体) 均相成核 n=生长维数+1 异相成核 n=生长维数
n=3+1=4 n=2+1=2 n=1+1=2
n=3+0=3 n=2+0=2 n=1+0=1
“退火”(热处理方法):
将成形后的制品升温到接近熔点的某一温度,以加速次 期结晶。
四川大学物理学院理论力学第五章课件 4
x
x
l
lM
M
y
y
y
xA A xA = sint
x
l
M
x2 + y2 = l2
张纪平 制作
x2 + y2 ≤ l2
(x − sint)2 + y2 = l2
1
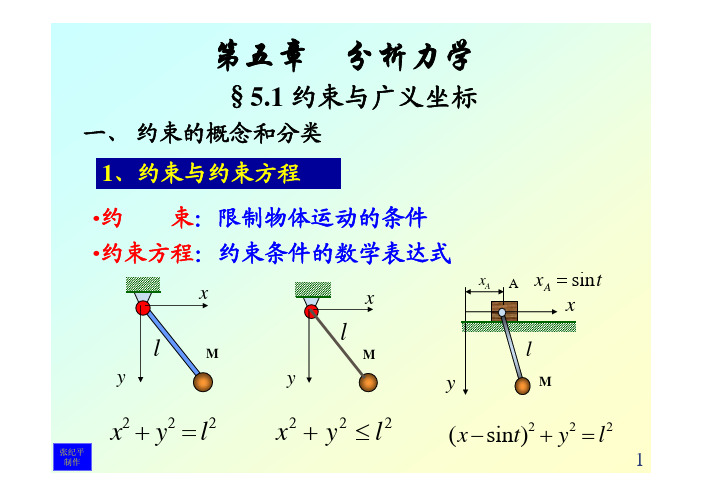
2、约束的分类
x 刚性杆
x
l
l
M
M
y
y
x2 + y2 = l2
x2 + y2 ≤ l2
xA A xA = sint
x
y
M
(x −sint)2 + y2 = l2
O
解: 解析法 2个自由度
α
取α、β 为广义坐标
系统所受约束符合虚功原理的适用条件
系统的主动力有 P1, P2 和 F
根据虚功原理,
P1iδ rC + P2 iδ rD + F iδ rB = 0
建立坐标系
P1δ xC + P2δ xD + Fδ yB = 0
张纪平 制作
A
β
F
O
B
α
y
C
l1 β
P1 A l2
F
x
D P2 B
18
P1δ xC + P2δ xD + Fδ yB = 0
yB = l1 cosα + l2 cos β
xC
=
1 2
l1 sin α
O
α
y
C
l1 β
xD
=
l1 sin α
+
1 2
l2
sin
β
大学物理(西南交大)作业参考答案5
NO.5 电势、导体与※电介质中的静电场 (参考答案)班级: 学号: 姓名: 成绩:一 选择题1.真空中一半径为R 的球面均匀带电Q ,在球心O 处有一带电量为q 的点电荷,如图所示,设无穷远处为电势零点,则在球内离球心O 距离为r 的P 点处的电势为: (A )r q04πε; (B ))(041R Qrq+πε;(C )r Qq 04πε+; (D ))(041R qQ r q-+πε;参考:电势叠加原理。
[ B ] 2.在带电量为-Q 的点电荷A 的静电场中,将另一带电量为q 的点电荷B 从a 点移动到b ,a 、b 两点距离点电荷A 的距离分别为r 1和r 2,如图,则移动过程中电场力做功为:(A ))(210114r r Q --πε; (B ))(210114r r qQ-πε;(C ))(21114r r qQ --πε; (D ))(4120r r qQ --πε。
参考:电场力做功=势能的减小量。
A=W a -W b =q(U a -U b ) 。
[ C ] 3.某电场的电力线分布情况如图所示,一负电荷从M 点移到N 点,有人根据这个图做出以下几点结论,其中哪点是正确的?(A )电场强度E M <E N ; (B )电势U M <U N ; (C )电势能W M <W N ; (D )电场力的功A >0。
[ C ]4.一个未带电的空腔导体球壳内半径为R ,在腔内离球心距离为d (d <R )处,固定一电量为+q 的点电荷,用导线把球壳接地后,再把地线撤去,选无穷远处为电势零点,则球心O 处的点势为:(A )0; (B )d q04πε; (C )-R q04πε; (D ))(1140R dq-πε。
参考:如图,先用高斯定理可知导体内表面电荷为-q ,外表面无电荷(可分析)。
虽然内表面电荷分布不均,但到O 点的距离相同,故由电势叠加原理可得。
[ D ] ※5.在半径为R 的球的介质球心处有电荷+Q ,在球面上均匀分布电荷-Q ,则在球内外处的电势分别为:(A )内r Q πε4+,外r Q04πε-; (B )内r Qπε4+,0; 参考:电势叠加原理。
四川大学物理习题册第五章解答2
x2
r02
真空中的静电场(二)
第五章 真空中的静电场
s E1 2 0
取x轴正方向为正
E2
s 2 0
1
x
x2
r02
x 0,
E
E1
E2
s 2 0
s 2 0
1
x x2
r02
2 0
sx
x2 r02
x 0,
面上均匀带电,电荷面密度为s.试求通过小孔中心O并
与平面垂直的直线上各点的场强和电势.(提示:选O 点的电势为零).
解: 用割补法,该带电体=无限大平面(+s) +圆屏(-s)
由高斯定理可得,无限大平面场强
s E1 2 0 x 由场强叠加原理可得,圆屏场强
E2
s 2 0
1
x
为常数,则场强分布为 Ex=
,Ey=
.
U Ex x 2Ax
Ey
U y
2By
真空中的静Hale Waihona Puke 场(二)第五章 真空中的静电场
三、计算题 1. 如图,带电细线弯成半径为R的半圆形,
电荷线密度为=0sinq,式中0为一常数,q为半径R与
x轴所成的夹角.试求环心O处的电场强度.
解: 在细线取一线段元,由点电荷的场强公式有
d
E
dq
4 0R2
er
0
sinq Rdq 4 0R2
cosq i sinq j
y E
dE
0
sinq cosq i sin2 q j dq
四川大学物理习题册第五版答案汇编
5.g/2; 2 3v 2 /3g
三、计算题
1. 解 : (1)v x / t 6m/s,
(n = 0, 1, 2,…)
(2)v dx/dt 10t 9t2 ,
v(2) 16 / s,
(3)a dv/ dt 10 18t,
大学物理练习册解答
一.力学部分 质点运动学(一) 质点运动学(二) 牛顿运动定律(一) 牛顿运动定律(二) 动量与角动量(一) 动量与角动量(二) 功和能(一) 功和能(二) 刚体定轴转动(一) 刚体定轴转动(二) 狭义相对论(一) 狭义相对论(二) 二.热学部分 温度 气体分子运动论(一) 气体分子运动论(二) 热力学第一定律(一) 热力学第一定律(二) 热力学第二定律(一) 热力学第二定律(二)
A2 。
at
Q
M
质点位于图中的 Q 点。显然质点在椭圆形轨
a
an
oo
x
道上沿反时针方向运动。在 M 点,加速度 a 的切
向分量 at 如图所示。可见在该点切向加速度 at 的方向
与速度 v 的方向相反。所以,质点在通过 M 点速率减小。
4.
解:先求质点的位置
t 2s,
a
s 20 2 5 22 60(m)( 在大圆)
t
2dt
0
vy 0
dvy
t 36t 2dt
0
vx 2t
vy 12t3
v 2ti 12t3 j
dx vx dt
dx 2tdt
x
t
0 dx 0 2tdt
x t2
dy vy dt
dy 12t3dt
y
dy
成都四川师范大学附属实验学校高中物理选修三第五章《原子核》知识点复习
一、选择题1.贝可勒尔在120 年前首先发现了天然放射现象,如今原子核的放射性在众多领域中有着广泛应用。
下列属于核聚变的是( )A .23411120H H He n +→+ B .427301213130He Al P n +→+ C .14140671C N e -→+D .2351131103192053390U n I Y 2n +→++2.下面关于结合能和比结合能的说法中,正确的有( ) A .原子核拆解成核子放出的能量称为结合能B .比结合能越大的原子核越稳定,因此它的结合能也一定越大C .重核与中等质量原子核相比较,重核的结合能和比结合能都大D .中等质量原子核的结合能和比结合能均比轻核的要大 3.以下说法正确的是( )A .β衰变所释放的电子是原子核内的中子转变为质子时产生的B .23290Th 成为原子核20882Pb ,要经过8次α衰变和6次β衰变C .α、β、γ三种射线中,γ射线的穿透能力和电离能力都最强D .2812Mg 半衰期为21小时,则10个2812Mg 原子核,经过21小时后还有5个未衰变 4.下列说法正确的是( )A .23892U 衰变为22286Rn 要经过4次α衰变和2次β衰变B .衰变中产生的β射线实际上是原子的核外电子挣脱原子核的束缚而形成的C .查德威克发现了中子,并第一次实现了人工合成放射性同位素D .汤姆孙在研究阴极射线时发现了电子,并准确测出了电子的电荷量 5.下列说法中正确的是( )A .机械波和光有波动性,实物粒子不具有波动性B .用弧光灯发出紫外线照射锌板并发生光电效应后,锌板带正电C .由于核聚变需要很高的环境温度,21H 和31H 发生聚变过程中是需要从外界吸收能量的 D .构成物体的质量是守恒不变的 6.下列说法中正确的是( ) A .钍的半衰期为24天。
1g 钍23490Th 经过 120 天后还剩0.2g 钍B .一单色光照到某金属表面时,有光电子从金属表面逸出,延长入射光照射时间,光电子的最大初动能不会变化 C .放射性同位素23490Th 经α、β衰变会生成22286Rn ,其中经过了2次α衰变和 3 次β衰变D .大量处于n =4激发态的氢原子向低能级跃迁时,最多可产生4种不同频率的光子 7.钍23490Th 具有放射性,它能放出一个新的粒子而变为镤23491Pa ,同时伴随γ射线产生,其方程为2342349091Th Pa x →+,钍的半衰期为24天,则下列说法中正确的是( )A .此反应为钍核裂变,释放大量的核能,方程中的x 代表质子B .x 是钍核中的一个中子转化成一个质子时产生的C .γ射线是镤原子核外电子跃迁放出的高速粒子D .1g 钍23490Th 经过120天后还剩0.2g 钍8.关于天然放射线性质的说法正确的是( )A .γ射线就是中子流B .α射线有较强的穿透性C .电离本领最强的是γ射线D .β射线是高速电子流 9.有一钚的同位素23994Pu 核静止在匀强磁场中,该核沿与磁场垂直的方向放出x 粒子后,变成铀(U )的一个同位素原子核.铀核与x 粒子在该磁场中的旋转半径之比为1:46,则( )A .放出的x 粒子是42He B .放出的x 粒子是01e -C .该核反应是β衰变反应D .x 粒子与铀核在磁场中的旋转周期相等10.铀(23892U )经过α、β衰变后形成稳定的铅(20682Pb ),在衰变过程中,中子转变为质子的个数为( )A .6个B .14个C .22个D .32个11.本题用大写字母代表原子核,E 经α衰变边长F ,再经β衰变变成G ,再经α衰变成为H ,上述系列衰变可记为下式:E F G βαα→→→H ;另一系列衰变如下:P Q R S ββα→→→,已知P 是F 的同位素,则下列判断正确的是( )A .Q 是G 的同位素,R 是H 的同位素B .R 是G 的同位素,S 是H 的同位素C .R 是E 的同位素,S 是F 的同位素D .Q 是E 的同位素,R 是F 的同位素12.2020年11月27日0时41分,华龙一号核电5号机组首次并网成功,标志着我国正式进入核电技术先进国家行列。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由电势的叠加原理有,
o 1 2 3q 4 p 2 q 0 d e3 q4 p0 6 eq a32 3 p3 0 q a e
3q
A eQ oEd lQ o3 2p3Q 0a e qA exa
a
O
q
a
2q
真空中的静电场(二)
第五章 真空中的静电场
8.空间某一区域的电势分布为=Ax2+By2,其中A、B
5.已知某电场的电场线分布情况如图所示.现观察到 一负电荷从M点移到N点.有人根据这个图作出下列几 点结论,其中哪点是正确的?
(A) 电场强度EM<EN. (B) 电势M<N.
(C) 电势能WM<WN. (D) 电场力的功A>0.
电场线密处,电场强度大.
电场线由高电位指向低电位.
-q
E M E N , M N , M 0 N M
真空中的静电场(二)
第五章 真空中的静电场
2.在一个带有负电荷的均匀带电球外,放置一电偶极
子,其电矩 的方向如图所示.当电偶极子被释放后,该
电偶极子将
(A) 沿逆时针方向旋转直到电矩 p 沿径向指向球面
而停止.
(B)沿逆时针方向旋转至 p 沿径向指向球面,同时沿
电场线方向向着球面移动.
(C) 沿逆时针方向旋转至 p 沿径向指向球面,同时
3 1 3
q 1 5
(B)
4pe 0l
5
(D)
q
4pe 0l
5 1 5
D l
C l -q
B l A +q
E lF
pe pepe A qC FC FC F 4 q 0 lq 4 q 0 l 4 1-1q 0 题5 图l
真空中的静电场(二)
第五章 真空中的静电场
逆电场线方向远离球面移动.
(D) 沿顺时针方向旋转至 p 沿径向朝
+
外,同时沿电场线方向向着球面移动.
- p
真空中的静电场(二)
第五章 真空中的静电场
3. 如图,A和B为两个均匀带电球体,A带电荷+q,B
带电荷-q,作一与A同心的球面S为高斯面.则
(A) 通过S面的电场强度通量为零,S面上各点的场
Rr
真空中的静电场(二)
第五章 真空中的静电场
6. 如图,一无限大平面中部有一半径为r0的圆孔,设平
面上均匀带电,电荷面密度为s.试求通过小孔中心O并
与平面垂直的直线上各点的场强和电势.(提示:选O 点的电势为零).
r= Cr (r≤R,C为常量)r= 0 (r>R)
试求:(1) 带电球体的总电荷; (2) 球内、外各点的电场
强度; (3) 球内、外各点的电势.
解:
R
R
1)Qrd V r4pr2d r4pC3d r rpC4R
0
0
2) r≤R时:
r
Cr 4pr2dr
E4pr2 0 e0
E
Cr 2
4e0
er
r>R时:
pe pqeq q q d E 4 d 0 R 2 q e r0 s 40 iR R 2 n d co i ssijn
yE
Rdq
R
dE p4p00eRp 0siqncpo qissi2n qjdq siqncoqdsq0,si2nqdqp2
q
0
0
dE O
x
3-2 题图
E 0 j 8e0R
pe p pe pe E 缺 口 4d 0 R 2 2R q d 4d 0 R 2 82 q0 R d 3
RoBiblioteka d真空中的静电场(二)
第五章 真空中的静电场
7.图示为一边长均为a的等边三角形,其三个顶点分 别放置着电荷为q、2q、3q的三个正点电荷,若将一电 荷为Q的正点电荷从无穷远处移至三角形的中心O处, 则外力需作功A=__________.
真空中的静电场(二)
第五章 真空中的静电场
2. 如图,一无限长圆柱面,其面电荷密度为s=s0cosa, 式中a为半径R与x轴所夹的角,试求圆柱轴线上一点的
场强.
解: 无限长圆柱面可以分为很多无限长条形面元,由
高斯定理有 2 pR d h E sh e0 R a dd E s 2 p d a 0 es0 c 2 pa o 0 d a es
B
-q
真空中的静电场(二)
第五章 真空中的静电场
4. 如图,CDEF为一矩形,边长分别为l和2l.在DC延 长线上CA=l处的A点有点电荷+q,在CF的中点B点有点 电荷-q,若使单位正电荷从C点沿CDEF路径运动到F点, 则电场力所作的功等于:
(A) q 5 1
4pe 0l 5 l
(C)
q
4pe 0l
da
dE
E xdxE dc Ea o s 2 0 ps0c 2 p2 o a 0d ea s 2 s e0 0 E ydyE dsE ian 2 0 ps0s4 pi2 a 0 n eda0
EExiEy j2se00i
真空中的静电场(二)
第五章 真空中的静电场
3. 一半径为R的带电球体,其电荷体密度分布为
N
Wp qp AqMN0 1 -2 题 图
真空中的静电场(二)
二、填空题
第五章 真空中的静电场
1.如图,一半径为R的带有一缺口的细圆环,缺口长
度为d(d<<R).环上均匀带正电,总电量为q.则圆
心O处的场强大小E=
.场强方向为
.
指向缺口
E 缺 环 E 整 环 E 缺 口 0 E 缺 口 E 缺口
R
E4pr2 Cr4pr2dre0
0
E
CR4
4e0r2
er
真空中的静电场(二)
第五章 真空中的静电场
rR,
EC4e0r2 er
rR,
E4C e0rR42 er
3)p PEd l R rrC 44C ee002rr4 R d2dr R r4C 4 C ee0r04 R r4 R 2dr4rC 1R 3 Re2 0C3r
强为零。
(B) 通过S面的电场强度通量为q/e0,S面上场强的
大小为E=q/(4pe0r2).
(C) 通过S面的电场强度通量为(-q/e0),S面上场强
的大小为E=q/(4pe0r2).
(D) 通过S面的电场强度通量为q/e0,但S面上各点
的场强不能直接由高斯定理求出.
S
r
S面上各点场强与两带电体均有关. A +q
为常数,则场强分布为 Ex=
,Ey=
.
Ex
U2Ax x
Ey
U y
2By
真空中的静电场(二)
第五章 真空中的静电场
三、计算题 1. 如图,带电细线弯成半径为R的半圆形,
电荷线密度为=0sinq,式中0为一常数,q为半径R与
x轴所成的夹角.试求环心O处的电场强度.
解: 在细线取一线段元,由点电荷的场强公式有
