钢结构设计课程 第四章
钢结构稳定计算

E ——欧拉临界应力, A ——压杆的截面面积 i ——回转半径( i2=I/A) l----构件的几何长度
1、理想轴心受压构件弯曲屈曲临界力随抗弯刚度的增加和构件长度 的减小而增大; 2、当构件两端为其它支承情况时,通过杆件计算长度的方法考虑。
钢结构设计原理 Design Principles of Steel Structure
长度l0x=6m ,l0y=3m,翼缘钢板为火焰切割边,钢材为Q345, f=315N/mm2,截面无削弱,试计算该轴心受压构件的整体稳
定性。
y
-250×8
x
x
y -250×12
钢结构设计原理 Design Principles of Steel Structure
第四章 构件稳定
1、截面及构件几何性质计算
钢结构设计原理 Design Principles of Steel Structure
第四章 构件稳定
§4.2 实腹式轴心受压构件的截面设计
轴心受压构件设计时应满足强度、刚度、整体稳定和局部稳定的要 求。设计时为取得安全、经济的效果应遵循以下原则。
截面设计原则
1.等稳定性原则
杆件在两个主轴方向上的整体稳定承载力尽量接近。因此尽可能 使两个方向的稳定系数或长细比相等,以达到经济效果。
截面关于x轴和y轴都属于b类,
x y
x
f y 50.4 235
345 61.1 235
查表得: 0.802
N 2000 103 311 .9N / mm 2 f 315 N / mm 2 A 0.802 8000
满足整体稳定性要求。
其整体稳定承载力为:
Nc Af 0.802 8000 315 2020000 N 2020 kN
钢结构设计原理 第四章-轴心受力构件

因此,失稳时杆件的整个截面都处于加载的过 程中,应力-应变关系假定遵循同一个切线模量 Et,此时轴心受压杆件的屈曲临界力为:
N cr ,t
2 Et I
2 二、实际的轴心受压构件的受力性能
在钢结构中,实际的轴压杆与理想的直杆受力性能之间差别很大,实 际上,轴心受压杆的屈曲性能受许多因素影响,主要的影响因素有:
一、理想轴压构件的受力性能 理想轴压构件是指满足下列4个条件: o杆件本身绝对直杆; o材料均质且各向同性; o无荷载偏心且在荷载作用之前无初始应力; o杆端为两端铰接。 在轴心压力作用下,理想的压杆可能发生三种形式的屈曲: 弯曲屈曲、扭转屈曲、弯扭屈曲——见教科书P97图4–6 轴心受压构件具体以何种形式失稳,主要取决于截面的形式 和尺寸、杆的长度以及杆端的支撑条件。
l N 2 EI 对一无残余应力仅存在初弯曲的轴压杆,杆件中点截面边缘开始 式中 N l2 NE 屈服的条件为:
0
1
经过简化为:
N N vm v0 v0 fy v m v0 v 1 1 N NE A W N N v0 N E fy A W NE N
An—构件的净截面面积_
N fy r f R An
P94式4-2
(1)当轴力构件采用普通螺栓连接时 螺栓为并列布置:
n1 n2 n3
按最危险的截面Ⅰ-Ⅰ 计算,3个截面净截面面积 相同,但 Ⅰ-Ⅰ截面受力最大。
N n
Ⅰ-Ⅰ:N Ⅱ-Ⅱ:N-Nn1/n Ⅲ-Ⅲ:N-N(n1+n2)/n
Ⅰ Ⅱ Ⅲ
2 2
从上面两式我们可以看出,绕不同轴屈曲时,不仅临界力不同,且残余 应力对临界应力的影响程度也不同。因为k1,所以残余应力对弱轴的 影响比对强轴的影响严重的多。
钢结构—第四章课后答案

P1084.1解: 示意图要画焊缝承受的剪力V=F=270kN ;弯矩M=Fe=270⨯300=81kN.mI x =[0.8⨯(38-2⨯0.8)3]/12+[(15-2)⨯1⨯19.52]⨯2=13102cm 4=腹板A e =0.8⨯(38-2⨯0.8)=29.12 cm 2截面最大正应力σmax =M/W= 81⨯106⨯200/13102⨯104=123.65 N/mm 2≤f t w =185N/mm 2剪力全部由腹板承担τ=V/A w =270⨯103/2912≤=92.72 N/mm 2 =f v w =125N/mm 2腹板边缘处”1”的应力σ1=(M/W)(190/200)=123.65(190/200)=210.19=117.47腹板边缘处的折算应力应满足1.1w zs t f σ=≤=2≤1.1f t w =203.5N/mm 2焊缝连接部位满足要求4.2解:(1) 角钢与节点板的连接焊缝“A ”承受轴力N=420kN连接为不等边角钢长肢相连 题意是两侧焊肢背分配的力N 1=0.65 ⨯420=273 kN肢背分配的力N 2=0.35 ⨯420=147 kNh fmin =1.5(t max )1/2=1.5(10)1/2=4.74mmh fmax =1.2(t min )=1.2(6)=7.2mm取h f =6mm肢背需要的焊缝长度l w1=273⨯103/(2⨯0.7⨯6⨯160)+2⨯6=203.12+12=215.13mm肢尖需要的焊缝长度l w2=147⨯103/(2⨯0.7⨯6⨯160)+2⨯6=109.38+12=121.38mm端部绕角焊2h f 时,应加h f (书中未加)取肢背的焊缝长度l w1=220mm ;肢尖的焊缝长度l w2=125mm 。
l wmax =60h f =360mm ;l wmin =8h f =48mm ;焊缝“A ”满足要求4.3解:节点板与端板间的连接焊缝“B ”承受拉力N 对焊缝“B ”有偏心,焊缝“B ”承受拉力N=(1.5/1.8) ⨯420=350kN ;剪力V=(1/1.8) ⨯420=233.33 kN ;弯矩M=350⨯50=17.5 kN.mh fmin =1.5(t max )1/2=1.5(20)1/2=6.71mmh fmax =1.2(t min )=1.2(10)=12mm焊缝“B ”h f =7mm焊缝“B ”A 点的力最大焊缝“B ”承受的剪应力τ=233.33⨯103/(2⨯0.7⨯7⨯386)=61.68 N/mm 2焊缝“B ”承受的最大正应力σ=N/Ae+M/W=350⨯103/(2⨯0.7⨯7⨯386)+17.5⨯106⨯200/(2⨯0.7⨯7⨯3863/12)=92.52+71.91 =164.43 N/mm 2验算焊缝“B ”的强度=148.19 N/mm 2<f f w 焊缝“B ”满足要求。
钢结构第四章习题答案

λx = 6000 / 167.936 = 35.7, λ y = 3000 / 56.93 = 52.7 ,均小于 [λ ] = 150 ,刚度满足。
根据 λ
345 查表 4.5(b)和 4.5(c)得绕 X 轴受压稳定系数 φx = 0.9151 235
1
算得绕 Y 轴受压稳定系数 φy = 0.7569
iy:30.6786 mm,
则长细比 λx = 6000 / 197.676 = 30.4, λ y = 3000 / 30.6786 = 97.8 ,刚度满足。 根据 λ
345 查表 4.5(b)得 ϕx 235
= 0.9622,ϕ y = 0.5694
1300 × 103 = 191.9 MPa < f = 205 N / mm 2 ,整体稳定满足。 0.5694 × 11900 型钢截面壁厚较大,局部稳定一般均能满足,此处不再验算。
2
2 4
绕 y 轴名义回转半径: iy =
I y / A = 15849 132
91.20
= 13.2cm ,
绕 y 轴名义长细比: λy = l0y / iy = 7200 绕 y 轴换算长细比: λ0y = 查 ϕ y = 0.785
= 54.5 ,
λy2 + λ12 = 54.52 + 342 = 64.2 < [λ ] = 12
图 4.32 缀板受力
/2
缀板柱所受最大剪力:
V=
Af 85
fy 235
=
9120 × 215 235 = 23068 N 85 235 V1l1 23068 / 2 × 960 = = 42653N a (259.6)
作用于缀板一侧的剪力:
04---钢结构深化设计方案

第四章钢构造深化设计方案4.1 深化设计总体思路及组织管理体系4.1.1 深化设计总体思路4.1.2 深化设计工作总流程4.1.3 深化设计组织管理体系4.1.3.1 公司层面深化设计组织管理体系我司重大项目实行需编制《深化设计方案》,会审图纸后,由各专业副总工程师部门根据合同及施工图规定旳设计工作内容、范畴、工期、质量原则、服务规定,并结合我司旳实际生产设备及工艺技术方案,分别编制《设计配合及优化方案》、《现场安装配合求》、《工艺技术配合规定》、《详图设计方案》,汇編形成《深化设计方案》后报总工程师审批,由深化设计部贯彻执行。
4.1.3.2 项目层面深化设计组织管理体系深化设计是钢构造工程实行旳源头,针对本工程地上钢构造旳深化设计,我司将从各专业技术线抽调骨干力量组建本工程深化设计部,由深化设计部长亲自兼任深化设计负责人,对设计方案编制、审批、执行等环节进行全过程管控,为工程旳顺利实行打下坚实旳基础。
图:深化设计组织架构4.1.3.3 岗位职责4.1.3.4 人员配备我公司为本工程旳深化设计组织了精良旳深化设计队伍,项目深化设计总负责人为专家级高工职称,从事专业工作年限46年;设计负责人、详图设计负责人、工艺负责人均为本科以上学历,从事专业工作年限均在6年以上;成员基本都为本科以上学历,深化设计工作年限基本在6-以上,为图纸深化设计旳质量提供了可靠旳人力保证。
根据本工程旳重要性,对本工程旳深化设计人员投入进行如下安排。
学历比例图工作年限比例图职称比例图4.1.3.5 硬件配备(一)电脑硬件配备考虑到诸暨市都市建设投资发展有限公司-剧院A、B区,地下室建设工程(钢构造制作与安装工程)重要限度,我公司配备了1台联想(Lenovo)锋行K330至尊版台式电脑作为本工程深化设计服务器,40台联想(Lenovo)扬天T3900d台式电脑作为本工程深化设计一般PC,为图纸深化设计旳质量提供了可靠旳电脑硬件保证,保证该工程深化设计旳圆满完毕。
钢结构设计原理第四章

第 一 T 类 形 第 二 类
1 fc bf x f y As M 1 fc bf x ( h0 x / 2)
1 fc ( bf b )hf 1 f c bx f y As M 1 fc ( bf b )hf ( h0 hf / 2)
M d —— 弯矩组合设计值;
目 录
f cd —— 混凝土轴心抗压强度设计值; f sd —— 钢筋抗拉强度设计值。
昆明理工大学建工学院
混凝土结构设计原理
4.5 公路桥涵工程中受弯构件正截面承载力计算
3、基本公式的适用条件: ⑴最小配筋率限制条件
As min bh
min 为最小配筋率, 0.15% ; 38 ftd / fsd (%)
目 录
5、在实际工程中,受弯构件应设计成适筋截面
昆明理工大学建工学院
混凝土结构设计原理
4.5 公路桥涵工程中受弯构件正截面承载力计算
建工与桥涵工程受弯构件承载力计公式比较
截面 类型 单筋 矩形
建
1 fc bx f y As
工
桥
fcd bx fsd As
涵
M 1 fc bx ( h0 x / 2)
0 M d fcd bx ( h0
x ) 2
目 录
昆明理工大学建工学院
混凝土结构设计原理
4.5 公路桥涵工程中受弯构件正截面承载力计算
计算公式:
X 0
M 0
f cd bx f sd As
x 0 M d fcd bx ( h0 ) 2
0 —— 桥梁结构的重要性系数; 特大桥、重要大桥 0 1.1 大桥、中桥、重要小桥 0 1.0 小桥、涵洞 0 0.9
第4章钢结构的连接-角焊缝
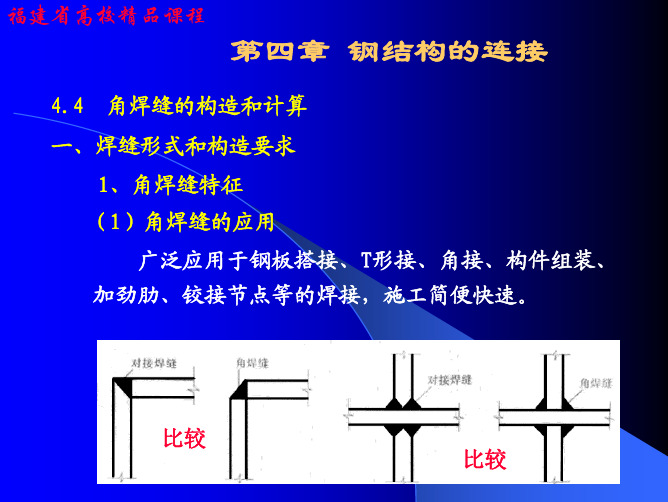
侧面角焊缝应力分布
福建省高校精品课程
第四章
钢结构的连接
B、正面角焊缝-端焊缝 作用力与焊缝方向垂直,焊缝应力复杂,焊缝根 部应力集中严重,易引起开裂破坏。
正面角焊缝应力分布
福建省高校精品课程
第四章
钢结构的连接
2、角焊缝的构造要求 (1)焊缝尺寸 焊脚尺寸hf(焊缝高度)-焊缝直边尺寸,设计标注的尺寸 有效厚度he-焊缝破坏面尺寸(45°垂直面焊缝高度) 焊缝的计算长度lw-有效受力长度,每条连续焊缝取实际 几何长度减去2hf 。
12
第四章 钢结构的连接
解: 采用如图所示的三面围焊
福建省高校精品课程
原lw=100-5 现lw=100-10
1、焊缝有效截面的几何特性 焊缝有效截面的形心位置
福建省高校精品课程
第四章 钢结构的连接
2、焊缝强度验算(A点)
⊥ ∥ ⊥
福建省高校精品课程
第四章 钢结构的连接
工程算例2: 试设计角钢与连接板的连接角焊缝。轴心力设计值N= 830kN(静力荷载)。角钢为2L125×80×10,长肢相连, 连接板厚度t=12mm,钢材Q235,手工焊,焊条E43型。
⎛σ +σ σ zs = ⎜ ⎜ βf ⎝
验算公式:
⎞ T V 2 w ⎟ + (τ Ax + τ Ax ) ≤ f f ⎟ ⎠
2
福建省高校精品课程
第四章 钢结构的连接
工程算例1: 试设计图所示厚度为12mm的支托板和柱搭接接头的角 焊缝。作用力设计值F=100kN(静力荷载),至柱翼缘边 缘的距离为200mm。钢材Q235,焊条E43系列。
T ⋅r τA = J
J=Ix+Iy
9-第四章-钢结构的延性设计

4 延性设计方法
框架结构的整体位移延性系数
控 制
构件截面的曲率延性系数
必须强迫结构按预定次序和位置出现塑 性铰以使结构按预定的模式破坏
钢结构延性设计的基本概念
钢结构延性设计的基础
截面、构件、结构(包括节点)的塑性分析
Ductile Design of Steel Structures
如何防止较脆的且只能承受有 限变形的非结构构件产生破坏
必须限制结构的弹性位移, 如层间位移等
钢结构延性设计的基本概念
一、结构抗震设计的三准则
2 中震可修
强度准则
对于不常发生的中等地震,允 许有一些非结构构件受到损坏。
但必须避免结构的某些不为由于大的非弹性 变形而损坏,以免昂贵而又困难的修复工作
在地震动荷载下总的结 构反应必须是弹性的
当抗震成为人们关注的热点后,研究方向主要朝两个方向发展:
一、建立更加完善的构件模型,把精力主要放在 构件与结构的稳定性上,当支撑设置适当,失稳 与塑性可能同时发生。
二、发展设计方法和构造措施,以使结构在地震荷载
下要构发造生措循施环保非证弹在性延此变性之形前和十不能分发保生持重失稳要稳定破的坏塑。性行为。需
钢结构延性设计的基本概念
三、结构的延性
* 延性概念的发展
根据上述概念,过去的观点一直认为:
钢材是目前建筑材料延性最好的,因此,在钢结构设
计中,想当然地利用了钢材的塑性变形能力;
但是,事实材表料明:的仅延仅材性料的良结好构延的性并延不性能保证结
构获得应具备的延性。
Material ductility alone is not a guarantee of ductile structural when steel components and connections can fail in brittle manner
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、稳定问题的整体性(稳定性不能就其本身孤立地分析,
4.2 轴心受压构件的整体稳定性
4.2.1 纵向残余应力对轴心受压构件整体稳定性的影响
1. 残余应力的测量及其分布
A、产生的原因
①焊接时的不均匀加热和冷却;
②型钢热扎后的不均匀冷却;
③板边缘经火焰切割后的热塑性收缩;
④构件冷校正后产生的塑性变形。
当σ >fp=fy-σ
rc时,截面出现塑性区,应力分布
如图4.7(d)。柱屈曲可能的弯曲形式有两种:沿强
轴(x轴)和沿弱轴(y轴),因此,临界应力为:
对x x轴屈曲时:
crx
2 E I ex 2 E 2t ( kb)h 2 4 2 E 2 2 2 k 2 x I x x 2tbh 4 x
4.1.4 稳定问题的多样性、整体性和相关性
1、稳定问题的多样性(结构所有受压部位在设计中都存 在处理稳定的问题,弯曲屈曲为轴心受压构件常见失稳
形式,但并非惟一形式,还存在扭转屈曲或弯扭屈曲等
失稳形式); 应考虑相邻构件对它的约束作用); 3、稳定问题的相关性(不同失稳模式的耦合作用表明稳 定具有相关性,弯曲和扭转的相关屈曲,局部和整体的 屈曲)。
一、简化方法: 1)切线模量理论 2)折算模量理论
二、数值方法: 1)数值积分法 2)有限单元法
4.1.3 稳定极限承载能力
一、切线模量理论: 在非弹性应力状态,应当取应力-应变关系曲线上 相应应力点的切线斜率(切线模量)代替线弹性模量。
二、折算模量理论(双模量理论): 荷载达到临界值后杆件即弯曲,这将导致截面上一 部分加压,一部分减压。减压区应当采用弹性模量,整 个截面的非弹性状态以折算模量反映。
程度时丧失稳定的能力,属于这一类。
4.1.1 失稳的类别
二、按屈曲后性能分类:
1)稳定分岔屈曲
稳定分岔屈曲
4.1.1 失稳的类别
2)不稳定分岔屈曲
不稳定分岔屈曲
4.1.1 失稳的类别
3)跃越屈曲
跃越屈曲
4.1.1 失稳的类别
第I类稳定:分岔屈曲--稳定分岔屈曲 第I类稳定:分岔屈曲--不稳定分岔屈曲 屈曲的特点: 屈曲后荷载显著降低方可保持平衡(有限干扰屈曲); 缺陷敏感性。 第II类稳定:极值点失稳 屈曲的特点: 偏心压杆及非完善构件;失稳时一般已进入塑性状态; 破坏的本质是 考虑双重非线性后的强度问题。
残余应力对短柱段的影响
4.2.1 纵向残余应力对轴心受压构件整体稳定性的影响 由于残余应力的存在导致比例极限 f p 降为:
f p f y rc
rc —截面中绝对值最大的残余应 y rc
或 p E f p 时,可采用欧拉公式计算临
第四章 单个构件的承载能力——稳定性
第一节
稳定问题的一般特点 第二节 轴心受压构件的整体稳定性 第三节 实腹式和格构式柱的截面选择计算 第四节 受弯构件的弯扭失稳 第五节 压弯构件的面内和面外稳定性及截面 选择计算 第六节 板件的稳定和屈曲后强度的利用
主要内容:
稳定问题的一般特点
轴心受力构件的整体稳定性 实腹式和格构式柱的截面选择计算 受弯构件的弯扭失稳 压弯构件的面内和面外稳定性及截面选择计算 板件的稳定和屈曲后强度的利用
重点:
轴心受力构件、梁及拉弯、压弯构件的整体稳定计算。
4.1
稳定问题的一般特点
4.1.1 失稳的类别
一、传统的分类: 1) 分支点(分岔)失稳:特点是在临界状态时, 结构(构件)从初始的平衡位形突变到与其临近的 另一个平衡位形,表现出平衡位形的分岔现象。包
4.1.2 一阶和二阶分析
二者的区别: 一阶分析:认为结构(构件)的变
形比起其几何尺寸来说很小,在分析 结构(构件)内力时,忽略变形的影 响。 二阶分析:考虑结构(构件)变形 对内力分析的影响。
注意:公式4-4的推导;
同时承受纵横荷载的构件
4.1.3 稳定极限承载能力
有两种方法可以用来确定构件的稳定极限承载能力:
4.2.1 纵向残余应力对轴心受压构件整体稳定性的影响 B、残余应力的测量方法:锯割法
锯割法测定残余应力的顺序
4.2.1 纵向残余应力对轴心受压构件整体稳定性的影响 实测的残余应力分布较复杂而离散,分析时常
采用其简化分布图(计算简图):
典型截面的残余应力
4.2.1 纵向残余应力对轴心受压构件整体稳定性的影响 2.从短柱段看残余应力对压杆的影响 以双轴对称工字型钢短柱为例:
界应力:
EI 2 EI NE 2 2 l l
2
E cr 2
2
4.2.1 纵向残余应力对轴心受压构件整体稳定性的影响 当 N A f p f y rc 或 p E f p 时,截面出现塑性区,由切线模量理论知,柱屈
曲时,截面不出现卸载区,塑性区应力不变而变形
第III种失稳类型:跃越失稳
屈曲的特点: 发生屈曲后,经历一个大变形过程到达一个新的强度回升的路径(但
是:此 时结构一般不能正常使用)。
4.1.1 失稳的类别
缺陷的存在使得结构不再呈分岔失稳形式; 缺陷的存在并不改变它们屈曲后的性态:在 稳定分岔屈曲中极限荷载仍高于临界荷载; 在不稳定分岔屈曲中,缺陷导致极限荷载大 幅度跌落。
增加,微弯时仅考虑截面的弹性区抵抗弯矩,因此
,用截面弹性区的惯性矩Ie代替全截面惯性矩I,即
得柱的临界应力:
2 EI e 2 EI I e N cr 2 2 l l I
2 E Ie cr 2 I
4.2.1 纵向残余应力对轴心受压构件整体稳定性的影响 仍以忽略腹板的双轴对称工字钢柱为例,推求临 界应力:
括稳定分岔和不稳定分岔。第一类稳定问题或者具
有平衡分岔的稳定问题。完善直杆轴心受压时的屈
曲和完善平板中面受压时的屈曲都属于这一类。
4.1
稳定问题的一般特点
4.1.1 失稳的类别
一、传统的分类: 2) 极值点失稳:特点是没有平衡位形的分岔,临界状
态表现为结构(构件)不能继续承受荷载增量。
由建筑钢材做成的偏心受压构件,在塑性发展到一定
