6工程力学材料力学答案
(完整版)材料力学课后习题答案
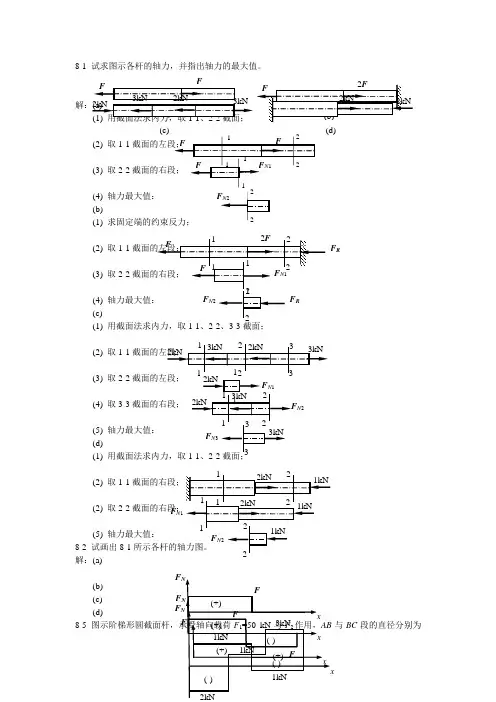
8-1 试求图示各杆的轴力，并指出轴力的最大值。
(2) 取1-1(3) 取2-2(4) 轴力最大值： (b)(1) 求固定端的约束反力； (2) 取1-1(3) 取2-2(4) (c)(1) 用截面法求内力，取1-1、2-2、3-3截面；(2) 取1-1(3) 取2-2 (4) 取3-3截面的右段；(5) 轴力最大值： (d)(1) 用截面法求内力，取1-1、(2) 取1-1(2) 取2-2(5) 轴力最大值： 8-2 试画出8-1解：(a) (b) (c) (d) 8-5与BC 段的直径分别为(c) (d)F RN 2F N 3 F N 1F F Fd 1=20 mm 和d 2=30 mm ，如欲使AB 与BC 段横截面上的正应力相同，试求载荷F 2之值。
解：(1) 用截面法求出(2) 求1-1、2-28-6 题8-5段的直径d 1=40 mm ，如欲使AB 与BC 段横截面上的正应力相同，试求BC 段的直径。
解：(1)用截面法求出1-1、2-2截面的轴力；(2) 求1-1、2-2截面的正应力，利用正应力相同；8-7 图示木杆，承受轴向载荷F =10 kN 作用，杆的横截面面积A =1000 mm 2，粘接面的方位角θ= 450，试计算该截面上的正应力与切应力，并画出应力的方向。
解：(1) (2) 8-14 2=20 mm ，两杆F =80 kN 作用，试校核桁架的强度。
解：(1) 对节点A(2) 列平衡方程 解得： (2) 8-15 图示桁架，杆1A 处承受铅直方向的载荷F 作用，F =50 kN ，钢的许用应力[σS ] =160 MPa ，木的许用应力[σW ] =10 MPa 。
解：(1) 对节点A (2) 84 mm 。
8-16 题8-14解：(1) 由8-14得到的关系；(2) 取[F ]=97.1 kN 。
8-18 图示阶梯形杆A 2=100 mm 2，E =200GPa ，试计算杆AC 的轴向变形 解：(1) (2) AC 8-22 图示桁架，杆1与杆2的横截面面积与材料均相同，在节点A 处承受载荷F 作用。
工程力学--材料力学(北京科大、东北大学版)第4版第六章习题答案
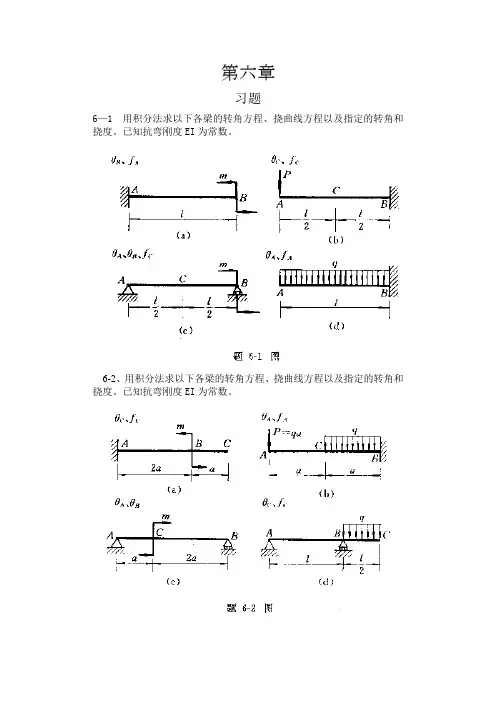
第六章习题6—1 用积分法求以下各梁的转角方程、挠曲线方程以及指定的转角和挠度。
已知抗弯刚度EI为常数。
6-2、用积分法求以下各梁的转角方程、挠曲线方程以及指定的转角和挠度。
已知抗弯刚度EI为常数。
6-3、用叠加法求图示各梁中指定截面的挠度和转角。
已知梁的抗弯刚读EI为常数。
6-4阶梯形悬臂梁如图所示，AC段的惯性矩为CB段的二倍。
用积分法求B端的转角以及挠度。
6-5一齿轮轴受力如图所示。
已知：a=100mm,b=200mm,c=150mm,l=300mm;材料的弹性模量E=210Pa;轴在轴承处的许用转角[]=0.005rad。
近似的设全轴的直径均为d=60mm,试校核轴的刚度。
回答：6-6一跨度为4m的简支梁，受均布载荷q=10Kn/m,集中载荷P=20Kn,梁由两个槽钢组成。
设材料的许用应力[]=160Ma,梁的许用挠度[]=。
试选择槽钢的号码，并校核其刚度。
梁的自重忽略不计。
6-7两端简支的输气管道，外径D=114mm。
壁厚=4mm,单位长度重量q=106N/m,材料的弹性模量E=210Gpa。
设管道的许用挠度试确定管道的最大跨度。
6-8 45a号工字钢的简支梁，跨长l=10m,材料的弹性模量E-210Gpa。
若梁的最大挠度不得超过，求梁所能承受的布满全梁的最大均布载荷q。
6-9一直角拐如图所示，AB段横截面为圆形，BC 段为矩形，A段固定，B段为滑动轴承。
C端作用一集中力P=60N。
有关尺寸如图所示。
材料的弹性模量E=210Gpa,剪切弹性模量G=0.4E。
试求C端的挠度。
提示：由于A端固定，B端为滑动轴承，所以BC杆可饶AB杆的轴线转动。
C端挠度由二部分组成；（1）把BC杆当作悬臂梁，受集中力P作用于C端产生的挠度，；（2）AB杆受扭转在C锻又产生了挠度，。
最后，可得C端的挠度6-10、以弹性元件作为测力装置的实验如图所示，通过测量BC梁中点的挠度来确定卡头A处作用的力P，已知,梁截面宽b=60mm,高h=40mm,材料的弹性模量E=210Gpa。
工程力学材料力学部分习题
工程力学——材料力学部分习题第六章变形体力学基础是非判断题1．材料力学是研究构件承载能力的一门学科。
（）2．材料力学的任务是尽可能使构件安全地工作。
（）3．材料力学主要研究弹性范围内的小变形情况。
（）4．因为构件是变形固体，在研究构件的平衡时，应按变形后的尺寸进行计算。
（）5．外力就是构件所承受的载荷。
（）6．材料力学研究的内力是构件各部分间的相互作用力。
（）7．用截面法求内力时，可以保留截开后构件的任一部分进行平衡计算。
( )8．压强是构件表面的正应力。
（）9．应力是横截面上的平均内力。
（）10．材料力学只研究因构件变形引起的位移。
（）11．线应变是构件中单位长度的变形量。
（）12．构件内一点处各方向线应变均相等。
（）13．切应变是变形后构件中任意两根微线段夹角角度的变化量。
（）14．构件上的某一点，若任何方向都无应变，则该点无位移。
（）15．材料力学只限于研究等截面直杆。
（）16．杆件的基本变形只是拉（压）、剪、扭、和弯四种，如果还有另一种变形，必定是这四种变形的某种组合。
（）填空题17．构件的承载能力包括____________、___________和____________三个方面；根据材料的主要性能作如下三个基本假设___________、___________、____________。
18．构件的强度是指___________________________________________________________；刚度是指_________________________________________________________________________；稳定性是指_______________________________________________________________________。
19．在材料力学中分析杆件内力的基本方法是__________，步骤是_____________________。
工程力学材料力学考研试题及答案
工程力学材料力学考研试题及答案### 工程力学材料力学考研试题及答案#### 一、选择题1. 下列哪项不是材料力学研究的范畴？（）A. 材料的应力-应变关系B. 材料的疲劳寿命C. 材料的热膨胀系数D. 材料的弹性模量答案： C2. 根据胡克定律，当材料受到正应力时，其应变与应力的关系是（）A. 正比B. 反比C. 无关D. 非线性答案： A3. 材料力学中的“屈服强度”指的是（）A. 材料开始发生塑性变形的应力B. 材料发生断裂的应力C. 材料的弹性模量D. 材料的硬度答案： A#### 二、简答题1. 简述材料力学中“弹性模量”和“剪切模量”的区别。
答案：弹性模量，也称为杨氏模量，是指材料在受到正应力作用下，其应变与应力之间的比值。
它反映了材料抵抗线性弹性变形的能力。
剪切模量，又称为刚度模量，是指材料在受到剪切应力作用下，其剪切应变与剪切应力之间的比值。
它描述了材料抵抗剪切变形的能力。
2. 解释什么是材料的“疲劳寿命”并简述其影响因素。
答案：疲劳寿命是指材料在重复或循环加载条件下，从开始加载到发生疲劳断裂的时间或循环次数。
影响疲劳寿命的因素包括应力水平、加载频率、材料的微观结构、表面处理和环境条件等。
#### 三、计算题1. 某材料的弹性模量为200 GPa，若该材料的一根长直杆受到100 MPa的正应力，求其应变。
答案：根据胡克定律，应变 \( \epsilon \) 与应力 \( \sigma \) 的关系为 \( \epsilon = \frac{\sigma}{E} \)，其中 \( E \) 是弹性模量。
代入数值得：\[ \epsilon = \frac{100 \times 10^6 \text{ Pa}}{200 \times 10^9 \text{ Pa}} = 5 \times 10^{-4} \]2. 已知某材料的屈服强度为250 MPa，若该材料的一根横截面积为50 mm²的杆件在受到2500 N的拉力作用下，判断是否会发生屈服。
工程力学习题及答案
1.力在平面上的投影（矢量）与力在坐标轴上的投影(代数量)均为代数量。
正确2.力对物体的作用是不会在产生外效应的同时产生内效应。
错误3.在静力学中，将受力物体视为刚体（D）A. 没有特别必要的理由B. 是因为物体本身就是刚体C. 是因为自然界中的物体都是刚体D. 是为了简化以便研究分析。
4.力在垂直坐标轴上的投影的绝对值与该力的正交分力大小一定相等。
正确5.轴力图、扭矩图是内力图，弯矩图是外力图。
错误6.胡克定律表明，在材料的弹性变形范围内，应力和应变（A）A .成正比B .相等C .互为倒数 D. 成反比7.材料力学的主要研究对象是（B）A.刚体B.等直杆C.静平衡物体D.弹性体8.通常工程中，不允许构件发生（A）变形A.塑性B.弹性C.任何D.小9.圆轴扭转时，同一圆周上的切应力大小（A）A.全相同B.全不同C.部分相同D.部分不同10.杆件两端受到等值、反向且共线的两个外力作用时，一定产生轴向拉伸或压缩变形。
正确1.材料力学的主要研究对象是（B）A.刚体B.等直杆C.静平衡物体D.弹性体2.构件的许用应力是保证构件安全工作的（B）A.最低工作应力B.最高工作应力C.平均工作应力D.极限工作应力3.低碳钢等塑性材料的极限应力是材料的（A）A.屈服极限B.许用应力C.强度极限D.比例极限4.一个力作平行移动后，新点的附加力偶矩一定（B）A.存在B.存在且与平移距离有关C.不存在D.存在且与平移距离无关5.力矩不为零的条件是（A）A.作用力和力臂均不为零B.作用力和力臂均为零C. 作用力不为零D.力臂不为零6.构件抵抗变形的能力称为（B）A.强度B.刚度C.稳定性D.弹性7.工程实际计算中，认为切应力在构件的剪切面上分布不均匀。
错误8.力在垂直坐标轴上的投影的绝对值与该力的正交分力大小一定相等。
正确9.圆轴扭转时，横截面上的正应力与截面直径成正比。
错误10.扭转时的内力是弯矩。
错误1.各力作用线互相平行的力系，都是平面平行力系。
材料力学全部习题解答
弹性模量
b
E 2 2 0 M P a 2 2 0 1 0 9P a 2 2 0 G P a 0 .1 0 0 0
s
屈服极限 s 240MPa
强度极限 b 445MPa
伸长率 ll010000m ax2800
由于 280;故0该50 材0料属于塑性材料;
13
解：1由图得
弹性模量 E0 3.550110063700GPa
A x l10.938m m
节点A铅直位移
A ytan 4 l150co sl4 2503.589m m
23
解：1 建立平衡方程 由平衡方程
MB 0 FN1aFN22aF2a
FN 2 FN1
得： FN12F1N22F
l1
l2
2.建立补充方程
3 强度计算 联立方程1和方
程（2）;得
从变形图中可以看出;变形几何关
l
l0
断面收缩率
AAA110000d22d22d2121000065.1900
由于 2故.4 属6 % 于 塑5 性% 材料;
15
解：杆件上的正应力为
F A
4F D2 -d2
材料的许用应力为
要求
s
ns
由此得
D 4Fns d2 19.87mm
s
取杆的外径为
D19.87m m
16
FN1 FN 2
Iz= I（ za） I（ zR ） =1 a2 4
2R4 a4 R 4 =
64 12 4
27
Z
解 a沿截面顶端建立坐标轴z;，y轴不变; 图示截面对z，轴的形心及惯性矩为
0 .1
0 .5
y d A 0 .3 5 y d y2 0 .0 5 y d y
工程力学课后习题答案（静力学和材料力学）
1 一 3 试画出图示各构件的受力图。
F
D
习题 1－3 图
C
F
D
C
A
B
FA
FB
习题 1－3a 解 1 图
F Ax
A
B
FAy
FB
习题 1－3a 解 2 图
C
BF
B
D
FB
FD
C
A
FA 习题 1－3b 解 2 图
W
FAx
FAy
习题 1－3c 解图
F
A
A
F
α
B C
FA
D
FAFD 习题 1－3d 解 2 图
FB2 x
B
FDy
C FB2 y
F Dx D
W
习题 1－4b 解 2 图
F'B1
B
F'B2x
F'B2 y F1
A B
F'B2x
习题 1－4c 解 1 图
F1 F'B2 y
FDx D FDy
F'B2x B
C
F'B2 y
W
F'B2 B
习题 1－4c 解 2 图
习题 1－4b 解 3 图
FA
A
B
F B1
习题 1－4d 解 1 图
可推出图（b）中 FAB = 10FDB = 100F = 80 kN。
FED αD
FDB FD′ B
FCB
α
B
F 习题 1－12 解 1 图
F AB 习题 1－12 解 2 图
1—13 杆 AB 及其两端滚子的整体重心在 G 点，滚子搁置在倾斜的光滑刚性平面上，如
工程力学材料力学部分课后习题详解
2-1 求下列结构中指定杆内的应力。
已知(a)图中杆的横截面面积A 1=A 2=1150mm 2； 解：（1）分析整体，作示力图∑=0)(i BF M：CB 041088=××−×A F AF N1F N2(c)40kN A F =（2）取部分分析，示力图见（b ）∑=0)(i CF M：02442.22=×+×−×q F F A N2(404402)36.36kN 2.2N F ×−×==3262236.361031.62MPa 115010N F A σ−×===×（3）分析铰E ，示力图见（c ）∑=0ix F ：0sin 12=−βN N F F1240.65kN N N F F == 3161137.961035.3MPa 115010N F A σ−×===×2-2 求下列各杆内的最大正应力。
（3）图(c)为变截面拉杆，上段AB 的横截面积为40mm 2，下段BC 的横截面积为30mm 2，杆材料的ρg =78kN/m 3。
解：1.作轴力图，BC 段最大轴力在B 处6N 120.530107812.0kN B F −=+×××AB 段最大轴力在A 处6N 12(0.5300.540)107812.0kN A F −=+×+×××3N 2612.010400MPa 30mm3010B B F σ−−×===× 3N 2612.010300MPa 40mm 4010AA F σ−−×===×杆件最大正应力为400MPa ，发生在B 截面。
EDF BF AF CxF N2(b)A120B120F NC2-4 一直径为15mm ，标距为200mm 的合金钢杆，比例极限内进行拉伸试验，当轴向荷载从零缓慢地增加58.4kN 时，杆伸长了0.9mm ，直径缩小了0.022mm ，确定材料的弹性模量E 、泊松比µ。
工程力学材料力学部分习题答案
b2.9 题图2.9所示中段开槽的杆件，两端受轴向载荷P 的作用，试计算截面1-1和2-2上的应力。
已知：P = 140kN ，b = 200mm ，b 0 = 100mm ，t = 4mm 。
题图2.9解：(1) 计算杆的轴力kN 14021===P N N(2) 计算横截面的面积21m m 8004200=⨯=⨯=t b A202mm 4004)100200()(=⨯-=⨯-=t b b A(3) 计算正应力MPa 1758001000140111=⨯==A N σ MPa 3504001000140222=⨯==A N σ (注：本题的目的是说明在一段轴力相同的杆件内，横截面面积小的截面为该段的危险截面)2.10 横截面面积A=2cm 2的杆受轴向拉伸，力P=10kN ，求其法线与轴向成30°的与45°斜截面上的应力ασ与ατ，并问m ax τ发生在哪一个截面？ 解：(1) 计算杆的轴力kN 10==P N(2) 计算横截面上的正应力MPa 501002100010=⨯⨯==A N σ(3) 计算斜截面上的应力MPa 5.37235030cos 2230=⎪⎪⎭⎫ ⎝⎛⨯==σσMPa 6.2123250)302sin(230=⨯=⨯=στ MPa 25225045cos 2245=⎪⎪⎭⎫⎝⎛⨯==σσMPa 251250)452sin(245=⨯=⨯=στ (4) m ax τ发生的截面 ∵0)2cos(==ασαταd d 取得极值 ∴0)2cos(=α 因此：22πα=， 454==πα故：m ax τ发生在其法线与轴向成45°的截面上。
（注：本题的结果告诉我们，如果拉压杆处横截面的正应力，就可以计算该处任意方向截面的正应力和剪应力。
对于拉压杆而言，最大剪应力发生在其法线与轴向成45°的截面上，最大正应力发生在横截面上，横截面上剪应力为零）2.17 题图2.17所示阶梯直杆AC ，P =10kN ，l 1=l 2=400mm ，A 1=2A 2=100mm 2，E =200GPa 。
工程力学复习题(材料力学部分)
工程力学作业（材料力学）第一、二章 拉伸、压缩与剪切一、填空题1、铸铁压缩试件，破坏是在 截面发生剪切错动，是由于引起的。
2、a 、b 、c 三种材料的应力－应变曲线如图所示。
其中强度最高的材料 是 ，弹性模量最小的材料是 ，塑性最好的材料是 。
3、图示结构中杆1和杆2的截面面积和拉压许用应力均相同，设载荷P 可在刚性梁AD 上移动。
结构的许可载荷[ P ]是根据P 作用于 点处确定的。
4、五根抗拉刚度EA 相同的直杆铰接成如图所示之边长为a 的正方形结构，a a 1 2 P C D BA OσεabcA 、B 两处受力 P 作用。
若各杆均为小变形，则A 、B 两点的相对位移∆AB ＝ 。
5、图示结构中。
若1、2两杆的EA 相同，则节点A 的竖向位移∆Ay ＝ ，水平位移为∆Ax ＝ 。
6、铆接头的连接板厚度t ＝ d ，则铆钉的切应力τ为 ， 挤压应力σ bs 为 。
二、选择题P / 2 P / 21、当低碳钢试件的试验应力σ ＝ σs 时，试件将：(A) 完全失去承载能力； (B) 破断；(C) 发生局部颈缩现象； (D) 产生很大的塑性变形。
正确答案是 。
2、图示木接头，水平杆与斜杆成α角，其挤压面积为A bs 为： （A ）b h ； （B ）b h tan α ； （C ）b h / cos α ； （D ）b h /（cos α sin α）。
正确答案是 。
3、图示铆钉联接，铆钉的挤压应力为：（A ）2 P / ( π d 2 )； （B ）P / (2 d t )； （C ）P / (2 b t )； （D ）4 P / ( π d 2 )。
正确答案是 。
4、等截面直杆受轴向拉力P 作用而产生弹性伸长，已知杆长为l ，截面积为A ，材料弹性模量为E ，泊松比为ν，拉伸理论告诉我们，影响该杆横截面上应力的因素是：（A ）E 、ν、P ； （B ）l 、A 、P ； （C ）l 、A 、E 、ν、P ； （D ）A 、P 。
工程力学(静力学和材料力学)课后习题答案
工程力学（静力学与材料力学）习题详细解答(第1章)(a) (b) 习题1－1图第1章 静力学基础1一1 图a 和b 所示分别为正交坐标系11y Ox 与斜交坐标系22y Ox 。
试将同一个力F 分别在两中坐标系中分解和投影，比较两种情形下所得的分力与投影。
解：图（a ）：11 sin cos j i F ααF F +=分力：11 cos i F αF x = ， 11 sin j F αF y = 投影：αcos 1F F x = ， αsin 1F F y =讨论：ϕ= 90°时，投影与分力的模相等；分力是矢量，投影是代数量。
图（b ）： 分力：22)tan sin cos (i F ϕααF F x −= ， 22sin sin j F ϕαF y =投影：αcos 2F F x = ， )cos(2αϕ−=F F y讨论：ϕ≠90°时，投影与分量的模不等。
1一2 试画出图a 和b 两种情形下各构件的受力图，并加以比较。
比较：解a 图与解b 图，两种情形下受力不同，二者的F R D 值大小也不同。
DR习题1－2b 解图DR习题1－2a 解2图C习题1－2a 解1图(a) (b)习题1－2图1一3 试画出图示各构件的受力图。
习题1－3图B F 习题1－3a 解2图 B习题1－3a 解1图习题1－3b 解1图F Ay Ax 习题1－3c 解图 A习题1－3b 解2图习题1－3d 解1图习题1－3e 解1图习题1－3e 解2图1－4 图a 所示为三角架结构。
荷载F 1作用在B 铰上。
AB 杆不计自重，BD 杆自重为W ，作用在杆的中点。
试画出图b 、c 、d 所示的隔离体的受力图，并加以讨论。
习题1－4图1习题1－3f 解1图F习题1－3e 解3图'A习题1－3f 解2图1O 习题1－3f 解3图F F'F 1习题1－4d 解2图F y B 21习题1－4c 解1图 AA B 1B FDx y2B 习题1－4b 解2图 1习题1－4b 解3图 F y B 2习题1－4c 解2图 F A B1B FAxF'习题1－5b 解3图E D(a-3)E B F习题1－5b 解2图习题1－5b 解1图'AxFF B习题1－5c 解图1一5 试画出图示结构中各杆的受力图。
工程力学静力学与材料力学习题及答案-力系的平衡
工程力学(静力学与材料力学)习题第3章力系的平衡3-1 试求图示两外伸梁的约束反力F RA 、F RB ,其中(a ) M = 60kN •m , F P = 20 kN ；(b ) F P =10 kN ,F P1 = 20 kN , q = 20kN/m , d = 0.8m 。
- (b )习题3-1图3-2直角折杆所受载荷，约束及尺寸均如图示。
试求A 处全部约束力。
3-3图示拖车重W = 20kN ，汽车对它的牵引力F S = 10 kN 。
试求拖车匀速直线行驶时，车轮A 、B 对地面的正压力。
3-4 图示起重机ABC 具有铅垂转动轴AB ，起重机重W = 3.5kN ,重心在D 。
在C 处吊有重％ = 10kN 的物体。
试求滑动轴承A 和止推轴承B 的约束力。
习题3-4图——19—习题3-2图I - 4 m L 4 m习题3-3图3 — 5图示钥匙的截面为直角三角形，其直角边AB = d 1, BC = d 2。
设在钥匙上作用一个力偶矩为M 的力偶。
试求其顶点A 、B 、C 对锁孔边上的压力。
不计摩擦，且钥匙与锁孔之间的隙缝很小。
习题3—5图一 “ 23 — 6图示一便桥自由放置在支座C 和D 上，支座间的距离CD = 2d = 6m 。
桥面重1g kN/m 。
试求当 汽车从桥上面驶过而不致使桥面翻转时桥的悬臂部分的最大长度l 。
设汽车的前后轮的负重分别为20kN 和 40kN ,两轮间的距离为3m 。
直解三角形平板OBC 的载荷，约束及尺寸(OB = d 1, OC = d 2)如图所示。
试求A 、O 处约束力。
3 — 8起重机装有轮子，可沿轨道A 、B 移动。
起重机桁架下弦DE 的中点C 上挂有滑轮(图未画出)， 用来提起挂在索链CG 上的重物。
从材料架上提起的物料重W = 50 kN ,当此重物离开材料架时，索链与铅 垂线成=20°角。
为了避免重物摆动，又用水平绳索GH 拉住重物。
材料力学课后答案d
-3-
工程力学习题解答
A． M 1 > M 2 > M 3 > M 4 C． M1 > M 2 = M 3 > M 4 E． FS1 = FS2 = FS3 = FS4
F
B． M1 = M 2 > M 3 > M 4 D． M 1 > M 2 > M 3 = M 4 F． FS1 > FS2 > FS3 > FS4
A
B
C
D
分析：这是对称结构承受对称荷载的情况，支反力偶矩必定对称，扭矩图必定反对称。
-2-
第 6 章 杆件的内力
因此只需根据支反力偶矩进一步判断扭矩正负即可。
6-2(4) 在梁的集中力作用处，其左、右两侧无限接近的横截面上的弯矩是 A 的。
A．相同
B．数值相等，符号相反
C．不相同
D．符号一致，数值不相等
−
1 4
q0 L
−
q0
⎜⎛ ⎝
x
−
L 2
⎟⎞ ⎠
−
FS
=
0
，
FS
=
1 4
q0 L
−
q0 x
。
∑m = 0 ，
M
+
q0 L 4
⎜⎛ x ⎝
−
L 2
⋅
2 ⎟⎞ 3⎠
+
q0
⎜⎛ ⎝
x
−
L 2
⎟⎞ ⋅ ⎠
1 ⎜⎛ x 2⎝
−
L 2
⎟⎞ ⎠
=
0，
M = − q0 (12x2 − 6Lx + L2 ) 。 24
工程力学(静力学和材料力学)课后习题答案解析(单辉祖)
WORD 格式.整理版1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解：1-2 试画出以下各题中AB 杆的受力图。
(a) B(b)(c)(d)A(e)A(a)(b) A(c)A(d)A(e)(c)(a)(b)解：1-3 试画出以下各题中AB 梁的受力图。
(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)解：1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ；(b) 半拱AB 部分；(c) 踏板AB ；(d) 杠杆AB ；(e) 方板ABCD ；(f) 节点B 。
解：(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b)B(c)BF D1-5 试画出以下各题中指定物体的受力图。
(a) 结点A ，结点B ；(b) 圆柱A 和B 及整体；(c) 半拱AB ，半拱BC 及整体；(d) 杠杆AB ，切刀CEF 及整体；(e) 秤杆AB ，秤盘架BCD 及整体。
解：(a)(d)FC(e)WB(f)F FBC(c)(d)AT F BAF (b)(e)(b)(c)(d)(e)CAA C’CDDC ’B2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445N ，F 2=535 N ，不计杆重，试求两杆所受的力。
解：(1) 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，(2) 列平衡方程：12140 sin 600530 cos6005207 164 o y AC ox BC ACAC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3 水平力F 作用在刚架的B 点，如图所示。
如不计刚架重量，试求支座A 和D 处的约束力。
解：(1) 取整体ABCD 为研究对象，受力分析如图，画封闭的力三角形：(2)F 1F FDF F AF D211 1.122D A D D A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o的力F ，力的大小等于20KN ，如图所示。
(完整版)材料力学习题册答案..
练习1 绪论及基本概念1-1 是非题（1）材料力学是研究构件承载能力的一门学科。
（ 是 ）（2）可变形固体的变形必须满足几何相容条件，即变形后的固体既不可以引起“空隙”，也不产生“挤入”现象。
（是 ）（3）构件在载荷作用下发生的变形，包括构件尺寸的改变和形状的改变。
（ 是 ） （4）应力是内力分布集度。
（是 ）（5）材料力学主要研究构件弹性范围内的小变形问题。
（是 ） （6）若物体产生位移，则必定同时产生变形。
（非 ） （7）各向同性假设认为，材料沿各个方向具有相同的变形。
（F ）（8）均匀性假设认为，材料内部各点的力学性质是相同的。
（是）（9）根据连续性假设，杆件截面上的内力是连续分布的，分布内力系的合力必定是一个力。
（非） （10）因为构件是变形固体，在研究构件的平衡时，应按变形后的尺寸进行计算。
（非 ）1-2 填空题（1）根据材料的主要性质对材料作如下三个基本假设：连续性假设 、均匀性假设 、 各向同性假设 。
（2）工程中的 强度 ，是指构件抵抗破坏的能力； 刚度 ，是指构件抵抗变形的能力。
（3）保证构件正常或安全工作的基本要求包括 强度 ， 刚度 ，和 稳定性 三个方面。
（4）图示构件中，杆1发生 拉伸 变形，杆2发生 压缩 变形， 杆3发生 弯曲 变形。
（5）认为固体在其整个几何空间内无间隙地充满了物质，这样的假设称为 连续性假设 。
根据这一假设构件的应力，应变和位移就可以用坐标的 连续 函数来表示。
（6）图示结构中，杆1发生 弯曲 变形，构件2发生 剪切 变形，杆件3发生 弯曲与轴向压缩组合。
变形。
（7）解除外力后，能完全消失的变形称为 弹性变形 ，不能消失而残余的的那部分变形称为 塑性变形 。
（8）根据 小变形 条件，可以认为构件的变形远 小于 其原始尺寸。
1-3 选择题（1）材料力学中对构件的受力和变形等问题可用连续函数来描述；通过试件所测得的材料的力学性能，可用于构件内部的任何部位。
工程力学(静力学与材料力学)答案
专业资料工程力学课后答案1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解：1-2 试画出以下各题中AB 杆的受力图。
BAO W (a) BAO W F(b)OW (c)AAO W(d)BAO W (e) BF BF ABO W (a) B AO W F(b) F AF B AO W(c)F AF O A O W(d) F B F AAOW (e)BF B F A AWC B(c)D (a)A WC E B(b)AWC D B解：1-3 试画出以下各题中AB 梁的受力图。
ABF(d)CABW(e)C ABW (e)CF B F AAB F(d)CF BF A(a) F D F BF ED A WCE B(b)AWC D B F D F BF A(c)AWC BF BF AAW CB(a)WABC D(c)ABF q D(b)CC A BFWDA ’ D ’B ’(d)ABFq(e)解：1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ；(b) 半拱AB 部分；(c) 踏板AB ；(d) 杠杆AB ；(e) 方板ABCD ；(f) 节点B 。
解：A WCB(a)F BF AA BF qD(b)F CF DWABC (c)F CF BCA BFWD(d)F BF AF DAB Fq(e)F BxF ByF AAB F (a) DCWAF (b) DB(c) FABD D ’ABF(d)CDW ABC D(e)WABC (f)AB F (a)DCWF AxF AyF DAF (b)BF BF A(c)FABDF BF D1-5 试画出以下各题中指定物体的受力图。
(a) 结点A ，结点B ；(b) 圆柱A 和B 及整体；(c) 半拱AB ，半拱BC 及整体；(d) 杠杆AB ，切刀CEF 及整体；(e) 秤杆AB ，秤盘架BCD 及整体。
解：(a)A B F(d) CF B F CW A B C D(e)F BF AWB(f)F ABF BCA B W (a) (c) B C W 1 W 2 FA F D A BC E F (d) A F AT BF BAF BT AB P P (b) W AB C C ’ DO G (e)(b)(c)(d)(e) F ABF AF CAPCF B BPCF’CF AABPPF BF NBCW1 W2FA FCxF CyF AxF AyBW1FA FAxF AyF BxF ByBCW2F CxF CyF’BxF’ByFABCF CF BDCE FF EF’CF FFDABCE FF E FFF BBCDGF BF CWA BCC’DOGF OyF OxF C’A BOWF BF OyF Ox2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445N ，F 2=535 N ，不计杆重，试求两杆所受的力。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
6-9 已知物体重W =100 N ，斜面倾角为30o (题6-9图a ，tan30o =0.577)，物块与斜面间摩擦
因数为f s =0.38，f ’s =0.37，求物块与斜面间的摩擦力？并问物体在斜面上是静止、下滑还是上滑？如果使物块沿斜面向上运动，求施加于物块并与斜面平行的力F 至少应为多大？
解：(1) 确定摩擦角，并和主动力合力作用线与接触面法向夹角相比较；
0.38
300.577
20.8
o f s o
f t
g f tg tg ϕαϕα
====∴=
(2) 判断物体的状态，求摩擦力：物体下滑，物体与斜面的动滑动摩擦力为
''cos 32 N s F f W α=⨯=
(3) 物体有向上滑动趋势，且静滑动摩擦力达到最大时，全约束力与接触面法向夹角等于摩擦角；
(4) 画封闭的力三角形，求力F ；
()()()
()sin sin 90sin 82.9 N
sin 90o f f f o f W F
F W αϕϕαϕϕ=
+-+=
=-
6-10 重500 N 的物体A 置于重400 N 的物体B 上，B 又置于水平面C 上如题图所示。
已知
f AB =0.3，f BC =0.2，今在A 上作用一与水平面成30o 的力F 。
问当F 力逐渐加大时，是A 先动呢？还是A 、B 一起滑动？如果B 物体重为200 N ，情况又如何？
(a)
(b)
解：(1) 确定A 、B 和B 、C 间的摩擦角：
12arctg 16.7arctg 11.3
o f AB o
f BC f f ϕϕ====
(2) 当A 、B 间的静滑动摩擦力达到最大时，画物体A 的受力图和封闭力三角形；
()()
1111
11sin sin 1809030sin 209 N
sin 60A
o o o f f f A o
f F W F W ϕϕϕϕ=
---∴=
⨯=-
(3) 当B 、C 间的静滑动摩擦力达到最大时，画物体A 与B 的受力图和封闭力三角形；
()()
2222
22sin sin 1809030sin 234 N
sin 60A B
o o o f f f A B o
f F W F W ϕϕϕϕ++=
---∴=
⨯=-
(4) 比较F 1和F 2；
12F F
物体A 先滑动；
(4) 如果W B =200 N ，则W A+B =700 N ，再求F 2；
()
2
2212
sin 183 N
sin 60f A B o
f F W F F ϕϕ+=
⨯=-
物体A 和B 一起滑动；
6-11 均质梯长为l ，重为P ，B 端靠在光滑铅直墙上，如图所示，已知梯与地面的静摩擦因
数f sA ，求平衡时θ=？
W
ϕf
解：(1) 研究AB 杆，当A 点静滑动摩擦力达到最大时，画受力图(A 点约束力用全约束力表
示)；
由三力平衡汇交定理可知，P 、F B 、F R 三力汇交在D 点； (2) 找出θmin 和ϕ f 的几何关系；
min min min
min sin tan cos 211tan 2tan 21arctan
2f f sA
sA l
l f f θϕθθϕθ⨯=⨯==∴= (3) 得出θ角的范围；
190arctan
2o sA
f θ≥≥ 6-13 如图所示，欲转动一置于V 槽型中的棒料，需作用一力偶，力偶矩M =1500 N ⋅cm ，已
知棒料重G =400 N ，直径D =25 cm 。
试求棒料与V 型槽之间的摩擦因数f s 。
解：(1) 研究棒料，当静滑动摩擦力达到最大时，画受力图(用全约束力表示)；
π/4)-ϕf
(2) 画封闭的力三角形，求全约束力；
12cos sin 4
4
R f R f F G F G ππϕϕ⎛⎫⎛⎫
=-=- ⎪ ⎪⎝⎭⎝⎭
(3) 取O 为矩心，列平衡方程；
12()0: sin sin 022
O R f R f D D
M F F F M ϕϕ=⨯⨯
+⨯⨯-=∑
sin 20.4243f ϕ=
= 12.55o f ϕ=
(4) 求摩擦因数；
tan 0.223s f f ϕ==
6-15 砖夹的宽度为25 cm ，曲杆AGB 与GCED 在G 点铰接。
砖的重量为W ，提砖的合力F
作用在砖对称中心线上，尺寸如图所示。
如砖夹与砖之间的摩擦因数f s =0.5，试问b 应为多大才能把砖夹起(b 是G 点到砖块上所受正压力作用线的垂直距离)。
解：(1) 砖夹与砖之间的摩擦角：
arctan arctan0.525.6o f s f ϕ===
(2) 由整体受力分析得：F=W
(2) 研究砖，受力分析，画受力图；
(3) 列y 方向投影的平衡方程；
0: 2sin 0
1.157y
R f R F
F W F W
ϕ=⨯-==∑
(4) 研究AGB 杆，受力分析，画受力图；
D
(5) 取G 为矩心，列平衡方程；
''
()0: sin 3cos 9.50
10.5 cm
G R f R f M
F F F b F b ϕϕ=⨯⨯-⨯⨯+⨯==∑
6-18 试求图示两平面图形形心C 的位置。
图中尺寸单位为mm 。
解:(a) (1) 将T 形分成上、下二个矩形S 1、S 2，形心为C 1、C 2；
(2) 在图示坐标系中，y 轴是图形对称轴，则有：x C =0 (3) 二个矩形的面积和形心；
2112
22501507500 mm 225 mm 5020010000 mm 100 mm
C C S y S y =⨯===⨯==
(4) T 形的形心；
0750022510000100
153.6 mm
750010000
C i i
C
i x S y y S
=⨯+⨯=
==+∑∑
(a)
(b)
(b) (1) 将L 形分成左、右二个矩形S 1、S 2，形心为C 1、C 2；
(3) 二个矩形的面积和形心；
21112
222101201200 mm 5 mm 60 mm 7010700 mm 45 mm 5 mm
C C C C S x y S x y =⨯====⨯===
(4) L 形的形心；
1200570045
19.74 mm
12007001200607005
39.74 mm
1200700
i i
C i i i
C
i
S x x S S y y S
⨯+⨯===+⨯+⨯=
=
=+∑∑∑∑
6-19试求图示平面图形形心位置。
尺寸单位为mm 。
解：(a) (1) 将图形看成大圆S 1减去小圆S 2，形心为C 1和C 2；
(2) 在图示坐标系中，x 轴是图形对称轴，则有：y C =0 (3) 二个图形的面积和形心；
(a)
(b)
22112
2
2220040000 mm 0806400 mm 100 mm
C C S x S x ππππ=⨯===⨯==
(4) 图形的形心；
6400100
19.05 mm
4000064000
i i
C i
C S x x S
y πππ-⨯=
=
=--=∑∑
(b) (1) 将图形看成大矩形S 1减去小矩形S 2，形心为C 1和C 2；
(2) 在图示坐标系中，y 轴是图形对称轴，则有：x C =0 (3) 二个图形的面积和形心；
2112
2216012019200 mm 60100606000 mm 50 mm
C C S y S y =⨯===⨯==
(4) 图形的形心；
01920060600050
64.55 mm
192006000
C i i
C i
x S y y S
=⨯-⨯=
=
=-∑∑
S S。