哈工大大学物理力学习题课

合集下载

理论力学(物理类)_哈尔滨工业大学中国大学mooc课后章节答案期末考试题库2023年

理论力学（物理类）_哈尔滨工业大学中国大学mooc课后章节答案期末考试题库2023年1.下列哪个结果等于拉格朗日函数对时间的导数？答案:_2.哈密顿量是广义坐标、广义速度和时间的函数答案:错误3.科里奥利力会改变物体的重力答案:错误4.张量连续与两个矢量点积，对其结果说法正确的是答案:其结果可以表示成一个行矩阵乘一个方阵，再乘一个列矩阵_其结果是一个数5.下列哪个结果是小振动问题的广义动量？答案:_6.下列运动中，加速度保持不变的是：答案:抛体运动7.一个刚体先进动30度，再章动90度，则若刚体上一质点在转前刚体坐标系下的分量是(6,4,2),则转后该质点在刚体坐标系下的分量是：答案:(6,4,2)8.若生成函数的形式为U=U(p,Q)，下列结果正确的是：答案:9.若生成函数的形式为U=U(q,P)，下列结果正确的是：答案:10.研究单摆在重力场中运动时，那些物理量可以作为广义坐标？答案:摆动的角度_摆球的横向位置11.关于平方反比引力作用下的可能的轨道形状有：答案:圆轨道_椭圆轨道_抛物线轨道_双曲线轨道12.牛顿力学有哪些获取运动积分的方案？答案:动量守恒定律_动量矩守恒定律_机械能守恒定律_角动量守恒定律13.一个刚体先进动30度，再章动90度，则若刚体上一质点在转前固定坐标系下的分量是(3,2,1),则转后该质点在固定坐标系下的分量是：答案:14.一个刚体先进动30度，再章动90度，则若刚体上一质点在转前刚体坐标系下的分量是(3,2,1),则转后该质点在刚体坐标系下的分量是：答案:(3,2,1)15.人造地球卫星绕地球作椭圆轨道运动，卫星轨道近地点和远地点分别为A和B。

用L和EK分别表示卫星对地心的角动量及其动能的瞬时值，则应有答案:LA=LB，EKA>EKB16.若质点组的质心做惯性运动，下列说法正确的是：答案:质点组的动量守恒17.下面关于质点组内力的说法，正确的是：答案:所有内力力矩的矢量和为零_所有内力的矢量和为零18.下列关于泊松定理，说法正确的是：答案:利用泊松定理的前提是先要得到两个运动积分_利用泊松定理可能无法获得新的运动积分19.下列那些量的结果为零答案:质点组所受内力的矢量和_质点组所受内力力矩的矢量和20.关于刚体维持平衡的充要条件，下列说法正确的是答案:主动力所做虚功为零_保守力场下势能的极值点21.下列那些结果不因坐标系的选择而变化？答案:标量_两个矢量的叉乘结果_两个矢量的点乘结果22.选择坐标系对张量的影响是：答案:没有改变张量的实体，但改变了其表示矩阵23.下列对于力的平移原理的说法正确的是：答案:利用力的平移原理可以将力的作用点平移到空间任意一点但需附加一个力偶24.下面那个结果正确反映了平面极坐标下基本矢量随时间的变化规律？答案:25.下列哪个结果是系统的广义能量？（T0、T1和T2分别是动能对于广义速度的零次、一次和二次齐次函数部分的结果）答案:-T0+T2+V26.历史上，最早得到速降线问题的正确解的科学家是：答案:约翰.伯努利27.以下转动，那些可以交换次序？答案:绕同一方向转动两次_一次无限小转动和一次有限大的定点转动_两次无限小转动28.有两个单摆，一个悬挂点静止，一个悬挂点在竖直方向做匀加速运动，则有：答案:二者都可以做简谐振动，频率大小无法判断29.有两个单摆，一个悬挂点静止，一个悬挂点在水平方向做匀加速运动，则有：答案:二者都可以做简谐振动，其中悬挂点静止的单摆频率较小30.关于欧拉运动学方程和欧拉动力学方程说法正确的是答案:欧拉运动学方程是建立角速度和欧拉角的关系_建立欧拉动力学方程需要用到惯量主轴来化简其形式_欧拉动力学方程是建立角速度和力矩的关系31.下列对于主矩的说法正确的是答案:主矩是作用在刚体上所有力的力矩的矢量和_力偶的主矩不依赖简化中心的选择32.下列关于角速度和角动量说法正确的是：答案:定轴转动角速度和角动量方向可能不相同_角速度沿着转轴方向33.一个质点做平面运动，如用平面极坐标系的参量（r ,θ）作为广义坐标来描述其运动，则广义力的两个分量为：答案:34.若生成函数的形式为U=U(p,P)，下列结果正确的是：答案:35.关于正则变换(q，p，H) —— (Q，P，K) 的条件，下列公式正确的是：答案:36.欧拉动力学方程对应定轴转动的哪一个知识点？（注：这里J 指角动量，I指转动惯量）答案:37.平方反比斥力下作用下，质点可能的轨道形状有：答案:双曲线38.一个均质的球形物体以角速度ω绕对称轴转动，如果仅仅靠自身的引力阻碍球体的离心分解，该物体的密度至少是多大？答案:39.下列对于力的可传性原理的说法正确的是：答案:利用力的可传性原理可以将力的作用点沿作用线平移40.下列关于虚功和功的关系，说法正确的是：答案:虚功与功具有同样的量纲_虚功与功都是标量41.下列关于广义力说法正确的是：答案:广义力的量纲与力的量纲未必相同_广义力的量纲依赖于广义坐标的选择_广义力是一个标量42.某人观测到一人造卫星始终停留在自己的垂直上空，问观察者的地点答案:赤道43.下列对于矢量场散度的写法正确的是：答案:44.可解约束的含义是问题可以求解答案:错误45.某质点处于平衡状态，下列说法正确的是：答案:加速度为零、速度不必为零46.关于平方反比力作用下的各类轨道的机械能大小顺序，正确的是：(以无穷远为势能零点)答案:抛物线大于椭圆轨道大于圆轨道47.关于质点的动量矩，下列说法正确的是答案:动量矩可以在任何参考系建立，动量矩定理在惯性系下成立48.以下各式，那个是正确的？答案:49.由于哈密顿-雅克比方程的解是作用量，可以通过将拉格朗日函数对时间积分的办法求解哈密顿-雅克比方程。

哈工大力学习题课下

1
2
共同角速度 J 11 J 22
啮合过程机械能损失J：1 J 2
E
E0 E

(1 2
J112

1 2
J
2
22
)

1 2
(
J1

J2
)
2
J1J2 (1 2 )2
2(J1 J2 )
7. 两个同样重的小孩，各抓着跨过滑轮绳子的两端。一个孩子用力向上爬，另一个则抓住绳子不动。若滑轮的质量
置的细杆处于非稳定平衡状态，当其受到微小扰动时，细杆将在重力作用下由静止开始绕铰链O 转动 .试计
算细杆转动到与竖直线成角时的角加速度和角速度 .
解细杆受重力和
铰链对细杆的约束力
FN
作用，由转动定律得
1 mgl sin J
2
式中 J 1 ml2 3
得 3g sin
和轴上的摩擦都可忽略，哪一个小孩先到达滑轮处？若两个小孩重量不等，情况又如何？
解：把每个小孩看成一个质点，以滑轮的
R
轴为参考点，把两个小孩和滑轮看成系统。规定向里为角动量和力矩的正方向。Biblioteka 1 2kxm2

(F
mg)2
2k
由质点系的功能原理：
(F
mg)xm

1 2
kxm2
得：
2(F mg)
xm
k
E p

1 2
kxm2

2(F
mg)2
k
1. 从一个半径为 R 的均匀薄圆板上挖去一个半径为 R/2 的圆板，所形成的圆洞的中心在距圆薄板中心 R/2 处，所剩薄板的质量为 m 。求此时薄板对通过圆中心与板面垂直的轴的转动惯量。

大学哈工大第八版理论力学-资料

二运动方程角速度角加速度
f (t)
角速度角加速度
d
dt
ddt dd2t2
转角角速度角加速度代数量正负规定要一致
图示
思考什么情况下刚体是加速转动?
什么情况下刚体减速转动?
！联想到了什么？
35
§7–3转动刚体内各点的速度和加速度
一转动刚体内各点的速度和加速度的计算
1 速度计算
s R
vds RdR
dt dt
d dt
vA 各点速度的大小与该点
vD D
A 到轴心的距离成正比
vB 速度的方向垂直于该点到
O
轴心的连线，指向图形
B 转动的一方。
36
§7–3转动刚体内各点的速度和加速度
一转动刚体内各点的速度和加速度的计算速度计算的逆运算
vds RdR
dt dt
vB OB
Δr M'
v*
r(t+Δt) O
B
lim v
r dr
t0 t dt
动点的速度矢沿着
动点运动轨迹的切线，并与此点运动的方向一致。
20
三加速度
§ 5-1 矢量法
alimv t0 t
dv dt
ddt2r2
a v r
此法常用于推导公式
lim v r dr t0 t dt
21
§ 5-2 直角坐标法
作业 1 P154 5-7
2 思考题P168 6-5 a) 平行四连杆机构。假设标有转动角速度刚体的长度为L 计算点M 的速度和加速度的大小并在图中画出它们的方向
❖ 3 思考题 6-5b) OA OB OC 设为已知,计算点 A B C 的速度和加速度的大小；并在图中画出它们的方向。

哈尔滨工业大学第7版理论力学第4章课后习题答案

解（1）方法 1，如图 4-6b 所示，由已知得
Fxy = F cos 60° ， Fz = F cos 30°
F = F cos 60°cos 30°i − F cos 60°sin 30° j − F sin 60°k = 3 i − 1 Fj − 3 Fk 44 2
41
理论力学（第七版）课后题答案哈工大.高等教育出版社
A
F
β
MA
C
MB
F
10 N
β M θ − 90° C
MB
(a)
(b)
(c)
图 4-11
解画出 3 个力偶的力偶矩矢如图 4-11b 所示，由力偶矩矢三角形图 4-11c 可见
MC =
M
2 A
+
M
2 B
=
3 0002 + 4 0002 = 5 000 N ⋅ mm
由图 4-11a、图 4-11b 可得
3 = 250 N 13
FRz = 100 − 200 ×
1 = 10.6 N 5
M x = −300 ×
3 × 0.1 − 200 × 1 × 0.3 = −51.8 N ⋅ m
13
5
M y = −100 × 0.20 + 200 ×
2 × 0.1 = −36.6 N ⋅ m 13
M z = 300 ×
z
F45° F3 F3′ B
F2A
E
F1
C
F5
F6
F F4 45°
D
y
K x
M
(a)
(b)
图 4-9
解 (1) 节点 A 为研究对象，受力及坐标如图 4-9b 所示

哈尔滨工业大学理论力学课后习题答案

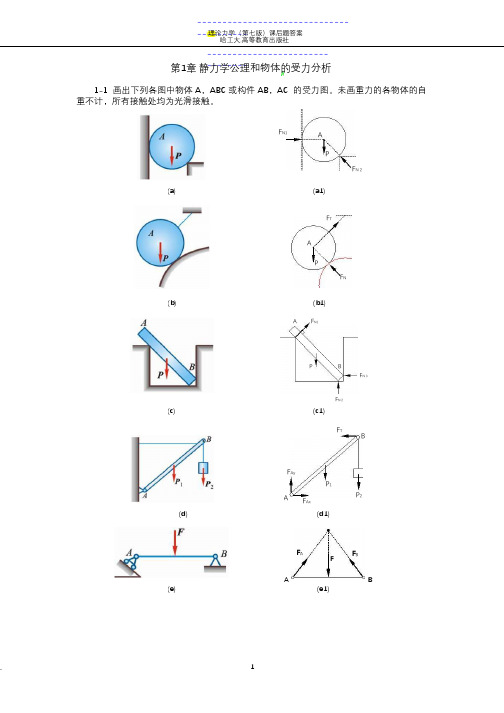
.----------------------------------------理论力学（第七版）课后题答案哈工大.高等教育出版社 -------------------------------- 第1章静力学公理和物体的受力分析1-1 画出下列各图中物体 A ，ABC 或构件 AB ，AC 的受力图。

未画重力的各物体的自重不计，所有接触处均为光滑接触。

F N1A PF N 2(a) (a1)F TA PF N(b)(b1)AF N1P BF N 3F N 2(c) (c1)F TBF AyP 1P 2AF Ax(d) (d1)F AF BFAB(e)(e1)qFF Ay F BF AxA B(f) (f1)FBC F CAF A(g) (g1)F Ay FCCA F Ax BP1 P2(h) (h1)BFCF CF AxDAF Ay(i) (i1)(j) (j1)BF B FCPF AyF AxA(k) (k1)F CAF AB 2 F AC CA2 F ABBF ACF BAA P (l) (l1)(l2)(l3)图 1-11-2 画出下列每个标注字符的物体的受力图。

题图中未画重力的各物体的自重不计，所有接触处均为光滑接触。

F N 2C2 F P 2(a1) F N1N(a)BF N1BC F N 2F NP 2P1P1F AyF Ay F AxF AxAA(a2) (a3)F N1AP1F N3B P 2F N 2(b) (b1)2 F NF N3F N1ABP 2P1F N F N 2(b2)(b3)F AyF AxA C D F N2BP 2P 1F N1(c)(c1)F AyF TAF AxD2 F F N2TBP 1F N1P 2(c2)(c3)F AyF BqBAF AxCDF C(d)(d1)F DyF AyF BqqD2 FDxBAF AxCF Dx D 2 FDyF C(d2) (d3)F Ay2 FBxqBF AyF AxqAB 2F ByF AxF CxC F CyP F BxAB PF Cx (e1)CF ByF Cy(e)(e2)(e3)F 1CF 2F AyF ByABF AxF Bx(f)(f1)F Cx2 FCxCCF 1F CyF 2 F 2F AyCyF ByAF BxF Ax B(f2)(f3)F BF AyCBAF AxP(g)(g1)2 F CyF T2 FCxCF AyF BF TDCF AxBAF Cx P (g2)(g3)DF 1F CyF B2 F 2F BBCF CxBF Ay AF Ax(h)(h1)(h2)A F AxF AyF CyF CxC2 A F EF CyF F OyCDF OxF Cx 2EOB(i)(i1)(i2)A A2 F Ax2 FE2 F AyFEC D F ByF ByF OyF BxF OxF BxOBB (i3)(i4)F AyDE F CxF TA F AxF ByC CHF By F Cy BPF BxF BxB(j)(j1)(j2)F Ay F Dy 22 F Ey2 F CF Cx 2 E F AxT 2 D F T 22FExF ExA D F Dx 2E F DxF T3F T12FCyF DyF Ey(j3)(j4)(j5)EFF BCED2 BF Cx⎝2 2 F DEF Cy(k)(k1)F BF FC BF Cx⎝EC F Cy90︒ ⎝FDED DF AyF AyAAF AxF Ax(k2) (k3)F B2 FBF 1F DBBDCAF AF C(l)(l1)(l2)F 22 DF DF 1F 2DBAC EE F EF AF C F E(l3)(l4)或2 2 F DyF2F 1F F Dy F 2F 1B 2 DF DxF DxBBD D F ExA C E C E F ExF CF EyF AF CF Ey(l2)’(l3)’(l4)’2 F ADAF CyF CxCF 1B(m)(m1)F ADDF ADHEF 2A DF EF HF AD 2(m2)(m3)F N AAF kF N BF OyF OxBO(n) (n1)F N1B Dq2 F BF N 2F N3(n2)FB D FF C F EF AF G GCEA(o)(o1)FBB DFDF BF E F FF C F D2 FEA F AF B 2CD(o2)(o3) (o4) 图 1-2第2章平面汇交力系与平面力偶系2-1 铆接薄板在孔心 A ，B 和 C 处受 3个力作用，如图 2-1a 所示。

哈工大大学物理第二章作业题+答案

方向向下。
T1 m1 ( g a1 ) 0.2 (9.8 1.96) 1.57 N 1 T2 T1 0.785 N 2 m g T2 0.1 9.8 0.785 a2 2 1.95 m s 2 m2 0.1
方向向下。
a3
方向向上。
m3 g T2 0.05 9.8 0.785 5.9 m s 2 m3 0.05
5
物体受力：真实力：重力 mg, 、斜面对它的正压力 N 惯性力： ma0
mg N ( ma0 ) mar
mgsin ma0sin mar mgcos N ma0cos 0
解得
N m ( g 0a) c o s; ar (g a0 ) sin
A

mg N ma
x 方向： mg sin max m(ar a0 sin ) y 方向： ma y N mg cos ma0 cos 解得
N m ( g 0a) c o s; ar (g a0 ) sin
解法二：以升降机为参考系（非惯性系），建立坐标系如图，
解当雨滴均匀运动时得所以当速率为 4.0 m s 时
1
mg k v 2 k mg / 25
F ma mg k v 2 mg
得
16 9 mg mg 25 25 a 9 g / 25
12. 2-12 质量为 m 的物体系于长度为 R 的绳子的一个端点上，在竖直平面内绕绳子另一端点（固定）作圆周运动．设时刻物体瞬时速度的大小为，绳子与竖直向上的方向成 θ 角，如图所示。(1) 求ｔ时刻绳中的张力 T 和物体的切向加速度 at；(2) 说明在物体运动过程中 at 的大小和方向如何变化？

哈尔滨工业大学大学物理热学部分部分习题

带入上式得出
5 5 E P V B 2 RT 0 0 2 2
（2）抽取绝热板，两种气体混合后处于平衡时的温度为多少？
混合后两种气体温度相同，温度与内能有关。因此应从内能入手。容器绝热，外界没有对气体做功，也没有热传递。系统内能量守恒。两种气体间存在能量转移，但是总内能不变。设混合后温度为T，则混合后 A气体内能 B气体内能
f ( v )d v
Nf ( v )d v

v2 v1
f (v )d v

v2
v1
Nf ( v )d v
(1) f ( v )d v 表示某气体分子的速率在 v v dv间隔内的概率。或者说，速率在 v v dv 间隔内的分子数占总分子数的百分比。 (2) Nf ( v )d v 表示在 v v dv 间隔的分子数
1 p r 2 3
因此，方均根速率为
2 3P r
（2）单位体积内气体的内能为多少？一个分子平均内能为
1 m 2 2
单位体积内有n个分子，内能为
1 2 1 2 3 E n nm r P 2 2 2
例5 ：已知某气体在温度T时的速率分布函数为
，
说明下列各表达式的意义 f (v )
(2) 麦克斯韦速率分布率相关问题
(3) 利用三种特征速率公式的一些计算 (4) 平均自由程相关问题
(5) 玻尔兹曼能量分布律的应用
10
例1. 体积和压强都相同的氦气和氢气（均视为刚性分子理想
气体），在某一温度T下混合，所有氢气分子所具有的热运
动动能在系统总热运动动能中所占的百分比是多少？
氢气为双原子分子，自由度为5，一个分子平均动能：
因此内能为

哈理工大学物理下习题解集

题9-19图9-19在磁感应强度为B的均匀磁场中，垂直于磁场向的平面有一段载流弯曲导线，电流为I ，如题9-19图所示．求其所受的安培力．解：在曲线上取ld则 baab B l I F d∵l d 与B 夹角l d ，2B 不变，B是均匀的．∴ b ab aab B ab I B l I B l I F)d (d向⊥ab 向上，大小BI F ab ab题9-20图9-20如题9-20图所示，在长直导线AB 通以电流1I =20A ，在矩形线圈CDEF 有电流2I =10 A ，AB 与线圈共面，且CD ，EF 都与AB 平行．已知a =9.0cm,b =20.0cm,d =1.0 cm ，求：(1)导线AB 的磁场对矩形线圈每边所作用的力； (2)矩形线圈所受合力和合力矩．解：(1)CD F向垂直CD 向左，大小4102100.82 dI bI F CD N 同理FE F向垂直FE 向右，大小5102100.8)(2 a d I bI F FE NCF F向垂直CF 向上，大小为ad dCF dad I I r r I I F 5210210102.9ln 2d 2N ED F向垂直ED 向下，大小为5102.9 CF ED F F N(2)合力ED CF FE CD F F F F F向向左，大小为4102.7 F N合力矩B P M m∵线圈与导线共面∴ B P m//0 M．10-1 一半径r =10cm 的圆形回路放在B =0.8T 的均匀磁场中．回路平面与B垂直．当回路半径以恒定速率trd d =80cm ·s -1 收缩时，求回路中感应电动势的大小．解: 回路磁通2πr B BS m 感应电动势大小40.0d d π2)π(d d d d 2trr B r B t t m V 10-4 如题10-4图所示，载有电流I 的长直导线附近，放一导体半圆环MeN 与长直导线共面，且端点MN 的连线与长直导线垂直．半圆环的半径为b ，环心O 与导线相距a ．设半圆环以速度v 平行导线平移．求半圆环感应电动势的大小和向及MN 两端的电压N M U U ．解:作辅助线MN ，则在MeNM 回路中，沿v向运动时0d m ∴ 0 MeNM 即 MN MeN 又∵ba ba MN ba ba Iv l vB 0ln 2d cos 0 所以MeN 沿NeM 向，大小为ba ba Iv ln20 M 点电势高于N 点电势，即ba ba Iv U U N Mln20 10-6如题10-6图所示，用一根硬导线弯成半径为r 的一个半圆．令这半圆形导线在磁场中以频率f 绕图中半圆的直径旋转．整个电路的电阻为R ．求：感应电流的最大值．题10-6图解: )cos(2π02t r B S B m ∴Bfr f r B r B t r B t m m i 222202ππ22π2π)sin(2πd d ∴RBf r R I m22π 10-7 如题10-7图所示，长直导线通以电流I =5A ，在其右放一长形线圈，两者共面．线圈长b =0.06m ，宽a =0.04m ，线圈以速度v =0.03m ·s -1垂直于直线平移远离．求：d =0.05m 时线圈中感应电动势的大小和向．题10-7图解: AB 、CD 运动速度v向与磁力线平行，不产生感应电动势． DA 产生电动势ADIvbvBb l B v d2d )(01BC 产生电动势)(π2d )(02d a Ivbl B v CB∴回路中总感应电动势8021106.1)11(π2ad d Ibv V 向沿顺时针．10-14 如题10-14图所示，在垂直于直螺线管管轴的平面上放置导体ab 于直径位置，另一导体cd 在一弦上，导体均与螺线管绝缘．当螺线管接通电源的一瞬间管磁场如题10-14图示向．试求：（1）ab 两端的电势差；（2）cd 两点电势高低的情况．解：由 l S t B l Ed d d d 旋知，此时旋E 以O 为中心沿逆时针向． (1)∵ab 是直径，在ab 上处处旋E与ab 垂直∴ll 0d 旋∴0 ab ,有b a U U (2)同理，0dl E cddc旋∴ 0 c d U U 即d c U U题10-15图10-15 一无限长的直导线和一正形的线圈如题10-15图所示放置(导线与线圈接触处绝缘)．求：线圈与导线间的互感系数．解：设长直电流为I ，其磁场通过正形线圈的互感磁通为32300122ln π2d π2a a Iar rIa∴2ln π2012aIM10-16 一矩形线圈长为a =20cm ，宽为b =10cm ，由100匝表面绝缘的导线绕成，放在一无限长导线的旁边且与线圈共面．求：题10-16图中(a)和(b)两种情况下，线圈与长直导线间的互感．解：(a)见题10-16图(a)，设长直电流为I ，它产生的磁场通过矩形线圈的磁通为2ln π2d 2πd 020)(12Iar r Ia S B b b S∴6012108.22ln π2a N I N M H (b)∵长直电流磁场通过矩形线圈的磁通012 ，见题10-16图(b) ∴0 M题10-16图题10-17图10-17 两根平行长直导线，横截面的半径都是a ，中心相距为d ，两导线属于同一回路．设两导线部的磁通可忽略不计，证明：这样一对导线长度为l 的一段自感为lL 0Inaad ．解：如图10-17图所示，取r l S d d 则ad aad aad da a d Il r r r Ilr l r Ir πI)ln (ln 2πd )d 11(π2d ))d (π22(0000 aad Illnπ0∴a a d l I L lnπ0 10-18 两线圈顺串联后总自感为1.0H ，在它们的形状和位置都不变的情况下，反串联后总自感为0.4H ．试求：它们之间的互感．解：∵顺串时M L L L 221 反串联时M L L L 221 ∴M L L 415.04L L M H 11-5 半径为R =0.10m 的两块圆板构成平行板电容器，放在真空中．今对电容器匀速充电，使两极板间电场的变化率为tEd d =1.0×1013 V ·m -1·s -1．求两极板间的位移电流，并计算电容器离两圆板中心联线r (r ＜R )处的磁感应强度Br 以及r =R 处的磁感应强度BR ．解:(1) tEt D j D 08.22 R j S j I D D D A(2)∵S j I l H SD ld d 0取平行于极板，以两板中心联线为圆心的圆r l 2 ，则22d d 2r tE r j r H D ∴tEr H d d 20tEr H B r d d 2000当R r 时，600106.5d d 2tER B R T12-1 某单色光从空气射入水中，其频率、波速、波长是否变化?怎样变化?解:不变，为波源的振动频率；nn 空变小； n u 变小．12-2 在氏双缝实验中，作如下调节时，屏幕上的干涉条纹将如变化?试说明理由． (1)使两缝之间的距离变小；(2)保持双缝间距不变，使双缝与屏幕间的距离变小； (3)整个装置的结构不变，全部浸入水中； (4)光源作平行于1S ，2S 联线向上下微小移动； (5)用一块透明的薄云母片盖住下面的一条缝．解:由 dDx知，(1)条纹变疏；(2)条纹变密；(3)条纹变密；(4)零级明纹在屏幕上作相反向的上下移动；(5)零级明纹向下移动． 12-3 什么是光程? 在不同的均匀媒质中，若单色光通过的光程相等时，其几路程是否相同?其所需时间是否相同?在光程差与位相差的关系式2 6中,光波的波长要用真空中波长,为什么?解:nr ．不同媒质若光程相等，则其几路程定不相同；其所需时间相同，为Ct．因为中已经将光在介质中的路程折算为光在真空中所走的路程。

大学物理力学习题课1 哈尔滨工程大学

根据题意：
2
at = an
c b ct / R
哈尔滨工程大学理学院孙秋华
t
R b c c
质点力学习题课 3.已知某些条件给出速度和运动方程作业2．以初速度 v0 向上抛出一小球，小球在运动过程中
受到阻力，其大小为
f kv ，k为常数，求：小球任
意时刻的速度及达到的最大高度。
哈尔滨工程大学理学院
孙秋华
质点力学习题课作业14. 质量为M=1.5kg的物体，用一根长为l=1.25m的细绳悬挂在天花板上，今有一质量为m=10g的子弹以 v0=500m/s的速度射穿物体，刚穿出物体时子弹的速度大小为v=30m/s, 设穿透时间极短，求（1）子弹刚穿出时绳中张力的大小；（2）子弹在穿透过程中所受的冲量。
哈尔滨工程大学理学院
孙秋华
质点力学习题课 1、力学中重要物理量的计算
作业4. 由楼窗口以水平初速度v 0射出一发子弹，求：（1）子弹在任意时刻的位置及轨迹方程；（2）子弹在任意时刻的速度、切向加速度和法向加速度；（3）任意时刻质点所在轨迹的曲率半径。
作业11. 一物体按规律x=ct2作直线运动（c为常数）。设媒质对物体的阻力正比于速度的平方，阻力系数为k，求：物体由 x=0到 x=l过程中，阻力所作的功。
I p2 p1
（3）质点系的动量守恒定律
条件: F 0
f 内 F
m i v ix c 1 i m i v iy c 2 i m i v iz c 3 i
p2 p1 mi v i
哈尔滨工程大学理学院孙秋华
哈尔滨工程大学理学院
孙秋华
质点力学习题课

哈工大大学物理课件(马文蔚教材)-第1章力学

结语
1 力学教育的重要性
力学教育是一个完整的物理课程的核心，是各种工程和科学领域成功的关键。
2 对未来学生的启示
力学对所有学生都有重大意义，是培养他们成为更好的科学家和工程师的必要过程。
课程内容适用于各种工程和科学领域，帮助学生建立牢固的基础。
力学主题与重要性
1
物理学基础
强化物理学概念，涵盖了牛顿三定律以及其他物理学基础。
2
应用广泛
力学是物理学分支的核心，对各种领域都有重大单果。
3
思维训练
强求物理学思维和技能，培养相应能力，提升学生成为更优秀的物理科学家或工程师。
基本概念
物理学与力学的定义
物理学是一门研究物质本质的自然科学，而力学是物理学最基本的分支之一。
牛顿三定律的解释与应用
牛顿三定律是物理学中的基本定理，被广泛应用于各种工程和科学领域。
质点、质量、力的概念
质点是指在物理问题中被简单地看作质点运动的物体，质量是质点所具有的固有量度，而力是物理学中最基本的物理量之一。
施密特原理与相对论运动学的简介
哈工大大学物理课件(马文蔚教材)-第1章力学
在哈尔滨工业大学的物理课程中，马文蔚的力学教材是必不可少的。本章介绍了力学这个重要的物理学分支，并解释了一些关键概念。
教材介绍
严谨详尽
由哈工大的教授编写，有趣的漫画，让学生更好地理解物理学概念。
实用性强
施密特原理和相对论运动学是物理学中的重要概念，用于描述物理学的运动和惯性。
运动学基础
位移、速度和加速度的概念
位移、速度和加速度是物理学运动学的基本概念。
直线运动和非直线运动的描述
直线运动和非直线运动分别是基于直线方向的运动和不规则方向的运动。

哈工大—大学物理习题课-稳恒电流的稳恒磁场

(2)由式可得
I
2 F
0
ln
a
r
r
2 ma
0
ln
a
r
r
0.317 1.8 105 9.8 A 4.1106 A 2 107 ln 1.2 6.7 6.7
(3)设电源功率为P，则
P Fv 0 I 2v ln a r
0.80 1.6
r
4 107 (4.1106 )2 4.2 103 1.2 6.7
• 电功率和焦耳定律
电功率 P A VI t
焦耳定律的微分表达式：
• 电源电动势
电动势 E(2) dr (电源内)
焦耳定律: Q I 2 Rt
p j2
E2
普遍表达式 E(2) dr L
• 磁现象本质：运动电荷对运动电荷的作用
• 磁感强度大小 B Fmax qv
沿着 Fmax v 的方向
dB1
0dI 2 d
0 Id 4 2d
方向如右图所示。
由于电流分布相对于z轴是轴对称的，所以dB1中只有z轴垂直的分量dB是有效的，与z轴平行的分量则被dB1’的相应分量所抵消。
dB dB1 cos cos r R cos
所以
d
dB
0 I (r R cos ) 4 2d 2
d
0 I (r R cos )d P点处的磁感应4强2 (度r 2 R2 2rR cos )
0I1I2 dl 2 R
方向：沿x轴正方向。
0I1I2
例2：空气中有一半径为r的“无限长”直圆柱金属导体，竖直线oo`为中心轴线，在圆柱体内挖一个直径为 1 r 的圆柱空洞，
2
空洞侧面与oo`相切，在未挖洞部分通以均匀分布的电流I，方

哈工大单自由度体系简谐荷载、周期荷载习题

习题部分A3.1 一个无阻尼单自由度体系，其质量m 、刚度k 和固有频率n ω未知，现用谐波激励试验确定这些特性。

当激励频率为4赫兹时，反应趋于无限增加（即共振条件）。

将5=ω∆磅力重的重物附于质量m 后，重做共振试验，这一次的共振发生于f =3赫兹处。

试确定体系的质量和刚度。

3.2 一个单自由度体系受到正弦力的激励。

测得共振时的位移幅值为2英寸；激励频率为固有频率的十分之一时，测得的位移幅值为0.2英寸。

试求体系的阻尼比。

3.3 在谐波激励受迫振动试验中，注意到共振时的运动幅值恰好是比共振频率高20%的激励频率时幅值的4倍。

试确定体系的阻尼比。

3.4 一个机器由四个钢弹簧支撑，阻尼可忽略不计。

机器—弹簧系统竖向振动的固有频率为每分钟200周。

机器产生竖向力0()sin p t p t ω=。

机器的稳态竖向位移幅值在机器以每分钟20转（rpm ）运转时为2.00=u 英寸，每分钟180转时为1.042英寸，每分钟600转时为0.0248英寸。

现用四个提供相同刚度的橡胶隔振垫取代钢弹簧，它们还为体系引入相当于ζ=25%的阻尼。

试计算机器竖向运动的幅值，并评论在不同机器速度时隔振的效果。

3.5 一个重1200磅力的空调装置用螺栓固定于两个平行简支钢梁的跨中（图P3.5）。

梁的净跨为8英尺。

每根梁横截面的面积二次矩为104英寸。

装置内的电动机以每分钟300转运转，在这个速度上产生一个60磅力的不平衡力。

忽略梁的重量，并假设体系有1%的粘滞阻尼。

对于钢材，E=30000千磅力/英寸2。

试确定由不平衡力引起的梁中点稳态挠度幅值和稳态加速度（用g 表示）。

图P3.53.6 (a) 证明：单自由度体系对余弦力0()cos p t p t ω=的稳态反应为(b) 证明：余弦力引起的最大变形与正弦力引起的相同。

3.7 (a) 证明：21/2(12)r n ωωζ=-是单自由度体系位移幅值的共振频率。

(b) 确定共振时的位移幅值。

[理学]哈工大版理论力学习题课期末复习

得: FAx 6 kN 得: FAy 2 kN
B C FBCx
q FAy A FFDxAx
M A(F ) 0, 得 : M A 18 kN m
D
FDMy A
[例] 图示结构，已知P和a的大小，且M=2Pa。求: A点的支座反力。
P
D
M
C E
A
a
a
a
a
B
[例] 图示结构，已知P和a的大小，且M=2Pa。求: A点的支座反力。
ve= v0 ae= a0
aan
va2 r
va
s
ve
in
[例]图示机构中杆O1A以匀角速度转动, O1A=AB=l , AB⊥O1A。求（1）图示瞬时AB杆和O2B杆的角速度；（2） B点的加速度。
O1
vA
A
O2 45°
B
vB
AB
vA PA
vB cos45vA
O2
vB O2 B
P
[例]图示机构中杆O1A以匀角速度转动, O1A=AB=l , AB⊥O1A。求（1）图示瞬时AB杆和O2B杆的角速度；（2） B点的加速度。
块B的质量为2m，绳AE段水平。系统初始静止。
求: （1）轮心C的加速度、物块B的加速度；
（2）AE段绳中的拉力。
A
E
解: (1) 利用动能定理求速度
(2) 求导求加速度
R C
OR
(3) 利用刚体平面运动微分
B
方程求AE段绳中的拉力
JC MC (F (e) )
max Fx(e)
T
C mg aC
FS FN
D
FDMy A
[例] 图示结构，已知P和a的大小，且M=2Pa。求: A点的支座反力。

哈工大理力习题及习题答案

理论力学（I）第六版哈尔滨工业大学理论力学教研室第二章平面汇交力系与平面力偶系2-1铆接薄板在孔心A 、B 和C 处受三力作用，如题2-1图（a ）所示。

F 1=100N ，沿铅直方向；F 3=50N ，沿水平方向，并通过点A ；F 2=50N ，力的作用线也通过点A ，尺寸如题2-1图(a)所示。

求此力系的合力。

解法一几何法。

应用力的多边形法，将力F 1、F 2和F 3首尾相接后，再从F 1的起点至F 3的终点连一直线，此封闭边便是三力的合力F R ，如题2-1图（b ）所示。

根据预先选好的比例尺，利用直尺和量角器便可确定合力F R 的大小和方向。

解法二解析法。

合力的矢量表达式为∑∑+=+=j F i F j F i F F y x Ry Rx R即合力R F 在x 轴和y 轴上的投影，分别等于力系各力在同一坐标轴上投影的代数和，所以有：N N F F F F xx x Rx 805080606050022321=⎪⎪⎭⎫ ⎝⎛++⨯+=++= N N F F F F yy y Rx 14008060805010022321=⎪⎪⎭⎫ ⎝⎛++⨯+=++= 所以，合力的大小为：N N F F F Ry Rx R2.161140802222=+=+=合力F R 与x 轴的夹角为：︒===24.602.16180arccos cosR Rx F F acr α 2-3物体重P=20kN ，用绳子挂在支架的滑轮B 上，绳子的另一端接在铰车D 上，如题2-3图（a ）所示。

转动铰车，物体便能升起。

设滑轮的大小、AB 与CB 杆自重及磨擦略去不计，A 、B 、C 三处均为铰链连接。

当物体处于平衡状态时，试求拉杆AB 和支杆CB 处受的力。

解：这是一个平面汇交力系的平衡问题。

选取滑轮B 为研究对象，并作B 点的受力图，如题2-3图（b ）所示。

由平衡方程∑∑==0,0y xF F，有：030sin 30cos =︒-︒+-T F F BC BA （1） 030cos 30sin =-︒-︒P T F BC （2）因忽略了滑轮B 的磨擦，所以P=T ，将P 、T 的数值代入（2）式，得KN F BC 64.74=将T 和F BC 的数值代入（1）式，得：kN F BA64.54=所以拉杆AB 和CB 分别受拉力54.64kN 和压力74.64kN 。

大学物理力学(黑龙江联盟)知到章节答案智慧树2023年哈尔滨工业大学

大学物理力学（黑龙江联盟）知到章节测试答案智慧树2023年最新哈尔滨工业大学绪论单元测试1.一质点沿x轴作直线运动，其v-t曲线如图所示，如t=0时，质点位于坐标原点，则t=4.5 s时，质点在x轴上的位置为参考答案:2m2.图中p是一圆的竖直直径pc的上端点，一质点从p开始分别沿不同的弦无摩擦下滑时，到达各弦的下端所用的时间相比较是参考答案:所用时间都一样3.一质点作直线运动，某时刻的瞬时速度 2 m/s，瞬时加速度，则一秒钟后质点的速度参考答案:不能确定4.如图所示，湖中有一小船，有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动．设该人以匀速率收绳，绳不伸长、湖水静止，则小船的运动是参考答案:变加速运动第一章测试1.某质点作直线运动的运动学方程为x＝3t-5t3 + 6 (SI)，则该质点作参考答案:变加速直线运动，加速度沿x轴负方向．2.一质点沿x轴作直线运动，其v-t曲线如图所示，如t=0时，质点位于坐标原点，则t=4.5 s时，质点在x轴上的位置为 ( )参考答案:2m．3.图中p是一圆的竖直直径pc的上端点，一质点从p开始分别沿不同的弦无摩擦下滑时，到达各弦的下端所用的时间相比较是参考答案:所用时间都一样4.几个不同倾角的光滑斜面，有共同的底边，顶点也在同一竖直面上．若使一物体（视为质点）从斜面上端由静止滑到下端的时间最短，则斜面的倾角应选参考答案:45°5.参考答案:不能确定第二章测试1.质量为m的小球，放在光滑的木板和光滑的墙壁之间，并保持平衡，如图所示．设木板和墙壁之间的夹角为a，当a逐渐增大时，小球对木板的压力将（）参考答案:减少2.两个质量相等的小球由一轻弹簧相连接，再用一细绳悬挂于天花板上，处于静止状态，如图所示．将绳子剪断的瞬间，球1和球2的加速度分别为（）参考答案:a1＝2ｇ，a2＝03.水平地面上放一物体A，它与地面间的滑动摩擦系数为．现加一恒力如图所示．欲使物体A有最大加速度，则恒力与水平方向夹角应满足（）参考答案:4.一只质量为m的猴，原来抓住一根用绳吊在天花板上的质量为M的直杆，悬线突然断开，小猴则沿杆子竖直向上爬以保持它离地面的高度不变，此时直杆下落的加速度为（）参考答案:5.如图所示，质量为m的物体A用平行于斜面的细线连结置于光滑的斜面上，若斜面向左方作加速运动，当物体开始脱离斜面时，它的加速度的大小为（）参考答案:第三章测试1.质量为m的质点，以不变速率v沿图中正三角形ABC的水平光滑轨道运动．质点越过A角时，轨道作用于质点的冲量的大小为（）参考答案:2.两辆小车A、B，可在光滑平直轨道上运动．第一次实验，B静止，A以0.5m/s的速率向右与B碰撞，其结果A以 0.1 m/s的速率弹回，B以0.3 m/s 的速率向右运动；第二次实验，B仍静止，A装上1 kg的物体后仍以 0.5m/s1的速率与B碰撞，结果A静止，B以0.5 m/s的速率向右运动，如图．则A和B的质量分别为（）参考答案:3.质量分别为m A和m B (m A>m B)、速度分别为和 (v A> v B)的两质点A和B，受到相同的冲量作用，则（）参考答案:A、B的动量增量相等4.质量为20 g的子弹，以400 m/s的速率沿图示方向射入一原来静止的质量为980 g的摆球中，摆线长度不可伸缩．子弹射入后开始与摆球一起运动的速率为（）参考答案:4 m/s5.一质量为M的斜面原来静止于水平光滑平面上，将一质量为m的木块轻轻放于斜面上，如图．如果此后木块能静止于斜面上，则斜面将（）参考答案:保持静止第四章测试1.一质点在如图所示的坐标平面内作圆周运动，有一力作用在质点上．在该质点从坐标原点运动到(0，2R）位置过程中，力对它所作的功为（）参考答案:2.对功的概念有以下几种说法：(1) 保守力作正功时，系统内相应的势能增加．(2) 质点运动经一闭合路径，保守力对质点作的功为零．(3) 作用力和反作用力大小相等、方向相反，所以两者所作功的代数和必为零．在上述说法中：参考答案:只有(2)是正确的3.质量分别为m和4m的两个质点分别以动能E和4E沿一直线相向运动，它们的总动量大小为参考答案:4.一个作直线运动的物体，其速度v与时间t的关系曲线如图所示．设时刻t1至t2间外力作功为W1 ；时刻t2至t3间外力作功为W2 ；时刻t3至t4间外力作功为W3 ，则（）参考答案:W1＝0，W2＜0，W3＞05.如图，在光滑水平地面上放着一辆小车，车上左端放着一只箱子，今用同样的水平恒力拉箱子，使它由小车的左端达到右端，一次小车被固定在水平地面上，另一次小车没有固定．试以水平地面为参照系，判断下列结论中正确的是参考答案:在两种情况下，由于摩擦而产生的热相等第五章测试1.一刚体的转动惯量只决定于（）参考答案:刚体的质量对给定转轴的分布2.两个匀质圆盘A和B的密度分别为和，若，但两圆盘的质量与厚度相同，如两盘对通过盘心垂直于盘面轴的转动惯量各为J A和J B，则（）参考答案:3.有两个半径相同，质量相等的细圆环A和B．A环的质量分布均匀，B环的质量分布不均匀．它们对通过环心并与环面垂直的轴的转动惯量分别为JA和JB，则（）参考答案:J A= J B4.一轻绳绕于半径r=0.2m的飞轮边缘，在轮缘切向施以F=98N的拉力，若不计摩擦，飞轮的角速度等于39.2 rad/s2，此飞轮的转动惯量为（）参考答案:0.5 kg·m25.一个作定轴转动的物体，对转轴的转动惯量为J，正以角速度w 0 =10 rad·s-1匀速转动，现对物体加一个恒定反向力矩M=-0.5N·m，经过时间t=5s后，物体停止了转动。