二阶效应(PPT)
合集下载
二阶效应的不同情况
N
NN
=N e1
Mi
Mmax= M0+ Nf Mi
混凝土结构•计原理 第七章
3
-两个端弯矩不相等且符号相反
-一阶弯矩端部最,大=J M2,二阶弯矩N在距端部某位置最大。,=J Mmax= Mo+ N有两种可能的分布。NM2=N eM2
N
N
N ei
1 =-N e1
Mi
Mmax= M0+ Nf
情形1最,=大J 弯矩M2,二阶弯矩不引起最大弯矩的增加 情形2最大弯矩Mmax，距离端部某距离，Nf只能使Mmax比M2稍
构件中任意点弯矩M= Ne+ Ny, Ne,——阶弯矩，Ny―二阶弯矩 最,=j 大弯矩心双广Mo+ Nf
©M°=N e
N
TLN f
M0 e
Mmax= M0+ Nf
混凝土结构•计原理 第七章
•两端弯矩不相等，但符号相同 -构件的最大挠度位于离端部某位置。
-最大弯矩Mo+ Nf
N (\^M2=N eo
混凝土结构•计原理—■第七章二
由上述分析可得到如下结论: (1)当一阶最大弯矩处与二阶最大弯矩处重合时，弯矩
增加得最多； (2)两个弯矩不等但单曲率弯曲时，弯矩仍将增l=加i 较多;
(3)当构件两端弯矩不相等且为双曲率弯曲时，沿构件产 生 一个反弯点，弯矩增l加=i 很少。 由轴压力在杆件自身挠曲后引起的局部二阶效应。仅在少 数 偏压构件中起控制作用，反弯点不在柱高范围内的较细长 偏 心压杆属于这类情况。
混凝土结构•计原理—■第七章
•:•二阶效应的不同情况
结构的二阶效应不仅与结构形式、 构件的几何尺寸有关, 还与构件有受力特点（变形曲率、 轴压比）有关。
NN
=N e1
Mi
Mmax= M0+ Nf Mi
混凝土结构•计原理 第七章
3
-两个端弯矩不相等且符号相反
-一阶弯矩端部最,大=J M2,二阶弯矩N在距端部某位置最大。,=J Mmax= Mo+ N有两种可能的分布。NM2=N eM2
N
N
N ei
1 =-N e1
Mi
Mmax= M0+ Nf
情形1最,=大J 弯矩M2,二阶弯矩不引起最大弯矩的增加 情形2最大弯矩Mmax，距离端部某距离，Nf只能使Mmax比M2稍
构件中任意点弯矩M= Ne+ Ny, Ne,——阶弯矩，Ny―二阶弯矩 最,=j 大弯矩心双广Mo+ Nf
©M°=N e
N
TLN f
M0 e
Mmax= M0+ Nf
混凝土结构•计原理 第七章
•两端弯矩不相等，但符号相同 -构件的最大挠度位于离端部某位置。
-最大弯矩Mo+ Nf
N (\^M2=N eo
混凝土结构•计原理—■第七章二
由上述分析可得到如下结论: (1)当一阶最大弯矩处与二阶最大弯矩处重合时，弯矩
增加得最多； (2)两个弯矩不等但单曲率弯曲时，弯矩仍将增l=加i 较多;
(3)当构件两端弯矩不相等且为双曲率弯曲时，沿构件产 生 一个反弯点，弯矩增l加=i 很少。 由轴压力在杆件自身挠曲后引起的局部二阶效应。仅在少 数 偏压构件中起控制作用，反弯点不在柱高范围内的较细长 偏 心压杆属于这类情况。
混凝土结构•计原理—■第七章
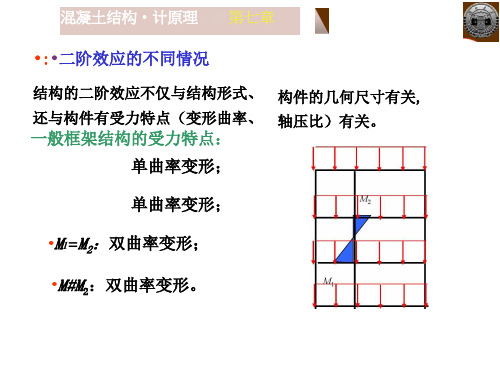
•:•二阶效应的不同情况
结构的二阶效应不仅与结构形式、 构件的几何尺寸有关, 还与构件有受力特点（变形曲率、 轴压比）有关。
第4章二阶非线性光学效应
0
1 n2
2
E0 0
1
n
2 y
,
1 n2
5
E0 0
0
1 n2
3
E0 0
1 nz2
,
1 n2
6
E0 0
0
(4.1-7)
第4章 二阶非线性光学效应
1） KDP（KH2PO4）晶体中的线性电光效应
KDP晶体属于42m对称群, 其光轴取为z轴, 另外两 个对称轴为x轴和y轴。 根据表4.1-1, 它的线性电光张量 的非零元素只有γ41=γ52和γ63, 其矩阵形式为
[ (2) (3,1)
:
a(2 )a(3)a(1)]E(3,
z)E(1,
z)eikz
(4.3-12)
dE(3, t )
dz
i32
k3c2
[ (2) (1,2 )
:
a(3)a(1)a(2 )]E(1,
z ) E (2 ,
z)eikz
(4.3-13)
第4章 二阶非线性光学效应
4.3.2 曼利-罗关系
乘 乘
第4章 二阶非线性光学效应
线性电光效应是一种特殊的二阶非线性光学效应。 在这里, 作用于介质的两个电场， 一个是光电场, 另一 个是低频场或直流场, 在这两个电场的作用下产生了二 阶非线性极化。 现在假定作用于介质的直流场为E0、 光电场为E exp(-iωt)+c.c., 则根据极化强度的一般表示 式（1.1-39）式和（1.1-40）式, 有
z )e ik 2 z
dE(3,
dz
z)
i320
2k3
a(3)
PNL (3,
z )e ik3 z
二阶效应规范规定(可直接使用).ppt
优选文档
4
◆说明：轴向压力在挠曲杆件中产生的二阶效应（效应）
是偏压杆件中由轴向压力在产生了挠曲变形的杆件内引起 的曲率和弯矩增量。例如结构中常见的反弯点位于柱高中 部的偏压构件中，这种二阶效应虽能增大构件除两端区域 外各截面的曲率和弯矩，但增大后的弯矩通常不可能超过 柱两端控制截面的弯矩。因此，在这种情况下，效应不会 对杆件截面的偏心受压承载能力产生不利影响。但是，在 反弯点不在杆件高度范围内（即沿杆件长度均为同号弯矩） 的较细长且轴压比偏大的偏压构件中，经效应增大后的杆 件中部弯矩有可能超过柱端控制截面的弯矩。此时，就必 须在截面设计中考虑效应的附加影响。因后一种情况在工 程中较少出现，为了不对各个偏压构件逐一进行验算，本
杆件挠曲二阶效应
优选文档
3
● 6.2.3条： 弯矩作用平面内截面对称的偏心受压构件，当同一主轴
方向的杆端弯矩比M1/M2不大于0.9且设计轴压比不大于0.9时，若构
件的长细比满足下式要求时，可不考虑轴向压力在该方向挠曲杆件 中产生的附加弯矩影响；否则应按截面的两个主轴方向分别考虑轴 向压力在挠曲杆件中产生的附加弯矩影响。
条给出了可以不考虑效应的条件。
优选文档
5
● 6.2.4条：考虑轴向压力在挠曲杆件中产生的二阶效应后控 制截面弯矩设计值应按下列公式计算：
M CmhnsM 2
Cm
0.7
0.3
M1 M2
hns
1 1300(M 2
1 /N
ea ) /h0来自lc h2c
c
0.5 fc A N
Cm—构件端截面偏心距调节系数，当小于0.7时取0.7；
hns—弯矩增大系数；
N —与弯矩设计值M2相应的轴向压力设计值；
二阶效应(PPT)
0.50
注：1、我国02规范、美国ACI规范规定：当验算表明剪力墙或筒体不 开裂时，剪力墙、筒体的刚度折减系数取为0.7；
2、在考虑内力的增大效应时，构件宜采用折减后的弹性弯曲刚度； 在考虑对层间位移的增大效应时，不对弹性弯曲刚度进行折减。
2、层增大系数法（P ）
➢ 层增大系数法
将产生侧移的框架结构中取出一根柱如图所示：
M B qH 2 3； yn 11qH 4 120Ec I0
带入上式得到最终表达式：
1
c 1 0.14H 2 Gi EcI0
实际结构并非等截面悬臂杆，可先求得实际结构在一 个给定倒三角形分布水平荷载下的顶点位移，并令这一顶 点位移与一个和实际结构等高的受同样倒三角形分布水平 荷载作用的等截面悬臂杆的顶点位移相等，从而求出这一 等截面悬臂杆对应的抗弯刚度，并以这一抗弯刚度作为真
B1
n
M B1 Gi yi
i1
各层水平位移将在 yi 的基础上产生增量 y1i，根据第二
项基本假定即可写出：
y1i yi
Gi yi M B
y1i
Gi yi MB
yi
取：C
Gi yi MB
（稳定系数）； 有：y1i Cyi
根据 P 效应迭代法的思路，在水平位移增大后，
各层竖向荷载又会在结构底截面引起弯矩增量，即：
yi 1 C C 2 C 3 L
当C<1.0时，上式即可改写为：yi f
yi
1 1C
这意味着各层位移具有相同的增大系数c ：
c
yi f
yi
1 1C
1
1 Gi yi M B
根据第一个假定位移曲线为一斜直线，则上式可改写
为：
混凝土结构的二阶效应
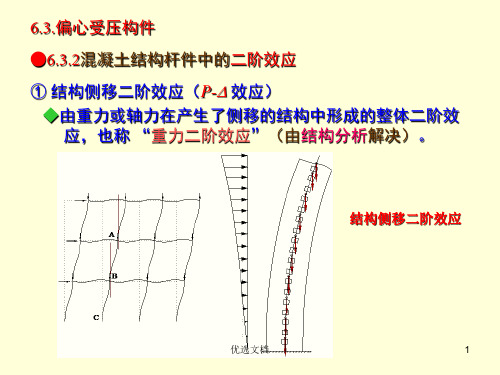
一、混凝土结构的二阶效应混凝土结构的二阶效应应由两部分组成：p-δ效应和P-Δ效应。
p-δ效应是指由于构件在轴向压力作用下，自身发生挠曲引起的附加效应，可称之为构件挠曲二阶效应，通常指轴向压力在产生了挠曲变形的构件中引起的附加弯矩，附加弯矩与构件的挠曲形态有关，一般中间大，两端部小。
P-Δ效应是指由于结构的水平变形而引起的重力附加效应，可称之为重力二阶效应，结构在水平力（风荷载或水平地震力）作用下发生水平变形后，重力荷载因该水平变形而引起附加效应，结构发生的水平侧移绝对值越大，P-Δ效应越显著，若结构的水平变形过大，可能因重力二阶效应而导致结构失稳。
1.重力二阶效应（P-Δ效应）计算计算P-Δ效应的近似方法有等效几何刚度的有限元法、等效水平力的有限元迭代法、折减弹性抗弯刚度的有限元、结构位移和构件内力增大系数法等。
1）等效几何刚度的有限元法在不考虑P-Δ效应影响时，是在结构的初始拓扑关系基础上建立结构的平衡方程。
一般可记为：[K]{u}=[F]考虑P-Δ效应影响时，对于结构的任一节点j，因P-Δ效应而引起的Mj=Gjuj，相应的等效附加水平力为Vj= 。
对于所有节点，则形成一个等效附加水平分力向量。
可以看出，考虑P-Δ效应相当于结构的初始刚度矩阵[K]修改为等效刚度矩阵[K-KG]。
新规范版的SATWE、TAT、PMSAP等软件都采用了等效几何刚度的有限元法，这种方法具有一般性，它既适用于采用刚性楼板假定的结构，也适用于存在独立弹性节点的结构。
与不考虑P-Δ效应的分析结果相比，结构的周期、位移和构件的内力都有所不同。
2）折减弹性抗弯刚度的有限元法折减弹性抗弯刚度的有限元法是今年来美国、加拿大等国设计规范推荐的一种考虑效益方法。
这种分析方法的基本思路是采用折减等效刚度，近似的考虑钢筋混凝土结构中各类构件在极限状态时因开裂而导致刚度减小现象，使分析结果与设计状态尽可能一致。
《混凝土结构设计规范》引进该方法，第7.3.12规定，当采用考虑二阶效应的弹性分析方法时，宜在结构分析中对钢筋混凝土构件的弹性抗弯刚度乘以一下折减系数：梁取0.4，柱取0.6，对未开裂的剪力墙和核心筒取0.7，对已开裂的剪力墙和核心筒壁取0.45。
二阶效应
M M ns s M s
(B.0.1-1） (B.0.1-1）
s 1
M M ns s M s
弯矩设计值；
端弯矩设计值；
s 1
B.0.2 框架结构中，所计算楼层各柱的 式计算（层增大系数法）：
可按下列 公
s
N 1
1
j
DH 0
B.0.3 剪力墙结构、框架－剪力墙结构、筒体结构中的 可按下列公式计算（整体增大系数法）：
M1 Cm 0.7 0.3 0.7 M2
M Cm ns M 2
M1 Cm 0.7 0.3 M2
1 lc ns 1 c 1300(M 2 / N ea ) / h0 h
2
0.5 f c A c N
6.2.20 轴心受压和偏心受压柱的计算长度 l0 可按 下列规定确定：
新修订规范解决方法：两种二阶效应分开考虑
P 效应：计算机计算 “考虑几何非线性的弹性有限元
法” 手算“层增大系数法”或“整体增大系数法”
P 效应：C
m
法（计算长度取支承长度） ns
5.3.4 混凝土结构的重力二阶效应可采用有限元分析方法
计算，也可采用本规范附录B的简化方法。当采用有限元 分析方法时，宜考虑混凝土构件开裂对构件刚度的影响。
1 s H 2G 1 0.14 Ec J d
对排架结构的二阶效应，近年来少有研究，故仍采 用原来的方法。 B.0.4 排架结构柱考虑二阶效应的弯矩设计值可按 下列公式计算：
M s M 0
l0 c h
2
1 s 1 1500 e0 / h0
0.5 f c A c N
(非线性光学课件)第三章 二阶非线性光学效应
i
D3
2cn3
(2)(3;1,2)E1(z)E2(z)exp(ikz)
12
dEd1z(z) i2Dcn11 (2)(1;2,3)E2*(z)E3(z)expi(kz)☆
dEd2z(z)
i
D2
2cn2
(2)(2;3,1)E3(z)E1*(z)expi( kz)
dE3(z) dz
i
D3
2cn3
(2)(3;1,2)E1(z)E2(z)exp(ikz)
P P12((22))((zz))D D00χχ((22))(( 12;;32, ,31))::eeˆˆ23eeˆˆ31E E32*EE1*3 P3(2)(z)D0χ(2)(3;1,2):eˆ1eˆ2E1E2
描述了两个差频过程与一个和频过程
9
E (zz)2i 0ce n ˆPN(L z)exi p kz)(
eˆ3
χ(2)(3;1,2):eˆ1eˆ2
极化率的三个分量写成如下标量形式
( 2 ) (1 ; 2 ,3 ) e ˆ 1 χ ( 2 ) (1 ; 2 ,3 ) :e ˆ 2 e ˆ 3
( 2 ) (2 ;3 , 1 ) e ˆ 2 χ ( 2 ) (2 ;3 , 1 ) :e ˆ 3 e ˆ 1
☆
dE3(z) dz
2ic3n3 Deˆ3
χ(2)(3;1,2):eˆ1eˆ2E1E2exp(ikz)
dEd1z(z) dEd2z(z)
i2Dcn11 (2)(1;2,3)E2*(z)E3(z)expi(kz)
i
D2
2cn2
(2)(2;3,1)E3(z)E1*(z)expi( kz)
dE3(z) dz
☆
并应用此方程组研究几种典型的二阶非线性光学效应：
【高中物理】优质课件：MOS器件的二阶效应
Cgd
W L
tox
R基本不变, 但是C减小， D 减小
结论：器件尺寸连同VDD同步缩小，器件的速度提高。
Scaling-down
MOSFET的跨导gm
MOSFET的跨导 gm的定义为：
gm
Ids Vgs Vdsconstant
MOSFET I-V特性求得
gm
W
tox L
Vgs VT
MOS管二阶效应
降低VT 的方法 ：
1) 降低衬底中的杂质浓度，采用高电阻率的衬底; 2) 减小SiO2介质的厚度 tox。
缩小尺寸后：栅长、阈值电压、与电源电压对比
L(m) 10
2
0.5 0.35 0.18
VT(V) 7-9
4
1
VDD(V) 20
12
50.Βιβλιοθήκη 0.4 3.3 1.8Scaling-down
式中0(T)是温度的函数， 0(T) = kT M ;
fv是垂直电场的退化函数； fh是水平电场的退化函数
MOS管二阶效应
迁移率的退化
1） 特征迁移率0
0与制造工艺密切相关，0还与温度T有关，温度升高 时，0就降低。如果从25℃增加到100℃，0将下降一半。
0 0
T2 T1
T2 T1
M
在半导体Si内一般认为，
Ldrawn是图上绘制的栅极长度。 Lfinal是加工完后的实际栅极长度。Lfinal = Ldrawn2Lpoly
MOS管二阶效应
迁移率的退化（二阶效应）
MOS迁移率并不是常数。从器件的外特性来看， 至少有三个因素影响值，它们是：温度T，垂直电场 Ev，水平电场Eh。
可以表示为：
= 0(T)fv(Vg,Vs,Vd)fh(Vg,Vs,Vd)
超快光学 第08章 非线性二阶效应
耦合波方程
02
01
03
耦合波方程是描述两个或多个波相互作用的数学模型 ，常用于描述非线性光学中的双波耦合现象。
它是一个非线性偏微分方程组，描述了不同波长或模 式的波在非线性介质中的相互作用和能量转换。
耦合波方程的解可以揭示双波耦合过程中的相位匹配 条件、能量转移速率等关键参数。
极化率与非线性折射率
光束整形与光束控制
光束整形是指改变光束的形状、大小、方向等参数的过程。 利用非线性二阶效应，可以对光束进行整形，实现光束的聚 焦、扩散、弯曲等操作。
光束控制是通过对光束的传播进行精确调控，实现光束的稳 定传输和精确指向。非线性二阶效应在光束整形与控制中的 应用，有助于提高光学系统的性能和稳定性。
04
得更加显著，影响非线性二阶效应的表现。
02
非线性二阶效应的数学模型
薛定谔方程
薛定谔方程是描述光场与物质相互作用的基本方程 ，用于描述光在非线性介质中的传播行为。
它是一个非线性偏微分方程，包含了光场与物质相 互作用的非线性项，能够描述光束在介质中的自聚 焦、自散焦等非线性现象。
薛定谔方程的解可以揭示光在非线性介质中的演化 过程，包括光束的形状变化、分裂、聚焦等。
实现信息处理，如光学倍 频、光学参量振荡等，为光学通信、光学传感等领 域提供技术支持。
非线性二阶效应的物理机制
01
光场与物质相互作用
非线性二阶效应的产生源于光场与物质的相互作用，当光场强度足够高
时，光子与物质中的电子发生相互作用，导致物质对光的响应表现出非
线性的行为。
高级量子理论
随着量子理论的深入发展，更高级的量子理论模型将为非线性二阶效应提供更 精确的描述和预测，有助于深入理解非线性光学的本质。
现代钢结构进展——二阶效应和半刚性-PPT课件
现 代 钢 结 构 进 展 —— 二阶效应
高等分析设计方法
是以整个结构体系为对象，考虑几何非线性和材料非线性（即二阶弹 塑性）的结构分析设计方法。由该方法可求得在特定荷载作用下结构 体系的极限承载力和失效模态，而无需对各个构件进行验算。 目前，欧洲钢结构规范（EC3）和澳大利亚钢结构标准都列有二阶弹 塑性分析或高等分析的条款。已颁布实施的《钢结构设计规范》 (GB50017—2019)也将钢框架二阶分析方法纳入设计条文，这表明二阶 分析设计方法用于工程设计已变得越来越重要。
图（a）的框架仅承受水平荷载H时，柱顶有位移△。此时 若在两柱顶施加竖载P，则力矩P△使框架两柱脚各增加水 平力P△／h，即相当于在柱顶作用有水平力2P△／h，如 图（b）所示。此水平力进一步产生附加水平位移，故总 位移应为△’ >△。此效应称为P—△效应，也称为框架 的二阶效应。
现 代 钢 结 构 进 展 —— 二阶效应
2 n P P P n * 01 0 i h S h S h S
总侧移和一阶分析的侧移的比值，定义为放大系数m ：
P P P m 1
现 代 钢 结 构 进 展 —— 二阶效应
二阶效应
现 代 钢 结 构 进 展 —— 二阶效应
构件的二阶效应
图（a）为受均布荷载作用的两端 铰接的受弯构件，最大挠度为δ。 图（b）为受均布荷载作用的两端 铰接的压弯构件，最大挠度为δ’ >δ 。 图（c）为考虑与不考虑P影响的 构件弯矩图。
q l2 q l2 M P m a x 8 8
二阶分析所得的柱端弯矩：
( ） H 2 H H Pm P m * 0 M Pm ( ） h h 1 h 1 H 0 2 2 2 S h h 2 H hmm M P 2P 。） 0 （注意：对上图，m中的 2
张毅 第三章 二阶非线性光学效应1资料讲解
☆
dE3(z) dz
2ic3n3 Deˆ3
χ(2)(3;1,2):eˆ1eˆ2E1E2exp(ikz)
dEd1z(z) dEd2z(z)
i2Dcn11 (2)(1;2,3)E2*(z)E3(z)expi(kz)
i
D2
2cn2
(2)(2;3,1)E3(z)E1*(z)expi( kz)
(E1E1*E2E2*)
可以用一个简单公式来概括， 即将二阶极化强度在频域内进行傅里叶展开
P (2)(t) P (n)ex i pnt)(
n
9
P (2)(t) P (n)ex i pnt)(
☆
n
这些频率成分以及它们对应的二阶非线性效应如下
PPP(((221 21))2)002((22)) EE01222(2)E1E2 P(1 2) 20(2)E1E2* P(0) 20(2)(E1E1* E2E2*)
4
本章将推导此方程组，
☆
并应用此方程组研究几种典型的二阶非线性光学效应：
光学倍频、和频、差频、参量过程，
推导出这些过程的光功率效率公式。
相位匹配和相位失配是非线性光学的重要概念， 相位匹配实质上是指光电场与介质没有动量交换， 即所谓的“动量守恒”；
相位失配就是光与介质之间有动量交换。
本章以二阶效应为例， 给出相位匹配的概念，相位匹配的条件， 以及实现相位匹配的方法。
eˆ3
χ(2)(3;1,2):eˆ1eˆ2
极化率的三个分量写成如下标量形式
( 2 ) (1 ; 2 ,3 ) e ˆ 1 χ ( 2 ) (1 ; 2 ,3 ) :e ˆ 2 e ˆ 3
( 2 ) (2 ;3 , 1 ) e ˆ 2 χ ( 2 ) (2 ;3 , 1 ) :e ˆ 3 e ˆ 1
版图二阶效应
版图二阶效应二阶效应可以分为重力二阶效应(p−Δ)和构件挠曲二阶效应(p−δ)，下面我们分别从这两者来探讨在混凝土结构设计中如何考虑二阶效应的影响:1.重力二阶效应当结构重力产生的附加弯矩大于初始弯矩的10%时需要考虑重力二阶效应，现行结构设计规范利用增大系数法（GB50010附录B、JGJ3-2010.5.4.3条和GB50010.3.6.3条文说明）考虑重力二阶效应的影响：M=Mns+ηsMs其中Ms为引起结构侧移的荷载所产生的一阶弹性分析构件端弯矩设计值（如水平地震作用）；Mns为不引起结构侧移的一阶弹性分析构件端弯矩设计值（如对称结构在均布重力荷载作用下）。
上式使用了叠加原理的概念，即设计弯矩可以拆分为产生侧移荷载产生的弯矩和不产生侧移的荷载的弯矩之和，而重力二阶效应仅增加产生层间侧移的部分。
变形增量也同样使用增大系数法考虑：Δ=ηsΔ1上述的Δ为一阶弹性分析的层间位移，ηs为增大系数。
增大系数以框架结构举例：ηs=11−∑inGjDH0上式中D为侧移刚度；H0为计算楼层的层高；∑inGj为第i层以上全部重力荷载设计值之和。
对上式分母第二项略作化简可以得到：∑inGjΔuiViH0其中Δui层平均层间侧移；Vi为楼层剪力；可以发现，上式即为“重力附加弯矩与初始弯矩的比值”（具体定义参见何时需要考虑二阶效应？），由此可以发现，增大系数的表达式含义其实十分“朴素”，简单来说就是：考虑重力二阶效应弯矩值一阶弹性分析的弯矩值ηs=考虑重力二阶效应弯矩值一阶弹性分析的弯矩值关于增大系数的计算有下面两点值得注意：计算位移增大系数时，不对构件的刚度进行折减（JGJ3-2010.5.4.3条，GB50010.B.0.5）。
因为设计规范中给出的限值均为弹性位移限制，弹性位移限值需要和弹性位移计算结果所匹配。
计算内力增大系数时，对构件刚度进行折减，《高规》折减系数取0.5，《混规》则对不同构件选取不同的折减系数，见B.0.5条。
二阶效应
小偏压构件截面曲率修正系数1：对于小偏压构件，离纵向力 较远一侧钢筋可能受拉不屈服或受压，且受压区边缘混凝土的 应变值 c一般也小于 0.0033，截面破坏时的曲率小于界限破坏 时曲率值b 。 偏心受压构件长细比对截面曲率的影响系数 2：随着长细比的 增大，达到最大承载力时截面应变值 c和 s减小，使控制截面
的极限曲率随l0/h的增加而减小。
结束！ 谢谢大家！
一般讲，长柱和细长柱必须考虑横向挠度af对构件承载力的影响。
—l0法：
偏心距增大系数： =
0.5 f c A 1 =
ei a f ei
1 l0 = 1 = 1 1 2 ei 1400 e i / h0 h
l0 h
af
2
2 = 1.15 0.01×
le
N( N (ee i+ ff)) i+a
x ei
N
①短柱：长细比 l0/h≤5 （对矩形、 T 形和 I 形截面），或 l0/d≤5 （对圆形、环形截面）； ②长柱：长细比l0/h或l0/d的值在5和30之间； ③细长柱：长细比l0/h或l0/d>30。 随着长细比的增大，构件的承 载力依次降低。从破坏形态分 析，短柱、长柱属于材料破坏， 而细长柱会发生失稳破坏。工 程中应尽可能避免采用细长柱， 以免使构件乃至结构整体丧失 稳定。
二阶效应
5 结构侧移和构件挠曲引起的附加内力 偏心受压构件会产生横向挠度 af，因此，横向总侧移为ei+af，构 件承担的实际弯矩M＝N(ei+af )=Nei(1+af/ei)，其值明显大于初始 ei 弯矩N· ei，称为“二阶效应”。
y 在有侧移框架中，二阶效应主要是指竖 向荷载在产生了侧移的框架中引起的附 px y = f × sin 加内力，通常称为P-Δ效应。在这类框架 le 的各个柱段中，P-Δ效应将增大柱端控制 af f 截面中的弯矩；在无侧移框架中，二阶 效应是指轴向压力在产生了挠曲变形的 柱段中引起的附加内力，就是 p-效应， 它有可能增大柱段中部的弯矩，但除底 层柱底外，一般不增大柱端控制截面的 弯矩 N N ei
混凝土结构的二阶效应
一、混凝土结构的二阶效应混凝土结构的二阶效应应由两部分组成：p-δ效应和P-Δ效应。
p-δ效应是指由于构件在轴向压力作用下，自身发生挠曲引起的附加效应，可称之为构件挠曲二阶效应，通常指轴向压力在产生了挠曲变形的构件中引起的附加弯矩，附加弯矩与构件的挠曲形态有关，一般中间大，两端部小。
P-Δ效应是指由于结构的水平变形而引起的重力附加效应，可称之为重力二阶效应，结构在水平力（风荷载或水平地震力）作用下发生水平变形后，重力荷载因该水平变形而引起附加效应，结构发生的水平侧移绝对值越大，P-Δ效应越显著，若结构的水平变形过大，可能因重力二阶效应而导致结构失稳。
1.重力二阶效应（P-Δ效应）计算计算P-Δ效应的近似方法有等效几何刚度的有限元法、等效水平力的有限元迭代法、折减弹性抗弯刚度的有限元、结构位移和构件内力增大系数法等。
1）等效几何刚度的有限元法在不考虑P-Δ效应影响时，是在结构的初始拓扑关系基础上建立结构的平衡方程。
一般可记为：[K]{u}=[F]考虑P-Δ效应影响时，对于结构的任一节点j，因P-Δ效应而引起的Mj=Gjuj，相应的等效附加水平力为Vj=。
对于所有节点，则形成一个等效附加水平分力向量。
可以看出，考虑P-Δ效应相当于结构的初始刚度矩阵[K]修改为等效刚度矩阵[K-KG]。
新规范版的SATWE、TAT、PMSAP等软件都采用了等效几何刚度的有限元法，这种方法具有一般性，它既适用于采用刚性楼板假定的结构，也适用于存在独立弹性节点的结构。
与不考虑P-Δ效应的分析结果相比，结构的周期、位移和构件的内力都有所不同。
2）折减弹性抗弯刚度的有限元法折减弹性抗弯刚度的有限元法是今年来美国、加拿大等国设计规范推荐的一种考虑效益方法。
这种分析方法的基本思路是采用折减等效刚度，近似的考虑钢筋混凝土结构中各类构件在极限状态时因开裂而导致刚度减小现象，使分析结果与设计状态尽可能一致。
《混凝土结构设计规范》引进该方法，第7.3.12规定，当采用考虑二阶效应的弹性分析方法时，宜在结构分析中对钢筋混凝土构件的弹性抗弯刚度乘以一下折减系数：梁取0.4，柱取0.6，对未开裂的剪力墙和核心筒取0.7，对已开裂的剪力墙和核心筒壁取0.45。
二阶效应分析课件
ABAQUS
总结词
高度模块化、易于扩展的有限元分析软件
详细描述
ABAQUS是一款高度模块化、易于扩展的 有限元分析软件，广泛应用于工程领域。它 可以进行二阶效应分析，包括结构、流体和
耦合场等问题。
MSC Nastran
要点一
总结词
专为航空航天领域设计的有限元分析软件
要点二
详细描述
MSC Nastran是一款专为航空航天领域设计的有限元分析 软件，可以进行二阶效应分析，包括结构、流体和声场等 问题。它具有高度的可靠性和精度，广泛应用于航空航天 工业。
模型建立复杂度高
二阶效应分析涉及到多个因素和多个层次的相互 作用，需要建立复杂的数学模型来描述这些关系。 然而，模型的建立需要高度的专业知识和技能， 同时也需要大量的计算资源。
缺乏统一的评价标准
目前，二阶效应分析还没有一个统一的评价标准， 不同的研究可能采用不同的评价方法，这使得结 果的比较和整合变得困难。
结果分析
提取关键数据
从结果中提取关键数据，如最大应力、 最大应变等。
绘制图表
根据关键数据绘制图表，应力云图、 应变云图等。
结果评估
根据分析目标和图表结果，评估结构 的性能和安全性。
优化建议
根据评估结果，提出优化建议，如改 进结构形状、调整材料属性等。
PART 04
二阶效应分析案例
案例一：桥梁结构的二阶效应分析
在实际应用中，需要根据问题的性质和要求选择合适的分析方法，以达到最好的 分析效果。
PART 03
二阶效应分析步骤
建立模型
确定分析目标
明确二阶效应分析的目的，如结构优化、振 动控制等。
选择模型类型
根据分析目标选择合适的模型类型，如有限 元模型、边界元模型等。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
➢ 整体增大系数法的推导如下：
假定一高层建筑结构在水平荷载作用下产生的一阶弹性水
平 位 移 如 图 ， 各 层 竖 向 荷 载 Gi 在 结 构 底 截 面 中 产 生
的附加弯矩为
M
，其值为：
B1
n
M B1 Gi yi
i1
各层水平位移将在 yi 的基础上产生增量y1i ，根据第二
项基本假定即可写出：
（c）没有用于计算杆件自身挠曲 P 变形的条文规定。 （d）各本规范之间二阶效应的计算方法不协调。
（e）用 增大组合弯矩 M (Mns Ms ) 的作法没有反映 P 效应的
实际规律，即引起结构侧移的弯矩
M
M
ns
M
才被
s
P 效应增大；
● 考虑折减构件刚度的弹性二阶分析方法，尽管规范条文有规定，
2、层增大系数法（P ）
➢ 层增大系数法
将产生侧移的框架结构中取出一根柱如图所示：
Vij
ij Nij
*i lij
Vi
n
ij Nij
j 1
*i lij
n
*i
Vi
n
Vi
Vi
j 1
ij Nij
n
lij
*i
Di*j
Di*j
j 1
j 1
则：Βιβλιοθήκη ni*i i
n
Dij
j 1
n
Di*j
材料非弹性的特点。否则计算出的附加弯矩可能
小 40~60%。
本次《规范》对二阶效应修订的内容
➢ 现行《规范》02有关二阶效应规定存在的不足：
● 对于简化计算方法“ l0 法”，主要有： （a）主要用于有侧移框架结构和排架结构的 P 效应计算，造成误
用于各种结构形式和用于 P 计算效应； （b）用于有侧移的框架结构时，不能满足“层效应”；
根据前式，水平位移增量也可表示为：
y2i
yi
M B2 MB
yiC
M B1 MB
C2yi
这样，第k次位移增量即为： yki Ck yi
第i层的最终位移可表示为：
y1i yi
Gi yi M B
y1i
Gi yi MB
yi
取：C
Gi yi MB
（稳定系数）； 有：y1i Cyi
根据 P 效应迭代法的思路，在水平位移增大后，
各层竖向荷载又会在结构底截面引起弯矩增量，即：
n
n
M B2 Gi y1i C Gi yi CM B1
i1
i1
则有： M B2 CM B1 C2M B
平荷载弯矩 M1 、M 2 之间的关系为：
Vclc M1 M 2
在考虑了 P 效应后，虽然柱上、下端弯矩增大为sM1 和 sM 2 ，但计算柱剪力时除这两个柱端弯矩外尚应考虑 P 效应弯矩，如上图：
Vclc s M1 M 2 Ns1
由于：Vclc M1 M 2 ，则 s 1 M1 M 2 Ns1 即考虑
4、整体增大系数法（ P ）
该方法针对高层建筑结构，有如下两点假设： 水平荷载沿结构高度的分布规律有一定变化时，结构水平
位移曲线形状的变化不显著，变形曲线假设为一直线。 当 P 效应导致结构的侧向变形增大时，认为结构的顶点
位移增长始终与结构底截面的倾覆弯矩的增长成正比。 有了结构水平位移曲线形状的假定，则任何一个楼层在水 平荷载下的水平位移 也与结构底截面倾覆力矩成比例。
二阶效应与不考虑二阶效应构件中的剪力是相同的。
3、 l0 法（P ）
➢ l0 法
我国以截面达到极限曲率推导出“极限曲率表达式”， 美国ACI规范以截面达到极限承载力推导出“极限轴力表
达
式”，二者相互等效。
➢ 以“极限曲率表达式”为例：
假设变形曲线为正弦曲线；
假设控制截面达到大、小偏心界限破坏的到对应的曲率
工程中结构二阶效应的计算方法
P 效应分析方法
1. 考虑构件刚度折减的弹性二阶 分析方法
① 整体增大系数法
2. 增大系数法
P 效应分析方法
② 层增大系数法
③ l0 法
①
法
适用范围
各类混凝土结构
剪力墙结构、框架-剪力墙结构、框架-核心筒结构、内筒-外框筒结构以及所有 符合这一方法基本假 定的其他高层结构
框架结构 框架结构 、排架结构
受压杆件
在二阶效应计算中需注意的主要问题：
➢
P 效应只增大引起结构侧移的弯矩
M
，不增
h
大不引起结构侧移的弯矩 Mv ，即：
M Mv Mh （ --弯矩增大系数）
➢ 同层各柱柱端 Mh 被 P 效应增大的比例应相同；
➢ 进行内力分析时，必须考虑钢筋混凝土结构构件
u ；
利用 1 和 2 分别对偏心距与长细比的影响进行修正，
得出：
1 1
1400 ei
h0
l0 h
2
1 2
➢ 侧移框架计算长度
l0 取值
l0 大小与构件两端的约 束有关。取构件两端A、B
反映约束条件的系数为 A、
B ,
A
EcIc lc
A
i1 A
EbIb lb
i1
B
EcIc lc
但工程中没有执行，用于工程的通用设计软件没有进行“构件刚度折减”
的弹性分析功能。
1、考虑折减构件刚度的弹性二阶 分析方法（P ）
➢ 对折减构件刚度后的结构进行弹性分析，并利用考虑
P 效应的结构进行非线性分析，对构件刚度的折减系
数进行校准。得出不同类型构件的刚度折减系数。
各国构件刚度折减系数
梁
B
i1 B
Eb Ib lb
i1
美国ACI规范有侧移框架 l0 取值
我国《规范》GB50010-2002的规定
我国规范框架结构柱的 l0 取值
楼盖类型
柱的类别
l0
现浇楼盖
底层柱 其余各层柱
1.0H 1.25H
装配式楼盖
底层柱
其余各层柱
1.25H 1.5H
当水平荷载产生的弯矩占总弯矩的75%以上时：
柱
剪力墙、
筒体
中国
0.4
0.6
0.45
美国
0.35
0.7
0.35
欧洲
0.5
0.5
0.50
注：1、我国02规范、美国ACI规范规定：当验算表明剪力墙或筒体不 开裂时，剪力墙、筒体的刚度折减系数取为0.7；
2、在考虑内力的增大效应时，构件宜采用折减后的弹性弯曲刚度； 在考虑对层间位移的增大效应时，不对弹性弯曲刚度进行折减。
ij Nij
lij
j 1
j 1
i
Vi
n
Dij
j 1
，由于是否考虑二阶效
n
应对各层的侧移刚度 Dij 影响不大，可以认为：
j 1
n
n
Dij
Di*j 1.0
j 1
j 1
有： i
1
n
n
1 ij Nij lij Dij
j 1
j1
值得注意的是构件中的剪力是不被增大的
对于未考虑二阶效应的柱中，柱剪力与柱上、下端一阶水