大学物理仿真实验凯特摆测量重力加速度
用凯特摆测量重力加速度 (7)

实验题目:用凯特摆测量重力加速度实验目的:学习凯特摆的实验设计思想和技巧,掌握一种比较精确的测量重力加速度的方法。
实验原理:设一质量为m 的刚体,其重心G 到转轴O 的距离为h ,绕O 轴的转动惯量为I ,当摆幅很小时,刚体绕O 轴摆动的周期T 为:mgh I T π2=(1)式中g 为当地的重力加速度.设复摆绕通过重心G 的轴的转动惯量为I G ,当G 轴与O 轴平行时,有I=I G +mh 2 (2)代入式(1)得:mgh mh I T G 22+=π (3)对比单摆周期的公式gl T π2= 可得 mhmh I l G 2+=(4),称为复摆的等效摆长。
因此只要测出周期和等效摆长便可求得重力加速度。
左图是凯特摆摆杆的示意图。
对凯特摆而言,两刀口间的距离就是该摆的等效摆长l 。
在实验中当两刀口位置确定后,通过调节A 、B 、C 、D 四摆锤的位置可使正、倒悬挂时的摆动周期T 1和T 2基本相等。
由公式(3)可得12112mgh mh I T G +=π (5) 22222mgh mh I T G +=π (6)其中T 1和h 1为摆绕O 轴的摆动周期和O 轴到重心G 的距离。
当T 1≈T 2时,h 1+h 2=l即为等效摆长。
由式(5)和(6)消去I G ,可得:()22222121214222T T T T a b g l h l π+-=+=+- (7)此式中,l 、T 1、T 2都是可以精确测定的量,而h 1则不易测准。
由此可知,a 项可以精确求得,而b 项则不易精确求得。
但当T 1=T 2以及 |2h 1-l | 的值较大时,b 项的值相对a 项是非常小的,这样b 项的不精确对测量结果产生的影响就微乎其微了。
实验仪器:凯特摆、光电探头、米尺、数字测试仪。
实验内容:1、仪器调节选定两刀口间得距离即该摆得等效摆长l ,使两刀口相对摆杆基本对称,并相互平行,用米尺测出l 的值,粗略估算T 值。
用凯特摆测量重力加速度

实验题目:用凯特摆测量重力加速度实验目的:学习凯特摆的实验设计思想和技巧,掌握一种比较精确的测量重力加速度的方法。
实验仪器:凯特摆、光电探头、米尺和VAFN多用数字测试仪。
实验原理:1,复摆。
质量为m的刚体,其重心G到转轴O的距离为h,绕O轴的转动惯量为I。
当摆幅很小时,刚体绕O转动的周期为(1)设复摆绕通过重心G的转动惯量为,当G轴与O轴平行时有:(2)代入(1)得:(3)对比单摆周期公式,可得:(4)l称为复摆的等效摆长,因此只要测出周期和等效摆长便可球的重力加速度。
2,凯特摆。
如左图对凯特摆而言,两刀口间距就是该摆的等效摆长l。
在实验种当两刀口位置确定后,通过调节A、B、C、D四摆锤的位置可以使正、倒悬挂时的摆动周期和基本相等,即。
由公式(3):(5)(6)当时,即为等效摆长。
由公式(5)和(6)可得:(7)此式中,l、T1、T2都是可以精确测定的量,而h1则不易测准。
由此可知,a项可以精确求得,而b项则不易精确求得。
但当T1=T2以及|2h1-l| 的值较大时,b项的值相对a项是非常小的,这样b项的不精确对测量结果产生的影响就微乎其微了。
实验步骤:1,仪器调节调节摆锤A、B、C、D到合适位置,是正,倒悬的摆动周期相等。
2,测量摆动周期测量凯特摆正,倒悬摆动10个周期的时间,等效摆长和转轴O到G的距离,记录如下:的A类不确定度:的B类不确定度:所以的展伸不确定度:同理,的展伸不确定度:同上,同上,将具体的数值代入一步写清楚3,计算重力加速度及其不确定度根据公式(7):所以:g=以下求的合成不确定度。
已知:(8)对(8)式等号两边取对数:等号两边求导并合并同类项:所以的合成不确定度公式为:(9)将上述数据代入(9):所以:注意单位由于,很小可以忽略,所以只合成g和的不确定度。
类似(8)到(9)的过程:所以:最后可得:不确定度取一到两位有效数字思考题:1,凯特摆测重力加速度,在实验设计上有什么特点?避免了什么量的测量?降低了哪个量的测量精度?实验上如何来实现?答:凯特摆测重力加速度设计特点是:减少一些量的测量,提高实验精度。
用凯特摆测量重力加速度实验报告 (7)

用凯特摆测量重力加速度化学物理系04级龚晓李PB042060022005-12-5实验目的:学习凯特摆的实验设计思想和技巧,掌握一种比较精确的测量重力加速度的方法。
实验原理:1、当摆幅很小时,刚体绕O轴摆动的周期:刚体质量m,重心G到转轴O的距离h,绕O轴的转动惯量I,复摆绕通过重心G的转轴的转动惯量为I G 。
当G轴与O轴平行时,有I=I G+mh2∴∴复摆的等效摆长l=( I G+mh2 )/mh2、利用复摆的共轭性:在复摆重心G旁,存在两点O和O´,可使该摆以O为悬点的摆动周期T₁与以O´为悬点的摆动周期T₂相同,可证得|OO´|=l,可精确求得l。
3、对于凯特摆,两刀口间距就是l,可通过调节A、B、C、D四摆锤得位置使正、倒悬挂时得摆动周期T₁≈T₂。
∴4π²/g=(T₁²+T₂²)/2l + (T₁²-T₂²)/2(2h₁-l) = a + b实验仪器:凯特摆、光电探头、米尺、数字测试仪。
实验内容:1、仪器调节选定两刀口间得距离即该摆得等效摆长l,使两刀口相对摆杆基本对称,并相互平行,用米尺测出l的值,粗略估算T值。
将摆杆悬挂到支架上水平的V形刀承上,调节底座上的螺丝,借助于铅垂线,使摆杆能在铅垂面内自由摆动,倒挂也如此。
将光电探头放在摆杆下方,让摆针在摆动时经过光电探测器。
让摆杆作小角度摆动,待稳定后,按下reset钮,则测试仪开始自动记录一个周期的时间。
2、测量摆动周期T₁和T₂调整四个摆锤的位置,使T₁和T₂逐渐靠近,差值小于0.001s,测量正、倒摆动10个周期的时间10T₁和10T₂各测5次取平均值。
3、计算重力加速度g及其标准误差σg 。
将摆杆从刀承上取下,平放在刀口上,使其平衡,平衡点即重心G。
测出|GO|即h₁,代入公式计算g。
推导误差传递公式计算σg 。
实验数据处理:1、l的值l=⅓(l₁+l₂+l₃)=74.17cmσ=0.03055cm,u A =σ/=0.01764cm,∴ΔA =t P·u A =1.32*0.01764=0.02328cmu B=ΔB /C=0.1/3=0.03333cm∴u L ==0.04066cmT e ==1.729s2、T₁和T₂的值T₁=1.72746sσ=2.525*10¯⁴s,u A =σ/=1.129*10¯⁴s∴ΔA =t P·u A =1.14*0.0001129=1.287*10¯⁴su B=ΔB /C=0.0001/3=0.3333*10¯⁴s∴u T1 ==1.329*10¯⁴sT₂=1.72751sσ=1.469*10¯⁴s,u A =σ/=0.6570*10¯⁴s∴ΔA =t P·u A =1.14*0.00006570=0.7489*10¯⁴su B=ΔB /C=0.0001/3=0.3333*10¯⁴s∴u T2 ==0.8197*10¯⁴s3、重力加速度gh₁=44.46cm∴g=4π²/[(T₁²+T₂²)/2l + (T₁²-T₂²)/2(2h₁-l)]=4π²/{(1.72746²+1.72751²)/(2*74.17*10¯²)+(1.72746²-1.72751²)/[2*(2*44.46*10¯²-74.17*10¯²)]}=9.813m/s²∴u g0.68 =g·{l¯²* u L²+[2 T₁/(T₁²+T₂²)]²·u T1²+[2 T₂/(T₁²+T₂²)]²·u T2²}=9.813*{(74.17*10¯²)¯²*(0.04066*10¯²)²+[2*1.72746/(1.72746²+1.72751²)]²*(1.329*10¯⁴)²+[2*1.72751/(1.72746²+1.72751²)]²*(0.8197*10¯⁴)²}=0.00545m/s²∴u g0.95 =2* u g0.68 =0.011 m/s²∴g=(9.813±0.011) m/s² P=0.95思考题:1、凯特摆测重力加速度,在实验设计上有什么特点?避免了什么量的测量?降低了哪个量的测量精度?实验上如何来实现?答:凯特摆测重力加速度在实验设计上把不可测的量转换成可测的量,利用复摆上两点的共轭性,对难以精确测定的量,有些避免了对其的测量,不能避免的则降低了其测量精度。
用凯特摆测量重力加速度 (4)
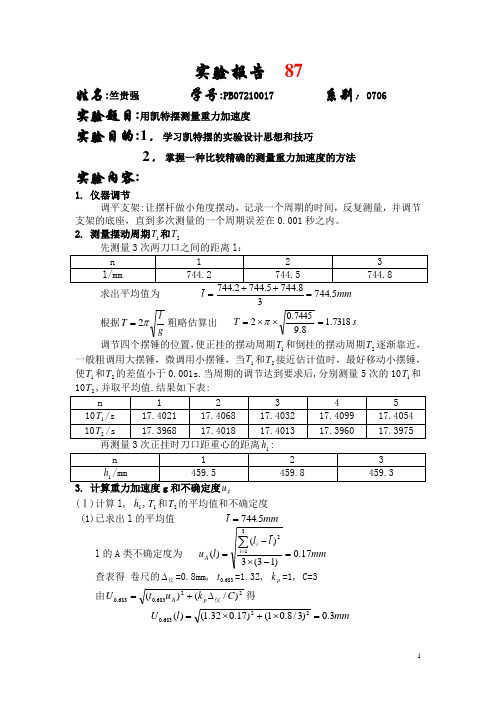
实验报告 87姓名:竺贵强 学号:PB07210017 系别:0706 实验题目:用凯特摆测量重力加速度实验目的:1.学习凯特摆的实验设计思想和技巧2.掌握一种比较精确的测量重力加速度的方法实验内容:1. 仪器调节调平支架:让摆杆做小角度摆动,记录一个周期的时间,反复测量,并调节支架的底座,直到多次测量的一个周期误差在0.001秒之内。
2. 测量摆动周期1T 和2T求出平均值为 mm l 5.7443== 根据gl T π2=粗略估算出 s T 7318.18.97445.02=⨯⨯=π 调节四个摆锤的位置,使正挂的摆动周期1T 和倒挂的摆动周期2T 逐渐靠近,一般粗调用大摆锤,微调用小摆锤,当1T 和2T 接近估计值时,最好移动小摆锤,使1T 和2T 的差值小于0.001s.当周期的调节达到要求后,分别测量5次的101T 和10g (Ⅰ)计算l, 1h ,1T 和2T 的平均值和不确定度 (1)已求出l 的平均值 mm l 5.744=l 的A 类不确定度为 mm l l l u i i A 17.0)13(3)()(312=-⨯-=∑= 查表得 卷尺的仪∆=0.8mm, 683.0t =1.32, p k =1, C=3由22683.0683.0)/()(C k u t U p A 仪∆+=得mm l U 3.0)3/8.01()17.032.1()(22683.0=⨯+⨯=所以 mm l )3.05.744(±= P=0.683(2)求出1h 的平均值 mm h 5.45933.4598.4595.4591=++=1h 的A 类不确定度为 mm h h h u i i A 15.0)13(3)()(312111=-⨯-=∑=查表得 卷尺的仪∆=0.8mm, 683.0t =1.32, p k =1, C=3由22683.0683.0)/()(C k u t U p A 仪∆+=得 mm h U 3.0)3/8.01()15.032.1()(221683.0=⨯+⨯=所以 mm h )3.05.459(1±= P=0.683(3)求出1T 的平均值 s T T i 74055.11010515111==∑=1T 的A 类不确定度为 s T T T u i i A 00014.0)15(5)()(512111=-⨯-=∑=取仪∆=0, 查表得 683.0t =1.14,由A u t U 683.0683.0=得s T U 00016.000014.014.1)(1683.0=⨯=所以 s T )00016.074055.1(1±= P=0.683(4)求出2T 的平均值 s T T i 73990.11010515122==∑=2T 的A 类不确定度为 s T T T u i i A 00011.0)15(5)()(512222=-⨯-=∑=取仪∆=0, 查表得 683.0t =1.14,由A u t U 683.0683.0=得s T U 00012.000011.014.1)(2683.0=⨯=所以 s T )00012.073990.1(2±= P=0.683(Ⅱ)计算g 及其不确定度已知b a l h T T l T T g +=--++=)2(2241222122212π(1)由l T T a 22221+=得 21220677.47445.0273990.174055.1s m a -=⨯+=下面求a 的不确定度传递公式:两边取对数 2ln ln )ln(ln 2221--+=l T T a求微分 dl l dT T T T dT T T T da a 1221222212122211-+++= 系数去绝对值并改成不确定度符号,最后写成不确定度传递公式为 2222212222211)1()2()2(21l T T a U l U T T T U T T T a U ++++= 带入数值可求求得a 的不确定度为2222222683.0)0003.07445.01()00012.073990.174055.173990.12()00016.073990.174055.174055.12(0677.4)(⨯+⨯+⨯+⨯+⨯⨯=a U 2-10.0017m s =所以 2-10.0017)m 0677.4(s a ±= P=0.683(2)由)2(212221l h T T b --=得 21220065.0)7445.04595.02(273990.174055.1s m b -=-⨯-= (3)比较a 和b 的大小,%15.0%100=⨯ab ,可见b 与a 相比,b 项可以忽略不计,从而可由a lT T g =+=2422212π求得a g 24π= 229.708m/s 0677.44==πg 再求g 的不确定度传递公式两边取对数 a g ln 4ln ln 2-=π求微分 da adg g 11-= 系数去绝对值并改成不确定度符号,最后写成不确定度传递公式为 a g U ag U = 带入数值可求的g 的不确定度为 2683.0/004.00017.00677.4708.9)(s m g U =⨯= 所以 20.004)m /s 9.708(±=g P=0.683误差分析:1. 使用米尺测量长度,误差太大;2. 在实验过程中支架底座很难调平,从而造成每个周期之间会有偏差;3. 实验中的偶然因素(比如振动)会造成周期的变化;4. 实验中发现凯特摆的周期与振幅有一定关系,从而每次的振幅不同也会造成周期的不同5. 在实验过程中,可能会形成不易察觉的锥面摆6. 从数据果看出,测得的十个周期数据并不理想,在调节时,两个周期分别为1.74005和1.74003,但在测量十个周期时周期的偏差比较大,可能是由于等待稳定的时间选的不好,导致周期有偏差改进方法:先测量一个周期,当稳定后,再迅速调到十个周期的档测量(这样能保证摆动已经稳定)。
大学物理实验报告 复摆法测重力加速度

大学物理实验报告复摆法测重力加速度内容
本实验旨在利用复摆法测量重力加速度。
实验仪器包括72 cm长铝管臂、影线、调整扳手、油流仪、抗干扰模块(磁力仪)等。
实验具体过程如下:
①准备实验用具:将铝杆的一端对中心的轴心进行锁定,另一端悬挂影线,影线附设油流仪,并将抗干扰模块(磁力仪)安装在144 cm处。
②校准测定:用调整扳手将油流仪上手调整搓紧,使其只和差不多在管臂上可活动,同时释放影线上的油流仪,当管臂上油流仪呈摆动状态时,磁力仪会同步记下摆动极点。
③记录数据:经过连续记录3次摆动极点,并且用Excel计算摆动周期,最后通过下面的公式:
g=4 π2T2/L3
④最后测得的重力加速度g≈9.80m/s2
实验最后的结果表明:通过复摆法可以得到准确的重力加速度,实验大多数结果符合物理原理以及数据的要求。
此外,实验者需要注意复摆实验中细节,以便获得更加精确的测量结果。
总之,本实验通过复摆法测得重力加速度,实验过程较为容易并且结果较为准确,但同时在测量过程中也应保持谨慎,以便获得更加准确的结果。
用凯特摆测量重力加速度实验报告

用凯特摆测量重力加速度实验目的:学习凯特摆的实验设计思想和技巧,掌握一种比较精确的测量重力加速度的方法。
实验原理:1、当摆幅很小时,刚体绕O轴摆动的周期:刚体质量m,重心G到转轴O的距离h,绕O轴的转动惯量I,复。
摆绕通过重心G的转轴的转动惯量为IG当G轴与O轴平行时,有I=I+mh2G∴+mh2 )/mh∴复摆的等效摆长l=( IG2、利用复摆的共轭性:在复摆重心G旁,存在两点O和O´,可使该摆以O为悬点的摆动周期T₁与以O´为悬点的摆动周期T₂相同,可证得|OO´|=l,可精确求得l。
3、对于凯特摆,两刀口间距就是l,可通过调节A、B、C、D四摆锤得位置使正、倒悬挂时得摆动周期T₁≈T₂。
∴4π²/g=(T₁²+T₂²)/2l + (T₁²-T₂²)/2(2h₁-l) = a + b实验仪器:凯特摆、光电探头、米尺、数字测试仪。
实验内容:1、仪器调节选定两刀口间得距离即该摆得等效摆长l,使两刀口相对摆杆基本对称,并相互平行,用米尺测出l的值,粗略估算T值。
将摆杆悬挂到支架上水平的V形刀承上,调节底座上的螺丝,借助于铅垂线,使摆杆能在铅垂面内自由摆动,倒挂也如此。
将光电探头放在摆杆下方,让摆针在摆动时经过光电探测器。
让摆杆作小角度摆动,待稳定后,按下reset钮,则测试仪开始自动记录一个周期的时间。
2、测量摆动周期T₁和T₂调整四个摆锤的位置,使T₁和T₂逐渐靠近,差值小于0.001s,测量正、倒摆动10个周期的时间10T₁和10T₂各测5次取平均值。
3、计算重力加速度g及其标准误差σg。
将摆杆从刀承上取下,平放在刀口上,使其平衡,平衡点即重心G。
测出|GO|即h₁,代入公式计算g。
推导误差传递公式计算σg。
实验数据处理:1、l的值l=⅓(l₁+l₂+l₃)=74.17cmσ=0.03055cm,uA=σ/=0.01764cm,∴ΔA =tP·uA=1.32*0.01764=0.02328cmu B=ΔB/C=0.1/3=0.03333cm∴uL==0.04066cmTe==1.729s2、T₁和T₂的值T₁=1.72746sσ=2.525*10¯⁴s,uA=σ/=1.129*10¯⁴s∴ΔA =tP·uA=1.14*0.0001129=1.287*10¯⁴su B=ΔB/C=0.0001/3=0.3333*10¯⁴s∴uT1==1.329*10¯⁴sT₂=1.72751sσ=1.469*10¯⁴s,uA=σ/=0.6570*10¯⁴s∴ΔA =tP·uA=1.14*0.00006570=0.7489*10¯⁴su B=ΔB/C=0.0001/3=0.3333*10¯⁴s∴uT2==0.8197*10¯⁴s3、重力加速度gh₁=44.46cm∴g=4π²/[(T₁²+T₂²)/2l + (T₁²-T₂²)/2(2h₁-l)]=4π²/{(1.72746²+1.72751²)/(2*74.17*10¯²)+(1.72746²-1.72751²)/[2*(2*44.46*10¯²-74.17*10¯²)]} =9.813m/s²∴ug0.68 =g·{l¯²* uL²+[2 T₁/(T₁²+T₂²)]²·uT1²+[2 T₂/(T₁²+T₂²)]²·uT2²}=9.813*{(74.17*10¯²)¯²*(0.04066*10¯²)²+[2*1.72746/(1.72746²+1.72751²)]²*(1.329*10¯⁴)²+[2*1.72751/(1.72746²+1.72751²)]²*(0.8197*10¯⁴)²}=0.00545m/s²∴ug0.95 =2* ug0.68=0.011 m/s²∴g=(9.813±0.011) m/s² P=0.95思考题:1、凯特摆测重力加速度,在实验设计上有什么特点?避免了什么量的测量?降低了哪个量的测量精度?实验上如何来实现?答:凯特摆测重力加速度在实验设计上把不可测的量转换成可测的量,利用复摆上两点的共轭性,对难以精确测定的量,有些避免了对其的测量,不能避免的则降低了其测量精度。
用凯特摆测量重力加速度(4)

⽤凯特摆测量重⼒加速度(4)实验报告 87姓名:竺贵强学号:PB07210017 系别:0706 实验题⽬:⽤凯特摆测量重⼒加速度实验⽬的:1.学习凯特摆的实验设计思想和技巧2.掌握⼀种⽐较精确的测量重⼒加速度的⽅法实验内容:1. 仪器调节调平⽀架:让摆杆做⼩⾓度摆动,记录⼀个周期的时间,反复测量,并调节⽀架的底座,直到多次测量的⼀个周期误差在0.001秒之内。
2. 测量摆动周期1T 和2T求出平均值为 mm l 5.7443== 根据gl T π2=粗略估算出 s T 7318.18.97445.02=??=π调节四个摆锤的位置,使正挂的摆动周期1T 和倒挂的摆动周期2T 逐渐靠近,⼀般粗调⽤⼤摆锤,微调⽤⼩摆锤,当1T 和2T 接近估计值时,最好移动⼩摆锤,使1T 和2T 的差值⼩于0.001s.当周期的调节达到要求后,分别测量5次的101T 和10g (Ⅰ)计算l, 1h ,1T 和2T 的平均值和不确定度 (1)已求出l 的平均值 mm l 5.744=l 的A 类不确定度为 mm l l l u i i A 17.0)13(3)()(312=-?-=∑= 查表得卷尺的仪?=0.8mm, 683.0t =1.32, p k =1, C=3由22683.0683.0)/()(C k u t U p A 仪?+=得mm l U 3.0)3/8.01()17.032.1()(22683.0=?+?=所以 mm l )3.05.744(±= P=0.683(2)求出1h 的平均值 mm h 5.45933.4598.4595.4591=++=1h 的A 类不确定度为 mm h h h u i i A 15.0)13(3)()(312111=-?-=∑=查表得卷尺的仪?=0.8mm, 683.0t =1.32, p k =1, C=3由22683.0683.0)/()(C k u t U p A 仪?+=得 mm h U 3.0)3/8.01()15.032.1()(221683.0=?+?=所以 mm h )3.05.459(1±= P=0.683(3)求出1T 的平均值 s T T i 74055.11010515111==∑=1T 的A 类不确定度为 s T T T u i i A 00014.0)15(5) ()(512111=-?-=∑=取仪?=0, 查表得 683.0t =1.14,由A u t U 683.0683.0=得s T U 00016.000014.014.1)(1683.0=?=所以 s T )00016.074055.1(1±= P=0.683(4)求出2T 的平均值 s T T i 73990.11010515122==∑=2T 的A 类不确定度为 s T T T u i i A 00011.0)15(5)()(51 2222=-?-=∑=取仪?=0, 查表得 683.0t =1.14,由A u t U 683.0683.0=得s T U 00012.000011.014.1)(2683.0=?=所以 s T )00012.073990.1(2±= P=0.683(Ⅱ)计算g 及其不确定度已知b a l h T T l T T g +=--++=)2(2241222122212π(1)由l T T a 22221+=得 21220677.47445.0273990.174055.1s m a -=?+=下⾯求a 的不确定度传递公式:两边取对数 2ln ln )ln(ln 2221--+=l T T a求微分 dl l dT T T T dT T T T da a 1221222212122211-+++= 系数去绝对值并改成不确定度符号,最后写成不确定度传递公式为 2222212222211)1()2()2(21l T T a U l U T T T U T T T a U ++++= 带⼊数值可求求得a 的不确定度为2222222683.0)0003.07445.01()00012.073990.174055.173990.12()00016.073990.174055.174055.12(0677.4)(?+?+?+?+??=a U 2-10.0017m s =所以 2-10.0017)m 0677.4(s a ±= P=0.683(2)由)2(212221l h T T b --=得 21220065.0)7445.04595.02(273990.174055.1s m b -=-?-= (3)⽐较a 和b 的⼤⼩,%15.0%100=?ab ,可见b 与a 相⽐,b 项可以忽略不计,从⽽可由a lT T g =+=2422212π求得a g 24π= 229.708m/s 0677.44==πg 再求g 的不确定度传递公式两边取对数 a g ln 4ln ln 2-=π求微分 da adg g 11-= 系数去绝对值并改成不确定度符号,最后写成不确定度传递公式为 a g U ag U = 带⼊数值可求的g 的不确定度为 2683.0/004.00017.00677.4708.9)(s m g U =?= 所以 20.004)m /s 9.708(±=g P=0.683误差分析:1. 使⽤⽶尺测量长度,误差太⼤;2. 在实验过程中⽀架底座很难调平,从⽽造成每个周期之间会有偏差;3. 实验中的偶然因素(⽐如振动)会造成周期的变化;4. 实验中发现凯特摆的周期与振幅有⼀定关系,从⽽每次的振幅不同也会造成周期的不同5. 在实验过程中,可能会形成不易察觉的锥⾯摆6. 从数据果看出,测得的⼗个周期数据并不理想,在调节时,两个周期分别为1.74005和1.74003,但在测量⼗个周期时周期的偏差⽐较⼤,可能是由于等待稳定的时间选的不好,导致周期有偏差改进⽅法:先测量⼀个周期,当稳定后,再迅速调到⼗个周期的档测量(这样能保证摆动已经稳定)。
利用凯特摆测定重力加速度g值(精)

複擺
5.移動滑體,改變重心位置,重覆步驟1.、 2.、3.、4.,求g值。 B.曲線法 1.量取O1O2距離L。 2.以O1為懸點,利用測量法之步驟2.並將滑體位置定在10公分, 測出週期T1, 重複三次,逐次移動滑體10公分再測量週期T1 , 至 位置80公分為止。 3.再以O2為懸點,仿步驟2.來量測週期T2。 4.以滑體位置為橫軸,週期T為縱軸,畫出T1 、 T2的曲線並找出 交點所對應的時間T0,帶入式(6) ,求g值。
複擺
一、目的 利用凱特擺測定重力加速度g值。 二.原理 (A)測量法:固定滑體和黑色圓形重物的位置, 找出質心並利用複擺求得重力加速度g值。 凱特(Kater)擺是兩端不對稱的複擺,做小角 度擺動時,運動方程式為τ = Iα (1)
(τ是力矩,I 是轉動慣量,α是角加速度,θ為擺角)
複擺
圖一 複擺結構裝置與示意圖
定值,即使不同交點,T1=T2=T0=T'1= T'2仍存在】
複擺
三、儀器與裝置 儀器:複擺支座、複擺刀口、複擺、水平儀、 平衡支架、光時閘、光電計時器 四、步驟
A.測量法 1.用平衡支架找出複擺重心位置G,量得O1G、O2G距離h1、h2。 2.先以O1為懸點,使其自由擺動,但擺幅不得超過5度,記錄擺 動10次的平均時間,即得擺動週期T1,重覆四次,取平均值。 3.以O2為懸點,重覆步驟2.,求得T2之平均值。 4.將T1、T2、h1、h2帶入式(5),即可求得g值。
複擺
以O1為懸點,轉動θ角時,複擺所受力矩大小為τ =-M g h1sinθ~-M g h1θ (2)其解 為 (A、δ為常數,由初始條件決定, I為複擺
對懸點O1的轉動慣量,且I=Icm+Mh12=M(R2+h12)【Icm為複擺 以質心G點為轉軸的轉動慣量,假設Icm=MR2,R未知且與質量 分佈有關】 )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
福建工程学院
实验报告
专业:通信工程
班级:1002
座号:3100205219
姓名:***
日期:2011-10-20
凯特摆测量重力加速度
实验目的:
1. 学习凯特摆的实验设计思想和技巧。
2. 掌握一种比较精确的测量重力加速度的方法。
3. 利用凯特摆测量重力加速度的方法
实验内容:
一.实验原理
图一是复摆的示意图,设一质量为m 的刚体,其重心G 到转轴O的距离为h ,绕O 轴的转动惯量为I ,当摆幅很小时,刚体绕O 轴摆动的周期T 为
mgh
I T π2= (1) 式中g 为当地的重力加速度。
设复摆绕通过重心G 的轴的转动惯量为I G ,当G 轴与O 轴平行时,有
2
mh I I G += (2)
代入式(1)得 mgh mh I T G 2
2+=π (3) 对比单摆周期的公式g
l T π2=,可得 mh mh I l G 2
+= (4)
l 称为复摆的等效摆长。
因此只要测出周期和等效摆长便可求得重力加速度。
复摆的周期我们能测得非常精确,但利用mh
mh I l G 2
+=来确定l 是很困难的。
因为重心G 的位置不易测定,因而重心G 到悬点O 的距离h 也是难以精确测定的。
同时由于复摆不可能做成理想的、规则的形状,其密度也难绝对均匀,想精确计算I G 也是不可能的。
我们利用复摆上两点的共轭性可以精确求得l 。
在复摆重心G 的两旁,总可找到两点
O 和O’,使得该摆以O 悬点的摆动周期T 1与以O’为悬点的摆动周期T 2相同,那么可以证明'OO 就是我们要求的等效摆长l 。
图一 复摆示意图 图二 凯特摆摆杆示意图
图二是凯特摆摆杆的示意图,对凯特摆而言,两刀口间的距离就是该摆的等效摆长l 。
在实验中当两刀口位置确定后,通过调节A 、B 、C 、D 四摆锤的位置可使正、倒悬挂时的摆动周期T 1和T 2基本相等,即T 1≈T 2。
由公式(3)可得
1
2
112mgh mh I T G +=π (5) 222
22mgh mh I T G +=π (6)
其中T 1和h 1为摆绕O 轴的摆动周期和O 轴倒重心G 的距离。
当T 1≈T 2时,h 1+h 2=l 即为等效摆长。
由式(5)和(6)消去I G ,可得
()b a l h T T l T T g +=--++=1222122212
2224π (7)
式中,l 、T 1、T 2都是可以精确测定的量,而h 1则不易测准。
由此可知,a 项可以精确求得,而b 项不易精确求得。
但当T 1 =T 2以及l h -12的值较大时,b 项的值相对a 项是非常小的,这样b 项的不精确对测量结果产生的影响就微乎其微了。
二.实验内容
1. 实验仪器
本实验装置包括凯特摆、光电探头和多用数字测试仪。
实验中将光电探头放在摆杆下方,调整它的位置和高度,让摆针在摆动时经过光电探测器。
电信号由B 插口输入到数字测试仪中,数字测试仪的功能选择旋钮放在“振动计数”档,时标旋钮放在“0.1ms ”档,计停开关置于“停止”,然后接通电源。
让摆杆作小角度的摆动,待其摆动若干次稳定后,按下数字测试仪的“复位”按钮。
此时测试仪开始自动记录一个周期的时间。
显示屏左边显示摆动的次数(即周期数),右边显示摆动数个周期的时间数值。
实验结果。
