0401七年级数学上册第四章《图形的初步认识》同步练习卷第1课生活中的立体图形
七年级上第四章《图形的初步认识》复习测试题含答案

北
B
A 西
东
54
北
D
西 B东
第 7题
第 8题
8. 如图所示 , 若 AB∥ CD,则∠ A+∠ M+∠ N+∠C=( C.540° )
第 9题
9. 如图所示 , 由 B 测 A 的方向是 (A. 北偏西 54° ) 10. 如图甲,用一块边长 10cm 的正方形 ABCD厚纸板,做了一套七巧板.将七巧板拼成一座桥(如图
七年级上第四章《图形的初步认识》复习测试题
(时间 120 分钟,满分 120 分) 一、选择题( 每题 3 分,满分 30 分) 1. 下列图形中 ,( A 2)(4)(5)) 不是多面体一
1
.
2
3
2. 如图所示 , 哪个图形不能折成一个正方体表面
4
.( b )
5
6
A
C
D
3. 下列语句中,正确的个数是( B.2 )个 ①两条直线相交 , 只有一个交点 . ②在∠ ABC的边 BC的延长线上取一点 D . ③若∠ 1+∠ 2+∠ 3=90° , 则∠ 1、∠ 2、∠ 3 互余 . ④一个角的余角比这个角的补角小 . 4. 在图中,不同的线段的条数是( C.10 )
∴AD∥ BC(同位角相等 , 两直线平行 )
A
B
25. (本题 12 分) 如图, ∠ 1=80°,∠ 2=100°,∠ BAD=60
(1)直线 AB与 CD是什么关系?请说明理由 .
( 2)求∠ D的度数 .
解 :(1)AB 与 CD平行 . ∵∠ 1=80°(已知)∴∠ ABE=80°(对顶角相等)
3
22
2
3
2020年人教版七年级数学上学期第4章几何图形初步 同步试卷(含答案)

人教版数学七年级上册第四章几何图形初步测试卷(时间90分钟,满分120分)题号一二三总分得分第Ⅰ卷(选择题)一.选择题(本大题共10小题,每小题3分,共30分)1.下列立体图形中,从上面看得到的图形是正方形的是( )2. 如图所示的几何体从左面看得到的图形是( )3.有如下说法:①平角是一条直线;②射线是直线的一半;③射线AB与射线BA表示同一射线;④用一个扩大2倍的放大镜去看一个角,这个角扩大2倍;⑤两点之间,线段最短;⑥12.5°=12°50′.其中正确的有( )A.4个B.3个C.2个D.1个4.把弯曲的河道改直,能够缩短船舶航行的路程,这样做的道理是( )A.垂线段最短B.两点确定一条直线C.两点之间,直线最短D.两点之间,线段最短5.下列说法不正确的是( )A.过两点有且只有一条直线B.连接两点线段的长度叫两点间的距离C.两点之间,线段最短D.如果AB=BC,则点B是线段AC的中点6.如图,从点O出发引四条射线OA,OB,OC,OD,则可组成角的个数是( )A.3个B.4个C.5个D.6个7.在广场的电子屏幕上有一个旋转的正方体,正方体的六个面上分别标有“恩施六城同创”六个字.如图是小明在三个不同时刻所观察到的图形,请你帮小明确定与“创”相对的面上的字是( )A.恩B.施C.城D.同8.如图,∠1=15°,∠AOC=90°,点B,O,D在同一条直线上,则∠2的度数为( ) A.75°B.95°C.105°D.165°9.如图,已知A,B,C,D,E五点在同一直线上,点D是线段AB的中点,点E是线段BC的中点,若线段AC=12,则线段DE等于( )A.10 B.8 C.6 D.410.一个正方体的平面展开图如图所示,折叠后可折成的图形是( )第Ⅱ卷(非选择题)二.填空题(共8小题,3*8=24)11.长方形绕其一边所在的直线旋转一周得到____.12.小朋友在用玩具枪瞄准时,总是用一只眼对准准星和目标,用数学知识解释为:.13.写出图中立体图形的名称:(1)_________________;(2);(3).14.若∠α的补角是125°,∠β的余角为37°,则∠α,∠β的大小关系为∠α___________∠β. 15.如图,点C 为线段AB 的中点,点D 为线段AC 上的一点,AC =4,BD =5,则CD =____,AD =____.16.计算:(1)49.9°=____°____′; (2)18°46′55″+27°17′24″=.17.两根木条,一根长60 cm ,一根长100 cm ,将它们的一端重合,顺次放在同一条直线上,此时两根木条的中点间的距离是cm.18. 如图,在正方形ABCD 中,点E 为DC 边上的一点,沿线段BE 对折后,若∠ABF 比∠EBF 大15°,则∠EBF 的度数为____.三.解答题(共7小题,66分)19. (8分)如图是由4个相同的小正方体搭成的几何体,请你画出它从正面、左面、上面三个不同的方向看得到的平面图形.20. (8分)一个角的余角比这个角的补角的13还小10°,求这个角的度数.21. (8分)已知线段AB ,延长AB 到点C ,使BC =12AB ,延长线BA 到点D ,使AD =2AB ,点M ,N 分别是BC ,AD 的中点,若MN =18 cm ,求AB 的长.22.(10分)已知线段AB =3 cm ,在线段AB 上取一点K ,使AK =BK ,在线段AB 的延长线上取一点C ,使AC =3BC ,在线段BA 的延长线上取一点D ,使AD =AK. (1)按以上叙述画出图形; (2)求线段BC ,DC 的长; (3)说出点K 是哪些线段的中点.23. (10分)已知∠AOB =80°,∠BOC =30°,求∠AOC 的大小.24. (10分)A,B两点在数轴上的位置如图所示,现A,B两点分别以1个单位/秒、4个单位/秒的速度同时向左运动.(1)几秒钟后,原点O恰好在两点正中间?(2)几秒钟后,恰好有OA∶OB=1∶2?25. (12分)如图,点O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.(1)请你数一数,图中有多少个小于平角的角;(2)求出∠BOD的度数;(3)请通过计算说明OE是否平分∠BOC.参考答案:1-5BADDD 6-10DDCCD 11. (1)、(2)、(3),(5)、(6),(4) 11. 圆柱12. 两点确定一条直线 13. 圆柱;五棱柱;四棱锥 14. > 15. 1,316. 49,54;46°4′19″ 17. 20或80 18. 25°19. 解:如图所示:20. 解:设这个角的度数为x°,则90-x =13(180-x)-10,解得x =60.则这个角的度数为60°21. 解:设AB =x cm ,则BC =12AB =x 2 cm ,BM =12BC =x4 cm ,AD =2x cm ,AN =12AD =x cm ,由MN =18 cm ,得x +x +x4=18,解得x =8, 则AB =8 cm22. 解:(1)如图所示:(2)因为AC =3BC ,AK =BK , 所以BC =AK =BK=12AB=1.5cm ,因为AD =AK ,所以AD= AK =BK =BC , 所以DC=2AB=6cm. (3) 点K 是AB ,DC 的中点23. 解:分两种情况讨论.①当∠BOC 在∠AOB 的内部时,∠AOC =∠AOB -∠BOC =80°-30°=50°; ②当∠BOC 在∠AOB 的外部时,∠AOC =∠AOB +∠BOC =80°+30°=110°, 故∠AOC 的度数为50°或110°24. 解:(1)由图可知OA =3,OB =12,设x 秒钟后, 原点O 恰好在两点正中间,则有3+x =12-4x ,解得x =95(2)设y 秒钟后,恰好有OA ∶OB =1∶2,则OB =2OA ,分两种情况: ①当B 在点O 的右边时,有12-4y =2(3+y), 解得y =1;②当点B 运动到点O 的左边时,有4y -12=2(3+y), 解得y =925.解:(1)图中有9个小于平角的角 (2)因为OD 平分∠AOC ,∠AOC =50°, 所以∠AOD =12∠AOC =25°,所以∠BOD =180°-25°=155° (3)因为∠BOE =180°-∠DOE -∠AOD =180°-90°-25° =65°,∠COE =90°-25°=65°,所以∠BOE =∠COE ,即OE 平分∠BOC1、老吾老以及人之老,幼吾幼以及人之幼。
人教版七年级上数学第4章几何图形初步:4.1几何图形同步练习(含答案)

4.1几何图形知识要点:1.立体图形定义:有些几何图形(如长方体、正方体、圆柱、圆锥、球等)的各部分不都在同一平面内,这样的几何图形叫做立体图形.2.常见的立体图形长方体、正方体、圆柱、圆锥、球等都是立体图形,棱柱、棱锥也是常见的立体图形3.点:线与线相交形成点.它是组成图形最基本的元素,一切图形都是由点组成的.如天上的星星、地图上的城市等4.线:面与面相交的地方形成线.线分为直线和曲线两种.如圆锥体的两个面相交形成曲线;正方体的两个面相交形成直线等5.面:包围着体的是面.面分为平面和曲面两种.一、单选题1.一个棱长为10分米的正方体,体积是( )立方分米.A.109B.106C.103D.10272.棱长为63的正方体,其表面积是()A.66B.67C.68D.693.如图,一个几何体的上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色.下列图形中,是该几何体的表面展开图的是()A.B.C.D.4.下列哪个正方体的展开图不可能如图所示()A.B.C.D.5.在如图所示的直三棱柱中,互相平行的棱有()A.3对B.4对C.5对D.6对6.将下面的纸片沿虚线折叠,不能折成长方体盒子的是( )A.B.C.D.7.组成如图的美丽图案的是( )A.三角形和扇形B.圆和四边形C.圆和三角形D.圆和扇形8.面与面相交成()A.点B.线C.面D.体9.图中的几何体有()条棱.A.3B.4C.5D.6二、填空题10.一个正方体有______个面,_______条棱,______个顶点.11.将如图所示半圆形薄片绕轴旋转一周,得到的几何体是_____,这一现象说明_____.12.天上一颗颗闪烁的星星给我们以“_____”的形象;中国武术中有“枪扎一条线,棍扫一大片”的说法,这句话给我们以“_____”的形象;宾馆里旋转的大门给我们以“_____”的形象.13.一枚硬币在桌面上快速旋转,给人的印象是一个球,这说明的数学原理是________.14.如图是一个正方体纸盒的展开图,当折成纸盒时,与点1重合的点是________.15.如图,是正方体的一个平面展开图,在这个正方体中,与“爱”字所在面相对的面上的汉字是______三、解答题16.如图是一个长为8cm,宽为6cm的长方形纸片,该长方形纸片分别绕长、宽所在直线旋转一周(如图1,图2),会得到两个几何体,请你通过计算说明哪种方式得到的几何体的体积大.(结果保留π)17.如图,第二行的图形绕虚线旋转一周,便能形成第一行的某个几何体.用线连一连.18.一个六棱柱模型如图所示,它的底面边长都是5cm,侧棱长是4cm.观察这个模型,回答下列问题.(1)这个六棱柱一共有多少个面?它们分别是什么形状?哪些面的形状、大小完全相同?(2)这个六棱柱一共有多少条棱?它们的长度分别是多少?答案 1.C 2.B 3.B 4.B 5.D 6.D 7.A 8.B 9.D10.6 12 8 11. 球 面动成体12.点, 线动成面, 面动成体. 13.面动成体 14.7和11 15.中.16.解:图1方式旋转得到几何体的体积:26888π2π⨯⨯=(3cm )图2方式旋转得到几何体的体积:286384ππ⨯⨯=(3cm ).因为384π288π>,所以图2方式得到的几何体的体积大.17.解:如图所示18.解:(1)这个六棱柱有6个侧面,2个底面,共8个面,它们分别是长方形、正六边形;6个侧面形状大小完全相同;2个底面的形状大小完全相同;故答案为:8,长方形,正六边形,6个侧面,2个底面。
华师大版2020-2021学年七年级数学上册第4章图形的初步认识单元同步试卷(含答案)
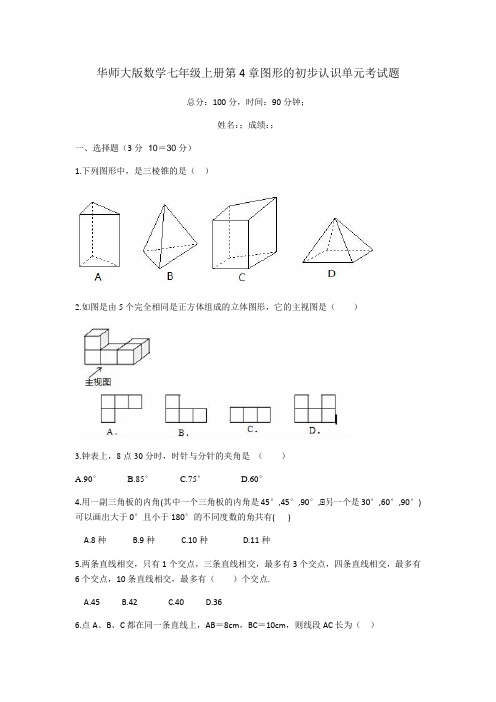
华师大版数学七年级上册第4章图形的初步认识单元考试题总分:100分,时间:90分钟;姓名:;成绩:;一、选择题(3分×10=30分)1.下列图形中,是三棱锥的是()2.如图是由5个完全相同是正方体组成的立体图形,它的主视图是()3.钟表上,8点30分时,时针与分针的夹角是()A.90°B.85°C.75°D.60°4.用一副三角板的内角(其中一个三角板的内角是45°,45°,90°,•另一个是30°,60°,90°)可以画出大于0°且小于180°的不同度数的角共有( )A.8种B.9种C.10种D.11种5.两条直线相交,只有1个交点,三条直线相交,最多有3个交点,四条直线相交,最多有6个交点,10条直线相交,最多有()个交点.A.45B.42C.40D.366.点A、B、C都在同一条直线上,AB=8cm,BC=10cm,则线段AC长为()A.18cm 或2cm B 、18cm C.2cm D 、8cm 或10cm7.下列四个生活中产生的现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵的位置,就能确定同一行树所在的直线;③从A 地到B 架设电线,总是尽可能沿着线段AB 方向架设;④把弯曲的公路改直,就能缩短路程。
其中可用公理“两点之间,线段最短”来解释的现象有( )A.①②B.①③C.②③D.③④8.如图,OC 平分∠AOD ,OD 平分∠BOC ,下列等式不成立的是( )A. ∠AOC=∠BODB.∠COD=21∠AOBC.∠AOC=21∠AODD.∠BOD=21∠BOC9.下列说法正确的是( )A 、一个锐角的余角比这个角的补角小90°;B 、如果一个角有补角,那么这个角必是钝角;C 、若∠1+∠2+∠3=180°,则∠1、∠2、∠3互为了补角;D 、如果∠α和∠β互为余角,∠β与∠θ互为余角,那么∠α与∠θ互为余角。
七年级数学上册 第4章 图形的初步认识同步练习 (新版)华东师大版

第4章图形的初步认识类型之一立体图形的识别1.下列说法错误的是( )A.长方体、正方体都是棱柱B.三棱柱的侧面是三角形C.直六棱柱有六个侧面,侧面为长方形D.球体是由曲面围成的2.在①球体;②柱体;③锥体;④棱柱;⑤棱锥中,必是多面体的是( )A.①~⑤ B.②③ C.④ D.④⑤类型之二立体图形的三视图3.下列四个几何体中,主视图与左视图相同的几何体有( )图4-X-1A.1个B.2个C.3个D.4个4.如图4-X-2为水平的讲台上放置的圆柱形笔筒和正方体形粉笔盒,其俯视图是( )图4-X-2图4-X-35.如图4-X-4是一个几何体的三视图,则这个几何体是( )图4-X-4图4-X-56.由一些完全相同的小正方体搭成的几何体的主视图和左视图如图4-X-6所示,则组成这个几何体的小正方体的个数可能是______________.图4-X-6类型之三图形的展开与折叠7.小亮为今年参加中考的好友小杰制作了一个正方体礼品盒(如图4-X-7),六个面上各有一个字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的表面展开图可能是图4-X-8中的( )图4-X-7图4-X -88.如图4-X -9是一个长方体形状包装盒的表面展开图.折叠制作完成后得到长方体的容积是(包装材料厚度不计)( )图4-X -9A .40×40×70B .70×70×80C .80×80×80D .40×70×80类型之四 直线、射线、线段9.如图4-X -10,已知线段AB ,在BA 的延长线上取一点C ,使CA =3AB ,则线段CA 与线段CB 的长度之比为( )图4-X -10A .3∶4B .2∶3C .3∶5D .1∶210.开学整理教室时,老师总是先把每一列最前和最后的课桌摆好,然后再依次摆中间的课桌,一会儿一列课桌就摆在一条线上了,整整齐齐,这是因为________________________________.11.如图4-X -11,已知线段AD =16 cm ,线段AC =BD =10 cm ,E ,F 分别是AB ,CD 的中点,则EF 的长为________cm .图4-X -1112.平面内不同的2个点确定1条直线,不同的3个点最多确定3条直线,不同的4个点最多确定6条直线,则平面内不同的10个点最多确定________条直线.13.如图4-X -12,已知线段AB 和CD 的公共部分BD =13AB =14CD.线段AB ,CD 的中点E ,F 之间的距离是10 cm ,求线段AB ,CD 的长.图4-X-12类型之五角的定义及运算14.4点10分,时针与分针所夹的小于平角的角为( )A.55° B.65°C.70° D.以上选项都不对图4-X-1315.如图4-X-13,A,O,B是同一直线上的三点,OC,OD,OE是从点O引出的三条射线,且∠1∶∠2∶∠3∶∠4=1∶2∶3∶4,则∠5=________度.16.如图4-X-14,∠AOC=∠BOD,∠AOD=120°,∠BOC=70°,求∠AOB的度数.图4-X-1417.如图4-X-15,已知O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,∠BOE=12∠EOC,∠DOE=70°,求∠EOC的度数.图4-X-15类型之六余角和补角18.已知∠α是锐角,∠α与∠β互补,∠α与∠γ互余,则∠β-∠γ的值等于( )A.45° B.60° C.90° D.180°19.若一个角的补角比它的余角的4倍少15°,则这个角的度数为________.类型之七分类讨论思想的应用20.已知一条射线OA,若从点O再引两条射线OB和OC,使∠AOB=80°,∠BOC =40°,若OD平分∠AOC,则∠BOD的度数为________.21.在一条直线上任取一点A,截取AB=20 cm,再截取AC=18 cm,M,N分别是AB,AC的中点,求M,N两点之间的距离.详解1.B [解析] 三棱柱的侧面应是四边形.故选B.2.D [解析] 多面体指四个或四个以上多边形所围成的立体图形.①只有一个面且是曲面;②可能是圆柱,也可能是棱柱,棱柱是多面体,圆柱则不是;③可能是棱锥也可能是圆锥,圆锥有两个面,一个曲面、一个平面,不是多面体;④至少有五个平面,故是多面体;⑤至少有四个平面,故是多面体.故选D.3.D4.D5.B6.4或5或6或77.C [解析] 正方体的表面展开图相对的面之间一定相隔一个正方形.A项,“预”的对面是“考”,“祝”的对面是“成”,“中”的对面是“功”,故本选项错误.B项,“预”的对面是“功”,“祝”的对面是“考”,“中”的对面是“成”,故本选项错误.C 项,“预”的对面是“中”,“祝”的对面是“考”,“成”的对面是“功”,故本选项正确.D项,“预”的对面是“中”,“祝”的对面是“成”,“考”的对面是“功”,故本选项错误.故选C.8.D9.A [解析] 不妨设AB=a,则CA=3a,CB=4a,因此,CA∶CB=3a∶4a=3∶4.10.两点确定一条直线11.1012.4513.解:设BD=x cm,则AB=3x cm,CD=4x cm.根据题意,得1.5x+2x-x=10,解得x=4,则3x=12,4x=16.答:线段AB的长为12 cm,线段CD的长为16 cm.14.B15.60 [解析] 因为A ,O ,B 是同一直线上的三点,即∠AOB =180°,∠1∶∠2∶∠3=1∶2∶3,所以∠1=30°,∠2=60°,∠3=90°.又因为∠1∶∠2∶∠3∶∠4=1∶2∶3∶4,所以∠4=120°,∠5=180°-120°=60°.16.解:∵∠AOB =∠AOC -∠BOC ,∠COD =∠BOD -∠BOC ,∠AOC =∠BOD , ∴∠AOB =∠COD .∵∠AOB +∠BOC +∠COD =∠AOD ,∴∠AOB =12(∠AOD -∠BOC )=12×(120°-70°)=25°.17.解:设∠BOE =x °.∵∠BOE =12∠EOC ,∴∠EOC =2x °.∵OD 平分∠AOB ,∴∠AOD =∠DOB =70°-x °.∵∠AOD +∠DOB +∠BOE +∠EOC =180°, ∴70°-x °+70°-x °+x °+2x °=180°, ∴x =40, ∴∠EOC =80°.18.C [解析] 由题意得∠α+∠β=180°,∠α+∠γ=90°,两式相减可得∠β-∠γ=90°.故选C.19.55°20.60°或20° [解析] 此题分两种情况:当射线OC 在∠AOB 内部时,∠AOC =∠AOB -∠BOC =40°,∠DOC =20°,则∠BOD =∠BOC +∠DOC =60°;当射线OC 在∠AOB 外部时,∠AOC =∠AOB +∠BOC =120°,∠DOC =60°,∠BOD =∠DOC -∠BOC =20°.故答案为60°或20°.21.解:①当点C 在BA 的延长线上时,如图①.图①∵M 是AB 的中点,N 是AC 的中点, ∴AM =12AB =10 cm ,AN =12AC =9 cm ,∴MN =AM +AN =19 cm ; ②当点C 在线段AB 上时,如图②.∵M 是AB 的中点,N 是AC 的中点, ∴AM =12AB =10 cm ,AN =12AC =9 cm ,∴MN =AM -AN =1 cm.综上,M ,N 两点之间的距离为19 cm 或1 cm.如有侵权请联系告知删除,感谢你们的配合!。
人教版七年级上册数学第四章几何图形初步单元测试题(含答案).doc

人教 , 版 , 七年级 , 上册 , 数学 , 第四章 , 几何图形 , 第四章几何图形初步第四章几何图形初步一、填空题 ( 每小题 3 分,共 18 分 )1.写出如图所示立体图形的名称:①____;② ____;③ ____.2.计算:(1)53 °19′42″+ 16°40′18″=____ ;(2)23 °15′16″× 5= ____ .3.延长线段AB到 C,使 BC= 4,若 AB= 8,则线段 AC的长是 BC的 ____ 倍.4.把一张长方形纸条按如图的方式折叠后,量得∠ AOB′=110°,则∠ B′OC的度数是____.5.如图,已知∠ COE=∠ BOD=∠ AOC=90°,则图中互余的角有___ _ 对,互补的角有 ____对.6.如图,点 A 在数轴上对应的数为 2,若点 B 也在数轴上,且线段 AB的长为 4,C 为 OB的中点,则点 C 在数轴上对应的数为 __ __ .二、选择题 ( 每小题 3 分,共 30 分 )7.下列能用∠C表示∠1 的是 ()8.已知∠ A=40°,则它的余角为()A.40° B .50°C.130° D .140°9.下列图形中可以作为一个三棱柱的展开图的是()10.下面四个几何体中,从左面看到的图形是四边形的几何体共有()A.1 个11.已知B.2个 C.3个M是线段AB的中点,那么:①AB=D.4 个2AM;② BM= AB;③ AM = BM;④ AM+ BM=AB,上面四个式子中,正确的个数有( )A.1 个12.如图,已知∠平分∠ DAF;④ AE B.2个C.3个D.4个1=∠ 2,∠ 3=∠ 4,则下列结论:①A D 平分∠ BAF;② AF平分∠ BAC,其中正确的个数是()平分∠ DAC;③ AEA. 1 B . 2 C . 3 D . 413.平面上五个点最多可以确定直线的条数为( ) A.5 条 B .8条C.10 条D.12 条14.如图,直线 l1 , l2 , l3 把平面分成 ( ) 部分.A. 4 B .5 C . 6 D . 715.如图,在时刻A.85° B8: 30,时钟上的时针和分针之间的夹角为.75° C .70°D.60°( )。
七年级数学上册第四章图形的初步认识单元综合测试题(新版)华东师大版(2021年整理)
七年级数学上册第四章图形的初步认识单元综合测试题(新版)华东师大版(word版可编辑修改)七年级数学上册第四章图形的初步认识单元综合测试题(新版)华东师大版(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(七年级数学上册第四章图形的初步认识单元综合测试题(新版)华东师大版(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为七年级数学上册第四章图形的初步认识单元综合测试题(新版)华东师大版(word 版可编辑修改)的全部内容。
第四章图形的初步认识测试卷一、 填空(每空2分,共40分)1、如图1,已知CB =5cm ,DB =7.5cm ,D 是AC 的中点,则AC =_________ 。
2、一个角的补角比它的余角大_____,若一个角的补角是它的余角的4倍,则这个角是_____度.3、时钟的时针和分针在3时20分时,所成的角度是_____度.4、45°36′48″=_________度,126。
31°=____°____′____″。
5、180°-67°43′38″=_____________6、如图2,CB ⊥AB ,∠CBA 与∠CBD 的度数比是4:1,则∠DBA =________度,<图4>7、如图3,AC ⊥BC ,CD ⊥AB ,点A 到BC 边的距离是线段_____的长,点B 到CD 边的距离是线段_____的长,图中的直角有__________ __,∠A 的余角有___________ ____,和∠A 相等的角有__________.8、如图4,当∠1=∠_____时,AB ∥CD ;当∠D +∠_____=180°时,∥;当∠B =∠_____时,AB ∥CD .9、如图5,∠1=055,∠3=055那么直线a 与b 的关系是 。
七年级数学上册第4章图形的初步认识4.1生活中的立体图形同步练习(新版)华东师大版
4.1 生活中的立体图形知识点 1 立体图形1.写出三个常见的立体图形的名称:____________.2.下面几种图形:①三角形;②长方形;③正方体;④圆;⑤圆锥;⑥圆柱.其中属于立体图形的是________(填序号).知识点 2 立体图形的分类3.下列物体的形状类似于球的是( )A.茶叶筒 B.羽毛球C.乒乓球 D.日光灯管4.图4-1-1中是圆柱的是( )图4-1-15.下列图形属于棱柱的有( )图4-1-2A.2个 B.3个C.4个 D.5个6.四棱柱、长方体和正方体之间的包含关系是图4-1-3中的( )图4-1-37.如图4-1-4所示的图形中,柱体有________,锥体有________,球体有________.(填序号)图4-1-48.请写出图4-1-5中立体图形的名称.图4-1-59.如图4-1-6所示,四棱锥有________条棱,________个顶点.图4-1-610.将下列几何体与它的名称连起来.图4-1-7知识点 3 多面体11.如图4-1-8所示的图形中,多面体有( )图4-1-8A.①② B.②③ C.②④ D.①④12.下列立体图形中,有五个面的是( )A.四棱锥 B.五棱锥C.四棱柱 D.五棱柱13.下列说法正确的有( )①圆柱的底面一定是圆;②棱锥的侧面是三角形;③柱体都是多面体;④锥体不一定是多面体.A.1个 B.2个 C.3个 D.4个14.观察如图4-1-9所示的几何体,请将符合条件的几何体的序号填在如图4-1-10所示的横线上.图4-1-9图4-1-1016.填空:(1)三棱柱有________个面,________个顶点,________条棱;(2)四棱柱有________个面,________个顶点,________条棱;(3)五棱柱有________个面,________个顶点,________条棱;(4)十棱柱有________个面,________个顶点,________条棱.16.一个棱柱有10个顶点,那么这个棱柱的底面是________边形,它________(填“是”或“不是”)多面体.17.如图4-1-11所示,第一行的图形绕虚线旋转一周,能形成第二行的某个几何体,用线连起来.图4-1-1118.小明为了做一个如图4-1-12所示的机器人,他应准备:图4-1-12(1)多少个?(2)多少个?(3)19.根据下列描述,分别判断该立体图形的名称:(1)一个立体图形是锥体,它的底面是六边形;(2)一个立体图形,无论怎样截,得到的截面都是圆.20.如图4-1-13所示,把这个几何体一刀切去一部分,如何把它变成三棱柱、三棱锥、四棱柱?动手试一试.图4-1-13详解1.答案不唯一,如圆柱、正方体、圆锥等2.③⑤⑥ 3.C 4.C5.B [解析] 第一、二、四个几何体是棱柱.故选B.6.A 7.①②③⑦⑤⑥④8.五棱柱圆锥圆柱球9.8 510.解:如图所示:11.D12.A [解析] 四棱锥由一个底面,四个侧面组成,共五个面.故选A.13.C [解析] ①②④正确.14.甲:(2)(4)(5)乙:(1) 丙:(1)(3)(6)15.(1)5 6 9 (2)6 8 12 (3)7 10 15 (4)12 20 3016.五是[解析] 一个棱柱有10个顶点,根据特点可知它是五棱柱,则底面是五边形,它是多面体.17.解:如图所示.18.解:(1)2个.(2)8个.(3)6个.19.解:(1)六棱锥.(2)球.20.解:答案不唯一,如图所示.。
2019—2020年最新人教版七年级数学上册第四章《图形认识初步》单元复习检测题及答案(同步试卷).doc
第4章 图形认识初步 复习练习题一、选择题1.如下图,下列四个几何体中,它们各自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不同的几何体是 ( )A .①②B .②③C .②④D .③④2.将下列图形绕直线l 旋转一周, 可以得到右图所示的立体图形的是()3. 如右图是每个面上都有一个汉字的正方体的一种展开图,那么在原正方体的“着”相对的面上的汉字是 ( ) A. 冷 B. 静 C. 应 D. 考4.下图是一个由6个相同的小立方体组成的几何体,从上面看得到的平面图形是( )A .B .C .D .5.如左图的几何体的俯视图是( )静 沉 着 应冷考(第8题图)正面5623 1 4第12题AB D(1)CA. B. C. D.6.右图是由几个相同的小正方体搭成的一个几何体,从左边看得到的平面图形是( )(A ) (B ) (C ) (D )7. 图中几何体的左视图是 ( )8.如上图,小芳的桌上放着一摞书和一个茶杯(见上方右图),那么小芳从正面看到的图形是( )9.如图,从正上方看下列各几何体,得到图形(1)的几何体是( )11.一个无盖的正方体盒子的平面展开图可以是下列图形中的( ).A .B .C .D .AB CDA.图①、图②B.图①、图③C.图②、图③D.只有图①12.如图是正方体的展开图,则正方体相对两个面上的数字之和的最小值是( ).A.4 B.6 C.7 D.813.下列图形中,不是正方体展开图形的是( )14. 下面哪个图形不是正方体的展开图()15.下列各图形经过折叠不能围成一个正方体的是()A B C D16.下面的平面图形中,是正方体的平面展开图的是()A B C D17.如右图,是一个不完整的正方体平面展开图,下面是四位同学补画的情况(图中阴影部分),其中补画正确....的是( )18.如左图,它需再添一个面,折叠后才能围成一个正方体,下图中的黑色小正方形分别由四位同学补画,其中正确的是( )19.如右图是某一立方体的侧面展开图 ,则该立方体是( )20.下列图中,左边的图形是立方体的表面展开图,把它折叠成立方体。
人教版七年级数学上册第四章几何图形初步单元练习题含答案
第四章《几何图形初步》单元练习题单元练习题一、选择题1.如果线段AB=4cm,BC=3cm,那么A、C两点的距离为()A. 1cmB. 7cmC. 1cm或7cmD.无法确定2.下列四个图形中是三棱柱的表面展开图的是()A.B.C.D.3.下列图形中,属于立体图形的是()A.B.C.D.4.把图1所示的正方体的展开图围成正方体(文字露在外面),再将这个正方体按照图2,依次翻滚到第1格,第2格,第3格,第4格,此时正方体朝上一面的文字为()A.富B.强C.文D.民5.在同一平面内,画出三条直线,使它们满足下列条件:①没有交点;②有一个交点;③有两个交点;④有三个交点.其中能画出图形的是()A.①②③④B.①②③C.①②④D.①③6.如图所示,OC,OD分别是∠AOB,∠BOC的平分线,且∠COD=26°,则∠AOB的度数为()A. 96°B. 104°C. 112°D. 114°7.如图,将正方形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF的大小为()A. 60°B. 45°C. 30°D. 15°8.一个六棱柱的顶点个数、棱的条数、面的个数分别是()A. 6、12、6B. 12、18、8C. 18、12、6D. 18、18、24二、填空题9.几何学中,有“点动成,线动成,动成体”的原理.10.如果一个棱锥一共有7个面,底边长是侧棱长的一半,并且所有的侧棱长相等,已知所有棱长的和是90cm,则它的每条侧棱长为.11.如图所示,点C在线段AB的延长线上,且BC=2AB,D是AC的中点,若AB=2cm,求BD 的长.解:∵AB=2cm,BC=2AB,∴BC=4cm.∴AC=AB+=cm.∵D是AC的中点,∴AD==cm.∴BD=AD-=cm.12.一个角的余角比它的补角的多1°,则这个角的度数为度.13.小明的家在车站O的北偏东60°方向的A处,学校B在车站O的南偏西30°方向的处,小明上车经车站所走的角∠AOB=.14.如图,已知∠AOB是直角,ON平分∠AOC,OM平分∠BOC,则∠MON的度数为°.15.如图是一个几何体的三视图,则这个几何体的形状是.16.根据几何体的特征,填写它们的名称.(1)上下两个底面是大小相同的圆,侧面展开后是长方形.(2)6个面都是长方形.(3)6个面都是正方形.(4)上下底面是形状大小相同的多边形,侧面是长方形.(5)下底面是圆,上方有一个顶点,侧面展开后是扇形.(6)下底面是多边形,上方有一个顶点.(7)圆圆的实体.三、解答题17.如图,直线AB,CD相交于点O,OA平分∠EOC.(1)若∠EOC=70°,求∠BOD的度数;(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.18.如图,已知∠AOC与∠BOD都是直角,∠BOC=65°(1)求∠AOD的度数;(2)∠AOB与∠DOC有何大小关系?(3)若不知道∠BOC的具体度数,其他条件不变,(2)的关系仍成立吗?19.我们知道,对于一些立体图形问题,常把它转化为平面图形来研究和处理,棱长为a的正方体摆成如图所示的形状,问:(1)这个几何体共有几个正方体?(2)这个几何体的表面积是多少?20.如图所示,点O在直线AB上,并且∠AOC=∠BOC=90°,∠EOF=90°,试判断∠AOE和∠COF,∠COE和∠BOF的大小关系.21.如图,甲、乙、丙三艘轮船从港口O出发,当分别行驶到A,B,C处时,经测量得,甲船位于港口的北偏东43°45′方向,乙船位于港口的北偏东76°35′方向,丙船位于港口的北偏西43°45′方向.(1)求∠BOC的度数;(2)求∠AOB的度数.第四章《几何图形初步》单元练习题单元练习题答案解析1.【答案】D【解析】解:(1)当A,B,C三点在一条直线上时,分点B在A、C之间和点C在A、B之间两种情况讨论.①点B在A、C之间时,AC=AB+BC=4+3=7cm;②点C在A、B之间时,AC=AB-BC=4-3=1cm.所以A、C两点间的距离是7cm或1cm.(2)当A,B,C三点不在一条直线上时,A,C两点之间的距离有多种可能.故选D.2.【答案】A【解析】A、是三棱柱的平面展开图;B、围成三棱柱时,两个三角形重合为同一底面,而另一底面没有,故不能围成三棱柱,故此选项错误;C、围成三棱柱时,缺少一个底面,故不能围成三棱柱,故此选项错误;D、围成三棱柱时,没有底面,故不能围成三棱柱,故此选项错误.故选A.3.【答案】C【解析】根据平面图形所表示的各个部分都在同一平面内,立体图形是各部分不在同一平面内的几何,由一个或多个面围成的可以存在于现实生活中的三维图形,可得答案.A、角是平面图形,故A错误;B、圆是平面图形,故B错误;C、圆锥是立体图形,故C正确;D、三角形是平面图形,故D错误.故选C.4.【答案】A【解析】由图1可得,“富”和“文”相对;“强”和“主”相对;“民”和“明”相对;由图2可得,小正方体从图2的位置依次翻到第4格时,“文”在下面,则这时小正方体朝上面的字是“富”,故选A.5.【答案】A【解析】①三条直线分别平行时,没有交点,故图形可以画出;②三条直线可以同时经过一个点,故图形可以画出;③其中两直线平行,第三条直线与平行的直线相交,故图形可以画出;④三条直线任意两条都相交时,有三个交点,故图形可以画出.故选A.6.【答案】B【解析】∵OC,OD分别是∠AOB,∠BOC的平分线,且∠COD=26°,∴∠BOC=2∠COD=52°,∴∠AOB=2∠BOC=104°,故选B.7.【答案】B【解析】∵四边形ABCD是正方形,∴∠ABC=90°,根据折叠可得∠1=∠2=∠ABD,∠3=∠4=∠DBC,∵∠1+∠2+∠3+∠4=∠ABC=90°,∴∠2+∠3=45°,即∠EBF=45°.故选B..8.【答案】B【解析】一个六棱柱的顶点个数是12,棱的条数是18,面的个数是8.故选B.9.【答案】线;面;面【解析】10.【答案】10cm【解析】∵一个棱锥一共有7个面,∴该棱锥是一个六棱锥.设每条侧棱为x cm,则底边长为12x cm.根据题意得:6x+6×12x=90.解得:x=10故答案为:10cm.11.【答案】BC;6;AC;3;AB;1【解析】求出BC长,根据线段中点求出AD,代入BD=AD-AB求出即可.12.【答案】63【解析】设这个角为x°,则它的余角为(90-x)°,补角为(180-x)°.根据题意有:(90-x)=(180-x)+1解得x=63,故这个角的度数为63度.13.【答案】150°【解析】如图所示:∵小明的家在车站O的北偏东60°方向A处,学校B在车站O的南偏西30°方向处,∴∠1=90°-60°=30°,∠2=30°,∴∠AOB=∠1+∠2+∠3=30°+30°+90°=150°,故答案为:150°.14.【答案】45【解析】∵∠AOB是直角,ON平分∠AOC,OM平分∠BOC,∴∠AON=∠CON=∠AOC,∠BOM=∠COM=∠BOC,∴∠MON=∠COM-∠CON=(∠BOC-∠AOC)=∠AOB=×90°=45°,故答案为:45.15.【答案】圆锥【解析】根据从上面看为圆的有球,圆锥,圆柱等几何体,从正面看和从左面看为三角形的只有圆锥,则这个几何体的形状是圆锥.故答案为:圆锥.16.【答案】(1)圆柱;(2)长方体;(3)正方体;(4)棱柱;(5)圆锥;(6)棱锥;(7)球.【解析】根据所给几何体的特征,直接填写它们的名称即可.17.【答案】解:(1)∵OA平分∠EOC,∴∠AOC=∠EOC=×70°=35°,∴∠BOD=∠AOC=35°;(2)设∠EOC=2x,∠EOD=3x,根据题意得2x+3x=180°,解得x=36°,∴∠EOC=2x=72°,∴∠AOC=∠EOC=×72°=36°,∴∠BOD=∠AOC=36°.【解析】(1)根据角平分线定义得到∠AOC=∠EOC=×70°=35°,然后根据对顶角相等得到∠BOD=∠AOC=35°;(2)先设∠EOC=2x,∠EOD=3x,根据平角的定义得2x+3x=180°,解得x=36°,则∠EOC=2x=72°,然后与(1)的计算方法一样.18.【答案】解:(1)∵∠DOC=∠DOB-∠BOC=90°-65°=25°,∴∠AOD=∠AOC+∠DOC=90°+25°=115°.(2)∵∠DOC=25°,∠AOB=∠AOC-∠BOC=90°-65°=25°,∴∠AOB=∠DOC.(3)成立,∵∠AOB=∠AOC-∠BOC=90°-∠BOC,∠COD=∠BOD-∠BOC=90°-∠BOC,∴∠AOB=∠COD.【解析】(1)先求出∠DCO,继而可得出∠AOD;(2)分别求出∠AOB和∠DOC的度数,可得∠AOB=∠DOC;(3)根据等角的余角相等,可得(2)的关系依然成立.19.【答案】解:(1)上面一层有1个正方体,中间层有3个正方体,底层有6个正方体,共10个正方体;(2)根据以上分析该物体的表面积为6×6×a2=36a2.【解析】(1)先找出每一层中正方体的个数,然后相加即可;(2)由题可知上下左右前后露出的面都为6个正方形,故总共的表面为36个表面,由此得出表面积.20.【答案】解:因为∠EOF=∠COF+∠COE=90°,∠AOC=∠AOE+∠COE=90°,即∠AOE和∠COF都与∠COE互余,根据同角的余角相等得:∠AOE=∠COF,同理可得出:∠COE=∠BOF.【解析】根据已知得出∠AOE和∠COF都与∠COE互余,进而得出∠AOE=∠COF,即可得出:∠COE=∠BOF.21.【答案】解:(1)∵甲船位于港口的北偏东43°45′方向,乙船位于港口的北偏东76°35′方向,丙船位于港口的北偏西43°45′方向,∴∠NOA=43°45′,∠NOB=76°35′,∠NOC=43°45′,∴∠BOC=∠NOB+∠NOC=76°35′+43°45′=120°20′;(2)∵∠NOA=43°45′,∠NOB=76°35′,∴∠AOB=∠NOB-∠NOA=76°35′-43°45′=32°50′.【解析】(1)根据方向角的表示方法,可得∠NOA,∠NOB,∠NOC的度数,根据∠BOC=∠NOB+∠NOC可得答案;(2)根据∠AOB=∠NOB-∠NOA,可得答案.。
