高考数学基础训练题三角函数函数图像与性质、函数y=Asin(wx+φ)的图像性质及应用
新高考数学考点12 y=Asin(wx+φ)的图像与性质考点分类讲义练习题附解析1

考点12 y=Asin(wx+φ)的图像与性质1、了解三角函数的周期性,画出 y =sin x , y =cos x , y =tan x 的图像,并能根据图像理解正弦函数、余弦函数在[ 0 ,2π ],正切函数的性质(如单调性、最大值和最小值、图像与 x 轴的交点等)2. 了解三角函数 y = A sin ( ωx + φ )的实际意义及其参数 A , ω ,φ 对函数图像变化的影响;能画出 y = A sin (ωx +φ )的简图,能由正弦曲线 y =sin x 通过平移、伸缩变换得到 y = A sin ( ωx + φ )的图像 .3. 会用三角函数解决一些简单的实际问题,体会三角函数是描述周期变化现象的重要函数模型 .1. 三角函数的图像与性质是高考中的必考点,对这部分内容的考查,高考中大多以中、低档题为主,主要集中于对函数的周期、图像、单调性、值域(或最值)等几个方面的考查 . 要解决此类问题,要求学生熟练地掌握三角函数的图像,及正弦函数、余弦函数、正切函数的最基本的性质,并能运用这些性质去熟练地解题 .2. 利用三角函数的性质解决问题时,要重视化归思想的运用,即将复杂的三角函数转化为基本的正弦、余弦、正切函数来处理1、函数 f ( x ) = A sin ( ωx + φ )的图像的平移和伸缩变换以及根据图像确定 A , ω ,φ 问题是高考的热点,题型多样,难度中低档,主要考查识图、用图的能力,同时考查利用三角公式进行三角恒等变换的能力 . 2、要牢牢记住函数 f ( x ) = A sin ( ωx + φ )的图像和性质。
1、【2020年江苏卷】.将函数y =πsin(2)43x ﹢的图象向右平移π6个单位长度,则平移后的图象中与y 轴最近的对称轴的方程是____.【答案】524x π=-【解析】3sin[2()]3sin(2)6412y x x πππ=-+=- 72()()122242k x k k Z x k Z πππππ-=+∈∴=+∈当1k =-时524x π=-故答案为:524x π=-2、【2020年全国1卷】设函数()cos π()6f x x ω=+在[π,π]-的图像大致如下图,则f (x )的最小正周期为( )A. 10π9 B.7π6 C. 4π3D. 3π2【答案】C【解析】由图可得:函数图象过点4,09π⎛⎫-⎪⎝⎭, 将它代入函数()f x 可得:4cos 096ππω⎛⎫-⋅+= ⎪⎝⎭又4,09π⎛⎫-⎪⎝⎭是函数()f x 图象与x 轴负半轴的第一个交点, 所以4962πππω-⋅+=-,解得:32ω=所以函数()f x 的最小正周期为224332T πππω=== 故选:C3、【2020年全国3卷】16.关于函数f (x )=1sin sin x x+有如下四个命题: ①f (x )的图像关于y 轴对称. ②f (x )的图像关于原点对称. ③f (x )的图像关于直线x =2π对称. ④f (x )的最小值为2.其中所有真命题的序号是__________. 【答案】②③【解析】对于命题①,152622f π⎛⎫=+= ⎪⎝⎭,152622f π⎛⎫-=--=- ⎪⎝⎭,则66f f ππ⎛⎫⎛⎫-≠ ⎪ ⎪⎝⎭⎝⎭, 所以,函数()f x 的图象不关于y 轴对称,命题①错误;对于命题②,函数()f x 的定义域为{},x x k k Z π≠∈,定义域关于原点对称,()()()()111sin sin sin sin sin sin f x x x x f x x x x ⎛⎫-=-+=--=-+=- ⎪-⎝⎭,所以,函数()f x 的图象关于原点对称,命题②正确;对于命题③,11sin cos 22cos sin 2f x x x x x πππ⎛⎫⎛⎫-=-+=+⎪ ⎪⎛⎫⎝⎭⎝⎭- ⎪⎝⎭, 11sin cos 22cos sin 2f x x x x x πππ⎛⎫⎛⎫+=++=+⎪ ⎪⎛⎫⎝⎭⎝⎭+ ⎪⎝⎭,则22f x f x ππ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭, 所以,函数()f x 的图象关于直线2x π=对称,命题③正确;对于命题④,当0x π-<<时,sin 0x <,则()1sin 02sin f x x x=+<<, 命题④错误. 故答案为:②③.4、【2020年天津卷】8.已知函数()sin 3f x x π⎛⎫=+ ⎪⎝⎭.给出下列结论: ①()f x 的最小正周期为2π;②2f π⎛⎫⎪⎝⎭是()f x 的最大值; ③把函数sin y x =的图象上所有点向左平移3π个单位长度,可得到函数()y f x =的图象. 其中所有正确结论的序号是 A. ① B. ①③C. ②③D. ①②③【答案】B【解析】因为()sin()3f x x π=+,所以周期22T ππω==,故①正确;51()sin()sin 122362f ππππ=+==≠,故②不正确; 将函数sin y x =的图象上所有点向左平移3π个单位长度,得到sin()3y x π=+的图象, 故③正确. 故选:B.5、【2020年山东卷】.下图是函数y = sin(ωx +φ)的部分图像,则sin(ωx +φ)= ( )A. πsin(3x +)B. πsin(2)3x - C. πcos(26x +)D. 5πcos(2)6x - 【答案】BC【解析】由函数图像可知:22362T πππ=-=,则222T ππωπ===,所以不选A, 当2536212x πππ+==时,1y =-∴()5322122k k Z ππϕπ⨯+=+∈, 解得:()223k k ϕππ=+∈Z ,即函数的解析式为:2sin 22sin 2cos 2sin 236263y x k x x x ππππππ⎛⎫⎛⎫⎛⎫⎛⎫=++=++=+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.而5cos 2cos(2)66x x ππ⎛⎫+=-- ⎪⎝⎭ 故选:BC.6、【2019年高考全国Ⅰ卷理数】函数f (x )=2sin cos ++x xx x在[,]-ππ的图像大致为 A .B .C .D .【答案】D 【解析】由22sin()()sin ()()cos()()cos x x x xf x f x x x x x-+----===--+-+,得()f x 是奇函数,其图象关于原点对称,排除A .又22π1π42π2()1,π2π()2f ++==>2π(π)01πf =>-+,排除B ,C ,故选D . 7、【2019年高考全国Ⅰ卷理数】关于函数()sin |||sin |f x x x =+有下述四个结论:①f (x )是偶函数②f (x )在区间(2π,π)单调递增③f (x )在[,]-ππ有4个零点 ④f (x )的最大值为2其中所有正确结论的编号是 A .①②④ B .②④ C .①④D .①③【答案】C 【解析】()()()()sin sin sin sin ,f x x x x x f x f x -=-+-=+=∴为偶函数,故①正确.当ππ2x <<时,()2sin f x x =,它在区间,2π⎛⎫π ⎪⎝⎭单调递减,故②错误. 当0πx ≤≤时,()2sin f x x =,它有两个零点:0,π;当π0x -≤<时,()()sin sin f x x x =--2sin x =-,它有一个零点:π-,故()f x 在[],-ππ有3个零点:0-π,,π,故③错误.当[]()2,2x k k k *∈ππ+π∈N时,()2sin f x x =;当[]()2,22x k k k *∈π+ππ+π∈N时,()sin sin 0f x x x =-=,又()f x 为偶函数,()f x ∴的最大值为2,故④正确.综上所述,①④正确,故选C .8、【2019年高考全国Ⅱ卷理数】下列函数中,以2π为周期且在区间(4π,2π)单调递增的是A .f (x )=|cos2x |B .f (x )=|sin2x |C .f (x )=cos|x |D .f (x )=sin|x |【答案】A【解析】作出因为sin ||y x =的图象如下图1,知其不是周期函数,排除D ; 因为cos cos y x x ==,周期为2π,排除C ;作出cos2y x =图象如图2,由图象知,其周期为π2,在区间(4π,2π)单调递增,A 正确; 作出sin 2y x =的图象如图3,由图象知,其周期为π2,在区间(4π,2π)单调递减,排除B ,故选A .图1图2图39、【2019年高考全国Ⅲ卷理数】设函数()f x =sin (5x ωπ+)(ω>0),已知()f x 在[]0,2π有且仅有5个零点,下述四个结论:①()f x 在(0,2π)有且仅有3个极大值点 ②()f x 在(0,2π)有且仅有2个极小值点③()f x 在(0,10π)单调递增 ④ω的取值范围是[1229510,)其中所有正确结论的编号是 A .①④ B .②③ C .①②③ D .①③④【答案】D【解析】①若()f x 在[0,2π]上有5个零点,可画出大致图象, 由图1可知,()f x 在(0,2π)有且仅有3个极大值点.故①正确;②由图1、2可知,()f x 在(0,2π)有且仅有2个或3个极小值点.故②错误;④当()f x =sin (5x ωπ+)=0时,5x ωπ+=k π(k ∈Z ),所以ππ5k x ω-=, 因为()f x 在[0,2π]上有5个零点,所以当k =5时,π5π52πx ω-=≤,当k =6时,π6π52πx ω-=>,解得1229510ω≤<,10、【2019年高考天津卷理数】已知函数()sin()(0,0,||)f x A x A ωϕωϕ=+>><π是奇函数,将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x .若()g x 的最小正周期为2π,且4g π⎛⎫= ⎪⎝⎭38f π⎛⎫= ⎪⎝⎭A .2-B . CD .2【答案】C【解析】∵()f x 为奇函数,∴(0)sin 0,=π,,0,f A k k k ϕϕ==∴∈∴=Z 0ϕ=; 又12π()sin,2π,122g x A x T ωω=∴==∴2ω=,又π()4g =2A =,∴()2sin 2f x x =,3π()8f =故选C. 11、【2018年高考江苏卷】已知函数()ππsin 2()22y x =+-<<ϕϕ的图象关于直线π3x =对称,则ϕ的值是________. 【答案】π6-【解析】由题意可得2sin π13⎛⎫+=± ⎪⎝⎭ϕ,所以2πππππ()326k k k +=+=-+∈Z ,ϕϕ,因为ππ22-<<ϕ,所以π0,.6k ==-ϕ 【名师点睛】由对称轴得2πππππ()326k k k +=+=-+∈Z ,ϕϕ,再根据限制范围求结果.函数()sin y A x B =++ωϕ(A >0,ω>0)的性质:(1)max min ,y A B y A B =+=-+; (2)最小正周期2πT =ω;(3)由()ππ2x k k +=+∈Z ωϕ求对称轴; (4)由()ππ2π2π22k x k k -+≤+≤+∈Z ωϕ求增区间;由()π3π2π2π22k x k k +≤+≤+∈Z ωϕ求减区间.12、【2019年高考浙江卷】设函数()sin ,f x x x =∈R .(1)已知[0,2),θ∈π函数()f x θ+是偶函数,求θ的值; (2)求函数22[()][()]124y f x f x ππ=+++的值域. 【答案】(1)π2θ=或3π2;(2)[1-+. 【解析】(1)因为()sin()f x x θθ+=+是偶函数,所以,对任意实数x 都有sin()sin()x x θθ+=-+, 即sin cos cos sin sin cos cos sin x x x x θθθθ+=-+, 故2sin cos 0x θ=, 所以cos 0θ=. 又[0,2π)θ∈, 因此π2θ=或3π2. (2)2222ππππsin sin 124124y fx f x x x ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+++=+++ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦ππ1cos 21cos 2136212sin 22222x x x x ⎛⎫⎛⎫-+-+ ⎪ ⎪⎫⎝⎭⎝⎭=+=--⎪⎪⎝⎭π1223x ⎛⎫=-+ ⎪⎝⎭.因此,函数的值域是[1+.题型一 三角函数的性质1、(2020届山东省枣庄市高三上学期统考)设函数2sin cos ()(,0)x x xf x a R a ax +=∈≠,若(2019)2f -=,(2019)f =( )A .2B .-2C .2019D .-2019【答案】B 【解析】因为2sin cos ()x x xf x ax +=,所以22sin()cos()sin cos ()()x x x x x xf x f x ax ax---+-==-=-, 因此函数()f x 为奇函数,又(2019)2f -=,所以(2019)(2019)2f f =--=-. 故选B2、(2020届山东省枣庄市高三上学期统考)已知函数()cos()(0)f x x ωϕω=+>的最小正周期为π,且对x ∈R ,()3f x f π⎛⎫⎪⎝⎭恒成立,若函数()y f x =在[0,]a 上单调递减,则a 的最大值是( )A .π6B .π3C .2π3D .5π6【答案】B 【解析】因为函数()()cos f x x ωϕ=+的最小正周期为π,所以22πωπ==,又对任意的x ,都使得()3f x f π⎛⎫≥ ⎪⎝⎭, 所以函数()f x 在3x π=上取得最小值,则223k πϕππ+=+,k Z ∈, 即2,3k k Z πϕπ=+∈,所以()cos 23f x x π⎛⎫=+ ⎪⎝⎭, 令222,3k x k k Z ππππ≤+≤+∈,解得,63k x k k Z ππππ-+≤≤+∈ ,则函数()y f x =在0,3π⎡⎤⎢⎥⎣⎦上单调递减,故a 的最大值是3π. 故选B3、(2020届山东省潍坊市高三上期中)已知函数()sin cos f x x x =+,则( ) A .()f x 的最小正周期为πB .()y f x =图象的一条对称轴方程为4x π=C .()f x 的最小值为2-D .()f x 的0,2π⎡⎤⎢⎥⎣⎦上为增函数【答案】B 【解析】()sin cos )4f x x x x π=+=+,对A ,()f x ∴的最小正周期为2π,故A 错误;对B ,()42f ππ==()y f x ∴=图象的一条对称轴方程为4x π=,故B 正确;对C ,()f x 的最小值为,故C 错误; 对D ,由[0,]2x π∈,得3[,]444x πππ+∈,则()f x 在[0,]2π上先增后减,故D 错误. 故选:B .4、(2020届山东实验中学高三上期中)已知函数()sin 2f x a x x =的图象关于直线12x π=-对称,若()()124f x f x ⋅=-,则12a x x -的最小值为( )A .4π B .2π C .πD .2π【答案】B 【解析】()f x 的图象关于直线12x π=-对称,(0)()6f f π∴=-,即-1a =,则()sin 222sin 26f x x x x π⎛⎫=-=- ⎪⎝⎭,12()()4f x f x =-,1()2f x ∴=,2()2f x =-或1()2f x =-,2()2f x =,即1()f x ,2()f x 一个为最大值,一个为最小值, 则12||x x -的最小值为2T, T π=,12||x x ∴-的最小值为2π, 即12a x x -的最小值为2π.故选:B .5、(2020届山东省滨州市三校高三上学期联考)设函数()sin 23f x x π⎛⎫=- ⎪⎝⎭,则下列结论正确的是( )A .π-是()f x 的一个周期B .()f x 的图像可由sin 2y x =的图像向右平移3π得到 C .()f x π+的一个零点为6x π=D .()y f x =的图像关于直线1712x π=对称 【答案】ACD 【解析】()sin 23f x x π⎛⎫=- ⎪⎝⎭的最小正周期为π,故π-也是其周期,故A 正确;()f x 的图像可由sin 2y x =的图像向右平移6π得到,故B 错误;()77()()sin sin 066323f f ππππππ⎛⎫+==-== ⎪⎝⎭,故C 正确; sin sin 17175()1262sin 132f πππππ⎛⎫⎛⎫⎛⎫-=== ⎪ =⎪ ⎪⎝⎭⎝⎭⎝⎭,故D 正确. 故选:ACD6、.(2020届江苏省南通市如皋市高三下学期二模)已知函数()()()sin 0f x x ωϕω=+>,将函数()y f x =的图象向右平移π4个单位长度后,所得图象与原函数图象重合,则ω的最小值等于__________.【答案】4【解析】由题得12=,4,()42n n n Z ππωω⨯⨯∴=∈, 因为0>ω,所以ω的最小值等于4.故答案为:47、(2020届江苏南通市高三基地学校第一次大联考数学试题)已知函数()2sin()(0)3f x x πωω=+>的图象关于点,02π⎛⎫⎪⎝⎭对称,则ω的最小值为_____. 【答案】43. 【解析】由题意可得,32k k Z ππωπ⨯+=∈,求得22,3k k Z ω=-∈, 又0>ω,则ω的最小值为43, 故答案为:43. 8、(2019南京学情调研)已知函数f(x)=2sin (2x +φ)⎝⎛⎭⎫-π2<φ<π2的图像关于直线x =π6对称,则f(0)的值为________.【答案】. 1【解析】由题意,f ⎝⎛⎭⎫π6=2sin ⎝⎛⎭⎫2×π6+φ=±2,即sin ⎝⎛⎭⎫π3+φ=±1,又因为-π2<φ<π2, -π6<π3+φ<5π6,所以π3+φ=π2,即φ=π6,所以f(x)=2sin ⎝⎛⎭⎫2x +π6,f(0)=1.9、(2019苏锡常镇调研)函数()cos()(0)3f x x πωω=->的图像关于直线2x π=对称,则ω的最小值为 .【答案】.32【解析】解法1:根据余弦函数的图像及性质,令ππωk x =-3,Z k ∈得ωππk x +=3,令23πωππ=+k 得k 232+=ω,Z k ∈,又因为0>ω,所以当0=k 时ω取得最小值为.32 解法2:由条件可得1)2(±=πf ,即1)32cos(±=-πωπ,则ππωπk =-32,Z k ∈,解得k 232+=ω,Z k ∈,又因为0>ω,所以当0=k 时ω取得最小值为.32解后反思:利用整体思想,结合三角函数的图像及性质是解决这类问题的关键!10、(2019苏州期初调查) 已知函数f(x)=sin (2x +φ)(0≤φ<π)的一条对称轴是x =-512π,则φ=________.【答案】 π3【解析】因为函数f(x)的一条对称轴是x =-512π,所以2×⎝⎛⎭⎫-5π12+φ=k π+π2,k ∈Z ,则φ=k π+4π3,k ∈Z ,又因为0≤φ<π,所以φ=π3.11、(2019南京、盐城二模)若函数f(x)=2sin (ωx +φ)(ω>0,0<φ<π)的图像经过点⎝⎛⎭⎫π6,2,且相邻两条对称轴间的距离为π2,则f ⎝⎛⎭⎫π4的值为________.【答案】.3【解析】由相邻两条对称轴间的距离为π2,知其最小正周期T =2×π2=π,从而得ω=2πT =2ππ=2,又f(x)=2sin (2x +φ)的图像经过点⎝⎛⎭⎫π6,2,所以2sin ⎝⎛⎭⎫π3+φ=2,解得φ=2k π+π6(k ∈Z ),又因为0<φ<π,所以φ=π6,故f (x )=2sin ⎝⎛⎭⎫2x +π6,即有f ⎝⎛⎭⎫π4=2sin 2π3= 3.题型二 三角函数图像的变换1、(2020届山东师范大学附中高三月考)为了得函数23y sin x π⎛⎫=+ ⎪⎝⎭的图象,只需把函数2y sin x =的图象( ) A .向左平移6π个单位 B .向左平移3π单位 C .向右平移6π个单位 D .向右平移3π个单位【答案】A 【解析】不妨设函数2y sin x =的图象沿横轴所在直线平移ϕ个单位后得到函数23y sin x π⎛⎫=+⎪⎝⎭的图象. 于是,函数2y sin x =平移ϕ个单位后得到函数,sin 2()y x ϕ=+,即sin(22)y x ϕ=+, 所以有223k πϕπ=+,6k πϕπ=+,取0k =,6π=ϕ.答案为A . 2、(2020届山东省枣庄、滕州市高三上期末)将曲线()cos 2y f x x =上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移4π个单位长度,得到曲线cos 2y x =,则6f π⎛⎫= ⎪⎝⎭( )A .1B .-1C D .【答案】D 【解析】把cos 2y x =的图象向左平移4π个单位长度,得cos 2()cos(2)sin 242y x x x ππ=+=+=-的图象,再把所得图象各点的横坐标变为原来的12倍,纵坐标不变,得图象的函数式为sin(22)sin 4y x x =-⨯=-, sin 42sin 2cos 2()cos 2y x x x f x x =-=-=,∴()2sin 2f x x =-,∴()2sin63f ππ=-=.故选:D.3、(2020届山东省潍坊市高三上学期统考)将函数()πsin 23f x x ⎛⎫=+ ⎪⎝⎭的图像向右平移()0a a >个单位得到函数()πcos 24g x x ⎛⎫=+ ⎪⎝⎭的图像,则a 的值可以为( )A .5π12B .7π12C .19π24D .41π24【答案】C【解析】由题意知,3()cos(2)sin(2)44g x x x ππ=+=+,其图像向左平移a 个单位得到函数3()sin(22)4f x x a π=++, 而函数()πsin 23f x x ⎛⎫=+⎪⎝⎭,所以有32243a k πππ+=+5224a k ππ=-+,取1k =得1924a π=.答案选C.4、(2020届浙江省宁波市余姚中学高考模拟)函数f(x)=sin(wx +φ)(w >0,φ<2π)的最小正周期是π,若将该函数的图象向右平移6π个单位后得到的函数图象关于直线x =2π对称,则函数f(x)的解析式为( )A .f(x)=sin(2x +3π) B .f(x)=sin(2x -3π) C .f(x)=sin(2x +6π) D .f(x)=sin(2x -6π) 【答案】D【解析】因为函数()()f x sin ωx φ=+的最小正周期是π,所以2ππω=,解得ω2=,所以()()f x sin 2x φ=+, 将该函数的图像向右平移π6个单位后,得到图像所对应的函数解析式为ππy sin 2x φsin 2x φ63⎡⎤⎛⎫⎛⎫=-+=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 由此函数图像关于直线πx 2=对称,得: πππ2φk π232⨯+-=+,即πφk π,k Z 6=-∈,取k 0=,得πφ6=-,满足πφ2<,所以函数()f x 的解析式为()πf x sin 2x 6⎛⎫=-⎪⎝⎭,故选D. 5、(2020·蒙阴县实验中学高三期末)关于函数()22cos cos(2)12f x x x π=-+-的描述正确的是( )A .其图象可由2y x =的图象向左平移8π个单位得到 B .()f x 在(0,)2π单调递增C .()f x 在[]0,π有2个零点D .()f x 在[,0]2π-的最小值为【答案】ACD【解析】由题:()22cos cos(2)1cos 2sin 2)24f x x x x x x ππ=-+-=+=+,由2y x =的图象向左平移8π个单位,得到)))84y x x ππ=+=+,所以选项A 正确;令222,242k x k k Z πππππ-≤+≤+∈,得其增区间为3[,],88k k k Z ππππ-+∈ ()f x 在(0,)8π单调递增,在(,)82ππ单调递减,所以选项B 不正确;解()0,2,4f x x k k Z ππ=+=∈,得:,28k x k Z ππ=-∈,[0,]x π∈, 所以x 取37,88ππ,所以选项C 正确;3[,0],2[,],sin(2)[24444x x x πππππ∈-+∈-+∈-,()[f x ∈, 所以选项D 正确. 故选:ACD6、(2020届山东省枣庄市高三上学期统考)将函数()sin 23f x x π⎛⎫=+ ⎪⎝⎭的图象向右平移2π个单位长度得到()g x 图象,则下列判断正确的是( ) A .函数()g x 在区间,122ππ⎡⎤⎢⎥⎣⎦上单调递增 B .函数()g x 图象关于直线712x π=对称 C .函数()g x 在区间,63ππ⎡⎤-⎢⎥⎣⎦上单调递减 D .函数()g x 图象关于点,03π⎛⎫⎪⎝⎭对称 【答案】ABD【解析】函数()sin 23f x x π⎛⎫=+⎪⎝⎭的图像向右平移2π个单位长度得到()ππsin 223g x x ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦2πsin 23x ⎛⎫=- ⎪⎝⎭.由于7π7π2ππsin sin 112632g ⎛⎫⎛⎫=-==⎪ ⎪⎝⎭⎝⎭,故7π12x =是()g x 的对称轴,B 选项正确. 由于π2π2πsin sin 00333g ⎛⎫⎛⎫=-==⎪ ⎪⎝⎭⎝⎭,故,03π⎛⎫ ⎪⎝⎭是()g x 的对称中心,D 选项正确.由π2ππ2232x -≤-≤,解得π7π1212x ≤≤,即()g x 在区间π7π,1212⎡⎤⎢⎥⎣⎦上递增,故A 选项正确、C 选项错误. 故选:ABD.7、(2019无锡期末) 已知直线y =a(x +2)(a>0) 与函数 y =|cos x|的图像恰有四个公共点A(x 1,y 1),B(x 2,y 2),C(x 3,y 3),D(x 4,y 4), 其中 x 1<x 2<x 3<x 4,则x 4+1tan x 4=________. 【答案】-2【解析】根据图形可得直线y =a(x +2)与函数y =-cos x 的图像相切于点(x 4,-cos x 4),其中x 4∈⎝⎛⎭⎫π4,π.因为y =sin x ,由导数的几何意义可得a =sin x 4=-cos x 4-0x 4+2,化简得x 4+1tan x 4=-2.8、(2020届江苏省南通市高三下学期3月开学考试)将函数()πsin 6f x x ω⎛⎫=- ⎪⎝⎭(0>ω)的图象向左平移π3个单位长度后,所得图象关于直线πx =对称,则ω的最小值为______. 【答案】12【解析】将函数f (x )=sin (ωx 6π-)(ω>0)的图象向左平移3π个单位后,可得函数y =sin (ωx 36πωπ+-)的图象,再根据所得图象关于直线x =π对称,可得ωπ36πωπ+-=k π2π+,k ∈Z , ∴当k =0时,ω取得最小值为12, 故答案为12.题型三 三角函数的解析式1、(2020届山东省滨州市高三上期末)已知函数()2sin(2)f x x ϕ=+的图象过点,26A π⎛⎫⎪⎝⎭,则( )A .把()y f x =的图象向右平移6π个单位得到函数2sin 2y x =的图象 B .函数()f x 在区间,02π⎛⎫- ⎪⎝⎭上单调递减C .函数()f x 在区间[]0,2π内有五个零点D .函数()f x 在区间0,3π⎡⎤⎢⎥⎣⎦上的最小值为1 【答案】D【解析】因为函数()2sin(2)f x x ϕ=+的图象过点,26A π⎛⎫⎪⎝⎭, 所以2sin 23πϕ⎛⎫+= ⎪⎝⎭,因此2,32k k Z ππϕπ+=+∈,所以2,6k k Z πϕπ=+∈,因此()2sin(2)2sin 222sin 266f x x x k x ππϕπ⎛⎫⎛⎫=+=++=+ ⎪ ⎪⎝⎭⎝⎭;A 选项,把()y f x =的图象向右平移6π个单位得到函数2sin 26y x π⎛⎫=- ⎪⎝⎭的图象,故A 错; B 选项,由3222,262k x k k Z πππππ+≤+≤+∈得2,63k x k k Z ππππ+≤≤+∈,即函数()2sin 26f x x π⎛⎫=+ ⎪⎝⎭的单调递减区间是:2,,63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦,故B 错; C 选项,由()2sin 206f x x π⎛⎫=+= ⎪⎝⎭得2,6x k k Z ππ+=∈,即,122k x k Z ππ=-+∈, 因此[]0,2x π∈,所以5111723,,,12121212x ππππ=,共四个零点,故C 错; D 选项,因为0,3x π⎡⎤∈⎢⎥⎣⎦,所以52,666x πππ⎡⎤+∈⎢⎥⎣⎦,因此1sin 2,162x π⎛⎫⎡⎤+∈ ⎪⎢⎥⎝⎭⎣⎦,所以[]2sin 21,26x π⎛⎫+∈ ⎪⎝⎭,即()2sin 26f x x π⎛⎫=+ ⎪⎝⎭的最小值为1,故D 正确;故选:D.2、(2020·浙江温州中学3月高考模拟)已知()sin()f x A x ωφ=+(0,04,)2A πωφ><<<)过点1(0,)2,且当6x π=时,函数()f x 取得最大值1.(1)将函数()f x 的图象向右平移6π个单位得到函数()g x ,求函数()g x 的表达式; (2)在(1)的条件下,函数2()()()2cos 1h x f x g x x =++-,求()h x 在[0,]2π上的值域.【答案】(1)()sin(2)6g x x π=-;(2)[1,2]-.【解析】 (1)由函数()f x 取得最大值1,可得1A =,函数过10,2⎛⎫ ⎪⎝⎭得12sin φ=,,26ππφφ<= 12,6662f k k Z ππππωπ⎛⎫=⇒+=+∈ ⎪⎝⎭,∵04ω<<,∴2ω=()26f x sin x π⎛⎫=+ ⎪⎝⎭,()266g x f x sin x ππ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭.(2) ()22226h x x cos x sin x π⎛⎫=+=+⎪⎝⎭, 710,,2,21266626x x sin x πππππ⎡⎤⎛⎫∈≤+≤-≤+≤ ⎪⎢⎥⎣⎦⎝⎭,12226sin x π⎛⎫-≤+≤ ⎪⎝⎭,值域为[]1,2-.。
1.8函数y=Asin(wx+φ)的图象基础练习题

3.A
【分析】
由三角函数图象平移的规律即可得解.
【详解】
若将函数 的图象向右平移 个单位,
所得函数图象对应的函数表达式是 .
故选:A.
4.A
【分析】
根据图象求出 即可得到函数解析式.
【详解】
显然 ,
因为 ,所以 ,所以 ,
由 得 ,
所以 ,即 , ,
因为 ,所以 ,
所以 .
故选:A
【点睛】
【点睛】
本题考查三角函数的伸缩变换,属于基础题.
7.C
【分析】
根据左加右减的原则,可得平移后的解析式为 ,化简整理,即可得出结果.
【详解】
将函数 的图象向右平移 个单位长度,所得图象的函数解析式为
,整理得 .
故选C
【点睛】
本题主要考查三角函数的图像变换问题,熟记平移原则即可,属于基础题型.
8.D
【分析】
【详解】
(1)由已知得 ,解得 .
将点 代入解析式, ,可知 ,
由 可知 ,于是 .
(2)令
解得 ,
于是函数 的单调递增区间为 .
【点睛】
本题考查正弦函数的图像和性质,基础题.
21.(1) ;(2)当 时, ;当 时, .
【分析】
(1)先由周期为 求出 ,再根据 , 进行求解即可;
(2)先求出 ,可得 ,进而求解即可
15.2
【分析】
根据所给的相邻的零点可求周期,从而得到 的值.
【详解】
因为 , 是函数 两个相邻的零点,
故 ,所以 ,故 ,
故答案为:2.
【点睛】
本题考查三角函数的图象性质,一般地,相邻两个零点之间的距离为半周期,相邻两条对称轴之间的距离也是半周期.
高考数学函数y=Asin(ωx+φ)的图象和性质

§3.3 函数y=Asin(ωx+φ)的图象和性质
知识清单
2
1.函数y=Asin(ωx+φ)和y=Acos(ωx+φ)的最小正周期都是① | ω | .
2.函数y=Atan(ωx+φ)的最小正周期是② | ω | .
3.y=Asin(ωx+φ)的有关概念
4.用五点法画y=Asin(ωx+φ)一个周期内的简图 用五点法画y=Asin(ωx+φ)一个周期内的简图时,要找五个关键点,如下表 所示:
(1)求A、B,确定函数的最大值M和最小值m,则A=
M
2
m
,B=
M
2
m
.
(2)求ω,确定函数的周期T,则ω=2T .
(3)求φ,常用代入法.
例1
已知函数f(x)=Asin(ωx+φ)
A>0,ω>0,|φ|<
2
,x∈R
的部分图象如
图所示.
(1)求f(x)的解析式;
(2)若g(x)=
3
f
5.确定y=Asin(ωx+φ)+k(A>0,ω>0,|φ|<π)中的参数的方法:
在由图象求解析式时,若最大值为M,最小值为m,则A= M m ,k= M m ,ω
2
2
由周期T确定,即由ω=2 求出,φ由特殊点的坐标确定.
T
方法技巧
方法 1 根据图象确定函数解析式
求函数y=Asin(ωx+φ)+B(A>0,ω>0,|φ|<π)的解析式的步骤:
=2sin 2x.
∵tan α=3,
∴g(α)=2sin
三角函数y=Asin(wx+φ)的图像和性质

专题:三角函数)sin(ϕ+=wx A y 的图像和性质一、知识点总结1、函数sin y x =的图象上所有点向左(右)平移ϕ个单位长度,得到函数()sin y x ϕ=+的图象;再将函数()sin y x ϕ=+的图象上所有点的横坐标伸长(缩短)到原来的1ω倍(纵坐标不变),得到函数()sin y x ωϕ=+的图象;再将函数()sin y x ωϕ=+的图象上所有点的纵坐标伸长(缩短)到原来的A 倍(横坐标不变),得到函数()sin y x ωϕ=A +的图象. 2、函数sin y x =的图象上所有点的横坐标伸长(缩短)到原来的1ω倍(纵坐标不变),得到函数sin y x ω=的图象;再将函数sin y x ω=的图象上所有点向左(右)平移ϕω个单位长度,得到函数()sin y x ωϕ=+的图象;再将函数()sin y x ωϕ=+的图象上所有点的纵坐标伸长(缩短)到原来的A 倍(横坐标不变),得到函数()sin y x ωϕ=A +的图象. 3、函数()()sin 0,0y x ωϕω=A +A >>的性质: ①振幅:A ;②周期:2πωT =;③频率:12f ωπ==T ;④相位:x ωϕ+;⑤初相:ϕ. ⑥函数()sin y x ωϕ=A ++B ,当1x x =时,取得最小值为min y ;当2x x =时,取得最大值为max y ,则()max min 12y y A =-,()max min 12y y B =+,()21122x x x x T=-< 二、课前热身1.函数())4f x x π=-(x ∈R )的最小正周期为2. 满足21)4sin(=-πx 的x 的集合为_____3. 已知函数sin()y A x ωϕ=+(0,||A ϕπ><)的一段图象如下图所示,则函数的解析式 . 4. 要得到)32sin(π-=x y 的图像,只要将y=sin2x 的图像向___移动___单位 5. 函数y=cos(2x-3π) 的单调递增区间是____________________ 6. 若函数()3sin 2f x x ω=+(0ω>)在区间3,34ππ⎡⎤-⎢⎥⎣⎦上是增函数,则ω的取值范围是 ___7. 函数y=3sin (2x-6π)-2(2π≤x ≤32π)的值域为___________8. 关于函数()4sin(2)3f x x π=+(x R ∈),有下列命题① 由12()()0f x f x ==得12x x -必是π的整数倍; ② ()y f x =的表达式可改为()4cos(2)6f x x π=-;③ ()y f x =的图象关于点(,0)6π-对称;④ ()y f x =的图象关于直线6x π=-对称.其中正确的命题的序号是 .(把你认为正确的命题的序号都填上) 三、典例分析例1:函数sin(A y =ωx )ϕ++B (0,0,>><ωπϕA )的最大值为22,最小值为-2,周期为32π,图象过点(0,42-),求此函数解析式例2:已知函数)2,0[],21,23[,1sin 2)(2πθθ∈-∈-+=x x x x f (1)当6πθ=时,求f(x)的最大值和最小值;(2)求θ的范围,使f(x)在区间]21,23[-上是单调递减函数。
高考数学函数y=Asin(ωx+φ)的图像及三角函数的应用

课堂考点探究
[思路点拨]根据≤x≤可得≤2x-≤,由此讨论函数g(x)的单调区间和取值范围.
例3 已知函数f(x)=sin+4cos2x,将函数f(x)的图像先向右平移个单位长度,再向下平移2个单位长度,得到函数g(x)的图像.(2)求函数g(x)在区间上的单调递减区间及取值范围.
课堂考点探究
课堂考点探究
变式题 (1)(多选题)函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图像如图4-25-4所示,则下列结论正确的是( )A.函数f(x)的最小正周期为πB.函数f(x)图像的一条对称轴为直线x=C.函数f(x)的单调递减区间为,k∈ZD.当x∈时,函数f(x)的取值范围为
课前基础巩固
[解析]将(0,1)代入函数f(x)的解析式,可得2sin φ=1,即sin φ=.因为|φ|<,所以φ=.
例1 (1)(多选题)为得到函数y=cos的图像,只需将y=cos 2x的图像上所有的点( ) A.横坐标伸长到原来的2倍(纵坐标不变),再向右平移个单位长度B.横坐标伸长到原来的2倍(纵坐标不变),再向右平移个单位长度C.向右平移个单位长度,再将横坐标伸长到原来的2倍(纵坐标不变)D.向右平移个单位长度,再将横坐标伸长到原来的2倍(纵坐标不变)
图4-25-4
课堂考点探究
(2)[2021·全国甲卷] 已知函数f(x)=2cos(ωx+φ)的部分图像如图4-25-5所示,则满足条件>0的最小正整数x为 .
Asin(ωx+φ)的图像与性质练习(含解析)
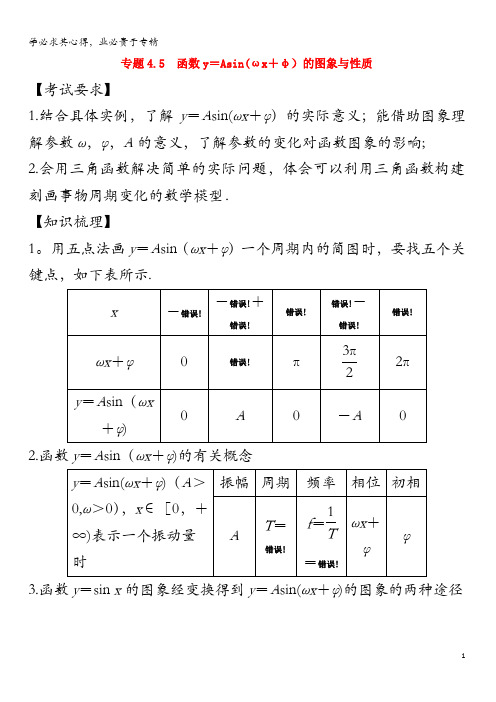
专题4.5 函数y=Asin(ωx+φ)的图象与性质【考试要求】1.结合具体实例,了解y=A sin(ωx+φ)的实际意义;能借助图象理解参数ω,φ,A的意义,了解参数的变化对函数图象的影响;2.会用三角函数解决简单的实际问题,体会可以利用三角函数构建刻画事物周期变化的数学模型.【知识梳理】1。
用五点法画y=A sin(ωx+φ)一个周期内的简图时,要找五个关键点,如下表所示.2.函数y=A sin(ωx+φ)的有关概念3.函数y=sin x的图象经变换得到y=A sin(ωx+φ)的图象的两种途径4。
三角函数应用(1)用正弦函数可以刻画三种周期变化的现象:简谐振动(单摆、弹簧等),声波(音叉发出的纯音),交变电流。
(2)三角函数模型应用题的关键是求出函数解析式,可以根据给出的已知条件确定模型f(x)=A sin(ωx+φ)+k中的待定系数。
(3)把实际问题翻译为函数f(x)的性质,得出函数性质后,再把函数性质翻译为实际问题的答案。
【微点提醒】1。
由y=sin ωx到y=sin(ωx+φ)(ω>0,φ〉0)的变换:向左平移错误!个单位长度而非φ个单位长度。
2。
函数y=A sin(ωx+φ)的对称轴由ωx+φ=kπ+错误!(k∈Z)确定;对称中心由ωx+φ=kπ(k∈Z)确定其横坐标。
3.音叉发出的纯音振动可以用三角函数表达为y=A sin ωx,其中x表示时间,y表示纯音振动时音叉的位移,错误!表示纯音振动的频率(对应音高),A表示纯音振动的振幅(对应音强)。
4。
交变电流可以用三角函数表达为y=A sin(ωx+φ),其中x表示时间,y表示电流,A表示最大电流,错误!表示频率,φ表示初相位。
【疑误辨析】1.判断下列结论正误(在括号内打“√"或“×”)(1)将函数y=3sin 2x的图象左移错误!个单位长度后所得图象的解析式是y=3sin错误!.()(2)利用图象变换作图时“先平移,后伸缩"与“先伸缩,后平移”中平移的长度一致.()(3)函数y=A cos(ωx+φ)的最小正周期为T,那么函数图象的两个相邻对称中心之间的距离为错误!.( )(4)由图象求解析式时,振幅A的大小是由一个周期内图象中最高点的值与最低点的值确定的。
高中 函数y=Asin(ωx+φ)的图象及性质 知识点+例题 全面
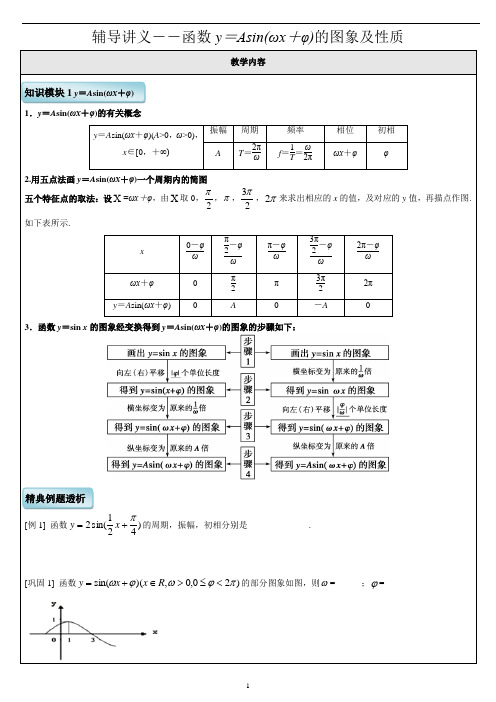
辅导讲义――函数y =Asin(ωx +φ)的图象及性质教学内容1.y =A sin(ωx +φ)的有关概念y =A sin(ωx +φ)(A >0,ω>0),x ∈[0,+∞)振幅 周期 频率 相位 初相 AT =2πωf =1T =ω2πωx +φφ2.用五点法画y =A sin(ωx +φ)一个周期内的简图 五个特征点的取法:设X =ωx +φ,由X 取0,2π,π,23π,π2来求出相应的x 的值,及对应的y 值,再描点作图.如下表所示.x0-φω π2-φω π-φω 3π2-φω 2π-φω ωx +φ 0 π2 π 3π2 2π y =A sin(ωx +φ)A-A3.函数y =sin x 的图象经变换得到y =A sin(ωx +φ)的图象的步骤如下:[例1] 函数)421sin(2π+=x y 的周期,振幅,初相分别是______________.[巩固1] 函数)20,0,)(sin(πϕωϕω<≤>∈+=R x x y 的部分图象如图,则ω=______;ϕ=______知识模块1 y =A sin(ωx +φ)精典例题透析[巩固] 若关于x 的方程01sin sin 2=+-+m x x 有解,则实数m 的取值范围为_____________.[例5] 要得到)21sin(x y -=的图象,只需将)621sin(π--=x y 的图象_______________.[巩固1] 为得到函数)3cos(π+=x y 的图象,只需将函数x y sin =的图象_____________________.[巩固2] 为得到函数)62sin(π-=x y 的图象,只需将函数x y 2cos =的图象_____________________.[例6] 已知函数x x f πsin )(=的图象的一部分如左图,则右图的函数图象所对的函数解析式为_____________.[巩固1] 函数)0,0,0)(sin()(πϕωϕω<<>>+=A x A x f 的部分图象如图所示,则)(x f 的解析式为____________.[巩固2] 已知函数),0,)(sin()(πϕπωϕω<<->∈+=R x x A x f 的部分图象如图所示,则函数)(x f 的解析式 是_______________.[例7] 设函数f (x )=3sin(ωx +φ)(ω>0,-π2<φ<π2)的图象关于直线x =2π3对称,它的周期是π,则下列说法正确的是________.(填序号)[例](1)已知函数f (x )=2sin(ωx +φ)(其中ω>0,|φ|<π2)的最小正周期是π,且f (0)=3,则ω=_____,φ=_______.(2)已知函数f (x )=A sin(ωx +φ) (A >0,|φ|<π2,ω>0)的图象的一部分如图所示,则该函数的解析式为____________.[巩固] 如图为y =A sin(ωx +φ)的图象的一段.(1)求其解析式;(2)若将y =A sin(ωx +φ)的图象向左平移π6个单位长度后得y =f (x ),求f (x )的对称轴方程.题型三:函数y =A sin(ωx +φ)的性质[例] (2014·重庆改编)已知函数f (x )=3sin(ωx +φ)(ω>0,-π2≤φ<π2)的图象关于直线x =π3对称,且图象上相邻两个最高点的距离为π.(1)求ω和φ的值;(2)当x ∈[0,π2]时,求函数y =f (x )的最大值和最小值.[巩固] 已知函数f (x )=A sin(ωx +φ)(x ∈R ,ω,A >0,0<φ<π2)的最大值为2,最小正周期为π,直线x =π6是其图象的一条对称轴.(1)求函数f (x )的解析式;(2)求函数g (x )=f (x -π12)-f (x +π12)的单调递增区间.1.(2013·山东)将函数y =sin(2x +φ)的图象沿x 轴向左平移π8个单位后,得到一个偶函数的图象,则φ的一个可能取值为( )A .3π4B .π4C .0D .-π42.(2013·浙江)函数f (x )=sin x cos x +32cos 2x 的最小正周期和振幅分别是__________.3.已知函数f (x )=2sin(ωx +φ)(ω>0,且|φ|<π2)的部分图象如图所示,则函数f (x )的一个单调递增区间是______________.4.电流强度I (安)随时间t (秒)变化的函数I =A sin(ωt +φ)(A >0,ω>0,0<φ<π2)的图象如右图所示,则当t =1100秒时,电流强度是_____________.5.已知函数f (x )=2sin ωx 在区间[-π3,π4]上的最小值为-2,则ω的取值范围是_________________.6.设偶函数f (x )=A sin(ωx +φ)(A >0,ω>0,0<φ<π)的部分图象如图所示,△KLM 为等腰直角三角形,∠KML =90°, KL =1,则f (16)的值为________.,7.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y =a +A cos ⎣⎡⎦⎤π6(x -6) (x =1,2,3,…,12,A >0)来表示,已知6月份的月平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温值 为________℃.夯实基础训练。
函数y=Asin(wx+φ)的性质与图象(典型题型)高一数学(北师大版2019必修第二册)

∴在规定的8∶00至20∶00之间,有6个小时时间可供冲浪者运动,即9∶00至15∶00.
题型五: 用方程思想求三角函数图象的解析式
第一步:根据图象确定第一个平衡点、第二个平衡点或最高点、最低点.第二步:将“ωx+φ ”作为一个整体,找到对应的值.第三步:列方程组求解.第四步:写出所求的函数解析式.
1.6函数y=Asin(x+)的性质与图象(典型题型)
横向伸缩
横向伸缩
温故知新
温故知新
0
温故知新
方法一
向左(>0)(右<0)平移|φ|个单位长度
各点的横坐标伸长(0<<1)(缩短>1)原来的
各点的纵坐标伸长(A>1)(缩短0<A<1)原来的A倍
倍
五.函数
在物理学中的几何意义
表示离开平衡位置的最大距离,
t(时)
0
3
6
9
12
15
18
21
24
y(米)
1.5
1.0
0.5
1.0
1.5
1.0
0.5
0.99
1.5
经长期观测,y=f(t)的曲线可近似地看成是函数y=Acosωt+b. (1)根据以上数据,求函数y=Acosωt+b(ω>0)的最小正周期T,振幅A及函数表达式. (2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的8∶00至20∶00之间,有多少时间可供冲浪者进行运动?
横坐标不变
纵坐标伸长到原来的 倍
向左平移
纵坐标不变
横坐标缩短到原来的 倍
变换二:
例2. 如何由 y=sinx 的图象得到 的图象?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
十四、三角函数函数图像与性质、函数sin()y A wx ϕ=+的图像性质及应用
1.求下列函数的定义域 (1)x
x y cos 2cos 1+=; (2)x y 2sin =. (3)y =tan ⎝ ⎛⎭⎪⎫
π4-x
2.求下列函数的最小正周期
(1))23πsin(x y -=; (2))4
π
2πtan(+=x y ; (3)y =|sin x |
(4) y =3cos ⎝ ⎛⎭⎪⎫
x 2-π4 (5))]1(2
πcos[)2πcos(-=x x y (6)f (x )=(1+3tan x )cos x
3.若函数cos()3y x πω=+(0)ω>的图象相邻两条对称轴间距离为2
π
,则ω等于 .
4.已知函数f (x )=sin x +cos x ,f ′(x )是f (x )的导函数.求f ′(x )及函数y =f ′(x )的最小正周期;
5.函数)3π
21sin(2-=x y 的一条对称轴方程为( )
A .3π4-=x
B .6π5-=x
C .3π-=x
D .3
π
2=x
6.函数sin(2)3
y x π
=+图像的对称轴方程可能是( )
A .6x π=-
B .12x π=-
C .6x π=
D . 12x π
=
7.y =sin ⎝ ⎛⎭
⎪⎫
x -π4的图象的一个对称中心是( ).
A .(-π,0) B.⎝ ⎛⎭⎪⎫-3π4,0 C.⎝ ⎛⎭⎪⎫3π2,0 D.⎝ ⎛⎭
⎪⎫π2,0
8.求函数)3
π
2cos(-=x y 的对称轴方程和对称中心的坐标
9.已知函数()2sin()f x x ωϕ=+对任意x 都有()(),66f x f x ππ
+=-则()6f π等于( )
A . 2或0
B . 2-或2
C . 0
D . 2-或0
10.函数)3π
2sin(+=x y 的图象( )
A .关于点(3π,0)对称
B .关于直线4π
=x 对称
C .关于点(4π,0)对称
D .关于直线3
π
=x 对称
11.函数y =tan ⎝ ⎛
⎭
⎪⎫2x +π4的图象与x 轴交点的坐标是 .
12.求下列函数的单调区间
(1))3
π
21cos(-=x y
(2)]0,π[),6
π
2sin(2-∈+=x x y
(3)x x y 2sin 32cos -=
(4))23π
sin(2x y -=
(5)y sin(2)6x π
=++1
(6)]),0[)(26
sin(2ππ
∈-=x x y
(7)y =2|cos x | (8))4sin 2cos 4cos
2(sin log 2
1π
π
x x y -=
13.设函数f (x )=sin ()2x +φ (-π<φ<0),y =f (x )图象的一条对称轴是直线x =π
8. (1)求φ; (2)求函数y =f (x )的单调增区间.
14.求下列函数的值域 (1) y =cos2x +cos x
(2))3π
2,6π(,sin 2-∈=x x y
(3))3
π
,2π(),3π2cos(2-∈+=x x y
(4)x x y 2cos 32sin -= )
66(π
π≤≤-x
(5) y =2sin ⎝ ⎛
⎭
⎪⎫2x +π3 (-π6<x <π6)(6)y =sin 2x +sin x -1
15.函数x x y cos 3sin +=在区间]2
,0[π
上的最小值为 .
16.函数)2
π
sin(sin 3)(x x x f ++=的最大值是______.
17.已知函数()sin sin(),2
f x x x x R π
=++∈.
(I)求()f x 的最小正周期; (II)求()f x 的的最大值和最小值;
18.试述如何由sin y x =的图像得到1sin(2)33
y x π
=+的图像。
反之呢?
19.把函数y =sin x (x ∈R )的图象上所有的点向左平行移动3
π
个单位长度,再把所得图象上所有点的横 坐标缩短到原来的
2
1
倍(纵坐标不变),得到的图象所表示的函数是 . 20.将函数sin()()6y x x R π=+∈的图象上所有的点向左平行移动4π
个单位长度,再把图象上各点的横
坐标扩大到原来的2倍(纵坐标不变),则所得到的图象的解析式为 . 21.将函数sin y x =的图像上所有的点向右平行移动
10
π
个单位长度,再把所得各点的横坐标伸长到原
来的2倍(纵坐标不变),所得图像的函数解析式是 . 22.为了得到函数)6
2sin(π
-=x y 的图象,可以将函数x y 2cos =的图象( )
A .向右平移
6π个单位长度 B .向右平移3π
个单位长度 C .向左平移6π个单位长度 D .向左平移3
π
个单位长度
23.为了得到函数y =sin (2x +1)的图像,只需把函数y =sin 2x 的图像上所有的点( ) A .向左平行移动12个单位长度 B .向右平行移动1
2个单位长度 C .向左平行移动1个单位长度 D .向右平行移动1个单位长度 24.为了得到函数y =sin 3x +cos 3x 的图像,可以将函数y =2cos 3x 的图像( ) A .向右平移π4个单位 B .向左平移π
4个单位 C .向右平移π12个单位 D .向左平移π
12个单位
25.函数y =cos(2x +φ)(-π≤φ<π)的图象向右平移π2个单位后,与函数y =sin ⎝ ⎛
⎭⎪⎫2x +π3的图象重合,则
φ=_ _.
26.将函数y =3sin ⎝ ⎛
⎭⎪⎫2x +π3的图像向右平移π2个单位长度,所得图像对应的函数( )
A .在区间⎣⎢⎡⎦⎥⎤π12,7π12上单调递减
B .在区间⎣⎢⎡⎦⎥⎤
π12,7π12上单调递增
C .在区间⎣⎢⎡⎦⎥⎤-π6,π3上单调递减
D .在区间⎣⎢⎡⎦⎥⎤
-π6
,π3上单调递增
27.函数y =-xc os x 的部分图象是( )
28.函数)2
π
2π(lncos <<-
=x x y 的图象( )
29.设函数f (x )=sin(ωx +φ)(ω>0,0<φ<π2)的部分图象如图所示,直线x =π
6是它的一条对称轴,则函数f (x )的解析式为( )
A .f (x )=sin ⎝ ⎛⎭⎪⎫x +π3
B .f (x )=sin ⎝ ⎛
⎭⎪⎫2x -π6
C .f (x )=sin ⎝ ⎛⎭⎪⎫4x +π3
D .f (x )=sin ⎝ ⎛
⎭
⎪⎫2x +π6
30.函数f (x )=A sin(ωx +φ)(x ∈R ,A >0,ω>0,0<φ<π
2)的部分图象如图所示.求f (x )的解析式;
31.已知函数y =sin(ωx +φ)(ω>0,-π≤φ<π)的图象如图所示,则φ=________.
32.已知函数y =sin(ωx +φ)(ω>0,|φ|<π)的图象如图所示,则φ=________.
33.已知函数f (x )=A cos(ωx +φ) 的图象如图所示,f (π2)=-2
3,则f (0)=________.
34.下列函数中,图像的一部分如右图所示的是( )
A .
sin()6y x π=+ B .cos(2)6
y x π
=- C .cos(4)3y x π=- D .sin(2)6
y x π
=-
35.已知函数)sin(φϖ+=x A y 在同一周期内,当3π
=x 时有最大值2,当x=0时有最小值-2,那么函
数的解析式为_______________.
36.已知函数f (x )=A sin(ωx +φ) (A >0,ω>0,|φ|<π
2)的部分图象如图所示. (1)求函数f (x )的解析式;
(2)如何由函数y =2sin x 的图象通过适当的变换得到函数f (x )的图象.
37.函数)3
2sin(3)(π
-
=x x f 的图象为C ,如下结论中正确的是________ (写出所有正确结论的编号).
① 图象C 关于直线π12
11=x 对称; ② 图象C 关于点)0,3
2(π
对称;
③ 函数125,
12()(π
π-
在区间x f )内是增函数;
④ 由x y 2sin 3=的图象向右平移3
π
个单位长度可以得到图象C.
38.设函数y =sin(ωx +φ) (ω>0,φ∈(-π2,π2))的最小正周期为π,且其图象关于直线x =π
12对称,则 在下面四个结论中:
① 图象关于点⎝ ⎛⎭⎪⎫π4,0对称; ②图象关于点⎝ ⎛⎭⎪⎫
π3,0对称;
③在⎣⎢⎡⎦⎥⎤0,π6上是增函数; ④在⎣⎢⎡⎦⎥⎤
-π6,0上是增函数,
所有正确结论的编号为________.。
