数学建模第二次作业(3)
股市分析数学建模.

数学建模第二次模拟赛题摘要针对于当前我国股市形势严峻这一情形,我们对国内股票市场的情况进行分析,使得我们能过更好地了解股市的风险程度,进而更好的增强抵抗能力并经得起利益的诱惑。
针对问题一:通过我们详细的查找资料,我们发现市盈率=每股股票价格/每股股票的收益,我们而市盈率以及股票的收益都有固定的值,这样我们就可以知道股票的内在价值了。
同时股票内在价值还有一些其他的模型算法,如:现金流贴现模型(DMM模型)、内部收益率模型(IRR模型)、零增长模型、不变增长模型等。
对于此题我们采用现金流贴现模型来计算股票的内在价值。
针对问题二:我们通过研究中国联通(SH600050)股票的发展走向来验证股票价格与股票内在价值之间的关联,用EXCEL软件作图进行分析比较,发现并不像经典理论所表达的那样“股市中股票价格是围绕股票内在价值上下波动的”。
针对问题三:关于政府救市的言论和措施,一开始没有起效果,主要是因为当时政府当时没有进行大规模的救市,政府在实行政策失误,以便聚集力量等待时机正确果断、准确、强力地出击救市,我们会给出数据分析来验证这一点。
针对问题四:政府救市是为了让股市稳定,让股市走向一个健康发展的道路是毋庸置疑的。
针对问题五:通过我们对历史数据的分析,我们发现当前股票还没调到位,其最有可能调到2700—2800左右。
针对问题六:对于当前的股票,我们发现股市有风险,入市须谨慎。
关键词:股票内在价值零增长模型不变增长模型 excel作图 MATLAB预测股市一、问题重述针对凶险的股市,对其风险程度的了解能更好的使我们增强抵抗能力和经得起其利益的诱惑。
股市里大家熟悉一个叫李大霄的,他在4月8号就说股市在4000点是地球顶,4月21号为止三遍说到顶。
其依据是:当前43%的股票市盈率已经超过100倍,50%的股票超过83%,70%的股票超过51倍,比较严重的特别是创业板已经整体接近100倍,风险比大盘6124时更甚。
产品销量预测模型

2012年河南科技大学数学建模第二次模拟训练承诺书我们仔细阅读了数学建模竞赛选拔的规则.我们完全明白,在做题期间不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人研究、讨论与选拔题有关的问题。
我们知道,抄袭别人的成果是违反选拔规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守选拔规则,以保证选拔的公正、公平性。
如有违反选拔规则的行为,我们将受到严肃处理。
我们选择的题号是(从A/B/C/D中选择一项填写): B队员签名:1.2.3.日期: 2012 年月--日2012年河南科技大学数学建模第二次模拟编号专用页评阅编号(评阅前进行编号):评阅记录(评阅时使用):评阅人评分备注B 题产品销量预测摘要对产品销售量的预测,无论是对于整体掌控市场的发育与成长态势的政策制定者,还是对于研究市场行情以制定营销策略的厂商而言,都具有极其重要的作用。
本文针对市场上新产品进入市场的销量预测的实际问题,确定模型应有的变量,做出一般的假设并确定约束条件,从而建立有效的模型,以更好的解决新产品进入市场的销量预测问题。
对于问题一,经过分析可设()=dxkx t dt ,从而建立简单的Malthus 模型,很好地解决了产品销售量的预测问题。
对于问题二,针对市场中存在市场容量N 这一约束条件,又有=k[N-x(t)]dxdt,则可建立阻滞增长模型,即可得到产品的销售量在一定时间内迅速增加,达到一定时期后销售量开始趋于稳定。
对于问题三,综合考虑各个影响产品销售量的因素,通过筛选和忽略微小因素,主要考虑产品价格、产品广告投入、消费者习惯等因素,并引用媒体广告产出的模型,分别建立各因素与销售量的函数关系式,并通过这些关系式的组合,得到一种新的新产品扩散模型。
通过该模型与logistic 模型和巴斯新产品扩散模型比较来进行模型检验,并通过Matlab 编程画图可以得出,该模型和两种已知的模型的曲线走向一致。
股市分析数学建模

数学建模第二次模拟赛题摘要针对于当前我国股市形势严峻这一情形,我们对国内股票市场的情况进行分析,使得我们能过更好地了解股市的风险程度,进而更好的增强抵抗能力并经得起利益的诱惑。
针对问题一:通过我们详细的查找资料,我们发现市盈率=每股股票价格/每股股票的收益,我们而市盈率以及股票的收益都有固定的值,这样我们就可以知道股票的内在价值了。
同时股票内在价值还有一些其他的模型算法,如:现金流贴现模型(DMM模型)、内部收益率模型(IRR模型)、零增长模型、不变增长模型等。
对于此题我们采用现金流贴现模型来计算股票的内在价值。
针对问题二:我们通过研究中国联通(SH600050)股票的发展走向来验证股票价格与股票内在价值之间的关联,用EXCEL软件作图进行分析比较,发现并不像经典理论所表达的那样“股市中股票价格是围绕股票内在价值上下波动的”。
针对问题三:关于政府救市的言论和措施,一开始没有起效果,主要是因为当时政府当时没有进行大规模的救市,政府在实行政策失误,以便聚集力量等待时机正确果断、准确、强力地出击救市,我们会给出数据分析来验证这一点。
针对问题四:政府救市是为了让股市稳定,让股市走向一个健康发展的道路是毋庸置疑的。
针对问题五:通过我们对历史数据的分析,我们发现当前股票还没调到位,其最有可能调到2700—2800左右。
针对问题六:对于当前的股票,我们发现股市有风险,入市须谨慎。
关键词:股票内在价值零增长模型不变增长模型 excel作图 MATLAB预测股市一、问题重述针对凶险的股市,对其风险程度的了解能更好的使我们增强抵抗能力和经得起其利益的诱惑。
股市里大家熟悉一个叫李大霄的,他在4月8号就说股市在4000点是地球顶,4月21号为止三遍说到顶。
其依据是:当前43%的股票市盈率已经超过100倍,50%的股票超过83%,70%的股票超过51倍,比较严重的特别是创业板已经整体接近100倍,风险比大盘6124时更甚。
多种类型的回归模型
数学建模第二次作业例一:(线性模型)针叶松数据该数据包含70棵针叶松的测量数据,其中y 表示体积(单位立方英尺),x 1为树的直径(单位:英寸),x 2为树的高度(单位:英尺)。
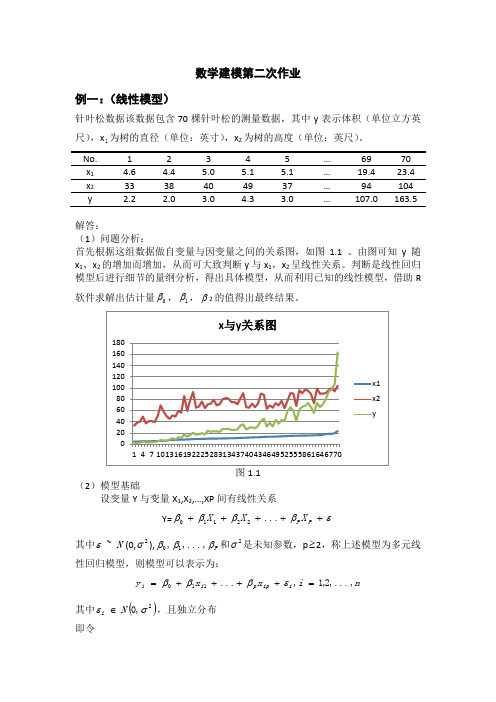
x 1 4.6 4.4 5.0 5.1 5.1 … 19.4 23.4 x 2 33 38 40 49 37 … 94 104 解答:(1)问题分析:首先根据这组数据做自变量与因变量之间的关系图,如图1.1 。
由图可知y 随x 1、x 2的增加而增加,从而可大致判断y 与x 1,x 2呈线性关系。
判断是线性回归模型后进行细节的量纲分析,得出具体模型,从而利用已知的线性模型,借助R 软件求解出估计量0β,1β,β2的值得出最终结果。
图1.1(2)模型基础设变量Y 与变量X 1,X 2,…,XP 间有线性关系Y=εββββ+++++P P X X X (22110)其中N ~ε(0,2σ),P βββ,...,,10和2σ是未知参数,p ≥2,称上述模型为多元线性回归模型,则模型可以表示为:n i x x y i ip p i i ,...,2,1,...110=++++=εβββ其中()2,0σεN i ∈,且独立分布 即令⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n y y y y 21,⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=p ββββ 10,⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=np n n p p x x x x x x x x x X ...1...1 (12)12222111211,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n εεεε 21则多元线性回归模型可表示为εβ+=X Y ,其中Y 是由响应变量构成的n 维向量,X 是n ⨯(p+1)阶设计矩阵,β是p+1维向量,并且满足E (ε)=0,Var (ε)=2σI n与一元线性回归类似,求参数β的估计值βˆ,就是求最小二乘函数 Q (β)=()()ββX y X y T--达到最小的β的值。
β的最小二乘估计()y X X X T T 1ˆ-=β从而得到经验回归方程P P X X Y βββˆˆˆˆ11+++=(3)问题求解:由于体积与长度的量纲不一致,为了使等式两边量纲统一,首先利用excel 软件对数据进行预处理,即对y 进行三次开方的处理。
数学建模(2)第二次作业word版
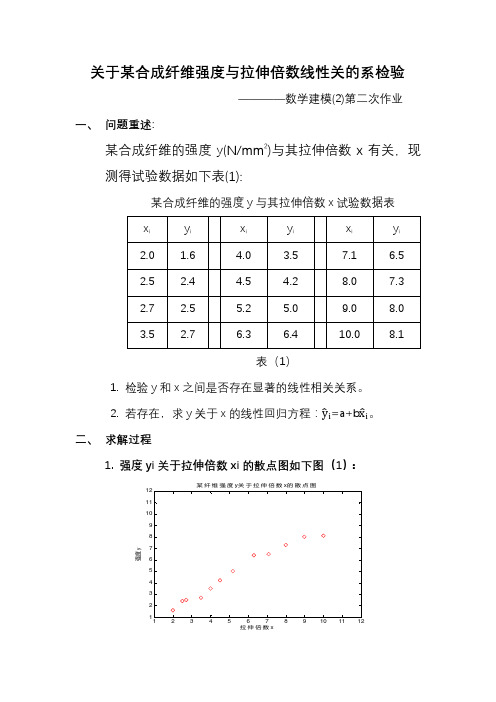
关于某合成纤维强度与拉伸倍数线性关的系检验————数学建模(2)第二次作业一、问题重述:某合成纤维的强度y(N/mm2)与其拉伸倍数x有关,现测得试验数据如下表(1):某合成纤维的强度y与其拉伸倍数x试验数据表表(1)1.检验y和x之间是否存在显著的线性相关关系。
2.若存在,求y关于x的线性回归方程:y i=a+b x i。
二、求解过程1.强度yi关于拉伸倍数xi的散点图如下图(1):图(1)2.样本相关系数计算 (1).计算公式r =nΣxy −ΣxΣynΣx 22nΣy 22(2)计算结果r =12∗382.17−3771.3612∗428.18−64.802∗ 12∗342.86−58.202=0.9859(3)结果分析r >0.8,说明该合成纤维强度y 与拉伸倍数x 成高度线性正相关关系。
2. 回归方程求解 (1).计算公式β1 =n ∑x i y i n i =1− ∑X i n i =1 ∑y i ni =1n x i2ni =1−∑x i n i =12某纤维强度y 关于拉伸倍数x 的散点图拉伸倍数x强度yβ 0=y −β1x (2).计算结果β 1= 12∗382.17−3771.3612∗428.18−64.802=0.8675β0=4.85−0.8675∗5.40=0.1655 (3).回归方程y i =0.1655+0.8675xi (4).回归前后图像对比图(2)回归系数β1=0.8675,表示拉伸倍数每增加一倍,该合成纤维强度增加0.08675。
三、 线性关系检验(1).提出假设123456789101112该纤维强度y 关于拉伸倍数x 的散点图及其线性回归方程拉伸倍数x强度yH0:β1=0线性关系不显著(2).计算检验统计量FF=SSR/1SSE/(n−2)= MSRMSE~F(1,n-2)F =58.89505/11.695902/(12−2)=347.2786(3).显著性水平α=0.05,根据分子自由度1和分母自由度12-2找出临界值Fα=4.965(4).F>Fα,拒绝H0,线性关系显著。
数学建模试题(带答案)三

数学建模试题(带答案)实验03 简单的优化模型(2学时)(第3章简单的优化模型)1. 生猪的出售时机p63~65目标函数(生猪出售纯利润,元):Q(t) = ( 8 – g t )( 80 + rt ) – 4t–640其中,t≥0为第几天出售,g为每天价格降低值(常数,元/公斤),r为每天生猪体重增加值(常数,公斤)。
求t使Q(t)最大。
1.1(求解)模型求解p63(1) 图解法绘制目标函数Q(t) = ( 8 – g t )( 80 + rt ) – 4t–640的图形(0 ≤t≤ 20)。
其中,g=0.1, r=2。
从图形上可看出曲线Q(t)的最大值。
(2) 代数法对目标函数Q(t) = ( 8 – g t )( 80 + rt ) – 4t–640用MATLAB求t使Q(t)最大。
其中,r, g是待定参数。
(先对Q(t)进行符号函数求导,对导函数进行符号代数方程求解)然后将代入g=0.1, r=2,计算最大值时的t和Q(t)。
要求:①编写程序绘制题(1)图形。
②编程求解题(2).③对照教材p63相关内容。
相关的MATLAB函数见提示。
★要求①的程序和运行结果:★要求②的程序和运行结果:syms g t r ;Q=(8-g.*t).*(80+r.*t)-4.*t-640;q=diff(Q,t);q=solve(q);g=0.1;r=2;tm=eval(q)Q=(8-g.*tm).*(80+r.*tm)-4.*tm-6401.2(编程)模型解的的敏感性分析p63~64对1.1中(2)所求得的符号表达式t(r,g),分别对g和r进行敏感性分析。
(1) 取g=0.1,对t(r)在r=1.5:0.1:3上求r与t的关系数据,绘制r与t的关系图形(见教材p65)。
(2) 取r=2,对t(g)在g=0.06:0.01:0.15上求g与t的关系数据,绘制g与t 的关系图形(见教材p65)。
要求:分别编写(1)和(2)的程序,调试运行。
高中数学北师大版 第四章 数学建模活动(三) 课后练习、课时练习

一、单选题
1. 对20不断进行“乘以2”或“减去3”的运算,每进行一次记作一次运算,若运算n
次得到的结果为23,则n的最小值为()
A.7 B.8 C.9 D.10
二、解答题
2. 吴淞口灯塔采用世界先进的北斗卫星导航遥测遥控系统,某校数学建模小组
测量其高度(单位:,如示意图,垂直放置的标杆的高度,使,,在同一直线上,也在同一水平面上,仰角,.(本题的距离
精确到
(1)该小组测得、的一组值为,,请据此计算的值;
(2)该小组分析若干测得的数据后,认为适当调整标杆到灯塔的距离(单位:,使与之差较大,可以提高测量精确度.若灯塔的实际高度为,试问为多少时,最大?。
数学建模第二次作业(章绍辉版)
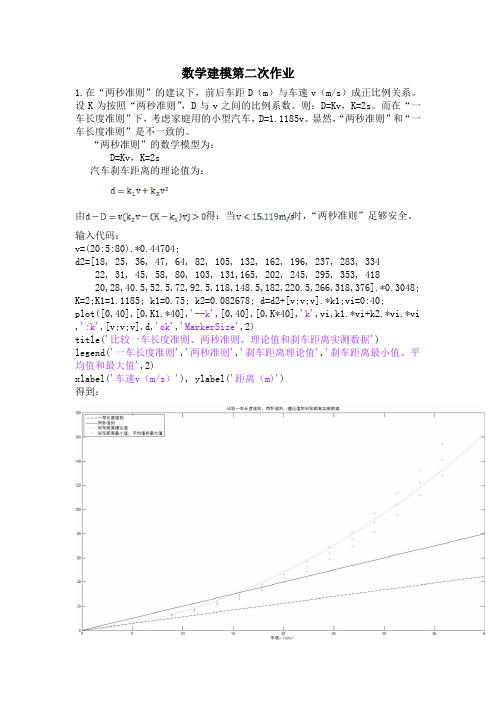
数学建模第二次作业1.在“两秒准则”的建议下,前后车距D(m)与车速v(m/s)成正比例关系。
设K为按照“两秒准则”,D与v之间的比例系数。
则:D=Kv,K=2s。
而在“一车长度准则”下,考虑家庭用的小型汽车,D=1.1185v。
显然,“两秒准则”和“一车长度准则”是不一致的。
“两秒准则”的数学模型为:D=Kv,K=2s汽车刹车距离的理论值为:由得:当时,“两秒准则”足够安全。
输入代码:v=(20:5:80).*0.44704;d2=[18, 25, 36, 47, 64, 82, 105, 132, 162, 196, 237, 283, 33422, 31, 45, 58, 80, 103, 131,165, 202, 245, 295, 353, 41820,28,40.5,52.5,72,92.5,118,148.5,182,220.5,266,318,376].*0.3048; K=2;K1=1.1185; k1=0.75; k2=0.082678; d=d2+[v;v;v].*k1;vi=0:40;plot([0,40],[0,K1.*40],'--k',[0,40],[0,K*40],'k',vi,k1.*vi+k2.*vi.*vi,':k',[v;v;v],d,'ok','MarkerSize',2)title('比较一车长度准则、两秒准则、理论值和刹车距离实测数据')legend('一车长度准则','两秒准则','刹车距离理论值','刹车距离最小值、平均值和最大值',2)xlabel('车速v(m/s)'), ylabel('距离(m)')得到:由上图也可以看出当车速超过15米每秒时,“两秒准则”不安全。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学建模
任意两个城市之间的最廉价路线
参与人员信息:
2012年 6 月 6 日
一、问题提出
某公司在六个城市C1、C2、C3、C4、C5、C6中都有分公司,从Ci 到Cj 的直达航班票价由下述矩阵的第i 行、第j 列元素给出(∞表示无直达航班),该公司想算出一张任意两个城市之间最廉价路线表,试做出这样的表来。
0 50 ∞ 40 25 10
50 0 15 20 ∞ 25
∞ 15 0 10 20 ∞
40 20 10 0 10 25
25 ∞ 20 10 0 55
10 25 ∞ 25 55 0
二 、问题分析
若网络中的每条边都有一个数值(长度、成本、时间等),则找出两节点(通常是源节点和阱节点)之间总权和最小的路径就是最短路问题。
最短路问题是网络理论解决的典型问题之一,可用来解决管路铺设、线路安装、厂区布局和设备更新等实际问题。
最短路问题,我们通常归属为三类:单源最短路径问题、确定起点终点的最短路径问题、全局最短路径问题———求图中所有的最短路径。
题中要求算出一张任意城市间的最廉价路线表,属于全局最短路问题,并且使得该公司总经理能够与各个子公司之间自由往返。
(此两点为主要约束条件) Floyd 算法,具体原理如下:
(1) 我们确定本题为全局最短路问题,并采用求距离矩阵的方法
根据路线及票价表建立带权矩阵W ,并把带权邻接矩阵我w 作为距离矩阵的初始值,即(0)(0)()ij v v D d W ⨯==
(2)求路径矩阵的方法
在建立距离矩阵的同时可建立路径矩阵R ,()ij v v R r ⨯=,ij r 的含义是从i v 到j v 的最短路径要经过点号为ij r 的点。
(3)查找最短路径的方法
若()1v ij r p =,则点1p 是点i 到j 的最短距离的中间点,然后用同样的方法再分头查找。
三、 模型假设:
1.各城市间的飞机线路固定不变
2.各城市间飞机线路的票价不改变
3.忽略乘客除票价以外的各项开销费用
4.不考虑雷雨云、低云、大风、雷暴、冰雹等主要天气因素对飞行的影响。
四、 模型建立
建立带权邻接矩阵:
根据飞机路线及票价表建立带权邻接矩阵, 在带权邻接矩阵中用插入顶点的方法依次构造出 6 个矩阵。
采用floyd 算法步骤为:
,i j D :i 到j 的最短距离
,i j R :i 到j 之间的插入点
输入带权邻接距阵 w
(1)赋初值:对所有,,,,,,, 1.i j i j i j i j w d j r k →→=
(2)更新,i j D ,,i j R :对所有i ,j 若,,,i k k j i j d d d +<,则
,,,i k k j i j d d d +→,,i j k r →.
(3)若k v =,停止;否则1k k +→,转(2).
运行程序得:
D (1)
D (2)、 D(3)、
D (4)、 D( 5)、
D(6),
使最后得到的矩阵 D ( 6 ) 为飞机的最廉价矩阵。
五、模型求解结果
根据模型求解,分析得出任意两个城市之间最廉价线路及票价为:
C1→C2: 1→6→2;35
C1→C3:1→5→3,1→6→4→3;45
C1→C4:1→6→4,1→5→4﹔35
C1→C5∶1→5﹔25
C1→C6:1→6﹔10
C2→C3∶2→3﹔15
C2→C4∶2→4﹔20
C2→C5∶2→4→5﹔30
C2→C6∶2→5﹔25
C3→C4∶3→4﹔10
C3→C5∶3→5∶3→4→5﹔20
C3→C6∶3→4→6﹔35
C4→C5∶4→5﹔10
C4→C6∶4→6﹔25
C5→C6∶5→4→6﹔35。
