控制系统仿真实训试题
《控制系统数字仿真》练习题及答案

《控制系统数字仿真》练习题及答案1. 单选题1. 某系统的函数关系式为y=1/(x3-2x+4),绘制x在0至10之间变化的图形,正确的是()。
A. fplot('1/(x*3-2*x+4)',[0 10])B. fplot('1/(x.^3-2*x+4)',[0 10])C. plot('1/(x.^3-2*x+4)',[0 10])D. plot('1/(x*3-2*x+4)',[0 10])正确答案:B2. 绘制系统零极点图的命令是()。
A. stepB. pzmapC. rlocusD. sgrid正确答案:B3. 将系统零极点形式变换为传递函数形式的命令是()。
A. tf2zpB. ss2tfC. ss2zpD. zp2tf正确答案:D4. AUTOCAD的坐标体系,包括世界坐标和()坐标系。
A. 绝对坐标B. 平面坐标C. 相对坐标D. 用户坐标正确答案:D5. 在MATLAB工作空间中,表示圆周率的特殊变量是()。
A. piB. ansC. iD. eps正确答案:A6. 下列哪条指令是求矩阵的行列式的值()。
A. invB. diagC. detD. eig正确答案:C7. 在CAD网络系统中,以下说法不正确的是()。
A. 设计资料可以共享B. 硬件可以共享C. 电脑文件可以共享D. 可以方便管理设计进度正确答案:C8. i=2; a=2i;b=2*i;c=2*sqrt(-1);程序执行后;a, b, c的值分别是()。
A. a=4,b=4,c=2.0000iB. a=4,b=2.0000i, c=2.0000iC. a=2.0000i, b=4,c=2.0000iD. a=2.0000i,b=2.0000i,c=2.0000i正确答案:C9. 在循环结构中跳出循环,执行循环后面代码的命令为()。
A. returnB. breakC. continueD. keyboard正确答案:B10. figure命令的作用是()。
控制系统仿真试题

结果:-25-20-15-10-505-15-10-5051015Root LocusReal AxisI m a g i n a r y A x i s(3)确定系统稳定时K 取值范围分析:当K=500>406.0748时,其阶跃响由下图可知是趋于发散的;当K=300<406.0748时,其阶跃响由下图可知是趋于收敛的;所以当系统稳定时,参数K的取值范围为:0<K<406.07482.试求以下系统单位阶跃响应曲线,并求其动态性能指标。
(20分)clear;clc;s=tf('s');g1=1/s;g2=1/(1+s);Gtf=g1*g2;G=feedback(Gtf,1);step(G);[y,t]=step(G);c=dcgain(G);disp('稳定值:');disp(c);[max_y,k]=max(y);peak_time=t(k);disp('峰值为:');disp(max(y));disp('到达峰值时间tp:');disp(peak_time);max_overshot=(max(y)-c)/c*100;sprintf('超调量: %f o/o',max_overshot)r1=1;while y(r1)<0.1*cr1=r1+1;endr2=1;while y(r2)<0.9*cr2=r2+1;endrise_time=t(r2)-t(r1);disp('上升时间为tr:')disp(rise_time)单位阶跃曲线如图: Step Response Time (sec)A m p l i t u d e0246810120.20.40.60.811.21.4System: G P eak amplitude: 1.16Overshoot (%): 16.3At time (sec): 3.64System: GSettling Time (sec): 8.08System: G Final Value: 1System: GRise Time (sec): 1.64运行结果: 结论:动态性能指标r p s t t t %σ分别为:%3.16%=σ超调量: s t s 0613.8=调节时间: s t p 6442.3=峰值时间:s t r 6564.1=上升时间:s=length(t);while (y(s)>0.98*c)&&(y(s)<1.02*c) s=s-1; endsetting_time=t(s); disp('调整时间ts:') disp(setting_time)3、已知单位负反馈系统的开环传递函数为)10)(5()(G ++=s s s Ks ,为使系统具有如下性能指标:速度误差系数130-=s K v ,相角裕度大于40。
控制系统数字仿真模拟题

控制系统数字仿真模拟题在控制系统数字仿真模拟中,我们将通过几个案例来展示数字仿真在控制系统设计和分析中的重要性和应用。
案例一:PID控制器调节系统在这个案例中,我们将模拟一个PID控制器调节系统。
首先,我们需要建立一个被控对象的数学模型,可以是一阶或二阶系统。
然后,我们根据实际的控制需求来确定PID控制器的参数。
接下来,我们使用数字仿真软件,比如MATLAB/Simulink来搭建系统模型,将被控对象和PID控制器连接起来并进行仿真。
通过改变PID参数的值,我们可以观察系统响应的变化并优化控制性能。
案例二:状态空间控制系统在这个案例中,我们将研究状态空间控制系统的数字仿真。
状态空间方法是一种描述系统动态特性的有效工具。
我们首先需要得到系统的状态空间表示,包括状态方程和输出方程。
然后,我们使用数字仿真软件来模拟系统的时间响应和频率响应。
通过改变初始状态和控制输入信号,我们可以观察系统的状态变化和输出响应。
通过数字仿真,我们可以更好地理解状态空间控制系统的特性和优化控制策略。
案例三:数字滤波器设计数字滤波器在控制系统中扮演着重要的角色。
在这个案例中,我们将研究数字滤波器的设计和性能评估。
首先,我们需要确定滤波器的类型,如低通滤波器、高通滤波器或带通滤波器。
然后,我们可以使用数字仿真软件来设计和仿真滤波器的频率响应和时域响应。
通过改变滤波器的参数,我们可以优化滤波器的性能和滤波效果。
通过上述案例,我们可以看到数字仿真在控制系统设计和分析中的重要性和灵活性。
它可以帮助工程师在设计前进行系统验证和仿真调试,避免了实际搭建系统的成本和风险。
数字仿真还可以快速优化控制策略和参数,提高系统的性能和鲁棒性。
因此,掌握数字仿真工具和方法对于控制系统工程师来说至关重要。
总结起来,数字仿真在控制系统设计和分析中具有重要的作用。
通过合理利用数字仿真软件和工具,工程师可以更好地理解系统的特性和优化控制策略。
数字仿真可以帮助工程师提高工作效率,节省成本,并减少了实际试验的风险。
控制系统仿真与计算机辅助设计试题
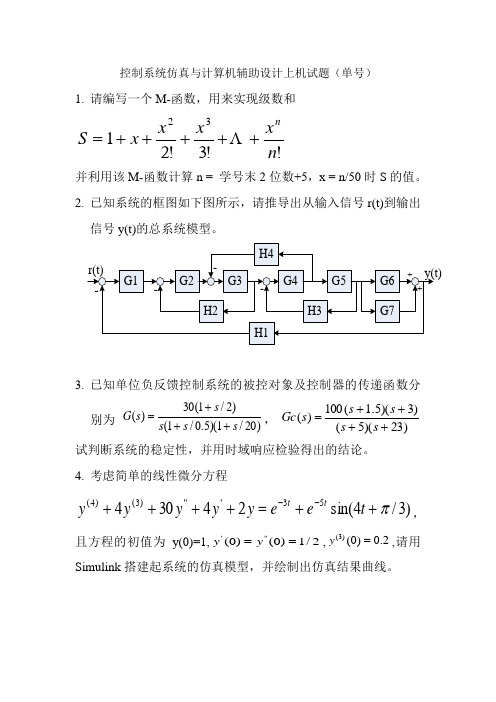
1. 请编写一个M-函数,用来实现级数和!!3!2132n xx x x S n+++++=并利用该M-函数计算n = 学号末2位数+5,x = n/50时S 的值。
2. 已知系统的框图如下图所示,请推导出从输入信号r(t)到输出信号y(t)的总系统模型。
3. 已知单位负反馈控制系统的被控对象及控制器的传递函数分别为 )20/1)(5.0/1()2/1(30)(s s s s s G +++=, )23)(5()3)(5.1(100)(++++=s s s s s Gc试判断系统的稳定性,并用时域响应检验得出的结论。
4. 考虑简单的线性微分方程)3/4sin(2430453''')3()4(π++=++++--t e e y y y y y tt ,且方程的初值为y(0)=1,2/1)0()0('''==y y ,2.0)0()3(=y ,请用Simulink 搭建起系统的仿真模型,并绘制出仿真结果曲线。
5. 请编写一个M-函数,用来实现级数和nx x x x S n+++++= 32132并利用该M-函数计算n = 学号末2位数+5,x = n/50时S 的值。
6. 已知系统的框图如下图所示,请推导出从输入信号r(t)到输出信号y(t)的总系统模型。
7. 已知单位负反馈控制系统的被控对象及控制器的传递函数分别为 )20/1)(5.0/1()2/1(30)(s s s s s G +++=, )23)(5.1()3)(1(100)(++++=s s s s s Gc试判断系统的稳定性,并用时域响应检验得出的结论。
8. 考虑简单的线性微分方程)4sin(2430453''')3()4(t e e y y y y y tt --+=++++,且方程的初值为y(0)=1,2/1)0()0('''==y y ,6.0)0()3(=y ,请用Simulink 搭建起系统的仿真模型,并绘制出仿真结果曲线。
控制系统仿真及CAD试题

控制系统仿真及CAD试题(研2010)一、(20分)试论述系统仿真的目的、意义、分类及应用与发展概况。
解:系统仿真的目的:在分析系统各要素性质及其相互关系的基础上,建立能描述系统结构或行为过程的、且具有一定逻辑关系或数量关系的仿真模型,据此进行试验或定量分析,以获得正确决策所需的各种信息。
系统仿真的意义:CAD不是简单的使用计算机代替人工计算、制图等“传统的设计方法”,而是通过CAD系统与设计者之间强有力的“信息交互”作用,从本质上增强设计人员的想象力与创造力,从而有效地提高设计者的能力与设计结果的水平,因此,CAD技术中所涉及的“设计”应该是以提高社会生产力的水平、加快社会进步为目的的创造性的劳动。
系统仿真的分类:按模型分类分为:物理仿真和数学仿真,物理仿真又分为实物仿真、实时仿真、半实物仿真、在线仿真;数学仿真又分为数字仿真、非实时仿真、模拟仿真、离线仿真。
系统仿真的应用:现代仿真技术经过近50年的发展与完善,已经在各行业做出卓越贡献,同时也充分体现出其在科技发展与社会进步中的重要作用。
仿真技术广泛应用在航空与航天工业、电力工业、原子能工业、石油、化工及冶金工业中。
仿真技术还广泛应用在医学、社会学、宏观经济与商业策略的研究等非工程领域中。
系统仿真的发展概况:(1)在硬件方面,基于多CPU并行处理技术的全数字仿真系统将有效提高系统仿真的速度,从而使仿真系统“实时性”得到进一步的加强。
(2)随着网络技术的不断完善与提高,分布式数字仿真系统将为人们广泛采用,从而达到“投资少、效果好”的目的。
(3)在应用软件方面,直接面向用户的高效能的数字仿真软件不断推陈出新,各种专家系统与智能化技术奖更深入的应用于仿真软件开发中,使得在人—机界面、结果输出、综合评判等方面达到更理想的境界。
(4)虚拟现实技术的不断完善,为控制系统数字仿真与CAD 开辟了一个新时代。
(5)随着FMS 与CIMS 技术的应用于发展,“离散事件系统”越来越多的为仿真领域所重视,离散事件仿真从理论到实现给我们带来许多新的问题。
(完整版)控制系统数字仿真题库

控制系统数字仿真题库一、填空题1. 定义一个系统时,首先要确定系统的边界;边界确定了系统的范围,边界以外对系统的作用称为系统的输入,系统对边界以为环境的作用称为系统的输出。
2.系统的三大要素为:实体、属性和活动。
3.人们描述系统的常见术语为:实体、属性、事件和活动。
4.人们经常把系统分成四类,它们分别为:连续系统、离散系统、采样数据系统和离散-连续系统。
5、根据系统的属性可以将系统分成两大类:工程系统和非工程系统。
6.根据描述方法不同,离散系统可以分为:离散时间系统和离散事件系统。
7. 系统是指相互联系又相互作用的实体的有机组合。
8.根据模型的表达形式,模型可以分为物理模型和数学模型二大类,其中数学模型根据数学表达形式的不同可分为二种,分别为:静态模型和动态模型。
9、采用一定比例按照真实系统的样子制作的模型称为物理模型,用数学表达式来描述系统内在规律的模型称为数学模型。
10.静态模型的数学表达形式一般是代数方程和逻辑关系表达式等,而动态模型的数学表达形式一般是微分方程和差分方程。
11.系统模型根据描述变量的函数关系可以分类为线性模型和非线性模型。
12 仿真模型的校核是指检验数字仿真模型和数学模型是否一致。
13.仿真模型的验证是指检验数字仿真模型和实际系统是否一致。
14.计算机仿真的三个要素为:系统、模型与计算机。
15.系统仿真的三个基本活动是系统建模、仿真建模和仿真试验。
16.系统仿真根据模型种类的不同可分为:物理仿真、数学仿真和数学-物理混合仿真。
17.根据仿真应用目的的不同,人们经常把计算机仿真应用分为四类,分别为:系统分析、系统设计、理论验证和人员训练。
18.计算机仿真是指将模型在计算机上进行实验的过程。
19. 仿真依据的基本原则是:相似原理。
20. 连续系统仿真中常见的一对矛盾为计算速度和计算精度。
21.保持器是一种将离散时间信号恢复成连续信号的装置。
22.零阶保持器能较好地再现阶跃信号。
控制系统数字仿真考试题

H《控制系统数字仿真》复习题一、选择1.将多项式展开的命令中正确的是 D 。
(A)conv([1,2,2],conv([4,1],[1,1])) (B)conv([2,2,1],conv([4,1],[1,1]))(C)conv([2,2,1],conv([1,4],[1,1])) (D)conv([1,2,2],conv([1,4],[1,1]))2.下列命令中可以创建起始值为0,增量值为0.5,终止值为10的等差数列的是A 。
(A)a=0:0.5:10 (B)a=linspace(0,10,0.5) (C)linspace(0,10,10)(D)logspace(0,1,11) 3.MATLAB系统中要清除工作区(Workspace)中的内容,只需在命令窗口输入 C 。
(A)clf (B)clc (C)Clear (D)clg4.列出工作内存中的变量名称以及细节,只需在命令窗口输入 A 。
(A)what (B)who (C)echo on (D)whos5.若B=[3 2 7 4 9 6 1 8 0 5],则B([end-3:end])为 C 。
(A)3 7 1(B)3 2 7 4 9 9 4 7 2 3(C)3 4(D)1 8 0 56.下列符号中可以引导注释行的是 D 。
(A)& (B)@ (C)$ (D)%7.MATLAB系统中合法的变量为 C 。
(A)25aa (B)f.3 (C)ha_23 (D)s\258.设A=[0 2 3 4;1 3 5 0],B=[1 0 5 3;1 5 0 5]则A>=B的结果为 B 。
(A)0 0 0 0 (B)0 1 0 1 (C)1 1 0 1 (D)1 1 0 01 0 0 0 1 0 1 0 0 0 1 0 0 0 1 09.用Matlab系统中的Format long命令设置显示格式后,430/12的显示结果为B 。
(A)35.833 3 (B)35.833 333 333 333 34(C)35.8 3e+01 (D)3.583 333 333 333 334e+0110.设a=1-5*i,则real(a)结果为 C 。
控制系统仿真试题及答案

《控制系统仿真》期终考查试题学生姓名:学号:班级:自动化101学院:电气工程学院老师:吴钦木2013 年12 月24 日一、程序设计题(给出程序和运行结果) 1、请编程实现求取满足12010mi i =>∑的m 的最小值。
答:>> mysum=0; >> for m=1:2010 mysum=mysum+m;if(mysum>2010)break;end end >> m m =63 >>2、已知多项式21()359f x x x =-+,22()41f x x x =+-,试编程求312()()()0f x f x f x =⨯=的解,并找出其解大于零的值。
答:>> p1=[3 -5 9]; >> p2=[1 4 -1]; >> p=conv(p1,p2); >> x=roots(p); >> b=x>0; >> c=x(x>0) c =0.8333 + 1.5184i 0.8333 - 1.5184i 0.2361 >>二、作图题(给出程序和运行结果)1、 已知220s in 100U t π=(伏), 23)B U t ππ=+(伏),43)C U t ππ=+(伏),0t =~0.1(秒),请利用MA TLAB 软件在一个图形界面的三个不同区域分别绘制A U ,B U ,C U 相对于时间t 的波形,并要求图形区域有栅格。
答:>> t=0:0.001:0.1;ua=220*sqrt(2)*sin(100*pi*t); subplot(3,3,1); plot(t,ua); gridub=220*sqrt(2)*sin(100*pi*t+2*pi/3);subplot(3,3,2); plot(t,ub); griduc=220*sqrt(2)*sin(100*pi*t+4*pi/3); subplot(3,3,3); plot(t,uc); gridA U ,B U ,C U 相对于时间t 的波形2、 已知一系统的传递函数为325()362s G s s s s +=+-+试利用MA TLAB 建立系统的零极点传函表达式和状态空间表达式,并绘制出系统的单位阶跃响应图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、某控制系统结构图如图所示,
(1) 试用SIMULINK 建立系统仿真模型,且该系统中K=1保存路径为:E :\lsfz ;
(2) 利用所建立的SIMULINK 仿真模型求该系统闭环传递函数及开环传递函数;
(3) 求该系统当K=1和K=2时的单位阶跃响应的峰值时间p t 、超调量o o σ
、调节时间s t 和稳态
值)(∞h ,分析系统性能,指出增益K 对系统的影响;
(4) 画出该系统的根轨迹,判断使系统稳定的K 的变化范围,求系统临界稳定时根轨迹增益。
(5) 画出系统的BODE 图,求出系统的频域性能指标幅值裕量和相角裕量。
二、已知某控制系统结构如下图,
(1)试用MATLAB 命令(编写m 文件),求出系统的开环和闭环传函;
(2)画出该系统的根轨迹,判断使系统稳定的K 的变化范围,求系统临界稳定时的增益及根值。
(3) 在K 值的稳定范围内绘制三组不同K 值的系统单位阶跃响应(同一坐标中),比较其峰值时间p t 、超调量o o σ
、调节时间s t 和稳态值)(∞h ,指出增益K 对系统的影响; (4)画出系统的BODE 图,求出系统的频域性能指标幅值裕量和相角裕量。
三、已知某控制系统结构如下图,
(1)当K=1和K=2时,试用时域法分析系统的稳定性。
(2)用根轨迹法确定使系统稳定的K 的范围
(3) 当K=1.5时,画出系统的BODE 图,求出系统的频域性能指标幅值裕量和相角裕量。
(4) 当K=1.5时,试用用奈氏稳定判据判断系统的稳定性。
四、单位负反馈系统的开环传递函数为:
3
)1
(
1
5.1
)
(
+
+
-
=
s
s
s
G
,
(1)求出闭环系统的单位阶跃响应曲线;
(2)使用Z-N第一法确定PID控制器的参数Kp、Ti、T d,求出PID控制后的系统单位阶跃响应曲线,与PID校正前进行对比。
五、单位负反馈系统的开环传递函数为:
)5
)(1
(
1
)
(
+
+
=
s
s
s
s
G
,
(1)求出闭环系统的单位阶跃响应曲线;
(2)使用Z-N第二法确定PID控制器的参数Kp、Ti、T d,并求出PID控制后的系统单位阶跃响应曲线,与PID校正前进行对比。
