初二数学综合能力测试题(含答案)
2022人教版初中八年级数学第十二章综合素质测评卷(二)含答案
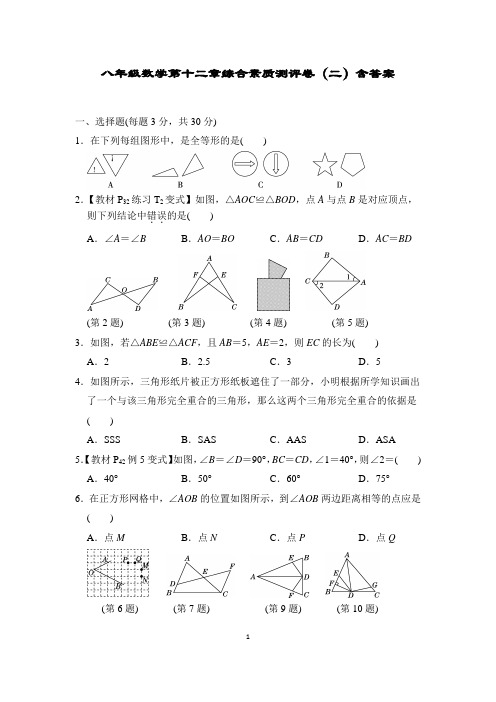
八年级数学第十二章综合素质测评卷（二）含答案一、选择题(每题3分，共30分)1．在下列每组图形中，是全等形的是()2．【教材P32练习T2变式】如图，△AOC≌△BOD，点A与点B是对应顶点，则下列结论中错误．．的是()A．∠A＝∠B B．AO＝BO C．AB＝CD D．AC＝BD(第2题)(第3题)(第4题)(第5题)3．如图，若△ABE≌△ACF，且AB＝5，AE＝2，则EC的长为() A．2 B．2.5 C．3 D．54．如图所示，三角形纸片被正方形纸板遮住了一部分，小明根据所学知识画出了一个与该三角形完全重合的三角形，那么这两个三角形完全重合的依据是()A．SSS B．SAS C．AAS D．ASA 5．【教材P42例5变式】如图，∠B＝∠D＝90°，BC＝CD，∠1＝40°，则∠2＝() A．40°B．50°C．60°D．75°6．在正方形网格中，∠AOB的位置如图所示，到∠AOB两边距离相等的点应是()A．点M B．点N C．点P D．点Q (第6题)(第7题)(第9题)(第10题)7．【教材P45习题T12改编】如图，已知D是△ABC的边AB上一点，DF交AC 于点E，DE＝EF，FC∥AB，若BD＝2，CF＝5，则AB的长为()A．1 B．3 C．5 D．78．在△ABC和△A′B′C′中，有下列条件：①AB＝A′B′；②BC＝B′C′；③AC＝A′C′；④∠A＝∠A′；⑤∠B＝∠B′；⑥∠C＝∠C′，则以下各组条件中不能．．保证△ABC≌△A′B′C′的一组是() A．①②③B．①②⑤C．①③⑤D．②⑤⑥9．如图，在△ABC中，AB＝AC，AD是角平分线，BE＝CF.下列说法正确的个数是()①DA平分∠EDF；②△EBD≌△FCD；③BD＝CD；④AD⊥BC.A．1个B．2个C．3个D．4个10．如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE＝DG，△ADG 和△AED的面积分别为50和25，则△EDF的面积为()A．25 B．35 C．15 D．12.5二、填空题(每题3分，共24分)11．【教材P33习题T3变式】如图，两个三角形全等，根据图中所给的条件可知∠α＝________．(第11题)(第12题)(第13题)12．【教材P38例2改编】如图，要测量池塘的宽度AB，在池塘外选取一点P，连接AP，BP并各自延长，使PC＝P A，PD＝PB，连接CD，测得CD长为25 m，则池塘宽AB为________m.13．如图，在△ABC中，∠C＝90°，AD平分∠BAC，AB＝5，CD＝1.6，则△ABD 的面积是________．14．如图，AB＝DB，∠ABD＝∠CBE，请你添加一个适当的条件：______________，使△ABC≌△DBE(只需添加一个即可)．(第14题)(第15题)(第16题)(第17题) 15．如图，点A，D，C，E在同一条直线上，AB∥EF，AB＝EF，∠B＝∠F，AE＝12，AC＝8，则CD的长为________．16．【教材P56复习题T9拓展】如图，在Rt△ABC中，∠ACB＝90°，BC＝3 cm，CD⊥AB，在AC上取一点E使EC＝BC，过点E作EF⊥AC交CD的延长线于点F，若EF＝5 cm，则AE＝________．17．如图，点B，C，D在同一条直线上，∠B＝∠D＝90°，AB＝CD，BC＝DE，则△ACE的形状为__________________________________．18．在△ABC中，点A的坐标为(0，1)，点B的坐标为(4，1)，点C的坐标为(4，3)，如果要使△ABD与△ABC全等(C与D不重合)，那么点D的坐标是________．三、解答题(19～22题每题10分，其余每题13分，共66分)19．【教材P44习题T11变式】已知：如图，点B，F，C，E在一条直线上，AB ＝DE，AC＝DF，BF＝EC.求证：△ABC≌△DEF.20．如图，点B，E，C，F在同一条直线上，AB∥DE，且AB＝DE，BE＝CF.求证：AC∥DF.21．如图，已知∠1＝∠2，∠3＝∠4，EC＝AD.求证：AB＝BE.22．如图，AD为△ABC的高，E为AC上一点，BE交AD于F，且BF＝AC，FD＝CD.猜想BE与AC的位置关系，并说明理由．23．如图，在△ABC中，D为BC边上一点，E为△ABC外部一点，DE交AC 于点O，且AC＝AE，AD＝AB，∠BAC＝∠DAE.(1)求证：△ABC≌△ADE；(2)若∠BAD＝20°，求∠CDE的度数．24．如图①，在△ABC中，∠ACB是直角，∠B＝60°，AD，CE分别是∠BAC，∠BCA的平分线，AD，CE相交于点F.(1)请你判断并写出FE与FD之间的数量关系(不需证明)；(2)如图②，如果∠ACB不是直角，其他条件不变，那么在(1)中所得的结论是否仍然成立？若成立，请证明；若不成立，请说明理由．答案一、1.C 2.C 3.C 4.D 5.B 6.A7．D 8.C 9.D 10.D二、11.51° 12.25 13.414．∠C ＝∠E (答案不唯一)15．4 16.2 cm 17.等腰直角三角形18．(4，－1)或(0，3)或(0，－1)三、19.证明：∵BF ＝EC ，∴BF ＋FC ＝EC ＋FC ，即BC ＝EF .在△ABC 和△DEF 中，⎩⎨⎧AB ＝DE ，AC ＝DF ，BC ＝EF ，∴△ABC ≌△DEF (SSS)．20．证明：∵BE ＝CF ，∴BE ＋EC ＝EC ＋CF ，即BC ＝EF .∵AB ∥DE ，∴∠B ＝∠DEF .在△ABC 和△DEF 中，⎩⎨⎧AB ＝DE ，∠B ＝∠DEF ，BC ＝EF ，∴△ABC ≌△DEF (SAS)．∴∠ACB ＝∠F .∴AC ∥DF .21．证明：∵∠1＝∠2，∴∠1＋∠EBD ＝∠EBD ＋∠2，即∠ABD ＝∠EBC .在△ABD 和△EBC 中，⎩⎨⎧∠ABD ＝∠EBC ，∠3＝∠4，AD ＝EC ，∴△ABD ≌△EBC (AAS)．∴AB ＝BE .22．解：BE ⊥AC .理由如下：∵AD 为△ABC 的高，∴∠BDF ＝∠ADC ＝90°.在Rt △BDF 和Rt △ADC 中，⎩⎨⎧BF ＝AC ，FD ＝CD ， ∴Rt △BDF ≌Rt △ADC (HL)．∴∠BFD ＝∠C .∵∠BFD ＝∠AFE ，∠C ＋∠DAC ＝90°，∴∠AFE ＋∠DAC ＝90°.∴∠AEF ＝90°，即BE ⊥AC .23．(1)证明：在△ABC 和△ADE 中，⎩⎨⎧AB ＝AD ，∠BAC ＝∠DAE ，AC ＝AE ，∴△ABC ≌△ADE (SAS)．(2)解：由(1)知△ABC ≌△ADE ，∴∠E ＝∠C .∵∠BAC ＝∠DAE ，∠BAC ＝∠BAD ＋∠DAC ，∠DAE ＝∠DAC ＋∠CAE ，∠BAD ＝20°，∴∠CAE ＝∠BAD ＝20°.∵∠E ＝∠C ，∠AOE ＝∠DOC ，∴∠CAE ＝∠CDE .∴∠CDE ＝20°.24. 点方法：解答探索结论问题的方法：在同一道题中，当前面的问题获得解答后，图形运动变化后要探索新的结论，常常根据已经解决问题的思路使相关探索问题得到解决．解：(1)FE ＝FD .(2)成立．证明：如图，在AC 上截取AG ＝AE ，连接FG .∵∠B ＝60°，AD ，CE 分别平分∠BAC ，∠BCA ，∴∠1＝∠2，∠3＝∠4，∠1＋∠2＋∠3＋∠4＝120°.∴∠2＋∠3＝60°.在△AEF 和△AGF 中，⎩⎨⎧AE ＝AG ，∠1＝∠2，AF ＝AF ，∴△AEF ≌△AGF (SAS)．∴∠AFE ＝∠AFG ，FE ＝FG .∵∠AFE ＝∠CFD ＝∠2＋∠3＝60°，∴∠AFG ＝∠AFE ＝60°.∴∠CFG ＝60°.在△CFG 和△CFD 中，⎩⎨⎧∠CFG ＝∠CFD ＝60°，CF ＝CF ，∠3＝∠4，∴△CFG ≌△CFD (ASA)．∴FG ＝FD .∴FE ＝FD .。
八年级综合数学测试题答案
八年级综合数学测试题答案一、选择题1. B2. C3. D4. A5. B6. C7. D8. A9. B10. C二、填空题1. 72. 153. 324. 645. 236. 568. 499. 8110. 98三、计算题1.解：首先将两边同时乘以3，得到：x + 4 = 7然后将4移到等号右边，得到：x = 7 - 4最后计算结果为：x = 32.解：首先将分数相加，得到：1/2 + 2/3然后需要找到两个分数的最小公倍数，最小公倍数为6，所以：3/6 + 4/6最后计算结果为：四、应用题解：让小明的年龄为x，则小刚的年龄为2x，他们年龄的和为12岁。
根据题意，我们可以列出等式：x + 2x = 12将等式简化为：3x = 12然后解方程：x = 12/3最后计算得出：x = 4所以小明的年龄为4岁，小刚的年龄为2 * 4 = 8岁。
五、解答题解：要证明两直线平行，需要证明它们具有相同的斜率。
首先，我们需要计算两条直线的斜率。
设直线AB的斜率为k1，直线CD的斜率为k2。
知道直线AB过点A(-3, 2)，过点B(1, 4)；直线CD过点C(-2, 5)，过点D(2, 7)。
直线AB的斜率为：k1 = (4 - 2) / (1 - (-3)) = 2 / 4 = 1/2。
直线CD的斜率为：k2 = (7 - 5) / (2 - (-2)) = 2 / 4 = 1/2。
由此可见，直线AB和直线CD的斜率相同，即k1 = k2 = 1/2。
因此，根据直线平行的判定定理，可知直线AB与直线CD平行。
六、解答题解：设小明吃的饺子数为x，则小红吃的饺子数为2x+3，根据题意可列出方程：x + (2x+3) = 31化简方程得：x + 2x + 3 = 313x + 3 = 313x = 31 - 33x = 28x = 28 / 3最后计算得出：x = 9 余 1所以小明吃的饺子数为9个。
综上所述，这是八年级综合数学测试题的答案。
初二数学综合试题及答案
初二数学综合试题及答案一、选择题（每题3分，共30分）1. 下列哪个选项是正整数？A. -5B. 0C. 3.5D. 22. 一个数的相反数是它本身，这个数是：A. 0B. 1C. -1D. 23. 以下哪个选项不是有理数？A. πB. √2C. 1/3D. 2.54. 一个数的绝对值是其本身，这个数是：A. 0B. 正数C. 负数D. 非负数5. 一个数的平方是9，这个数是：A. 3B. -3C. 3或-3D. 以上都不对6. 一个数的立方是-8，这个数是：A. 2B. -2C. 2或-2D. 以上都不对7. 下列哪个选项是无理数？A. 2.5B. √4C. √2D. 0.58. 一个数的倒数是它本身，这个数是：A. 0B. 1C. -1D. 以上都不对9. 一个数的绝对值是其相反数，这个数是：A. 0B. 正数C. 负数D. 非负数10. 一个数的平方是16，这个数是：A. 4B. -4C. 4或-4D. 以上都不对二、填空题（每题4分，共20分）1. 一个数的相反数是-4，这个数是______。
2. 一个数的绝对值是5，这个数可以是______或______。
3. 一个数的倒数是1/2，这个数是______。
4. 一个数的平方是25，这个数是______或______。
5. 一个数的立方是27，这个数是______。
三、解答题（每题10分，共50分）1. 计算：(-2) × (-3) × 4。
2. 计算：(-5) ÷ (-2) × 3。
3. 计算：(-3)² - 4 × (-2)。
4. 计算：(-1)³ + 2 × (-3)。
5. 计算：5 × (-3) + 4 × (-2) - 3。
答案：一、选择题1. D2. A3. A4. D5. C6. B7. C8. D9. C10. C二、填空题1. 42. 5，-53. 24. 5，-55. 3三、解答题1. 242. 7.53. 64. -75. -17。
2022人教版初中八年级数学期末综合素质检测卷(二)含答案
八年级数学期末综合素质检测卷（二）含答案一、选择题(每题3分，共30分)1．【教材P104习题T1变式】下列运算正确的是()A．a·a2＝a2B．(a5)3＝a8C．(ab)3＝a3b3D．a6÷a2＝a3 2．【教材P4练习T2改编】下列长度的三条线段，不能．．构成三角形的是() A．3，3，3 B．3，4，5 C．5，6，10 D．4，5，9 3．【教材P147习题T8变式】世界上最小的开花结果植物是澳大利亚的出水浮萍，这种植物的果实像一个微小的无花果，质量只有0.000 000 076 g．将数0.000 000 076用科学记数法表示为()A．7.6×10－9B．7.6×10－8C．7.6×109D．7.6×108 4．【教材P60练习T1拓展】在如图所示的4个图案中，属于轴对称图案的有()A．1个B．2个C．3个D．4个5．如果把分式xyx＋y中的x和y都扩大为原来的5倍，那么分式的值() A．扩大为原来的10倍B．扩大为原来的5倍C．不变D．缩小为原来的1 56．如图，在△ABC中，∠ABC，∠ACB的平分线BE，CD相交于点F，∠A＝60°，则∠BFC等于()A．100°B．110°C．120°D．150°(第6题)(第9题)(第10题)7．下列各式中，计算结果是x2＋7x－18的是()A．(x－1)(x＋18) B．(x＋2)(x＋9)C．(x－3)(x＋6) D．(x－2)(x＋9)8．已知y2＋10y＋m是完全平方式，则m的值是()A．25 B．±25 C．5 D．±59．如图，沿过点A的直线折叠这个直角三角形纸片的直角，使点C落在AB边上的点E处，折痕为AD.若BC＝24，∠B＝30°，则DE的长是() A．12 B．10 C．8 D．610．已知，如图，△ABC是等边三角形，AE＝CD，BQ⊥AD于Q，BE交AD于点P，下列说法：①∠APE＝∠C，②AQ＝BQ，③BP＝2PQ，④AE＋BD＝AB，其中正确的有()A．1个B．2个C．3个D．4个二、填空题(每题3分，共24分)11．若式子(x－4)0有意义，则实数x的取值范围是______________．12．【教材P117练习T2(3)变式】分解因式：xy－xy3＝________________．13．【教材P24练习T2改编】一个多边形的每个内角都是150°，这个多边形是________边形．14．如图，在△ABC和△DEF中，已知CB＝DF，∠C＝∠D，要使△ABC≌△EFD，还需添加一个条件，那么这个条件可以是____________．(第14题)(第15题)(第18题)15．【教材P56复习题T10改编】如图，在△ABC中，DE是AC的垂直平分线，AB＝4，△ABD的周长为12，则BC＝________.16．已知点P(1－a，a＋2)关于y轴的对称点在第二象限，则a的取值范围是____________．17．已知3x＋5y－5＝0，则8x×32y的值是________．18．如图，在平面直角坐标系中，点A，B分别在x轴和y轴上，∠BAO＝60°，在坐标轴上找一点P，使得△P AB是等腰三角形，则符合条件的P点共有________个．三、解答题(19～21题每题8分，22～24题每题10分，25题12分，共66分) 19．先化简后求值：(x＋3)2－(x－4)(x＋4)．其中x＝－2.20. 解方程：1－xx－2＝12－x－2.21．如图，已知EC＝AC，∠BCE＝∠DCA，∠A＝∠E.求证：∠B＝∠D.22．如图，在平面直角坐标系中，每个小正方形的边长都为1个单位长度，△ABC 的顶点都在格点上，点A的坐标为(－3，2)．请按要求完成下列问题：(1)把△ABC先向下平移7个单位长度，再向右平移7个单位长度，得到△A1B1C1，画出△A1B1C1；(2)画出△A1B1C1关于x轴对称的△A2B2C2；画出△A1B1C1关于y轴对称的△A3B3C3；(3)求△ABC的面积．23．如图，在△ABC中，AB＝BC，DE⊥AB于点E，DF⊥BC于点D，交AC 于点F.(1)若∠AFD＝155°，求∠EDF的度数；(2)若点F是AC的中点，求证：∠CFD＝12∠ABC.24．某商店老板第一次用1 000元购进了一批口罩，很快销售完；第二次购进时发现每只口罩的进价比第一次上涨了2.5元．老板用2 500元购进了第二批口罩，所购进口罩的数量是第一次购进口罩数量的2倍，同样很快销售完，两批口罩的售价均为每只15元．(1)第二次购进了多少只口罩？(2)商店老板第一次购进的口罩有3%的损耗，第二次购进的口罩有5%的损耗，商店老板销售完这些口罩后是盈利还是亏本？盈利或亏本多少元？25．(1)在等腰直角三角形ABC中，∠BAC＝90°，AB＝AC，点A，B分别是y 轴，x轴上的两个动点，直角边AC交x轴于点D，斜边BC交y轴于点E.①如图①，当点C的横坐标为－1时，求点A的坐标；②如图②，当点D恰好为AC中点时，连接DE，求证：∠ADB＝∠CDE.(2)如图③，点A在x轴上，且A(－4，0)，点B在y轴的正半轴上，分别以OB，AB为直角边在第一、二象限作等腰直角三角形BOD和等腰直角三角形ABC，且∠OBD＝90°，∠ABC＝90°，连接CD交y轴于点P，当点B在y轴的正半轴上运动时，BP的长度是否变化？若变化，请说明理由；若不变化，请求出BP的长．答案一、1.C 2.D 3.B 4.B 5.B 6.C7．D 8.A 9.C 10.C二、11.x ≠4 12.xy (1＋y )(1－y )13．十二 14.AC ＝ED (答案不唯一)15．8 16.－2＜a ＜1 17.32 18.6三、19.解：原式＝x 2＋6x ＋9－(x 2－42)＝x 2＋6x ＋9－x 2＋16＝6x ＋25，当x ＝－2时，原式＝6×(－2)＋25＝－12＋25＝13.20．解：方程两边同时乘(x －2)，得1－x ＝－1－2(x －2)，解得x ＝2.检验：当x ＝2时，x －2＝0，故此方程无实数根．21．证明：∵∠BCE ＝∠DCA ，∴∠BCE ＋∠ACE ＝∠DCA ＋∠ACE ，即∠ACB ＝∠ECD .在△ACB 和△ECD 中，⎩⎨⎧∠A ＝∠E ，AC ＝EC ，∠ACB ＝∠ECD ，∴△ACB ≌△ECD (ASA)．∴∠B ＝∠D .22．解：(1)如图所示，△A 1B 1C 1即为所求．(2)如图所示，△A 2B 2C 2，△A 3B 3C 3即为所求．(3)S △ABC ＝2×3－12×2×1－12×1×2－12×1×3＝6－1－1－32＝52.23．(1)解：∵∠AFD ＝155°，∴∠DFC ＝25°.∵DF ⊥BC ，DE ⊥AB ，∴∠FDC ＝∠AED ＝90°.∴∠C ＝180°－90°－25°＝65°.∵AB ＝BC ，∴∠A ＝∠C ＝65°.∴∠EDF ＝360°－65°－155°－90°＝50°.(2)证明：如图，连接BF .∵AB ＝BC ，且点F 是AC 的中点，∴BF ⊥AC , ∠ABF ＝∠CBF ＝12∠ABC .∴∠CFD ＋∠BFD ＝90°.∵FD ⊥BC ，∴∠CBF ＋∠BFD ＝90°.∴∠CFD ＝∠CBF .∴∠CFD ＝12∠ABC .24. 点方法：利润问题的相关公式及其数量关系：1．相关公式．售价＝进价×(1＋利润率)；售价＝标价×折扣；利润率＝利润进价×100%.2．基本数量关系．利润＝售价－进价；利润＝进价×利润率；销售额＝销售量×销售单价．进价×(1＋利润率)＝标价×折扣．解：(1)设第一次购进了x只口罩，则第二次购进了2x只口罩，依题意，得1 000x＝2 5002x－2.5，解得x＝100.经检验，x＝100是原方程的解，且符合题意．则2x＝2×100＝200.答：第二次购进了200只口罩．(2)[100×(1－3%)＋200×(1－5%)]×15－1 000－2 500＝805(元)．答：商店老板销售完这些口罩后盈利，盈利805元．25．(1)①解：如图①，过点C作CF⊥y轴于点F，则∠CAF＋∠ACF＝90°.∵∠BAC＝90°，即∠BAO＋∠CAF＝90°，∴∠ACF＝∠BAO.又∵∠AFC＝∠BOA＝90°，AC＝BA，∴△AFC≌△BOA(AAS)．∴AO＝CF＝1.∴点A的坐标是(0，1)．②证明：如图②，过点C作CG⊥AC，交y轴于点G.∵CG⊥AC，∴∠ACG＝90°.∴∠CAG＋∠AGC＝90°.∵∠AOD＝90°，∴∠ADO＋∠DAO＝90°.∴∠AGC＝∠ADO.又∵∠ACG＝∠BAD＝90°，AC＝BA，∴△ACG≌△BAD(AAS)．∴CG＝AD＝CD.∵∠BAC＝90°，AB＝AC，∴∠ACB＝45°.又∵∠ACG＝90°，∴∠DCE＝∠GCE＝45°.又∵CD＝CG，CE＝CE，∴△DCE≌△GCE(SAS)．∴∠CDE＝∠CGE.∴∠ADB＝∠CDE.(2)解：BP的长度不变化．如图③，过点C作CH⊥y轴于点H.∵∠ABC＝90°，∴∠CBH＋∠ABO＝90°.∵∠BAO＋∠ABO＝90°，∴∠CBH＝∠BAO.又∵∠CHB＝∠AOB＝90°，BC＝AB，∴△CBH≌△BAO(AAS)．∴CH＝BO，BH＝AO＝4.∵BD＝BO，∴CH＝BD.又∵∠CHP＝∠DBP＝90°，∠CPH＝∠DPB，∴△CPH≌△DPB(AAS)．∴BP＝HP＝12BH＝2.。
初二数学综合能力测试题(含答案)
初二数学综合能力测试题(含答案)1、已知$a>b$，则下列不等式中成立的是（）。
A。
$ac>bc$。
B。
$-a>-b$。
C。
$-2a3-b$2、若$\frac{ac}{bd}\neq1$，则下列各式正确的是（）。
A。
$\frac{ac+1}{a+ca}=\frac{cx}{a+2b}+\frac{2d}{bd+1}$B。
$\frac{ac+1}{b+db}=\frac{cx}{a+2b}+\frac{2d}{bd+1}$ C。
$\frac{ac+1}{c+ac}=\frac{cx}{a+2b}+\frac{2d}{bd+1}$D。
$\frac{ac+1}{d+bd}=\frac{cx}{a+2b}+\frac{2d}{bd+1}$3、下列图形中不是中心对称图形的是（）。
A。
B。
C。
D。
4、如图，直线$l_1$、$l_2$被直线$l_3$所截，且$l_1\parallel l_2$，若$\angle1=50^\circ$，则$\angle2$的度数为（）。
A。
$130^\circ$。
B。
$50^\circ$。
C。
$40^\circ$。
D。
$60^\circ$5、下列调查方式中，适宜采用抽样调查的是（）。
A。
了解重庆市所有九年级学生每天参加体育锻炼的平均时间B。
审查一篇科学论文的正确性C。
对你所在班级同学的身高的调查D。
对“瓦良格”号航母的零部件性能的检查6、已知数据2，3，x，4，8的平均数是4，则这组数据的中位数和众数是（）。
A。
3和3.B。
3和4.C。
2和3.D。
4和47、某厂接到加工720件衣服的订单，预计每天做48件，正好按时完成，后因客户要求提前5天交货，设每天应多做$x$件，则$x$应满足的方程为（）。
A。
$\frac{720}{48+x}=\frac{720}{48}-5$B。
$\frac{720}{48+x}=\frac{720}{48}+5$C。
$\frac{720}{48+x}=5$D。
初二数学综合练习题及答案
初二数学综合练习题及答案1. 以分数的形式写出下列小数：a. 0.6b. 0.25c. 0.75d. 0.125答案：a. 6/10b. 25/100c. 75/100d. 125/10002. 两数的和是30，差是14，求这两个数。
答案：设其中一个数为x，根据题意可得：x + (x - 14) = 302x - 14 = 302x = 30 + 142x = 44x = 22所以这两个数分别为22和8。
3. 甲、乙两人一起修一段铁轨，甲单独修完需要4天，乙单独修完需要6天。
如果两人一起修，他们需要多少天才能完成？答案：甲单独修完的工作效率是1/4，乙单独修完的工作效率是1/6，设两人一起修完的时间为x天，则他们一起的工作效率是1/x。
根据题意可得：1/4 + 1/6 = 1/x3/12 + 2/12 = 1/x5/12 = 1/x将等式两边取倒数，得：12/5 = x/1x = 12/5x = 2.4所以，甲乙两人一起修完需要2.4天。
4. 小明有5张红色的卡片，6张黄色的卡片，他从两堆卡片中分别取出一张，那么取出的两张卡片中至少有一张红色卡的概率是多少？共有5 + 6 = 11张卡片，从中任意取出两张的情况总数为C(11, 2) = 55。
取出的两张卡片中，至少有一张红色卡的情况总数为：只有一张红色卡的情况：5 * 6 = 30两张卡片都是红色卡的情况：5 * 4 = 20所以，取出的两张卡片中至少有一张红色卡的概率为(30 + 20)/55 = 50/55 = 10/11。
5. 甲、乙两数之和是65，差是15，求甲、乙两数分别是多少。
答案：设甲、乙两数分别为x和y，根据题意可得：x + y = 65x - y = 15将第二个等式两边同时加上y，得：x = y + 15将上面的表达式代入第一个等式中，得：(y + 15) + y = 652y + 15 = 652y = 65 - 152y = 50y = 50/2y = 25将y的值代入第一个等式中，得：x + 25 = 65x = 65 - 25x = 40所以，甲、乙两数分别为40和25。
八年级上册数学综合测试题及答案
八年级上册数学综合测试题及答案一、单选题（18分）1.（3分）在代数式枭，，巳$/,亮，攀，--：中，分式共有（ ）A.2个B.3个C.4个D.5个 2 .（3分）图中有三个正方形，其中构成的三角形中全等三角形的对数有（）3 . （3分）下列运算正确的是（ ）4 . （3分）下列式子变形是因式分解的是（A.2对B.3对C.4对D.5对 A 3o ¥b a+l =T B.2X& 辿 3 3C.Vo 5 =0D./a/ = a(a >0)Ax7 - 5x + 6 = K(X - 5)+ 6 B.x2- 5x + 6 = (x - 2)(x - 3J5 . （3分）对于实数a 、b ,定义一种新运算"® "为：a ® b 二高,这里等式右边是实数运算.例如：1® 3二合=4-则方程x ® （-2）=合1的解是（ ）6 .（3分）如图，已知，BD 为SBC 的角平分线，且BD=BC , E 为BD 延长线上 的一点，BE=BA .下面结论:①2ABDaEBC ;②AC=2CD ;③AD=AE=EC ; ④N BCE+N BCD=180° .其中正确的是（ ）A.①②③B.①②④C.①③④D.②③④二.填空题（18分）7 .（3分）在直角坐标平面里，MBC 三个顶点的坐标分别为A （-2,0）、B （0 , 3） 和C （-3 , 2）,若以y 轴为对称轴作轴反射ABC 在轴反射下的像是△A'B'C', 则C 点坐标为 .C.(x - 2)(x - 3/ = x 2 - 5K + 6 Dy-5x+6=a + 2J(x+3)A.x=4B.x=5C.x 二 6D.x=78. （3分）若关于x的分式方程看#告二念解，则m= .9. （3分）计算：咛尸“多环/_ .10. （3分）如图所示，MBC的两条外角平分线AP、CP相交于点P, PH±AC 于H .若nABC=60° ,则下面的结论:①N ABP=30°;②N APC=60°;③PB=2PH ;④/APH二N BPC ,其中正确的结论是.11. （3分）关于x的方程：x+：=c+弼解是xi=c , X2W ； X-：=日的解是xi=c , X2 = ~ ,贝U X+2=C+S的解是Xi = C , X2=.12.（3分）我们知道："两边及其中一边的对角分别相等的两个三角形不一定全等〃.但是，小亮发现：当这两个三角形都是锐角三角形时，它们会全等，除小亮的发现之外，当这两个三角形都是一时，它们也会全等；当这两个三角形其中一个三角形是锐角三角形,另一个是时，它们一定不全等.三、解答题（84分）13. （6 分）计算：- 2）° +1+4cos30°- |\3 - y[17\ .14. （6分）如图,方格纸中每个小正方形的边长都是1「ABC在平面直角坐标系中的位置如图所示：⑴将占ABC向右平移4个单位后,得到&A1B1C1,请画出^AiBiCi,并直接写出⑵作出5面的关于x轴的对称图形S2B2c2并直接写出点A2的坐标(3)在第二象限5x5的网格中作△ ABC的轴对称图形，要求各顶点都在格点上, 共能作一个.15. (6分)列分式方程解应用题：北京第一条地铁线路于1971年1月15日正式开通运营.截至2017年1月，北京地铁共有19条运营线路，覆盖北京市11个辖区.据统计，2017年地铁每小时客运量是2002年地铁每小时客运量的4倍,2017年客运240万人所用的时间比2002年客运240万人所用的时间少30小时，求2017年地铁每小时的客运量？16 .（6 分）已知AD 为SBC 的内角平分线，AB=7 cm , AC=8 cm , BC=9 cm .7 cm_______ gem __________ 9cm(1)请画出图形，(必须保留作图痕迹).(2)求CD的长.17 . (6分)如图，ABIICD ,以点A为圆心，小于AC长为半径作圆弧，分别交AB , AC于E , F两点，再分别以E , F为圆心，大于狂眠为半径作圆弧,两条圆弧交于点P,作射线AP ,交CD于点M .(1)若/ACD= 114。
初二数学综合试卷答案
一、选择题1. 答案：D解析：根据题意，设圆的半径为r，则圆的面积为πr²。
由题意知，圆的面积为36π，即πr²=36π，解得r=6。
因此，圆的直径为2r=12。
2. 答案：A解析：根据题意，设正方形的边长为a，则正方形的周长为4a。
由题意知，正方形的周长为24，即4a=24，解得a=6。
因此，正方形的面积为a²=6²=36。
3. 答案：C解析：根据题意，设等腰三角形的底边长为a，腰长为b。
由题意知，底边长为4，腰长为6，即a=4，b=6。
根据勾股定理，可得三角形的高h=√(b²-a²)=√(6²-4²)=√(36-16)=√20=2√5。
4. 答案：B解析：根据题意，设一次函数的解析式为y=kx+b。
由题意知，当x=1时，y=2；当x=2时，y=3。
根据这两个点，可以列出方程组：$$\begin{cases}k+b=2 \\2k+b=3\end{cases}$$解得k=1，b=1。
因此，一次函数的解析式为y=x+1。
5. 答案：D解析：根据题意，设等差数列的首项为a₁，公差为d。
由题意知，等差数列的前三项分别为2，5，8。
因此，可得方程组：$$a₁+d=2 \\a₁+2d=5\end{cases}$$解得a₁=1，d=1。
因此，等差数列的第六项为a₁+5d=1+5×1=6。
二、填空题6. 答案：-2解析：由题意知，a²+b²=17，ab=6。
根据平方差公式，可得(a+b)²=a²+2ab+b²=17+2×6=29。
因此，a+b=±√29。
7. 答案：2解析：根据题意，设梯形的上底为a，下底为b，高为h。
由题意知，梯形的面积S=15，上底a=3，下底b=5。
根据梯形面积公式，可得h=S×2/(a+b)=15×2/(3+5)=6。
人教版八年级数学上册全册综合测试题含答案
人教版八年级数学上册全册综合测试题一、选择题(本大题共7小题，每小题3分，共21分．在每小题列出的四个选项中，只有一项符合题意)1．计算(－12)0－4的结果是( )A ．－1B ．－32C ．－2D ．－522．下列长度的三条线段，不能组成三角形的是( ) A ．9，15，8 B ．4，9，6 C ．15，20，8 D ．3，8，4 3．下列计算正确的是( )A ．(－x 3)2＝x 5B ．(－3x 2)2＝6x 4C ．(－x )－2＝1x2 D ．x 8÷x 4＝x 24．衡阳市某生态示范园计划种植一批梨树，原计划总产量为30万千克，为了满足市场需求，现决定改良梨树品种，改良后平均每亩产量是原来的1.5倍，总产量比原计划增加了6万千克，种植亩数减少了10亩，则原来平均每亩产量是多少万千克？设原来平均每亩产量为x 万千克，根据题意，列方程为( )A.30x －361.5x ＝10B.30x －301.5x ＝10C.361.5x －30x ＝10 D.30x ＋361.5x＝10 5．如图1，在△ABC 中，AB ＝AC ，AD 平分∠BAC ，DE ⊥AB 于点E ，DF ⊥AC 于点F ，有下列结论：①BD ＝DC ；②DE ＝DF ；③AD 上任意一点到AB ，AC 的距离相等；④AD 上任意一点到点B 与点C 的距离不等．其中正确的是( )A ．①②B ．③④C ．①②③D ．①②③④图16．如图2①是长方形纸带，∠DEF ＝30°，将纸带沿EF 折叠成图②，再沿BF 折叠成图③，则图③中∠CFE 的度数为( )A ．60°B ．90°C ．120°D ．150°图27．如图3，在四边形ABCD 中，∠BAD ＝120°，∠B ＝∠D ＝90°，在BC ，CD 上分别找一点M ，N ，当△AMN 的周长最小时，∠AMN ＋∠ANM 的度数为( )A ．130°B ．120°C ．110°D ．100°图3二、填空题(本大题共7小题，每小题3分，共21分) 8．0.000608用科学记数法表示为__________．9．在平面直角坐标系中，将点A (－1，2)向右平移3个单位长度得到点B ，则点B 关于x 轴的对称点C 的坐标是________．10．已知a ＋b ＝32，ab ＝1，则(a －2)(b －2)＝________．11．一个多边形的内角和是四边形内角和的4倍，则这个多边形的边数是________． 12．如图4，在Rt △ABC 中，∠B ＝90°，ED 是AC 的垂直平分线，交AC 于点D ，交BC 于点E .已知∠BAE ＝16°，则∠C 的度数为________．413．如图5，在△ABC 中，∠C ＝90°，∠ABC ＝60°，BD 平分∠ABC ，若AD ＝6，则CD ＝________．图514．请你写一个能先用提公因式法，再用公式法来分解因式的三项式，并写出因式分解的结果：____________________.三、解答题(共58分)15．(8分)计算：(1)(－2x3y2－3x2y2＋2xy)÷2xy；(2)(x＋2y－3)(x－2y＋3)(运用乘法公式)．16．(8分)解分式方程：xx－1－1＝2x3x－3.17．(9分)先化简，再求值：8x2－4x＋4÷(x2x－2－x－2)，其中||x＝2.18．(10分)如图6，在平面直角坐标系中，每个小正方形的边长均为1，点A 的坐标为(－3，2)．(1)把△ABC 向下平移4个单位长度得到△A 1B 1C 1，画出△A 1B 1C 1，则点A 1的坐标是________； (2)画出△ABC 关于y 轴对称的△A 2B 2C 2，则点C 2的坐标是________； (3)求△ABC 的面积．图619．(11分)某自动化车间计划生产480个零件，当生产任务完成一半时，停止生产进行自动化程序软件升级，用时20分钟，恢复生产后工作效率比原来提高了13，结果完成任务时比原计划提前了40分钟，求软件升级后每小时生产多少个零件．20．(12分)已知△ABC 为等腰三角形，AB ＝AC ，点D 为直线BC 上一动点(点D 不与点B ，C重合)．以AD为边作△ADE，且AD＝AE，连接CE，∠BAC＝∠DAE.(1)如图7①，当点D在边BC上时，试说明：①△ABD≌△ACE；②BC＝DC＋CE.(2)如图②，当点D在边BC的延长线上时，其他条件不变，探究线段BC，DC，CE之间存在的数量关系，并说明理由．图71．A 2．D 3．C 4．A 5．C 6．B 7．B 8．6.08×10－49．(2，－2) 10．2 11．10 12．37° 13．314．答案不唯一，如9x 3＋6x 2y ＋xy 2＝x (9x 2＋6xy ＋y 2)＝x (3x ＋y )215．解：(1)原式＝－2x 3y 2÷2xy －3x 2y 2÷2xy ＋2xy ÷2xy ＝－x 2y －1.5xy ＋1.(2)原式＝[x ＋(2y －3)][x －(2y －3)]＝x 2－(2y －3)2＝x 2－(4y 2－12y ＋9)＝x 2－4y 2＋12y －9.16．解：方程左右两边同乘3(x －1)，得 3x －3(x －1)＝2x . 3x －3x ＋3＝2x . 2x ＝3.x ＝1.5.检验：当x ＝1.5时，3(x －1)≠0. ∴原分式方程的解为x ＝1.5.17．解：原式＝8（x －2）2÷⎣⎢⎡⎦⎥⎤x 2x －2－（x ＋2）（x －2）x －2＝8（x －2）2÷x 2－x 2＋4x －2 ＝8（x －2）2·x －24＝2x －2. ∵||x ＝2，∴x ＝±2.∵x －2≠0，∴x ＝2舍去，即x ＝－2. 当x ＝－2时，2x －2＝－12. 18．解：(1)△A 1B 1C 1如图所示． 由图可知A 1(－3，－2)．。
八年级下册数学期末综合能力测试题
八年级下册数学期末综合能力测试题1.如图①是一个长为2a,宽为2b的长方形纸片,其长方形的面积显然为4ab,现将此长方形纸片沿图中虚线剪开,分成4个小长方形,然后拼成如图②的一个正方形.(1)图②中阴影正方形EFGH的边长为:_________________;(2)观察图②,代数式(a -b)2表示哪个图形的面积?代数式(a+b)2呢?(3)用两种不同方法表示图②中的阴影正方形EFGH的面积,并写出关于代数式(a+b)2、(a -b)2和4ab之间的等量关系;(4)根据(3)题中的等量关系,解决如下问题:若a+b=7,ab=5,求:(a -b)2的值.2.如图(1)线段AB、CD相交于点O,连接AD、CB.如图(2),在图(1)的条件下,ang;DAB和ang;BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N.试解答下列问题：(1)在图(1)中,请直接写出ang;A、ang;B、ang;C、ang;D之间的等量关系;(2)在图(2)中,若ang;D=40deg;,ang;B=30deg;,试求ang;P的度数;(写出解答过程)(3)如果图(2)中,ang;D和ang;B为任意角,其他条件不变,试写出ang;P与ang;D、ang;B之间数量关系.(直接写出结论即可)3.某同学在一次课外活动中，用硬纸片做了两个直角三角形，见图①、②.图①中，ang;B=90deg;，ang;A：30deg;;图②中，ang;D= 90deg;，ang;F=45deg;.图③是该同学所做的一个实验：他将△DEF的直角边DE与△ABC的斜边AC重合在一起，并将△DEF沿AC方向移动.在移动过程中，D、E 两点始终在AC边上(移动开始时点D与点A重合).(1)在△DEF沿AC方向移动的过程中，该同学发现：F、C两点间的距离逐渐_______;连接FC，ang;FCE的度数逐渐_______.(填“不变”、“变大”或“变小”)(2)△DEF在移动的过程中，ang;FCE与ang;CFE度数之和是否为定值，请加以说明;(3)能否将△DEF移动至某位置，使F、C的连线与AB 平行?请求出ang;CFE的度数.4.平面内的两条直线有相交和平行两种位置关系.(1)如图a，若AB∥CD，点P在AB、CD外部，则有ang;B=ang;BOD.又因ang;BOD与ang;POD的互补，ang;POD+ang;BPD+ang;D=180 ordm;，故ang;BOD=ang;BPD+ang;D，得ang;BPD=ang;B-ang;D.将点P移到AB、CD内部，如图b，以上结论是否成立?若成立，说明理由;若不成立，则ang;BPD、ang;B、ang;D之间有何数量关系?请证明你的结论;(4分)(2)在图b中，将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q，如图c，则ang;BPD、ang;B、ang;D、ang;BQD之间有何数量关系?(不需证明)(3分)(3)根据(2)的结论求图d中ang;A+ang;B+ang;C+ang;D+ang;E+ang;F的度数.(4分)5.用水平线和竖直线将平面分成若干边长为1的小正方形网格,小正方形的顶点叫格点，以格点为顶点的多边形叫格点多边形.利用小正方形网格，可以求出格点多边形的面积.下图在网格中画出了按一定规律排列的一些格点多边形，观察图形，找出规律，解答下列问题.⑴对照图形，把下表空格填写完整.多边形的序号① ② ③ ④ ⑤ ，多边形内的格点数 1 2 3 4 5 ， n多边形边界上的格点数 6 6 8 ， ----多边形的面积(平方单位) 3 4 6 ， ----⑵根据①-⑤个多边形的内部格点数、边界上的格点数和多边形面积的关系，用含n(n为奇数时)的代数式表示按此规律排列的第个多边形内部的格点数、边界上的格点数和面积.⑶求在网格中按图中排列规律排列的n个多边形面积的和(用含n的代数式表示).6. 小明和小刚玩猜数游戏，小明说：“你任意选择三个一位数，按下列步骤计算：①把第一个数乘以5;②加上2;③乘以4;④加上第二个数的2倍;⑤乘以5;⑥加上第三个数.只要你告诉我计算的最后结果，我就知道你选择的三个一位数分别是多少.”⑴第一次小刚计算的结果是163，小明说小刚选择的三个数分别是1、2、3;第二次小刚计算的结果是829，小明说小刚选择的三个数分别是7、8、9;又试了几次，小明都说对了.若小刚计算的结果是199，你能说出小刚选择的三个数吗?⑵请你用所学的数学知识说明小明为什么每次都能说对小刚选择的三个一位数?7.一列火车从A站开往B站，沿途经过n个车站(包括起点站A和终点站B).该车挂有一节邮政车厢，厢内装有从A站发往沿途每车站的邮包各1个.运行时，需要在每个车站停靠，每停靠一个站不仅要卸下已通过各车站发给该车站的邮包各1个，还要装上发给下面行程中每个车站的邮包各1个(到终点站B不再装进邮包).⑴火车从A站开出后(未到达第二站前)，邮政车厢内装有多少个邮包?⑵当火车驶过第二站后(未到达第三站前)、驶过第三站后(未到达第四站前)、驶过第x个站后(未到达下站前)，邮政车厢内各装有多少个邮包?⑶若沿途共有车站20个(包括A、B两站)，当驶过第10个站后(未到达下站前)，邮政车厢内装有多少个邮包?8、2005年6月1日以来，台湾的十多种水果陆续地以零关锐登陆福建、上海等地.某水果商户抓住商机，准备用24000元从福建采购两种畅销水果到内地销售.经市场调查，台湾芒果的批发价为每箱40元，台湾凤梨的批发价为每箱50元，同时了解到，投入市场销售后，芒果和凤梨分别可获得25%与30%的利润.由于受保持期的销售量的限制，芒果的进购量(箱数)不得超过凤梨进购量的，凤梨的进购量不得超过320箱，如果没芒果的进购量的x(箱)，两种水量全部销售完后所获得的利润为y(元).?(1)求所获利润y(元)与进购量x(箱)之间的函数关系式.?(2)水果商应怎样进购两种水果，经销售完后所获利润最大，最大利润是多少??9.近年来，全市中小学校在校人数呈逐年减少的趋势，但城区各中小学的在校人数不但没有减少，反而有增加的趋势，镇(处)学校的部分学生流向城区学校，在学校现有教育资源有限的情况下，给城区学校方面带来了很大的压力.某校2005年的毕业人数占学校总人数的13 ，根据当年招生计划，该校招收的新生将比已毕业的年级减少一个班.由于服务区外的新生大量涌入，使得招收的新生年级班级名额严重超编，学校只能扩大班级的数目，新生班级数目在原计划的基础上增加了13 ，使学校实际招收的新生人数占到学校在校人数的411 .若各年级按平均每班60人计算，设2005届学生毕业前学校共有班级x个.(现在校人数=上年在校人数+招收新生数-毕业人数)⑴用含x的代数式表示2005年该校计划招生的班级数;⑵求该校现有的班级数及在校人数.。
初二数学上册全等三角形综合能力测试题及答案
初二数学全等三角形练习题一、填空题1．如图1所示，两个三角形全等，其中已知某些边的长度和某些角的度数，•则x=_______．(1) (2)2．如图2所示，在△ABC和△DEF中，AB=DE，∠B=∠E，要使△ABC≌△DEF，•需要补充的一个条件是____________．3．把“两个邻角的角平分线互相垂直”写成“如果……，那么……”的形式为_______________．4．在△ABC和△A′B′C中，∠A=∠A′，CD与C′D′分别为AB边和A′B•′边上的中线，再从以下三个条件：①AB=A′B′；②AC=A′C′；③CD=C′D•′中任取两个为题设，另一个作为结论，请写出一个正确的命题：________（用题序号写）．5．如图3所示，△ABC中，∠C=90°，AD平分∠CAB，BC=8cm，BD=•5cm，则D点到直线AB 的距离是______cm．(3) (4)6．如图4所示，将一副七巧板拼成一只小动物，则∠AOB=•_______．7．如图5所示，P、Q是△ABC的边BC上的两点，且BP=PQ=QC=•AP=AQ，则∠BAC的大小等于__________．(5) (6) (7)8．已知等腰△ABC中，AB=AC，D为BC边上一点，连结AD，若△ACD•和△ABD都是等腰三角形，则∠C的度数是________．9．如图6所示，梯形ABCD中，AD∥BC，∠C=90°，且AB=AD，•连结BD，过A点作BD的垂线，交BC于E，如果EC=3cm，CD=4cm，则梯形ABCD•的面积是_______cm．10．如图7所示，△ABC、△ADE与△EFG都是等边三角形，D•和G分别为AC和AE的中点，若AB=4时，则图形ABCDEFG外围的周长是________．二、选择题11．如图8所示，在∠AOB的两边截取AO=BO，CO=DO，连结AD、BC交于点P，考察下列结论，其中正确的是（）①△AOD≌△BOC ②△APC≌△BPD ③点P在∠AOB的平分线上A．只有① B．只有②C．只有①② D．①②③12．下列判断正确的是（）A．有两边和其中一边的对角对应相等的两个三角形全等B．有两边对应相等且有一角为30°的两个等腰三角形全等 (8)C．有一角和一边相等的两个直角三角形全等D．有两角和一边对应相等的两个三角形全等13．如果两个三角形的两条边和其中一边上的高对应相等，那么这两个三角形的第三边所对的角的关系是（）A．相等 B．互余 C．互补或相等 D．不相等14．如图9所示，在下面图形中，每个大正方形网格都是由边长为1的小正方形组成，则图中阴影部分面积最大的是（）(9)15．将五边形纸片ABCDE按如图10所示方式折叠，折痕为AF，点E、D分别落在E′，D′，已知∠AFC=76°，则∠CFD′等于（）A．31° B．28° C．24° D．22°(10) (11) (12)16．如图11所示，在菱形ABCD中，E、F分别是AB、AC的中点，如果EF=2，那么ABCD的周长是（）A．4 B．8 C．12 D．1617．如图12所示，在锐角△ABC中，点D、E分别是边AC、BC的中点，且DA=DE，那么下列结论错误的是（）A．∠1=∠2 B．∠1=∠3 C．∠B=∠C D．∠3=∠B18．如图13所示，把腰长为1的等腰直角三角形折叠两次后，得到的一个小三角形的周长是（）A．． C．(13) (14) (15)19．如图14所示中的4×4的正方形网格中，∠1+∠2+∠3+∠4+∠5+∠6+•∠7=（ ）A ．245°B ．300°C ．315°D ．330°20．已知：如图15所示，CD ⊥AB ，BE ⊥AC ，垂足分别为D 、E ，BE 、CD•相交于点O ，∠1=∠2，图中全等的三角形共有（ ）A ．1对B ．2对C ．3对D ．4对三、解答题21．（9分）如图所示，有一池塘，要测量池塘两端A 、B 的距离，请用构造全等三角形的方法，设计一个测量方案（画出图形），并说明测量步骤和依据．22．（9分）如图所示，已知∠1=∠2，∠C=∠D ，求证：AC=BD ．23．（9分）如图所示，D 、E 分别为△ABC 的边AB 、AC 上点，•BE 与CD 相交于点O ．现有四个条件：①AB=AC ；②OB=OC ；③∠ABE=∠ACD ；④BE=CD ．（1）请你选出两个条件作为题设，余下作结论，写一个正确的命题：命题的条件是_______和_______，命题的结论是_______和________（均填序号）（2）证明你写的命题．24．（10分）如图所示，△ABC 为等边三角形，BD 为中线，延长BC 至E ，•使DE=BD. 求证：CE=12BC ．25．（11分）如图①所示，把一张矩形纸片ABCD沿对角线BD折叠，将重合部分△BFD剪去，得到△ABF和△EDF．①（1）判断△ABF与△EDF是否全等？并加以证明；（2）把△ABF与△EDF不重合地拼在一起，可拼成特殊三角形和特殊四边形，将下列拼图（图②）按要求补充完整．②26．（12分））如图（1）所示，OP是∠MON的平分线，•请你利用该图形画一对以OP所在直线为对称轴的全等三角形．请你参考这个作全等三角形方法，解答下列问题：（1）如图（2），在△ABC中，∠ACB=90°，∠B=60°，AC、CE分别是∠BAC，∠BCA 的平分线交于F，试判断FE与FD之间的数量关系．（2）如图（3），在△ABC中，若∠ACB≠90°，而（1）中其他条件不变，请问（1）中所得的结论是否仍然成立？若成立，请证明；若不成立，说明理由．1．60° 2．BC=EF或∠D=∠A或∠C=∠F3．如果作两个邻补角的角平分线，那么这两条角平分线互相垂直4．如果①②，那么③ 5．36．135° 7．120° 8．36°或45°9．26 10．15 11．D 12．D 13．C 14．D15．B 16．D 17．D 18．B 19．C 20．D21．在平地任找一点O，连OA、OB，延长AO至C使CO=AO，延BO至D，使DO=•BO，•则CD=AB，依据是△AOB≌△COD（SAS），图形略．22．证△ACB≌△BDA即可．23．（1）条件①、③结论②、④，（2）证明略24．略25．（1）△ABF≌△EDF，证明略（2）如图:26．（1）FE=FD（2）（1）中的结论FE=FD仍然成立．在AC上截取AG=AE，连结FG．证△AEF≌△AGF得∠AFE=∠AFG，FE=FG．由∠B=60°，AD、CE分别是∠BAC，∠BCA的平分线得∠DAC+∠ECA=60°．所以∠AFE=∠CFD=∠AFG=60°，所以∠CFG=60°．由∠BCE=∠ACE及FC为公共边．可证△CFG≌△CFD，所以FG=FD，所以FE=FD．。
初二数学初中数学综合库试题答案及解析
初二数学初中数学综合库试题答案及解析1.（本题9分）已知△ABC为正三角形，点M是射线BC上任意一点，点N是射线CA上任意一点，且BM="CN，直线BN与AM相交于点Q。
下面给出了三种情况（如图" ①,②,③）,请回答下列问题:【1】（1）利用图①证明。
【答案】【2】（2）先用量角器分别测量∠BQM的大小，然后猜测∠BQM是否为定值？利用图③证明你的猜想【答案】2.我校准备挑选一名跳高运动员参加区中学生运动会，对跳高队的甲、乙两名运动员进行了8次选拔比赛，他们的成绩（单位：cm）如下：【1】甲、乙两名运动员的跳高平均成绩分别是多少？【答案】甲169，乙168；【2】哪名运动员的成绩更为稳定？为什么？【答案】甲6 乙31.5选甲【3】若预测，跳过165cm就很可能获得冠军。
该校为了获得冠军，可能选哪位运动员参赛？若预测跳过170cm才能得冠军呢？为什么？【答案】甲、乙3.（10分）如图，在△ABC中，O是AC上的一个动点（不与点A、C重合），过O点作直线MN//BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F。
【1】（1）试说明：OE=OF。
【答案】略【2】（2）当O点运动到何处时，四边形AECF是矩形？并证明你的结论。
【答案】略4.下列各组数中，是勾股数的是（）A．2，3，4B．4，5，6C．7，8，9D．9，40，41【答案】D【解析】利用勾股数的定义进行判断，逐个计算即可．因为92＋402＝412，又9，40，41都是正整数，故D为勾股数．5.先化简，再求值：，其中x=﹣1．【答案】原式=，当x=﹣1时，原式=﹣3．【解析】先根据分式运算的法则把分式进行化简，再把x=﹣1代入求值即可．试题解析：原式===．当x=﹣1时，原式=﹣=﹣3．【考点】分式的化简求值．6.（9分）探究题：如图：（1）△ABC为等边三角形，动点D在边CA上，动点P在边BC上，若这两点分别从C、B点同时出发，以相同的速度由C向A和由B向C运动，连接AP，BD交于点Q，两点运动过程中AP=BD成立吗？请证明你的结论；（2）如果把原题中“动点D在边CA上，动点P边BC上，”改为“动点D，P在射线CA和射线BC上运动”，其他条件不变，如图（2）所示，两点运动过程中∠BQP的大小保持不变．请你利用图（2）的情形，求证：∠BQP=60°；（3）如果把原题中“动点P在边BC上”改为“动点P在AB的延长线上运动，连接PD交BC于E”，其他条件不变，如图（3），则动点D，P在运动过程中，DE始终等于PE吗？写出证明过程．【答案】（1）（2）见解析（3）DE=PE【解析】（1）由△ABC为等边三角形，可得∠C=∠ABP=60°，AB=BC，又由这两点分别从C、B点同时出发，以相同的速度由C向A和由B向C运动，可得BP=CD，即可利用SAS，判定△ABP≌△BCD，继而证得结论；（2）同理可证得△ABP≌△BCD（SAS），则可得∠APB=∠BDC，然后由∠APB+∠PAC=∠ACB=60°，∠DAQ=∠PAC，求得∠BDC+∠DAQ=∠BQP=60°；（3）首先过点D作DG∥AB交BC于点G，则可证得△DCG为等边三角形，继而证得△DGE≌△PBE（AAS），则可证得结论．试题解析：解：（1）成立．理由：∵△ABC是等边三角形，∴∠C=∠ABP=60°，AB=BC，根据题意得：CD=BP，在△ABP和△BCD中，，∴△ABP≌△BCD（SAS），∴AP=BD；（2）根据题意，CP=AD，∴CP+BC=AD+AC，即BP=CD，在△ABP和△BCD中，，∴△ABP≌△BCD（SAS），∴∠APB=∠BDC，∵∠APB+∠PAC=∠ACB=60°，∠DAQ=∠PAC，∴∠BDC+∠DAQ=∠BQP=60°；（3）DE=PE．理由：过点D作DG∥AB交BC于点G，∴∠CDG=∠C=∠CGD=60°，∠GDE=∠BPE，∴△DCG为等边三角形，∴DG=CD=BP，在△DGE和△PBE中，，∴△DGE≌△PBE（AAS），∴DE=PE．【考点】全等三角形的判定与性质；等边三角形的判定与性质7.（本题满分12分）如图，已知的中垂线交于点，交于点，有下面3个结论：①是等腰三角形；②∽；③点D是线段AC的黄金分割点．请你从以上结论中只选一个加以证明（友情提醒：证明①得8分，证明②得10分，证明③得12分）．【答案】详见解析．【解析】（1）根据三角形的内角和定理及线段垂直平分线的性质易证∠BDC=∠ACB=72°，即可得是等腰三角形；（2）由（1）即可判定∽；（3）由（2）可得AB：BD=BC：DC，又因BD=AD=BC，AB=AC，所以AD2=DC·AC，即可判定点D是线段AC的黄金分割点．试题解析：①∵AB=AC，∠A=36°∴∠ABC=∠ACB=∵AB垂直平分线交AC于D，有 AD=BD，∴∠A=∠ABD=36°，∴∠DBC=∠ABC-∠ABD=72°-36°=36°，∴∠BDC=180°-∠C-∠DBC=180°-72°-36°=72°，∴BD=BC，∴△BCD是等腰三角形．‚由①得，∠ABC=∠ACB=∠BDC=∠C=72°，∴△ABC∽△BCD③由 得，AB：BD=BC：DC，又因BD=AD=BC，AB=AC∴AD2=DC·AC即点D是线段AC的黄金分割点．【考点】等腰三角形的判定及性质；相似三角形的判定及性质．8.如图，一个直角三角形纸片，剪去直角后，得到一个四边形，则∠1+∠2= ．【答案】270°．【解析】如图，由四边形的内角和定理可得∠3+∠4+∠1+∠2=360°，根据直角三角形的两锐角互余可得∠3+∠4=90°，所以∠1+∠2=270°．【考点】四边形的内角和定理；直角三角形的两锐角互余．9.（本题6分）计算：．【答案】．【解析】由零指数幂、立方根、负整数指数幂的法则，以及绝对值的概念计算即可．试题解析：原式==．【考点】1．实数的运算；2．零指数幂；3．负整数指数幂；4．立方根．10.已知三角形的两边长为4，8，则第三边的长度可以是（）．A．16B．8C．4D．1【答案】B．【解析】根据三角形三边关系：三角形两边之和大于第三边，两边之差小于第三边，所以本题第三边的范围应该是大于4，小于12，只有B选项的长度符合，故本题选B．【考点】三角形三边关系．11.如图所示，已知△ABC中，AB=6，AC=9，AD⊥BC于D，M为AD上任一点，则等于．【答案】45【解析】在Rt△CDM和Rt△BDM中，=+，=+，则－=－；在Rt△ABD和Rt△ACD中，=，，则－=，所以－==81－36=45．【考点】直角三角形的勾股定理12.【答案】．【解析】首先对各二次根式进行化简，然后合并同类二次根式．试题解析：解：原式= =．【考点】二次根式的加减法运算．13.下列长度的各组线段能组成一个三角形的是（）A．4cm，6cm，11cm B．4cm，5cm，1cmC．3cm，4cm，5cm D．2cm，3cm，6cm【答案】C【解析】根据三角形的三边关系“任意两边之和大于第三边，任意两边之差小于第三边”，A、4+6＜11，不能组成三角形；B、1+4=5，不能组成三角形；C、3+4＞5，能够组成三角形；D、2+3＜6，不能组成三角形．故选C．【考点】三角形三边关系．14.（2015秋•潮南区月考）计算：m•m2•m3+（m3）2﹣（2m2）3．【答案】﹣6m6【解析】直接利用同底数幂的乘法运算法则以及幂的乘方和积的乘方运算法则分别化简得出答案．解：m•m2•m3+（m3）2﹣（2m2）3=m6+m6﹣8m6=﹣6m6．【考点】幂的乘方与积的乘方；同底数幂的乘法．15.（2015秋•开江县期末）某文具经销店在开学时购进了A、B两种型号的计算器，已知：购进A型号的计算器20个，B型号的计算器25个需用1265元；购进A型号的计算器16个，B型号的计算器12个需用748元．求：（1）A、B两种型号的计算器进价分别是多少元？（2）在（1）的条件下，若A型号的计算器的售价是30元/个，B型号的计算器的售价是45元/个，商店一次性购进两种型号的计算器各20个，并全部销售，求商店所获利润是多少元？（3）在两种型号计算器的进价和售价均保持不变的情况下，该商店准备购进A、B两种型号的计算器共40个，且A型号的计算器的数量不得少于5个，问：商店应怎样进货，才能使所获利润最大？最大利润是多少元？【答案】（1）A型号的计算器进价为22元，B型号的计算器进价为33元．（2）商店所获利润是400元．（3）商店应购进A计算器5个、B计算器35个，才能使所获利润最大，最大利润是460元．【解析】（1）根据：A计算器20个费用+B计算器25个费用=1265、A计算器16个费用+B计算器12个费用=1265，即可列方程组求解；（2）所获利润=A型号计算器利润+B型号计算器利润，计算可得；（3）根据（2）中相等关系列出，总利润与A型号计算器数量间的函数关系式，结合函数增减性可得最大利润．解：（1）设A型号的计算器进价为x元，B型号的计算器进价为y元，根据题意得：解得：，答：A型号的计算器进价为22元，B型号的计算器进价为33元．（2）（30﹣22）×20+（45﹣33）×20=400（元）答：商店所获利润是400元．（3）设购进A型号计算器m个，则购进B型号计算器有（40﹣m）个，所获得总利润为W，由题意得：W=（30﹣22）m+（45﹣33）（40﹣m）=﹣4m+480∵﹣4＜0，∴W随m的增大而减小，∵A型号的计算器的数量不得少于5个，即m≥5，∴当m=5时，W最大，最大值为：W=﹣4×5+480=460元；答：商店应购进A计算器5个、B计算器35个，才能使所获利润最大，最大利润是460元．【考点】一次函数的应用；二元一次方程组的应用；一次函数的性质；根据实际问题列一次函数关系式．16.规定用符号[m]表示一个实数m的整数部分，例如：[]=0，[3.14]=3．按此规定[]的值为（）A．3B．4C．5D．6【答案】B【解析】先求出+1的范围，再根据范围求出即可．解：∵3＜＜4，∴4＜+1＜5，∴[+1]=4，故选B．【考点】估算无理数的大小．17.一列快车从甲地匀速驶往乙地，一列慢车从乙地匀速驶往甲地．设先发车辆行驶的时间为x h，两车之间的距离为y km．当两车均到达各自终点时，运动停止．如图是y与x之间函数关系的部分图象．（1）由图象知，慢车的速度为 km/h，快车的速度为 km/h；（2）请在图中补全函数图象；（3）求当x为多少时，两车之间的距离为300km．【答案】(1)80,120；(2)补图见解析；（3）x=1．2 h或4．2 h【解析】（1）根据AB段可以确定先出发的车的速度，然后根据BC段确定两车速度的和，则后出发的车的速度可以求得；（2）根据路程是480km，则可以求得两辆车到达时的时间，然后求得各组到达的所需要的时间，再求得相距的距离即可确定；（3）两车之间的距离是300km时有两个位置，分成相遇前和相遇后两种情况讨论即可列方程求解．试题解析：（1）先出发的车的速度是（480-440）÷0．5=80km/h，两车的速度的和是440÷（2．7-0．5）=200km/h，则另一辆车的速度是120km/h．则慢车的速度是80km/h，快车120km/h．故答案是：80，120；（2）如下图，注意端点值．（3）由题意，可知两车行驶的过程中有2次两车之间的距离为300km．即（80+120）×（x-0．5）=440-300，解得x=1．2（h）；（8分）或（80+120）×（x-2．7）=300，解得x=4．2（h）．（10分）故x=1．2 h或4．2h，两车之间的距离为300km．【考点】一次函数的应用．18.如图，四边形ABCD是菱形，对角线AC、BD相交于点O，DH⊥AB于H，连接OH，求证：∠DHO=∠DCO．【答案】证明见解析【解析】根据菱形的对角线互相平分可得OD=OB，再根据直角三角形斜边上的中线等于斜边的一半可得OH=OB，然后根据等边对等角求出∠OHB=∠OBH，根据两直线平行，内错角相等求出∠OBH=∠ODC，然后根据等角的余角相等证明即可．证明：∵四边形ABCD是菱形，∴OD=OB，∠COD=90°，∵DH⊥AB，∴OH=BD=OB，∴∠OHB=∠OBH，又∵AB∥CD，∴∠OBH=∠ODC，在Rt△COD中，∠ODC+∠DCO=90°，在Rt△DHB中，∠DHO+∠OHB=90°，∴∠DHO=∠DCO．【考点】菱形的性质．19.在菱形ABCD中，E为AB的中点，OE=3，则菱形ABCD的周长为．【答案】24【解析】根据菱形的对角线互相平分可得OB=OD，然后判断出OE是△ABD的中位线，再根据三角形的中位线等于第三边的一半求出AD，然后根据菱形的周长进行计算即可得解．解：在菱形ABCD中，OB=OD，∵E为AB的中点，∴OE是△ABD的中位线，∵OE=3，∴AD=2OE=2×3=6，∴菱形ABCD的周长为4×6=24．故答案为：24．【考点】菱形的性质．20.如图，在平行四边形ABCD中，AB=3cm，BC=5cm，对角线AC，BD相交于点O，则OA 的取值范围是（）A．1cm＜OA＜4cm B．2cm＜OA＜8cmC．2cm＜OA＜5cm D．3cm＜OA＜8cm【答案】A【解析】根据三角形的三边关系定理得到AC的取值范围，再根据平行四边形的性质即可求出OA的取值范围．解：∵AB=3cm，BC=5cm，∴2cm＜AC＜8cm，∵四边形ABCD是平行四边形，∴AO=AC，∴1cm＜OA＜4cm，故选：A．【考点】平行四边形的性质；三角形三边关系．21.下面的图像反映的过程是：小明从家去超市买文具，又去书店购书，然后回家．其中x表示时间，y表示小明离他家的距离，若小明家、超市、书店在同一条直线上．根据图像回答下列问题：（1）超市离小明家多远，小明走到超市用了多少时间？（2）超市离书店多远，小明在书店购书用了多少时间？（3）书店离小明家多远，小明从书店走回家的平均速度是每分钟多少米？【答案】（1）1．1千米；15分钟；（2）0．9千米；18分钟；（3）80米．分．【解析】（1）根据图像得出所求的信息；（2）根据图像信息得出我们所需要求的信息；（3）根据路程÷时间得出速度．试题解析：（1）由图像可以看出超市离小明家1．1千米，小明走到超市用了15分；（2）超市离书店：2-1．1=0．9千米，小明在书店购书用了55-37=18分；（3）由图像可以看出书店离小明家2千米，小明从书店走回家的平均速度是米/分．【考点】一次函数图象的性质．22. 如图，P 是矩形ABCD 的边AD 上一个动点，矩形的两条边AB 、BC 的长分别为6和8，那么点P 到矩形的两条对角线AC 和BD 的距离之和是 ． 【答案】4.8 【解析】首先连接OP ，由矩形的两条边AB 、BC 的长分别为6和8，可求得OA=OD=5，△AOD 的面积，然后由S △AOD =S △AOP +S △DOP =OA•PE+OD•PF 求得答案．解：连接OP ，∵矩形的两条边AB 、BC 的长分别为6和8， ∴S 矩形ABCD =AB•BC=48，OA=OC ，OB=OD ，AC=BD==10，∴OA=OD=5，∴S △ACD =S 矩形ABCD =24，∴S △AOD =S △ACD =12，∵S △AOD =S △AOP +S △DOP =OA•PE+OD•PF=×5×PE+×5×PF=（PE+PF ）=12，解得：PE+PF=4.8． 故答案为：4.8．23. 如图，△ABC 中，∠B=90°，AB=BC ，AD 是△ABC 的角平分线，若BD=1，求DC 的长．【答案】【解析】过D作DE⊥AC于E，根据角平分线性质求出DE=1，求出∠C=45°，解直角三角形求出DC即可．解：过D作DE⊥AC于E，∵△ABC中，∠B=90°，AD是△ABC的角平分线，BD=1，∴DE=BD=1，∵∠B=90°，AB=BC，∴∠C=∠BAC=45°，在Rt△DEC中，sin45°=，∴DC==．点评：本题考查了三角形内角和定理，等腰三角形的性质，角平分线的性质，解直角三角形的应用，主要考查学生综合运用性质进行推理和计算的能力．24.如图，下列各点在阴影区域内的是（）A．（3，2）B．（﹣3，2）C．（3，﹣2）D．（﹣3，﹣2）【答案】A【解析】应先判断出阴影区域在第一象限，进而判断在阴影区域内的点．解：观察图形可知：阴影区域在第一象限，A、（3，2）在第一象限，故正确；B、（﹣3，2）在第二象限，故错误；C、（3，﹣2）在第四象限，故错误；D、（﹣3，﹣2）在第三象限，故错误．故选A．【点评】解决本题的关键是掌握好四个象限的点的坐标的特征：第一象限正正，第二象限负正，第三象限负负，第四象限正负．25.如图所示：是一段楼梯，高BC是3m，斜边AC是5m，如果在楼梯上铺地毯，那么至少需要地毯（）A．5m B．6m C．7m D．8m【答案】C【解析】先根据直角三角形的性质求出AB的长，再根据楼梯高为BC的高=3m，楼梯的宽的和即为AB的长，再把AB、BC的长相加即可．解：∵△ABC是直角三角形，BC=3m，AC=5m∴AB===4m，∴如果在楼梯上铺地毯，那么至少需要地毯为AB+BC=7米．故选C．点评：本题考查的是勾股定理，解答此题的关键是找出楼梯的高和宽与直角三角形两直角边的等量关系．26.如图，已知Rt△ABC中，∠ABC=90°，先把△ABC绕点B顺时针旋转90°至△DBE后，再把△ABC沿射线平移至△FEG，DE、FG相交于点H．（1）判断线段DE、FG的位置关系，并说明理由；（2）连结CG，求证：四边形CBEG是正方形．【答案】（1）FG⊥ED；（2）见解析【解析】（1）根据旋转和平移可得∠DEB=∠ACB，∠GFE=∠A，再根据∠ABC=90°可得∠A+∠ACB=90°，进而得到∠DEB+∠GFE=90°，从而得到DE、FG的位置关系是垂直；（2）根据旋转和平移找出对应线段和角，然后再证明是矩形，后根据邻边相等可得四边形CBEG是正方形．（1）解：FG⊥ED．理由如下：∵△ABC绕点B顺时针旋转90°至△DBE后，∴∠DEB=∠ACB，∵把△ABC沿射线平移至△FEG，∴∠GFE=∠A，∵∠ABC=90°，∴∠A+∠ACB=90°，∴∠DEB+∠GFE=90°，∴∠FHE=90°，∴FG⊥ED；（2）证明：根据旋转和平移可得∠GEF=90°，∠CBE=90°，CG∥EB，CB=BE，∵CG∥EB，∴∠BCG=∠CBE=90°，∴四边形BCGE是矩形，∵CB=BE，∴四边形CBEG是正方形．点评：此题主要考查了图形的旋转和平移，关键是掌握新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行且相等．27.实数在数轴上的位置如图所示，则化简的结果是（）A．1B．b+1C．D．【答案】A【解析】根据数轴可得：a-10，a-b0，则原式=1-a+a-b+b=1.【考点】二次根式的化简28.如图是4×4正方形网络，其中已有3个小方格涂成了黑色．现在要从其余13个白色小方格中选出一个也涂成黑色的图形成为轴对称图形，这样的白色小方格有个．【答案】3【解析】根据轴对称图形的性质可得：白色小方格的有3个.【考点】轴对称图形的性质29.在△ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．（1）如图1，当点D在线段BC上，如果∠BAC=90°，则∠BCE 度；（2）设∠BAC=a，∠BCE=b．①如图2，当点D在线段BC上移动，则a，b之间有怎样的数量关系？请说明理由；②当点D在直线BC上移动，则a，b之间有怎样的数量关系？请直接写出你的结论，不必说明理由．【答案】(1)、90°；(2)、①、α+β=180°；理由见解析；②、当点D在射线BC上时，α+β=180°；当点D在射线BC的反向延长线上时，α=β．【解析】(1)、根据∠BAC=∠DAE得出∠BAD=∠CAE，然后利用SAS判定△ABD和△ACE全等，从而得出∠B=∠ACE，则∠B+∠ACB=∠ACE+∠ACB，从而得出∠BCE=90°；(2)、①、、根据∠BAC=∠DAE得出∠BAD=∠CAE，然后利用SAS判定△ABD和△ACE全等，从而得出∠B=∠ACE，则∠B+∠ACB=∠ACE+∠ACB，从而得出α+β=180°；②、根据题意分别画出两个图形，然后分别进行计算得出答案，当点D在射线BC上时，α+β=180°；当点D在射线BC的反向延长线上时，α=β．试题解析：(1)、90°．∵∠BAC=∠DAE，∴∠BAC-∠DAC=∠DAE-∠DAC．即∠BAD=∠CAE．在△ABD与△ACE中，AB=AC，∠BAD=∠CAE，AD=AE ∴△ABD≌△ACE（SAS），∴∠B=∠ACE．∴∠B+∠ACB=∠ACE+∠ACB，∴∠BCE=∠B+∠ACB，又∵∠BAC=90°∴∠BCE=90°(2)、①α+β=180°，∵∠BAC=∠DAE，∴∠BAD+∠DAC=∠EAC+∠DAC．即∠BAD=∠CAE．在△ABD与△ACE中，AB=AC，∠BAD=∠CAE，AD=AE ∴△ABD≌△ACE（SAS），∴∠B=∠ACE．∴∠B+∠ACB=∠ACE+∠ACB．∴∠B+∠ACB=β，∵α+∠B+∠ACB=180°，∴α+β=180°；②、当点D在射线BC上时，α+β=180°；当点D在射线BC的反向延长线上时，α=β．【考点】三角形全等的判定与性质30.在下列四个角的度数中，一个不等边三角形的最小角度数可以是（）.A．80°B．65°C．60°D．59°【答案】D【解析】根据题意可得：等边三角形的每一个内角的度数都是60°，则不等边三角形最小角的度数为59°.【考点】三角形最小内角31.如图，在△ABC中（AB＞BC），AC=2BC，BC边上的中线AD把△ABC的周长分成60和40两部分，求AC和AB的长．【答案】AC=48；AB=28【解析】首先设BD=CD=x，AB=y，则AC=4x，然后分AC+CD=60，AB+BD=40和AC+CD=40，AB+BD=60两种情况分别求出x和y的值，然后看三角形的三边关系判定是否都符合条件.试题解析：∵AD是BC边上的中线，AC=2BC，∴BD=CD，设BD=CD=x，AB=y，则AC=4x，分为两种情况：①AC+CD=60，AB+BD=40，则4x+x=60，x+y=40，解得：x=12，y=28，即AC=4x=48，AB=28；②AC+CD=40，AB+BD=60，则4x+x=40，x+y=60，解得：x=8，y=52，即AC=4x=32，AB=52，BC=2x=16，此时不符合三角形三边关系定理；综合上述：AC=48，AB=28．【考点】(1)、中线的性质；(2)、分类讨论思想.32.实数、在数轴上的位置如图所示，请化简：。
八年级上学期数学综合能力测试(二)参考答案
八年级上学期数学综合能力测试（二）参考答案一、填空题（共5小题，每小题4分，满分20分） 1、33333223()333a b c abc a b c a b ab abc ++-=++---22[()][()()]3()a b c a b a b c c ab a b c =+++-++-++ 222()()a b c a b c ab bc ca =++++---，∴22222()()()()a b b c a b b c a b c a b b cc a-+-+--=++--- 33333a b c abca b c++-==++。
2、由211a b c=+，可得2bc ac ab =+，即()()0a b c a c b -+-=， 由于c ，b 为正数，则(),()a b a c --必定一正一负，那么A ∠的大小介于B ∠与C ∠之间，不妨假定B A C ∠≤∠≤∠， 则有1802A B C A C A ︒=∠+∠+∠>∠+∠≥∠，即90A ︒∠<。
3、命题①，一般地，依题意可得：45,21m n n -+=-=，于是3,6n m ==-或4； 但对于单项式4(5)m n m xy -++，当5m =-时，它的值为零，此时n 只需取大于2的整数，则必定有单项式522n x y -与4(5)m n m x y -++的和为单项式；故命题①错误；命题②，2M N -的次数不超过6，但它并不一定是多项式；如取631,1M x N x =+=+，则232M N x -=-为三次单项式；故命题②错误；命题③，当0,1m ≠时，原方程可化为：67()mm x x -=，此时方程的解为1,0x =-或1；当0m =时，原方程可化为：21()()()x x x x x -----=，此时x 不能为零，则方程的解为1x =-或1；当1m =时，原方程可化为：20425()()()x x x x x ---=，此时x 不能为零，则方程的解为1x =-或1；故命题③错误；命题④，当DN 在DEF ∆的外部时，易知DFE ACB ∠=∠180()1804035105CAB CBA ︒︒︒︒=-∠+∠=--=； 当DN 在DEF ∆的内部时，如右图所示，,AC DF AM DN ==，ACM DFN ∴∆≅∆，403575DFE ACM CAB CBA ︒︒︒∴∠=∠=∠+∠=+=； 故命题④错误。
数学八年级上册 全册全套试卷综合测试卷(word含答案)
数学八年级上册全册全套试卷综合测试卷（word含答案）一、八年级数学三角形填空题（难）1．一机器人以0.3m/s的速度在平地上按下图中的步骤行走，那么该机器人从开始到停止所需时间为__s．【答案】160.【解析】试题分析：该机器人所经过的路径是一个正多边形，利用360°除以45°，即可求得正多边形的边数，即可求得周长，利用周长除以速度即可求得所需时间．试题解析：360÷45=8，则所走的路程是：6×8=48m，则所用时间是：48÷0.3=160s．考点：多边形内角与外角．2．已知a、b、c为△ABC的三边，化简：|a+b﹣c|-|a﹣b﹣c|+|a﹣b+c|=______．--【答案】3a b c【解析】【分析】根据三角形的三边关系判断绝对值内式子的正负，然后利用绝对值的性质去掉绝对值，再去括号合并同类项即可．【详解】解：∵a、b、c为△ABC的三边，∴a+b＞c，a-b＜c，a+c＞b，∴a+b-c＞0，a-b-c＜0，a-b+c＞0，∴|a+b-c|-|a-b-c|+|a-b+c|=(a+b-c)+(a-b- c)+(a-b+c)=a+b-c+a-b- c+a-b+c=3a-b-c．故答案为：3a-b-c．【点睛】本题主要考查了三角形的三边关系定理和利用绝对值的性质进行化简，利用三角形的三边关系得出绝对值内式子的正负是解决此题的关键．3．已知a，b，c是△ABC的三边长，a，b满足|a﹣7|+（b﹣1）2=0，c为奇数，则c=_____．【答案】7【分析】根据非负数的性质列式求出a 、b 的值，再根据三角形的任意两边之和大于第三边，两边之差小于第三边求出c 的取值范围，再根据c 是奇数求出c 的值．【详解】∵a ，b 满足|a ﹣7|+（b ﹣1）2=0，∴a ﹣7=0，b ﹣1=0，解得a=7，b=1，∵7﹣1=6，7+1=8，∴68c <<，又∵c 为奇数， ∴c=7，故答案为7．【点睛】本题考查非负数的性质：偶次方，解题的关键是明确题意，明确三角形三边的关系．4．如图所示，小明从A 点出发，沿直线前进10米后向左转30°，再沿直线前进10米，又向左转30°，…，照这样下去，他第一次回到出发地A 点时，（1）左转了____次；（2）一共走了_____米．【答案】11 120【解析】∵360÷30=12，∴他需要走12−1=11次才会回到原来的起点，即一共走了12×10=120米.故答案为11，120.5．如图，△ABC 中，∠B 与∠C 的平分线交于点O ，过O 作EF ∥BC 交AB 、AC 于E 、F ，若△ABC 的周长比△AEF 的周长大12cm ，O 到AB 的距离为4cm ，△OBC 的面积_____cm 2．【答案】242cm ．【解析】由BE=EO可证得EF∥BC，从而可得∠FOC=∠OCF，即得OF=CF；可知△AEF等于AB+AC，所以根据题中的条件可得出BC及O到BC的距离，从而能求出△OBC的面积．【详解】∵BE=EO，∴∠EBO=∠EOB=∠OBC，∴EF∥BC，∴∠FOC=∠OCB=∠OCF，∴OF=CF；△AEF等于AB+AC，又∵△ABC的周长比△AEF的周长大12cm，∴可得BC=12cm，根据角平分线的性质可得O到BC的距离为4cm，∴S△OBC=12×12×4=24cm2．考点：1．三角形的面积；2．三角形三边关系．6．如图，∠A=50°，∠ABO=28°，∠ACO=32°，则∠BOC=______°.【答案】110【解析】已知∠A=50°，∠ABO=28°，∠ACO=32°，根据三角形外角的性质可得∠BDC=∠A+∠ABO=78°，∠BOC=∠BDC+∠ACO=110°．二、八年级数学三角形选择题（难）7．已知△ABC，(1)如图①，若P点是∠ABC和∠ACB的角平分线的交点，则∠P＝90°＋12∠A；(2)如图②，若P点是∠ABC和外角∠ACE的角平分线的交点，则∠P＝90°－∠A；(3)如图③，若P点是外角∠CBF和∠BCE的角平分线的交点，则∠P＝90°－12∠A.上述说法正确的个数是()A．0个B．1个C．2个D．3个【答案】C【解析】【分析】根据三角形的内角和外角之间的关系计算．解：（1）∵若P 点是∠ABC 和∠ACB 的角平分线的交点，∴∠ABP=∠PBC ，∠ACP=∠PCB∵∠A=180°-∠ABC-∠ACB=180°-2（∠PBC+∠PCB ）∠P=180°-（∠PBC+∠PCB ）∴∠P=90°+12∠A ； 故（1）的结论正确；（2）∵∠A=∠ACB-∠ABC=2∠PCE-2∠PBC=2（∠PCE-∠PBC ）∠P=∠PCE-∠PBC∴2∠P=∠A故（2）的结论是错误．（3）∠P=180°-（∠PBC+∠PCB ）=180°-12（∠FBC+∠ECB ） =180°-12（∠A+∠ACB+∠A+∠ABC ） =180°-12（∠A+180°） =90°-12∠A ． 故（3）的结论正确．正确的为：（1）（3）．故选：C【点睛】主要考查了三角形的内角和外角之间的关系．（1）三角形的外角等于与它不相邻的两个内角和；（2）三角形的内角和是180度．求角的度数常常要用到三角形的内角和是180°这一隐含的条件．8．如图，三角形ABC 内的线段,BD CE 相交于点O ,已知OB OD =,2OC OE =.若BOC ∆的面积=2，则四边形AEOD 的面积等于（ ）A．4 B．5 C．6 D．7【答案】D【解析】【分析】连接AO，利用等高不等底的三角形面积比等于底长的比，可求出△COD与△BOE的面积．列出关于△AOE与△AOD的面积的方程即可求出四边形AEOD的面积．【详解】连接OA，∵OB=OD，∴S△BOC=S△COD=2，∵OC=2OE，∴S△BOE=12S△BOC=1，∵OB=OD，∴S△AOB=S△AOD，∴S△BOE+S△AOE=S△AOD，即：1+S△AOE=S△AOD①，∵OC=2OE，∴S△AOC=2S△AOE，∴S△AOD+S△COD=2S△AOE，即：S△AOD+2=2S△AOE②，联立①和②：解得：S△AOE=3，S△AOD=4，S四边形AEOD=S△AOE+S△AOD=7，故选D．本题考查三角形面积问题，涉及方程组的解法，注意灵活运用等高不等底的三角形面积比等于底长的比这一结论．9．一正多边形的内角和与外角和的和是1440°，则该正多边形是（）A．正六边形B．正七边形C．正八边形D．正九边形【答案】C【解析】【分析】依题意，多边形的内角与外角和为1440°，多边形的外角和为360°，根据内角和公式求出多边形的边数．【详解】解：设多边形的边数为n，根据题意列方程得，（n﹣2）•180°+360°＝1440°，n﹣2＝6，n＝8．故这个多边形的边数为8．故选：C．【点睛】考查了多边形的外角和定理和内角和定理，熟练记忆多边形的内角和公式是解答本题的关键．10．如图，若∠A=27°，∠B=45°，∠C=38°，则∠DFE等于（）A．110︒B．115︒C．120︒D．125︒【答案】A【解析】【分析】根据三角形外角的性质三角形的一个外角等于和它不相邻的两个内角的和可得∠AEB=∠A+∠C=65°，∠DFE=∠B+∠AEC，进而可得答案．【详解】解：∵∠A=27°，∠C=38°，∴∠AEB=∠A+∠C=65°，∵∠B=45°，∴∠DFE=65°+45°=110°，【点睛】此题主要考查了三角形外角的性质，关键是掌握三角形的一个外角等于和它不相邻的两个内角的和．11．以下列数据为长度的三条线段，能组成三角形的是（）A．2 cm、3cm、5cm B．2 cm、3 cm、4 cmC．3 cm、5 cm、9 cm D．8 cm、4 cm、4 cm【答案】B【解析】【分析】三角形的任何一边大于其他两边之差，小于两边之和，满足此关系的可组成三角形，其实只要最小两边的和大于最大边就可判断前面的三边关系成立．【详解】A、2+3=5，故本选项错误．B、2+3＞4，故本选项正确．C、3+5＜9，故本选项错误．D、4+4=8，故本选项错误．故选B．【点睛】本题考查三角形的三边关系，根据三角形的任何一边大于其他两边之差，小于两边之和，满足此关系的可组成三角形．12．如图，AB∥CD，DE⊥BE，BF、DF分别为∠ABE、∠CDE的角平分线，则∠BFD＝（）A．110°B．120°C．125°D．135°【答案】D【解析】【分析】【详解】如图所示，过E作EG∥AB．∵AB∥CD，∴EG∥CD，∴∠ABE+∠BEG=180°，∠CDE+∠DEG=180°，∴∠ABE+∠BED+∠CDE=360°．又∵DE⊥BE，BF，DF分别为∠ABE，∠CDE的角平分线，∴∠FBE+∠FDE=12（∠ABE+∠CDE）=12（360°﹣90°）=135°，∴∠BFD=360°﹣∠FBE﹣∠FDE﹣∠BED=360°﹣135°﹣90°=135°．故选D．【点睛】本题主要考查了平行线的性质以及角平分线的定义的运用，解题时注意：两直线平行，同旁内角互补．解决问题的关键是作平行线．三、八年级数学全等三角形填空题（难）13．如图，四边形ABCD中，AB＝AD，AC＝5，∠DAB＝∠DCB＝90°，则四边形ABCD的面积为_____．【答案】12.5【解析】【分析】过A作AE⊥AC，交CB的延长线于E，判定△ACD≌△AEB，即可得到△ACE是等腰直角三角形，四边形ABCD的面积与△ACE的面积相等，根据S△ACE=12×5×5=12.5，即可得出结论．【详解】如图，过A作AE⊥AC，交CB的延长线于E，∵∠DAB=∠DCB=90°，∴∠D+∠ABC=180°=∠ABE+∠ABC，∴∠D=∠ABE，又∵∠DAB=∠CAE=90°，∴∠CAD=∠EAB，又∵AD=AB，∴△ACD≌△AEB（ASA），∴AC=AE，即△ACE是等腰直角三角形，∴四边形ABCD的面积与△ACE的面积相等，∵S△ACE=12×5×5=12.5，∴四边形ABCD的面积为12.5，故答案为12.5．【点睛】本题主要考查了全等三角形的判定与性质，解题的关键是学会添加常用辅助线，构造全等三角形解决问题14．如图，已知△ABC为等边三角形，点D，E分别在边BC，AC上，且BD＝CE，若BE交AD于点F，则∠AFE的大小为_____（度）．【答案】60【解析】【分析】根据△ABC为等边三角形得到AB＝BC，∠ABD＝∠BCE＝60°，再利用BD＝CE证得△ABD≌△BCE，得到∠BAD＝∠CBE，再利用内角和外角的关系即可得到∠AFE＝60°.【详解】∵△ABC为等边三角形，点D，E分别在边BC，AC上，且BD＝CE，∴AB＝BC，∠ABD＝∠BCE＝60°，在△ABD和△BCE中，AB BCABD BCEBD CE=⎧⎪∠∠⎨⎪=⎩＝,∴△ABD≌△BCE（SAS），∴∠BAD＝∠CBE，∵∠ABF+∠CBE＝∠ABC＝60°，∴∠ABF+∠BAD＝60°，∵∠AFE＝∠ABF+∠BAD，∴∠AFE＝60°，故答案为：60．【点睛】此题考查三角形全等的判定定理及性质定理，题中证明三角形全等后得到∠BAD＝∠CBE，再利用外角和内角的关系求∠AFE是解题的关键.15．如图，在Rt△ABC中，∠BAC＝90°，AD⊥BC于D，BE平分∠ABC交AC于E，交AD于F，FG∥BC，FH∥AC，下列结论：①AE＝AF；②AF＝FH；③AG＝CE；④A B＋FG＝BC，其中正确的结论有________________．(填序号)【答案】①②③④【解析】①正确.∵∠BAC＝90°∴∠ABE+∠AEB=90°∴∠ABE=90°-∠AEB∵AD⊥BC∴∠ADB=90°∴∠DBE+∠BFD=90°∴∠DBE=90-∠BFD∵∠BFD=∠AFE∴∠DBE=90°-∠AFE∵BE平分∠ABC∴∠ABE=∠DBE∴90°-∠AEB=90°-∠AFE∴∠AEB=∠AFE∴AE=AF②正确.∵∠BAC=90°∴∠BAF+∠DAC=90°∴∠BAF=90°-∠DAC∵AD⊥BC∴∠ADC=90°∴∠C+∠DAC=90°∴∠C=90°-∠DAC∴∠C=∠BAF∵FH∥AC∴∠C=∠BHF∴∠BAF=∠BHF在△ABF和△HBF中ABE CBEBAF BHFBF BF∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABF≌△HBF∴AF=FH③正确.∵AE=AF，AF=FH∴AE=FH∵FG∥BC，FH∥AC∴四边形FHCG是平行四边形∴FH=GC∴AE=GC∴AE+EG=GC+EG∴AG=CE④正确.∵四边形FHCG是平行四边形∴FG=HC∵△ABF≌△HBF∴AB=HB∴AB+FG=HB+HC=BC故正确的答案有①②③④.16．如图，Rt△ABC中，∠C=90°．E为AB中点，D为AC上一点，BF∥AC交DE的延长线于点F．AC=6，BC=5．则四边形FBCD周长的最小值是______．【答案】16【解析】四边形FBCD周长=BC+AC+DF；当DF BC⊥时，四边形FBCD周长最小为5+6+5=1617．AD，BE是△ABC的高，这两条高所在的直线相交于点O，若BO=AC，BC=a，CD=b，则AD的长为______.【答案】AD的长为a-b或b-a或a+b或12a或b.【解析】【分析】分别讨论△ABC为锐角三角形时、∠A、∠B、∠C分别为钝角时和∠A为直角时五种情况，利用AAS证明△BOD≌△ACD，可得BD=AD，根据线段的和差关系即可得答案.【详解】①如图，当△ABC为锐角三角形时，∵AD、BE为△ABC的两条高，∴∠CAD+∠AOE=90°，∠CBE+∠BOD=90°，∵∠BOD=∠AOE，∴∠CAD=∠OBD，又∵∠ODB=∠ADC=90°，OB=AC，∴△BOD≌△ACD，∴AD=BD，∵BC=a，CD=b，∴AD=BD=BC-CD=a-b.②如图，当∠B为钝角时，∵∠C+∠CAD=90°，∠O+∠CAD=90°，∴∠C=∠O，又∵∠ADC=∠ODB=90°，OB=AC，∴△BOD≌△ACD，∴BD=AD，∴AD=CD-BC=b-a.③如图，当∠A为钝角时，同理可证：△BOD≌△ACD，∴AD=BC-CD=a-b.④如图，当∠C为钝角时，同理可证：△BOD≌△ACD，∴AD=BD=BC+CD=a+b.⑤当∠B为直角时，点O、D、B重合，OB=0，不符合题意，当∠C为直角时，点O、C、D、E重合，CD=0，不符合题意，如图，当∠A为直角时，点A、E、O重合，∵OB=AC，∠CAB=90°，∴△ABC是等腰直角三角形，∵AD⊥BC，∴AD是Rt△ABC斜边中线，∴AD=AD=12BC=12a=b.综上所述：AD的长为a-b或b-a或a+b或12a或b.故答案为：a-b或b-a或a+b或12a或b【点睛】本题主要考查全等三角形的判定与性质，全等三角形的判定方法有：SSS 、AAS 、ASA 、SAS 、HL 等，注意：SAS 时，角必须是两边的夹角，SSA 和AAA 不能判定两个三角形全等.灵活运用分类讨论的思想是解题关键.18．如图，已知AB ∥CD ，O 为∠CAB 、∠ACD 的角平分线的交点，OE ⊥AC 于E ，且OE ＝2，CO ＝3，则两平行线间AB 、CD 的距离等于________．【答案】4【解析】试题解析：如图，过点O 作MN ，MN ⊥AB 于M ，交CD 于N ，∵AB ∥CD ，∴MN ⊥CD ，∵AO 是∠BAC 的平分线，OM ⊥AB ，OE ⊥AC ，OE=2，∴OM=OE=2，∵CO 是∠ACD 的平分线，OE ⊥AC ，ON ⊥CD ，∴ON=OE=2，∴MN=OM+ON=4，即AB 与CD 之间的距离是4．点睛：要明确：①角的平分线上的点到角的两边的距离相等，②从一条平行线上的任意一点到另一条直线作垂线，垂线段的长度叫两条平行线之间的距离，③平行线间的距离处处相等．四、八年级数学全等三角形选择题（难）19．如图，AOB ∆的外角,CAB DBA ∠∠的平分线,AP BP 相交于点P ，PE OC ⊥于E ，PF OD ⊥于F ，下列结论：（1）PE PF =；（2）点P 在COD ∠的平分线上；（3）90APB O ∠=︒-∠，其中正确的有 （ ）A ．0个B ．1个C ．2个D ．3个【答案】C【解析】【分析】 过点P 作PG ⊥AB ，由角平分线的性质定理，得到PE PG PF ==，可判断（1）（2）正确；由12APB EPF ∠=∠，180EPF O ∠+∠=︒，得到1902APB O ∠=︒-∠，可判断（3）错误；即可得到答案．【详解】解：过点P 作PG ⊥AB ，如图：∵AP 平分∠CAB ，BP 平分∠DBA ，PE OC ⊥，PF OD ⊥，PG ⊥AB ，∴PE PG PF ==；故（1）正确；∴点P 在COD ∠的平分线上；故（2）正确；∵12APB APG BPG EPF ∠=∠+∠=∠， 又180EPF O ∠+∠=︒， ∴11(180)9022APB O O ∠=⨯︒-∠=︒-∠；故（3）错误； ∴正确的选项有2个；故选：C ．【点睛】 本题考查了角平分线的判定定理和性质定理，解题的关键是熟练掌握角平分线的判定和性质进行解题．20．如图，△ABC 中，P 、Q 分别是BC 、AC 上的点，作PR ⊥AB ，PS ⊥AC ，垂足分别是R 、S ，若AQ =PQ ，PR =PS ，下面四个结论：①AS =AR ；②QP ∥AR ；③△BRP ≌△QSP ；④AP 垂直平分RS ．其中正确结论的序号是（ ）．A．①②B．①②③C．①②④D．①②③④【答案】C【解析】【分析】如图，连接AP,根据HL判定△APR和△APS全等，即可说明①正确；由△APR和△APS 全等可得∠RAP=∠PAC，再根据等腰三角形性质推出∠QAP=∠QPA，得到∠QPA=∠BAP，根据平行线判定推出OP//AB，即②正确；在Rt△BRP和Rt△QSP中，只有PR=PS.无法判断Rt△BRP和Rt△QSP是否全等；连接RS，与AP交于点D，先证△ARD≌△ASD，即RD=SD；运用等腰三角形的性质即可判定.【详解】解：如图，连接AP∵PR⊥AB，PS⊥AC，PR=PS∴△APR≌△APS∴AS=AR，∠RAP=∠PAC即①正确；又∵AQ=PQ∴∠QAP=∠QPA∴∠QPA=∠BAP∴OP//AB，即②正确.在Rt△BRP和Rt△QSP中，只有PR=PS.无法判断Rt△BRP和Rt△QSP是否全等,故③错误.如图，连接PS∵△APR≌△APS∴AR=AS，∠RAP=∠PAC∴AP垂直平分RS，即④正确；故答案为C.【点睛】本题主要考查了全等三角形的性质和判定，角平分线性质的应用，熟练掌握全等三角形的判定和性质是解答本题的关键21．如图，已知五边形ABCDE中，∠ABC=∠AED=90°，AB=CD=AE=BC+DE=2，则五边形ABCDE的面积为（）A．2 B．3 C．4 D．5【答案】C【解析】【分析】可延长DE至F，使EF=BC，利用SAS可证明△ABC≌△AEF，连AC，AD，AF，再利用SSS证明△ACD≌△AFD，可将五边形ABCDE的面积转化为两个△ADF的面积，进而求解即可．【详解】延长DE至F，使EF=BC，连AC，AD，AF，在△ABC与△AEF中，=90AB AEABC AEFBC EF⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ABC≌△AEF（SAS），∴AC=AF，∵AB=CD=AE=BC+DE，∠ABC=∠AED=90°，∴CD=EF+DE=DF，在△ACD与△AFD中，AC AFCD DFAD AD⎧⎪⎨⎪⎩＝＝＝，∴△ACD≌△AFD（SSS），∴五边形ABCDE的面积是：S=2S△ADF=2×12•DF•AE=2×12×2×2=4．故选C.【点睛】本题主要考查了全等三角形的判定及性质以及三角形面积的计算，正确作出辅助线，利用全等三角形把五边形ABCDE的面积转化为两个△ADF的面积是解决问题的关键．22．如右图，在△ABC中，点Q，P分别是边AC，BC上的点，AQ=PQ，PR⊥AB于R，PS⊥AC于S，且PR=PS，下面四个结论：①AP平分∠BAC；②AS=AR；③B P=QP；④QP∥AB．其中一定正确的是( )A．①②③B．①③④C．①②④D．②③④【答案】C【解析】试题解析：∵PR⊥AB于点R，PS⊥AC于点S，且PR=PS，∴点P在∠BAC的平分线上，即AP平分∠BAC，故①正确；∴∠PAR=∠PAQ，∵AQ=PQ，∴∠APQ=∠PAQ，∴∠APQ=∠PAR，QP AB∴，故④正确；在△APR与△APS中,AP AP PR PS=⎧⎨=⎩，(HL)APR APS∴≌，∴AR=AS，故②正确；△BPR和△QSP只能知道PR=PS,∠BRP=∠QSP=90∘，其他条件不容易得到，所以，不一定全等.故③错误.故选C.23．如图，在△ABC和△DCB中，AB=DC，AC与BD相交于点E，若不再添加任何字母与辅助线，要使△ABC≌△DCB，则还需增加的一个条件是（）A ．AC=BDB ．AC=BC C ．BE=CED ．AE=DE【答案】A【解析】 由AB=DC ，BC 是公共边，即可得要证△ABC≌△DCB，可利用SSS ，即再增加AC=DB 即可. 故选A.点睛：此题主要考查了全等三角形的判定，解题时利用全等三角形的判定：SSS ，SAS ，ASA ，AAS ，HL ，确定条件即可，此题为开放题，只要答案符合判定定理即可.24．在ABC 中，2,72A B ACB ∠=∠∠≠︒，CD 平分ACB ∠，P 为AB 的中点，则下列各式中正确的是（ ）A ．AD BC CD =-B ．AD BC AC =- C ．AD BC AP =-D ．AD BC BD =-【答案】B【解析】【分析】 可在BC 上截取CE=CA ，连接DE ，可得△ACD ≌△ECD ，得DE=AD ，进而再通过线段之间的转化得出线段之间的关系．【详解】解：∵∠A=2∠B，∴∠A﹥∠B∴BC﹥AC∴可在BC上截取CE=CA，连接DE(如图)，，∴∠ACD=∠BCD∵CD平分ACB又∵CD=CD，CE=CA∴△ACD≌△ECD，∴AD=ED，∠CED=∠A=2∠B又∠CED=∠B+∠BDE∴∠B=∠BDE∴AD=DE=BE，∴BC=BE+EC=AD+AC所以AD=BC-AC故选：B若A选项成立，则CD=AC，∴∠A=∠CDA=∠CDE=∠CED=2∠B=2∠EDB∴∠CDA+∠CDE+∠EDB=180°即5∠EDB=180°∴∠EDB=36°∴∠A=72°，∠B=36°∴∠ACB=72°与已知∠ACB≠72°矛盾，故选项A不正确;假设C选项成立，则有AP=AC，作∠BAC的平分线，连接FP，∴△CAF≌△PAF≌△PBF，∴∠CFA=∠AFP=∠PFB=60°∠B=30°，∠ACB=90°当∠ACB=90°时，选项C才成立，∴当∠ACB≠72°时，选项C不一定成立；假设D选项成立，则AD=BC-BD由图可知AD=BA-BD∴AB=BC∴∠A=∠ACB=2∠B∴∠A+∠ACB+∠B=180°∴∠B=36°，∠ACB=72这与已知∠ACB≠72°矛盾，故选项D不成立．故选：B【点睛】本题考查的是考查的是利用角的平分线的性质说明线段之间的关系．,,五、八年级数学轴对称三角形填空题（难）25．我们知道，经过三角形一顶点和此顶点所对边上的任意一点的直线，均能把三角形分割成两个三角形（1）如图，在ABC∆中，25,105A ABC∠=︒∠=︒，过B作一直线交AC于D，若BD 把ABC∆分割成两个等腰三角形，则BDA∠的度数是______．（2）已知在ABC∆中，AB AC=，过顶点和顶点对边上一点的直线，把ABC∆分割成两个等腰三角形，则A∠的最小度数为________．【答案】130︒1807︒⎛⎫⎪⎝⎭【解析】【分析】（1）由题意得：DA=DB，结合25A∠=︒，即可得到答案；（2）根据题意，分4种情况讨论，①当BD=AD，CD=AD，②当AD=BD，AC=CD，③AB=AC，当AD=BD=BC，④当AD=BD，CD=BC，分别求出A∠的度数，即可得到答案．【详解】（1）由题意得：当DA=BA，BD=BA时，不符合题意，当DA=DB时，则∠ABD=∠A=25°，∴∠BDA=180°-25°×2=130°．故答案为：130°；（2）①如图1，∵AB=AC，当BD=AD，CD=AD，∴∠B=∠C=∠BAD=∠CAD，∵∠BAC+∠B+∠C=180°，∴4∠B=180°，∴∠BAC=90°．②如图2，∵AB=AC，当AD=BD，AC=CD，∴∠B=∠C=∠BAD，∠CAD=∠CDA，∵∠CDA=∠B+∠BAD=2∠B，∴∠BAC=3∠B，∵∠BAC+∠B+∠C=180°，∴5∠B=180°，∴∠B=36°，∴∠BAC=108°．③如图3，∵AB=AC，当AD=BD=BC，∴∠ABC=∠C，∠BAC=∠ABD，∠BDC=∠C，∵∠BDC=∠A+∠ABD=2∠BAC，∴∠ABC=∠C=2∠BAC，∵∠BAC+∠ABC+∠C=180°，∴5∠BAC=180°，∴∠BAC=36°．④如图4，∵AB=AC，当AD=BD，CD=BC，∴∠ABC=∠C，∠BAC=∠ABD，∠CDB=∠CBD，∵∠BDC=∠BAC+∠ABD=2∠BAC，∴∠ABC=∠C=3∠BAC，∵∠BAC+∠ABC+∠C=180°，∴7∠BAC=180°，∴∠BAC=180 ()7︒．综上所述，∠A的最小度数为：180 ()7︒．故答案是：180 ()7︒．【点睛】本题主要考查等腰三角形的性质定理以及三角形内角和定理与外角的性质，根据等腰三角形的性质，分类讨论，是解题的关键．26．在平面直角坐标系中，点A在x轴的正半轴上，点B在y轴的正半轴上，∆为等腰三角形，符合条件的C点有∠=︒，在x轴或y轴上取点C，使得ABCABO36__________个．【答案】8【解析】【分析】观察数轴，按照等腰三角形成立的条件分析可得答案．【详解】解：如下图所示，若以点A为圆心，以AB为半径画弧，与x轴和y轴各有两个交点，但其中一个会与点B重合，故此时符合条件的点有3个；若以点B为圆心，以AB为半径画弧，同样与x轴和y轴各有两个交点，但其中一个与点A重合，故此时符合条件的点有3个；线段AB的垂直平分线与x轴和y轴各有一个交点，此时符合条件的点有2个．∴符合条件的点总共有：3＋3＋2=8个．故答案为：8．【点睛】本题考查了等腰三角形的判定，可以观察图形，得出答案．27．如图，∠MON＝30°，点A1、A2、A3…在射线ON上，点B1、B2，B3…在射线OM上，△A1B1A2，△A2B2A3，△A3B3A4…均为等边三角形，从左起第1个等边三角形的边长记a1，第2个等边三角形的边长记为a2，以此类推，若OA1＝3，则a2=_______，a2019=_______.【答案】6； 3×22018.【解析】【分析】根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3，以及a2=2a1=6，得出a3=4a1，a4=8a1，a5=16a1…进而得出答案．【详解】解：如图，∵△A1B1A2是等边三角形，∴A1B1=A2B1，∠3=∠4=∠12=60°，∴∠2=120°，∵∠MON=30°，∴∠1=180°-120°-30°=30°，又∵∠3=60°，∴∠5=180°-60°-30°=90°，∵∠MON=∠1=30°，∴OA1=A1B1=3，∴A2B1=3，∵△A2B2A3、△A3B3A4是等边三角形，∴∠11=∠10=60°，∠13=60°，∵∠4=∠12=60°，∴A1B1∥A2B2∥A3B3，B1A2∥B2A3，∴∠1=∠6=∠7=30°，∠5=∠8=90°，∴a2=2a1=6，a3=4a1，a4=8a1，a5=16a1，以此类推：a2019=22018a1=3×22018故答案是：6；3×22018．【点睛】此题主要考查了等边三角形的性质以及等腰三角形的性质，根据已知得出a2=2a1=6，a3=4a1，a4=8a1，a5=16a1…进而发现规律是解题关键．28．如图，在△ABC中，∠C＝90°，∠B＝30°，以点A为圆心，任意长为半径画弧分别交AB，AC于点M和N，再分别以点M，N为圆心，大于12MN的长为半径画弧，两弧交于点P，连接AP并延长交BC于点D，则下列说法：①AD是∠BAC的平分线；②∠ADC＝60°；③点D在AB的垂直平分线上；④S△DAC：S△ABC＝1：3.其中正确的是__________________．(填所有正确说法的序号)【答案】4【解析】【分析】①连接NP，MP，根据SSS定理可得△ANP≌△AMP，故可得出结论；②先根据三角形内角和定理求出∠CAB的度数，再由AD是∠BAC的平分线得出∠1=∠2=30°，根据直角三角形的性质可知∠ADC=60°；③根据∠1=∠B可知AD=BD ，故可得出结论；④先根据直角三角形的性质得出∠2=30°，CD=12AD，再由三角形的面积公式即可得出结论．【详解】①连接NP，MP．在△ANP与△AMP中，∵AN AMNP MPAP AP=⎧⎪=⎨⎪=⎩，∴△ANP≌△AMP，则∠CAD=∠BAD，故AD是∠BAC的平分线，故此选项正确；②∵在△ABC中，∠C=90°，∠B=30°，∴∠CAB=60°．∵AD是∠BAC的平分线，∴∠1=∠2=12∠CAB=30°，∴∠3=90°﹣∠2=60°，∴∠ADC=60°，故此选项正确；③∵∠1=∠B=30°，∴AD=BD，∴点D在AB的中垂线上，故此选项正确；④∵在Rt△ACD中，∠2=30°，∴CD=12AD，∴BC=BD+CD=AD+12AD=32AD，S△DAC=12AC•CD=14AC•AD，∴S △ABC=12AC•BC=12AC•32AD=34AC•AD，∴S△DAC：S△ABC=1：3，故此选项正确．故答案为①②③④．【点睛】本题考查的是作图﹣基本作图，熟知角平分线的作法是解答此题的关键．29．如图,在ABC中,90,ACB ABD︒∠=是ABC的轴对称图形,点E在AD上,点F在AC的延长线上.若点B恰好在EF的垂直平分线上,并且5AE=,13AF=,则DE=______．【答案】4．【解析】【分析】连接BE ，BF ，根据轴对称的性质可得△ABD ≌△ACB ，进而可得DB=CB ，AD=AC ，∠D=∠BCA=90°，再利用线段垂直平分线的性质可得BE=BF ，然后证明Rt △DBE ≌Rt △CBF 可得DE=CF ，然后可得ED 长．【详解】解：连接BE ，BF ，∵△ABD 是△ABC 的轴对称图形，∴△ABD ≌△ACB ，∴DB=CB ，AD=AC ，∠D=∠BCA=90°，∴∠BCF=90°，∵点B 恰好在EF 的垂直平分线上，∴BE=BF ，在Rt △DBE 和Rt △CBF 中BD BC EB FB =⎧⎨=⎩，∴Rt △DBE ≌Rt △CBF （HL ），∴DE=CF ，设DE=x ，则CF=x ，∵AE=5，AF=13，∴AC=AD=5+x ，∴AF=5+2x ， ∴5+2x=13，∴x=4，∴DE=4，故答案为：4．【点睛】此题主要考查了轴对称和线段垂直平分线的性质，关键是掌握成轴对称的两个图形全等．30．如图，ABC ∆中，AB AC =，点D 是ABC ∆内部一点，DB DC =，点E 是边AB 上一点，若CD 平分ACE ∠，100AEC =∠，则BDC ∠=______°【答案】80【解析】【分析】根据角平分线得到∠ACE=2∠ACD，再根据角的和差关系得到∠ECB =∠ACB－2∠ACD，然后利用外角定理得到∠ABC+∠ECB=100°，代换化简得出∠ACB－∠ACD=50°，即∠DCB=50°，从而求出∠BDC即可.【详解】∵CD平分∠ACE，∴∠ACE=2∠ACD=2∠ECD，∴∠ECB=∠ACB－∠ACE=∠ACB－2∠ACD，∵∠AEC=100°，∴∠ABC+∠ECB=100°，∴∠ABC+∠ACB－2∠ACD=100°，∵AB=AC，∴∠ABC=∠ACB,∴2∠ACB－2∠ACD=100°，∴∠ACB－∠ACD=50°，即∠DCB=50°，∵DB=DC，∴∠DBC=∠DCB，∴∠BDC=180°－2∠DCB=180°－2×50°=80°.【点睛】本题考查了角平分线，三角形内角和，外角定理，及等边对等角的性质等知识，熟练掌握基本知识，找出角与角之间的关系是解题的关键.六、八年级数学轴对称三角形选择题（难）31．如图，△ABC的周长为32，点D、E都在边BC上，∠ABC的平分线垂直于AE，垂足为Q，∠ACB的平分线垂直于AD，垂足为P，若BC＝12，则PQ的长为（）A ．3B ．4C ．5D ．6【答案】B【解析】【分析】 首先判断△BAE 、△CAD 是等腰三角形，从而得出BA ＝BE ，CA ＝CD ，由△ABC 的周长为32以及BC ＝12，可得DE ＝8，利用中位线定理可求出PQ ．【详解】∵BQ 平分∠ABC ，BQ ⊥AE ，∴∠ABQ ＝∠EBQ ，∵∠ABQ+∠BAQ ＝90°，∠EBQ+∠BEQ ＝90°，∴∠BAQ ＝∠BEQ ，∴AB ＝BE ，同理：CA ＝CD ，∴点Q 是AE 中点，点P 是AD 中点（三线合一），∴PQ 是△ADE 的中位线，∵BE+CD ＝AB+AC ＝32﹣BC ＝32﹣12＝20，∴DE ＝BE+CD ﹣BC ＝8，∴PQ ＝12DE ＝4． 故选：B ．【点睛】本题考查了三角形的中位线定理和等腰三角形的性质和判定，解答本题的关键是判断出△BAE 、△CAD 是等腰三角形，利用等腰三角形的性质确定PQ 是△ADE 的中位线．32．如图，ABC ∆中，60BAC ∠=︒，BAC ∠的平分线AD 与边BC 的垂直平分线MD 相交于点D ，DE AB ⊥交AB 的延长线于点E ，DF AC ⊥于点F ，现有下列结论：①DE DF =；②DE DF AD +=；③DM 平分EDF ∠；④2AB AC AE +=，其中正确的是（ ）A．①②B．①②③C．①②④D．①②③④【答案】C【解析】【分析】①由角平分线的性质可知①正确；②由题意可知∠EAD=∠FAD=30°，故此可知ED=12AD，DF=12AD，从而可证明②正确；③若DM平分∠EDF，则∠EDM=90°，从而得到∠ABC为直角三角形，条件不足，不能确定，故③错误；④连接BD、DC，然后证明△EBD≌△DFC，从而得到BE=FC，从而可证明④．【详解】解：如图所示：连接BD、DC．①∵AD平分∠BAC，DE⊥AB，DF⊥AC，∴ED=DF．∴①正确．②∵∠EAC=60°，AD平分∠BAC，∴∠EAD=∠FAD=30°．∵DE⊥AB，∴∠AED=90°．∵∠AED=90°，∠EAD=30°，∴ED=12 AD．同理：DF=12AD．∴DE+DF=AD．∴②正确．③由题意可知：∠EDA=∠ADF=60°．假设MD平分∠EDF，则∠ADM=30°．则∠EDM=90°，又∵∠E=∠BMD=90°，∴∠EBM=90°．∴∠ABC=90°．∵∠ABC是否等于90°不知道，∴不能判定MD平分∠EDF，故③错误．④∵DM是BC的垂直平分线，∴DB=DC．在Rt△BED和Rt△CFD中DE DFBD DC⎧⎨⎩＝＝，∴Rt△BED≌Rt△CFD．∴BE=FC．∴AB+AC=AE-BE+AF+FC又∵AE=AF，BE=FC，∴AB+AC=2AE．故④正确．综上所述，①②④正确，故选：C．【点睛】本题主要考查的是全等三角形的性质和判定、角平分线的性质、线段垂直平分线的性质，掌握本题的辅助线的作法是解题的关键．33．如图，在△ABC中，BC的垂直平分线分别交AC，BC于点D，E,若△ABC的周长为24，CE＝4，则△ABD的周长为（）A．16 B．18 C．20 D．24【答案】A【解析】【分析】根据线段的垂直平分线的性质和三角形的周长公式进行解答即可.【详解】解：∵DE是BC的垂直平分线，∴DB=DC，BC=2CE=8又∵AABC的周长为24，∴AB+BC+AC=24∴AB+AC=24-BC=24-8=16∴△ABD的周长=AD+BD+AB=AD+CD+AB=AB+AC=16，故答案为A【点睛】本题考查的是线段的垂直平分线的性质，理解并应用线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.34．如果三角形有一个内角为120°，且过某一顶点的直线能将该三角形分成两个等腰三角形，那么这个三角形最小的内角度数是( )A．15°B．40 C．15°或20°D．15°或40°【答案】C【解析】【分析】依据三角形的一个内角的度数为120°，且过某一顶点能将该三角形分成两个等腰三角形，运用分类思想和三角形内角和定理，即可得到该三角形其余两个内角的度数．【详解】如图1，当∠A=120°，AD=AC，DB=DC时，∠ADC=∠ACD=30°，∠DBC=∠DCB=15°，所以，∠DBC=15°，∠ACB=30°+15°=45°；故∠ABC=60°，∠C=80°；如图2，当∠BAC=120°，可以以A为顶点作∠BAD=20°，则∠DAC=100°，∵△APB，△APC都是等腰三角形；∴∠ABD=20°，∠ADC=∠ACD=40°，如图3，当∠BAC=120°，以A为顶点作∠BAD=80°，则∠DAC=40°，∵△APB，△APC都是等腰三角形，∴∠ABD=20°，∠ADC=100°，∠ACD=40°．故选C．【点睛】本题主要考查了三角形内角和定理以及等腰三角形的性质的运用，解决问题的关键是掌握等腰三角形的性质以及三角形内角和定理．35．如图，已知长方形ABCD，AB＝1，BC＝2，点M为矩形内一点，点E为BC边上任意一点，则MA＋MD＋ME的最小值为( )A．1 B．3C．3D．3【答案】B【解析】【分析】将△AMD绕点A逆时针旋转60°得到△AM’D’，MD=M’D’，易得到△ADD’和△AMM’均为等边三角形，推出AM=MM’可得MA+MD+ME=D’M+MM’+ME，共线时最短；由于点E 也为动点，可得当D’E⊥BC时最短，此时易求得D’E=DG+GE的值.【详解】将△AMD绕点A逆时针旋转60°得到△AM’D’，MD=M’D’，易得到△ADD’和△AMM’均为等边三角形，∴AM=MM’，∴MA+MD+ME=D’M+MM’+ME，∴D′M、MM′、ME共线时最短，由于点E也为动点，∴当D’E⊥BC时最短，此时易求得3∴MA+MD+ME的最小值为3故选B ．【点睛】本题考查轴对称、旋转变换、矩形的性质等知识，解题的关键是学会添加常用辅助线，构造等边三角形解决问题，学会用转化的思想思考问题．36．如图，ABC △中，60BAC ∠=︒，ABC ∠、ACB ∠的平分线交于E ，D 是AE 延长线上一点，且120BDC ∠=︒．下列结论：①120BEC ∠=︒；②DB DE =；③2BDE BCE ∠=∠．其中所有正确结论的序号有（ ）．A ．①②B ．①③C ．②③D ．①②③【答案】D【解析】 分析：根据三角形内角和等于180°求出∠ABC+∠ACB ，再根据角平分线的定义求出∠EBC+∠ECB ，然后求出∠BEC=120°，判断①正确；过点D 作DF ⊥AB 于F ，DG ⊥AC 的延长线于G ，根据角平分线上的点到角的两边的距离相等可得DF=DG ，再求出∠BDF=∠CDG ，然后利用“角边角”证明△BDF 和△CDG 全等，根据全等三角形对应边相等可得BD=CD ，再根据等边对等角求出∠DBC=30°，然后根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义求出∠DBE=∠DEB ，根据等角对等边可得BD=DE ，判断②正确，再求出B ，C ，E 三点在以D 为圆心，以BD 为半径的圆上，根据同弧所对的圆周角等于圆心角的一半可得∠BDE=2∠BCE ，判断③正确．详解：∵60BAC ∠=︒，∴18060120ABC ACB ∠+∠=︒-︒=︒，∵BE 、CE 分别为ABC ∠、ACB ∠的平分线，∴12EBC ABC ∠=∠，12ECB ACB ∠=∠， ∴11()1206022EBC ECB ABC ACB ∠+∠=∠+∠=⨯︒=︒， ∴180()18060120BEC EBC ECB ∠=︒-∠+∠=︒-︒=︒， 故①正确．如图，过点D 作DF AB ⊥于F ，DG AC ⊥的延长线于G ，∵BE 、CE 分别为ABC ∠、ACB ∠的平分线，∴AD 为BAC ∠的平分线，∴DF DG =，∴36090260120FDG ∠=︒-︒⨯-︒=︒，又∵120BDC ∠=︒，∴120BDF CDF ∠+∠=︒，120CDG CDF ∠+∠=︒．∴BDF CDG ∠=∠，∵在BDF 和CDG △中，90BFD CGD DF DGBDF CDG ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩， ∴BDF ≌()CDG ASA ，∴DB CD =，∴1(180120)302DBC ∠=︒-︒=︒， ∴30DBC DBC CBE CBE ∠=∠+∠=︒+∠，∵BE 平分ABC ∠，AE 平分BAC ∠，∴ABE CBE ∠=∠，1302BAE BAC ∠=∠=︒， 根据三角形的外角性质，30DEB ABE BAE ABE ∠=∠+∠=∠+︒，∴DEB DBE ∠=∠，∴DB DE =，故②正确．∵DB DE DC ==，∴B 、C 、E 三点在以D 为圆心，以BD 为半径的圆上，∴2BDE BCE ∠=∠，故③正确，综上所述，正确结论有①②③，故选：D ．点睛：本题考查了角平分线的性质，全等三角形的判定与性质，等角对等边的性质，圆内接四边形的判定，同弧所对的圆周角等于圆心角的一半性质，综合性较强，难度较大，特别是③的证明．七、八年级数学整式的乘法与因式分解选择题压轴题（难）37．已知a ＝2018x ＋2018，b ＝2018x ＋2019，c ＝2018x ＋2020，则a 2＋b 2＋c 2－ab －ac －bc 的值是( )A ．0B ．1C ．2D ．3 【答案】D【解析】【分析】 把已知的式子化成12[（a-b ）2+（a-c ）2+（b-c ）2]的形式，然后代入求解即可． 【详解】原式=12（2a 2+2b 2+2c 2-2ab-2ac-2bc ） =12[（a 2-2ab+b 2）+（a 2-2ac+c 2）+（b 2-2bc+c 2）] =12[（a-b ）2+（a-c ）2+（b-c ）2] =12×（1+4+1） =3，故选D.【点睛】 本题考查了因式分解的应用，代数式的求值，正确利用因式分解的方法把所求的式子进行变形是关键．38．（2017重庆市兼善中学八年级上学期联考）在日常生活中如取款、上网等都需要密码．有一种用“因式分解法”产生的密码方便记忆，如：对于多项式44x y -，因式分解的结。
双柏县八年级(上)期末综合素质测评数学试卷及答案-精选
双柏县2019-2020学年上学期末综合素质测评八年级数学试卷命题：双柏县教研室（全卷满分100分，考试时间120分钟）（本大题共8个小题，每小题只有一个正确选项，每小题3分，满分24分）1．计算）A．-3 B．3 C．-9 D．92．下列几组数能作为直角三角形的三边长的是（）A．1，2，3 B．2，3，4C．3，4，5 D．4，5，63．下列说法正确的是（）A．所有无限小数都是无理数B．所有无理数都是无限小数C．有理数都是有限小数D．不是有限小数的不是有理数4．已知一组数据：12，5，9，5，14，下列说法不正确的是（）A．平均数是9 B．中位数是9C ．众数是5D ．极差是55．在平面直角坐标系中，已知点P 的坐标是（-1，-2），则点P 关于x 轴对称的点的坐标是（ ） A ．（-1，2） B ．（1，-2） C ．（1，2）D ．（2，1）6．如图，AB ∥CD ，∠D =∠E =35°， 则∠B 的度数为（ ）A ．60°B ．65°C ．70°D ．75°7．一次函数y kx b =-，当k <0，b <0时的图象大致位置是（ ）A ．B ．C ．D ．8．下列计算正确的是（ ）BA CDEABC．2D二、填空题（本大题共6个小题，每小题3分，满分18分）9．25的算术平方根是．10= ．11．某水池有水15m3，现打开进水管进水，进水速度5m3/ h；xh后这个水池内有水y m3，则y关于x的关系式为．12．命题“对顶角相等”的条件是，结论是．13．如果a、b同号，则点P（a，b）在象限．14．方程组521x yx y+=⎧⎨-=⎩的解是.三、解答题（本大题共有9个小题，满分58分）O A BDF341 2CE 15．（本小题4）16．（本小题5分）已知13x y =⎧⎨=⎩ 和02x y =⎧⎨=-⎩都是方程ax -y =b 的解，求a 与b 的值．17．（本小题6分）如图,直线CD 、EF 被直线OA 、OB 所截，∠1 +∠2 =180°．求证：∠3=∠4．18．（本小题5分）长方形的两条边长分别为4，6，建立适当的直角坐标系，使它的一个顶点的坐标为（-2，-3）．请你写出另外三个顶点的坐标．19．（本小题5分）某中学为了绿化校园，计划购买一批榕树和香樟树，经市场调查榕树的单价比香樟树少20元，购买3棵榕树和2棵香樟树共需340元．请问榕树和香樟树的单价各多少？20．（本小题6分）已知直线y =2x 与y =-x +b 的交点为（1，a ），试确定方程组2y 0+y 0x x b -=⎧⎨-=⎩ 的解和a 、b 的值．21．（本小题9分）已知一次函数y =kx -3的图象与正比例函数12y x =的图象相交于点（2，a ）． （1）求a 的值．（2）求一次函数的表达式．（3）在同一坐标系中，画出这两个函数的图象．22．（本小题9分）甲、乙两名工人同时加工同一种零件，现根据两人7天产品中每天出现的次品数情况绘制成如下不完整的统计图和表，依据图、表信息，解答下列问题： 相关统计量表：x（2）判断谁出现次品的波动小．（3）估计乙加工该种零件30天出现次品多少件？23．（本小题9分）汽车出发前油箱有油50L ，行驶若干小时后，在加油站加油若干升．图象表示的是从出发后，油箱中剩余油量y （L ）与行驶时间t （h ）之间的关系．（1）汽车行驶 h 后加油，中途加油L ；（2）求加油前油箱剩余油量y 与行驶时间t 的函数关系式；（3）已知加油前、后汽车都以70km /h 匀速行驶，如果加油站距目的地210km ，那么要到达目的地，油箱中的油是否够用？请说明理由．甲 乙数量O 2 4 6 8 t/h 2013-2014学年上学期末综合素质测评八年级数学参考答案一、选择题（每小题只有一个正确的选项，每小题3分，共24分）1．A2．C3．B4．D5．A6．C7．C8．A 二、填空题（每小题3分，共18分）OABDF342C E1 59．5 10．2 11．y =5x +15 12．如果两个角是对顶角，那么它们相等 13．一或三 14．2y 3x =⎧⎨=⎩ 三、解答题（共58分）15．（每小题4）×（= -616．（本小题5分）解：因为13x y =⎧⎨=⎩ 和02x y =⎧⎨=-⎩都是方程ax -y =b 的解 所以，35,22a b a b b -==⎧⎧⎨⎨==⎩⎩解得 17．（本小题6分）证明：∵∠2与∠5是对顶角 ∴∠2=∠5∵∠1 +∠2 =180° ∴∠1 +∠5 =180° ∴CD ∥EF ∴∠3=∠4 18．（本小题5分） 解：如图建立直角坐标系， 因为长方形的一个顶点的 坐标为A （-2，-3）所以长方形的另外三个顶点 的坐标分别为： B （2，-3），C （2，3），D （-2，3） （答案不唯一）19．（本小题5分）解：设榕树的单价为x 元/棵，香樟树的单价是y 元/棵，则： y 203+2y 340x x =-⎧⎨=⎩，解得60y 80x =⎧⎨=⎩ 答：榕树和香樟树的单价分别是60元/棵，80元/棵 20．（本小题6分）解：因为直线y =2x 与y =-x +b 的交点为（1，a ），所以221+3a a a b b ==⎧⎧⎨⎨=-=⎩⎩，解得 则有 2y 02y 01,,+y 30+y 3y 2x x x x x -=-==⎧⎧⎧⎨⎨⎨-===⎩⎩⎩即解得 因此，方程组2y 0+y 0x x b -=⎧⎨-=⎩ 的解是1y 2x =⎧⎨=⎩，a 、b21．（本小题9分） 解：（1）∵ 正比例函数12y x =的图象过点（2，a ∴ a =1（2）∵一次函数y =kx -3的图象经过点（2，1）∴1=2k -3 ∴k =2∴y =2x -3 （3）函数图像如右图 22．（本小题9分）解：（1）补全的图如下。
初二数学经典综合试卷答案
一、选择题1. 选择题答案：C解析：题目中给出的方程为x+3=2x-5，移项得x=8，代入原方程检验，8+3=2×8-5，等式成立，故x=8是方程的解。
2. 选择题答案：B解析：题目中给出的方程为2(x-3)=3(x+2)，展开得2x-6=3x+6，移项得x=-12，代入原方程检验，2×(-12-3)=3×(-12+2)，等式成立，故x=-12是方程的解。
3. 选择题答案：A解析：题目中给出的方程为x^2-5x+6=0，因式分解得(x-2)(x-3)=0，解得x=2或x=3。
4. 选择题答案：D解析：题目中给出的方程为(x-1)^2=4，开平方得x-1=±2，解得x=3或x=-1。
5. 选择题答案：C解析：题目中给出的方程为(x+2)^2=0，开平方得x+2=0，解得x=-2。
二、填空题1. 填空题答案：x=2解析：题目中给出的方程为x+3=2x-5，移项得x=8，代入原方程检验，8+3=2×8-5，等式成立，故x=8是方程的解。
2. 填空题答案：x=3解析：题目中给出的方程为2(x-3)=3(x+2)，展开得2x-6=3x+6，移项得x=-12，代入原方程检验，2×(-12-3)=3×(-12+2)，等式成立，故x=-12是方程的解。
3. 填空题答案：x=2解析：题目中给出的方程为x^2-5x+6=0，因式分解得(x-2)(x-3)=0，解得x=2或x=3。
4. 填空题答案：x=3解析：题目中给出的方程为(x-1)^2=4，开平方得x-1=±2，解得x=3或x=-1。
5. 填空题答案：x=-2解析：题目中给出的方程为(x+2)^2=0，开平方得x+2=0，解得x=-2。
三、解答题1. 解答题答案：步骤一：将方程x^2-5x+6=0因式分解得(x-2)(x-3)=0。
步骤二：解得x=2或x=3。
步骤三：代入原方程检验，2^2-5×2+6=0，3^2-5×3+6=0，等式成立。
双柏县八年级(上)期末综合素质测评数学试卷及答案
双柏县2019-2020学年上学期末综合素质测评八年级数学试卷命题：双柏县教研室（全卷满分100分，考试时间120分钟）一、选择题（本大题共8个小题，每小题只有一个正确选项，每小题3分，满分24分）1．计算）A．-3 B．3 C．-9 D．92．下列几组数能作为直角三角形的三边长的是（）A．1，2，3 B．2，3，4C．3，4，5 D．4，5，63．下列说法正确的是（）A．所有无限小数都是无理数 B．所有无理数都是无限小数C．有理数都是有限小数 D．不是有限小数的不是有理数4．已知一组数据：12，5，9，5，14，下列说法不正确的是（）A．平均数是9 B．中位数是9C ．众数是5D ．极差是55．在平面直角坐标系中，已知点P 的坐标是（-1，-2），则点P 关于x 轴对称的点的坐标是（ ） A ．（-1，2） B ．（1，-2） C ．（1，2）D ．（2，1）6．如图，AB ∥CD ，∠D =∠E =35°， 则∠B 的度数为（ ）A ．60°B ．65°C ．70°D ．75°7．一次函数y kx b =-，当k <0，b <0时的图象大致位置是（ ）A ． B． C ． D ．8．下列计算正确的是（ ）A B BA CDEC．2 D49-二、填空题（本大题共6个小题，每小题3分，满分18分）9．25的算术平方根是．10= ．11．某水池有水15m3，现打开进水管进水，进水速度5m3/ h；xh后这个水池内有水y m3，则y关于x的关系式为．12．命题“对顶角相等”的条件是，结论是．13．如果a、b同号，则点P（a，b）在象限．14．方程组521x yx y+=⎧⎨-=⎩的解是 .三、解答题（本大题共有9个小题，满分58分）15．（本小题4）O A BDF341 2C E16．（本小题5分）已知13x y =⎧⎨=⎩ 和02x y =⎧⎨=-⎩都是方程ax -y =b 的解，求a 与b 的值．17．（本小题6分）如图,直线CD 、EF 被直线OA 、OB 所截，∠1 +∠2 =180°．求证：∠3=∠4．18．（本小题5分）长方形的两条边长分别为4，6，建立适当的直角坐标系，使它的一个顶点的坐标为（-2，-3）．请你写出另外三个顶点的坐标．19．（本小题5分）某中学为了绿化校园，计划购买一批榕树和香樟树，经市场调查榕树的单价比香樟树少20元，购买3棵榕树和2棵香樟树共需340元．请问榕树和香樟树的单价各多少？20．（本小题6分）已知直线y=2x与y=-x+b的交点为（1，a），试确定方程组2y0+y0xx b-=⎧⎨-=⎩的解和a、b的值．21．（本小题9分）已知一次函数y=kx-3的图象与正比例函数12y x=的图象相交于点（2，a）．（1）求a的值．（2）求一次函数的表达式．（3）在同一坐标系中，画出这两个函数的图象．22．（本小题9分）甲、乙两名工人同时加工同一种零件，现根据两人7天产品中每天出现的次品数情况绘制成如下不完整的统计图和表，依据图、表信息，解答下列问题： 相关统计量表：次品数量统计表：xO 2 4 6 8 t /h（1）补全图、表．（2）判断谁出现次品的波动小．（3）估计乙加工该种零件30天出现次品多少件？23．（本小题9分）汽车出发前油箱有油50L ，行驶若干小时后，在加油站加油若干升．图象表示的是从出发后，油箱中剩余油量y （L ）与行驶时间t （h ）之间的关系．（1）汽车行驶 h 后加油，中途加油 L ；（2）求加油前油箱剩余油量y 与（3）已知加油前、后汽车都以70km /h 210km ，那么要到达目的地，油箱说明理由．甲 乙数量2013-2014学年上学期末综合素质测评八年级数学 参考答案一、选择题（每小题只有一个正确的选项，每小题3分，共24分）1．A 2．C 3．B 4．D 5．A 6．C 7．C 8．A二、填空题（每小题3分，共18分）9．5 10．2 11．y =5x +15 12．如果两个角是对顶角，那么它们相等 13．一或三 14．2y 3x =⎧⎨=⎩ 三、解答题（共58分）OABDF342C E1515．（每小题4= -616．（本小题5分）解：因为13x y =⎧⎨=⎩和02x y =⎧⎨=-⎩都是方程ax -y =b 的解 所以，35,22a b a b b -==⎧⎧⎨⎨==⎩⎩解得 17．（本小题6分）证明：∵∠2与∠5是对顶角 ∴∠2=∠5∵∠1 +∠2 =180° ∴∠1 +∠5 =180° ∴CD ∥EF ∴∠3=∠4 18．（本小题5分） 解：如图建立直角坐标系， 因为长方形的一个顶点的 坐标为A （-2，-3）所以长方形的另外三个顶点 的坐标分别为：B （2，-3），C （2，3），D （-2，3）（答案不唯一）19．（本小题5分）解：设榕树的单价为x 元/棵，香樟树的单价是y 元/棵，则：y 203+2y 340x x =-⎧⎨=⎩，解得60y 80x =⎧⎨=⎩ 答：榕树和香樟树的单价分别是60元/棵，80元/棵 20．（本小题6分）解：因为直线y =2x 与y =-x +b 的交点为（1，a ），所以221+3a a a b b ==⎧⎧⎨⎨=-=⎩⎩，解得 则有 2y 02y 01,,+y 30+y 3y 2x x x x x -=-==⎧⎧⎧⎨⎨⎨-===⎩⎩⎩即解得因此，方程组2y 0+y 0x x b -=⎧⎨-=⎩ 的解是1y 2x =⎧⎨=⎩，a 、b21．（本小题9分） 解：（1）∵ 正比例函数12y x =的图象过点（2，a ∴ a =1 （2）∵一次函数y =kx -3的图象经过点（2，1）∴1=2k -3 ∴k =2 ∴y =2x -3 （3）函数图像如右图22．（本小题9分）解：（1）补全的图如下。
双柏县八年级(上)期末综合素质测评数学试题及答案
双柏县2019-2020学年上学期末综合素质测评八年级数学试卷命题：双柏县教研室（全卷满分100分，考试时间120分钟）（本大题共8个小题，每小题只有一个正确选项，每小题3分，满分24分）1．计算）A．-3 B．3 C．-9 D．92．下列几组数能作为直角三角形的三边长的是（）A．1，2，3 B．2，3，4C．3，4，5 D．4，5，63．下列说法正确的是（）A．所有无限小数都是无理数B．所有无理数都是无限小数C．有理数都是有限小数D．不是有限小数的不是有理数4．已知一组数据：12，5，9，5，14，下列说法不正确的是（）A．平均数是9 B．中位数是9C．众数是5 D．极差是55．在平面直角坐标系中，已知点P的坐标是（-1，-2），则点P关于轴对称的点的坐标是（）A．（-1，2）B．（1，-2）C．（1，2）D．（2，1）6．如图，AB∥CD，∠D =∠E =35°，则∠B的度数为（）A．60°B．65°C．70°D．75°7．一次函数y kx b=-，当<0，b<0时的图象大致位置是（）A．8．下列计算正确的是（）A BC．2D．49-二、填空题（本大题共6个小题，每小题3分，满分18分）9．25的算术平方根是．10= ．11．某水池有水15m3，现打开进水管进水，进水速度5m3/ h；h后这个水池内有水y m3，则y关于的关系式为．12．命题“对顶角相等”的条件是，结论是．BA CDEOAB DF 3412 CE13．如果a 、b 同号，则点P （a ，b ）在 象限．14．方程组521x y x y +=⎧⎨-=⎩的解是 .三、解答题（本大题共有9个小题，满分58分）15．（本小题416．（本小题5分）已知13x y =⎧⎨=⎩ 和02x y =⎧⎨=-⎩都是方程a -y =b 的解，求a 与b 的值．17．（本小题6分）如图,直线CD 、EF 被直线OA 、OB 所截，∠1 +∠2 =180°． 求证：∠3=∠4．18．（本小题5分）长方形的两条边长分别为4，6，建立适当的直角坐标系，使它的一个顶点的坐标为（-2，-3）．请你写出另外三个顶点的坐标．19．（本小题5分）某中学为了绿化校园，计划购买一批榕树和香樟树，经市场调查榕树的单价比香樟树少20元，购买3棵榕树和2棵香樟树共需340元．请问榕树和香樟树的单价各多少？20．（本小题6分）已知直线y=2与y=-+b的交点为（1，a），试确定方程组2y0+y0xx b-=⎧⎨-=⎩的解和a、b的值．21．（本小题9分）已知一次函数y=-3的图象与正比例函数12y x的图象相交于点（2，a）．（1）求a的值．（2）求一次函数的表达式．（3）在同一坐标系中，画出这两个函数的图象．x22．（本小题9分）甲、乙两名工人同时加工同一种零件，现根据两人7天产品中每天出现的次品数情况绘制成如下不完整的统计图和表，依据图、表信息，解答下列问题： 相关统计量表：（2）判断谁出现次品的波动小．（3）估计乙加工该种零件30天出现次品多少件？甲 乙数量23．（本小题9分）汽车出发前油箱有油50L，行驶若干小时后，在加油站加油若干升．图象表示的是从出发后，油箱中剩余油量y（L）与行驶时间t（h）之间的关系．（1）汽车行驶h后加油，中途加油L；（2）求加油前油箱剩余油量y与行驶时间t的函数关系式；（3）已知加油前、后汽车都以70m/h匀速行驶，如果加油站距目的地210m，那么要到达目的地，油箱中的油是否够用？请说明理由．hOABDF342C E1 5上学期末综合素质测评八年级数学 参考答案一、选择题（每小题只有一个正确的选项，每小题3分，共24分）1．A 2．C 3．B 4．D 5．A 6．C 7．C 8．A二、填空题（每小题3分，共18分）9．5 10．2 11．y =5+15 12．如果两个角是对顶角，那么它们相等 13．一或三 14．2y 3x =⎧⎨=⎩ 三、解答题（共58分）15．（每小题4）×（-）= -616．（本小题5分）解：因为13x y =⎧⎨=⎩和02x y =⎧⎨=-⎩都是方程a -y =b 的解 所以，35,22a b a b b -==⎧⎧⎨⎨==⎩⎩解得 17．（本小题6分） 证明：∵∠2与∠5是对顶角 ∴∠2=∠5 ∵∠1 +∠2 =180° ∴∠1 +∠5 =180° ∴CD ∥EF ∴∠3=∠4 18．（本小题5分） 解：如图建立直角坐标系， 因为长方形的一个顶点的 坐标为A （-2，-3） 所以长方形的另外三个顶点 的坐标分别为：B （2，-3），C （2，3），D （-2，3）（答案不唯一）19．（本小题5分）解：设榕树的单价为元/棵，香樟树的单价是y 元/棵，则：y 203+2y 340x x =-⎧⎨=⎩，解得60y 80x =⎧⎨=⎩ 答：榕树和香樟树的单价分别是60元/棵，80元/棵20．（本小题6分）解：因为直线y =2与y =-+b 的交点为（1，a ），所以221+3a a ab b ==⎧⎧⎨⎨=-=⎩⎩，解得 则有 2y 02y 01,,+y 30+y 3y 2x x x x x -=-==⎧⎧⎧⎨⎨⎨-===⎩⎩⎩即解得 因此，方程组2y 0+y 0x x b -=⎧⎨-=⎩ 的解是1y 2x =⎧⎨=⎩，a 、b21．（本小题9分） 解：（1）∵ 正比例函数12y x =的图象过点（2，a ∴ a =1（2）∵一次函数y =-3的图象经过点（2，1）∴1=2-3 ∴=2 ∴y =2-3 （3）函数图像如右图 22．（本小题9分） 解：（1）补全的图如下。
双柏县八年级(上)期末综合素质测评数学试卷及答案
双柏县2019-2020学年上学期末综合素质测评八年级数学试卷命题：双柏县教研室（全卷满分100分，考试时间120分钟）一、选择题（本大题共8个小题，每小题只有一个正确选项，每小题3分，满分24分）1．计算）A．-3 B．3 C．-9 D．92．下列几组数能作为直角三角形的三边长的是（）A．1，2，3 B．2，3，4C．3，4，5 D．4，5，63．下列说法正确的是（）A．所有无限小数都是无理数 B．所有无理数都是无限小数C．有理数都是有限小数 D．不是有限小数的不是有理数4．已知一组数据：12，5，9，5，14，下列说法不正确的是（）A．平均数是9 B．中位数是9C ．众数是5D ．极差是55．在平面直角坐标系中，已知点P 的坐标是（-1，-2），则点P 关于x 轴对称的点的坐标是（ ） A ．（-1，2） B ．（1，-2） C ．（1，2）D ．（2，1）6．如图，AB ∥CD ，∠D =∠E =35°， 则∠B 的度数为（ ）A ．60°B ．65°C ．70°D ．75°7．一次函数y kx b =-，当k <0，b <0时的图象大致位置是（ ）A ． B． C ． D ．8．下列计算正确的是（ ）A B BA CDEC．2 D49-二、填空题（本大题共6个小题，每小题3分，满分18分）9．25的算术平方根是．10= ．11．某水池有水15m3，现打开进水管进水，进水速度5m3/ h；xh后这个水池内有水y m3，则y关于x的关系式为．12．命题“对顶角相等”的条件是，结论是．13．如果a、b同号，则点P（a，b）在象限．14．方程组521x yx y+=⎧⎨-=⎩的解是 .三、解答题（本大题共有9个小题，满分58分）15．（本小题4）O A BDF341 2C E16．（本小题5分）已知13x y =⎧⎨=⎩ 和02x y =⎧⎨=-⎩都是方程ax -y =b 的解，求a 与b 的值．17．（本小题6分）如图,直线CD 、EF 被直线OA 、OB 所截，∠1 +∠2 =180°．求证：∠3=∠4．18．（本小题5分）长方形的两条边长分别为4，6，建立适当的直角坐标系，使它的一个顶点的坐标为（-2，-3）．请你写出另外三个顶点的坐标．19．（本小题5分）某中学为了绿化校园，计划购买一批榕树和香樟树，经市场调查榕树的单价比香樟树少20元，购买3棵榕树和2棵香樟树共需340元．请问榕树和香樟树的单价各多少？20．（本小题6分）已知直线y=2x与y=-x+b的交点为（1，a），试确定方程组2y0+y0xx b-=⎧⎨-=⎩的解和a、b的值．21．（本小题9分）已知一次函数y=kx-3的图象与正比例函数12y x=的图象相交于点（2，a）．（1）求a的值．（2）求一次函数的表达式．（3）在同一坐标系中，画出这两个函数的图象．22．（本小题9分）甲、乙两名工人同时加工同一种零件，现根据两人7天产品中每天出现的次品数情况绘制成如下不完整的统计图和表，依据图、表信息，解答下列问题： 相关统计量表：次品数量统计表：xO 2 4 6 8 t /h（1）补全图、表．（2）判断谁出现次品的波动小．（3）估计乙加工该种零件30天出现次品多少件？23．（本小题9分）汽车出发前油箱有油50L ，行驶若干小时后，在加油站加油若干升．图象表示的是从出发后，油箱中剩余油量y （L ）与行驶时间t （h ）之间的关系．（1）汽车行驶 h 后加油，中途加油 L ；（2）求加油前油箱剩余油量y 与（3）已知加油前、后汽车都以70km /h 210km ，那么要到达目的地，油箱说明理由．甲 乙数量2013-2014学年上学期末综合素质测评八年级数学 参考答案一、选择题（每小题只有一个正确的选项，每小题3分，共24分）1．A 2．C 3．B 4．D 5．A 6．C 7．C 8．A二、填空题（每小题3分，共18分）9．5 10．2 11．y =5x +15 12．如果两个角是对顶角，那么它们相等 13．一或三 14．2y 3x =⎧⎨=⎩ 三、解答题（共58分）OABDF342C E1515．（每小题4= -616．（本小题5分）解：因为13x y =⎧⎨=⎩和02x y =⎧⎨=-⎩都是方程ax -y =b 的解 所以，35,22a b a b b -==⎧⎧⎨⎨==⎩⎩解得 17．（本小题6分）证明：∵∠2与∠5是对顶角 ∴∠2=∠5∵∠1 +∠2 =180° ∴∠1 +∠5 =180° ∴CD ∥EF ∴∠3=∠4 18．（本小题5分） 解：如图建立直角坐标系， 因为长方形的一个顶点的 坐标为A （-2，-3）所以长方形的另外三个顶点 的坐标分别为：B （2，-3），C （2，3），D （-2，3）（答案不唯一）19．（本小题5分）解：设榕树的单价为x 元/棵，香樟树的单价是y 元/棵，则：y 203+2y 340x x =-⎧⎨=⎩，解得60y 80x =⎧⎨=⎩ 答：榕树和香樟树的单价分别是60元/棵，80元/棵 20．（本小题6分）解：因为直线y =2x 与y =-x +b 的交点为（1，a ），所以221+3a a a b b ==⎧⎧⎨⎨=-=⎩⎩，解得 则有 2y 02y 01,,+y 30+y 3y 2x x x x x -=-==⎧⎧⎧⎨⎨⎨-===⎩⎩⎩即解得因此，方程组2y 0+y 0x x b -=⎧⎨-=⎩ 的解是1y 2x =⎧⎨=⎩，a 、b21．（本小题9分） 解：（1）∵ 正比例函数12y x =的图象过点（2，a ∴ a =1 （2）∵一次函数y =kx -3的图象经过点（2，1）∴1=2k -3 ∴k =2 ∴y =2x -3 （3）函数图像如右图22．（本小题9分）解：（1）补全的图如下。
初二数学能力测试卷电子版
一、选择题（每题3分，共30分）1. 下列各数中，有理数是（）A. √2B. πC. -√3D. 0.1010010001…2. 已知 a + b = 5，a - b = 1，则a² + b² 的值为（）A. 21B. 22C. 23D. 243. 在直角坐标系中，点 P（-2，3）关于 x 轴的对称点坐标为（）A. （-2，-3）B. （2，3）C. （-2，3）D. （2，-3）4. 下列函数中，一次函数是（）A. y = x² + 2x + 1B. y = 2x - 3C. y = √xD. y = log₂x5. 一个长方形的长是 8 厘米，宽是 4 厘米，它的对角线长是（）A. 6 厘米B. 8 厘米C. 10 厘米D. 12 厘米6. 若 a、b 是方程x² - 5x + 6 = 0 的两个根，则 a + b 的值为（）A. 5B. -5C. 6D. -67. 在三角形 ABC 中，∠A = 45°，∠B = 90°，∠C = 45°，则三角形 ABC 是（）A. 直角三角形B. 等腰三角形C. 等边三角形D. 不等腰三角形8. 下列命题中，正确的是（）A. 若 a > b，则a² > b²B. 若 a > b，则 a - b > 0C. 若 a > b，则 a + c > b + cD. 若 a > b，则 ac > bc9. 已知函数 y = kx + b（k ≠ 0），当 x = 1 时，y = 2；当 x = 2 时，y = 4，则 k 的值为（）A. 1B. 2C. 3D. 410. 一个圆的半径增加了 20%，则圆的面积增加了（）A. 20%B. 40%C. 44%D. 45%二、填空题（每题4分，共20分）11. 若 a、b、c 成等差数列，且 a + b + c = 12，则 b 的值为 _______。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（满分150分，120分钟完卷）： 得分： 一、选择题：（4X10=40）1、已知b a >，则下列不等式中成立的是（ ）A. bc ac > B ．b a ->- C ．b a 22-<- D ．b a ->-33 2、若0≠=dcb a ，则下列各式正确的是（ ）． A ． dx cx b a = B ． 11++=d c b a C ． b a d b c a =++ D ． d dc b b a 22+=+ 3、下列图形中不是．．中心对称图形的是（ ）A B C D4、如图，直线21l l 、被直线3l 所截，且1l ∥2l ，若∠1=50°，则∠2的度数为（ ）A 、︒130B 、︒50C 、︒40D 、︒605、下列调查方式中，适宜采用抽样调查的是（ ） A 、了解市所有九年级学生每天参加体育锻炼的平均时间 B 、审查一篇科学论文的正确性C 、对你所在班级同学的身高的调查D 、对“瓦良格”号航母的零部件性能的检查6、已知数据2，3，x ，4，8的平均数是4，则这组数据的中位数和众数是（ ） A ．3和3 B. 3和4 C.2和3 D.4和47、某厂接到加工720件衣服的订单，预计每天做48件，正好按时完成，后因客户要求提前5天交货，设每天应多做x 件，则x 应满足的方程为（ ）．A ．x +48720548720=- B ．x +=+48720548720C ．572048720=-xD ．-48720x +48720=5 8、如图，A 为反比例函数xky =图象上一点，AB 垂直x 轴于B 点，若S △AOB ＝3，则k 的值为（ ）ABOxyA. 6B. 3C.23 D. 不能确定9. 2012中国（）国际云计算博览会简称“云博会”于3月22日—24日在南坪国际会展中心隆重举行。
小明开车从家去看展览，预计1个小时能到达，行驶了半个小时，刚好行驶了一半路程，遇到堵车道路被“堵死”，堵了几分钟突然发现旁边刚好有一个轻轨站，于是小明将车停在轻轨站的车库，然后坐轻轨去观看“云博会”，结果按预计时间到达。
下面能反映该小明距离会展中心的距离y （千米）与时间x （小时）的函数关系的大致图象是H I M N第4题图210.正方形ABCD 的对角线交于点O 过顶点D 作AC 的平行线，在这条线上取一点E ，连接AE,CE,使AE=AC ,AE 交CD 于F .则下列结论①CE=CF ②∠ACE=︒75 ③△DFE 是等腰三角形 ④ 若AB =1则CE =13- ⑤232-=∆∆CFA DFE S S 正确的个数是（ ）A. 2 B. 3 C. 4 D. 5二、填空题：（4x6=24） 11、 a:b:c=3:5:7且2a+3b-c=28, 3a-2b+c=12、如图，在平行四边形ABCD 中， E 是BC 边上的中点，则△AFD 和△EFB 的周长之比为__________.13、分式方程0221=----x xx m 有增根，则=m . 14、若不等式组245x a x a <-⎧⎨>-⎩无解，则a 的取值围是__________15、一天晚上，小伟帮妈妈清洗茶杯，三个茶杯只有花色不同，其中一个无盖（如图），突然停电了，小伟只好把杯盖与茶杯随机地搭配在一起，则花色完全搭配正确的概率是 ． 16、=三、计算题： 17、每题6分(1) 102128)2010(23-⎪⎭⎫⎝⎛-+-+-π （2）2)12(832-+-A B C D第10题 FOEA BCD第12题 F E D C B A.. . .18、（6分）先化简，再求值：111(112+---÷--m m m m m ），其中01222=--m m .19、（8分）已知：如图，梯形ABCD 中，AB ∥DC ，E 是AB 的中点，直线ED 分别与对角线AC 和BC 的延长线交于M 、N 点求证：MD ：ME ＝ND ：NE20、（8分）已知a,b,c 是△ABC 的三边的长，且满足: a 2+2b 2+c 2-2b(a+c)=0,试判断此三角形的形状.ND CA EB M4F N EAB DC M 21、（10分）如图，在正方形ABCD 中，M 是AD 的中点，连接BM ，BM 的垂直平分线交BC 的延长线于F ，连接MF 交CD 于N .求证：（1） BM =EF ； （2） 2CN =DN .22、（10分）如图，在平面直角坐标系xOy 中，一次函数)0(≠+=k b kx y 的图象与反比例函数()0my m x=≠的图象交于二、四象限的A 、B 两点，与x 轴交于C 点，点B 的坐标为(n ,6)．线段5=OA ，E 为x 轴上一点，AE=AC ，tan ∠AOE =34．（1）求该反比例函数和一次函数的解析式；（2）连接BE ，求△AEB 的面积．.. . .23、（10分）百货超市到厂家购进A 、B 两种酱油，A 种酱油每瓶进价6.5元，B 种酱油每瓶进价8元，购进140瓶共花了1000元.（1）超市到厂家购进A 、B 两种酱油各多少瓶？（2）百货超市再以原来的进价购进A 、B 两种酱油共200瓶，计划投资不超过1420元，A 、B 两种酱油的售价分别是每瓶8元和10元，并且将这200瓶酱油卖完获利不低于339元，请你写出所有的进货方案.24、 (10分)为了保护环境，某化工厂一期工程完成后购买了3台甲型和2 台乙型污水处理设备，共花费资金54万元，且每台乙型设备的价格是每台甲型设备价格的75%，实际运行中发现，每台甲型设备每月能处理污水200吨，每台乙型设备每月能处理污水160吨，且每年用于每台甲型设备的各种维护费和电费为1万元，每年用于每台乙型设备的各种维护费和电费为1.5万元.今年该厂二期工程即将完成，产生的污水将大大增加，于是该厂决定再购买甲、乙两型设备共8台用于二期工程的污水处理，预算本次购买资金不．超过．．84万元，预计二期工程完成后每月将产生不少于．．．1300吨污水. （1）请你计算每台甲型设备和每台乙型设备的价格各是多少元？ （2）请你求出用于二期工程的污水处理设备的所有购买方案；（3）若两种设备的使用年限都为10年，请你说明在（2）的所有方案中，哪种购买方案的总费用最少？（总费用＝设备购买费＋各种维护费和电费） 25、（12分）如图，在矩形ABCD 中，AB=18cm ，AD=9cm ，点M 沿AB 边从A 点开始向B 以2cm/s 的速度移动，点N 沿DA 边从D 点开始向A 以1cm/s 的速度移动．如果点M 、N 同时出发，用t （s ）表示移动时间（0≤t6N M D C B A ≤9），求：（1）当t 为何值时，︒=∠45ANM ？（2）计算四边形AMCN 的面积，根据计算结果提出一个你认为合理的结论； （3）当t 为何值时，以点M 、N 、A 为顶点的三角形与△BCD 相似？参考答案：一、选择题：.. . .1-5 CDCBA 6-10 A DA DC 二、填空题： 11、425-12、 13、m=3 14、3a ≤ 15、61 16、三．解答题17、(1) 12128)2010(23-⎪⎭⎫⎝⎛-+-+-π （2）2)12(832-+-=33 =318、解：原式=)111)1)(1(()1)(1(1+--++-÷-+-m m m m m m m m （2分） =111112++--÷+m m m m （4分） =m m m m -+⨯+2111 （6分） =mm -21（8分） 由01222=--m m 得212=-m m （9分 ∴原式=2 （10分）19、∵DC ∥AB∴△NDC ∽△NEB∴ND/NE=NC/NB=DC/EB ∵EB=AE∴DC/EB=DC/AE ∵△DCM ∽△EAM ∴DC/AE=MD/ME ∴MD/ME=ND/NE20、解: a 2+2b 2+c 2-2b(a+c)=0 a 2+b 2+ b 2+c 2-2ba-2bc=0(a-b) 2+(b-c) 2=0 即: a-b=0 , b-c=0 a=b= c 所以△ABC 是等边三角形.21、解：（1）过A 作AK ⊥x 轴，垂足为K 在Rt △AKO 中，∵tan ∠AOE =34，设AK=4x,则OK=3x,OA=5x OA =5, ∴x =1,则OK =3，AK =4，∴A （-3,4）代入x m y =得12-=m ∴反比例函数是xy 12-= （3分）∵点B （6，n ）在反比例函数图象上 ∴B （6，-2）将点A(-3,4),B(6,-2)代入b kx y +=得，⎩⎨⎧+=-+-=b k b k 6234 解之得⎪⎩⎪⎨⎧=-=232b k ∴232+-=x y （6分） （2）∵AE=AC ∴E （-9,0）B BEC AEC AEB y EC AM EC S S S ⋅+⋅=+=∆∆∆2121 =362122141221=⨯⨯+⨯⨯ （4分） 22、（1）证明：过E 点作EK ⊥BC 垂足为K ，过M 作MH ⊥BC 垂足为H ∴EK ∥AH8∵EF 是BM 的垂直平分线 ∴E 是BM 中点，∴EK =21AH=AB 21∵M 是AD 中点 ∴AM=AD 21∴EK=AM （2分） ∵四边形ABCD 是正方形 ∴∠ABC=︒90∵EF 是BM 的垂直平分线 ∴∠BEF=︒90∴∠ABM+∠MBF=︒90∠MBF+∠EFB=︒90∴∠ABM=∠EFB （4分）在∴在△ABM 和△EFK 中AM=EK ∠ABM=∠EFB ∠A=∠EKF=︒90∴△ABMC ≌△EFK (AAS) ∴AB= EF 6分）23、（10分）百货超市到厂家购进A 、B 两种酱油，A 种酱油每瓶进价6.5元，B 种酱油每瓶进价8元，购进140瓶共花了1000元.（1）超市到厂家购进A 、B 两种酱油各多少瓶？（2）百货超市再以原来的进价购进A 、B 两种酱油共200瓶，计划投资不超过1420元，A 、B 两种酱油的售价分别是每瓶8元和10元，并且将这200瓶酱油卖完获利不低于339元，请你写出所有的进货方案. 解： （1）超市到厂家购进A 、B 两种酱油各80瓶和60瓶；（2）A 种酱油进120瓶，B 种酱油进80瓶； A 种酱油进121瓶，B 种酱油进79瓶； A 种酱油进122瓶，B 种酱油进78瓶. 24、 解：（1）设一台甲型设备的价格为x 万元，由题54%7523=⨯+x x ，解得x ＝12，∵ 12×75%＝9 ，∴ 一台甲型设备的价格为12万元，一台乙型设备的价格是9万元 (2)设二期工程中,购买甲型设备a 台,由题意有⎩⎨⎧≥-+≤-+1300)8(16020084)8(912a a a a ，解得：421≤≤a由题意a 为正整数,∴a ＝1,2,3,4 ∴所有购买方案有四种,分别为方案一:甲型1台,乙型7台； 方案二:甲型2台,乙型6台 方案三:甲型3台,乙型5台； 方案四:甲型4台,乙型4台 (3)设二期工程10年用于治理污水的总费用为W 万元)8(105.1101)8(912a a a a w -⨯+⨯+-+=化简得: =w －2a ＋192,∵W 随a 的增大而减少 ∴当a ＝4时, W 最小（逐一验算也可） ∴按方案四甲型购买4台,乙型购买4台的总费用最少. 25、解：（1）对于任何时刻t ，AM=2t ，DN=t ，NA=9-t ，当AN=AM 时，△MAN 为等腰直角三角形，即：9-t=2t ， 解得：t=3（s ），所以，当t=3s 时，△MAN 为等腰直角三角形．(2)在△NAC 中，NA=9-t ，NA 边上的高DC=12， ∴t t DC NA s NAC 98118)9(2121-=•-=•=∆ 在△AMC 中，AM=2t,BC=9,.. . .81s 9922121=+=∴=••=•=∴∆∆∆AMC NAC NAMC AMC s s t t BC AM s 四边形 由计算结果发现：在M 、N 两点移动过程中，四边形NAMC 的面积始终不变（或者提出：M 、N 两点到对角线AC 的距离之和保持不变）（3）根据题意，可分为两种情况来研究，在矩形ABCD 中： ①当 NA ：AB=AM ：BC 时，△NAP ∽△ABC ，那么有： （ 9-t ）：18=2t ：9，解得t=1.8（s ）， 即当t=1.8s 时，△NAP ∽△ABC ；②当 NA ：BC=AM ：AB 时，△MAN ∽△ABC ，那么有： （ 9-t ）：9=2t ：18，解得t=3（s ）， 即当t=3s 时，△MAN ∽△ABC ；所以，当t=1.8s 或3s 时，以点N 、A 、M 为顶点的三角形与△ABC 相似．。