小学五年级奥数题及答案:平行四边形
《平行四边形》习题精选及参考答案

《平行四边形》习题精选及参考答案一、填空题1.过□ABCD的顶点A、C分别作对角线BD的垂直线,垂足为E、F,则四边形AECF是 .2.延长△ABC的中线AD到E,使DE=AD 则四边形ABEC是四边形.3.在四边形ABCD中∠A=50°欲使四边形为平行四边形,则∠B= ,∠C=,∠D= .4.在四边形中,任意相邻两个内角互补,则这个四边形是四边形.5.如图12-1-29,在□ABCD中,E、F为AB、CD的中点,连结DE、EF、BF则图中共有个平行四边形.6.在□ABCD中连结BD作AE⊥BD,CF⊥BD,垂足分别为E、F,连结CE、AF,点P、Q在线段BD上,且BP=DQ,连结AP、CP、AQ、CQ,MN分别交AB、CD于M、N连结AM、CM、NA、NC,那么图中平行四边形(除□ABCD外)有个,它们是 .二、判断题1.平行四边形的对边分别相等()2.平行四边形的对角线相等()3.平行四边形的邻角互补()4.平行四边形的对角相等()5.平行四边形的对角线互相平分一组对角()6.对角线平分平行四边形的四个三角形的面积相等()三、选择题1.能判断四边形是平行四边形的条件是()A.一组对边平行,另一组对边相等B.一组对边平行,一组对角相等C.一组对边平行,一组邻角互补D.一组对边相等,一组邻角相等2.能确定平行四边形的大小和形状的条件是()A.已知平行四边形的两邻边B.已知平行四边形的两邻角C.已知平形四边形的两对角线D.已知平行四边形的两边及夹角3.平行四边形一边为32,则它的两条对角线长不可能为()A.20和18 B.40和50C.60和30 D.32和504.如图12-1-30所示,已知□ABCD的对角线的交点是O,直线EF过O点且平行于BC,直线GH过O且平行AB,则图中有()个平行四边形.A.5个B.6个C.7个D.10个5.能判定四边形为平行四边形的是()A.一组对角相等B.两条对角线互相垂直C.两条对角线互相平分 D.一对邻角互补6.以下结论正确的是()A.对角线相等,且一组对角也相等的四边形是平行四边形.B.一边长为5,两条对角线分别是4和6的四边形是平行四边形.C.一组对边平行,且一组对角相等的四边形是平行四边形.D.对角线相等的四边形是平行四边形.7.在□ABCD中,点E、F分别在边BC、AD上,如果点E,F分别由下列各种情况得到的,那么四边形AECF不一定是平行四边形的是()A.AE、CF分别平分∠DAB、∠BCDB.AE,CF使∠BEA=∠CFDC.E、F分别是BC、AD的中点D.BE=BC,AF=AD8.□ABCD对角线交点为O,△OBC的周长为59cm,且AD=28cm,两对角线之差为14cm,则对角线长为()A.12cm和9cm B.24cm 和38cmC.8.5cm和22.5cm D.15.5cm 和29.5cm四、解答题1.如图12-1-31所示,在□ABCD中,AE平分∠BAD,CF平分∠BCD,四边形AECF是平行四边形吗?2.如图12-1-32所示,四边形ABCD中∠B=∠D,∠1=∠2,则四边形ABCD是平行四边形吗?为什么?3.如图12-1-33所示,四边形ABCD的对角线AC、BD相交于点O,E、F分别是OD、OB上一点,若∠ECD=∠FAB,EC=AF,则四边形AECF是平行四边形吗?为什么?4.如图12-1-34所示,四边形ABCD中AB=CD,∠DBC=90°,FD⊥AD于D,求证四边形ABCD 是平行四边形.5.如图12-1-35所示,△ABC中DE在BC边上,N、M在AB、AC上,且EN与DM互相平分,MD ∥AB,NE∥AC求证:BD=DE=CE五、证明题1.已知:如图12-1-18,在□ABCD中,E、F是对角线BD上的两点,且BE=DF.求证:(1)AE=CF(2)AE∥CF2.已知:如图12-1-19,四边形ABCD为平行四边形,E、F是直线BD延长线上的两点,且DE =BF,求证AE=CF参考答案一、填空题1.平行四边形点拨:由一组对边平行且相等,即可判断2.平行四边形3.130°,50°,130°4.平行四边形点拨:由题意可得两组对边分别平行5.4个点拨:□ABCD,□ADFE,□EFCB,□EDFB6.3个□AECF,□APCQ,□AMCN二、判断题1.√ 2.×点拨:对角线不一定相等,但互相平分3.√ 4.√5.×点拨:对角线不平分一组对角,只是自己互相平分 6.√三、选择题1.B 2.D 3.A 4.D 5.C 6.C 7.B 8.B四、解答题1.解:四边形AECF是平行四边形点拨:由□ABCD知∠BCD=∠BAD,又AE平分∠BAD,CF平分∠BCD,故∠EAF=∠ECF,又∠AF ∥EC,故∠AEC+∠EAF=18O°,即∠AEC+∠ECF=18O°,所以AE∥CF,故四边形AECF是平行四边形.2.解:四边形ABCD是平行四边形由∠1=∠2得DC∥AB,所以∠D+∠DAB=18O°,又∠B=∠D,所以∠DAB+∠B=180°,所以AD∥BC,即四边形ABCD为平行四边形.3.解:是平行四边形点拨:AB∥CD,故∠ACD=∠CAB,又∠ECD=∠FAB,故∠ACD-∠ECD=∠CAB-∠FAB,即∠ACE =∠CAF,所以CE=AF,CE=AF,故AFCE是平行四边形.4.证明:∵BD⊥AD ∴∠BDA=90°∵∠DBC=90°,DC=AB,DB=DB∴△ADB≌△CBD ∴AD=BC∴四边形ABCD是平行四边形5.证明:∵NE,MD互相平分∴四边形MNDE为平行四边形∴MN DE又∵MD∥AB,NE∥AC ∴四边形MNBD、MNEC为平行四边形∵MN=BD,MN=CE ∴BD=DE=CE五、证明题1.证明:∵四边形ABCD为平行四边形∴AB DC ∴∠ABE=∠CDF在△ABE和△CDF中∴△ABE≌△CDF(SAS)∴AE=CF ∴∠AEB=∠CFD∴∠AED=∠BFC(等角的补角相等)∴AE∥CF2.证明:如图(3)所示∵四边形ABCD是平行四边形∴AD∥BC,AD=BC ∴∠1=∠2∵BD是直线∴∠1+∠3=180°,∠2+∠4=180°∴∠3=∠4∴△ADE≌△CBF ∴AE=CF。
五年级上学期平行四边形周长奥数题

五年级上学期平行四边形周长奥数题问题:求下列平行四边形的周长:1. 平行四边形ABCD,其中AB=6cm,AD=8cm,角D为直角。
2. 平行四边形EFGH,其中EF=10cm,GH=7cm,角E为直角。
3. 平行四边形IJKL,其中IJ=5cm,KL=12cm,角K为直角。
解答:1. 平行四边形ABCD的周长可以通过将所有边的长度相加得到。
根据题目给出的信息,AB=6cm,AD=8cm,角D为直角。
因此,BC和CD的长度与AB和AD相等。
所以BC=6cm,CD=8cm。
将所有边的长度相加:周长 = AB + BC + CD + DA = 6cm + 6cm + 8cm + 8cm = 28cm。
2. 平行四边形EFGH的周长可以通过将所有边的长度相加得到。
根据题目给出的信息,EF=10cm,GH=7cm,角E为直角。
同样地,FG和EH的长度与EF和GH相等。
所以FG=10cm,EH=7cm。
将所有边的长度相加:周长 = EF + FG + GH + HE = 10cm + 10cm +7cm + 7cm = 34cm。
3. 平行四边形IJKL的周长可以通过将所有边的长度相加得到。
根据题目给出的信息,IJ=5cm,KL=12cm,角K为直角。
同样地,JK和LI的长度与IJ和KL相等。
所以JK=5cm,LI=12cm。
将所有边的长度相加:周长 = IJ + JK + KL + LI = 5cm + 5cm + 12cm +12cm = 34cm。
结论:根据题目给出的信息,我们通过将平行四边形的边长相加,得到了每个平行四边形的周长。
平行四边形ABCD的周长为28cm,平行四边形EFGH的周长为34cm,平行四边形IJKL的周长为34cm。
(苏教版)五年级数学上册平行四边形面积的计算及答案(二).doc
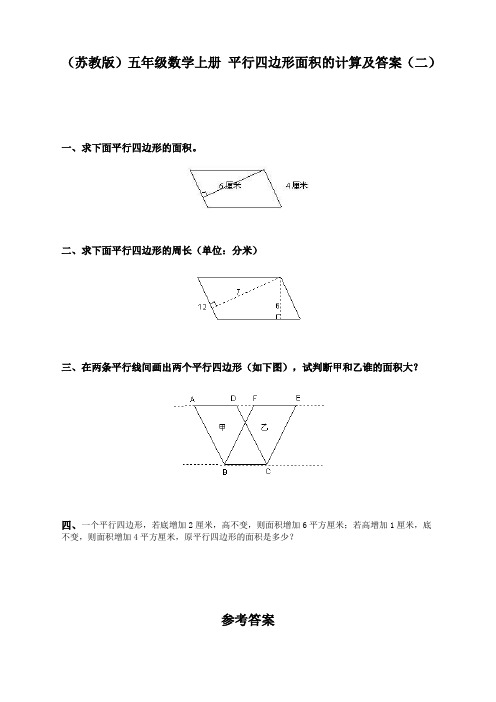
(苏教版)五年级数学上册平行四边形面积的计算及答案(二)一、求下面平行四边形的面积。
二、求下面平行四边形的周长(单位:分米)三、在两条平行线间画出两个平行四边形(如下图),试判断甲和乙谁的面积大?四、一个平行四边形,若底增加2厘米,高不变,则面积增加6平方厘米;若高增加1厘米,底不变,则面积增加4平方厘米,原平行四边形的面积是多少?参考答案一、解答:(平方厘米)答:这个平行四边形的面积是24平方厘米。
二、已知平行四边形的一组底和高分别是12分米和7分米,可以求出它的面积是(平方分米),通过“平行四边形面积=底×高”,可以逆推出:底=平行四边形面积÷高,已知面积是84平方分米,高是6分米,可以求出和6分米相对应的底,用分米),平行四边形对边相等,已知平行四边形相邻的两条边分别是12分米和14分米,就可以求出它的周长。
解答:(分米)。
答:这个平行四边形的周长是52分米。
三、平行四边形ABCD和BCEF是画在两条平行线之间,那么这两个平行四边形的高相等,因为两条平行线间的距离处处相等。
这两个平行四边形都是以BC为底,所以说这两个平行四边形的底也相等的,底和高都分别相等,那么底和高的乘积(面积)也相等,从两个面积相等的平行四边形中减去同样的一个三角形,剩下的面积也相等,所以甲和乙的面积是一样大的。
四、根据第一组条件,增加部分是一个底是2厘米,面积是6平方厘米的平行四边形,根据平行四边形的面积公式可以求出这个平行四边形的高,即求出原平行四边形的高。
根据第二组条件,,增加部分是一个高为1厘米,面积为4平方厘米的平行四边形,由此可以求出增加部分的底,即求出原平行四边形的底。
解答:(平方厘米)答:原平行四边形的面积是12平方厘米。
五年级数学 思维训练--平行四边形和三角形 - 答案

平行四边形和三角形(答案)一、我会填1、把一个平行四边形转化成一个长方形,它的面积与原来平行四边形的面积(相等),这个长方形的长等于原来平行四边形的(底),长方形的宽等于平行四边形的(高)。
长方形的面积等于长乘宽,所以平行四边形的面积等于(底)乘(高),用字母表示的公式为( S=ab )。
2、一个平行四边形的底为15分米,高为18分米,面积为( 270 )平方分米。
如果一个平行四边形底为12分米,面积为180平方分米,则高为( 15 )分米。
3、一个平行四边形的底扩大4倍,高缩小2倍,则面积(扩大2倍);如果他的底缩小3倍,高扩大3倍,则面积(不变)。
做错※=2ab求证方法:S1=ab S2=4a×b24、一个平行四边形的面积为64平方厘米,高为8厘米,底为( 8 )厘米。
5、填上“>”、“<”或“=”符号。
① A的面积(=)B的面积② A的面积(<)B的面积A 8B A B8③ A的面积(=)B的面积④空白的面积(=)阴影的面积5A B106、把一个长8厘米,宽4厘米的长方形框架拉成一个平行四边形,这时面积减少8平方厘米,平行四边形的面积为( 24 )平方厘米,这时平行四边形的高为( 3 )厘米。
二、认真选(每题只有唯一正确的答案,请将正确答案序号填入括号内)1、下面四个平行四边形,根据已知条件(①)的面积可以算出。
55 6 5 6 7 4.56①②③④2、将一个平行四边形拼成一个长方形,面积(③),周长(②);将一个平行四边形拉成一个长方形,面积(①),周长(③);不错※①变大②变小③不变④无法比较图形变化判断:3、能拼成一个平行四边形的两个三角形必须具备(②)。
①面积相等②形状相同③完全一样④任意两个均可4、周长相等的一个正方形,一个长方形,一个平行四边形,(①)面积最大。
①正方形②长方形③平行四边形④无法比较 a×a面积最大5、梯形ABCD中,三角形AOD和BOC的面积相比(③①三角形AOD ②三角形③同样④无法比较解:三角形ACD和BCD的面积:DC×h÷2 ,h一样,共同减去三角形OCD的面积。
平行四边形专题训练(含答案)
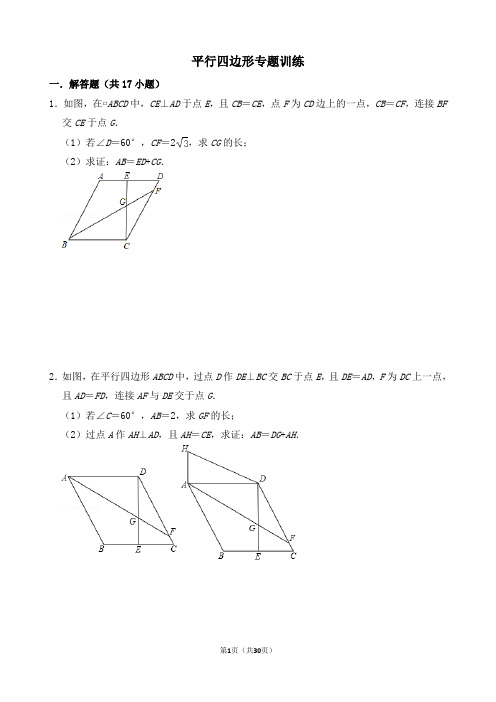
平行四边形专题训练一.解答题(共17小题)1.如图,在▱ABCD中,CE⊥AD于点E,且CB=CE,点F为CD边上的一点,CB=CF,连接BF 交CE于点G.(1)若∠D=60°,CF=2,求CG的长;(2)求证:AB=ED+CG.2.如图,在平行四边形ABCD中,过点D作DE⊥BC交BC于点E,且DE=AD,F为DC上一点,且AD=FD,连接AF与DE交于点G.(1)若∠C=60°,AB=2,求GF的长;(2)过点A作AH⊥AD,且AH=CE,求证:AB=DG+AH.3.如图,已知▱ABCD中,DE⊥BC于点E,DH⊥AB于点H,AF平分∠BAD,分别交DC、DE、DH 于点F、G、M,且DE=AD.(1)求证:△ADG≌△FDM.(2)猜想AB与DG+CE之间有何数量关系,并证明你的猜想.4.如图,已知▱ABCD中,AE平分∠BAD交DC于E,DF⊥BC于F,交AE于G,且AD=DF.过点D作DC的垂线,分别交AE、AB于点M、N.(1)若M为AG中点,且DM=2,求DE的长;(2)求证:AB=CF+DM.5.在平行四边形ABCD中,BE⊥AD,F为CD边上一点,满足BF=BC=BE.(1)如图1,若BC=12,CD=13,求DE的长;(2)如图2,过点G作DG∥BE交BF于点G.求证:BG=AE+DG.6.如图,在平行四边形ABCD中,∠ACB=45°,点E在对角线AC上,BE的延长线交CD于点F,交AD的延长线于点G.(1)若BE=,EC=,求△BCE的面积;(2)若∠ABE=2∠EBC,且AB=BE,求证:EC=DG.7.如图1,在平行四边形ABCD中,AE⊥BC于点E,E恰为BC的中点,tan B=2.(1)求证:AD=AE;(2)如图2,点P在线段BE上,作EF⊥DP于点F,连接AF,求证:;(3)请你在图3中画图探究:当P为射线EC上任意一点(P不与点E重合)时,作EF 垂直直线DP,垂足为点F,连接AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论.8.如图①,在平行四边形ABCD中,对角线AC、BD交于点O,AB=AC,AB⊥AC,过点A作AE⊥BD于点E.(1)若BC=6,求AE的长度;(2)如图②,点F是BD上一点,连接AF,过点A作AG⊥AF,且AG=AF,连接GC交AE 于点H,证明:GH=CH.9.在▱ABCD中,点E是BC的中点,过点A作AF⊥CD交直线CD于点F,连接AE、DE(1)如图1,当点F与点C重合时,AB=AC=2,求线段DE的长;(2)如图2,若∠EAF=30°,AE=CF,求证:BE=AF.10.已知,在▱ABCD中,AB⊥AC,点E是AC上一点,连换BE,延长BE交AD于点F,BE=CE.(1)如图1,当∠AEB=60°,BF=2时,求▱ABCD的面积;(2)如图2,点G是过点E且与BF垂直的直线上一点,连接GF,GC,FC,当GF=GC时,求证:AB=2EG.ABCD BD AD E CD AE BD F G为AF的中点,连接DG.(1)如图1,若DG=DF=1,BF=3,求CD的长;(2)如图2,连接BE,且BE=AD,∠AEB=90°,M、N分别为DG,BD上的点,且DM=BN,H为AB的中点,连接HM、HN,求证:∠MHN=∠AFB.12.在△BCF中,点D是边CF上的一点,过点D作AD∥BC,过点B作BA∥CD交AD于点A,点G是BC的中点,点E是线段AD上一点,且∠CDG=∠ABE=∠EBF.(1)若∠F=60°,∠C=45°,BC=2,请求出AB的长;(2)求证:CD=BF+DF.13.已知在平行四边形ABCD中,过点D作DE⊥BC于点E,且AD=DE.连接AC交DE于点F,作DG⊥AC于点G.(1)如图1,若,AF=,求DG的长;(2)如图2,作EM⊥AC于点M,连接DM,求证:AM﹣EM=2DG.14.已知,在平行四边形ABCD中,点E是AD边上一点,且DE=DC.(1)若点E与点A重合(如图1),点B沿MN翻折后的点B1恰好落在AC上,且∠MNB1=45°,AB1=1,AM=2,BM=.求:①∠AMN的度数;②BN的长;(2)如图2,若CE交对角线BD于F,∠ABD=2∠DBC,求证:BC=DF+AB.15.在平行四边形ABCD中,点E是AD边上的点,连接BE.(1)如图1,若BE平分∠ABC,BC=8,ED=3,求平行四边形ABCD的周长;(2)如图2,点F是平行四边形外一点,FB=CD.连接BF、CF,CF与BE相交于点G,若∠FBE+∠ABC=180°,点G是CF的中点,求证:2BG+ED=BC.16.如图,在平行四边形ABCD中,点O是对角线AC的中点,点E是BC上一点,且AB=AE,连接EO并延长交AD于点F.过点B作AE的垂线,垂足为H,交AC于点G.(1)若AH=3,HE=1,求△ABE的面积;(2)若∠ACB=45°,求证:DF=CG.17.如图,在▱ABCD中,∠ACB=45°,点E在对角线AC上,BE=BA,BF⊥AC于点F,BF的延长线交AD于点G.点H在BC的延长线上,且CH=AG,连接EH.(1)若BC=12,AB=13,求AF的长;(2)求证:EB=EH.18.如图,平行四边形ABCD中,过点C作CE⊥AB于点E,点F是AD上一点,连结BF、CF,交CE于点G。
数学五年级上册平行四边形的面积解决问题练习题(含答案)

6.1平行四边形的面积1.一个平行四边形果园,底长150米,高40米.如果这个果园一共种了1000棵果树,那么每棵果树平均占地多少平方米?2.一块平行四边形形稻田,底是90米,高60米,如果每平方米施肥0.2千克,这块稻田需施肥多少千克?3.一个平行四边形的面积是90平方厘米.它的底是15厘米,高是多少厘米?(列方程解)4.有一块平行四边形的菜地,底和高都是12米,它的面积是多少平方米?如果每平方米种10颗白菜,那么这块菜地一共可以种多少棵白菜?5.李大伯家有一块平行四边形的稻田,底是110m,是高的0.25倍.他今年计划每公顷稻田需施肥45kg,那么这块稻田共要施肥多少千克?6.有一块平行四边形的瓜地,底是6.8m,是高的2倍,如果每平方米栽瓜苗5棵,大约可栽多少棵瓜苗?7.如图,红星广告公司要将一块平行四边形的铁板的一面刷上油漆,如果每千克油漆能刷1.2平方米,这块铁板共需多少千克油漆?8.(如图)请回忆老师引导你推导平行四边形面积公式进的情境,给(1)、(2)填空;(3)计算.(1)以将平行四边形转化为长方形来推导平行四边形的面积公式.把平行四边形转化成长方形采用的方法是:(2)观察转化前的平行四边形与转化后的长方形,你发现了什么?(请写在下面的横线上,至少写三条)(3)计算上面平行四边形的面积.(先动手在图中量出计算时需要的数据,再算出它的面积)9.自己测量需要的数据,并求出图中草地的总面积.(测量数据以厘米为单位四舍五入到整数)10.张大爷有一块平行四边形的地,底长175米,高80米,今年共收绿豆2856千克,平均每公顷收绿豆多少千克?这块平行四边形的面积是多少平方米?合多少公顷呢?11.一块底长1.5米,高1.2米的平行四边形铁板.现在要油漆它的两面,每平方米用油漆0.3千克,一共要油漆多少千克?12.学校要制作一块平行四边形宣传牌,底长4米,高2米,如果广告公司制作广告牌每平方米收费30元,那么学校应支付给这个广告公司多少元?13.一块平行四边形的地,底边长250m,高84m,在这块地里种小麦,共收小麦14.7吨,平均每公顷收小麦多少吨?14.在一块底50m,高30m的平行四边形地里栽桃树,平均每6m2栽一棵,这块地能栽多少棵桃树?如果每棵收4.5kg桃子,这块土地共收桃子多少千克?15.有一块平行四边形的菜地,底长48米,高是底的一半,这块地的面积是多少平方米?16.画出下面图形的高,并量出有用的数据标在图上,再计算图形的面积.17.有一块平行四边形的麦田,底225米,高60米,共收小麦10.8吨,这块麦田有多少公顷?平均每公顷收小麦多少吨?18.一块平行四边形的花生地,底长45米,高18米,每平方米种花生6棵,每棵花生的产量约是0.8千克,这块花生地共收花生多少千克?19.一块平行四边形的地共收油菜籽3400kg,它的底长250m,高68m.平均每公顷收油菜籽多少千克?20.某乡镇中学开垦了一块平行四边形荒地种油菜,这块平行四边形地的底是32米,高是35米.如果平均每平方米收油菜1.5千克.这块地一共收油菜多少千克?21.如图,一块长方形草地,长方形的长是16米,宽是10米,中间铺了一条石子路。
苏教版数学五年级上册:平行四边形面积的计算及答案(二)

苏教版数学五年级上册平行四边形面积的计算及答案(二)一、求下面平行四边形的面积。
二、求下面平行四边形的周长(单位:分米)三、在两条平行线间画出两个平行四边形(如下图),试判断甲和乙谁的面积大?四、一个平行四边形,若底增加2厘米,高不变,则面积增加6平方厘米;若高增加1厘米,底不变,则面积增加4平方厘米,原平行四边形的面积是多少?参考答案一、解答:(平方厘米)答:这个平行四边形的面积是24平方厘米。
二、已知平行四边形的一组底和高分别是12分米和7分米,可以求出它的面积是(平方分米),通过“平行四边形面积=底×高”,可以逆推出:底=平行四边形面积÷高,已知面积是84平方分米,高是6分米,可以求出和6分米相对应的底,用分米),平行四边形对边相等,已知平行四边形相邻的两条边分别是12分米和14分米,就可以求出它的周长。
解答:(分米)。
答:这个平行四边形的周长是52分米。
三、平行四边形ABCD和BCEF是画在两条平行线之间,那么这两个平行四边形的高相等,因为两条平行线间的距离处处相等。
这两个平行四边形都是以BC为底,所以说这两个平行四边形的底也相等的,底和高都分别相等,那么底和高的乘积(面积)也相等,从两个面积相等的平行四边形中减去同样的一个三角形,剩下的面积也相等,所以甲和乙的面积是一样大的。
四、根据第一组条件,增加部分是一个底是2厘米,面积是6平方厘米的平行四边形,根据平行四边形的面积公式可以求出这个平行四边形的高,即求出原平行四边形的高。
根据第二组条件,,增加部分是一个高为1厘米,面积为4平方厘米的平行四边形,由此可以求出增加部分的底,即求出原平行四边形的底。
解答:(平方厘米)答:原平行四边形的面积是12平方厘米。
奥数-平行四边形-特殊2学

⑽如右下图,以正方形ABCD的一边向正方形外作等边三角形ABE,BD与EC交于F,则 等于()
A. B. C. D.
【例 3】 如图,将矩形 沿 翻折,使点 落在点 处,连接 、 ,过点 作 ,垂足为 .
特殊平行四边形
1矩形
①定义:
有一个角是直角的平行四边形叫做矩形.
②性质:
是矩形 ;
是矩形
③性质推论:
.
④判定:
是矩形;
是矩形.
2菱形
①定义:
有一组邻边相等的平行四边形叫做菱形.
②性质:
是菱形 ;
是菱形
③判定:
是菱形;
是菱形.
3正方形
①定义:
有一个角是直角且有一组邻边相等的四边形是正方形.
②性质:
具有菱形、矩形的所有性质.
A.有一组对边平行且相等,有一个角是直角
B.有一组对边平行,另一组对边相等,两条对角线互相垂直
C.两组对边分别相等,且有一组相邻的角相等
D.一组对边相等,一组相邻的边相等,一组对角相等
⑻如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转 ,则这两个正方形重叠部分的面积是.
求证: .
【例 13】 如图,矩形 中, , ,若将该矩形折叠,使点 与点 重合,求折痕 的长.
【例 14】如图,折叠长方形的一边 ,使点 落在 边的点 处,如果 , ,求 的长.
习题1.如图,四边形 是正方形, , ,那么 __________.
习题2. 如图,已知正方形 中,点 在 上,并且 , 垂直平分 分别交 、 、 于 、 、 ,若 ,则 __________.
