第二章 静电场和稳恒磁场
静电场与稳恒磁场的异同

静电场与稳恒磁场的异同
静电场和稳恒磁场是两种不同的物理场,它们具有一些相似之处,但也存在一些显著的差异。
相似之处:
1.无源性:静电场和稳恒磁场都是无源场,它们不依赖于电荷或电流的变化而产生。
差异之处:
1.作用粒子不同:静电场与电荷粒子(例如电子或质子)相互作用,而稳恒磁场则与运动带电粒子(电流)相互作用。
2.相关物理量不同:静电场与电荷的位置和电荷量有关,通常用电场强度(单位电荷受到的力)来描述;而稳恒磁场与电流的位置和大小有关,通常用磁感应强度(单位电流受到的力)来描述。
3.引力与斥力:静电场中的电荷之间可以相互吸引或排斥,根据电荷的正负性质决定;而稳恒磁场中的磁荷(即电流)之间不存在引力或斥力的作用。
4.能量流动方式:静电场中的能量流动是通过电磁辐射进行的,即光的形式;而稳恒磁场中的能量流动主要是通过电流在导体中的传输进行的。
总体而言,静电场和稳恒磁场在物理特性和相互作用方面存在一些重要的区别,但它们都是电磁场的重要组成部分,共同构成了电磁学的基础。
1/ 1。
电动力学-选择题填空题判断题问答题复习

《电动力学1》随教材复习题目一、章节容:第0章 矢量分析第一章 电磁现象的普遍规律第二章 静电场第三章 静磁场第四章 电磁波的传播第五章 电磁波的辐射二、题型1. 选择题,填空题,判断题、问答题2. 计算题(见教材例题)2018年5月第0章 矢量分析一、选择题0.1设222)()()(z z y y x x r '-+'-+'-=为源点到场点的距离,r 的方向规定为从源点指向场点,则有 ( B )A. 0=∇rB. r r r ∇=C. 0=∇'rD. r r r'∇= 0.2位置矢量r 的散度等于 (B )A .0 B.3 C.r1 D. r 0.3位置矢量r 的旋度等于 (A )A.0B.3C.r rD.3rr 0.4位置矢量大小r 的梯度等于 ( C )A.0 B .r 1 C. r r D.3rr 0.5r 1∇=? ( B ) A. 0 B.3r r - C.r r D .r 0.6⨯∇3r r =? (A ) A. 0 B .r r C.r D.r 1 0.7⋅∇3rr =?(其中r ≠0) ( A ) A.0 B.1 C.r D.r1 二、填空题0.1位置矢量r 的散度等于( 3 )。
0.2位置矢量r 的旋度等于( 0 )。
0.3位置矢量大小r r r 。
0.4无旋矢量场可以引入(标)势来处理,无源矢量场可以引入(矢)势来处理。
0.5(无旋)矢量场可以引入标势来处理,(无源)矢量场可以引入矢势来处理。
三、判断题0.1标量场的梯度必为无旋场。
(√)0.2矢量场的旋度不一定是无源场。
(×) 0.3无旋场必可表示为标量场的梯度。
(√) 0.4无源场必可表示为另一矢量的旋度。
(√)第一章 电磁现象的普遍规律一、选择题1.1对于感应电场下面哪一个说确 ( D )A 感应电场的旋度为零B 感应电场散度不等于零C 感应电场为无源无旋场D 感应电场由变化磁场激发1.2从麦克斯韦方程组可知变化电场是 ( B )A 有源无旋场B 有源有旋场C 无源无旋场D 无源有旋场1.3从麦克斯韦方程组可知变化磁场是 ( D) A 有源无旋场 B 有源有旋场 C 无源无旋场 D 无源有旋场。
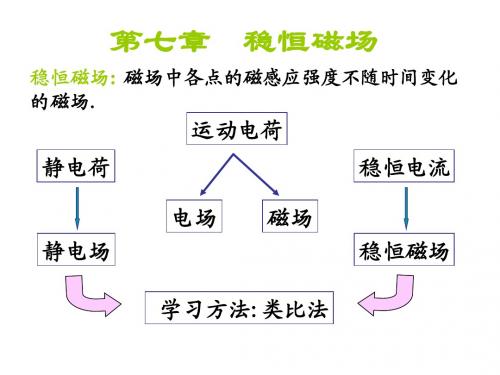
静电场与稳恒磁场对比教学文稿

R
以无限远作 为电势零点
稳恒磁场
.30.
均匀带电无限长圆柱面的电场 无限长均匀通电直圆柱面的磁场
E 2 0r
(r R)
0
(r R)
均匀带电无限长圆柱体的电场
E
2 0r r
2 0 R 2
(r R) (r R)
均匀带电圆环轴线上的电场
E
40
xQ x2 R2
32
B
0 2
I r
(r R)
0 (r R)
L
i
表二 作用力
1.点(元)受力
2.电荷(电流)受力
静电场
f qE
f dqE
(Q)Biblioteka 稳恒磁场 类比总结fqB
f Idl B
(I)
表三、 场量计算
E
1.点电荷(电流元)场
的叠加
•方法
d
Q
q
r
dE
dq
4π0r2
rˆ
•典型题目
x
B
类比总结
Idl
r
I dB04Idπlr2rˆ
I
x
2.某些对称性
B Fm
q0
高斯定理 S E dS10 i qi内
静电场的环路定理 Edl 0
高斯定理
q0
BdS0
S
磁场的安培环路定理 Bdl0
v
Ii内
L
静止电荷的电场
E
Q
40r2
rˆ
L
i
运动电荷产生的磁场 B0qvrˆ
4r2
均匀带电无限长直线的电场 无限长直线电流的磁场
E
2 0r
B 0I 2r
电动力学——精选推荐

电动⼒学电动⼒学第⼀章静电场⼀、考核知识点1、真空与介质中静电场场⽅程,场的性质、物理特征。
2、电场的边值关系、在两种介质分界⾯上电场的跃变性质。
3、由场⽅程、边值关系,通过电荷分布确定场分布及极化电荷的分布。
4、静电场的势描述。
由势分布确定场分布、荷分布;通过静电势的定解问题,确定静电势的分布、场分布及介质极化性质的讨论。
⼆、考核要求(⼀)、场⽅程、场的确定1、场⽅程,场的边值关系,体、⾯极化电荷密度的确定式等规律的推导。
2、识记:(1)、真空与介质静电场⽅程。
(2)、电场的边值关系。
(3)、体、⾯极化电荷密度的确定式。
3、领会与理解:(1)、静电场的物理特征。
12(2)、P D E ,,与电荷的关系,⼒线分布的区别与联系。
(3)、在介质分界⾯上场的跃变性质。
4、应⽤:通过对称性分析,运⽤静电场的⾼斯定理确定场,讨论介质的极化,正确地由电荷分布画出场的⼒线分布。
(⼆)、静电势1、静电势⽅程、边值关系的推导。
2、识记:静电势的积分表述、势⽅程、势的边值关系、势的边界条件、唯⼀性定理。
3、领会与理解:势的边值关系与边界条件,荷、势与场的关系,解的维数的确定,电像法的指导思想与像电荷的确定。
4、应⽤:求解静电势定解问题的⽅法(分离变量法、电像法)的掌握及应⽤,求解的准确性,场的特征分析及由势对介质极化问题的讨论。
第⼆章稳恒磁场⼀、考核知识点1、电荷守恒定律。
2、稳恒磁场场⽅程,场的性质特点。
3、由场⽅程,通过流分布确定场分布与磁化流。
4、磁场的边值关系。
5、稳恒磁场的⽮势。
6、由磁标势法确定场。
3⼆、考试要求1、规律的推导:真空、介质中稳恒磁场场⽅程,电荷守恒定律的微分表述,体、⾯磁化电流密度的确定式,磁场的边值关系,⽮势⽅程及其积分解,磁标势⽅程和边值关系等。
2、识记:电荷守恒定律,稳恒磁场场⽅程,体、⾯磁化电流密度的确定式,⽮势引⼊的定义式,磁标势引⼊条件,磁场的边值关系,0=f α情况磁标势的边值关系。
麦克斯韦方程组的推导及说明

13-6麦克斯韦方程组关于静电场和稳恒磁场的基本规律,可总结归纳成以下四条基本定理:静电场的高斯定理:静电场的环路定理:稳恒磁场的高斯定理:磁场的安培环路定理:上述这些定理都是孤立地给出了静电场和稳恒磁场的规律,对变化电场和变化磁场并不适用。
麦克斯韦在稳恒场理论的基础上,提出了涡旋电场和位移电流的概念:1.麦克斯韦提出的涡旋电场的概念,揭示出变化的磁场可以在空间激发电场,并通过法拉第电磁感应定律得出了二者的关系,即上式表明,任何随时间而变化的磁场,都是和涡旋电场联系在一起的。
2.麦克斯韦提出的位移电流的概念,揭示出变化的电场可以在空间激发磁场,并通过全电流概念的引入,得到了一般形式下的安培环路定理在真空或介质中的表示形式,即上式表明,任何随时间而变化的电场,都是和磁场联系在一起的。
综合上述两点可知,变化的电场和变化的磁场彼此不是孤立的,它们永远密切地联系在一起,相互激发,组成一个统一的电磁场的整体。
这就是麦克斯韦电磁场理论的基本概念。
在麦克斯韦电磁场理论中,自由电荷可激发电场,变化磁场也可激发电场,则在一般情况下,空间任一点的电场强度应该表示为又由于,稳恒电流可激发磁场,变化电场也可激发磁场,则一般情况下,空间任一点的磁感强度应该表示为因此,在一般情况下,电磁场的基本规律中,应该既包含稳恒电、磁场的规律,如方程组(1),也包含变化电磁场的规律,根据麦克斯韦提出的涡旋电场和位移电流的概念,变化的磁场可以在空间激发变化的涡旋电场,而变化的电场也可以在空间激发变化的涡旋磁场。
因此,电磁场可以在没有自由电荷和传导电流的空间单独存在。
变化电磁场的规律是:1.电场的高斯定理在没有自由电荷的空间,由变化磁场激发的涡旋电场的电场线是一系列的闭合曲线。
通过场中任何封闭曲面的电位移通量等于零,故有:2.电场的环路定理由本节公式(2)已知,涡旋电场是非保守场,满足的环路定理是3.磁场的高斯定理变化的电场产生的磁场和传导电流产生的磁场相同,都是涡旋状的场,磁感线是闭合线。
第二章场和波

二. 描述电场的物理量 1. 电场对电荷的力作用
电场强度 E 是反映电场的力性质的物理量。
实验表明, 在电场中的固定点所放电荷受到的电场
力
F
的大小与所放电荷的电量 q成正比。两者的比值
F/q是一常量, 与所放电荷的电量无关。这个比值反映
的是电场自身的属性。 放入电场中某点的电荷所受的电场力跟这电荷的 电量的比值叫作该点的电场强度, 简称场强。用符号E 表示
q1q0 F1 k 2 b
且
,
q2 q0 F2 k 2 b
2
• q0
b
q1
b a
q2
F1 F2
2
•
•
a 2 (b ) 合力的大小 q1q0 4 F 2 F cos 2k 2 b b 2 2 1/ 2 2 9 109 5 1011 109 ( [ 5 102) (4 102) ] 7 2 . 16 10 N 方向 2 2 (5 10 )
解 在距点电荷r 处,放置电量很小的正电荷(称 为检验电荷),q0 所受静电场力为 qq0 F=k 2 r 又据电强度的定义得该点场强为 q F E= =k 2 r q0 可见点电荷电场中某点的场强与该点到点电荷的距离 平方成反比,所有与点电荷距离相同点的场强相同。
且q>0,电场线是发散的;q<0,电场线指向点电荷。
指南针。
地球地理上的南北极 与磁针的南北极不重合。
地磁场 的北极 地理上的 南极
二. 运动电荷的磁现象
虽然人们很早就发现了电和磁,但19世纪初科学界 仍普遍认为电和磁是两种独立的作用。丹麦物理学家 奥斯特接受德国哲学家康德和谢林关于自然力统一的 哲学思想,坚信电与磁之间一定有某种联系。 1820 年 奥斯特终于发现了电流的磁效应,宣布当电流通过导 线时,引起导线旁的磁针偏转。 法国物理学家安培进一步努力于同一年建立了电
稳恒磁场
安培定律
一、安培力
安培力:电流元在磁场中受到的磁力. 安培力:电流元在磁场中受到的磁力. 一个自由电子受的洛仑兹力为: 一个自由电子受的洛仑兹力为
f 洛 = qv × B = −ev × B
电流元所受磁力: 电流元所受磁力
方向: 方向:×
v
dl
B
I
设截面积为S,单位体积电子数为 设截面积为 单位体积电子数为n 单位体积电子数为
1 2 m = NISn = NI πR n 2
方向:与 B 成600夹角. 夹角. 方向: (2)此时线圈所受力矩的大小为: )此时线圈所受力矩的大小为:
)60
0
B
3 2 πR M = mB sin60 = NIB 4 方向: m× B 方向: ×
0
n
即垂直于 B向上,从上往下俯视,线圈是逆时针转动。 向上,从上往下俯视,线圈是逆时针转动。
1T = 1N ⋅ S ⋅ m−1 ⋅ C−1
磁通量
一、磁力(感)线 磁力( 直线电流的磁力线
磁场的高斯定理
圆电流的磁力线
通电螺线管的磁力线
I
I
I
I
通量(通过一定面积的磁力线数目) 二、磁通量(通过一定面积的磁力线数目)
v v dΦ = B ⋅ dS
v v Φ = ∫s B ⋅ dS
单位
1Wb= 1T ⋅ m
I
该式对任意形状的线圈都适用. 该式对任意形状的线圈都适用.
例1如图,求圆心O点的 B . 如图,求圆心 点的 I O
• × R
B=
µ0 I
4R
I
O• •
R
B=
µ0 I
8R
R
• •O
大学物理电磁学总结

大学物理电磁学总结电磁学部分总结静电场部分第一部分:静电场的基本性质和规律电场是物质的一种存在形态,它同实物一样也具有能量、动量、质量等属性。
静电场的物质特性的外在表现是:(1)电场对位于其中的任何带电体都有电场力的作用(2)带电体在电场中运动, 电场力要作功——电场具有能量1、描述静电场性质的基本物理量是场强和电势,掌握定义及二者间的关系。
电场强度 E =q 0∞ W a 电势 U a ==E ⋅d rq 0a2、反映静电场基本性质的两条定理是高斯定理和环路定理Φe =E ⋅d S =ε0∑qL E ⋅d r =0要掌握各个定理的内容,所揭示的静电场的性质,明确定理中各个物理量的含义及影响各个量的因素。
重点是高斯定理的理解和应用。
3、应用(1)、电场强度的计算1q E =r 02a) 、由点电荷场强公式 4πεr 及场强叠加原理 E = ∑ E 计i 0算场强一、离散分布的点电荷系的场强1q i E =∑E i =∑r 2i 0i i 4πεr 0i二、连续分布带电体的场强 d q E =⎰d E =⎰r 204πε0r其中,重点掌握电荷呈线分布的带电体问题b) 、由静电场中的高斯定理计算场源分布具有高度对称性的带电体的场强分布一般诸如球对称分布、轴对称分布和面对称分布,步骤及例题详见课堂笔记。
还有可能结合电势的计算一起进行。
c) 、由场强和电势梯度之间的关系来计算场强(适用于电势容易计算或电势分布已知的情形),掌握作业及课堂练习的类型即可。
(2)、电通量的计算a) 、均匀电场中S 与电场强度方向垂直b) 、均匀电场,S 法线方向与电场强度方向成θ角E =-gradU =-∇U∂U ∂U ∂U =-(i +j +k )∂x ∂y ∂zc) 、由高斯定理求某些电通量(3)、电势的计算a) 、场强积分法(定义法)——计算U P =⎰E ⋅d rb) 、电势叠加法——q i ⎰电势叠加原理计算⎰∑U i =∑4πεr⎰0iU =⎰dq ⎰dU =⎰⎰⎰4πε0r ⎰第二部分:静电场中的导体和电介质一、导体的静电平衡状态和条件导体内部和表面都没有电荷作宏观定向运动的状态称为静电平衡状态。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ρ r (r ′) ε0
案 网
co
r r r dv r r | r − r ′ |3
m
电动力学习题解答参考
第二章 静电场和稳恒电磁场
r r 3ql cosθer − qle z = 4πε 0 r3 1
4.在原点有一个 p = pe x 的偶极子,另在 x=0,y=0,z= l 处偶极矩为 − p 的偶极子,求两个 偶极子在 r >> l 处产生的电势。 解:原点处的偶极子在场点产生的电势为
1
co
m
p cos α ,其中 cos α = cos ϕ sin θ 4πε 0 r 2
1
电动力学习题解答参考
第二章 静电场和稳恒电磁场
2
6.在以 O 为中心,R 为半径的球面上,已知电势分布为 φ (r = R, θ ) = a (1 + cos θ ) ,其中 a 为已知正常量,θ为球坐标的极角。试求球外的电势分布。 解:要求的定解问题为 ∇
r
球壳外边界 E | r = R = 3 cosθE 0 er 因为球壳内部电场强度为 0,作用在球壳上电荷的电场为 E =
da
(r > R)
课
后
答
两个(相等的)半球壳,为了使这两个半球壳不至于分开,需要加多大的外力? 解:易知球壳内部电场强度为 0,球外电势满足的定解问题为:
E0 R 3 cosθ r2
m =1
后
r = ∫∫ σ 0 cosθ ⋅ r r 2 sin θdθdφ
da
-3-
r =a
答
解:电偶极矩 p =
r
∫ σr dS
v
w.
案 网
co
代入边界条件解得:
m
根据题目条件,场具有轴对称性,那么 φ 的通解为 φ =
∑ (a r
∞
n
+ bn / r n +1 ) Pn (cosθ )
电动力学习题解答参考 它们还受如下边界条件的限制:
-5-
后
答
那么 φ 2 =
球壳上电荷分步 σ = ε 0 (
ww
19. 一半径为 a 的无限长接地圆柱形导体,一线电荷密度为 λ 的无限长直线放在圆柱外且 与圆柱轴线平行,带电直线与圆柱轴线的距离为 d,求圆柱外任一点的电势。 解:如图,选择 A 点的电势为 0,则直线在场点 Q 产生的电势为
w.
=
2
φ =0
(r > R)
φ | r = R = a(1 + cosθ ) 2
φ |∞ = 0
n
n =0
φ=
A3 A0 A1 4R 2R 2 + 2 P1 (cosθ ) + 3 P2 (cosθ ) ,其中 A0 = a , A1 = 2 R 2 a , A0 = a r 3 3 r r
7.已知半径为 R 的球壳表面电荷面密度为 σ = σ 0 cos θ ,求电偶极矩及球外电势。
E0 R 3 E0 R 3 r r cos θ ) + ( − sin θ + sin θ )eθ e E r 0 3 3 r r
-4-
co
r
ε − ε0 R2 r r E 0 (cosθer + sin θeθ ) 2 ε + ε0 r
r 3 cosθE 0 er 2
m
电动力学习题解答参考 那么电场作用在一个半球壳上的力 F = 考虑到对称性
m =1
代入边界条件解得:
φ=
E a2 λ a ln − E 0 ρ cosθ + 0 cosθ 2πε 0 ρ ρ
kh
2
φ =0
0
−
∫ε
φ |r =a = C φ |∞ = − E 0 r cosθ
答
w.
案 网
φ2 = −
r p cos α ′ ,其中 cos α ′ = cos ϕ sin θ ′ = cos ϕ sin θ 2 4πε 0 (r − l cosθ ) r − l cosθ
ww
3.一对电量相等的正负电荷相距为 l ,求该系统在远处的电场强度。 解:具有偶极矩 p z = ql 的电偶极子产生的电势为 φ =
w.
1
r er r ( p ⋅ ∇) 2 =− 4πε 0 r
kh
v r ql cosθ ) 4πε 0 r 2
1
r r r 1 p ⋅ er 解: E = −∇φ = −∇( ) 4πε 0 r 2
1 1 q+Q q Rq / a + − 2 2 1/ 2 2 2 4πε 0 R 4πε 0 [a + r − 2ar cosθ ] 4πε 0 [b + r − 2br cosθ ]1 / 2 1
∂φ 2 ∂φ1 ) |r =R − ∂r ∂r
ϕ1 = −
λ ( ρ 2 + d 2 − 2 ρd cos θ )1 / 2 ln 2πε 0 d −a
球外电势为 φ =
w.
=
kh
r r p⋅r 4πε 0 r 3
1
=
课
4πR 3 r σ 0 ez 3
R 3 σ 0 cosθ 3ε 0 r2
r
ww
8.将一个半径为 R,介电常数为ε的无限长圆柱形均匀电介质放入均匀外电场 E 0 中,圆 柱轴线与 E 0 垂直。试求介质极化电荷所产生的电势和电场强度。 解:令柱外电势为 φ1 ,柱内电势为 φ 2 ,由第 5 题容易知道它们的通解分别为:
电动力学习题解答参考
第二章 静电场和稳恒电磁场
r 1.对电场强度的表示式 E =
1 4πε 0
∫
ρ (r ′)(r − r ′)
r r 3 r − r′
r
r
r
V
dV ′
进行直接微分。证明
r r ρ ∇ × E = 0及 ∇ ⋅ E =
ε0
r 证明: ∇ × E =
1 4πε 0
=0
∫v ρ (r ′)∇ × r r
∇⋅∫
v
r r (r − r ′) dv | r − r ′ |3
r ∇⋅E =
1 4πε 0 1
ρ (r ′)(r − r ′)
v
r r r (r − r ′) = ρ (r ′)∇ ⋅ r r 3 dv 4πε 0 ∫v | r − r′| =
r r er er r v =− [ p × ∇ × 2 + ( p ⋅ ∇) 2 ] 4πε 0 r r 1
柱外、柱内电场强度为: E1 = −∇φ1 =
r
r ε − ε0 E 2 = −∇φ 2 = − E0 ε + ε0
12. 半径为 R 的导体球壳,放入均匀电场 E 0 中。设想这个球壳被垂直于 E 0 的平面分割成
r
w.
E0 R 3 cosθ ) r2
r
案 网
∇ 2φ = 0
φ |r =R = C
m
r′ d λ 2 2 1/ 2 ln ,其中 r = ( ρ + d − 2 ρd cos θ ) 2πε 0 r a
B A
kh
球壳本身带电,其上电势并不为 0,球内电势 φ 2 | r = R = φ1 | r = R =
1 q+Q q( R − a cosθ ) Rq / a(b cosθ − R ) − 2 [ 2 − 2 2 3/ 2 4π R [a + R − 2aR cosθ ] [b + R 2 − 2bR cosθ ]3 / 2
w.
q+Q 4πε 0 r
1
案 网
co
q+Q 4πε 0 R
1
壳上的电荷分布。
m
电动力学习题解答参考
第二章 静电场和稳恒电磁场
a2 假定在 B 点有一电象,B 点距离轴线 ,线电荷密度为 − λ ,它在场点产生的电势为 d
ϕ2 =
λ [ ρ 2 + (a 2 / d ) 2 − 2 ρ (a 2 / d ) cos θ ]1 / 2 , ln 2πε 0 a − a2 / d
容易得出在圆柱面上 ϕ 2 + ϕ 2 为 0,满足原有的边界条件,可以用该电象替代圆柱的影响。 那么圆柱外任一点的电势为 ϕ =
度。 解:磁偶极矩 m =
课
磁感应强度 B = −
r
µ0 r r (m ⋅ ∇) 3 4π r
=
ww
w.
-6-
kh
3r
3
µ 0α 0 a 3
r r (2 cos θer + sin θeθ )
r
5.半径为 a 的无限长导体圆柱,带线电荷密度为λ,置于均匀电场 E 0 中,电场和圆柱体轴 线垂直,求柱外电势。
解:要求的定解问题为 ∇
w.
r =a
ww
根据题目条件,场与 z 无关,那么 φ 的通解为:
∞
φ = a 0 + b0 ln r + ∑ [(a m r m + bm / r m ) cos mθ + (c m r m + d m / r m ) sin mθ ]
π /2
第二章 静电场和稳恒电磁场
r
0< < / 2
Eσds ∫ θ π r 3 cos 2 θE 0 er 3ε 0 cosθE 0 R 2πR sin θdθ 2
r
F=
∫
0
9 = πε 0 E 02 R 2 4
14.有一个半径为 R 的薄导体球壳,带电量为 Q。壳内距中心为 a (< R ) 处有一点电荷 q.求
第二章 静电场和稳恒电磁场
