距离保护整定计算例题
第5章 保护计算举例
第5章 保护计算举例5.1 距离保护计算举例以215、216断路器为例整定计算()Ω=⨯=⨯=97.2926.3585.085.01Z Z dz Ⅰ0=dz tⅡdz Z ，Ⅱ段与相邻211断路器Ⅰ段配合。
()Ω=⨯=⋅3.525.6185.0211Ⅰdz Zmin 211⋅⋅⋅⋅+=fz dz k dz dz K Z K Z Z ⅠⅠⅡ 85.0=k K分支系数：9727.1163.0/6128.0min =+=⋅fz K系统Ⅰ最小，系统Ⅱ最大，故B —C 单回路分支系数()16.7142.0/085.12min =+⨯=⋅fz K 。
所以：min 211⋅⋅⋅⋅+=fz dz k dz dz K Z K Z Z ⅠⅠⅡ9727.13.5285.097.29⨯⨯+=()Ω=5.112灵敏度校验：75.397.29/5.112==lm K ＞1.25动作时间：5.0=Ⅱdz t （S ）ⅢdzZ ，Ⅲ段与相邻线路211断路器Ⅱ段配合。
ⅡⅢ211min 18.085.0⋅⋅⨯+=dz fz dz Z K Z Z=4575.459127.18.026.3585.0⨯⨯+⨯()Ω=99()39.397.2999=÷=近lm K ＞1.5()()35.036.3616.797.29/99=⨯+=远lm K ＜1.2因为不满足远后备灵敏度的要求，所以按躲开线路流过的最大负荷电流来整定。
()Ω==428min fh dz Z Z (最小负荷阻抗)()()42.136.3616.797.29/428=⨯+=远lm K ＞1.2()3.1497.29428=÷=近lm K ＞1.5动作时间：3=Ⅲdz t (S)距离保护计算结果见后表4--1。
5.2 相差高频保护整定计算举例5.2.1启动元件(以210、211断路器为例进行计算整定)。
()120/10cos 2423/5002.05.23max 2⨯⨯⨯⨯=⋅=⋅φbp k dzj I K I058.0120/14002.05.2=⨯⨯= (A) 4.0120150127.05.2/=÷⨯⨯=⋅⋅=l zc k dzj n l I K I (A)相差启动元件可以整定在1A 左右。
距离保护整定计算例题
精心整理距离保护整定计算例题题目：系统参数如图，保护1配置相间距离保护，试对其距离I段、II段、III段进行整定，并校验距离II段、III段的灵敏度。
取z1=0.4?/km，线路阻抗角为75?，Kss=1.5，返回系数Kre=1.2，III段的可靠系数Krel=1.2。
要求II段灵敏度?1.3~1.5，III段近后备?1.5，远后备?1.2。
解：1、计算各元件参数，并作等值电路ZMN=z1lMN=0.4?30=12.00?ZNP=z1lNP=0.4?60=24.00?ZT=100%K U?TTSU2=1005.10?5.311152=44.08?2、整定距离I段Z Iset1=K IrelZMN=0.85?12=10.20?t I1=0sZ Iset3=K IrelZNP=0.85?24=20.40?t I3=0s3、整定距离II1)整定阻抗计算(1)与相邻线路I段配合Z II II I?20.40)=43.38?(2)Z II?44.08)=72.27?取Z II?2)K IIsen=MNsetIIZZ1=43.38/12=3.62(?1.5)，满足规程要求3）时限t II1=0.5s4、整定距离III段并校验灵敏度1)最小负荷阻抗ZLminZLmin=LmanLIU min=LmanNIU9.0=35.3/1109.0⨯=163.31?Cos?L =0.866，?L=30?2）负荷阻抗角方向的动作阻抗Zact（30?）Zact（30?）=ressrelLKKKZ min=2.15.12.131.163⨯⨯=75.61?3）整定阻抗Z IIIset1，?set=75?(1)采用全阻抗继电器Z IIIset1=Zact（30?）=75.61?，?set=75?（2）采用方向阻抗继电器附录:助增分支系数的计算分支系数：.1.2I I K b ==.1.3.1I I I +=.1.3.1I I +=211s MNs x Z x ++，与故障点的位置无关。
距离保护例题
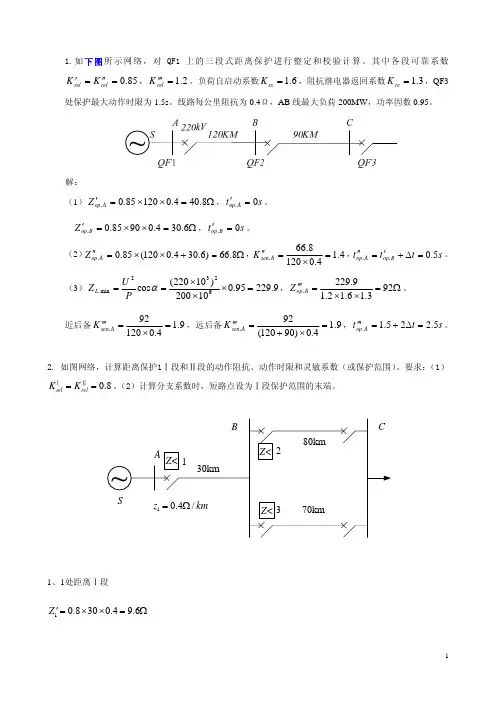
1.如下图所示网络，对QF1上的三段式距离保护进行整定和校验计算。
其中各段可靠系数85.0=′′=′rel relK K ，2.1=′′′rel K ，负荷自启动系数6.1=ss K ，阻抗继电器返回系数3.1=re K ，QF3处保护最大动作时限为1.5s 。
线路每公里阻抗为0.4Ω，AB 线最大负荷200MW ，功率因数0.95。
解：（1）Ω=××=′8.404.012085.0.A opZ ，s t A op 0.=′。
Ω=××=′6.304.09085.0.B opZ ，s t B op 0.=′。
（2）Ω=+××=′′8.66)6.304.0120(85.0.A opZ ，4.14.01208.66.=×=′′A sen K ，s t t t B op A op 5.0..=Δ+′=′′。
（3）9.22995.010200)10220(cos 6232min .=×××==αP U Z L ，Ω=××=′′′923.16.12.19.229.A op Z 。
近后备9.14.012092.=×=′′′A senK ，远后备9.14.0)90120(92.=×+=′′′A sen K ，s t t A op 5.225.1.=Δ+=′′′。
2. 如图网络，计算距离保护1Ⅰ段和Ⅱ段的动作阻抗、动作时限和灵敏系数（或保护范围）。
要求：（1）0.8rel rel K K ==ⅠⅡ。
（2）计算分支系数时，短路点设为Ⅰ段保护范围的末端。
Z<Z<70km1、1处距离Ⅰ段10.8300.49.6Z ′=××=Ω.10op t s ′=。
保护范围为线路全长的80%。
2、2处和3处距离Ⅰ段 20.8800.425.6Z ′=××=Ω， 20.8700.422.4Z ′=××=Ω。
距离保护的整定计算实例
例3-1 在图3—48所示网络中，各线路均装有距离保护，试对其中保护1的相间短路保护Ⅰ、Ⅱ、Ⅲ段进行整定计算。
已知线路AB 的最大负荷电流350max L =⋅I A,功率因数9.0cos =ϕ，各线路每公里阻抗Ω=4.01Z /km ，阻抗角 70k =ϕ，电动机的自起动系数1ss =K ,正常时母线最低工作电压min MA ⋅U 取等于110(9.0N N =U U kV )。
图3—48 网络接线图解： 1.有关各元件阻抗值的计算AB 线路的正序阻抗 Ω=⨯==12304.0L 1AB AB Z ZBC 线路的正序阻抗 Ω=⨯==24604.0L 1BC BC Z Z变压器的等值阻抗 Ω=⨯=⋅=1.445.311151005.10100%2T 2T k T S U U Z 2．距离Ⅰ段的整定(1)动作阻抗： Ω=⨯==2.101285.0rel 1.AB op Z K Z ⅠⅠ(2)动作时间：01=Ⅰt s3．距离Ⅱ段(1)动作阻抗：按下列两个条件选择。
1)与相邻线路BC 的保护3(或保护5)的Ⅰ段配合)(min b rel rel 1.op BC AB Z K K Z K Z ⋅+=ⅠⅡⅡ式中，取8.0,85.0rel rel ==ⅡⅠK K ， min b ⋅K 为保护3的Ⅰ段末端发生短路时对保护1而言的图3-49 整定距离Ⅱ段时求min .jz K 的等值电路最小分支系数，如图3-49所示，当保护3的Ⅰ段末端1d 点短路时， 分支系数计算式为 215.112)15.01(B A B B A 12b ⨯⎪⎪⎭⎫ ⎝⎛++=+⨯++==X Z X Z Z X X Z X I I K AB BC BC AB 为了得出最小的分支系数min b ⋅K ,上式中A X 应取可能最小值，即A X 最小，而B X 应取最大可能值，而相邻双回线路应投入，因而19.1215.11301220min .b =⋅⎪⎭⎫ ⎝⎛++=K 于是Ω=⨯⨯+=''02.29)2485.019.112(8.01.dzZ 2)按躲开相邻变压器低压侧出口2d 点短路整定（在此认为变压器装有可保护变压器全部的差动保护，此原则为与该快速差动保护相配合），)(T min .b rel 1.op Z K Z K Z AB ⋅+=ⅡⅡ此处分支系数min b ⋅K 为在相邻变压器出口2k 点短路时对保护1的最小分支系数，由图3-53可见Ω=⨯+==++=++==⋅3.72)1.4407.212(7.007.2130122011.op max .B min .A 13min b ⅡZ X Z X I I K AB此处取7.0rel =ⅡK 。
电力系统继电保护距离保护(例题)
本章是本课程的重点之一。要求掌握： 1、概念和基本原理。包括：测量阻抗、整定阻抗、 动作阻抗、最大灵敏角、精工电流、分支系数。 2、动作特性和动作方程，幅值比较与相位比较之 间的转换关系。 3、接线方式及其反映的故障类型（最好能推导）。 4、整定原则和计算。 5、振荡轨迹、振荡中心，振荡闭锁措施。 6、选相方法。 7、过渡电阻的影响。 8、工频故障分量距离继电器的基本原理。
I I 而 Z set.3 K rel Z 34 0.85 24 20.4()
- 5 /14-
Kb.min的计算
Xs1.min
A
Z1-2
B
0.85Z3-4
k1 0.15Z3-4 C
Xs2.max
I 1
I 2
Z5-6
K b.min
I 2 X s1.min Z1 2 X s2.max (1 0.15) Z 34 I1 X s2.max 2 Z 34
- 10 /14-
(2) 灵敏性校验 1) 本线路末端短路时的灵敏系数
K sen
Z 110.2 9.18 1.5 Z1-2 12
III set
满足要求
- 11 /14-
2) 相邻元件末端短路时的灵敏系数
相邻线路末端短路时
III Z set Z1-2 K b.max Z 34
K sen
K b.max
X s1.max Z12 X s2.min 25 12 1 2.48 X s2.min 25
K sen
110.2 1.2 12 2.48 24
- 12 /14-
满足要求
相邻变压器低压侧出口k2点短路时
K b.max
距离保护例题
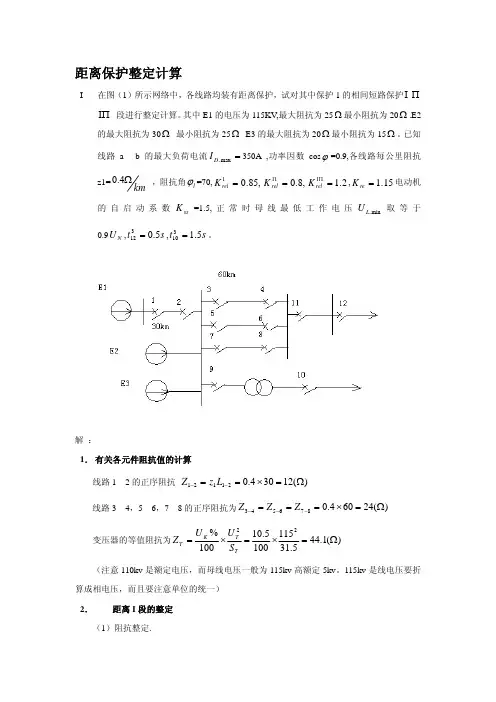
距离保护整定计算I 在图（1）所示网络中，各线路均装有距离保护，试对其中保护1的相间短路保护ΙΠ 段进行整定计算。
其中E1的电压为115KV ,最大阻抗为25ΙΠΩ最小阻抗为20Ω.E2的最大阻抗为30Ω 最小阻抗为25Ω E3的最大阻抗为20Ω最小阻抗为15。
已知线路a----b 的最大负荷电流Ω=max .D I 350A ,功率因数cos ϕ=0.9,各线路每公里阻抗z1=km Ω4.0 ，阻抗角l ϕ=70,,电动机的自启动系数=1.5,正常时母线最低工作电压取等于0.9,t ,。
,85.0=Ιrel K ,8.0=Πrel K 2.1=ΙΠrel K 15.1=re K ss K min .L U N U s 5.0312=s t 5.1310=解 ：1． 有关各元件阻抗值的计算线路1—2的正序阻抗 )(12304.021121Ω=×==−−L z Z线路3—4，5—6，7—8的正序阻抗为)(24604.0876543Ω=×===−−−Z Z Z 变压器的等值阻抗为)(1.445.311151005.10100%22Ω=×=×=T T K T S U U Z （注意110kv 是额定电压，而母线电压一般为115kv 高额定5kv 。
115kv 是线电压要折算成相电压，而且要注意单位的统一）2． 距离I 段的整定（1）阻抗整定.)(2.101285.02111Ω=×==−Z K Z rel set 2）动作时间。
s t 01=3． 距离II 段的整定(1)整定阻抗：按下列两个条件选择1）与相邻下一级线路3—4（或5—6或7—8）的保护3（或保护5或保护7）的1段配合)(3.min .ΙΠΠ+=set b AB rel set Z K Z K Z 式中，可取而,85.0=Ιrel K ,8.0=Πrel K )(4.202485.0433.Ω=×==−ΙΙZ K Z rel set 分支系数的计算：设B 母线上的电压为U 。
继电保护距离保护的整定计算和校验
继电保护距离保护的整定计算和校验4.1 断路器1距离保护的整定计算和校验4.1.1距离保护І段的整定计算(1)动作阻抗对输电线路，按躲过本线路末端短路来整定。
取K K'=0.85；Z dz'=K K'Z L3=0.85×36=30.6Ω；(2)动作时限距离保护І段的动作时限是由保护装置的继电器固有动作时限决定，人为延时为零，即t'=0s。
4.1.2距离保护П段的整定计算和校验(1)动作阻抗：按下列三个条件选择。
①与相邻线路L4的保护的І段配合Zdz''=K K''(Z L3+K'K f h·min Z L4)式中，取K'=0.85, K K''=0 .8，K f h·min为保护7的І段末端发生短路时对保护7而言的最小分支系数。
当保护7的І段末端发生短路时，分支系数为：K f h·min=I L3/I L4=1于是Zdz''=K K''(Z L3+K'K f h·min Z L4)=0.8×(36+0.85×1×10)=35.6Ω；②与相邻线路L2的保护的І段配合Zdz''=K K''(Z L3+K'K f h·min Z L2)式中，取K'=0.85, K K''=0 .8，K f h·min为保护5的І段末端发生短路时对保护7而言的最小分支系数。
当保护5的І段末端发生短路时，分支系数为：K f h·min=I L3/I L4=1于是Zdz''=K K''(Z L3+K'K f h·min Z L2)=0.8×(36+0.85×1×16)=39.68Ω；③按躲开相邻变压器低压侧出口短路整定Zdz''=K K''(Z L3+K f h·min Z TC)式中，取K K''=0 .8，K f h·min为保护7的І段末端变压器低压侧出口发生短路时对变压器低压侧出口而言的最小分支系数。
距离保护的整定计算
距离保护的整定计算一、距离保护第一段 1.动作阻抗(１)对输电线路，按躲过本线路末端短路来整定，即取AB K dzZ k Z '='⋅12．动作时限0≈'t 秒。
二、距离保护第二段1．动作阻抗（1）与下一线路的第一段保护范围配合，并用分支系数考虑助增及外汲电流对测量阻抗的影响，即()BC k fz AB k dzZ K K Z K Z '+''=''⋅1式中fz K 为分支系数min ⎪⎪⎭⎫ ⎝⎛=ABBCfz II K（2）与相邻变压器的快速保护相配合()B fz AB k dzZ K Z K Z +''=''⋅1取（1）、（2）计算结果中的小者作为1⋅''dzZ 。
2. 动作时限保护第Ⅱ段的动作时限，应比下一线路保护第Ⅰ段的动作时限大一个时限阶段，即12CABA '图3-50 电力系统接线图AZ 'BABZ BCZ Z 'Z ''Z '''00.5tZ 'Z ''Z '''00.5t3AZ 12CABA '图3-50 电力系统接线图AZ 'BABZ BCZ Z 'Z ''Z '''00.5tZ 'Z ''Z '''00.5t3AZt t t t ∆≈∆+'=''213.灵敏度校验5.1≥''=ABdzlm Z Z K如灵敏度不能满足要求，可按照与下一线路保护第Ⅱ段相配合的原则选择动作阻抗，即()2.dz fz AB k dzZ K Z K Z ''+''=''这时，第Ⅱ段的动作时限应比下一线路第Ⅱ段的动作时限大一个时限阶段，即t t t ∆+''=''21三、 距离保护的第三段1．动作阻抗按躲开最小负荷阻抗来选择，若第Ⅲ段采用全阻抗继电器，其动作阻抗为min.1.1fh zqh k dzZ K K K Z '''='''式中2．动作时限保护第Ⅲ段的动作时限较相邻与之配合的元件保护的动作时限大一个时限阶段，即t t t ∆+'''='''23．灵敏度校验作近后备保护时5.11.≥'''=⋅ABdzlm Z Z K 近作远后备保护时2.1≥+'''=⋅BCfz ABdzlm Z K Z Z K 远式中，K fz 为分支系数，取最大可能值。
距离保护例题
Z dz.A 0.8 (0.4 85 0.85 0.4 65) 44.88
K lm 44.88 1.32 1.3 0.4 85
满足要求
若在距A侧40km处发生Rg=16Ω的相间弧光短路
如图所示电网已知线路的正序阻抗线路l1l2上装有三段式距离保护测量元件zq13线路l2距离段的动作时限为2s试求距离保护1的段的动作阻抗整定阻抗及动作时限
距离保护例题
电力工程系 荣雅君
题1．有一方向阻抗继电器，其整定阻抗 Z zd 7.560 ，若测量阻抗为 Z J 7.230， 该继电器能否动作?为什么? ＋j Z 7.560
U f . min I f . max 0.9 110/ 3 163.3 0.35
保护装置的起动阻抗： 1 1 Z dz1 Z f . min 163.3 91 K k K zq K h 1.2 1.3 1.15 动作时限：
t1 t 2 t 2 0.5 2.5s
Z dz. j 25.0230
Z dz . j 44.88 cos(60 30) 38.86
Zd
Rg
Zj.A
60
Z dz. j 38.8630
30
O
Z j. A Z dz. j Z j. A Z dz. j
Ⅰ段不动作 Ⅱ段动作，以0.5s切除故障。
若在距A侧60km处发生金属性相间短路，测量阻 抗 Z J . A 0.4 60 24 Z dz. A ，距离Ⅰ段瞬时动作，切 除故障。
若在距A侧70km处发生金属性相间短路，测量阻 抗 Z J . A 0.4 70 28 Z dz. A ，距离Ⅰ段不动作， 由于 Z J . A Z dz. A ，故距离Ⅱ动作，以0.5s延时切除故障。
20距离保护的整定计算实例教学文案
20距离保护的整定计算实例仅供学习与交流，如有侵权请联系网站删除 谢谢2例3-1 在图3—48所示网络中，各线路均装有距离保护，试对其中保护1的相间短路保护Ⅰ、Ⅱ、Ⅲ段进行整定计算。
已知线路AB 的最大负荷电流350max L =⋅I A,功率因数9.0cos =ϕ，各线路每公里阻抗Ω=4.01Z /km ，阻抗角 70k =ϕ，电动机的自起动系数1ss =K ,正常时母线最低工作电压min MA ⋅U 取等于110(9.0N N =U U kV )。
图3—48 网络接线图解： 1.有关各元件阻抗值的计算AB 线路的正序阻抗 Ω=⨯==12304.0L 1AB AB Z ZBC 线路的正序阻抗 Ω=⨯==24604.0L 1BC BC Z Z变压器的等值阻抗 Ω=⨯=⋅=1.445.311151005.10100%2T 2T k T S U U Z 2．距离Ⅰ段的整定(1)动作阻抗： Ω=⨯==2.101285.0rel 1.AB op Z K Z ⅠⅠ(2)动作时间：01=Ⅰt s3．距离Ⅱ段(1)动作阻抗：按下列两个条件选择。
1)与相邻线路BC 的保护3(或保护5)的Ⅰ段配合仅供学习与交流，如有侵权请联系网站删除 谢谢3)(min b rel rel 1.op BC AB Z K K Z K Z ⋅+=ⅠⅡⅡ式中，取8.0,85.0rel rel ==ⅡⅠK K ， min b ⋅K 为保护3的Ⅰ段末端发生短路时对保护1而言的图3-49 整定距离Ⅱ段时求min .jz K 的等值电路最小分支系数，如图3-49所示，当保护3的Ⅰ段末端1d 点短路时， 分支系数计算式为215.112)15.01(B A B B A 12b ⨯⎪⎪⎭⎫ ⎝⎛++=+⨯++==X Z X Z Z X X Z X I I K AB BC BC AB 为了得出最小的分支系数min b ⋅K ,上式中A X 应取可能最小值，即A X 最小，而B X 应取最大可能值，而相邻双回线路应投入，因而19.1215.11301220min .b =⋅⎪⎭⎫ ⎝⎛++=K 于是Ω=⨯⨯+=''02.29)2485.019.112(8.01.dzZ 2)按躲开相邻变压器低压侧出口2d 点短路整定（在此认为变压器装有可保护变压器全部的差动保护，此原则为与该快速差动保护相配合），)(T min .b rel 1.op Z K Z K Z AB ⋅+=ⅡⅡ仅供学习与交流，如有侵权请联系网站删除 谢谢4此处分支系数min b ⋅K 为在相邻变压器出口2k 点短路时对保护1的最小分支系数，由图3-53可见Ω=⨯+==++=++==⋅3.72)1.4407.212(7.007.2130122011.op max .B min .A 13min b ⅡZ X Z X I I K AB此处取7.0rel =ⅡK 。
第三章距离保护3
0.9 110 163.5 3 0.35
若保护1的对应的III段采用方向阻抗继电器，则其整定值为：
Z III set.1
K Z rel L.min
Kss Kre cos set
L
0.83 163.5 1.151.5 cos 70 arccos(0.9)
110.2
（2）灵敏性校验
1）本线路末端短路时的灵敏系数为：
Z12
29 12
2.47 1.25
满足灵敏度的要求。
（3）再在计算保护1距离II段的动作延时
8
t III
8
0.5s
按原则，保护1距离II段的动作延时与保护3的I段的动作延时相配合，为：
t1II t3I t 0.5s
按原则，保护1的距离II段的动作延时还要与相邻变压器的动作延时相配合，
为：
t1II tTI t 0.5s
3.4.1 距离保护的整定计算
（五）整定计算举例
A
X s1
Z12
B
k1
C
0.85Z34
0.15Z34
B3
4C
A1
2
60km
7
~
E1 115 / 3kV
X s1.max 25
X s1.min 20
30km
5
6
I D.max
60km
9
10
~
E2 115 / 3kV
Uk % 10.5
t III
t III
10
1.5s
X s2.max 25
ST 31.5MVA
X s2.min 20
图3.26 [例3.1]的网络连接图
（2）动作延时为：
距离保护例题
t1 = t 2 + ∆t = 2 + 0.5 = 2.5s
题3
5．各段整定阻抗 ． 设nl=ny=1 距离Ⅰ段整定阻抗 距离Ⅰ 距离Ⅱ段整定阻抗 距离Ⅱ 负荷的阻抗角 距离Ⅲ 距离Ⅲ段整定阻抗
Z zd .1 Z dz .1 91 = ∠70° = ∠70° = 126.9∠70°Ω cos(70° − 25.8°) 0.72 ′ ′ Z zd .1 = Z dz .1∠70° = 11.9∠70°Ω
O
＋1
故该继电器不能动作。 故该继电器不能动作。
题2．有一方向阻抗继电器，若正常运行时的 ．有一方向阻抗继电器， 测量阻抗为 Z J = 3.5∠30°Ω ，要使该方向阻抗继 电器在正常运行时不动作， 电器在正常运行时不动作，则整定阻抗最大不 能超过多少( 能超过多少 ϕ d = 75° )? ＋j Z = Z ∠75°Ω
路时，距离保护 各段的动作情况 各段的动作情况。 路时，距离保护A各段的动作情况。
′ ′ 解： Z dz. A = K k Z AB = 0.85 × 0.4 × 80 = 27.2Ω
′′ ′ ′ Z dz. A = K k′ ( Z AB + K k Z BC ) = 0.80(32 + 0.85 × 0.4 × 60) = 41.92Ω
如图所示电网，已知：线路的正序阻抗Z1＝ 题6 如图所示电网，已知：线路的正序阻抗 ＝0.4Ω ／km，线路阻抗角 ϕ d = 60° ，A、B变电所装有反应相 ， 、 变电所装有反应相 间短路的两段式距离保护， 间短路的两段式距离保护，其Ⅰ、Ⅱ段的测量元件均 采用方向阻抗继电器和0 接线方式。试求保护AⅠ 采用方向阻抗继电器和 0接线方式。试求保护 Ⅰ、 段的动作阻抗及Ⅱ段的灵敏系数，并分析在距A侧 Ⅱ段的动作阻抗及Ⅱ段的灵敏系数，并分析在距 侧 40km处发生 g＝16Ω的相间弧光短路时，A变电所距 处发生R 的相间弧光短路时， 变电所距 处发生 的相间弧光短路时 离保护各段的动作情况。 离保护各段的动作情况。 解：
距离保护习题
3-24 在校验距离Ⅲ段远后备灵敏系数时，分支系数Kb应取
(
)
A．最大值
B．最小值
C．1
D．0
3-25 利用动作时间来躲过振荡影响的保护是(
)
A．距离I段保护 B．距离Ⅱ段保护
C．距离Ⅲ段保护 D．距离Ⅱ、Ⅲ段保护
3-26 正方向出口相间短路，存在动作“死区”的阻抗继电器是
（
）
A．全阻抗继电器
B．方向阻抗继电器
相位差 作为判别的依据，当_____，继电器动作；当_____，继电
器不动作。
3-3
方向阻抗继电器幅值比较式电气动作方程为
. U
J
1 2
.
I
J
Zzd则 其12 I.相J Zzd
位比较式电气动作方程为_____。偏移阻抗继电器相位比较式电气
.
.
动作方程为
90 ，arg则UJ其幅IJ Z值ZD 比 9较0 式电气动作方程为_____。
3-8 距离保护对反应BC相间短路的阻抗继电器，加入继电器的电压 为_____，加入继电器的电流为_____。对反应A相接地短路的阻抗 继电器，加入继电器端子的电压为_____，加入继电器端子的电流 为_____。
3-9 阻抗继电器通常采用_____接线方式，该接线方式的优点是测 量阻抗与_____无关，且基本不随运行方式变化。
.
.
继电器的幅值比较回路可采用IJ Z_Z_D __U_J 和_____两种类型。
3-4实用的方向阻抗继电器的插入电压(又称极化电压)来自两个 方面：①_____②_____。
3-5若方向阻抗元件的整定阻抗为 1075，0 则方向阻抗继电器比 幅式动作方程为_____，其比相式动作方程为_____。
(完整)距离保护例题
2。
对0º接线的相间方向阻抗继电器， 1）说明其接线方式；2）写出其相位比较式动作方程; 3)画出动作特性；4)当加入继电器的电压和电流相位差mm I Uarg 为65º和85º时，测得的动作阻抗均为12.5Ω。
计算该阻抗继电器的整定阻抗和最大灵敏角。
解： （1) 0°接线的相间方向阻抗继电器的接线方式为：U I ∆∆，三个相间阻抗继电器接线分别为： ABAB A B U Z I I =-；BC BC B C U Z I I =-;CA CA C AU Z I I =- (2）其相位比较式动作方程为： 0090270mm m setU argU I Z ≤≤- 或 0090arg90m set mmI Z U U --≤≤或 0090270m m setZ arg Z Z ≤≤-或 0090arg90set mmZ Z Z --≤≤（3)动作特性如下:(4) 0008565752senϕ+==； 0012.512.7cos(7565)set Z ==Ω-4。
如图所示，各线路均装有距离保护，单位长度阻抗为km 1/4.0Ω=z ，试对保护1的距离II段进行整定计算，并校验灵敏系数。
（85.0=I relK ，8.0=IIrel K ）解： 20.85900.430.6set Z I=⨯⨯=Ω保护1的Ⅱ段与保护1的Ⅰ段配合时,最小分支系数为:min 0.5b k =所以:10.8(600.40.530.6)31.44set Z =⨯⨯+⨯=Ω 131.441.310.460sen k ==⨯6. 图示系统，保护1装有0º接线的相间方向阻抗继电器.12ME δj e E E -=MN 20∠80ºΩ12∠80ºΩ22∠80ºΩ1）计算保护1的距离I 段的定值（85.0=Irel K ）；2）画出系统振荡时，保护1的阻抗继电器测量阻抗变化轨迹； 3）计算当 180=δ时，保护1的阻抗继电器的测量阻抗； 4)保护1的距离I 段在系统振荡情况下是否会误动？5)设 0=δ，在线路出口发生经过渡电阻Ω=4g R 的三相短路，计算保护1的阻抗继电器的测量阻抗。
整定计算例题
b)如图 4-15 所示相邻线路末端短路时的灵敏系数为
K
sen.1( 2 )
Z AB
Z set .1 K b. max Z next
（4-4）
其中，求取 K b. max 时，X sA 应取最大值 X sA. max ；而 X sB 应取最小值 X sB. min ，则
Z set .1 K rel ( L A BZ 1 K b. min Z set .3 ) 1.2 (30 0.4 1.667 28.032) 70.475
应取 Z set 69.806 为相间距离保护第Ⅲ段的整定值。 2） 灵敏度校验： a）本线路末端短路时的灵敏系数为
如下图所示网络中 采用三段式 相间距离保护 为相 间短路保护。已知 线路每公里 阻抗 Z 1 =0.4 / km ，线路阻抗角 1 65 ，线路 AB 及线路 BC 的最大负荷电流 I L. max =400A，
功率因数 cos =0.9。K rel =K rel =0.8，K rel =1.2，K ss =2，K re =1.15，电源电动势 E=115kV
69.806
b)与相邻线路距离保护第 段相配合，即
Z set .1 K rel ( L A BZ 1 K b. min Z set.3 ) Z set .4 K rel LC DZ 1 0.8 62 0.4 19.84
Z set .3 K re; ( LB CZ1 K b. min Z set .4 ) 0.8 (38 0.4 1 19.84) 28.032
距离保护定值整定计算
距离保护定值整定计算(1):IBL 电流比例系数电流比例系数表示每个脉冲对应的电流幅值(A),这个定值是厂家提供的,使用时根据CT二次最小电流及最大电流选用相应的比例系数,并利用跳线选择装置上电流互感器二次并联电阻是一个还是两个。
此系数不允许在试验有误差时进行修改。
本网络电流互感器二次额定电流为5A且电流变换器二次负载电阻为一个，所以此处选择IBL定值为0.178。
（2）:VBL 电压比例系数电压比例系数表示每个脉冲对应的电压幅值(V)此系数也由厂家提供, 本网络VBL定值为 0.125。
（3） KG 控制字控制字是一个四位十六进制的数,由十六位二进制数换算而成,控制字置“1”有效,不用或备用置“0”.（4）IQD 相电流差突变量起动元件电流定值此定值应满足最小运行方式下本线路末端故障时有足够灵敏度.相电流差突变量起动元件是分相起动,相当于模拟型保护的负序起动元件,负序元件考虑三相短路短时出现负序时灵敏度,定值取的较低,而相电流差突变量起动元件在任何故障下都有灵敏度,所以可以取的稍高,否则在重负荷时容易频繁起动.对110KV线路IQD一次值取300A.（5）IWI 无电流鉴别相电流元件定值整定原则:a 躲开本线路电容电流的稳态值.b 最小方式下本线路末端故障应有足够的灵敏度1～2A作用:a 发出跳闸令后,判断故障是否切除。
b 判断断路器是否已合上,以便使程序进入后加速状态。
c 作电流不平衡的判据。
（6）DI2健全相相电流差突变量元件.作用:在本线路非全相过程中高频零序保护退出工作,此时高频保护不再利用通道.此时健全相再发生故障,利用两个健全相的相电流差突变量DI2加阻抗判的方法瞬时切除三相。
整定原则:本线路在非全相期间末端故障灵敏度大于2.整定建议:DI2与IQD整定相同值.（7） KX零序电抗补偿系数KX=(X0-X1)/3X1，X0、X1最好实测（8） KR零序电阻补偿系数KR=(R0-R1)/3R1（9） R/X线路正序电阻与正序电抗的比值用于高阻算法，距离保护用常规算法算出电阻分量大于电抗分量的1/3时，认为是经高阻接地，调用特殊算法，此算法可使电抗分量较少受过渡电阻的影响。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
距离保护整定计算例题
题目：系统参数如图，保护1配置相间距离保护，试对其距离I 段、II 段、III
段进行整定，并校验距离II 段、III 段的灵敏度。
取z1=0.4Ω/km ，线路阻抗角为75︒，Kss=1.5，返回系数Kre=1.2，III 段的可靠系数Krel=1.2。
要求II 段灵敏度≥1.3~1.5，III 段近后备≥1.5，远后备≥1.2。
解：
1、计算各元件参数，并作等值电路
Z MN =z 1l MN =0.4⨯30=12.00 Ω Z NP =z 1l NP =0.4⨯60=24.00 Ω
Z T =100%K U ⨯T T S U 2=1005.10⨯5
.311152
=44.08 Ω
2、整定距离I 段
Z I set1=K I rel Z MN =0.85⨯12=10.20 Ω t I 1=0s Z I set3=K I rel Z NP =0.85⨯24=20.40 Ω t I 3=0s 3、整定距离II 段并校验灵敏度 1)整定阻抗计算
(1)与相邻线路I 段配合
Z II set1=K II rel (Z MN +Kbmin Z I set3 )=0.8(12+2.07⨯20.40)=43.38Ω (2)与变压器速断保护配合
Z II set1=K II rel (Z MN +Kbmin Z T )=0.7(12+2.07⨯44.08)=72.27 Ω 取Z II set1=Min( (1),(2))=43.38Ω
2)灵敏度校验
K II sen =
MN
set II Z Z 1
=43.38/12=3.62 (>1.5)，满足规程要求 3）时限 t II 1=0.5s 4、整定距离III 段并校验灵敏度 1)最小负荷阻抗 Z Lmin Z Lmin =
Lman L I U min =Lman
N I U 9.0=35.03
/1109.0⨯=163.31 Ω
Cos ϕL =0.866， ϕL=30︒
2）负荷阻抗角方向的动作阻抗Z act （30︒） Z act （30︒）=
re ss rel L K K K Z min =2
.15.12.131
.163⨯⨯=75.61 Ω
3）整定阻抗Z III set1，ϕset =75︒ (1)采用全阻抗继电器
Z III set1= Z act （30︒）=75.61Ω， ϕset =75︒ （2）采用方向阻抗继电器 Z III set1 =
)cos()
30(L set act Z ϕϕ-︒=)
3075(61.75︒-︒COS =106.94Ω
4）灵敏度校验
方向阻抗：近后备：Ksen=
MN
set III Z Z 1
=106.94/12=8.91
远后备：（1）线路NP Ksen=NP MN set III Z K Z Z max 1
+=2448.21294.106⨯+=1.5
（2）变压器Ksen=T MN set III Z K Z Z max 1
+=08.4448.21294.106⨯+=0.88
定值清单
附录: 助增分支系数的计算
KN MN NK
MN M m Z I I Z I Z I Z I I U Z 1
.
2.
1
.
2.
1.1
+
=+=
=
⋅
⋅
KN b MN Z K Z +=
分支系数：.
1
.
2I I K b =
=
.
1
.
3
.
1I I I +=.
1
.
3.
1I I +
=2
11s MN
s x Z x ++
，与故障点的位置无关。
min 2max 1max 1s MN s b X Z X K ++= =2512
251++=2.48
max
2min 1min 1s MN
s b X Z X K ++= = 1+(20+12)/30=2.07。