机械原理习题全解
机械原理习题全解
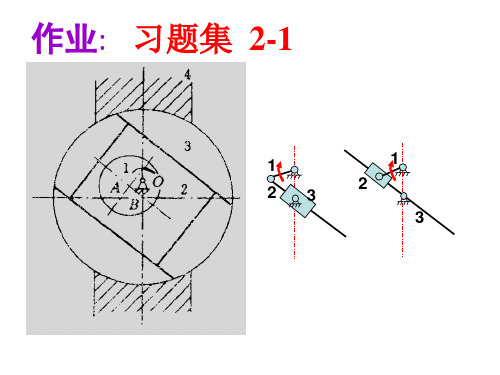
作业: 习题集 2-2
1 2 3 4
5
解: n = 4,pl = 5,ph = 1,F’ = 0,p’ = 0 F= 3n- (2pl+ph-p’ ) - F’ = 1 机构自由度数=机构原动件数 所以,机构具有确定的运动。
2-3 图示为一简易冲床的初拟设计方案。设计者的思路是:动力由 齿轮1输入,使轴A 连续回转;而固装在轴 A 上的凸轮2 与杠杆3 组成 的凸轮机构使冲头 4上下运动,以达到冲压的目的。试绘出其机构 运动简图(各尺寸由图中量取),分析是否能实现设计意图,并提 出修改方案。 3
5
4
解:n 3, P
l
2
(1)
4, Ph 1
F 3 3 (2 4 1 0) 0 0
原方案不可行。 改进措施: 1、增加一个低副和一个活动构件; 2、用一个高副代替低副。
修 改 方 案
3
2
3
5
4
(1)
2
5
4
(1)
习题2-4 图示牛头刨床设计方 案草图。 设计思路为:动力由 曲柄1输入,通过滑块2使 摆动导杆 3 作往复摆动, 并带动滑枕4作往复移动 , 已达到刨削加工目的。 试问图示的构件组合是否 能达到此目的? 如果不 能,该如何修改?
4
F’ = 1
F= 3n- (2pl+ph) - F’ = 1
1
机构自由度数=机构原动件数
所以,机构具有确定的运动。
作业: 习题集 2-2
4 3 2 1 5
6
解: n = 5,pl = 5,ph = 2,F’ = 1,p’ = 0 F= 3n- (2pl+ph-p’ ) - F’ = 2 机构自由度数=机构原动件数 所以,机构具有确定的运动。
机械原理习题(附答案解析)

第二章一、单项选择题:1.两构件组成运动副的必备条件是。
A.直接接触且具有相对运动;B.直接接触但无相对运动;C.不接触但有相对运动;D.不接触也无相对运动。
2.当机构的原动件数目小于或大于其自由度数时,该机构将确定的运动。
A.有;B.没有;C.不一定3.在机构中,某些不影响机构运动传递的重复部分所带入的约束为。
A.虚约束;B.局部自由度;C.复合铰链4.用一个平面低副联二个做平面运动的构件所形成的运动链共有个自由度。
A.3;B.4;C.5;D.65.杆组是自由度等于的运动链。
A.0;B.1;C.原动件数6.平面运动副所提供的约束为A.1;B.2;C.3;D.1或27.某机构为Ⅲ级机构,那么该机构应满足的必要充分条件是。
A.含有一个原动件组;B.至少含有一个基本杆组;C.至少含有一个Ⅱ级杆组;D.至少含有一个Ⅲ级杆组。
8.机构中只有一个。
A.闭式运动链;B.原动件;C.从动件;D.机架。
9.要使机构具有确定的相对运动,其条件是。
A.机构的自由度等于1;B.机构的自由度数比原动件数多1;C.机构的自由度数等于原动件数二、填空题:1.平面运动副的最大约束数为_____,最小约束数为______。
2.平面机构中若引入一个高副将带入_______个约束,而引入一个低副将带入_____个约束。
3.两个做平面平行运动的构件之间为_______接触的运动副称为低副,它有_______个约束;而为_______接触的运动副为高副,它有_______个约束。
4.在平面机构中,具有两个约束的运动副是_______副或_______副;具有一个约束的运动副是_______副。
5.组成机构的要素是________和________;构件是机构中的_____单元体。
6.在平面机构中,一个运动副引入的约束数的变化范围是_______。
7.机构具有确定运动的条件是____________________________________________。
机械原理课后答案
习题解答第一章绪论1-1 答:1 )机构是实现传递机械运动和动力的构件组合体。
如齿轮机构、连杆机构、凸轮机构、螺旋机构等。
2 )机器是在组成它的实物间进行确定的相对运动时,完成能量转换或做功的多件实物的组合体。
如电动机、内燃机、起重机、汽车等。
3 )机械是机器和机构的总称。
4 )a. 同一台机器可由一个或多个机构组成。
b. 同一个机构可以派生出多种性能、用途、外型完全不同的机器。
c. 机构可以独立存在并加以应用。
1-2 答:机构和机器,二者都是人为的实物组合体,各实物之间都具有确定的相对运动。
但后者可以实现能量的转换而前者不具备此作用。
1-3 答:1 )机构的分析:包括结构分析、运动分析、动力学分析。
2 )机构的综合:包括常用机构设计、传动系统设计。
1-4 略习题解答第二章平面机构的机构分析2-1 ~2-5 (答案略)2-6(a) 自由度F=1 (b) 自由度F=1(c) 自由度F=12-7题2 -7 图F =3 × 7 -2 × 9 -2 =12 -8a) n =7 =10 =0 F =3×7-2×10 =1b) B 局部自由度n =3 =3 =2 F=3×3 -2×3-2=1c) B 、D 局部自由度n =3 =3 =2 F=3×3 -2×3-2 =1d) D( 或C) 处为虚约束n =3 =4 F=3×3 -2×4=1e) n =5 =7 F=3×5-2×7=1f) A 、B 、C 、E 复合铰链n =7 =10 F =3×7-2×10 =1g) A 处为复合铰链n =10 =14 F =3×10 -2×14=2h) B 局部自由度n =8 =11 =1 F =3×8-2×11-1 =1i) B 、J 虚约束C 处局部自由度n =6 =8 =1 F =3×6 -2×8-1=1j) BB' 处虚约束A 、C 、D 复合铰链n =7 =10 F =3×7-2×10=1 k) C 、D 处复合铰链n=5 =6 =2F =3×5-2×6-2 =1l) n =8 =11 F =3×8-2×11 =2m) B 局部自由度I 虚约束4 杆和DG 虚约束n =6 =8 =1 F =3×6-2×8-1 =12-9a) n =3 =4 =1 F =3 × 3 -2 × 8 -1 =0 不能动。
机械原理习题解答(第1-3章)

vB
+
vC2B
=
vC3
+
vC2C3
方向
? ?
ω1lAB
?
BC
AB
0
? ∥BC
b
C(C2,C3,C4)
p
C3
C2
d
e
再根据速度影像原理,作△bde ∽ △ BDE 求得d及e,由图可得
b
vD v pd 0.23m / s
C(C2,C3,C4)
p' C '
(3)加速度分析
' C2
3
答:(1)机构所有的瞬心数:K=(N-1)/2=6(6-1)/2=15。 (2)求出如下三个瞬心P16,P36,P13,如下图所示。
P23 K(P13) P36
P12 P16
1 / 3 P P / P P 36 13 16 13
3-11 速度多边形和加速度多边形有哪些特性?试标出图 中VAB、VBC、VCA及VA、VB、VC的方向? 答:速度多边形具有以下特点: (1)作图起点p称为速度多边形的极点p,它代表机构中速 度为零的点。 (2)在速度多边形中,连接p点和任一点的矢量代表该点 在机构图中同名点的绝对速度,其指向是从p点指向该点。
答:速度瞬心是互作平面相对运动的两构件上瞬时相对速 度为零的重合点,也就是具有同一瞬时绝对速度的重合点 (即瞬时绝对速度速度相等的重合点),简称瞬心。若瞬心 处的绝对速度为零,则该瞬心称为绝对瞬心,否则称为相 对瞬心。 3-2 何为三心定理?何种情况下的瞬心需用三心定理来确 定? 答: 三心定理是指三个彼此作平面平行运动的构件的三 个瞬心必位于同一直线上。 对于不通过运动副直接相连的两构件间的瞬心位置,需用 三心定理来确定。
机械原理习题及问题详解
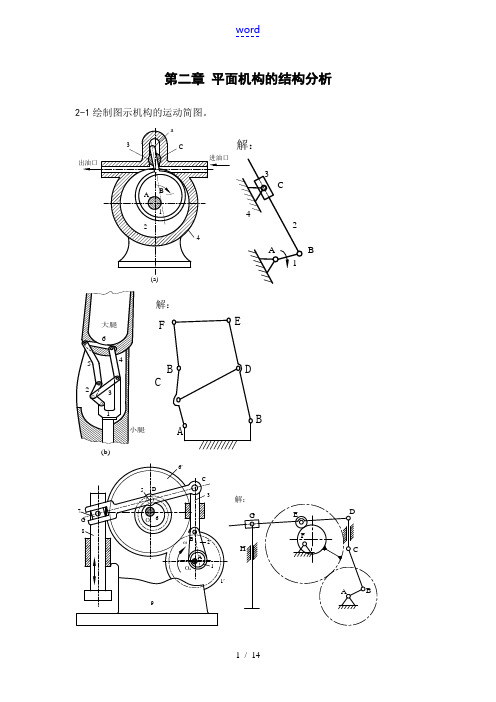
第二章 平面机构的结构分析2-1绘制图示机构的运动简图。
B解:大腿 小腿213456(b)ACB FEDB解:2-3计算图示机构的自由度,并指出复合铰链、局部自由度和虚约束。
ABCDE(a)ABDCE(b)ABCDE(c)(e)(f)H(g)解:(a) C 处为复合铰链。
7,n =p h =0,p l =10。
自由度323721001W l h F n p p =--=⨯-⨯-=。
(b) B 处为局部自由度,应消除。
3n =,p h =2,p l =2自由度323323121W l h F n p p =--=⨯-⨯-⨯=。
(c) B 、D 处为局部自由度,应消除。
3n =,p h =2,p l =2。
自由度323323121W l h F n p p =--=⨯-⨯-⨯=。
(d) CH 或DG 、J 处为虚约束,B 处为局部自由度,应消除。
6n =,p h =1,p l =8。
自由度32362811W l h F n p p =--=⨯-⨯-=。
(e) 由于采用对称结构,其中一边的双联齿轮构成虚约束,在连接的轴颈处,外壳与支架处的连接构成一个虚约束转动副,双联齿轮与外壳一边构成虚约束。
其中的一边为复合铰链。
其中4n =,p h =2,p l =4。
自由度32342422W l h F n p p =--=⨯-⨯-=。
(f) 其中,8n =,p h =0,p l =11。
自由度323821102W l h F n p p =--=⨯-⨯-=。
(g) ①当未刹车时,6n =,p h =0,p l =8,刹车机构自由度为32362802W l h F n p p =--=⨯-⨯-=②当闸瓦之一刹紧车轮时,5n =,p h =0,p l =7,刹车机构自由度为32352701W l h F n p p =--=⨯-⨯-=③当两个闸瓦同时刹紧车轮时,4n =,p h =0,p l =6,刹车机构自由度为32342602W l h F n p p =--=⨯-⨯-=2-3 判断图示机构是否有确定的运动,假如否,提出修改方案。
机械原理习题及解答

第二章习题及解答2-1 如题图2-1所示为一小型冲床,试绘制其机构运动简图,并计算机构自由度。
(a)(b)题图2-1解:1)分析该小型冲床由菱形构件1、滑块2、拨叉3和圆盘4、连杆5、冲头6等构件组成,其中菱形构件1为原动件,绕固定点A作定轴转动,通过铰链B与滑块2联接,滑块2与拨叉3构成移动副,拨叉3与圆盘4固定在一起为同一个构件且绕C轴转动,圆盘通过铰链与连杆5联接,连杆带动冲头6做往复运动实现冲裁运动。
2)绘制机构运动简图选定比例尺后绘制机构运动简图如图(b)所示。
3)自由度计算其中n=5,P L=7, P H=0,F=3n-2P L-P H=3×5-2×7=1故该机构具有确定的运动。
2-2 如题图2-2所示为一齿轮齿条式活塞泵,试绘制其机构运动简图,并计算机构自由度。
(a)(b)题图2-2解:1)分析该活塞泵由飞轮曲柄1、连杆2、扇形齿轮3、齿条活塞4等构件组成,其中飞轮曲柄1为原动件,绕固定点A作定轴转动,通过铰链B与连杆2联接,连杆2通过铰链与扇形齿轮3联接,扇形齿轮3通过高副接触驱动齿条活塞4作往复运动,活塞与机架之间构成移动副。
2) 绘制机构运动简图选定比例尺后绘制机构运动简图如图(b)所示。
3)自由度计算其中n=4,P L=5, P H=1F=3n-2P L-P H=3×4-2×5-1=1故该机构具有确定的运动。
2-3 如图2-3所示为一简易冲床的初步设计方案,设计者的意图是电动机通过一级齿轮1和2减速后带动凸轮3旋转,然后通过摆杆4带动冲头实现上下往复冲压运动。
试根据机构自由度分析该方案的合理性,并提出修改后的新方案。
题图2-3解:1)分析2)绘制其机构运动简图(图2-3 b)选定比例尺后绘制机构运动简图如图(b )所示。
3)计算机构自由度并分析其是否能实现设计意图由图b 可知,45200l h n p p p F ''===== 故3(2)34(2520)00l h F n p p p F ''=-+--=⨯-⨯+--=因此,此简易冲床根本不能运动,需增加机构的自由度。
机械原理部分试题及解答
第一章机构的组成和结构1-1 试画出图示平面机构的运动简图,并计算其自由度。
F=3×3-2×4=1 F=3×3-2×4=1F=3×3-2×4=1 F=3×3-2×4=11-2 计算图示平面机构的自由度。
将其中高副化为低副。
确定机构所含杆组的数目和级别,以及机构的级别。
(机构中的原动件用圆弧箭头表示。
)F=3×7-2×10=1 F=3×7-2×10=1 含3个Ⅱ级杆组:6-7,4-5,2-3。
含3个Ⅱ级杆组:6-7,4-5,2-3。
该机构为Ⅱ级机构构件2、3、4连接处为复合铰链。
该机构为Ⅱ级机构F=3×4-2×5-1=1 F=3×3-2×3-2=1F=3×5-2×7=1(高副低代后)F=3×5-2×7=1(高副低代后)含1个Ⅲ级杆组:2-3-4-5。
含2个Ⅱ级杆组:4-5,2-3。
该机构为Ⅲ级机构构件2、3、4连接处为复合铰链。
该机构为Ⅱ级机构F=3×8-2×11-1=1 F=3×6-2×8-1=1F=3×9-2×13=1(高副低代后)F=3×7-2×10=1(高副低代后)含4个Ⅱ级杆组:8-6,5-7,4-3,2-11。
含1个Ⅱ级杆组6-7。
该机构为Ⅱ级机构含1个Ⅲ级杆组2-3-4-5。
第二章 连 杆 机 构2-1 在左下图所示凸轮机构中,已知r = 50mm ,l OA =22mm ,l AC =80mm,︒=901ϕ,凸轮1的等角速度ω1=10rad/s ,逆时针方向转动。
试用瞬心法求从动件2的角速度ω2。
解:如右图,先观察得出瞬心P 13和P 23为两个铰链中心。
再求瞬心P 12:根据三心定理,P 12应在P 13与P 23的连线上,另外根据瞬心法,P 12应在过B 点垂直于构件2的直线上,过B 点和凸轮中心O 作直线并延长,与P 13、P 23连线的交点即为P 12。
机械原理课后全部习题解答
机械原理课后全部习题解答文档编制序号:[KKIDT-LLE0828-LLETD298-POI08]《机械原理》习题解答机械工程学院目录第1章绪论 (1)第2章平面机构的结构分析 (3)第3章平面连杆机构 (8)第4章凸轮机构及其设计 (15)第5章齿轮机构 (19)第6章轮系及其设计 (26)第8章机械运动力学方程 (32)第9章平面机构的平衡 (39)第一章绪论一、补充题1、复习思考题1)、机器应具有什么特征机器通常由哪三部分组成各部分的功能是什么2)、机器与机构有什么异同点3)、什么叫构件什么叫零件什么叫通用零件和专用零件试各举二个实例。
4)、设计机器时应满足哪些基本要求试选取一台机器,分析设计时应满足的基本要求。
2、填空题1)、机器或机构,都是由组合而成的。
2)、机器或机构的之间,具有确定的相对运动。
3)、机器可以用来人的劳动,完成有用的。
4)、组成机构、并且相互间能作的物体,叫做构件。
5)、从运动的角度看,机构的主要功用在于运动或运动的形式。
6)、构件是机器的单元。
零件是机器的单元。
7)、机器的工作部分须完成机器的动作,且处于整个传动的。
8)、机器的传动部分是把原动部分的运动和功率传递给工作部分的。
9)、构件之间具有的相对运动,并能完成的机械功或实现能量转换的的组合,叫机器。
3、判断题1)、构件都是可动的。
()2)、机器的传动部分都是机构。
()3)、互相之间能作相对运动的物件是构件。
()4)、只从运动方面讲,机构是具有确定相对运动构件的组合。
()5)、机构的作用,只是传递或转换运动的形式。
()6)、机器是构件之间具有确定的相对运动,并能完成有用的机械功或实现能量转换的构件的组合。
()7)、机构中的主动件和被动件,都是构件。
()2 填空题答案1)、构件 2)、构件 3)、代替机械功 4)、相对运动 5)、传递转换6)、运动制造 7)、预定终端 8)、中间环节 9)、确定有用构件3判断题答案1)、√ 2)、√ 3)、√ 4)、√ 5)、× 6)、√ 7)、√第二章 机构的结构分析2-7 是试指出图2-26中直接接触的构件所构成的运动副的名称。
机械原理习题及答案讲解
第1章平面机构的结构分析1.1解释下列概念1.运动副;2.机构自由度;3.机构运动简图;4.机构结构分析;5.高副低代。
1.2验算下列机构能否运动,如果能运动,看运动是否具有确定性,并给出具有确定运动的修改办法。
题1.2图题1.3图1.3 绘出下列机构的运动简图,并计算其自由度(其中构件9为机架)。
1.4 计算下列机构自由度,并说明注意事项。
1.5计算下列机构的自由度,并确定杆组及机构的级别(图a所示机构分别以构件2、4、8为原动件)。
题1.4图题1.5图第2章平面机构的运动分析2.1试求图示各机构在图示位置时全部瞬心。
题2.1图2.2在图示机构中,已知各构件尺寸为l AB=180mm , l BC=280mm , l BD=450mm ,l CD=250mm ,l AE =120mm ,φ=30º, 构件AB上点E的速度为v E=150 mm /s ,试求该位置时C、D两点的速度及连杆2的角速度ω2。
2.3 在图示的摆动导杆机构中,已知l AB=30mm , l AC=100mm , l BD=50mm ,l DE=40mm ,φ1=45º,曲柄1以等角速度ω1=10 rad/s沿逆时针方向回转。
求D点和E点的速度和加速度及构件3的角速度和角加速度(用相对运动图解法)。
题2.2图题2.3图2.4 在图示机构中,已知l AB=50mm , l BC=200mm , x D=120mm , 原动件的位置φ1=30º, 角速度ω1=10 rad/s,角加速度α1=0,试求机构在该位置时构件5的速度和加速度,以及构件2的角速度和角加速度。
题2.4图2.5 图示为机构的运动简图及相应的速度图和加速度图。
(1)在图示的速度、加速度多边形中注明各矢量所表示的相应的速度、加速度矢量。
(2)以给出的速度和加速度矢量为已知条件,用相对运动矢量法写出求构件上D 点的速度和加速度矢量方程。
机械原理_课后习题答案免费(全面)高教版 西北工大
2) 求vC2
v C 2 = v B + v C 2 B = v C 3 + vC 2 C 3
方向: 大小: ⊥AB
√
⊥BC ?
0 0
∥BC ?
取
μv = 0.005
m/s mm
作速度图
b
题3-10 解(续2)
[解] (2)速度分析
v B → vC 2 → v D , v E → ω 2
1) 求vB 2) 求vC2 3) 求vD 和求vE 用速度影像法
C
E
vC = v B + vCB v D = v B + v DB
(2) 求vE
D p(a, f )
v E = vC + v EC = v D + v ED
b d e c
题3-5 解
b) 解: 顺序 (1) 求vC
v B → vC → v E → v F
D B vB A E G F C
vC = v B + vCB
√
0 0
∥CD ?
b2 (b1) (b3)
其中 a B3B2 = 2ω2 v B3B2 = 0(∵ v B3B2 = 0)
a B1 ⎛ m / s 2 ⎞ 取 μa = ⎜ ⎟ 作加速度图 p ' b '1 ⎝ mm ⎠
题3-8 c) 解(续2)
[解] (3)加速度分析 a B 2 ( = a B1 ) → a B 3 → a C 3 1) 求aB2 A 1 ω1 2) 求aB3
取
√ v ⎛m/s⎞ μ v = B1 ⎜ ⎟ 作速度图 pb1 ⎝ mm ⎠
3) 求vC3 : 用速度影像法
v C 3 = 0 同时可求得 ω3 =
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
c ∈ [340 , 600 )
c ∈ [600 ,860 ]
c ∈ [140 , 240 ]
非最短杆, 240 ≤ c ≤ 600 (2)c非最短杆, ) 非最短杆 c ∈ [240 , 340 240 + 600 ≥ c + 500 也非最长杆 c > 600 为最长杆, (3)c为最长杆, ) 为最长杆 c ∈ [860 ,1340 240 + c ≥ 600 + 500 且满足安装条件 c ≤ 600 + 240 + 500 综合以上结果, 综合以上结果,得:c ∈ 140,1340
习题集 3-1
P34在∞ P24
P13
P12
P23
P12 P23 P14 P34 P13
P14
P12 P14 P23 P34 P24
作业: 作业 习题集 3-1
P13在∞
P12 P23
作业: 作业 习题集 3-1
P13
P34在∞
P14 P23 P24 P12 P14 P23 P34 P24
P12 P12 P23 P14 P34 P13
作业: 习题集 2-2 作业
解:
5 4 3 2 1
n=4 pl = 4 ph = 2 F’ = 1 F= 3n- (2pl+ph) - F’ = 1 机构自由度数=机构原动件数 机构自由度数 机构原动件数 所以,机构具有确定的运动。 所以,机构具有确定的运动。
作业: 习题集 2-2 作业
4 3 2 1 5
a +e αmax = arcsin( ) b
a +e γ min = −αmax = − arcsin( ) 2 2 b
故A点运动到最高位置时压力 角最大, 角最大,传动角最小
π
π
(2)导杆机构有曲柄的条件及最小传动角
A
l4
l1
B
1)若A、D整周转动,应满足: 、
l4为 短 l4 + e ≤ l1 最 杆
VE = ω3 ⋅ PE P ⋅ µl = 0.357m / s 13
_______
3)当Vc=0时,瞬心 ) 点将重合, 时 瞬心P13与C点将重合,即处于 与 点将重合 即处于AB 共线的两个极限位置( 与BC共线的两个极限位置(如图所示), 共线的两个极限位置 如图所示), 由图量得两极限位置所对应的Φ的值分别为: 由图量得两极限位置所对应的 的值分别为: 的值分别为 =26.4° Φ 1=26.4°; Φ 2=226.6° =226.6°
1
解:以选定的比例尺ul 作运动简图 以选定的比例尺பைடு நூலகம்
ω2
1)由题意知P23是构件 和构件 上的等速重合点 )由题意知 是构件2和构件 和构件3上的等速重合点 2构件上 23点的速度 构件上P 构件上
VP 23 = ω2 ⋅ P23 P ⋅ µl 12
_______
_______
3构件上 23点的速度 VP 23 = ω3 ⋅ P23 P ⋅ µl 构件上P _______ 构件上 13
若lmin+lmax≤其余两杆长度之和 Y N
以最短杆 为机架
以最短杆的邻边 为机架 曲柄摇杆 机构
以最短杆的对边 为机架 双摇杆 机构
双曲柄 机构
6-1 在图示的运动链中,各构件的尺寸如图(单 在图示的运动链中,各构件的尺寸如图( )。试问 位mm)。试问,分别采用哪个构件为机架,可 )。试问,分别采用哪个构件为机架, 获得曲柄摇杆机构、双曲柄机构和双摇杆机构? 获得曲柄摇杆机构、双曲柄机构和双摇杆机构? 解:由已知条件知该四杆机构满足杆长条件 lmin+lmax(25+60=85)≤其余两杆长度之和(40+50=90) 其余两杆长度之和 所以: 为机架可得曲柄摇杆 曲柄摇杆机构 所以: 以AB或O1O2为机架可得曲柄摇杆机构 或 为机架可得双曲柄 双曲柄机构 以AO1为机架可得双曲柄机构 为机架可得双摇杆 双摇杆机构 以BO2为机架可得双摇杆机构
c ≤ 240 c + 600≥ 240+ 500
c ∈ [140 ,240 ]
2)c非最短杆 2)c非最短杆,取c为机架,则只需满足安装条件, 非最短杆, c为机架 则只需满足安装条件, 为机架, 该机构就一定为双摇杆机构
c > 240 c ≤ 600+ 240+ 500
c ∈ [240 ,1340 ]
4
1
2
3
改进措施: 改进措施: 1、增加一个低副和一个活动构件; 增加一个低副和一个活动构件; 2、用一个高副代替低副。 用一个高副代替低副。
改进方案
改进方案
作业: 作业 习题集 3-1
P13在∞ P24 P23 P34 P14在∞
P12 P12 P23 P14 P34 P13在∞ P12 P14 P23 P34 P24
6
解: n = 5,pl = 5,ph = 2,F’ = 1,p’ = 0 F= 3n- (2pl+ph-p’ ) - F’ = 2 机构自由度数=机构原动件数 机构自由度数 机构原动件数 所以,机构具有确定的运动。 所以,机构具有确定的运动。
作业: 习题集 2-2 作业
1 2 3 4
5
解: n = 4,pl = 5,ph = 1,F’ = 0,p’ = 0 F= 3n- (2pl+ph-p’ ) - F’ = 1 机构自由度数=机构原动件数 机构自由度数 机构原动件数 所以,机构具有确定的运动。 所以,机构具有确定的运动。
2)不满足杆长条件 ) c ≤ 240 为最短杆: (1)c为最短杆: ) 为最短杆 c + 600 ≥ 240 + 500
]
]
[
]
思路2: 思路 : 假设c长度未定 长度未定, 为机架, 为机架 解:假设 长度未定,以CD为机架,且能使该机构为双 摇杆机构, 摇杆机构,则可以考虑如下两种情况 : 1)c为最短杆,但不满足杆长条件 为最短杆, ) 为最短杆
长杆) 长杆)
240 < c < 600 (1)c非最短杆 ) 非最短杆 也非最长杆: 也非最长杆: 600 + 240 ≤ c + 500 c ≥ 600 (2)c为最长杆: ) 为最长杆: 为最长杆 c + 240 ≤ 600 + 500
解:1)满足杆长条件 )
a = 240mm, b = 600mm, c = ? mm, d = 500mm
2
5
(1)
4
习题2 习题2-4 图示牛头刨床设计方 案草图。 案草图。 设计思路为: 设计思路为:动力由 曲柄1输入,通过滑块2 曲柄1输入,通过滑块2使 作往复摆动, 摆动导杆 3 作往复摆动, 并带动滑枕4 并带动滑枕4作往复移动 , 已达到刨削加工目的。 已达到刨削加工目的。 试问图示的构件组合是否 能达到此目的? 能达到此目的? 如果不 该如何修改? 能,该如何修改?
D
e
摆动导杆机构( 为周转副 为周转副) 2) 摆动导杆机构(A为周转副)
l1 + e ≤ l 4
α max = ?
A
l1
α
B
α
F vB3
sin α =
e l BD
α = arcsin
e l BD
l4
D
在B、D距离最短时出现. 距离最短时出现.
e
α max
γ min =
e = arcsin | l1 − l4 |
4
1
2
3
即表示如果按 此方案设计机 构,机构是不 能运动的。 能运动的。必 须修改, 须修改,以达 到设计目的。 到设计目的。
解:首先计算设计方案草图的自由度
F = 3n − 2PL − PH = 3 × 4 − 2 × 6 = 0
F = 3n − 2PL − PH = 3 × 4 − 2 × 6 = 0
图示为一简易冲床的初拟设计方案。设计者的思路是: 2-3 图示为一简易冲床的初拟设计方案。设计者的思路是:动力由 齿轮1输入,使轴A连续回转;而固装在轴A上的凸轮2与杠杆3 齿轮1输入,使轴A 连续回转;而固装在轴A 上的凸轮2 与杠杆3 组成 的凸轮机构使冲头4上下运动,以达到冲压的目的。 的凸轮机构使冲头4 上下运动,以达到冲压的目的。试绘出其机构 运动简图(各尺寸由图中量取) 分析是否能实现设计意图, 运动简图(各尺寸由图中量取),分析是否能实现设计意图,并提 出修改方案。 出修改方案。 3
6-2 如图所示,设已知四杆机构各构件的长度分别 如图所示, 为: = 240mm, b = 600mm, c = 400mm, d = 500mm a 试问要使此机构成为双摇杆机构, 试问要使此机构成为双摇杆机构,则应取哪个杆为 机架?且其长度的允许变动范围为多少? 机架?且其长度的允许变动范围为多少? 解:以题意知该四杆机构满足杆长条件 lmin+lmax(240+600=840)≤其余两杆长度之和(400+500=900) 其余两杆长度之和 所以,选最短杆的对边CD为机架可得双摇杆 为机架可得双摇杆机构 所以,选最短杆的对边CD为机架可得双摇杆机构 假设c长度未定, 为机架, 假设 长度未定,以CD为机架, 长度未定 为机架 且能使该机构为双摇杆机构, 且能使该机构为双摇杆机构, 则可以考虑如下两种情况 : 1)满足杆长条件( c不为最短杆也不为最长杆、 c为最长杆); 不为最短杆也不为最长杆、 为最长杆 为最长杆); ) 不为最短杆也不为最长杆 2)不满足杆长条件(c为最短杆、c非最短杆也非最长杆、 c为最 为最短杆、 非最短杆也非最长杆 非最短杆也非最长杆、 为最 ) 为最短杆
c 综合以上结果,可得: 综合以上结果,可得: ∈
[140 ,1340 ]
