工程流体力学(英文版)第七章.pdf
第七章 管内流体流动分析

第九章 管内流体流动
§9.1 粘性流体的两种流动状态(内部结构) §9.2 圆管中充分发展的层流流动 §9.3 湍流(紊流)的半经验公式 §9.4 圆管中充分发展的湍流流动 §9.5 管道入口段中的流动
§9.1 粘性流体的两种流动状态
一、层流与湍流
1.流动形态 雷诺试验揭示出粘性流体有两种性
层流 过渡状态
紊流
§9.1 粘性流体的两种流动状态
雷诺实验(续)
实验现象(续)
§9.1 粘性流体的两种流动状态
2.两种流动状态的判定
a、实验发现
v vcr v vcr
流动较稳定 流动不稳定
b、临界流速
vcr ——下临界流速
vcr ——上临界流速
层 流: v vcr
不稳定流: vcr v vcr
§9.2 圆管中充分发展的层流流动
4. 阻力系数与 流动损失
定义式
p
L D
um2 2
um
p L
R2
8
p L
D2
32
阻力系数
64
Re
水平管:
hf
p
gL uΒιβλιοθήκη 2 D 2gRe Dum
雷诺数
结论:层流流动的沿程损失与平均流速的一次方成正比。
§9.3 湍流的半经验理论
一、湍流假说---普朗特混合长度理论
紊 流: v vcr
§9.1 粘性流体的两种流动状态
2、两种流动状态的判定(续)
c、临界雷诺数 雷诺数
Re ud
Recr 2300 ——下临界雷诺数
Recr 4000 ——上临界雷诺数
工程上常用的圆管临界雷诺数
工程流体力学英文原版

工程流体力学英文原版Engineering Fluid Mechanics: An Introduction.Engineering fluid mechanics is a crucial discipline within the field of engineering that deals with the study of fluids and their interactions with solid boundaries. It is a fundamental branch of physics and engineering that finds applications in various fields such as civil, mechanical, aerospace, and chemical engineering. The study of fluid mechanics involves the understanding of fluid properties, fluid statics, fluid dynamics, and fluid control.1. Fluid Properties.Fluids are substances that continuously deform under the application of shear stress. They lack a fixed shape and take the shape of the container in which they are contained. Fluids can be classified as liquids or gases, depending on their state and properties. Liquids have adefinite volume but no fixed shape, while gases expand tofill the available space.Some important fluid properties include density, viscosity, compressibility, and surface tension. Density is the mass per unit volume of a fluid. Viscosity representsthe internal friction of a fluid and affects its flow behavior. Compressibility describes how a fluid responds to changes in pressure, while surface tension arises from the intermolecular forces at the fluid's surface.2. Fluid Statics.Fluid statics deals with the behavior of fluids at rest, or in equilibrium. It involves the study of pressure distribution in fluids, buoyancy, and hydrostatics.Pressure is a force per unit area acting perpendicular tothe surface, and it is a fundamental quantity in fluid mechanics. Buoyancy is the upward force exerted by a fluid on an immersed object, and it is responsible for thefloating of objects on water. Hydrostatics deals with the equilibrium of fluids under the influence of gravity andother external forces.3. Fluid Dynamics.Fluid dynamics is concerned with the motion of fluids and the forces acting on them. It involves the study of fluid flow, fluid mechanics equations, and fluid control. Fluid flow can be laminar or turbulent, depending on the velocity and other fluid properties. Laminar flow is smooth and orderly, while turbulent flow is chaotic and irregular.The fundamental equations of fluid dynamics include the conservation of mass, momentum, and energy. The conservation of mass states that the rate of change of mass within a control volume is equal to the net mass flow rate into the volume. The conservation of momentum relates the forces acting on a fluid element to its acceleration, while the conservation of energy accounts for the conversion of energy forms within a fluid system.4. Fluid Control.Fluid control involves the manipulation and manipulation of fluid flow using pumps, valves, and other devices. Pumps are used to increase the pressure or flow rate of a fluid, while valves are used to control the direction or amount of fluid flow. Other devices such as nozzles, diffusers, and turbines are also employed to modify fluid flow characteristics.In conclusion, engineering fluid mechanics is a crucial discipline that deals with the study of fluids and their interactions with solid boundaries. It involves the understanding of fluid properties, fluid statics, fluid dynamics, and fluid control. This knowledge is essentialfor engineers to design, analyze, and optimize fluid systems in various engineering applications.。
《工程流体力学》第七章 粘性流体动力学
x方向 : 1)表面力:作用在左右两面上力的合力:
作用在上下两面上力的合力:
作用在前后两面上力的合力:
作用在整个六面体上表面力沿x轴方向的合力:
2) x方向质量力 : 单位质量流体受到的质量力分量:X;
六面体受到的质量力: Xrdxdydz
牛顿第二定律:
—— 以应力形式表示的粘性流体运动微分方程 再把表面应力和变形率之间关系代入上3式:
应力:各向同性
运动粘性流体:存在法向、切向表面力 应力:各向异性
流体中:任一点c :绕c任意方位
c点应力定义: 要计算两个向量的比值
用作用在dAx, dAy, dAz上的dFx, dFy, dFz:定义c上的应力
需要2个下标表示:9个应力分量
第1个下标i:应力作用方向 第2个下标j:作用面方向
第七章 粘性流体动力学
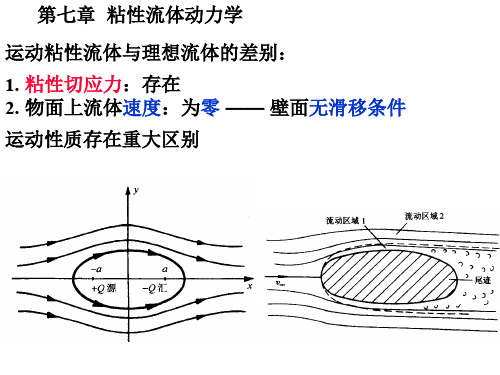
运动粘性流体与理想流体的差别: 1. 粘性切应力:存在 2. 物面上流体速度:为零 —— 壁面无滑移条件 运动性质存在重大区别
第一节 粘性流体中作用力
一、粘性应力: 1.质量力:与流体质量有关
与流体粘性无关 粘性流体中质量力考虑方法:和理想流体相同
2. 表面力: 静止和运动理想流体:仅存在指向作用面法向表面力
由于外部无粘流:受到分离流的排挤 明显改变:其中压强分布 实际计算:用实测物面压力分布计算分离点前附面层流动 附面层分离:使流体一部分机械能损失在涡流中
绕流物体阻力增加 流体机械效率降低 甚至产生不稳定流动 导致机器损坏 防止或推迟附面层分离现象发生:是工程上一个重要问 题
边界层分离后:形成尾涡区 尾涡区压强:基本上等于分离点压强 压强:上下对称 若将压强在圆柱面上积分:则得压差阻力
流体在y+l层时均速度:
工程流体力学第七章 理想不可压缩流体的有旋流动和无旋流动讲解

x
vx
y
v y
z
vz
t
0
或
(v) 0
t
连续性方程表示了单位时间内控制体内流体质量的增量等于流体在控
制体表面上的净通量。它适用于理想流体和粘性流体、定常流动和非定常
流动。
在定常流动中,由于 0 t
x
0
对于不可压缩流体 vr 1 v vz vr 0
r r z r
式中 r 为极径; 为极角
球坐标系中的表示式为:
1 (vrr 2 ) 1 (v sin ) 1 v 0
t r 2 r
r sin
r sin
在某流场O点邻近的任意点A上的速度可以分成三个部分: 分别为与O点相同的平移速度(平移运动);绕O点转动在A点 引起的速度(旋转运动);由于变形(包括线变形和角变形) 在A点引起的速度(变形运动)。
第三节 有旋流动和无旋流动
根据流体微团在流动中是否旋转,可将流体的流动分为两 类:有旋流动和无旋流动。
vx y
2 x
2 y
2 z
前面在流体微团的分析中,已给出E点的速度为 :
vxE
vx
vx x
dx
vx y
dy
vx z
dz
v yE
vy
vy x
dx
vy y
dy
vy z
dz
vzE
《工程流体力学》第七章 粘性流体动力学

2.附面层位移厚度d*: 设物面P点附面层厚度d ,在垂直于纸面方向取单位宽度,
则该处通过附面层的质量流量:
通过同一面积理想流体流量:
ro, Vo —— 附面层外边界处理想
流体的密度和速度
以d*高度作一条线平行于物面,
使两块阴影处面积相同:
即在流量相等条件下将理想流体流动区从物面向外移动了
流体绕物体流动,整个流场分为三个区域:
1)附面层: 流速:由壁面上零值急剧增加到自由来流速度同数量级值 沿物面法线方向:速度梯度很大
即使流体粘性系数小:粘性应力仍可达到一定数值
由于速度梯度很大: 使得通过附面层物体 涡旋强度很大,流体 是有旋的
2)尾迹流: 附面层内流体:离开物体流入下游,在物体后形成尾迹流
各物理量都是统计平均值, \ 瞬时物理量=平均物理量+脉动物理量, 对整个方程进行时间平均的运算。
一、常用时均运算关系式:
时均运算规律:
推论:脉动量对空间坐标各阶导数的时均值=0。
二、连续方程:对二维流动,瞬态运动连续方程 进行时均运算:
\ 可压缩紊流运动连续方程:
进行时均运算: 上两式相减:
\ 附加法向应力
法向应力: l: 比例系数,与体积变化率有关
三个法向应力平均值的负值:为粘性流体在该点压强
最后得表面应力与变形率之间的关系:
第二节 粘性流体运动的基本方程
一、连续方程:
粘性流体运动:服从质量守恒定律 连续方程:不涉及力的作用 仍能得出与理想流体相同形式的方程
二、运动微分方程: 粘性流体中:微元六面体 微元六面体中心:c
三、雷诺方程: 二维不可压缩粘性流,不考虑质量力,N-S为:
对上式进行时均运算:
第七章流体在管路中的流动

U max
J 2 J 2 r0 d 4 16
(6)
二、流量及平均流速
现求圆管中层流的流量:取半径r处厚度为d 的一个微小环形 r 面积,每秒通过这环形面积的流量为
dqV u 2rdr
由通过圆管有效截面上的流量为
Q udA
A ro
o
故油在管中是层流状态。
[例5-2] 水流经变截面管道,已知d2/d1=2,则相应的 Re2/Re1=?
解题分析
[解 ] 因
Re
Vd
4Q 1 d d
V
4Q d 2
故
d1 Re 2 / Re1 (1 / d 2 ) /(1 / d1 ) 0.5 d2
5.2 流动损失分类
沿程水头损失计算 局部水头损失计算 章目解析 从力学观点看,本章研究的是流动 阻力。
产生流动阻力的原因:
内因——粘性+惯性 外因——流体与固体壁面的接触情况流
体的运动状态(外界干扰)
从能量观看,本章研究的是能量损 失(水头损失)。
研究内容 管流:研究hw的计算(本章重 点)。 水头损失的两种形式 hf :沿程水头损失(由摩擦引 起); hj :局部水头损失(由局部干 扰引起)。
w
总水头损失: h
hf hj
5.1 层流与湍流流动
粘性流体两种流动状态:
紊流状态 层流状态
一、雷诺实验.
1. 装置
2. 实验条件
液面高度恒定. 水温恒定
图5-1 雷诺实验装置
3.实验步骤
层流状态
(a)
工程流体力学课程教学大纲双语

《工程流体力学》课程教学大纲(双语)一、课程基本信息课程代码:050246课程名称:工程流体力学英文名称:Engineering Fluid Mechanics课程类别:专业基础课specialized basic course学时:54Class hours: 54学分:3.0Credits: 3.0适用对象: 热能与动力工程专业的学生考核方式:考试(平时成绩占总成绩的30%)先修课程:高等数学,大学物理,工程力学Pre-sessional course: Advanced Mathematics, University Physics, Engineering Mechanics二、课程简介工程流体力学是研究流体(包括气体和流体)的平衡和运动规律的科学。
它是一门横跨各领域,各不同专业的重要技术基础课。
能源、动力、环境、设备、化工,航空、国防等领域均需要流体力学知识。
热能与动力工程专业学生尤其需要流体力学知识作为工程设计或从事其他专业技术工作的理论基础。
通过本课程的学习,使学生掌握流体力学的基本概念,基本原理和实验技能,为将来的学习和工作打下基础。
本课程的前四章为双语教学。
Course Description:Engineering Fluid Mechanics is the science of the law of equilibrium and motion of fluids, which include gases and liquids. It is an important basic technical course stretching across various field and various specialty. A knowledge of fluid mechanics is required in various fields such as energy, power, environment, industry, chemistry, building, aviationand national defense, etc. Students of Thermal Energy and Power Engineering Specialty need the knowledge of fluid mechanics in Engineering design or other technical work. This course provides students with basic concepts,basic theories and experimental techniques of fluid mechanics needed in future study or work. Chapter 1 to chapter 4 will be taught in both Chinese and English (bilingual education).三、课程性质与教学目的本课程是热能与动力工程专业的专业基础课。
工程流体力学7.2气体一维定常等熵流动

cp c p cV
p p 1
代入
h v2 2
h0
得
p -1
v2 2
h0
c2 v2
-1
2
h0
c K RT
RT -1
v2 2
h0
二、滞止状态
cp
R 1
Ma 2
v2 c2
v2
T
2c p
T0
能量方程的另一种形式
c2
v2
v2 max
c02
1 2 2 1
四、临界状态
ccr
2 1c0
1 1vmax
或者
c
c0
Ma 1
ccr
RTcr
2R 1
T0
Ma 1
ccr
Ma 1
0
vcr
vmax
v
令Ma=1
Tcr cc2r 2
Ma2
2M
2
1
1M
2
用速度系数表示
T T0
c2 c02
1-
-1 1
M
2
p p0
1 -
-1 1
M
2
1
1
0
1
-
-1 1
M
2
1
T0 c02 1
pcr p0
2
1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
prototype
model
1. Geometric similitude
(basic and the most obvious requirement) The model is an exact geometric replica of the prototype. All the linear dimensions of the model and prototype are in the same ratio
ratio of area:
ratio of volume:
Ω l3 CΩ = = 3 = Cl3 Ωm lm
prototype
model
2. Motion Similitude (result)
Velocity of the model and the prototype are in the same ratio throughout the entire flow field. ratio of velocity
1. Dynamic Similitude of Fluid Motion
Dynamic Similitude of Fluid Motion:
At any time, all the parameters of the model and prototype are in the same ratio throughout the entire flow field: Geometric similitude (basic) Motion similitude (result) Dynamic similitude (condition)
Ne equals
2.2 Euler number, Froud number, Reynolds number, Mach number
1. Similitude Principle of flow acted by pressure force
Pressure force
F = Ne 2 2 ρl V
Cω =
C V l ω = = V ω m Vm lm Cl
3. Dynamic simiห้องสมุดไป่ตู้itude (condition)
All the forces that act on corresponding masses in the model and the prototype are in the same ratio throughout the entire flow field.
Em
E = ρ a2
ρV 2 V 2 Ca = = 2 2 a ρa
Mach number:
V 12 M = = ( Ca ) a
3. Dimensional Analysis
1.Principle of identical dimensions for physical equations Dimension: Unit types of physical variables Fundamental dimension: the dimension of time T (hour, minute, second) the dimension of length L (m, cm, mm) the dimension of mass M (ton, kilogram, gram) the dimension of temperature (oC, K)
ρVl ρ mVm lm Re = = µ µm
Reynolds number:
4. Similitude Principle of flow acted by elastic force
Elastic force For fluid:
Fs = EA = El 2
a= E ρ
Ca =
ρV 2
E
=
ρ mVm 2
Fp = ( ∆ p ) A = ( ∆ p ) l 2
F Ne = 2 2 ρl V
Eu =
(∆ p)l2
ρ l 2V 2
=
∆p ρV 2
Euler number:
Eu =
∆ pm ∆p = ρV 2 ρ mVm 2
2. Similitude Principle of flow acted by gravity
V3 V1 V2 = = = CV V1m V2 m V3m
Cl V l t = = Ct = Vm lm tm CV
ratio of time:
prototype
model
Cl l t V CV = = = Vm lm tm Ct
ratio of acceleration:
CV CV 2 V t a Ca = = = = am Vm tm Ct Cl
l1 l2 d = = = Cl l1m l2 m d m
scale ratio between model and prototype
prototype
model
scale ratio:
l1 l2 d = = = Cl l1m l2 m d m
A l2 CA = = 2 = Cl 2 Am l m
prototype
model
2. How to design:
One type of flow Geometric similitude Similitude of initial and boundary condition The same similitude dimensionless number
Cl 3 l3 t Q CQ = = 3 = = Cl 2 CV Qm l m tm Ct
ratio of volume rate:
ratio of kinematic viscosity:
Cl 2 l2 t ν Cν = = 2 = = Cl CV ν m l m t m Ct
ratio of rotation:
kν = 1 k L kV
kν =1 1/ 2 kL kL
1 kv = 10
3/ 2
VL
kV = k L = 1 ν '≠ ν = ?
3/2 kν = k L
if
1 kL = , 10
1 = 31 .62
3. Model experiment
* the most important force (dimensionless number) * laminar or complete turbulence rough zone
n y = k x x x ... x a n a1 1 a2 2 a3 3
example
3. Buckingham
π
Method (group Method)
The number of independent dimensionless groups of variables needed to correlate the variables in a given process is equal to n-m, where n is the number of variables involved and m is the number dimensions included in the variables.
Gravity:
Fg = mg = ρΩ g = ρ l 3 g
Froud number:
Fr =
V gl
=
Vm g m lm
3. Similitude Principle of flow acted by viscous force
Viscous force
F = Ne ρ l 2V 2
du du 2 Fτ = τ A = µ A=µ l dy dy
φ ( x1 , x2 , x3 , ⋅ ⋅ ⋅⋅, xn ) = 0
πi =
xi x x
a1 a2 i +1 i + 2 am ... x x i +m a3 i +3
f (π 1 , π 2 , π 3 , ⋅ ⋅ ⋅⋅, π m ) = 0
example
4. Model experiment
Derived dimension: velocity: LT-1 acceleration: LT-2 density: ML-3 force: MLT-2 pressure: ML-1T-2 dynamic viscosity: ML-1T-1 kinematic viscosity: L2T-1
F3 F1 F2 = = = CF F1m F2 m F3m
CF = ma = Cm Ca = Cρ Cl 2 CV 2 mm am
prototype
model
4. Relationship
Geometric similitude
(basic and the most obvious requirement)
Dimensional analysis:
How to operate an experiment and analysis experimental date…)
2. Why need we study?
a. The need for developing Fluid Mechanics FM: Theoretical FM Experimental FM Computational FM b. The need of engineering practice
1. Condition of Similitude
Geometric similitude (basic) Motion similitude (result) Dynamic similitude (condition) Similitude of initial and boundary condition
