简支梁计算表
简支梁正截面抗弯承载力计算表格
4 砼弹性模量
5 钢筋弹性模量
6 预应力弹性模量
7 主筋抗拉强度设计值
8
9 板的铰缝截面积
fcd MPa 13.8 fsd MPa 195 fpd MPa Ec MPa 31500 Es MPa 210000 Ep MPa fsd MPa 280
mm2
三 计算系数及其他参数
1 桥梁结构的重要性系数 γo 2 钢筋与砼的弹性模量比 αES 3 预筋与砼的弹性模量比 αEp 4 纵向受拉钢预筋配筋率 ρ
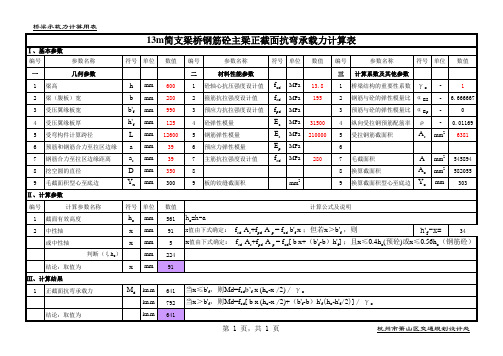
桥梁承载力计算用表
Ⅰ、基本参数
编号
参数名称
13m简支梁桥钢筋砼主梁正截面抗弯承载力计算表
符号 单位 数值 编号
参数名称
符号 单位 数值 编号
参数名称
符号 单位 数值
一
几何参数
1 梁高
2 梁(腹板)宽
3 受压翼缘板宽
4 受压翼缘板厚
5 受弯构件计算跨径
6 预筋和钢筋合力至拉区边缘
7 钢筋合力至拉区边缘距离
224
91
641 当x≤b'f,则Md=fcdb’f x (ho-x /2) / γo 792 当x>b'f,则Md=fcd[ b x (ho-x /2)+(b'f-b)h'f(ho-h'f/2)] / γo
641
第 1 页,共 1 页
杭州市萧山区交通规划设计处
-
1
- 6.666667
-
0
- 0.01169
5 受拉钢筋截面积
As mm2 6381
6
7 毛截面积
A mm2 545894
8 换算截面积
Ao mm2 582055
简支梁和悬臂梁的弯矩挠度计算

0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
#DIV/0!
第四章简支梁设计计算(1)

第四章简支梁设计计算(1)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第四章 简支梁(板)桥设计计算第一节 简支梁(板)桥主梁内力计算对于简支梁桥的一片主梁,知道了永久作用和通过荷载横向分布系数求得的可变作用,就可按工程力学的方法计算主梁截面的内力(弯矩M 和剪力Q ),有了截面内力,就可按结构设计原理进行该主梁的设计和验算。
对于跨径在10m 以内的一般小跨径混凝土简支梁(板)桥,通常只需计算跨中截面的最大弯矩和支点截面及跨中截面的剪力,跨中与支点之间各截面的剪力可以近似地按直线规律变化,弯矩可假设按二次抛物线规律变化,以简支梁的一个支点为坐标原点,其弯矩变化规律即为:)(42maxx l x lM M x -=(4-1) 式中:x M —主梁距离支点x 处的截面弯矩值;m ax M —主梁跨中最大设计弯矩值;l —主梁的计算跨径。
对于较大跨径的简支梁,一般还应计算跨径四分之一截面处的弯矩和剪力。
如果主梁沿桥轴方向截面有变化,例如梁肋宽度或梁高有变化,则还应计算截面变化处的主梁内力。
一 永久作用效应计算钢筋混凝土或预应力混凝土公路桥梁的永久作用,往往占全部设计荷载很大的比重(通常占60~90%),桥梁的跨径愈大,永久作用所占的比重也愈大。
因此,设计人员要准确地计算出作用于桥梁上的永久作用。
如果在设计之初通过一些近似途径(经验曲线、相近的标准设计或已建桥梁的资料等)估算桥梁的永久作用,则应按试算后确定的结构尺寸重新计算桥梁的永久作用。
在计算永久作用效应时,为简化起见,习惯上往往将沿桥跨分点作用的横隔梁重力、沿桥横向不等分布的铺装层重力以及作用于两侧人行道和栏杆等重力均匀分摊给各主梁承受。
因此,对于等截面梁桥的主梁,其永久作用可简单地按均布荷载进行计算。
如果需要精确计算,可根据桥梁施工情况,将人行道、栏杆、灯柱和管道等重力像可变作用计算那样,按荷载横向分布的规律进行分配。
excel计算大全-钢结构计算表格-单跨变截面简支梁

一.1b=100t=10h=230s=6B=#VALUE!mm 2#VALUE!#VALUE!mm#VALUE!mm 3#VALUE!mm 32混凝土等级C208.08板厚h d 100梁跨度6000梁左相邻净距1800梁右相邻净距1800板托顶宽b 0b 1 =600b 2 =6001500mm 150000mm 2#VALUE!mm 2#VALUE!mm混凝土板顶面至组合截面中和轴的距离 x= [b e *h d 2/(2*αE )+A*y]/A 0 =#VALUE!mm混凝土截面惯性矩 I c = b e *h d 3/12=125000000mm 4换算成钢截面的组合截面惯性矩 I 0 = I c /αE + A c *(x-0.5h d )2/αE + I + A(y-x)2 =#VALUE!mm 4#VALUE!mm 4#VALUE!mm 4#VALUE!mm 4#VALUE!mm 43#VALUE!mm 2混凝土板顶面至组合截面中和轴的距离x c = [b e *h d 2/(4*αE )+A*y]/A 0c =#VALUE!mm #VALUE!#VALUE!mm 4#VALUE!mm 4#VALUE!mm 4#VALUE!mm 4二施工阶段的验算1弯矩和剪力钢梁自重:#VALUE!kN/m 板自重: 6.00kN/m 2000mm)板托重:0.90kN/m #VALUE!kN/m自重标准值 g 1:#VALUE!kN/m施工荷载:2.80kN/m钢梁中和轴至钢梁顶面的距离为 y t = [0.5b*t 2 + h*s*(0.5h + t) + B*T*(t+h+0.5T)] / A =钢梁中和轴至钢梁顶面的距离为 y b = h + t + T - y t =钢梁截面惯性矩 I= (b*t 3 + s*h 3 + B*T 3) / 12 + b*t*(yt-0.5t)2 + s*h*(y t -0.5h-t)2 + B*T*(0.5T+h+t-y t )2 =钢梁上翼缘的弹性抵抗矩 W 1 = I / y t =屋面檩条计算截面特征计算钢梁截面特征计算钢梁面积 A =b*t + h*s +B*T =混凝土板截面面积A c = b e * h d =换算成钢截面的组合截面面积A 0=A c /αE +A =混凝土板顶面至钢梁截面中和轴的距离 y = h d + h t +y t =对混凝土板顶面的组合截面弹性抵抗矩 w 0c t = αE *I 0 / x=钢梁上翼缘的弹性抵抗矩 W 2 = I / y b =组合截面特征计算钢与混凝土弹性模量比αE =混凝土板计算宽度b e =换算成钢截面的组合截面面积 A 0c = A c / 2αE + A =换算成钢截面的组合截面惯性矩 I 0c = I c /(2*αE ) + A c *(x c -0.5h d )2/(2*αE) + I + A(y-x c )2 =对混凝土板顶面的组合截面弹性抵抗矩 w 0c tc = 2αE *I 0c / x c =对混凝土板底面的组合截面弹性抵抗矩 w 0c bc =2αE *I 0c / (x c - h d ) =对混凝土板底面的组合截面弹性抵抗矩 w 0c b =αE *I 0 / (x - h d ) =对钢梁上翼缘的组合截面弹性抵抗矩 w 0t = I 0 / (d-x) =对钢梁下翼缘的组合截面弹性抵抗矩 w 0b = I 0 / (H-x) =考虑混凝土徐变的组合截面特征计算对钢梁上翼缘的组合截面弹性抵抗矩 w 0tc = I 0c / (d-x c ) =对钢梁下翼缘的组合截面弹性抵抗矩 w 0bc = I 0c / (H-x c ) =(平台梁间距:自重标准值 g 1k :施工阶段弯矩设计M #VALUE!kN.m 梁跨度:6000mm)施工阶段剪力设计V#VALUE!kN2钢梁抗弯强度设计#VALUE!N/mm 2<215N/mm 2#VALUE!N/mm 2<215N/mm 23钢梁剪应力计算面积矩 S=#VALUE!mm 3#VALUE!N/mm 2<125N/mm 24挠度计算△=5*g*l 4/(384*E*I)=#VALUE!mm < L/400 =15mm三使用阶段的验算1弯矩及剪力找平层重:1.9kN/m 活荷载:15.6kN/m (活荷载:6kn/m 2)78.84kN.m 52.56kN22.1#VALUE!N/mm 2<10N/mm 2#VALUE!N/mm 2<10N/mm 2#VALUE!N/mm 2<215N/mm 2#VALUE!N/mm 2<215N/mm 22.2#VALUE!N/mm 2<10N/mm 2#VALUE!N/mm 2<10N/mm 2#VALUE!N/mm 2<215N/mm 2#VALUE!N/mm 2<215N/mm 22.3(略)2.4(略)3钢梁的剪应力钢梁上翼缘应力 M / r x *W 1 =钢梁下翼缘应力 M / r x *W 2 =钢梁剪应力τ1max = v 1*s 1/I*t w =使用阶段弯矩设计混凝土板底面应力σ0c b =-M/W 0c b =钢梁上翼缘应力σ0t = -M 1/W 1+M 2/W 0t =钢梁下翼缘应力σ0b = -M 1/W 2+M 2/W 0b =考虑混凝土徐变在垂直荷载作用下的正应力使用阶段剪力设计组合梁的抗弯强度在垂直荷载作用下的正应力混凝土板顶面应力σ0c t =-M/W 0c t =钢梁上翼缘应力σ0tc = -M 1/W 1+(M 2g /W 0tc +M 2q /W 0t )=钢梁下翼缘应力σ0bc = -M 1/W 2+(M 2g /W 0bc +M 2q /W 0b )=混凝土板顶面应力:σ0c tc =-(M 2g /W 0c tc +M 2q /W 0c t )=混凝土板底面应力:σ0c bc =-(M 2g /W 0c bc +M 2q /W 0c b )=温度差产生的应力组合梁中由于混凝土收缩引起的内力#VALUE!mm 3#VALUE!mm 3#VALUE!N/mm 2<125N/mm 24组合梁的挠度#VALUE!mm < L/400 =15mm两个受力阶段的荷载对组合梁的钢梁产生的剪应力τ=V 1S 1/It w +V 2S o /I o T w =△=5q k l 4/384EI o +5g k l 4/384EI o c =钢梁腹板顶面处对钢梁中和轴的面积矩S 1=钢梁腹板顶面以外的砼及钢梁上翼缘对组合截面中和轴的面积S o =200T=10 mm#VALUE!mm4300板托高度h t150 mm4#VALUE! #VALUE!#VALUE! #VALUE!#VALUE! #VALUE! #VALUE! #VALUE!#VALUE! #VALUE! #VALUE! #VALUE!#VALUE! #VALUE!。
简支梁固有频率计算公式表

简支梁固有频率计算公式表
简支梁的固有频率可以通过以下公式进行计算:
f = (1/2π) sqrt(k/m)。
其中,f代表梁的固有频率,k代表梁的弹性系数,m代表梁的
质量。
在这个公式中,弹性系数k可以通过梁的材料特性和几何形状
来计算,而梁的质量m可以通过梁的密度和几何形状来计算。
另外,对于简支梁来说,其固有频率的计算还需要考虑梁的长
度L和杨氏模量E。
简支梁的固有频率可以通过以下公式进行计算: f = (1/2L) sqrt(E/m)。
在这个公式中,L代表梁的长度,E代表梁的杨氏模量,m代表
梁的质量。
除了上述的公式,还可以通过有限元分析等方法来计算简支梁
的固有频率。
这些方法可以更加精确地考虑梁的几何形状和边界条件等因素,得到更加准确的固有频率值。
总的来说,简支梁的固有频率可以通过多种公式和方法进行计算,需要考虑梁的材料特性、几何形状、边界条件等因素,以得到准确的结果。
简支梁计算(双向板)

梁截面:b=0.24m L= 4.6mh=0.4m h 0=0.375m梁自重: 2.592KN/m梁两侧板:Q (面)= 5.2KN/(m*m)板1:跨度:L1(长)= 4.6mL1(短)= 3.3m板2:跨度:L2(长)= 4.6m L2(短)= 3.3m 27KN/m Q1=29.592KN/m fc=14.3放大系数1a1=1fy=360放大系数12、计算配筋:Q2=8.58KN/m Q (总)=Q1+Q2=38.172KN/m100.9649KN*m0.20920.23737905.18mm*mm=14.0824KN/m Q (总)=Q1+Q2=43.67439KN/m115.5188KN*m0.239360.2781060.09mm*mm=11.3312KN/mQ (总)=Q1+Q2=40.9232KN/m108.2419KN*m0.224280.25741981.576mm*mmξ=1-SQRT(1-2*as)=板传给梁的线荷载为:Q2=(2*L1(长)-0.5*L1(短))*L1(短)*Q (面)/4/L1(长)+L2(短)*Q (面)/4as=M/(a1*fc*b*h 0*h 0*1000)=M=Q (总)*L*L/8=梁配筋面积As:As=(a1*fc*b*h*ξ*1000000)/fy=(类型三):当梁一侧板为长垮(板1);一侧板为短垮(板2)时:Q2=(2*L1(长)-0.5*L1(短))*L1(短)*Q (面)/4/L1(长)+(2*L2(长)-0.5*L2(短))*L2(短)*Q (面)/4/L2(长)M=Q (总)*L*L/8=梁配筋面积As:as=M/(a1*fc*b*h 0*h 0*1000)=(L1(短)+L2(短))*Q (面)/4=M=Q (总)*L*L/8=(类型二):当梁两侧板均为其长垮时:作用在梁上的总荷载:类型(一):当梁两侧板均为其短垮时:ξ=1-SQRT(1-2*as)=As=(a1*fc*b*h*ξ*1000000)/fy=作用在梁上的总荷载:板传给梁的线荷载为:梁配筋面积As:材料数据:ξ=1-SQRT(1-2*as)=As=(a1*fc*b*h*ξ*1000000)/fy=板传给梁的线荷载为:作用在梁上的总荷载:次梁计算L-1(类型二)1、基本资料:楼板面荷载(包括板自重):作用在梁上墙体线荷载:as=M/(a1*fc*b*h 0*h 0*1000)=需修改计算结果最终结果KN/(m*m)分类。
excel计算大全-钢结构计算表格-简支钢梁计算

excel计算大全-钢结构计算表格-简支钢梁计算简支钢梁计算基本数据输入:梁跨度: l=9000mm梁间距a=2400mm钢材:Q 345f =315N/mm 2fv =185N/mm 2 上翼缘:b 1=400mm t 1=14mm 下翼缘:b 2=300mm t 2=12mm 腹板:h w =574mm t w =8mm即: 断面BH 600x8x400x14x300x12截面特性计算:钢梁截面:A 0=13792mm 2 重量108.3kg/m 钢梁中和轴的位置:y 0=342mm钢梁对X轴截面惯性矩:I z =8.94E+08mm 4 钢梁上翼缘的弹性抵抗矩:W 1x = 3.46E+06mm 3 钢梁下翼缘的弹性抵抗矩:W 2x = 2.61E+06mm 3钢梁对Y轴截面惯性矩:I y = 1.02E+08mm 4i y =85.9 mm y =104.8上翼缘对Y 轴的惯性矩:I 1=7.47E+07mm 4 下翼缘对Y 轴的惯性矩:I 2= 2.70E+07mm 40.73 截面不对称影响系数:0.380.53 工字形截面简支梁的系数0.76 梁的整体稳定系数:0.74 修正后:0.672.截面验算:(1)弯矩及剪力的计算:=+=211I I I b α=-=)12(8.0b b αη=bβ==hb t l 111ξ=bφ='bφλ钢梁自重: 1.30KN/m恒载: 4.00KN/m2=10.90KN/mg1k活载:q c= 3.0KN/m2p k=18.10KN/m p=23.16KN/m 弯矩:M=234.49KN·m 剪力:V=104.22KN(2)钢梁的强度、稳定和挠度的验算:梁的整体稳定应力:σ=101.01N/mm2钢梁上翼缘应力:σ1=67.70N/mm2钢梁下翼缘应力:σ2=89.68N/mm2钢梁剪应力:τ=22.70N/mm2挠度:w=8.4mmw/l=1/1072。
单跨等截面简支梁钢筋计算表(带公式程序)
KN/m
(2)钢梁 的强度、稳 定和挠度的 验算:
钢梁 上翼缘应 力:
钢梁 下翼缘应 力:
钢梁 剪应力:
挠 度:
σ 1= 263.19 N/mm 2
σ 2=
τ=
w= w / l=
263.19 N/mm 2
45.47 N/mm 2
30.2 mm 1/ 199
2/7
U.S.A.
3.参数统计
1.构件总 重:
0.63
0.21 0.18
0.71
14.40 1.00 5/7
U.S.A.
JOB No.:__________
BY________________ DATE______________ CHK'D_____________
6/7
U.S.A.
JOB No.:__________
BY________________ DATE______________ CHK'D_____________
2.截面验 算:
(1)弯矩 及剪力的验 算:
钢梁换算 平均自 重:
恒 载:
0.40 KN/m 4.50 KN/m 2
活 载:
g = 1k 11.65 KN/m q c = 2.50 KN/m 2
pk=
弯矩: 剪力:
17.90
KN/m
M= V=
p = 22.73
102.30 KN ·m
68.20 KN
JOB No.:__________
BY________________ DATE______________ CHK'D_____________
W 2x = 3.89E+05 mm 3 I y = 7.78E+06 mm 4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
U.S.A.
钢梁上翼 缘的弹性 抵抗矩:
钢梁下翼 缘的弹性 抵抗矩:
钢梁对Y 轴截面惯 性矩:
上翼缘对 Y轴的惯性 矩:
下翼缘对 Y轴的惯性 矩:
平面外 稳定系数 计算:
截面不 对称影响 系数:
工字形截 面简支梁 的系数
JOB No.:__________
BY________________ DATE______________ CHK'D_____________
钢梁截 面钢:梁中和 轴的位 置:
钢梁对X 轴截面惯 性矩:
钢梁上翼 缘的弹性 抵抗矩:
钢梁下翼 缘的弹性 抵抗矩:
钢梁对Y 轴截面惯 性矩:
上翼缘对 Y轴下的翼惯缘性对 Y轴的惯性
截面特 性计算:
钢梁截 面钢:梁中和 轴的位 置:
钢梁对X 轴截面惯 性矩:
A 0 = 7884 mm 2 重量 61.9 y 0 = 425 mm
t 1= 8 mm t 2= 8 mm t w= 6 mm
t 1= 8 mm t 2= 8 mm t w= 6 mm
kg/m
1/7
U.S.A.
JOB No.:__________
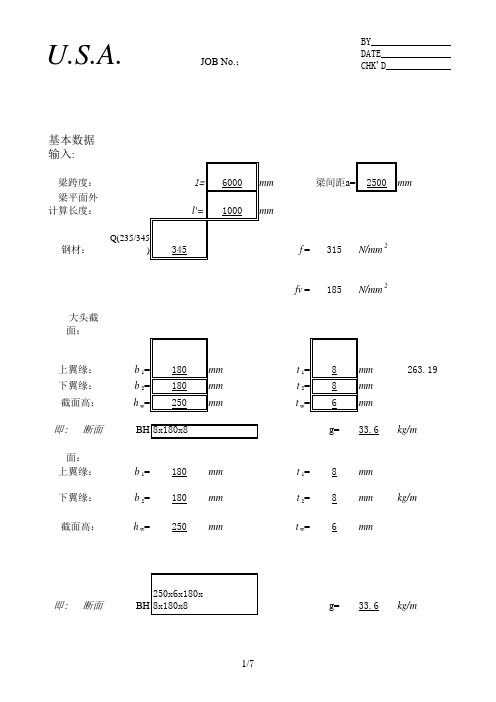
即 : 断面
350x6x180x BH 8x180x8
BY________________ DATE______________ CHK'D_____________
U.S.A.
JOB No.:__________
BY________________ DATE______________ CHK'D_____________
基本数据 输入:
梁跨度: 梁平面外 计算长度:
l= 18000 mm l'= 3500 mm
梁间距a= 6000 mm
钢材: (235/345) 235
BY________________ DATE______________ CHK'D_____________
1.22 0.81
6/7
U.S.A.
JOB No.:__________
BY________________ DATE______________ CHK'D_____________
kg/m 7/7
2.截面验 算:
(1)弯矩 及剪力的验 算:
钢梁换算 平均自 重:
恒 载:
活 载:
0.65 KN/m
0.25 KN/m 2
g = 1k 2.15 KN/m q c = 0.35 KN/m 2
pk=
弯矩: 剪力:
4.25
KN/m
p = 5.52
M = 223.49 KN ·m
V = 49.66 KN
KN/m
f = 215 N/mm 2
大头截 面:
fv = 125 N/mm 2
上翼缘: 下翼缘: 截面高:
即 : 断面 小头截 面:
上翼缘:
下翼缘:
截面高:
b 1= 180 mm b 2= 180 mm h w= 850 mm
850x6x180x BH 8x180x8
b 1= 180 mm b 2= 180 mm h w= 350 mm
W 1x = 5.88E+05 mm 3
W 2x = 5.88E+05 mm 3 I y = 7.78E+06 mm 4
iy=
46.5 mm
y=
75.3
I 1 = 6.67E+06 mm 4
I 2 = 3.89E+06 mm 4
0.63 0.21 0.18
0.71 5/7
U.S.A.
JOB No.:__________
I z = 8.01E+08 mm 4
W 1x = 1.88E+06 mm 3 W 2x = 1.88E+06 mm 3
I y = 7.79E+06 mm 4
iy=
36.6 mm
y=
95.7
I 1 = 6.67E+06 mm 4
I 2 = 3.89E+06 mm 4
A 0 = 4884 mm 2 重量 38.3 y 0 = 175 mm I z = 1.03E+08 mm 4
(2)钢梁 的强度、稳 定和挠度的 验算:钢梁 上翼缘应 力:
钢梁 下翼缘应 力:
σ 1= 145.75 N/mm 2 σ 2= 118.65 N/mm 2 2/7
U.S.A.
钢梁 剪应力挠: 度:
3.参数统计
1.构件总 重:
2.构件实 际重量:
JOB No.:__________
BY________________ DATE______________ CHK'D_____________
τ= w= w / l=
23.65 N/mm 2 62.4 mm
1/ 288
扩大系
ቤተ መጻሕፍቲ ባይዱ
902.1 Kg
数:
1.2
1082.5 Kg
3/7
U.S.A.
JOB No.:__________
BY________________ DATE______________ CHK'D_____________
截面特 性计算:
