第一章《直角三角形》奥数题
八年级下册第一章《直角三角形》培优习题

八年级下册第一章《直角三角形》培优习题一、知识要点填空:1、直角三角形的性质:(1)直角三角形的两个锐角_________(2)直角三角形斜边上的中线等于斜边的_________;(3)直角三角形30°角所对的直角边是______的一半;(4)直角三角形中,如果有一条直角边是斜边的一半,那么这条直角边所对的角是30°.2、直角三角形的判定方法:(1)有一个角是直角的三角形是直角三角形;(2)有两个角______的三角形是直角三角形;(3)如果一条边上的中线等于这边的一半,那么这个三角形是直角三角形。
3、等腰直角三角形是特殊的直角三角形,它的两个底角都是_____,且两条直角边相等。
等腰直角三角形具有等腰三角形和直角三角形的所有性质,是很常见的特殊三角形。
二、练习题1、如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则则∠1+∠2等于__________.2、设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形,则下列四个图中,能表示它们之间关系的是()A. B.C. D.3、如图,Rt△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交AD于E,EF∥AC,下列结论一定成立的是()A.AB=BF B.AE=ED C.AD=DC D.∠ABE=∠DFE4、如图,在△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP的长不可能的是()A.3.5 B.4.2 C.5.8 D.75、如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交于BC的延长线于F,若∠F=30°,DE=1,则EF的长是() A.3 B.2 C.3 D.16、已知等腰△ABC 中,AD ⊥BC 于点D ,且AD=21BC ,则△ABC 底角的度数为___________________.7、四边形ABCD 由一个∠ACB=30°的Rt △ABC 与等腰Rt △ACD 拼成,E 为斜边AC 的中点,则∠BDE=__________.8、已知:在△ABC 中,∠BAC=90°,AD ⊥BC 于点D ,∠ABC 的平分线BE 交AD 于点F ,试说明AE=AF.9、在△ABC 中,∠A=90°,AB=AC ,∠ABC 的平分线BD 交AC 于D ,CE ⊥BD 的延长线于点E .求证:CE =21BD10、一根长2a 的木棍(AB ),斜靠在与地面(OM )垂直的墙(ON )上,设木棍的中点为P .若木棍A 端沿墙下滑,且B 端沿地面向右滑行.木棍滑动的过程中,点P 到点0的距离不变化,在木棍滑动的过程中,△AOB 的面积最大为______________.11、如图在Rt △ABC 中,∠ACB=90°,CD 、CE 分别是斜边AB 边上的高与中线,CF 是∠ACB 的平分线,则∠1与∠2的大小关系是( )A .∠1>∠2 B. ∠1=∠2 C. ∠1<∠2 D.不能确定12、如图,在Rt △ABC 中,∠ACB=90°,AB=2BC ,在直线BC 或AC 上取一点P ,使得△PAB 为等腰三角形,则符合条件的点P 共有( )A .4个B .5个C .6个D .7个13、如图,在直角三角形ABC 中,CM 是斜边AB 上的中线,MN ⊥AB ,∠ACB 的平分线CN 交MN 于N ,求证:CM=MN .14、如图,在斜边长为1的等腰直角三角形OAB 中,作内接正方形A 1B 1D 1C 1;在等腰直角三角形OA 1B 1中作内接正方形A 2B 2D 2C 2;在等腰直角三角形OA 2B 2中作内接正方形A3B3D3C3;…;依次做下去,则第n个正方形A nB n D nC n的边长是_______________.15、下面的方格图案中的正方形顶点叫做格点,图1中以格点为顶点的等腰直角三角形共有4个,图2中以格点为顶点的等腰直角三角形共有________个,图3中以格点为顶点的等腰直角三角形共有_________个,图4中以格点为顶点的等腰直角三角形共有_________个.16、如图,在△ABC中,∠B=90°,∠BAC=78°,过C作CF∥AB,连接AF于BC相交于G,若GF=2AC,则∠BAG=17、如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DFE是等腰直角三角形;②DE长度的最小值为4;③四边形CDFE的面积保持不变;④△CDE面积的最大值为8.其中正确的结论是()A.①②③B.①③ C.①③④D.②③④18、如图,已知OA=a,P是射线ON上一动点(即P可以在射线ON上运动),∠AON=60°,填空:(1)当OP=_________时,△AOP为等边三角形;(2)当OP=__________时,△AOP为直角三角形;(3)当OP满足___________时,△AOP为钝角三角形.GF CB A。
小学奥数-几何五大模型(直角三角形)

小学奥数-几何五大模型(直角三角形)导语:几何学是数学的一个重要分支,对于学生的综合能力和逻辑思维有很大的培养作用。
直角三角形是几何学中的基础概念之一,它具有很多有趣的性质和特点。
本文将介绍直角三角形的定义、性质以及在奥数竞赛中的应用。
一、直角三角形的定义直角三角形是指其中一个角为90°的三角形。
在直角三角形中,我们将直角所在的边称为斜边,另外两个边分别称为直角边。
直角三角形经常用符号∆ABC表示,其中A、B、C分别表示三角形的顶点,而∠C是直角。
二、直角三角形的性质1. 两腰的平方和等于斜边的平方:根据勾股定理,在直角三角形ABC中,我们可以得出以下关系式:AB² + BC² = AC²。
2. 边长关系:如果两个直角三角形的对应直角边相等,那么它们的斜边也相等。
3. 高度关系:直角三角形的高等于斜边的两条直角边的乘积除以斜边。
三、直角三角形在奥数竞赛中的应用直角三角形是数学竞赛中经常出现的题型之一。
通过掌握直角三角形的性质和相关公式,我们可以解决以下类型的问题:1. 求边长:已知一个直角三角形的两个直角边,可以使用勾股定理求解斜边的长度。
2. 求面积:已知直角三角形的两个直角边,可以利用面积公式S = 1/2 * 直角边1 * 直角边2来求解三角形的面积。
3. 判定形状:根据已知边长关系和角度关系,可以判断一个三角形是否为直角三角形。
结语:直角三角形是小学奥数几何学的重要内容,掌握直角三角形的定义、性质和应用是解决几何学问题的基础。
希望本文能够帮助大家加深对直角三角形的理解,并在奥数竞赛中取得更好的成绩。
一年级认识图形奥数题有答案

一年级认识图形奥数题有答案It was last revised on January 2, 2021一年级。
上册第一讲认识图形(一)1.这叫什么?这叫“点”。
用笔在纸上画一个点,可以画大些,也可以画小些。
点在纸上占一个位置。
2.这叫什么?这叫“线段”。
沿着直尺把两点用笔连起来,就能画出一条线段。
线段有两个端点。
3.这叫什么?这叫“射线”。
从一点出发,沿着直尺画出去,就能画出一条射线。
射线有一个端点,另一边延伸得很远很远,没有尽头。
4.这叫什么?这叫“直线”。
沿着直尺用笔可以画出直线。
直线没有端点,可以向两边无限延伸。
5.这两条直线相交。
两条直线相交,只有一个交点。
6.这两条直线平行。
两条直线互相平行,没有交点,无论延伸多远都不相交。
7.这叫什么?这叫“角”。
角是由从一点引出的两条射线构成的。
这点叫角的顶点,射线叫角的边。
角分锐角、直角和钝角三种。
直角的两边互相垂直,三角板有一个角就是这样的直角。
教室里天花板上的角都是直角。
锐角比直角小,钝角比直角大。
习题一1.点(1)看,这些点排列得多好!(2)看,这个带箭头的线上画了点。
2.线段下图中的线段表示小棍,看小棍的摆法多有趣!(1)一根小棍。
可以横着摆,也可以竖着摆。
(2)两根小棍。
可以都横着摆,也可以都竖着摆,还可以一横一竖摆。
(3)三根小棍。
可以像下面这样摆。
3.两条直线哪两条直线相交?哪两条直线垂直?哪两条直线平行?4.你能在自己的周围发现这样的角吗?第二讲认识图形(二)一、认识三角形1.这叫“三角形”。
三角形有三条边,三个角,三个顶点。
2.这叫“直角三角形”。
直角三角形是一种特殊的三角形,它有一个角是直角。
它的三条边中有两条叫直角边,一条叫斜边。
3.这叫“等腰三角形”。
它也是一种特殊的三角形,它有两条边一样长(相等),相等的两条边叫“腰”,另外的一条边叫“底”。
4.这叫“等腰直角三角形”或叫“直角等腰三角形”。
它既是直角三角形,又是等腰三角形。
奥数题20道

奥数题20道1. 直角三角形的勾股定理:a^2 + b^2 = c^2,其中a,b为直角边的长度,c为斜边的长度。
2. 等差数列的通项公式:an = a1 + (n-1)d,其中an为第n个数,a1为首项,d为公差。
3. 等差数列的前n项和公式:Sn = n/2*(a1 + an),其中Sn为前n项和,a1为首项,an为第n个数。
4. 等差数列的首项和公差的关系:d = (an - a1)/(n-1),其中d为公差,an为第n个数,a1为首项。
5. 等比数列的通项公式:an = a1 * r^(n-1),其中an为第n个数,a1为首项,r为公比。
6. 等比数列的前n项和公式:Sn = (a1 * (r^n - 1))/(r - 1),其中Sn为前n项和,a1为首项,r为公比。
7. 二次函数的一般式:y = ax^2 + bx + c,其中a,b,c为常数。
8. 二次函数的顶点坐标公式:xv = -b/(2a),yv = -D/4a,其中xv,yv为顶点的横纵坐标,D为判别式。
9. 二次函数的判别式公式:D = b^2 - 4ac,其中D为判别式,a,b,c为二次函数的系数。
10. 平行四边形的性质:对角线相等且互相平分,相邻角互补,同时对角线之间的夹角相等。
11. 三角形的内角和定理:三角形的三个内角之和等于180度。
12. 正多边形的内角和公式:(n-2) * 180度,其中n为正多边形的边数。
13. 四边形的内角和公式:360度,即四边形的四个内角之和等于360度。
14. 连续整数的和公式:n个连续整数的和为(n/2)(2a + (n-1)d),其中a为第一个整数,d为公差。
15. 组合公式:C(n, r) = n!/(r!(n-r)!),其中C(n, r)为从n个元素中选取r个元素的组合数。
16. 相似三角形的性质:对应角相等,对应边成比例。
17. 直角三角形的正弦定理:sinA/a = sinB/b = sinC/c,其中A,B,C为三角形的角度,a,b,c为对应的边的长度。
小学奥数三角形习题及答案

三角形习题1.如图,在直角AOB 内有一条射线OC,并且AOC ∠比BOC ∠大20︒.则BOC ∠=________.ACOB 2.如图所示,已知∠4的度数是∠1度数的3倍,求∠1,∠2,∠3,∠4分别是多少度?3.如图,已知O 是直线AD 上一点,∠AOB ,∠BOC ,∠COD 三个角从小到大依次相差25°,求这三个角的度数。
4.如图,图中的3∠=________度.5.如图,直角的顶点在直线l 上,则图中所有小于平角的角之和是________度.参考答案1.【答案】35︒【解析】()9020235︒︒︒-÷=2.【答案】45,135,45,135【分析】由和倍问题,∠4是∠1的3倍,而且∠1+∠4=180°,所以∠1=1801+3=45÷()°,则∠4=18045135︒-︒=︒,同理,3180418013545∠=︒-∠=︒-︒=°,2=1801=135∠︒-∠°3.【答案】35;60;85【分析】由和差问题:∠AOB=180-25-25-25=︒︒︒︒÷()335°,∠OBC=+=︒︒352560°,∠COD=60+25=85︒︒°4.【答案】60【解析】因为∠2和30°角组成一个平角,所以218030150︒︒︒∠=-=;因为∠2和∠1组成一个平角,所以1180218015030︒︒︒︒∠=-∠=-=;因为∠1、∠3和图中直角组成一个平角,所以3180190180309060︒︒︒︒︒︒∠=-∠-=--=.5.【答案】450【解析】由一部分组成的角之和是180度,由两部分组成的角之和是18090+度,一共180********++=度.180⎫⎪⎪︒⎬⎪⎪⎭。
直角三角形奥数题
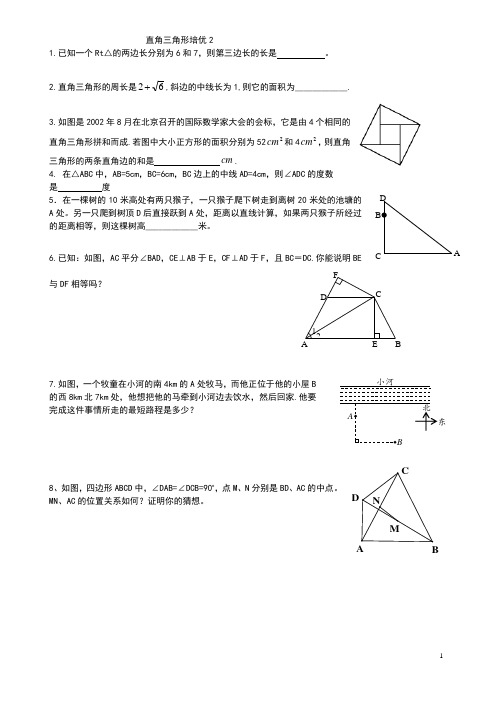
直角三角形培优21.已知一个Rt △的两边长分别为6和7,则第三边长的长是 。
2.直角三角形的周长是62,斜边的中线长为1,则它的面积为____________.3.如图是2002年8月在北京召开的国际数学家大会的会标,它是由4个相同的直角三角形拼和而成.若图中大小正方形的面积分别为522cm 和42cm ,则直角三角形的两条直角边的和是 cm .4. 在△ABC 中,AB=5cm ,BC=6cm ,BC 边上的中线AD=4cm ,则∠ADC 的度数 是 度5.在一棵树的10米高处有两只猴子,一只猴子爬下树走到离树20米处的池塘的A 处。
另一只爬到树顶D 后直接跃到A 处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高____________米。
6.已知:如图,AC 平分∠BAD ,CE ⊥AB 于E ,CF ⊥AD 于F ,且BC =DC.你能说明BE与DF 相等吗?7.如图,一个牧童在小河的南4km 的A 处牧马,而他正位于他的小屋B的西8km 北7km 处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?8、如图,四边形ABCD 中,∠DAB=∠DCB=90o ,点M 、N 分别是BD 、AC 的中点。
MN 、AC 的位置关系如何?证明你的猜想。
A ABCDE F1 2小河D9.如图,在Rt △ABC 中,∠BAC=90°,AC=2AB ,点D 是AC 的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A 、D 重合,连接BE 、EC .试猜想线段BE 和EC 的数量及位置关系,并证明你的猜想.10. 已知,如图,在Rt △ABC 中,∠ACB=90°,∠A=30°,CD ⊥AB 交AB 于点E ,且CD=AC ,DF ∥BC ,分别与AB 、AC 交于点G 、F .(1)求证:GE=GF ;(2)若BD=1,求DF 的长.12、如图,一根长2a 的木棍(AB ),斜靠在与地面(OM )垂直的墙(ON )上,设木棍的中点为P .若木棍A 端沿墙下滑,且B 端沿地面向右滑行.木棍滑动的过程中,点P 到点0的距离不变化,在木棍滑动的过程中,△AOB 的面积最大为______________.13、如图,已知△ABC 为直角三角形,∠C=90°,若沿图中虚线剪去∠C ,则则∠1+∠2等于__________.14.已知,如图△ABC 是边长4cm 的等边三角形. 动点P 从点A 出发,沿AB 向点B 运动,动点Q从点B出发,沿BC 向点C 运动,如果动点P 、Q 都以1cm/s 的速度同时出发.设运动时间为t (s ),那么t 为何值时,△PBQ 是直角三角形?B CQ。
九年级奥数培训解直角三角形-奥数精讲与测试

知识点、重点、难点直角三角形中角与角之间关系为两锐角互余;边与边之问的关系为勾股定理;边与角之间的关系则可由两锐角的正余弦、正余切公式给出.三角形A BC 中,2sin sin sin a b cR A B C===,其中a 、b 、c 分别为 ∠A 、∠B 、∠C 所对的边,R 为△ABC 外接圆半径,称为三角形的正弦定理.图中BD =c cos B ,DC = a -c cos B .所以2222b AC AD DC ==+22(sin )(cos )c B a c B =+- 222cos a c ac B =+-①同理可得 2222cos .a b c bc A =+- ②2222cos .c a b ab C =+-③上述三式称为三角形的余弦定理.将①②③式变形可得222222cos ,cos ,22a c b b c a B A ac bc+-+-== 222cos .2a b c C ab+-=此三式用于已知三角形三边求三角形内角,而且容易验证:当三角形内角为钝角时,其余弦值小于零,这为判断钝角增加了一种新方法.三角形的面积的另一个公式为:三角形面积等于两边及其夹角正弦的乘积的一半,即111sin sin sin .222ABC S ab C bc A ac B ∆=== 直角三角形的边角关系、三角形的正余弦定理,为解直角三角形和有关三角形边角的问题提供了多种方法.例题精讲例1:如图,△ABC 中,∠C =90°,AB =10,AC =6,AD 是∠BAC 的平分线,求点B 到直线AD 的距离BH . 已知Rt △ABH 中AB =10,要求BH ,可求出∠BAH 的正弦值,而∠BAH =∠CAD ,因而可先 求出DC 的长.解:作DE ⊥AB 于E ,有AE =AC =6,ED =CD .设DC =3k ,由三角形内角平分线性质有106BD DC =,则5.BD k =Rt △BDE 中,222,DE BE BD +=即222(3)(106)(5)k k +-=,得 1.k =2233,6335CD k AD ===+=,sin ,105BHDAC ∠==故2 5.BH =例2:如图,证明单位圆(半径为1)上的锐角三角形的三个角的余弦之和小于该三角形周长之半.证明:锐角△ABC 中,有A +B > 90°,A > 90°-B ,则cos A <cos(90°-B )= sin B .同理有cos B <sin C ,cos C <sin A ,故cos A +cos B +cos C <sin A +sin B +sin C .根据正正弦定理有22sin sin sin a b cR A B C====,所以2sin sin sin a b c A B C ++=++,即sin sin sin A B C ++=1()2a b c ++,故1cos cos cos ().2A B C a b c ++<++例3:已知△ABC 的面积2224a b c S ∆+-=,试求内角C 的大小.解:2224a b c S ∆+-=,又有1sin 2S ab C ∆=,则2221sin ,42a b c ab C +-=222sin .2a b c C ab +-=由余弦定理知222cos 2a b c C ab+-=,故sin cos ,C C =两边除以cos C ,有sin tan 1,cos CC C==故45.C =例4:如图,某污水处理站计划砌一段截面为等腰梯形的排污渠.如果渠深为h ,截面积为S ,试求当倾角θ为多少时造价最小?分析 要使造价最小,只需考虑AD +DC +CB 最小,故首先设法用h 、S 、θ表示AD +DC +CB .解:11()(22cot )(cot )22S AB CD h CD h h CD h h θθ=+=+=+,有cot S CD h h θ=-,则22(sin h S AD DC CB AD CD hθ++=+=+-(2cos )cot ).sin S h h h θθθ-=+因S 、h 为常数,则要求AD +DC +CB 的最小值,只需求2cos sin θθ-的最小值.设2cos ,sin m θθ-=两边平方整理得222(1)cos 4cos (m m θθ+-- 4)0-=,222224(1)(4)2(3)cos .m m m m θ±++-±-==由上式知22(3)0m m -≥,解得3m ≥,故当3m =时,2cos sin θθ-有最小值.当3m =时,221cos 12m θ==+,从而60θ=,此时排污渠造价最小.例5:如图,在△ABC 中,已知最大内角A 是最小内角C 的2倍,且三边的长a 、b 、c 是三个连续自然数,求三角形各边的长.解:设三角形三边分别是a =n +1,b =n 、c =n -1(n 为自然数,且n ≥2). 如图作∠A 的平分线AD 交BC 于D ,再作DE ⊥AC 于E .因为∠1=∠2,所以AB BDAC DC=,所以AB AC BC AC DC +=,所以(1).21n n DC n +=- 又因为∠2=∠C ,所以AD CD =,所以1.22n EC AC ==在Rt △EDC 中,21cos .2(1)EC n C DC n -==+又在ABC ∆中,由余弦定理有222222(1)(1)4cos .22(1)2(1)BC CA AB n n n n C BC CA n n n +-++--+===++所以2142(1)2(1)n n n n -+=++,所以5n =,所以此三角形的三边长为4、5、6.A 卷一、填空题1.一个三角形的一边长为2,这条边上的中线是1,另两边之和是31+, 则这个三角形的另两边之长分别是 和 .2.在Rt △ABC 中,∠C = 90°,AC=6,CA 的平分线AD=43,则AB = .3.在Rt △ABC 中,∠C = 90°,BC=35,AC=315,则∠A = ,外接圆的半径是 .4.梯形的两底长分别等于13厘米和5厘米,两底角分别是30°和60°,则梯形的周长是 厘米.5.在Rt △ABC 中,∠C = 90°,AC=2,cosB=35,则ABC S ∆= .6.已知直角三角形斜边的长是斜边上的高的4倍,那么这个三角形的两个锐角度数分别是 度和 度.7.若0°<α <90°,那么以sin α、cos α、tan α·cot α为三边的三角形ABC 的内切圆半径和外接圆半径这和等于 .8.计算200120001(tan 60)(3tan 30)3= .9.已知tan α=2,α为锐角,4cos 5sin 2cos 3sin αααα-=+ .10.如果等腰三角形ABC 中,底角是30°,面积为1003,那么ABC ∆的周长是 .二、解答题11.已知等腰直角三角形ABC 中,∠C =90°,点D 在直线BC 上,且BD = AB ,求∠ADB 的余切值.12.如图,已知△ABC 中,∠C = 90°,E 、F 在AB 边上,AF=EF=EB ,且CF = sin α,CE =cos α,求斜边AB 的长. B 卷一、填空题1.在△ABC 中,有一个角为60°,103S ∆=,它的周长是20,则它的三边之长分别为 、 和 .2.如图,在Rt △ABC 中,E 、D 分别是边AC 、BC 的中点,BE =222,AB =10,∠C =90°,则AD = .3.计算tan 1°·tan 2°·tan 3°·…·tan 88°·tan 89°= .4.已知在直角三角形ABC 中,∠C = 90°,tan 2A +cot 2A = 5,则tan A +cot A = .5.在直角三角形中,斜边长为C ,面积为S ,那么这个三角形的两直角边长 分别是 和 .6.在△ABC 中,∠B =30°,∠BAC =135°,BC =10,则AB = .7.计算tan 15°= .8.如图,在等腰直角三角形ABC 中,斜边AB 上有两点M 、N ,且∠MCN = 45°.记AM = m ,MN =x ,BN = n ,则以x 、m 、n 为三边长的三角形是 三角形.9.如图,在△ABC 中AB = AC ,∠ABN =∠MBC ,BM = NM , BN = 2a ,则点N 到边BC 的距离是 (用含a 的代数式表示).10.在△ABC 中,∠BAC =120°,∠ABC =15°,∠A 、∠B 、∠C 的对边分别为a 、b 、c ,那么a :b :c =二、解答题11.如图,城市规划期间欲拆除一电线杆AB .已知距电线杆AB 水平距离14米的D 处有一大坝,背水坡CD 的坡度i =2:1,坝高CF 为2米,在坝顶C 处测得杆顶A 的仰角为30°,D 、E 之间是宽为2米的人行道,试问在拆除电线杆AB 时,为确保行人安全,是否需要将此人行道封上?请说明理由(地面上以点B 为圆心、以AB 长为半径的圆形区域为危险区域)(3=1.732 ,2=1.414).12.如图,在△ABC中,∠A=45°,CB =5,BD=3,CD=7,D在边AB的延长线上,求∠CBD和AC的大小.13.在Rt△ABC中,已知两直角边的差为22,两直角边在斜边上的射影的差为23,求△ABC的三边的长.14.如图,ABCD是正方形,E为BC上一点.将正方形折叠,使A点、E点重合,折痕为MN.若tan∠AEN=13DC+CE=10,求(1)△ANE的面积;(2)sin∠ENB的值.C卷一、填空题1. ABC中,∠C=90°,∠A的平分线AD交BC于D,则CDAB AC=-.2.等腰△ABC中,AB=AC,BC=8,且△ABC的内切圆半径是2,则AB= .3. ⊙O的半径为2, ⊙O内的点P到圆心O的距离为1,过P点的弦AB与劣弧AB组成一个弓形,则此弓形面积的最小值是.4.如图,△ABC中,∠C=90°,CD是∠C的平分线,CA=3,CB=4,则CD=.5.已知在直角三角形ABC中,∠C=90°,a、b是∠A、∠B的对边,且220a ab b--=,则tan A=.6.如图,∠C=90°,∠BAC = 30°,BC=1,D为BC边上一点,tan∠ADC是方程22113()5()2x xx x+-+=的较大的根,那么CD的长是.7.已知1sin cos,01805xαα-=<<,则tanα=.8.△ABC中,a cos B=b cos A,关于x的方程22(1)(1)200b xc x x-++-=的两根相等,则△ABC是三角形.9.在△ABC中,BC=3,内切圆半径3r=,则cot cot22B C+=. 10.若0°<θ<30°,sin13kmθ=+(k为常数,0k<),那么m的取值范围是.二、解答题11.设m 、n 、p 是正数,且222m n p +=,求m np+的最大值.12.如图,△ABC 中,⊙O 内切于△ABC ,切点分别为D 、E 、F ,BD =3,DC =2,∠BAC =60°,求.ABC S ∆13.如图,CD 是直角三角形ABC 斜边AB 上的高,2BDC ABC ADC S S S ∆∆∆=, 求sin B 的值.14.已知P 是矩形ABCD 内任意一点,连结PA 、PB 、PC 、PD ,求证:在 ∠PAB 、∠PBC 、∠PCD 、∠PDA 四个角中,必有一个不小于45°,也必有一个不大于45°.。
三角形奥数1练习题及答案

三角形奥数1练习题及答案班别:姓名:成绩:1.一个三角形的三个内角中 A 、至少有一个钝角B 、至少有一个直角 C 、至多有一个锐角 D、至少有两个锐角.下列长度的三条线段能组成三角形的是A、,4,B、,6,11C、 1,2,3D、,6,10. 如图在△ABC 中,∠ACB=900,CD是边AB上的高。
那么图中与A、∠BB、∠ACDC、∠BCDD、∠BDCAD第题B∠A相等的角是C4.如图,AC⊥BD,DE⊥AB,下列叙述正确的是A、∠A=∠BB、∠B=∠DC、∠A=∠DD、∠A+∠D=9005.如图,∠A+∠B+∠C+∠D+∠E+∠F的和为 A.180°B.360°C.540°D.720°BC第题EDAABCDF16.等腰三角形两边长分别为,7,则它的周长为 A、13B、 1C、 13或1D、不能确定.如图所示,在△ABC 中,∠B=∠C,FD⊥BC,DE⊥AB,EAF∠AFD=158°, 则∠EDF=________度. A.58° B.68° C.78° D.32°BDC8.一个多边形的内角和等于它的外角和,这个多边形是 A 、三角形B、四边形C、五边形D、六边形.能将三角形面积平分的是三角形的A、角平分线B、高C、中线D、外角平分线B第题CA10.如图,AB∥CD,∠A=700,∠B=400,则∠ACD= A、50 B、00 C、00 D、 1100二,填空11.长为11,8,6,4的四根木条,选其中三根组成三角形有种选法,它们分别是12.一个多边形的内角和是外角和的3倍,它是_____边形;一个多边形的各内角都等于1200度,它是_____边形。
13.已知△ABC为等腰三角形,①当它的两个边长分别为cm和cm时,它的周长为_____;②如果它的周长为1cm,一边的长为cm,则腰长为_____.14.如果一个多边形的每一外角都是240,那么它边形BA80EDxy15.如图,∠1=∠2=30,∠3=∠4,∠A=80,则x?,2第题C16.如图飞机要从A地飞往B地,因受大风影响,一开始就偏离航线18°,飞到了C地,已知∠ABC=10°,现在飞机要达到B地需以_____的角飞行.17.如图,△ABC中,高AD与CE的长分别为2㎝,4㎝求AB与BC的比是多少?BDCAE18.如图,△ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于E,∠A=60°,∠BDC=95°,求△BDE各内角的度数. AE319.如图,△ABC中,∠A=36°,∠ABC=40°,BE平分∠ABC,∠E=18°,CE平分∠ACD吗?为什么?20.如图所示,已知∠1=∠2,∠3=∠4,∠C=32°,∠D=28°,求∠P的度数.CAPD1-5.DBCCB-10BBBCB 11. ①、6、②4、6、11 ③4、8、11. ④6、8、11 12.,6;13.19;14. 十五15.110°130°16.28° 1因为s?ABC?12AB?CE?12BC?AD高AD=2㎝CE=4ABBC?AD21CE?4?218.略19. 解:设AP与BC交于K,∵在△ACK与△BPK中,∠AKC=∠PKB,∴∠P+∠3=∠1+∠C,即∠P=∠1-∠3+∠C,① 设AD与BP 交于F,同理有∠P=∠4-∠2+∠D,② 由于∠1=∠2,∠3=∠4,则①+②得,2∠P=∠C+∠D=32°+28°=60°,∴∠P=30°故答案为:30°.5㎝所以一年级奥数题图形的变化规律在下图的一组图形中,”?”处应填什么样的图形?图形的等份划分在右图中画一条直线,把图形分成形状相同、大小相等的两部分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章《直角三角形》培优试题
1.已知一个Rt △的两边长分别为6和7,则第三边长的长是 。
2.直角三角形的周长是62 ,斜边的中线长为1,则它的面积为____________.
3.如图是2002年8月在北京召开的国际数学家大会的会标,它是由4个相同的直角三角形拼和而成.若图中大小正方形的面积分别为522
cm 和42
cm ,则直角
三角形的两条直角边的和是 cm .
4. 在△ABC 中,AB=5cm ,BC=6cm ,BC 边上的中线AD=4cm ,则∠ADC 的度数 是 度
5.在一棵树的10米高处有两只猴子,一只猴子爬下树走到离树20米处的池塘的
A 处。
另一只爬到树顶D 后直接跃到A 处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高____________米。
6.已知:如图,AC 平分∠BAD ,CE ⊥AB 于E ,CF ⊥AD 于F ,且BC =DC.你能说明BE
与DF 相等吗?
7.如图,一个牧童在小河的南4km 的A 处牧马,而他正位于他的小屋B
的西8km 北7km 处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?
8、如图,四边形ABCD 中,∠DAB=∠DCB=90o
,点M 、N 分别是BD 、AC 的中点。
MN 、AC 的位置关系如何?证明你的猜想。
A
A B C D
E F
1 2
小河
D
9.如图,在Rt △ABC 中,∠BAC=90°,AC=2AB ,点D 是AC 的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A 、D 重合,连接BE 、EC . 试猜想线段BE 和EC 的数量及位置关系,并证明你的猜想.
10. 已知,如图,在Rt △ABC 中,∠ACB=90°,∠A=30°,CD ⊥AB 交AB 于点E ,且CD=AC ,DF ∥BC ,分别与AB 、AC 交于点G 、F . (1)求证:GE=GF ;
(2)若BD=1,求DF 的长.
12、如图,一根长2a 的木棍(AB ),斜靠在与地面(OM )垂直的墙(ON )上,设木棍的中点为P .若木棍A 端沿墙下滑,且B 端沿地面向右滑行.木棍滑动的过程中,点P 到点0的距离不变化,在木棍滑动的过程中,△AOB 的面积最大为______________.
13、如图,已知△ABC 为直角三角形,∠C=90°,若沿图中虚线剪去∠C ,则则∠1+∠2等于__________.
14.已知,如图△ABC 是边长4cm 的等边三角形. 动点P 从点A 出发,沿AB 向点B 运动,动点
Q
从点
B
出发,沿
BC 向点C 运动,如果动点P 、Q 都以1cm/s 的速度同时出发.
设运动时间为
t (s ),那么t 为何值时,△PBQ 是直角三角形?
B
C
Q。
