集合的运算交和并(20200926054838)
集合中元素的交并补运算

集合中元素的交并补运算一、集合的基本概念1.集合的定义:集合是由确定的、互异的元素构成的整体。
2.集合的表示方法:用大括号括起来,如{a, b, c}。
3.集合的元素:集合中的每一个成员称为元素。
二、集合的基本运算1.交集(∩):两个集合中共同拥有的元素构成的新集合。
2.并集(∪):两个集合中所有元素(包括重复元素)构成的新集合。
3.补集(’):一个集合在全集中所没有的元素构成的新集合。
三、交集的性质1.交换律:A∩B=B∩A2.结合律:(A∩B)∩C=A∩(B∩C)3.对于任何集合A,A∩∅=∅=A∩A四、并集的性质1.交换律:A∪B=B∪A2.结合律:(A∪B)∪C=A∪(B∪C)3.对于任何集合A,A∪∅=A=A∪A4.分配律:A∪(B∩C)=(A∪B)∪(A∪C)五、补集的性质1.A’∪A=∅,A’∩A=U(其中U为全集)2.(A’∪B)’=A∩B3.(A’∩B)’=A∪B六、交、并、补运算的应用1.集合的划分:将一个集合分成若干个互不交集的过程。
2.集合的覆盖:用若干个集合覆盖一个集合的过程,涉及到并集的性质。
3.集合的包含关系:通过交集和补集判断两个集合的包含关系。
七、注意事项1.集合运算中,元素必须满足确定性和互异性。
2.集合运算中,要注意区分集合与元素的关系,遵循运算法则。
3.在解决实际问题时,要灵活运用集合的交、并、补运算,简化问题。
通过以上知识点的学习,学生可以掌握集合中元素的交并补运算的基本概念、性质和应用,为后续数学学习打下坚实的基础。
习题及方法:1.习题:设集合A={1, 2, 3},集合B={2, 3, 4},求A∩B和A∪B。
解题方法:根据交集和并集的定义,可以直接找出A和B中共同的元素和所有元素。
解:A∩B={2, 3},A∪B={1, 2, 3, 4}。
2.习题:如果集合A={x | x是小于5的整数},集合B={x | x是小于6的整数},求A∩B和A’∪B。
集合的运算---交、并

-2
3
从图形可以看出,阴影部分即是集合A 与集合B 的交集
A B { x | x 2 } { x | x 3} { x | 2 x 3}
例5:设A={x|x是等腰三角形},B={x|x是直角三角形},求A∩B 分析:此题仍是求交集,如果用文氏图表示各个集合,可能会 方便我们的理解
1
①
4
2
3
(1)
A B A A B, A B B A B
B
A(Leabharlann 2)A B AA B B
②如果集合A是集合B的子集:则有 A B A , A B B
即: A
B A B A
?
A B A B B
?
例1:设A={4,5,6,8},B={3,5,7,8},求A∪B 分析:此题是求两个集合的并集,如果用文氏出表示各个集合, 可能会方便我们的理解 A 4, 5, 3,
1
4
2
3
注意:定义中的“或”字,它说明A∪B中的元素有下列三种情况: x A, x B 或 x A, x B 或 x A, x B 2、交集:一般地,由所有属于集合A,且属于集合B的元素所组成的 集合,叫做集合A与集合B的交集。 记作:A B 读作:“A交B” 即 A B { x | x A , 且 x B } 注意:定义中的“且”字,它说明A∩B中的任一元素x都是A与B的 公共元素。由此可知, A∩B必是A和B的公共子集。 即: A B A , A B B 所以 A B A A B , A B B A B
A
B
解:将集合A,集合B用上图表示 A∩B ={x|x是等腰三角形}∩{x|x是直角三角形} ={x|x是等腰直角三角形}
集合的运算律公式(二)

集合的运算律公式(二)集合的运算律公式交换律交换律指的是集合的并、交运算,在交换操作的顺序不影响最终结果。
具体公式如下:•并运算交换律:A ∪ B = B ∪ A•交运算交换律:A ∩ B = B ∩ A例如:设集合 A = {1, 2, 3},集合 B = {3, 4, 5}。
则根据并运算交换律,有A ∪ B = B ∪ A = {1, 2, 3, 4, 5}。
根据交运算交换律,有A ∩ B = B ∩ A = {3}。
结合律结合律指的是集合的并、交运算,在结合操作的顺序不影响最终结果。
具体公式如下:•并运算结合律:(A ∪ B) ∪ C = A ∪ (B ∪ C)•交运算结合律:(A ∩ B) ∩ C = A ∩ (B ∩ C)例如:设集合 A = {1, 2, 3},集合 B = {3, 4, 5},集合 C = {1, 3, 5}。
则根据并运算结合律,有(A ∪ B) ∪ C = A ∪ (B ∪C) = {1, 2, 3, 4, 5}。
根据交运算结合律,有(A ∩ B) ∩ C = A ∩ (B ∩ C) = {3}。
分配律分配律指的是集合的并、交运算之间的关系。
具体公式如下:•并运算对交运算的分配律:A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)•交运算对并运算的分配律:A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)例如:设集合 A = {1, 2, 3},集合 B = {3, 4, 5},集合 C = {1, 3, 5}。
根据并运算对交运算的分配律,有 A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) = {1, 2, 3, 4, 5}。
根据交运算对并运算的分配律,有A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) = {1, 3}。
吸收律吸收律指的是集合的并、交运算与集合的子集之间的关系。
具体公式如下:•并运算对子集的吸收律:A ⊆ (A ∪ B)•交运算对子集的吸收律:(A ∩ B) ⊆ A例如:设集合 A = {1, 2, 3},集合 B = {3, 4, 5}。
高中数学课件集合的运算交、并

2021/4/27
例2:设A={x|x是锐角三角形},B={x|x是钝角三角形},求A∪B
解:A∪B ={x|x是锐角三角形} ∪{x|x是钝角三角形} ={x|x是斜三角形}
例3:设 A { x | 1 x 2 } , B { x | 1 x 3 } 求 A , B
分析:此题与例1类似,与实数大小有关系,利用数轴处理
-1
1 23
解:将集合A,集合B用上图表示
A B {x| 1x2 } {x|1x3 } {x| 1x3 }
练习:设 A { x | 1 x 0 } , B { x |1 x 3 } 求 A ,B
2021/4/27
例4:设 A { x |x 2 } , B { x |x 3 } , A B 求 .
分析:求两个集合的交集即是求既属于集合A又属于集合B的元素, 此题与实数大小有关系,利用数轴处理会是问题简便
解:在数轴上分别作出集合A 集合B所对应的部分
-2
3
从图形可以看出,阴影部分即是集合A 与集合B 的交集
A B { x |x 2 } { x |x 3 } { x | 2 x 3 }
2021/4/27
14Βιβλιοθήκη 32注意:定义中的“或”字,它说明A∪B中的元素有下列三种情况:
xA,xB或 xA,xB或 xA,xB 2、交集:一般地,由所有属于集合A,且属于集合B的元素所组成的
集合,叫做集合A与集合B的交集。
记作:AB 读作:“A交B” 即 A B { x |x A ,且 x B }
注意:定义中的“且”字,它说明A∩B中的任一元素x都是A与B的 公共元素。由此可知, A∩B必是A和B的公共子集。
交集和并集的计算方法

交集和并集的计算方法嘿,咱今儿来聊聊交集和并集的计算方法哈!这可有意思啦!你看哈,交集就像是两个圈子重叠的那一块儿。
比如说,咱有一堆水果,一个圈子里是苹果、香蕉、橘子,另一个圈子里是香蕉、梨、葡萄,那它们重叠的部分,也就是香蕉,这就是交集啦!这多形象啊!计算交集呢,就是找出那些同时属于两个集合的元素。
那并集呢,就像是把两个圈子里的所有东西都合到一块儿。
还是刚才那堆水果,把两个圈子里的所有水果都算上,苹果、香蕉、橘子、梨、葡萄,这就是并集啦!是不是很好理解呀?咱举个具体的例子呗,有集合A 是{1,2,3,4},集合 B 是{3,4,5,6}。
那它们的交集不就是{3,4}嘛,因为 3 和 4 是这两个集合都有的呀。
它们的并集呢,就是{1,2,3,4,5,6},把两个集合里的数都搁一块儿啦!再想想,交集是不是有点像咱找朋友,得是两边都有的那几个特别的人;并集呢,就像是把两边认识的人都拢到一起,人可就多啦!这计算方法不难吧?可别小瞧了它哟!在好多地方都用得到呢。
比如说,咱统计喜欢不同运动的人,那喜欢篮球和喜欢足球的人的交集,就是既喜欢篮球又喜欢足球的人呗;它们的并集就是喜欢篮球或者喜欢足球的人啦。
还有啊,生活中也能找到交集和并集的影子呢!比如说你有一堆爱好,我也有一堆爱好,那咱俩爱好的交集,就是咱俩都喜欢的东西呀,说不定还能因为这个成为好朋友呢!而咱俩爱好的并集,那可就是丰富多彩啦,能一起玩的东西可多了去了。
学了交集和并集的计算方法,就像是掌握了一把钥匙,能打开好多知识的大门呢!以后遇到更复杂的问题,咱也不怕啦,就用这方法去分析分析,肯定能找到答案。
总之呢,交集和并集的计算方法真的很有用,很有趣呀!咱可得好好掌握,以后肯定用得上,对吧?。
集合的并、交、补基本运算法则
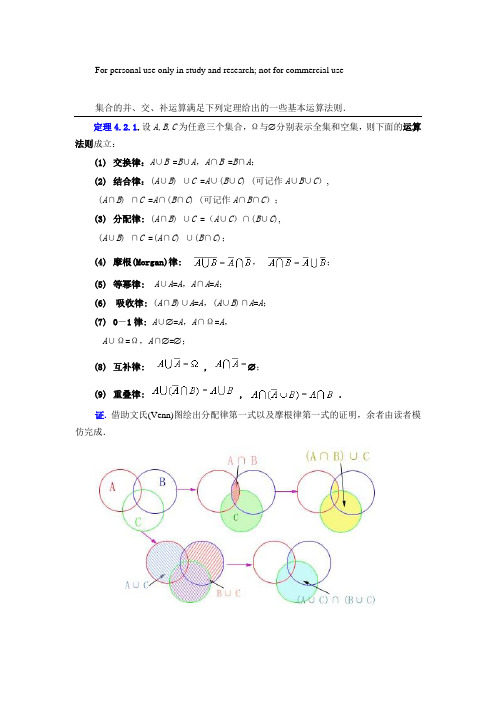
For personal use only in study and research; not for commercial use集合的并、交、补运算满足下列定理给出的一些基本运算法则.定理4.2.1.设A,B,C为任意三个集合,Ω与∅分别表示全集和空集,则下面的运算法则成立:(1)交换律:A∪B =B∪A,A∩B =B∩A;(2)结合律:(A∪B) ∪C =A∪(B∪C) (可记作A∪B∪C),(A∩B) ∩C =A∩(B∩C) (可记作A∩B∩C);(3)分配律: (A∩B) ∪C =(A∪C)∩(B∪C),(A∪B) ∩C =(A∩C) ∪(B∩C);(4)摩根(Morgan)律: ,;(5)等幂律: A∪A=A,A∩A=A;(6)吸收律: (A∩B)∪A=A,(A∪B)∩A=A;(7)0―1律: A∪∅=A,A∩Ω=A,A∪Ω=Ω,A∩∅=∅;(8)互补律: , ∅;(9)重叠律: , .证.借助文氏(Venn)图绘出分配律第一式以及摩根律第一式的证明,余者由读者模仿完成.例4.2.1 试证明等式证.=Ω∩C=C对偶.定理4.2.1的九条定律中的每一条都包含两个或四个公式,只要将其中一个公式中的∪换成∩,同时把∩换成∪,把∅换成Ω,同时把Ω换成∅,这样就得到了另一个公式,这种有趣的规则称为对偶原理. 例如,摩根定律中的∪换成∩,∩换成∪,就得到了另一个摩根公式.例4.2.2 的对偶为;的对偶为;的对偶式是仅供个人用于学习、研究;不得用于商业用途。
For personal use only in study and research; not for commercial use.Nur für den persönlichen für Studien, Forschung, zu kommerziellen Zwecken verwendet werden.Pour l 'étude et la recherche uniquement à des fins personnelles; pas à des fins commerciales.толькодля людей, которые используются для обучения, исследований и не должны использоваться в коммерческих целях.以下无正文仅供个人用于学习、研究;不得用于商业用途。
集合中的运算和关系

集合中的运算和关系集合是数学中的一个基本概念,它是由一些确定的、互不相同的对象构成的整体。
集合中的运算和关系是研究集合性质和结构的重要内容。
一、集合的运算集合的运算包括并集、交集、差集和补集等。
1.并集:设A、B是两个集合,它们的并集记为A∪B,表示A和B中所有元素的集合。
2.交集:设A、B是两个集合,它们的交集记为A∩B,表示同时属于A和B的元素的集合。
3.差集:设A、B是两个集合,它们的差集记为A-B,表示属于A但不属于B的元素的集合。
4.补集:设U是一个全集,A是U的一个子集,A的补集记为A’,表示U中不属于A的元素的集合。
二、集合的关系集合之间的关系主要包括包含关系、相等关系和不相交关系等。
1.包含关系:设A、B是两个集合,如果A中的所有元素都属于B,则称A包含于B,记为A⊆B。
如果A包含于B且B包含于A,则称A等于B,记为A=B。
2.相等关系:设A、B是两个集合,如果A包含于B且B包含于A,则称A等于B,记为A=B。
3.不相交关系:设A、B是两个集合,如果A和B没有共同的元素,则称A和B不相交,记为A∩B=∅。
三、集合的性质1.确定性:集合中的元素是确定的,不含有不确定性。
2.互异性:集合中的元素是互不相同的。
3.无序性:集合中的元素没有顺序。
四、集合运算的性质1.结合律:对于集合的并集、交集和差集运算,都满足结合律。
2.交换律:对于集合的并集、交集和差集运算,都满足交换律。
3.分配律:对于集合的并集和交集运算,满足分配律。
五、集合的关系的性质1.自反性:对于任意集合A,A包含于A。
2.对称性:对于任意集合A、B,如果A包含于B,则B包含于A。
3.传递性:对于任意集合A、B、C,如果A包含于B且B包含于C,则A包含于C。
以上是集合中的运算和关系的基本知识点,希望对你有所帮助。
习题及方法:1.习题:设集合A={1, 2, 3},集合B={2, 3, 4},求A∪B、A∩B、A-B、A’。
集合 运算

集合运算集合运算集合论是数学中最基础的部分之一,而集合运算就是我们对集合之间关系的描述和运算规律的探讨。
在实际生活和学术研究中,集合运算起着极为重要的作用,无论从数学上还是其他领域的应用来看,集合运算都是不可或缺的工具。
在此,我们将重点介绍集合运算的基础知识,按照不同的类别进行分类介绍。
一、集合的基本运算集合基本运算有三个:并集、交集和差集。
并集:当A和B是两个集合时,集合A和集合B的并集(记作A∪B)是由属于集合A或属于集合B的元素构成的新集合。
交集:当A和B是两个集合时,集合A和集合B的交集(记作A∩B)是由属于集合A且属于集合B的元素构成的新集合。
差集:当A和B是两个集合时,集合A和集合B的差集(记作A-B)是由属于集合A但不属于集合B的元素构成的新集合。
二、补集运算补集是指一个集合与它的全集的差集,即一个集合中所有不属于自己的元素的集合。
与其他运算不同,这是只需要一个集合即可完成运算的一种特殊运算方式。
补集常用符号为C(A),表示集合A的补集,C(A)=U-A 。
其中, U 表示构成某一集合的所有元素的全部可能的“全集”。
三、笛卡尔积当A和B是两个集合时,笛卡尔积(记作A×B)是由所有形如(a,b)的有序对构成的集合,其中a∈A,b∈B。
四、集合运算除了以上几种基本运算,还有一些其它的常规运算,这里简单介绍两种:并集和交集的笛卡尔积:集合A和B的并集与交集的笛卡尔积分别是(A×B)∪(A×B) 和(A×B)∩(A×B) 。
幂集:集合A的所有子集构成的集合称为 A 的幂集。
极其重要的一点是将幂集定义为集合 A 的所有子集,不包括空集,因此 A 的幂集元素个数是 2^n,n 为集合 A 中元素的个数。
总结:集合运算是集合论中重要的一个部分,集合之间的基本运算包括并集、交集、差集以及补集等。
此外,还有笛卡尔积和幂集等其他重要概念。
在实际生活和学术研究中,集合运算帮助我们更好地描述和计算不同集合之间的关系,并提供了大量的重要工具和方法。
