不同温度和压力下的声速
空气的声速和声波的特性

空气的声速和声波的特性空气,作为一种常见的气体,具有一定的声速和声波特性。
本文将从声速和声波传播特性两个方面来探讨空气的声学性质。
一、空气的声速特性声速是声波在介质中传播的速度,在空气中的声速受到多个因素的影响。
1. 温度:空气的声速与温度密切相关。
一般情况下,温度越高,声速越快;温度越低,声速越慢。
这是因为温度升高会导致空气分子的平均速度增加,分子之间的碰撞频率也增加,从而加快声波的传播速度。
2. 湿度:湿度对空气的声速也有一定的影响。
相对湿度越高,空气中的水蒸气分子越多,导致声波传播的速度稍慢于干燥的空气。
这是因为水蒸气分子比空气分子要重,会影响声波在介质中的传播速度。
3. 气压:气压的变化对声速也有一定的影响。
一般情况下,气压越高,声速越快;气压越低,声速越慢。
这是因为空气分子受到的压力越大,分子之间的碰撞频率也增加,从而加快声波的传播速度。
二、声波的特性声波是一种机械波,是由物体振动引起的,通过介质传播的能量传递。
1. 频率:声波的频率是指单位时间内声波振动的次数,单位为赫兹(Hz)。
不同频率的声波对应着不同的音调,人耳能够听到的频率范围通常为20Hz至20kHz。
2. 波长:声波的波长是指在媒质中传播一个完整的波的距离。
波长和频率有关系,其计算公式为λ = v / f,其中λ表示波长,v表示声速,f表示频率。
3. 强度:声波的强度是指单位面积上通过的声能,与声波的振幅相关。
强度越大,声音越响亮;强度越小,声音越轻。
一般以分贝(dB)为单位来衡量声波的强度。
4. 反射和折射:当声波遇到障碍物时,会发生反射和折射现象。
反射使声波在障碍物表面发生反向传播,折射则是指声波从一个介质传播到另一个介质时改变传播方向。
5. 干涉和衍射:声波也会发生干涉和衍射现象。
干涉是指两个或多个声波相遇时形成增强或减弱的现象,衍射是指声波绕过障碍物传播的现象。
总结:空气作为一种常见的介质,具有一定的声速和声波特性。
空气中的声速与温度关系

空气中的声速与温度关系在自然界中,声音是通过介质传播的,包括空气、水和固体等。
而在空气中传播的声音速度与温度之间存在着一定的关系。
本文将探讨空气中声速与温度的关系,并解释其原因。
一、声速与温度的基本关系根据实验数据和理论计算,可以得出声速与温度之间的关系式:声速(V)与温度(T)成正比,即V ∝ T。
换言之,当温度升高时,声速也会相应地增加;当温度降低时,声速则会减小。
这与我们的日常经验是相符合的。
二、声速与分子速度的关系要深入理解声速与温度关系的原理,我们需要了解气体分子的运动特性。
在空气中,气体分子具有极高的运动速度,它们不断地无规律地碰撞和运动。
当温度升高时,气体分子的平均动能也会增加,分子的碰撞频率也会增加。
而声音的传播就是通过气体分子的碰撞和振动来实现的。
在空气中,声波的传播是通过分子之间的相互碰撞传递的。
当声波通过一个分子时,这个分子会将振动能量传递给下一个分子,并继续传递下去。
而当温度升高时,分子的运动速度增加,它们之间的碰撞频率增加,传递能量的速度也会变快,从而导致声速的增加。
三、声速与温度的具体关系实际上,声速与温度的关系可以通过一个较为简单的公式来表示,即V = V₀ + 0.6T。
其中,V₀是声速在0摄氏度时的数值,而T表示气体的温度。
这个公式的推导基于理想气体状态方程和声学原理。
根据这个公式,我们可以清楚地看到,声速与温度的关系是线性的。
也就是说,当温度升高1摄氏度时,声速也会相应地增加0.6米/秒。
这个关系在一定范围内是成立的,尤其在常规温度下。
四、应用与影响了解声速与温度的关系对许多实际应用领域都有重要意义。
例如在航空航天和气象学中,声速与温度的变化对飞行器的设计和性能有直接影响。
由于声速与温度成正比,所以在高温环境下,高速飞行器的空气动力学性能可能会发生变化。
此外,在声波传播和声学测量领域中,也需要考虑温度对声速的影响。
因为声速与温度有明确的关系,所以在测量和计算声波传播距离、时间和频率时,需要准确考虑气温因素。
音速在不同气体的速度
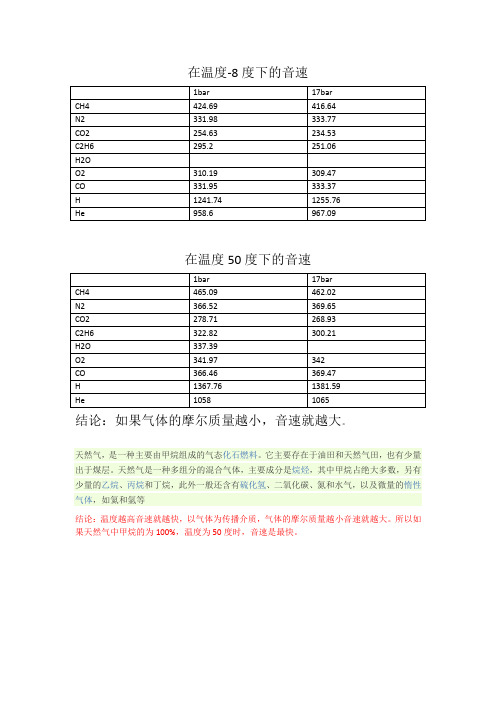
在温度-8度下的音速
在温度50度下的音速
结论:如果气体的摩尔质量越小,音速就越大。
天然气,是一种主要由甲烷组成的气态化石燃料。
它主要存在于油田和天然气田,也有少量出于煤层。
天然气是一种多组分的混合气体,主要成分是烷烃,其中甲烷占绝大多数,另有少量的乙烷、丙烷和丁烷,此外一般还含有硫化氢、二氧化碳、氮和水气,以及微量的惰性气体,如氦和氩等
结论:温度越高音速就越快,以气体为传播介质,气体的摩尔质量越小音速就越大。
所以如果天然气中甲烷的为100%,温度为50度时,音速是最快。
音速随高度的变化公式

音速随高度的变化公式
声速=20.05×(288-高度×0.65/100)的平方根。
在11000米高空(对流层顶)温度=-56.5摄氏度=216.5K,声速=295m/s。
利用上面的公式计算不同海拔的气温,再综合前面的音速经验公式,就可以推算不同海拔的音速了。
在11000~20000m的高空(属平流层,气温基本没有变化,所以又叫"同温层"),温度下降到零下57℃(15-11x6.5=-
56.5℃),这里的音速是u=331.3+[0.606x(-
57)]=296.7m/s(约1068km/h)。
喷气式飞机都喜欢在1万米左右的高空巡航,因为这里是平流层的底部,可以避开对流层因对流活动而产生的气流。
在11000~20000m的同温层内,音速的标准值是1062km/h,而且基本稳定。
喷气式飞机都用马赫数Ma来表示速度,而不用对地速度。
这是因为物体在空气中飞行时,前端会压缩空气形成波动,这个波动是以音速传播的(因为声波也是波动的一种)。
如果物体的飞行速度超过音速,那么这些波动无法从前端传播,而在物体前端堆积,压力增大,最终形成激波。
激波是超音速飞行的主要阻力源。
水中的声波传播与声速分析

水中的声波传播与声速分析水是一个极具特殊性质的物质,它具有良好的介质特性,可以有效传播声波。
声波是一种纵波,通过分子振动和传递振动的能量来传播。
在水中,声波的传播速度与多种因素相关,其中最主要的因素是水的温度、盐度、压力以及浮游生物的存在。
首先,水温是影响声波传播速度的重要因素之一。
一般来说,水的温度越高,其分子的热运动越剧烈,导致分子之间相互碰撞的频率增加,从而使声波传播的速度增大。
相反,水温越低,分子热运动减慢,声波的传播速度也相应减小。
这就解释了为什么在温暖的夏季,我们在游泳池中听到的声音会比在寒冷的冬季听到的声音更响亮。
盐度是另一个影响声波传播速度的重要因素。
普通海水中含有各种溶解的盐类,然而,若海水中的盐度过高或过低,都会影响声波的传播速度。
高盐度会增加水的密度,而密度是声波传播速度的重要参量,所以高盐度会导致声速增大;低盐度则会降低声速。
因此,不同海域的海水盐度不同,导致声波的传播速度也会有所差异。
除了温度和盐度外,水的压力也会对声波传播速度产生影响。
水的压力与深度呈正相关,它会使水分子之间的距离缩小,分子间相互影响的频率增加,从而使声波传播速度增大。
因此,在较深的水域,声波的传播速度会大于浅水域。
此外,水中存在大量的浮游生物,如鱼类、海藻等,它们的存在对声波传播速度也有影响。
浮游生物可以对水的密度和粘度产生影响,改变声波在水中的传播速度。
此外,如鱼类等大型浮游生物还可以对声波进行散射和吸收,使声音的传播距离减小。
为了准确分析水中声波的传播速度,科学家们通过实验和模型研究,利用声速仪或声速计进行测量。
采集到的数据被用于声速剖面测量,可以详细描绘出声波在水中的传播速度随深度变化的情况。
这些数据对于海洋勘探、声纳定位、水下通信等领域具有重要意义。
综上所述,水中的声波传播速度受到多种因素的影响,包括水的温度、盐度、压力以及水中浮游生物的存在。
科学家们通过实验和模型研究,利用声速仪进行测量,为深入了解水中声波传播速度提供了重要依据。
声的传播速度和频率

声的传播速度和频率声波是一种机械波,它通过介质(如空气、水或固体)的振动传播。
声的传播速度和频率是声波传播过程中的两个重要参数。
一、声的传播速度声的传播速度是指声波在介质中传播的速度。
不同介质的声速不同,通常用符号v表示。
声速的大小取决于介质的性质,如介质的密度、弹性模量和泊松比等。
1.空气中的声速:在常温常压下(0°C,1个大气压),空气中的声速约为343米/秒。
声速在空气中的大小还与空气的温度、压力和湿度等因素有关。
空气温度越高,声速越快;空气压力越大,声速也越快。
2.水中的声速:水中声速约为1480米/秒。
声速在水中的大小还与水的温度、盐度和深度等因素有关。
水温越低,声速越快;水中盐度越高,声速也越快。
3.固体中的声速:固体中的声速一般比空气和水中的声速快。
在钢铁中,声速约为5000米/秒;在橡胶中,声速约为40-150米/秒。
二、声的频率声的频率是指声波振动的次数,通常用符号f表示,单位是赫兹(Hz)。
频率表示声波的音高,频率越高,声音听起来越尖锐;频率越低,声音听起来越低沉。
1.人耳的听觉频率范围:人耳能够听到的声波频率范围大约是20Hz到20000Hz。
低于20Hz 的声波称为次声波,高于20000Hz的声波称为超声波。
2.声波的波长和频率的关系:根据波动方程,声波的波长(λ)与声速(v)和频率(f)之间的关系为:λ = v/f。
即波长与声速成正比,与频率成反比。
三、声的传播速度和频率的关系声的传播速度和频率之间没有直接的关系,但它们之间存在间接的影响。
在同一介质中,声速是一定的,当声波的频率发生变化时,其波长也会发生变化。
1.声波在介质中的传播:声波在介质中传播时,遇到不同密度的介质界面,会发生反射、折射和透射等现象。
这些现象会影响声波的传播速度和频率。
2.声波的多普勒效应:当声源和观察者相对运动时,观察者接收到的声波频率会发生变化,这就是多普勒效应。
多普勒效应说明了声的传播速度和频率之间的关系。
超声波速度与温度的关系

超声波速度与温度的关系超声波速度与温度的关系是物理、声学和工程学领域中一个重要的研究课题。
理解超声波在不同温度下的速度变化对于超声波技术在医学成像、材料检测、地震勘探等领域的应用具有重要意义。
本文将从理论基础、实验研究和应用领域三个方面进行阐述,以使读者全面了解超声波速度与温度的关系。
理论基础超声波是一种机械波,它是以固体、液体和气体为传播介质的波动现象。
超声波的速度由介质的物理参数决定,其中温度是一个重要的影响因素。
在固体和液体介质中,声速随温度的升高而增大,而在气体介质中,声速随温度的升高而减小。
这是由于介质分子在不同温度下的振动和相互作用引起的。
根据理想气体状态方程,声速和温度的关系可由下式表示:c = (γRT/M)^0.5其中,c为声速,γ为绝热指数,R为气体常数,T为温度,M为分子量。
根据该公式可知,在一定温度范围内,声速和温度呈线性关系,而且不同介质的声速和温度之间存在一定的函数关系。
因此,了解超声波速度和温度的关系,有助于深入理解声波在介质中的传播机理,从而为超声波技术的应用提供理论基础。
实验研究超声波速度与温度的关系在实验室中经过了大量的研究验证。
科研人员通过一系列的实验手段,探究了超声波在不同温度下的传播特性。
其中,最常用的方法是采用声速计测定不同温度下介质的声速。
以水为例,科研人员将温度分别控制在不同水平,通过声速计测得水中超声波的速度,并分析得出声速与温度之间的变化规律。
实验结果表明,在常见的实验温度范围内,声速与温度之间存在一定的函数关系。
同时,还有研究采用声学共振法、声子结构法、分子动力学模拟等手段对超声波速度与温度的关系进行研究,这些实验结果都为理论模型的建立和完善提供了有力支持。
值得注意的是,除了标准环境条件下进行的实验研究外,科研人员还进行了在极端条件下的实验,如在超低温、高温和高压环境下进行了声速测定,以验证理论模型的适用性。
这些实验结果为超声波在极端环境下的应用提供了重要数据支持,也深化了对超声波速度与温度关系的理解。
超声波温度与声速的曲线

超声波温度与声速的曲线
超声波在传播过程中,其声速与温度之间的关系呈现抛物线状的曲线。
从0℃开始,随着温度的升高,声速逐渐加快,当温度达到大约74℃时,声速达到最快。
然后随着温度的继续升高,声速会缓慢下降。
此外,超声波的频率也会影响其在水中传播的衰减速度和传播距离。
实验结果表明,超声波在水中的衰减速率与频率的平方成正比,即频率越大,衰减速率越高。
在管道流体中,超声波的传播速度与温度变化也呈非线性变化。
当管道流体温度低于50℃时,超声波的传播速度与温度变化呈现微线性关系。
而当管道流体温度大于50℃时,声速与温度对应值不再具有唯一性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
-------------精选文档-----------------
不同温度和压力下的声速
The classical ideal gas law may be written as pV=nRT, from which the expression for gas density ρ relating to pressure p could be deduced: ρ=pM/RT, wherein V and n correspond to volume and number of moles of a substance, respectively; T, M and R are respectively corresponding to absolute temperature, molar mass and ideal gas constant, approximately 8.3144621 J/(mol·K).
The sound speed of sound in an ideal gas depends only on its temperature and composition. The speed has a weak dependence on frequency and pressure in ordinary air, deviating slighty from ideal behavior. In general, the speed of sound c is given by the Newton-Laplace equation: c=(K f/ρ)1/2, in which the bulk modulus K f is simply the gas pressure p multiplied by the dimensionless adiabatic indexγ, which is about 1.4 for air.
理想气体状态方程PV=nRT, 推导得ρ=PM/RT.
0°C,1标准大气压下空气密度约为1.293g/L, 就用空气做个例子算一算.P=101325(标准大气压),M=29(空气摩尔质量),R=8.314J/(mol·k)(理想气体常数,定值),T=0+273.15K(开尔文温度),代入公式,计算出结果,这里要注意的是R值对应压力和体积的单位是Pa和M3,所以算出的ρ单位是KG/M3
声速的平方跟压力成正比,跟密度成反比;跟温度成线性关系所以声速不仅仅受压力影响气体中:u=√(γP/ρ),其中γ为比热比,P为压力,ρ为密度
可编辑。
