AHP中判断矩阵一致性改进的一种新方法
AHP中判断矩阵一致性的可控标准

判断矩阵的建立广泛使用 Sa 提出的 1 尺度法 , at y - 9 即对各层 中的因素进行两两相互对 比, 从而得到 判断矩阵.- 尺度法受限制于决策者 的知识结构 、 1 9 判断水平和个人偏好等 因素影响 , 在实际问题 中判断 矩 阵常 出现 不完 全 一致 的情 形 . 判 断矩 阵一 致性 的检 验 直接影 响决 策结 果 的正确 性 . 对 Sa at y建议 使 用一 致性 比率 C R对 判 断矩 阵一 致性 进行 检 验 , 内容 为 : 于 r阶判 断矩 阵 A, 算 一 其 对 t 计
wi
计 算 出在不 同显 著性水 平下 c 的临界值 , 方法 偏差项 , , 该 的分 布形 式 的选取标 准 较 随意 , 待验证 ; 者 有 后 定义 偏差 项 a i8 q一w ~N( , ) i O ,, 12 … , 并 将统 计量 . j= , , , s
,
( 一
定 义 1 如果 r阶矩 阵 A = ( , t a ) 满足下 列 条件 :
1 )非负性 : >0 i 0 ,, 1 2 … , ; j= , , n
2 互 反 性 : = ,√ =1 2 … ,. ) a i ,, n
于是 口 =1 : l2 … ,. 称矩 阵 A = ( 是 正互 反 阵. , ,, n则 a)
由于人 的 主观 理性 判 断可 以认 为存 在着 一致 性趋 势 , 而不 一致 性 判 断矩 阵 的产 生可 以认 为是 众 多 随 机 干扰 联合 作 用 的结果 . 因此 , 可将 偏差 项 占 看 成 均值 为零 、 同方差 的正 态 随机变 量 , 即 ~N( , ) 其 O , 中 为未 知参 数. 并假 设 决策 者严 格按 照 AH P要 求 对层 中各 因素两 两 比较 ( 果 与其他 因素无 关 ) 根 据 结 ,
幸福感的量化与评价模型

y ij =
x ij − x min ( j) x max ( j) − x min(j)
(1)
其中: x max( j) = max i {x ij };x min ( j) = min i {x ij }(i = 1,2, ⋯5;j = 1,2, ⋯19) 经过以上的变化之后,指标中的原始数据 x ij 转化成用于评价的值 y ij ,使所有值 集中在[0,1]之间。 ⑵计算均值 y j :
三、问题假设
1、附表所给数据真实可靠。 2、调查问卷随机且均匀分布,信息量足够大。 3、忽略被调查者性别、年龄及地域的差异性; 4、假设被调查者在调查时均处于正常的情绪状态下; 5、该样本容量对于分析数据足够大,不带有地区以及其他方面的差异性。
四、符号和定义说明 4.1 符号说明
表二:符号说明
符号
定义及说明 每个指标的票数 归一化后的评价值
表三:网民幸福感的评价指标表
一级指标(五个)
二级指标 自己目前的身体健康状况
分值 1-5 1-5 1-5 1-5 1-5 1-5 1-5 1-5 1-5 1-5 1-5 1-5 1-5 1-5 1-5 1-5 1-5 1-5 1-5
身心健康
工作压力情况 业余生活 对自己目前的收入 对自己目前的住房条件 目前社会经济发展状况 对城市出行便利情况 对城市的生活节奏 对城市的治安情况 对城市的环境情况 自信程度 事业发展前途 在工作或学习中有无成就感 和家人的关系 和朋友(同学)关系良好 和邻居关系 和同事关系 对生活的态度 自认为幸福程度
3
图一:层次分析模型图
幸 福 指 数
家 庭 因 素
个 人 因 素
生 活 因 素
自 我 价 值
家 庭 经 济
AHP的一致性问题

AHP的一致性问题第21卷第3期淮北煤师院2000年9月JournalofHuaibeiCoal—Industry.Tea—chersCollegeV0I_21No3Sen2000摘要:本文对AHP的和校正方法,AHP的一致性问题孔宪明赵文才颗学,.致性问题作了较为系统的研究和整理,介绍了几种较为简便且实用的检验关键词:—二塾堡重至查望分类号:0223文献标识码:Af’j~iil,f’¨}文章编号:1000—2227(2000)03—0021—05AHP中判断矩阵的一致性是层次分析法能否使用的关键,许多学者对一致性检验及校正方法作了大量探讨.本文对层次分析法中的一致性问题进行了较为系统的整理,介绍了几种较为简便易行的检验及校正方法.1一致性的概念在层次分析法中,为了形成判断矩哞,引人了l一9比率标度方法,这就使得决策者判断思维数学化.应用层次分析法保持判断思维的一致性是非常重要的. SaatyAL教授将判断矩阵–(.)…的一致性定义为:若对任意k,∈【l,2,…,},总有n=n成立,称判断矩阵A=(蛳)…是一致的.文【l】进一步给出,满足上述条件的判断矩阵称为具有基本一致性.AHP中的一致性除满足基本一致性外,还应满足次序一致性.所谓次序一致性是指,若元素甲比元素乙重要,元素乙比元素丙重要,则元素甲比元素丙重要.由于客观世界的复杂性及人们认识能力的局限性,利用AHP比例标度构造两两比较判断矩阵时,很难保证其具有完全一致性,特别是因素多规模大的问题更是如此.因此,为了保证层次分析法得到的结论基本合理,需要对构造的判断矩阵进行比称为随机一致性比率,记为cR.即cR=莆当CR<..10时,即认为判断矩阵具有满意的一致性.2.2统计检验法若A:(aJ…为n阶判断矩阵,W=(,…,)为其排序向量,c=(c)…为其导出矩阵,其中q1.根据文【2】的结论,判断矩阵为完全一致性矩阵的充要条件是其导出矩阵C中元素全部为1,即C=由人的主观判断偏差造成的判断矩阵不一致,可认为是众多随机干扰联合作用的结果,因而,q可视作以1为均值的正态随机变量.定理设为n阶判断矩阵,c:(c)…为其导出矩阵.c~Ⅳ(1,5),其中8为常数,且各q(,=1,2,一,n)相互独立,则统计量=∑∑(c一1)服从自由度为n的的u‘分布.定理的结论是显然的.且A满足完全一致性当且仅当=0.常数i可根据对判断矩阵的”满意的一致性”的不同要求来选取,通常取吉s5s寺8越小,对判断矩阵一致性的要求越高于是判断矩阵A的一致性检验即为如下的统计假设检验问题::s;对于给定的显着性水平嵋令P(≥)=峨查自由度为的分布表可得临界值瑶.当判断矩阵的观测值<时,即可认为A具有满意的一致性;反之,则认为不具备一致性.2.3次序一致-陛检验保持判断矩阵满足次序一致性是判断矩阵可用的前提条件,因而还需对比较判断矩阵进行次序一致性检验.在1—9比例标度下,判断矩阵:(q)…满足次序一致性的数学描述为: 对任意,,E{1,2,…,n),有(1)若蛳≥1且%>1,则0.±>1(2)若0¨>1且≥1,则o>1(3)若哪≤1且咏<1,则a<1(4)若鲫<1且%≤1,则0.±<1(5)若=l且蛳=1,则m=l第3期孔宪明等AI’Ip的一致性问题由此得次序一致性检验方法如下:(I)给定判断矩阵4=()…(2)令1(3)令=1(4)令=1(5)若满足田≥l且印>1或满足>1且≥1,转步骤(8)(6)若满足q≤l且(1或满足<l且≤1,转步骤(9)(7)若满足哪=1且蛳=1,转步骤(1o)(8)若.≤1,转步骤(11),否则转(14)(9)若.≥1,转步骤(12),否则转(14J(10)若n:1,转步骤(14),否则转(13】(11)输出哪,,∞,指出‰应大于1,转步骤(14)(12)输出,,‰,指出应小于1,转步骤(14)(13)输出%,,,指出口应等于1(14)令=—1(15)若≤n,返回步骤(5)(16)令J=J+1(17)若≤返回步骤(4){18)令i=i+1(19)若≤,返回步骤(3)(20)结束对经检验出现违反次序一致性的判断,应重新予考虑3一致性的校正方法对不满足一致性的判断矩阵,下面介绍两种校正方法3.1向量校正法设4为判断矩阵,将A=()…各列进行规一化后得矩阵=(,m,…),其中为n维列向量(i=1,2,…,n).用和积法求出A的最大特征根所对应的特征向量,得到A的规~他特征向量百=若4完全一致,刚=i=1,2,….n)若A不完全一致,则每个∞与保持一种近似比例关系,而这种近似的比例关系程度可采用向量夹角来度量.记为a与的夹角(i:I,2,….).令p=eosO-黼(其中∞.内积)=s;n=称为∞相对于的一致性系数,为相对于的偏差系数.显然,有性质(1)0≤P.≤1,0≤≤1(i=1.2,…,n)24淮北煤师院2000年(2)当A完全一致时,P.=1,d=O(i=1,2,…,)(3)越小,越大,∞与的一致性程度越好.【4)若p>P/,则<aj,d比∞的一致性好.将所有d按由小到大顺序排列:击l≤d≤…≤dl≤当判断矩阵不满足一致性时,当然需要首先校正偏差最大的列.因而我们选取偏差最大的两个d一.与所对应的两列作为首先调整的对象.假设一.与分别对应原矩阵的第i列与第列,则校正蛳与.为保证新矩阵仍为正互反矩阵,将原嘶=1/校正为n=1/靠.同时,确定n时,应以偏差最小的一对应的㈨列为准,使校正后的两列尽量保持与∞的近似比例关系.对校正后的新矩阵进行一致性检验若仍不满足一致性,则重复上述过程直到满意为止.归纳向量校正法的步骤如下(1)将判断矩阵A=(哪)…各列规一化,得=(d-,--,)(2)计算A的规一化特征向量五(3)计算并按从小到大顺序排列:】≤d&≤…≤d结束由此得到的矩阵A”即为符合满意一致性的判断矩阵,即为其特征向量参考文献:[1]马维野.一种检验判断矩阵次序一致性的实用方法[J】,系统工程理论与实践.1996,I6(11):103—105【2】刘万里,雷治军关于AHP中判断矩阵校正方法的研究.】】系统工程理论与实践.1997,17(6):30—29f3]赵焕臣,许树柏,和金生层次分析法[M]北京:科学出版社.1986. 【4]杜之韩判断矩阵一致性检验的新途径【】]系统工程理论与实践.1998,18(6):102—104.【5】徐泽水判断矩阵一致性改进的一种实用方法【J].系统工程.1998,16(6):61—63.TheProblemofConsistencyinAHPKONGXian-ruingZHAOWen—cai{皿mmMathemag~,Tai∞Educationaltns~e,Taim27/000Abstract:Thispaperpresentsquitesystematicstudyandarrangementofconsi steneyinAHP,also imredueesseveralkindsofeasyandpracticalmethodsofverificationandrecti fication.Keywords:AHP;consistency;rectification旦m。
AHP法的随机一致性(RC)指标
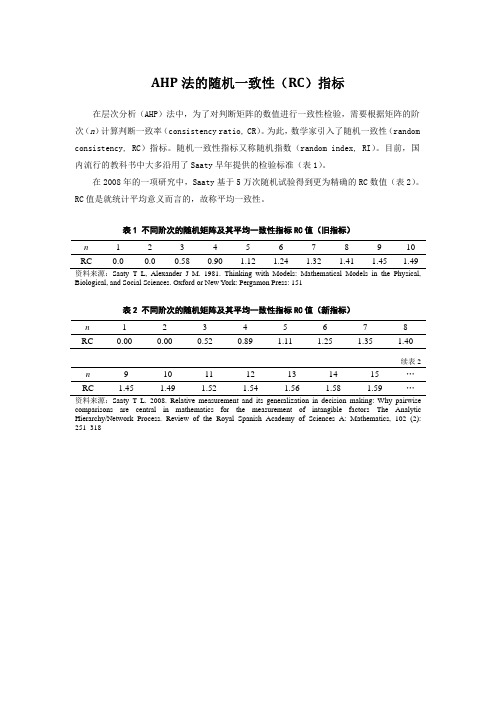
AHP法的随机一致性(RC)指标在层次分析(AHP)法中,为了对判断矩阵的数值进行一致性检验,需要根据矩阵的阶次(n)计算判断一致率(consistency ratio, CR)。
为此,数学家引入了随机一致性(random consistency, RC)指标。
随机一致性指标又称随机指数(random index, RI)。
目前,国内流行的教科书中大多沿用了Saaty早年提供的检验标准(表1)。
在2008年的一项研究中,Saaty基于5万次随机试验得到更为精确的RC数值(表2)。
RC值是就统计平均意义而言的,故称平均一致性。
表1 不同阶次的随机矩阵及其平均一致性指标RC值(旧指标)n 1 2 3 4 5 6 7 8 9 10 RC 0.0 0.0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49资料来源:Saaty T L, Alexander J M. 1981. Thinking with Models: Mathematical Models in the Physical, Biological, and Social Sciences. Oxford or New York: Pergamon Press: 151表2 不同阶次的随机矩阵及其平均一致性指标RC值(新指标)n 1 2 3 4 5 6 7 8 RC 0.00 0.00 0.52 0.89 1.11 1.25 1.35 1.40续表2 n 9 10 11 12 13 14 15 …RC 1.45 1.49 1.52 1.54 1.56 1.58 1.59 …资料来源:Saaty T L. 2008. Relative measurement and its generalization in decision making: Why pairwise comparisons are central in mathematics for the measurement of intangible factors—The Analytic Hierarchy/Network Process. Review of the Royal Spanish Academy of Sciences A: Mathematics, 102 (2):251–318。
模糊互补判断矩阵一致性修正新方法

p ,) I l=∑ ∑ l 一 I ( = 尺一 J R r
定义 5
“
对 于模 糊 判断 矩 阵 R 一 ( ) , R 中存在 ( 若 2≤ ≤ ) 不小 于 0 5的元素使 得 个 .
…
z“
:
…
.
.
¨' 且在这 个 方 案优 劣循环 链 中至 少有一 个 元素 大于 0 5 则称 判 I并 .,
断矩 阵 尺 是不 一致 的 ; 则判 断 矩阵 尺具 有 满意一 致 性 . 否 定义 6 称如 下判 断矩阵 为 互补 判断 矩 阵 R 一 (。 的可达 矩 阵 , — Q + Q。 … + , r) T +
矩Q (x元定为 ; : 喜’ 中 ” 布运符 布运规定 阵= )的% 0式 + 示 5 其
( ) 其 e J eI r 一a w 一 』 +o 5, ≥ ( ) . 口 . 然 R。 ( ) 为 模 糊 一 致 矩 阵 , 过 代 换 有 显 ; r 经
r = .+告 ∑ l = 5 ( 一∑ ,R 一( 为 的 征 阵 j= 0 ) r 称 ) R 特 矩 .
摘 要 断 矩 阵 的一 致 性 修 正 是 利 用 层 次 分 析 法 进 行 决 策 的 一 个 重 要 步 骤 。 文 利 用 几何 平 均 法 对 由 专 家 构 判 本
造 的模糊 互补判断矩 阵进行修正 , 证明了满意一致性矩 阵的存在性与所给方法的收敛性 . 最后给 出了一算例. 关键词 : 模糊 互补判断矩 阵; 几何平均 ; 满意一致性 ; 收敛
一
致性 修 改方 法. 本文 在此 基础 上 探讨 对基 于模 糊一 致 矩 阵 的修 正方 法.
1 基 本 定 义 及 主 要 结 论
层次分析法中判断矩阵一致性的改进方法

[ 摘要】 判断矩阵也叫 成对比较阵, 它是通过对定 性指标进行 量化得到的; 通过一个敷学 建模的实例, 建立相应的判 断矩阵并判定 其一致性,进 而对达不到要 求的
翔断矩阵提m笔者的改进方 法。
[ 关键词】层次分析法判断矩阵一致性数学建模
中图分类号:01- o
文献标识码; A 文章 编号 :167 1- - 7 597( 2 008) 1 22018 1- - 01
其中R=Ⅸ=( 而, 屯,…,善。) 7 l毛>0,i =1,2,…,一}· 引理2设彳=( 口Ⅳ) 。.是判断矩阵.A。是A的最大特征值,则五。
≥刀, 等号成立 当且仅当^是 一致性矩 阵.
定理设彳=( 口口) 。是判断矩阵,红是A的最大特征值,历=( w1, w2,…,毗)7为k对应的特征向量,取口E( o’1) ,并令占=( 钆) 。,其中
取=0. 1,得修改 后的矩阵和 各项指标 如下
l
●9
9
;, r 。 On 9 5 n● 诌2
I .391 l ,5
6.522 2
1
O.3l l
3.216 l
( 下转第170页)
圃Байду номын сангаас
教■ 科学
Ⅵ
盟
爵
●_§;
浅谈音乐教学中情感的培养
马淑 华 ( 白城职业技术学院吉林白城137000)
[ 擅要】在音 乐教育中,教师要善于 动脑,组织好各个环 节的教学,用生动、形 象、甜美的教学语言和 动听的歌声与伴奏打动 学生的心库,唤起学生 的美感. [ 关键词]音乐教学 情感 培养 中图分类号:G4 2文献标识码:A 文章 编号 ;167 1- - 7 507( 2 008) 1 22017 0—01
AHP中正互反判断矩阵一致性调整的新方法
S a a t y 教授于2 0 世纪7 0 年代提出的层次分析法( A n a l y t i c H i e r a r c h y P r o c e s s , 简称A H P ) [ 】 是一种 把定性分析与定量建模巧妙结合, 解决具有复杂层次结构的多维群决策问题的系统化 、 层次化
DO h 1 0 . 3 9 6 9 / j . i s s n . 0 4 6 9 — 5 0 9 7 . 2 0 1 3 . 0 1 . O 0
AHP中正 互 反 判 断矩 阵一 致 性 调 整 的新 方 法
江 正 华
( 南京大学数学系, 南京 2 1 0 0 9 3 )
摘要
全面阐释了层次分析法( A H P ) 中一种针对正互反判断矩阵进行一致性调整的
南京大学学报数学半年刊
第3 0 卷 第2 期
2 0 1 3 年l 1 月
J OURNAL OF NANJ I NG UNI VERS I TY Vo 1 . 3 0 , No . 2
MA TH EMA T I C AL B I QUA R T E RL Y
No v . , 2 0 1 3
不但能够满足一致性比率要求, 而且可以很好地代表专家意见即具有满意的可信度, 最终达到
对原 判 断矩 阵一致 性 改进 的 目的.
1 正 互反 判断矩阵及其一致性
在多维决策中, 记Ⅳ = { 1来自, 2 , … , n ) . 设X = { x d i ∈Ⅳ} 为一有限的决策因素集( 或称指标
可 能始 终保 持判 断 的 完全 一致 , 判 断存在 一 定 的误差 实难 避 免, 其给 定 的判 断矩 阵 也就常 常 是 非 一致 性 的 . 而 判 断矩 阵 是否 具 有一 致 性将 直接 影 响 到 由判 断矩 阵所 求 得 的权重 向量或 称 排 序 向量 能否 精 确 地反 映 各 系统 要 素 间 的客 观 排序 . 故 需要对 决策 专家 给 出 的判 断矩 阵作 一致 性分 析和 校 正, 使之 具有 满 意一 致性 , 以便用 于 实际 决策 . 数十 年 来 , 有 关AH P  ̄ I J 断矩 阵的一 致 性调 整 方法 的研 究 已取 得 了相 当成 果 【 2 — 7 l , 如最 小 二 乘法 与广 义最 d ' - 乘法 [ 2 ] 、 最 优传 递矩 阵法 【 3 】 、 模糊 一致性 变换 法 【 4 】 、 标 度构造 法 【 5 】 等. 本 文在 已有 的专 家 判 断矩 阵排 序方 法 的基 础上 , 提 出 了一种 新 的确 定排序 权 重 的方法 . 在 充 分提 取专 家全 部判 断 信 息 的基础 上 , 导 出一 个 对应 于 原判 断矩 阵 的完 全一 致性 矩 阵, 特 别 关键 的是 将 导 出 的完 全 一致 性矩 阵与 原判 断矩 阵按 一定 的几 何调 和 比组 合得 到 新 的调和 矩 阵. 此 调和矩 阵
AHP判断矩阵一致性调整的前瞻算法
的 互反性 , 以 后涉 及元素 的调 整不 特别 说明 都是 成对 调 整) , 即 s= i , t = j ( 1) 其他 ) n ×n , 其中 a
(k ) st
=
1/ askakt , s= j , t= i ast ,
而可知 T = ( T i j ) n×n 是 对称阵。 d 定义 8 ( d i, j ) = argmax ( $ ij )
率变小的数值 , 表征了 aij 的第 k 种调整对矩阵 一致性的改 善程度。 如果 $ (ijk ) > C. R. ( A) - C. R. ( A(i jk) ) ≤ 0, 说明 第 k 种调整无助于甚至有碍于改善判断矩阵 的一致性 , 在我 们 的算 法实现中 就把它置 0。 由于 aij 有 n- 2 种调整 策略 , 因 此就有 n - 2个可能的改善程度 , 分别是 $ (ijk ) > C. R. ( A ) ) (k ) C. R. ( A(i jk) ) , k ∈ N , k ≠ i , j . 由 于 A (ij k) = A (j k i , 故 $ ij = (k ) $ ji .
AHP ( Analytic Hier archy Process ) [1, 2] 是经 济管 理 领 域广泛应 用的决策方法 , 运用 AHP 法进行决策 分析 , 关 键是专家能够构造出能够通过一致性检 验的判断矩阵。 如 果判 断矩阵 不能通 过一致 性检验 , 就要 对判断 矩阵进 行 调整。 目前已经有很多一致性调 整算法 [311]
X 收稿日期 : 2006-09-06 作者简 介 : 叶跃祥 ( 1978-) , 男 , 福建厦门人 , 中国科学技术大学管理 学院博士研究生 , 研究方向 : 经济决策分析 , 信息 管理 ; 糜仲春 ( 1945-) , 男 , 浙江绍兴人 , 中国科学技术大学管理学院教授 , 博士生导师 , 研究方向 : 经济决策 分析 , 信息管理 , 商务智能 ; 王宏宇 ( 1981-) , 男 , 山西忻州人 , 中国科学技术大学管理学院博士研究生 , 研究方向 : 商务智能 , 经济决策分析 ; 梁晓艳 ( 1979-) , 女 , 新疆库尔勒人 , 中国科 学技术大学管理学院博士研究生 , 研究方向 : 金融工程 , 经济决策分析。
新的改进AHP算法研究及应用
第 l 2期
计 算 机 技 术 与 发 展
C OMP UTE C NOL Y N D V OP R TE H OG A D E EL ME T N
V 1 0 1 o2 . N 2
De . 2 c 0 O l
21 0 0年 l 2月
新 的改进 A P算 法研 究及 应用 H
Ab t c : o s u tdte u g n mar s a t C n t ce h j d me t t xwhc r r i i hme t t ecn i e c q i me ts n o t e e su z f e h o s tn yr u e n io e f h yi e o s s e r k s
t mp v r ia t x cn itn yp siit nteb ss fmane a c h a d t .Frm h e esr n u f in o dt n f o i m eo i n lmar o sse c o sblyo a i itn n eterw aa g i i h o o ten csaya ds fi e tc n io o c is
法【2。它通过建 立 问题 的层次结 构模 型 、 1 ’ J 构造 各层
学生考查课成绩 的评 定 , 一般 是通过 授课 教师 打
的判断矩阵 、 进行层次单排序及一致性检验 、 进行层次 总排序及 一致性检验 四个步骤来 完成指标排序或权值 的确定 l3 _] 1 。在利用 层次 分析 法分 析 问题 时 , 造满 , 构 足一致性要求 的判断矩 阵 A : ( a 是 A P的关 H 键之一 。 但通常情况下 给出的判断信 息难 以达 到完 全
Ke 0 : ; u g n t x c n i e c ;ts c s yw 州s A jd me t mar ; s t y et l s i o s n a
AHP中判断矩阵的几种构造方法综述
关于反对称矩阵的标度选取的问题研究者提出可以采用ln1ln9标度比如两者如果重要程度相同则赋值于ln1则元素记为0依次类推该标度即可得到需要的矩阵即aij式在国内也有其他不同的标度方法不同的标度选取导致不同的权重度中的数字不应太多因为两个元素的对比毕竟是带有主观色彩的对于需要快速足够了太繁琐的标度方法只适合于一些特殊的案例
On Me t h o d s o f Ma t r i x J u d g me n t i n AHP
H UA We i
( C h a n g j i a n g E n g i n e e r i n g Vo c a t i o n a l C o l l e g e , Wu h a n 4 3 0 2 1 2 , C h i n a )
提出 了几种判断矩阵 的构造方法 , 本文介绍 了目前 的三 种方 法, 提 出了各 自的优缺点及笔者的建议 。
2 判 断 矩 阵 的构 造 方 法
( 1 )1 ~9 标度判 断矩阵的构造方法 各个因素对于 目标 的权重是不 同的, 判断矩阵给出 了如
1 层 次 分 析 法 与判 断矩 阵 的构 造 介 绍
结 了近几 年国内外对于判断矩阵构造问题的研究 , 并 进行 了归纳分类 , 给 出了对 于各种构造 方法选取 的评价标准 ,
指 出 推 广 这 些 方 法 才 是 研 究 者 需 要 关 心 的问 题 。 关键 词 : 判断矩 阵; 标度评价 ; 层次分析法 ( AHP ) 中图分类号 : 02 2 3 文献标识码 : A 文章编号 : 1 6 7 3 — 0 4 9 6 ( 2 0 1 4 ) 0 4 — 0 0 6 5 — 0 2 D O I : 1 0 . 1 4 0 7 9 / j . c n k i . c n 4 2 — 1 7 4 5 / t v . 2 0 1 4 . 0 4 . 0 2 7
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
系统工程理论与实践SYSTEMS ENGINEERING----THEORY & PRACTICE2000 Vol.20 No.2 P.122-125AHP中判断矩阵一致性改进的一种新方法李梅霞摘要: 通过分析诱导矩阵与判断矩阵不一致性的关系,提 出了一种新的改进判断矩阵一致性的方法。
关键词: 诱导矩阵; 一致性; 和积法中图分类号: O223 A New Method for Improving the Consistency ofthe Comparis on Matrix in AHPLI Mei-xia(Changwei Teachers College, Weifang 261043)Abstract: In this paper, a new method for improv ing the consistency of comparison matrix was presented by analyzing the relatio nship between the induced matrix and the inconsistency of comparison matrix. Keywords: induced matrix; consistency; ANC1 引言 T.L. Saaty于70年代提出的层次分析法(AHP)为解决多目标决策问题提供了很大的方便,在 社 会、经济、管理中得到了广泛应用。
其关键步骤是由专家给出判断矩阵,然后计算排序向量 。
因此专家给出的判断矩阵是否能具有满意的 一致性是一个很重要的问题。
它直接影响到由此判断矩阵得到的排序向量是否能真实地反映 各比较方案之间的客观排序。
因此,对判断矩阵一致性的改进是AHP中一个很重要的内容。
文献[1~3]中提出了几种一致性改进的方法,取得了一定的效果。
但是有些方法比较复 杂,有些方法缺乏一定的理论依据,因此寻求一种更好的改进判断矩阵一致性的方法仍具有 重要意义。
本文首先定义了一种特殊的矩阵——诱导矩阵,然后通过分析诱导矩阵与判断矩 阵不一致性的关系,提出了一种新的改进判断矩阵一致性的方法。
通过多例验证,该方法简 单有效且符合实际。
2 问题的提出 为以后叙述方便,记Ω={1,2,…,n}。
设A=(a ij)n× n为判断矩阵,若其元素满足a ij>0, a ji=1/a ij, a ii=1, i,j∈Ω,则称A为正互反矩阵。
若此正互反矩阵又满足a ij=a ik/a jk, i, j, k∈Ω, 则称A为完全一致性矩阵。
一般情况下,专家给出 的判断矩阵很难满足完全一致性条件。
文献[4]中指出当时即认为A具有满意的一致性。
因此当专家给出的判断矩阵不具有满意一致 性时,可通过征求专家意见,应用合理的方法对判断矩阵的元素进行适当调整,从而使判 断矩阵达到满意的一致性。
文献[5]中指出,“和积法”是一种比较好的计算判断矩阵排序向量的方法。
其步骤为 :设A=(a ij)n× n为判断矩阵,令B=(b ij)n× n,其中则βj为判断矩阵A的第j个列向量的归一化向量。
再令由此求得判断矩阵 排序向量w=(w1, w2, …, w n)T的方法称为“和积法”。
定义 称矩阵C=(c ij)n× n为判断矩阵A的诱导矩阵,其中 , 定理 判断矩阵A为完全一致性矩阵的充要条件是矩阵C中元素全部为1,即 证明 必要性。
若判断矩阵A为完全一致性矩阵,则A的每一列向量的归一 化向量均相等,从而其与“和积法”求得的排序向量相等,即 b ij=w i, i,j∈ Ω,从而c ij=1, 即 充分性。
若即 c ij=1,从而b ij=w i, i,j∈Ω,即各列归一化向量均相等,从而A为完全一 致性矩阵。
由定理可知,若C中存在某个元素c ij不为1,则说明判断矩阵A不为完全一致性矩阵, 且c ij偏离1越大,说明a ij对A的不一致性的影响越大。
当c ij>1时,a ij偏大,应适当减小;当c ij<1时,a ij偏小,应适当增大。
由于专家的判 断一般不会出现很大的失误,因此对影响判断矩阵一致性的元素可进行适当微调。
通过某些 元素(或其分母)增加1或减小1的方法使判断矩阵逐步达到满意的一致性。
3 判断矩阵一致性改进的方法 通过2中的分析,改进判断矩阵A的一致性的方法可按如下步骤进行: 1) 计算A 的各列归一化向量βj, j∈Ω及“和积法”求得的排序向量w; 2) 求出诱导矩阵C=(c ij)n×n; 3) 找出使|c ij-1|( i, j∈Ω)达到最大值的i,j,记为k,l; 4) 若c kl>1,则若a kl为整数,令a′kl=a kl-1,否则令a′kl=1/(1/a kl+1); 若c kl<1, 则若a kl为整数, 令a′kl=a kl+1,否则令a′kl=1/(1/a kl-1); 5) 令a′lk=(1)/(a′kl), a′ij=a ij, i,j∈ Ω且i,j≠k,l; 6) 若A′=(a′ij)具有满意的一致性,则停止,A′即为求得的具有满意一致性的 判断矩阵;否则,用A′代替A转1)。
4 应用举例 例1 设CR(A)=0.1407>0.1,A不具有满意的一致性。
“和积法”求得的排序向量从而诱导矩阵C中偏离1最大的元素为c32=1.619>1,且a32=2为整数,因此需将a32减小 1,即a′32=1, a′23=1,从而可得CR(A′)=0.0250<0.1,A′具有满意的一致性。
例2 设CR(A)=0.1720>0.1,A不具有满意的一致性。
“和积法”求得的排序向量从而诱导矩阵C中偏离1最大的元素为c13=2.406>1且a13=3为整数,因此需将a13减小1 ,即 从而可得CR(A′)=0.1036>0.1,A′仍不具有满意的一致性,需继续进行调整。
“和积法”求得的排序向量的诱导矩阵偏离1最大的元素为c′13=2.106>1,因此需将a′13减小1, 即a″ 13=1, a″31=1,从而可得CR(A″)=0.0292<0.1,A″具有满意的一致性。
本文作者对章志敏教授的指导和帮助表示衷心的感谢!李梅霞(昌潍师专数学系,山东 潍坊 261043)参考文献:[1] 陈宝谦等.正互反矩阵的一个特征值问题.高校应用数学学报,1991,6(1) :57~65.[2] Ma Weiye etc. A Practical Approach to Modifying Pairwise Compariso n Matrices and Two Criteria of Modificatory Effectiveness. Journal of Systems S cience & Systems Engineering, 1993, 2(4):334~338.[3] 刘万里,雷治军.关于AHP中判断矩阵校正方法的研究.系统工程理论与实 践,1997,17(6):30~39.[4] Saaty T L. A Scaling Method for Priorities in Hierarchical Structu res. Journal of Math. Psychology, 1997,15:234~281.[5] 王应明.判断矩阵排序方法综述.决策与决策支持系统,1995,(3):101~114收稿:1998-05-15AHP中判断矩阵一致性改进的一种新方法作者:李梅霞, LI Mei-xia作者单位:昌潍师专数学系,山东,潍坊,261043刊名:系统工程理论与实践英文刊名:SYSTEMS ENGINEERING--THEORY & PRACTICE年,卷(期):2000,20(2)被引用次数:87次1.陈宝谦正互反矩阵的一个特征值问题[期刊论文]-高校应用数学学报A辑 1991(01)2.Ma Weiye.etc A Practical Approach to Modifying Pairwise Compariso n Matrices and Two Criteria of Modificatory Effectiveness 1993(04)3.刘万里.雷治军关于AHP中判断矩阵校正方法的研究 1997(06)4.Saaty T L A Scaling Method for Priorities in Hierarchical Structu res 19975.王应明判断矩阵排序方法综述 1995(03)1.期刊论文姜艳萍.樊治平.王欣荣AHP中判断矩阵一致性改进方法的研究-东北大学学报(自然科学版)2001,22(4)针对AHP中判断矩阵一致性改进问题,提出了一种新的改进判断矩阵一致性的方法.首先,给出了诱导矩阵的定义,然后通过分析诱导矩阵与判断矩阵之间的关系,给出了将判断矩阵改进为满意一致性矩阵的简洁、实用的迭代算法.最后给出了两个算例.2.期刊论文樊爱宛.樊爱京.FAN Ai-wan.FAN Ai-jing改进的AHP算法在计算机实验考核中的应用-电脑知识与技术2009,5(35)针对计算机实验考核评价遇到的实际问题,采用构建诱导矩阵的方法,对传统层次分析法(AHP)的判断矩阵的一致性检验进行了研究改进;解决了决策者调整判断矩阵的盲目性.应用这种改进的AHP法对计算机实验考核评估,结果证明了该方法的可行性和实用性.3.期刊论文待发表文章摘要预报-东北大学学报(自然科学版)2001,22(3)冷连轧过程控制在线负荷分配及修正计算王军生, 赵启林, 矫志杰, 刘相华提出应用Newton-Raphson法直接对冷连轧过程控制负荷分配进行求解计算,从计算精度、计算时间、求解稳定性方面探讨了该算法的特点.给出了初始值计算方法,并对雅可比矩阵进行了简化计算.针对轧制过程中的打滑现象提出对负荷分配得到的压下率进行修正.该方法已被用于冷连轧机组在线控制,实践证明了该算法的准确性和可靠性.具有热致/溶致液晶性能的系列主链液晶聚合物的合成与性能研究支俊格, 张宝砚, 张爱玲, 史国华介晶单体4,4′—二羟基-α,α′—二甲基苄联氮(DDBA)与不同摩尔比的对苯二甲酰氯和癸二酰氯采用界面聚合的方法共聚而得系列聚合物P1~P7.通过傅立叶转换红外光谱(FT-IR)、差示扫描量热仪(DSC)、热失重分析(TGA)、偏光显微镜(POM),X-射线衍射分析(WAXD)等手段对聚合物的结构、热致及溶致液晶性能、热性能进行了表征.单体DDBA与聚合物P1~P6均为向列型液晶,呈现清晰的丝状织构,但聚合物的热致液晶性能随刚性链段对苯二甲酰含量的增加而逐渐减弱;所有的聚合物均具有溶致液晶性能,其织构从柳叶状逐渐变为砂粒状;聚合物均具有较高的热稳定性,热分解温度在320℃以上,且其热稳定性随刚性链段对苯二甲酰含量的增大而升高.快凝AlFeVSiNd纳米合金薄带时效过程研究贾威, 张彤, 曾梅光采用透射电镜研究了快凝Al-Fe-V-Si-Nd弥散纳米晶合金薄带在时效处理过程中,其内部微结构变化,首先出现元素偏聚现象;再提高热处理温度,Al8Fe4Nd相开始溶解,同时α-Al13(Fe,V)3Si相开始析出.在同一温度下,随热处理时间增加,α-Al13(Fe,V)3Si相析出量增加;测量了时效处理前后样品的力学性能,出现类似传统铝合金时效硬化的现象.复映射z←zw+c(w=α+iβ)构造广义J集的外部结构王兴元推广了美国Alaska大学的Philip教授提出的用来探讨Mandelbrot集外部结构的“区域分解”和“角度分解”的方法,提出了等势线和色彩调配法,并利用这四种方法构造了复映射的广义Julia集(简称广义J集)的一系列外部结构图.研究了广义J集外部结构的分形特征及演化过程.岩石裂纹相互作用的应力场分析黄明利, 唐春安, 梁正昭运用岩石破裂过程分析RFPA2D系统,通过对岩石试样中预置的一组雁列式裂纹相互作用应力场的数值模拟,探讨了不同几何排布的雁列式裂纹应力场的相互作用的4种模式,模拟结果和相关的理论和实践结果具有较好的一致性.AHP中判断矩阵一致性改进方法的研究姜艳萍, 樊治平, 王欣荣针对AHP中判断矩阵一致性改进问题,提出了一种新的改进判断矩阵一致性的方法.首先,给出了诱导矩阵的定义,然后通过分析诱导矩阵与判断矩阵之间的关系,给出了将判断矩阵改进为满意一致性矩阵的简洁、实用的迭代算法.最后给出了两个算例.由时序立体数据表支持的综合评价方法郭亚军, 潘建民, 曹仲秋在经济管理与决策中,经常遇到大量的动态综合评价问题.但遗憾的是决策者常常将动态的综合评价问题“简化”为静态的综合评价问题,而使得综合评价结果不同程度的“失真”.针对由时序立体数据表支持的综合评价问题的特殊性,提出了一种新的“‘纵横向’拉开档次”法,并给出一个实际例子.该方法具有原理简单、直观意义明显、评价过程“透明”等特点.金融产品管理的模型与优化黄小原, 庄新田分析研究了宏观金融产品的模型和优化问题,这一问题的目标函数是股东资产净值盈利的极大化,决策变量是金融杠杆和债务结构.文中给出了金融产品管理模型与优化的不确定情景条件的构造过程.最后,给出一个不同债务结构下的金融杠杆变化及其资产净值盈利的案例仿真.工程机械驾驶员座椅主动悬架最优控制黄英, 张以忱建立了车辆-座椅两自由度悬架系统的力学和数学模型,应用线性随机最优控制理论(LQG),根据路面随机振动输入的统计特性,在状态变量不全知的情况下,通过Kalman-Bucy滤波器对其进行无偏最优估计,设计出控制系统的最优反馈规律.应用MATLAB仿真语言对该模型进行编程设计和计算机仿真实验.关联规则发现的一种改进算法张晓辉, 何耀东, 万家华, 赵宏给出一个改进的关联规则发现算法.由于这个算法只需搜索交易数据库一次,从而大量减少了所需的I/O次数,因此这个算法尤其适合于大型交易数据库.使用合成数据作试验表明这个算法尤其对大型数据库的性能优于先前已有的一些关联规则算法.一种基于移动网络的网络重组与恢复策略冯永新, 赵林亮, 王光兴将重新划分网络边界和周界的思想引入网络重组,并且将几种实现网络重组的机制有机地结合起来,提出一种新的基于移动网络的重组与恢复策略.对于这种网络重组和恢复策略,在时间和有效性上进行了分析和讨论.一种新的无信元丢失的ATM通信网络拥塞控制方法关少颖, 王光兴提出了一种新的融合速率和凭证流量控制方法、无丢失的ATM通信网络拥塞控制方法.实验结果表明,该方法硬件实现简单并能动态分配带宽、充分利用网络资源、及时解除网络拥塞,尤其采用了共享缓存器,信元的丢失率趋于零.模糊聚类挖掘方法在电子商务中的应用郝先臣, 张德干, 赵海利用模糊关系矩阵,给出了一种模糊聚类的方法,并将这些技术应用到具体电子商务平台的数据挖掘工作中,得到了可行性验证,从而为此技术在电子商务领域的广泛应用起到了示范作用.基于神经网络的永磁同步电机的鲁棒控制李鸿儒, 白湘波, 顾树生提出一种基于神经网络的永磁同步电机的鲁棒控制策略.基于此策略设计了神经网络PID速度控制器,使速度控制器能实时在线调整.由一种混合型神经网络作为辨识器,利用神经网络的学习特性实现对永磁同步电机系统不确定性的鲁棒控制.为了加快响应速度,提高响应性能,采用多步预测性能指标函数下的反传算法.仿真和实验结果表明,所提出的控制方法明显优于一般永磁同步电机系统的控制方法,具有较强的鲁棒性.神经网络过学习问题的统计学分析及改进算法王振雷, 李鸿儒, 顾树生着重分析了神经网络自学习过程中出现的问题,并提出了一种新的函数及检测预测算法对网络结构进行学习,该准则函数综合考虑了网络的逼近性、容错性和归纳性并且算法实现起来简单,容易实现在线选择.一类非线性相似广义组合系统的鲁棒控制石海彬, 刘晓平, 张嗣瀛研究了一类具有非线性互联作用的广义组合系统,在其互联项中含有不确定性,以前人对广义系统和相似性的研究为基础,定义了这类系统的相似结构,提出了新的相似性概念,对系统设计了鲁棒分散控制器.由于控制器本身也具有相似结构,因此易于工程实现.复映射Z←Zα+C(α<0)所构造的广义M-集中Bk′的自相似嵌套研究朱志良, 曹林, 刘向东, 朱伟勇研究了复映射Z←Zα+C(α<0)所产生的广义Mandelbrot集的内部结构,利用逃逸时间算法改变参数α,作出一系列分形图,通过具体的实验数据论证了这些分形图中逃逸点的分布规律,特别阐述了其中Bk′偏卫星系自相似嵌套规律.高炉煤粉喷吹系统的动态辨识刘克显, 王玉涛, 王师高炉煤粉喷吹是一个时变、非线性复杂系统,采用常规方法无法建立起精确的数学模型.通过对煤粉喷吹系统的研究,提出一种带可调因子的模糊神经网络(AFNN),它通过调节可调因子的大小,实现喷吹对象的动态辨识.实验结果表明,该网络具有快速的学习能力,较强的自适应性.无损耗电阻器的端口特性及应用研究吴建华, 殷洪义, 徐心和对无损耗电阻器的特性和功能进行了分析和探讨,建立了无损耗电阻器的数学模型和应用算法,并用无损耗电阻器代替电路中的电阻器,实现了动态电路的特性校正,大大减少了电路的能量损耗.实验结果验证了特性分析和算法的正确性,说明了无损耗电阻器可用于各类电系统及自动控制系统.基于D-S理论与嵌入式传感器的发电机温度监控与故障诊断杜庆东, 徐凌宇, 赵海在水电站的故障监控与报警系统中一般都采用实时采集传感器数据并进行处理分析的方法,这不仅增加了通信的负担而且由于恶劣的电磁环境也容易造成数据的误传;为了克服这些缺点,提出了一种采用嵌入式传感器与数据融合理论相结合的故障监控与诊断的方案,并且在吉林丰满水电站的发电机线圈温度的监控系统中得到了实际应用,取得了较好的效果.虚拟企业中多媒体信息的混沌加密方法王丽娜, 于戈, 梅哲论述了混沌加密原理,设计了混沌加密算法,分析了混沌加密的效率及安全性.提出混沌加密是非常有效的加密方法.对使用Java实现虚拟企业中信息的混沌加密的一些技术问题做了讨论和处理.混沌加密算法是对称加密算法,使用RSA算法来保护混沌加密密钥.Sialon/SiC复相材料的高温氧化行为茹红强, 张宁, 于佩志研究利用粘土直接合成的低成本Sialon/SiC复相材料的氧化行为,并对Sialon相含量、氧化温度以及氧化时间对氧化过程的影响进行了研究,结果表明,这种材料的氧化反应是一种钝化反应,具有较好的抗氧化性,Sialon相含量的增加能提高材料的抗氧化性.超声波作用下悬浮液中微粒凝聚过程参数的研究白晓清, 赫冀成针对利用超声波去除或分离悬浮液中微小颗粒(以下简称微粒)过程和复合材料生产过程悬浮液中的微粒凝聚过程参数进行了分析研究.利用数值模拟预测了微粒达到最终平衡状态时所需要的凝聚时间和凝聚位置,也预测了不同初始位置的微粒达到指定位置所需要的凝聚时间和在指定时刻微粒所处的凝聚位置.将数值模拟结果与其解析解进行了比较,表明数值计算结果是可靠的,并且数值模拟很好地弥补了解析解的不足.基于观测器的具有对称结构的广义大系统的H∞分散控制陈跃鹏, 张庆灵, 徐天群讨论具有对称结构的广义大系统的H∞分散控制问题.通过设计基于状态观测器的状态反馈,借助于广义代数Riccati不等式,给出具有对称结构的闭环广义大系统的H∞分散控制的充要条件.采用低温急冷大压下细化铁素体组织张红梅, 刘相华, 王国栋, 乔立峰, 曹刚以SS400为研究对象,在Gleeble1500热模拟上,测定了在850℃变形的奥氏体CCT曲线,研究了低温急冷大变形条件下变形温度、应变量、过冷度对铁素体变形行为以及对铁素体晶粒细化的影响.结果发现通过采用大变形低温轧制可以得到特别细小的铁素体组织平均晶粒直径约为2.66μm,铁素体体积分数可达85%以上,在铁素体边界有碳化物的析出.研究表明,低温、急冷、大变形可以有效地提高铁素体形核的驱动力,增加铁素体形核率,使晶粒大大地细化.SiCp/2024Al铝基复合材料及其阳极氧化膜的腐蚀行为贺春林, 刘常升, 李凤琴, 才庆魁用电化学方法研究了碳化硅颗粒增强2024铝(SiCp/2024Al)基复合材料及其硫酸阳极氧化膜在3.5%NaCl水溶液中的耐蚀性;作为比较,对2024Al的耐蚀性也进行了研究.结果表明,SiCp/2024Al复合材料在3.5%NaCl水溶液中比相应的基体金属有较大的腐蚀敏感性.SiCp/2024Al复合材料的阳极氧化膜具有良好的耐NaCl溶液腐蚀的能力,但其耐蚀性不如2024Al合金的阳极氧化膜,这是由于氧化膜中SiC颗粒的存在破坏了氧化膜的完整性和均匀性所致.WSGGM结合离散坐标法研究非灰气体辐射换热问题聂宇宏, 陈海耿推导了描述非灰气体辐射特性的灰气体加权和模型(WSGGM)与离散坐标法结合的公式,通过数值模拟以及与段法的比较,表明在WSGGM参数相同的情况下,该方法与段法的结果相吻合,证明将WSGGM引入离散坐标法能成功地用于模拟非灰气体辐射问题.4.学位论文李伯德AHP判断矩阵一致性改进方法研究2007层次分析法(AHP)在T.L.Saaty等人于20世纪70年代正式提出之后,由于它在处理复杂的定性与定量相结合的决策问题上的有效性,很快在世界范围内得到了普遍的重视和广泛的应用。
