高等流体力学课件 高等流体力学(7)
合集下载
高等流体力学课件

静止流体满足力的平衡条件,即合力为零。
流体静力学的基本概念
流体静力学是研究流体平衡和压力分布的学 科。
压力分布
静止流体的压力分布与重力场和其他外力场 有关,可以通过静力学方程求解。
流体动力学
总结词
流体动力学的基本概念、一维流动、层流与湍流
一维流动
一维流动是指流体沿着一条线的流动,可以用于 描述长距离管道内的流动或某些对称的流动。
水利工程
机械工程
流体动力学在水力发电、水利枢纽设计、 灌溉系统优化等方面具有广泛应用,为水 利工程提供了重要的技术支持。
流体动力学在机械工程领域的应用也十分 广泛,如内燃机、通风 system等的设计和 优化。
流体在自然界中的应用
气候变化
流体动力学在气候变化研究中发挥着重要作用,如风场、洋流等 对气候的影响研究。
详细描述
连续性方程是流体动力学的基本方程之一,它表达了单位时间内流经某一封闭 曲面微元体的流体质量的增加等于该微元体所受质量源的净增量,用于描述流 体运动的连续性。
动量方程
总结词
描述流体动量守恒的方程
详细描述
动量方程是流体动力学的基本方程之一,它表达了流体动量的变化率等于作用在 流体上的外力之和,包括重力、压力、摩擦力等。
方法
02
常用的线性稳定性分析方法包括特征值分析、傅里叶分析和庞
加莱截面法等。
应用
03
线性稳定性分析在气象、海洋、航空航天等领域有广泛应用,
用于预测和控制流体运动的稳定性。
非线性稳定性分析
定义
非线性稳定性分析是研究流体运动在较大扰 动下的响应,需要考虑非线性效应对流体运 动的影响。
方法
非线性稳定性分析需要求解非线性偏微分方程,常 用的方法包括数值模拟和近似解析法。
流体静力学的基本概念
流体静力学是研究流体平衡和压力分布的学 科。
压力分布
静止流体的压力分布与重力场和其他外力场 有关,可以通过静力学方程求解。
流体动力学
总结词
流体动力学的基本概念、一维流动、层流与湍流
一维流动
一维流动是指流体沿着一条线的流动,可以用于 描述长距离管道内的流动或某些对称的流动。
水利工程
机械工程
流体动力学在水力发电、水利枢纽设计、 灌溉系统优化等方面具有广泛应用,为水 利工程提供了重要的技术支持。
流体动力学在机械工程领域的应用也十分 广泛,如内燃机、通风 system等的设计和 优化。
流体在自然界中的应用
气候变化
流体动力学在气候变化研究中发挥着重要作用,如风场、洋流等 对气候的影响研究。
详细描述
连续性方程是流体动力学的基本方程之一,它表达了单位时间内流经某一封闭 曲面微元体的流体质量的增加等于该微元体所受质量源的净增量,用于描述流 体运动的连续性。
动量方程
总结词
描述流体动量守恒的方程
详细描述
动量方程是流体动力学的基本方程之一,它表达了流体动量的变化率等于作用在 流体上的外力之和,包括重力、压力、摩擦力等。
方法
02
常用的线性稳定性分析方法包括特征值分析、傅里叶分析和庞
加莱截面法等。
应用
03
线性稳定性分析在气象、海洋、航空航天等领域有广泛应用,
用于预测和控制流体运动的稳定性。
非线性稳定性分析
定义
非线性稳定性分析是研究流体运动在较大扰 动下的响应,需要考虑非线性效应对流体运 动的影响。
方法
非线性稳定性分析需要求解非线性偏微分方程,常 用的方法包括数值模拟和近似解析法。
高等流体力学的讲义课件流体力学的基本概念

t x y z
D lim 1 (xx,yy,zz,tt)(x,y,z,t)
Dt t0t
lit m0t
x t
x
y t
y
z t
z
uvw
t x y z
1.2 欧拉和拉格朗日参考系
1.1 连续介质假说
当流体分子的平均自由程远远小于流场的最小宏观尺度时, 可用统计平场的方法定义场变量如下:
ur lim(vrm) V m
lim(m)
V V
在微观上充分大统计平均才有确
定的值;宏观上充分小,统计平均 才能代表一点的物理量变化。
V
vr
•
m
连续介质方法的适用条件
1.2 欧拉和拉格朗日参考系
系统和控制体
通常力学和热力学定律都是针对系统的,于是需要在拉格朗日参考 系下推导基本守恒方程,而绝大多数流体力学问题又是在欧拉参考 系下求解的,因此需要寻求联系两种参考系下场变量及其导数的关 系式
欧拉和拉格朗日参考系中的时间导数
1.2 欧拉和拉格朗日参考系
欧拉参考系: u u (x,y,z,t)
x - x0 = u ( t - t0) y - y0 = v (t - t0) z - z0 = w (t - t0)
用 x0 , y0 , z0 来区分不同的流体质点,而用 t 来确定流体质点
的不同空间位置。
1.2 欧拉和拉格朗日参考系
系统和控制体
系统 某一确定流体质点集合的总体。 随时间改变其空间位置、大小和形状;系统边界上没有质量交换; 始终由同一些流体质点组成。 在拉格朗日参考系中,通常把注意力集中在流动的系统上,应用质 量、动量和能量守恒定律于系统,即可得到拉格朗日参考系中的基 本方程组。
D lim 1 (xx,yy,zz,tt)(x,y,z,t)
Dt t0t
lit m0t
x t
x
y t
y
z t
z
uvw
t x y z
1.2 欧拉和拉格朗日参考系
1.1 连续介质假说
当流体分子的平均自由程远远小于流场的最小宏观尺度时, 可用统计平场的方法定义场变量如下:
ur lim(vrm) V m
lim(m)
V V
在微观上充分大统计平均才有确
定的值;宏观上充分小,统计平均 才能代表一点的物理量变化。
V
vr
•
m
连续介质方法的适用条件
1.2 欧拉和拉格朗日参考系
系统和控制体
通常力学和热力学定律都是针对系统的,于是需要在拉格朗日参考 系下推导基本守恒方程,而绝大多数流体力学问题又是在欧拉参考 系下求解的,因此需要寻求联系两种参考系下场变量及其导数的关 系式
欧拉和拉格朗日参考系中的时间导数
1.2 欧拉和拉格朗日参考系
欧拉参考系: u u (x,y,z,t)
x - x0 = u ( t - t0) y - y0 = v (t - t0) z - z0 = w (t - t0)
用 x0 , y0 , z0 来区分不同的流体质点,而用 t 来确定流体质点
的不同空间位置。
1.2 欧拉和拉格朗日参考系
系统和控制体
系统 某一确定流体质点集合的总体。 随时间改变其空间位置、大小和形状;系统边界上没有质量交换; 始终由同一些流体质点组成。 在拉格朗日参考系中,通常把注意力集中在流动的系统上,应用质 量、动量和能量守恒定律于系统,即可得到拉格朗日参考系中的基 本方程组。
流体力学课件(全)

X 1 p 0 x
Y 1 p 0 y
欧拉平衡方程
Z 1 p 0 z
p p( , T )
t
1 V V T p
1 V V p T
p p(V , T )
1 t T p
p
p
1 p T
V
p y = pn pz = pn
px = p y = pz = pn = p
28/34
第二章
流体静力学
§1 静压强及其特性 §2 流体静力学平衡方程 §3 压力测量 §4 作用在平面上的静压力 §5 作用在曲面上的静压力 §6 物体在流体中的潜浮原理
29/34
§2流体静力学平衡方程
通过分析静止流体中流体微团的受力,可以建立 起平衡微分方程式,然后通过积分便可得到各种不同 情况下流体静压力的分布规律。 why 因此,首先要建立起流体平衡微分方程式。 现在讨论在平衡状态下作用在流体上的力应满足 的关系,建立平衡条件下的流体平衡微分方程式。
《流体力学》
汪志明教授
5/24
第一章 流体的流动性质
§1 流体力学的基本概念
§2 流体的连续介质假设 §3 状态方程 §4 传导系数 §5 表面张力与毛细现象
《流体力学》
汪志明教授
6/24
§2 流体的连续介质假设
虽然流体的真实结构是由分子构成,分子间有一定的孔隙,但流 体力学研究的并不是个别分子微观的运动,而是研究大量分子组成的 宏观流体在外力的作用下所引起的机械运动。 因此在流体力学中引入连续介质假设:即认为流体质点是微观上 充分大,宏观上充分小的流体微团,它完全充满所占空间,没有孔隙 存在。这就摆脱了复杂的分子运动,而着眼于宏观机械运动。
Y 1 p 0 y
欧拉平衡方程
Z 1 p 0 z
p p( , T )
t
1 V V T p
1 V V p T
p p(V , T )
1 t T p
p
p
1 p T
V
p y = pn pz = pn
px = p y = pz = pn = p
28/34
第二章
流体静力学
§1 静压强及其特性 §2 流体静力学平衡方程 §3 压力测量 §4 作用在平面上的静压力 §5 作用在曲面上的静压力 §6 物体在流体中的潜浮原理
29/34
§2流体静力学平衡方程
通过分析静止流体中流体微团的受力,可以建立 起平衡微分方程式,然后通过积分便可得到各种不同 情况下流体静压力的分布规律。 why 因此,首先要建立起流体平衡微分方程式。 现在讨论在平衡状态下作用在流体上的力应满足 的关系,建立平衡条件下的流体平衡微分方程式。
《流体力学》
汪志明教授
5/24
第一章 流体的流动性质
§1 流体力学的基本概念
§2 流体的连续介质假设 §3 状态方程 §4 传导系数 §5 表面张力与毛细现象
《流体力学》
汪志明教授
6/24
§2 流体的连续介质假设
虽然流体的真实结构是由分子构成,分子间有一定的孔隙,但流 体力学研究的并不是个别分子微观的运动,而是研究大量分子组成的 宏观流体在外力的作用下所引起的机械运动。 因此在流体力学中引入连续介质假设:即认为流体质点是微观上 充分大,宏观上充分小的流体微团,它完全充满所占空间,没有孔隙 存在。这就摆脱了复杂的分子运动,而着眼于宏观机械运动。
流体力学 第7章

3. 短管直径计算 【例7-4】 圆形有压涵管,管长l=50m,上、下游水位差 H=2.5m,涵管为钢筋混凝土管,各局部阻碍的水头损失 系数:进口ζe=0.5,转弯ζb=0.55 ,出口ζ0=1,通过流量 Q=2.9m3/s,计算所需管径。 【解】 列1-1和2-2断面的伯 努利方程,忽略上下 游流速,得
2 0v0
2g
,代入上式,整理得
管嘴出口流速
1 v n 2 gH0 n 2 gH0 (7 - 8)
7.2 管嘴出流
1 v n 2 gH0 n 2 gH0 (7 - 8)
管嘴流量
Q vA n A 2 gH0 (7 - 9)
式中 n n 0.82
7.1 孔口出流
2. 淹没出流 列1-1和2-2断面的伯努利方程
vc2 vc2 H1 H2 se 2g 2g 2g 2g
0 0
1v12
2 2v2
令 H 0 H1 H 2
1v12
2g
,又v2忽略
不计,代入上式,整理得 收缩断面流速
1 vc se 2 gH0 2 gH0 (7 - 4)
Qmax——开始出流时的最大流量。
7.1 孔口出流
【例7-1】 贮水罐底面积3m×2m,贮水深H1=4m,由于 锈蚀,距罐底0.2m处形成一个直径d=5mm的孔洞,试求 (1)水位恒定,一昼夜的漏水量;(2)因漏水水位下降, 一昼夜的漏水量。
【解】(1)按薄壁小孔口恒定出流计算
Q A 2gH
管道 长管:水头损失以沿程水头损失为主,局部损失 和流速水头的总和同沿程水头损失相比很小,忽 略不计,或按沿程水头损失的某一百分数估算, 仍能满足工程要求的管道,如城市室外给水管道 就属于长管。
2 0v0
2g
,代入上式,整理得
管嘴出口流速
1 v n 2 gH0 n 2 gH0 (7 - 8)
7.2 管嘴出流
1 v n 2 gH0 n 2 gH0 (7 - 8)
管嘴流量
Q vA n A 2 gH0 (7 - 9)
式中 n n 0.82
7.1 孔口出流
2. 淹没出流 列1-1和2-2断面的伯努利方程
vc2 vc2 H1 H2 se 2g 2g 2g 2g
0 0
1v12
2 2v2
令 H 0 H1 H 2
1v12
2g
,又v2忽略
不计,代入上式,整理得 收缩断面流速
1 vc se 2 gH0 2 gH0 (7 - 4)
Qmax——开始出流时的最大流量。
7.1 孔口出流
【例7-1】 贮水罐底面积3m×2m,贮水深H1=4m,由于 锈蚀,距罐底0.2m处形成一个直径d=5mm的孔洞,试求 (1)水位恒定,一昼夜的漏水量;(2)因漏水水位下降, 一昼夜的漏水量。
【解】(1)按薄壁小孔口恒定出流计算
Q A 2gH
管道 长管:水头损失以沿程水头损失为主,局部损失 和流速水头的总和同沿程水头损失相比很小,忽 略不计,或按沿程水头损失的某一百分数估算, 仍能满足工程要求的管道,如城市室外给水管道 就属于长管。
流体力学 7-4-5-粘性流体湍流流动
内区粘流与外区无粘流是渐进衔接的。
5.2
边界层流动的分离
边界层流动的动力学过程:惯性力、压力梯度、粘性力之 相对平衡。 (动能) (层外主流) (阻滞)
边界层外缘
1-3:顺压梯度区 3-5:逆压梯度区 S:分离点 S点后:分离区
u y 0 0
E
2
3
dp 0 dx
S
dp 0 dx
u y 0 0
1
dp 0 dx
5
u y 0 0
边界层内的流动示意图
边界层分离的条件:①存在逆压梯度区;
②壁面或粘性对流动的阻滞。 分离流动的特点:边界层离体,形成尾流(旋涡)。 分离的结果:产生压差阻力(形状阻力)。
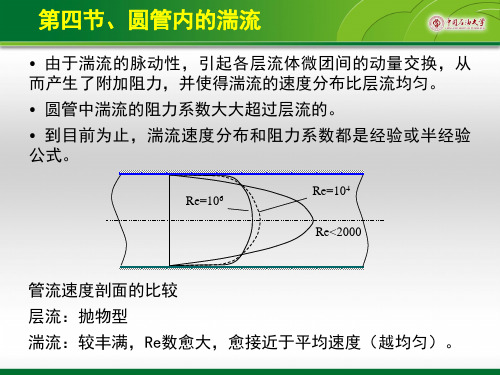
Re
过渡区
湍流区
?
水力光滑区 f (Re) 混合摩擦区 f (Re, 水力粗糙区 f ( )
d
) d
莫迪(Moody)图
d
层流区、临界区、光滑管区、过渡区、完全湍流粗糙管区。
对应关系:
莫迪图(汪158) • 层流区 尼古拉兹曲线(汪156) 层流区
• 临界区
• 光滑管区 • 过渡区 • 完全湍流粗糙管区
4.1
管内湍流结构
• 管中心处大部分区域的 流动是不规则的脉动运动 ——湍流核心区;
• 靠近固体壁面的一个薄 层内,脉动运动受到壁面 的限制,流动呈平滑的层 流运动特征——层流底层 (或粘性底层); • 层流底层与湍流核心区 之间,两种流动状态并存 ——过渡区。
湍流核心区 过渡区 层流底层
层流底层的厚度б0很薄,通常 只有几分之一毫米(与 Re 数有 关),但它的速度梯度很大, 对湍流流动的能量损失以及流 体与壁面间的热传导现象有重 要影响,这种影响与管道壁面 的粗糙程度直接相关。
《高等工程流体力学》课件

明确学习和掌握流体力学的预期成果和学术目标。
课程大纲
概述课程重点和每个章节的内容概要,为学习提供指引。
流体力学基础知识
打下坚实的基础,掌握流体的基本性质、流动的描述方法和流体静力学的重要概念。
1
流体的基本性质
深入了解液体和气体的特性,包括密度、
流动的描述方法
2
粘度和表面张力。
学习流体力学中的常见描述方法,如拉
《高等工程流体力学》PPT课 件
欢迎来到《高等工程流体力学》PPT课件,本课程将帮助您深入了解流体力学 的基础知识、流体动力学和应用与案例分析。让我们开始吧!
课程介绍
探索流体力学的世界,从课程背景、目标和大纲开始,为您提供全面的课程导引。
课程背景
介绍流体力学作为工程学科的重要性和应用领域。
课程目标
格朗日和欧拉描述。
3
流体静力学
探索液体和气体的静力学特性,包括压 力分布和浮力原理。
流体动力学
进入流体的动态世界,研究流体的动量方程、能量方程和连续性方程。
流体的动量方程
了解流体的质量、惯性和力之间 的关系,并探讨动量守恒定律。
流体的能量方程
研究流体中的能量传输,包括势 能和动能的转换。
流体的连续性方程
识别并解决在流体力学中可能遇到的常见问题和挑战。
了解质量守恒定律,并学习如何 应用连续性方程解决流体流动问 题。
应用与案例分析
将学到的理论知识应用于实际工程中,深入分析实际案例及潜在问题与解决方案。
流源等领域中的广泛应用。
工程实例分析
通过实例研究,深入分析流体力学在具体工程中的应用和解决方案。
潜在问题与解决方案
课程大纲
概述课程重点和每个章节的内容概要,为学习提供指引。
流体力学基础知识
打下坚实的基础,掌握流体的基本性质、流动的描述方法和流体静力学的重要概念。
1
流体的基本性质
深入了解液体和气体的特性,包括密度、
流动的描述方法
2
粘度和表面张力。
学习流体力学中的常见描述方法,如拉
《高等工程流体力学》PPT课 件
欢迎来到《高等工程流体力学》PPT课件,本课程将帮助您深入了解流体力学 的基础知识、流体动力学和应用与案例分析。让我们开始吧!
课程介绍
探索流体力学的世界,从课程背景、目标和大纲开始,为您提供全面的课程导引。
课程背景
介绍流体力学作为工程学科的重要性和应用领域。
课程目标
格朗日和欧拉描述。
3
流体静力学
探索液体和气体的静力学特性,包括压 力分布和浮力原理。
流体动力学
进入流体的动态世界,研究流体的动量方程、能量方程和连续性方程。
流体的动量方程
了解流体的质量、惯性和力之间 的关系,并探讨动量守恒定律。
流体的能量方程
研究流体中的能量传输,包括势 能和动能的转换。
流体的连续性方程
识别并解决在流体力学中可能遇到的常见问题和挑战。
了解质量守恒定律,并学习如何 应用连续性方程解决流体流动问 题。
应用与案例分析
将学到的理论知识应用于实际工程中,深入分析实际案例及潜在问题与解决方案。
流源等领域中的广泛应用。
工程实例分析
通过实例研究,深入分析流体力学在具体工程中的应用和解决方案。
潜在问题与解决方案
流体力学7 6水面曲线分析讲解

水跃 h→hc dh/ds→∞ 正交
工程实例 修挡水建筑物
末端跌坎
挡水建筑物下泄
7
h0
hc
水平线 M1
N-N M2
C-C
M3
i<ic
水平线
hc h0 i>ic
S1 C-C S2 N-N S3
8
2、急坡渠道 i>ic h0<hc
分区 曲线 水深h 流态 i-J 1-Fr dh/ds 曲线形状
1 S1 h> hc > h 0 缓流 + + + 上凸的壅水曲线 2 S2 hc > h> h0 急流 + - - 下凹的降水曲线 3 S3 hc >h 0 > h 急流 - - + 上凸的壅水曲线
?分析i-J/(1-Fr) 的正负(单调增减性 ),便可得到水面 曲线沿程变化的趋势及两端极限情况
4
1、分界线h0、hc
?正常水深线:N-N(分子为零) i-J=0
J=i
h=h 0 (渐近线)
?临界水深线:c-c(分子为零) 1-Fr =0
h=h c (正交)
2、流动分区
? 1区: N-N 、c-c线之上 ? 2区: N-N 、c-c线之间 ? 3区: N-N 、c-c线之下
时,最终都要趋于水平线 8、急流状态水面线控制水深在上游,缓流状态水面线控
制水深在下游,是由于微幅干扰波的影响 9、共有12条水面曲线,其中缓坡、急坡各 3条,临界坡、
平坡、逆坡各 2条,常用 M1、M2、M3、S2四条曲线
13
七、水面曲线的定性绘制步骤
1、绘出N-N线和C-C 线,将流动空间分成1、2、3三区,每个区域 只相应一种水面曲线。
工程实例 修挡水建筑物
末端跌坎
挡水建筑物下泄
7
h0
hc
水平线 M1
N-N M2
C-C
M3
i<ic
水平线
hc h0 i>ic
S1 C-C S2 N-N S3
8
2、急坡渠道 i>ic h0<hc
分区 曲线 水深h 流态 i-J 1-Fr dh/ds 曲线形状
1 S1 h> hc > h 0 缓流 + + + 上凸的壅水曲线 2 S2 hc > h> h0 急流 + - - 下凹的降水曲线 3 S3 hc >h 0 > h 急流 - - + 上凸的壅水曲线
?分析i-J/(1-Fr) 的正负(单调增减性 ),便可得到水面 曲线沿程变化的趋势及两端极限情况
4
1、分界线h0、hc
?正常水深线:N-N(分子为零) i-J=0
J=i
h=h 0 (渐近线)
?临界水深线:c-c(分子为零) 1-Fr =0
h=h c (正交)
2、流动分区
? 1区: N-N 、c-c线之上 ? 2区: N-N 、c-c线之间 ? 3区: N-N 、c-c线之下
时,最终都要趋于水平线 8、急流状态水面线控制水深在上游,缓流状态水面线控
制水深在下游,是由于微幅干扰波的影响 9、共有12条水面曲线,其中缓坡、急坡各 3条,临界坡、
平坡、逆坡各 2条,常用 M1、M2、M3、S2四条曲线
13
七、水面曲线的定性绘制步骤
1、绘出N-N线和C-C 线,将流动空间分成1、2、3三区,每个区域 只相应一种水面曲线。
高等流体力学第7讲

因此
dz
d
0
lim 0
z z0
0
在奇点附近
z
z0
0
dz
d
0
F (
)
Q i
2
ln
0
dz
d
0
Q i
2
a2
z zj
和 z=0
而它们都在圆内,因而圆外并未增加奇点。
y
O
x
g(z) f (z) f ( a2 ) 确实是满足物面条件及奇点条件的 z
圆外流场的解。
例:在 z a 的圆外有均匀来流如图所示,求相应的复势。
y V
O
x
已知均匀流的复势为
f (z) Vei( ) z
在 - 平面上仍是解析函数。
2、若在z - 平面上,复势 f (z) 在 z = zi 点上有奇点,
则在 - 平面上,在对应点 = i 上 F( ) 也具有
同样性质的奇点。
例:在z - 平面上 z = z0 点处有源和涡
f
(
z)
Q i
2
ln
z
z0
已知变换关系为 z = g ( )
L
L
O
x
O
z- 平面
- 平面
设有解析复变函数 z = g (),它把 z = x + i y 平面上的几何曲线L: z(t)= x (t) + i y (t)变换到
= + i 平面上的几何曲线L : (t)= (t) + i (t) 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
dp
1 2
u
u
G
u
沿流线取线元 dl ,
dl
dp
u2 2
G dl
u
d
dp
u2 2
G
0
dp u2
2 GC
伯努利方程,或伯努利积分;C 称伯努利常数,C 沿同一条流线为常数;
伯努利方程成立条件:理想流体,外力有势,正压流体,定常流 动,沿流线。
20
沿流线的伯努利方程
u
u 2
(u
)
p
2u G
(u ) 2 t (u ) ( )u (u ) u( ) ( u) ( )u (u )
(u ) ( )u 2 t
35
涡量方程
涡量方程的物理意义
第一节:粘性,斜压与外力无势是引起速度环 量和涡通量发生变化的三大因素.
D
Dt
C (t )
Du Dt
dr
C (t )
Dui Dt
dxi
沿一条确定的由流体质点组成的物质周线的速度环量的随体导数等 于该周线上的加速度的环量。 以上结论是纯运动学性质的,因此对任何流体都成立。
5
因为:
Du p 1 ( • u) 2u f
Dt
3
Du p u f
Dt
在运动过程中, 涡管会发生变形:当涡管被拉伸时, 涡量增大, 涡管 被压缩时, 涡量减小, 以保持通过横截面的总的涡通量不变。
15
涡管强度保持定理
涡量场的散度为 0, 0 , 由此得出在每一瞬时通过同一涡管 任意截面的涡通量处处相等, 即涡管强度在空间上守恒, 以上结论对 任意流体都是正确的。 当满足开尔文定理成立条件时, 涡管强度不但具有空间上的守恒性, 而且具有时间上的守恒性。
u
C(t)
dr
C(t)
Du Dt
dr
u
D(dr ) Dt
C(t)
Du Dt
dr
u
du
其中
D(dr ) Dt
d
Dr Dt
du
4
沿物质周线的速度环量的随体导数
u
u(r,t)
为单值函数, u du
C(t)
C(t)
d
u2 2
0
D
Dt
C (t )
Du Dt
dr
u
du
16
理想不可压缩流体在重力场作用下的流动
(1) 均匀来流定常不脱体绕流 (2) 物体从静止状态开始运动 满足理想、正压、质量力有势; 第 1 种情况下, 流体质点来自无穷远处,无穷远处无旋, 所以整个 流场无旋; 第 2 种情况下, 初始时刻, 静止状态的流体无旋, 所以任意时刻流体 无旋。
17
3.2 伯努利方程
u dl t
+dl
dp
u2 2
G
0
u
dp u2
t
dl
+d
2
G 0
很难计算,只是在某 些特定条件下求解
2 u dl
1 t
2
1
d
dp
u2 2
G
0
质量力只有重力且重力加速度沿负 z 轴方向,流体密度为常数,
p1
u12 2
gz1
p2
u22 2
gz2
2
1
u dl t
成立条件:理想流体,流体密度为常数,重力加速度沿 Z 轴负方向,
23
伯努利方程的条件虽然苛刻,但揭示的规律 可应用于实际流动中去,例如解释河道流动 规律,虹吸管原理(连通管原理)及机翼升 力产生原因等。
伯努利方程是物理学能量守恒和转换定律在流 体运动中的表现形式之一。
24
沿流线的伯努利方程
非定常流动
u t
dp
1 2
u
u
G
u
等式两边同时点乘 dl , dl 平行于 u ,即沿流线方向,
z
k
dx dy dz d
x y z
dr d
式中d 表示对空间的全微分。
8
正压流体
( p) 等密度面和等压强面是重合的
流体作等熵流动,等温流动,不可压缩均质流体均可视为正压流体。
( p)
d
dp
( p)
dp
dr
p
dp
d
dp
( p)
dr
dp
( p)
因为 dr 是任选的,所以对正压流体流场中任一点有,
解:液体是不可压缩的,故液体在同一瞬时的速度 v v(t) 沿U形 管处处相等,只是时间的函数,且等于,
v d (速度正向从1指向2)
dt
是液面至平衡位置的距离。非定常流沿流 线的伯努利方程,
1
v
p1
v12 2
gz1
p2
v22 2
gz2
2 1
v dl t
z1
因为 z1 h , z2 h ,v1 v2 , p1 p2 pa ,
(u ) ( )u 2 t
涡量的随体导数 u D
t
Dt
粘性项影响:粘性对涡量变化的影响主要是粘性扩散,而运动粘 性系数在这里相当于扩散系数。在粘性流体中,由于粘性的作用, 涡量强的地方将向涡量弱的地方输运涡量,正像热量由温度高的 地方向温度低的地方传播和扩散一样,扩散的作用是抹平差距, 直至全流场涡量强度相等为止
v
2
h
z2
2g
2 1
v t
dl
v t
2 1
dl
=
d 2
dt 2
L
d 2 2g 0
dt2 L
p1
u12 2
gz1
p2
u22 2
gz2
2 1
u dl t
33
求方程的解,
d 2 2g 0
dt2 L
c1 cos
2g L
t c2 sin
2g L
t
初始条件:t 0 时 A ,d 0
D Du dr p dr f dr 2u dr
Dt C(t) Dt
C (t )
C(t)
C (t )
6
欧拉方程 理想流体,
Du p f
Dt 设质量力有势且为单值函数,
f G Du p G
Dt
7
场论公式
dr
(dxi
dyj
dzk
)
x
i
y
j
21
伯努利方程的水力学意义 单位质量流体沿流线的水头形式
v2 z
p
H 常数
(沿流线)
2g ρg
v2
速度水头
2g
z
位置水头
p
压强水头 测压管水头
H
总水头
22
若忽略重力(空气),则 v2 p H 常数 (沿流线) 2ρ
由上式可解释两船在行驶时,如果靠的太近就 会相互碰撞
高速公路上行驶的两列汽车,小车不能太靠 近大车
涡量方程
理想流体
(u ) ( )u 2
t (u ) ( )u t
以上涡量方程中没有压强 p 出现,于是可在压强场未知情况下求 解速度场和涡量场。
39
已知涡量场求解压强场
u t
(u
)u
p
2u
u t
(u
)u
p
2u
(u
)u
p
练习题 3.1 (p.84),
14
涡管强度保持定理(亥姆霍兹第二定律)
取 C(t) 是涡管横截面 A(t) 上并围绕涡管一周的封闭物质周线,则 在某一瞬时 ,
u dr ndA
C (t )
A(t )
D u dr D ndA 0
Dt C(t)
Dt A(t)
涡管在随流体运动过程中通过其任一横截面的涡通量, 即涡管强度, 不随时间改变。
26
势流伯努利方程
定常流动
t
dp
2
G
f
(t)
dp
2
G
f
上式中 f 在全流场为常数, 且不随时间变化;在伯努利积分中的 C 只是沿同一条流线为常数
27
伯努利方程应用
28
伯努利方程应用
29
伯努利方程应用
30
伯努利方程应用
31
伯努利方程应用
32
例1 液体在两头开口的等横截面 U 形管中振荡,液柱长 L,液面上 方为大气压强 pa , 忽略粘性摩擦力和表面张力。求液柱运动规律。
12
亥姆霍兹定律
当流体正压 , 理想流体 , 质量力有势,即 生成环量的所有扭矩为零,则开尔文定理 可给出流体流动很漂亮的几何描述,即亥 姆霍兹定律
涡线无始无终,并生成封闭环,即涡管, 涡管的速度环量沿涡管长度方向不变,为 常数,即亥姆霍兹第一定律
13
涡旋不生不灭定理 若流体理想,正压,且外力有势,如果初始 时刻在某部分流体内无旋,则以前或以后 任一时刻这部分流体皆无旋;反之,若初 始时刻该部分流体有旋,则以前或以后的 任何时刻这部分流体皆为有旋。
36
涡量方程 涡量方程的物理意义
涡线的拉伸和扭曲
u
l
u l
| | lim u pQ0 PQ
u
u
| | lim | | lim
pQ0 PQ
pQ0 PQ
PΩ
u
Q u u
使涡线拉伸或压缩,或而使涡线扭曲,结果都会导致涡量的变化。
37
花样滑冰运动员就是利用减小惯性距来增 大旋转。
38
dt
Acos
2g L
t
c1 A ,c2 0
振动周期: 2 L
2g
速度: d
