第3章 参考答案
逻辑第三章习题参考答案(0710)

30
III. 三、2. P94
【原题】 ⒉ 已知“有S不是p”为假
【参考答案】
SP
SOP
0
例S 蕃茄
例P 西红柿
2021/4/14
PS
SP
0
1
美国人
人
SP
1
SP
1
31
III. 三、3. P94
【原题】 ⒊ 已知“有S是P”为真
【参考答案】
SP
SIP
1
例S 蕃茄
2021/4/14
36
III. 四、2. P94
【原题】 ⒉ 这架飞机上的乘客都是去英国旅游的。
【参考答案】
整理:所有乘客是去英国旅游的。SAP为真
SIP:有的乘客是去英国旅游的。 真 SOP:有的乘客不是去英国旅游的。假 SEP:所有乘客不是去英国旅游的。假
【参考答案】
不表达判断
因为是一般疑问句,是有疑而问,无所断定。
2021/4/14
3
III. 一、2. P93
【原题】 ⒉ 没有耕耘,哪来收获?
【参考答案】
间接表达判断:没有耕耘就没有收获。 因为是反诘句。
2021/4/14
第三章练习题
(共一讲)
III. 一、P93 (共 10 小题)
【原题】 一、下列语句是否表达判断?为什么?
【知识点】
语句和判断的关系 何种语句表达判断?何种语句不表达判断?
2021/4/14
2
III. 一、1. P93
【原题】 ⒈ 为什么说社会主义制度有无比的优越性?
2021/4/14
15
III. 二、3. P93
数据与计算机通信答案(第3章)

而对于数字彩色电视机,相当不错了。如果不提高数据率,还可以通过降低分辨率或刷新速 率,来换取色彩数的提高,但这也不实用的方法。
已知视频带宽 B=5MHz,所以有 5=P/105,则每行的像素数 P=5x105=525。 然而,通常 CCIR-M/NTSC 制式每行只约有 450 像素,带宽 B=P/105=450/105=4.3MHz (实 际技术指标 4.2Hz) 。 带宽由 4.2MHz 增加到 5MHz 时,水平分辨率约增加 75 像素,增幅 16.7%。 (2)计算垂直分辨率的增幅 由于信号最高频率 fH=5MHz,即最短的信号周期 1/fH=0.2υs。 又因为每个最短周期包含 2 个像素,则有 225 周期/行。那么,每行扫描时间为 0.2υs×225=45υs。加上水平回扫 11υs,每行往返扫描时间为 56υs ,即 56x10-6 s, 假定每屏 V 行,每秒扫描 30 场(帧、屏),则每秒扫描行数为 30V。 因此对于画面刷新,有 30V×56x10-6 = 1s,V = 595 行/屏。目前 NSTL 制式每行只有 525 行。垂直分辨率增加了 70 行,增幅 13.3%。
cos 2 t = cos t cos t = 1 (cos 2t + cos 0) = 1 (cos 2t + 1)
2
2
所以, f (t) = (10 cos t)2 = 100 cos 2 t = 50 + 50 cos 2t
中国近代史纲要第三章习题参考答案

第三章习题参考答案第三章辛亥革命与君主专制制度的终结一、单项选择题1.B2.C3.C4.C5.A6.C7.C8.D9.D 10.C11.B 12.B 13.C 14.A 15.B16.B 17.B 18.B 19.D 20.C21.D 22. A 23. C 24. A 25.C26.D 27. D 28.C 29. A 30. B 31. A二、多项选择题1. ABCD2. ABCD3. AB4. ABD5.BCD6. ABCD7. ABD8.ABC9.CD 10. ABD11. ABC 12.BCD 13.BCD 14.ABC 15.ABCD16.ABCD 17.ABC 18.AC三、简答题1.简述资产阶级革命派形成的阶级基础参考答案:19 世纪末20 世纪初,中国民族资本主义得到了初步的发展。
随着民族资本主义企业发展数量的增多和规模的扩大,民族资产阶级及与它相联系的社会力量也有了较大的发展。
民族资产阶级为了冲破帝国主义、封建主义的桎梏,发展资本主义,需要自己政治利益的代言人和经济利益的维护者。
这正是资产阶级革命派形成的阶级基础。
2.简述资产阶级革命派所进行的宣传和组织工作答:历史进入20 世纪,随着一批新兴知识分子的产生,各种宣传革命的书籍报刊纷纷涌现,民主革命思想得到广泛传播。
1903 年,章炳麟发表了《驳康有为论革命书》,反对康有为的保皇观点,强调中国人民完全有能力建立民主共和制度。
邹容创作了《革命军》,阐述在中国进行民主革命的必要性和正义性,号召人民推翻清朝统治,建立“中华共和国”。
陈天华创作了《警世钟》、《猛回头》两本小册子,痛陈帝国主义侵略给中国带来的沉重灾难,揭露清政府已经成了帝国主义统治中国的工具,号召人民推翻清政府。
在资产阶级革命思想的传播过程中,资产阶级革命团体也在各地相继成立。
从1904 年开始,出现了10 多个革命团体,其中重要的有华兴会、科学补习所、光复会等。
这些革命团体的成立为革命思想的传播及革命运动的发展提供了不可缺少的组织力量。
第3章 问题及习题参考答案

Cl 2HCl Cl H ++CH 4Cl CH 3Cl H +++Cl +CH 4CH 3HCl +Cl +CH 3Cl CH 3Cl 2第3章 思考题及习题参考答案思考题3-1用纽曼投影式画出下列化合物的对位交叉和全重叠式构象。
1. 解: 1-氯-2-溴乙烷;2. 解:3-羟基丙酸。
对位交叉式; 全重叠式 对位交叉式; 全重叠式。
思考题3-2利用键能数据的计算,判断下列A 和B 两种甲烷氯代的反应历程,哪个较合理?A.B.解:从图3-7可以看出链传递的第一步反应是反应的速度决定步骤。
根据键能分别计算两个历程的此步反应的焓变:历程A. ∆H = 434.7 一 351.1 = 83.6 kJ ·mol -1,活化能 > 83.6 kJ ·mol -1历程B. ∆H = 434.7 一 430.5 = 4.2 kJ ·mol -1,活化能为16.7 kJ·mol -1答:历程A 的速度决定步骤的活化能必须大于83.6 kJ · mol -1,而历程B 的活化能为16.7 kJ·mol -1,因此,历程B 较为合理。
习题3.1. 在标准状况下37.0g 由甲烷与另一种烷烃两种气态烷烃组成的混合物完全燃烧消耗4.25 molO 2,计算两种可能的混合物的摩尔组成。
解:设气态烷烃混合物的组成为CnHm ,完全燃烧的反应方程式为:++CnHm O 2CO 2H 2O n +m 4n m 2(12n + m)g 4m +n mol 37.0g 4.25 mol 4m +n 4.25×(12n + m) = 37.0× 4.25m - (37.0/4)m = 37.0n - 4.25×12nm = 4.25×12 - 37.0 37.0/4 - 4.25n m = 2.8n m/n = 2.8气体烷烃中:甲烷CH 4的m/n = 4 > 2.8,乙烷C 2H 6的m/n = 3 > 2.8;丙烷C 3H 8的m/n = 2.7 < 2.8,丁烷C 4H 10的m/n = 2.5 < 2.8。
化工原理 第3章 参考答案 (期末专用)

T 46℃ 46℃ T1 t2 32℃ T2 =10℃
Q=QL=Q1+Q'1=qm1r1+qm1cp1(T1-T2) Q=QL=Q1+Q'1=Q2=qm2cp2(t2-t1)→qm2 Q'1=qm1cp1(T1-T2)=qm2cp2(t-t1)→t
求:∆tm1、∆t'm1→求A2=A1+A'1 t t1 =5℃ 已知r=351.6[kJ/kg] →A CS2平均温度tm=(46+10)/2=28℃ 查:28℃下CS2比热cp=0.963[kJ/kg·℃] Q1=qm1r1=(300/3600)×351.6=29.3[kW] Q'1=(300/3600)×0.963×103×(46-10)=2.89[kW] Q=QL=Q1+Q'1=29.3+2.89=32.19[kW] Q L Q=QL=Q1+Q'1=Q2=qm2cp2(t2-t1) qm2 = cp2(t2 - t1) 2 返回
解出: t′ =34.1 ℃ 2 ′ ∆m Q K′A t′ q′ 1 ⋅ r q′ 2cp2 (t′ - t1) 2(34.1-30) m 2 m = = = = =1.64 Q K ∆ m qm1 ⋅ r qm2cp2 (t2 - t1) At 35-30 冷却水流量增加一倍,蒸汽冷凝量q'm1将增加64%
Q=QL=Q1+Q 32.19×103 L qm2 = = =0.285 kg/ s] [ 3 cp2(t2 - t1) 4.187×10 ×(32-5)
Q'1=qm1cp1(T1-T2)=qm2cp2(t-t1)=2.89[kW] Q'1=0.285×4.187×103×(t-5)=2.89[kW] →t=7.45℃
大学物理第三章课后习题答案

L 时时, (1)摩擦力做功多少? (2)弹性力做功多少? (3)其他力做功多少? (4)外力做的总功是多少? 8. 小球系于细绳的一端,质量为 m ,并以恒定的角速
度 ω 0 在光滑水平面上围绕一半径为 R 的圆周运动。细 绳穿过圆心小孔, 若手握绳的另一端用力 F 向下拉绳,使小球运转的半径减小一半, 求 力对小球所做的功。 9. 如图所示, 一小车从光滑的轨道上某处由
9. 解:由题意知小车飞越 BC 缺口时做斜抛运动,其射程 BC = 2 R sin α 。 设小车在 B 点时的速度为 υ B , 欲使小车 刚 好 越 过 BC , 应 满 足 2υ B ⋅ sin α g
-7-
2 R sin α = υ B ⋅ cos α ⋅
自治区精品课程—大学物理学
题库
gR (1) cos α 由 A 点运动到 B 点时机械能守恒得: 1 2 mgh = mg ( R + R cos α ) + mυ B (2) 2 由式(1)与(2)得 1 h = (1 + cos α + )R 2 cos α
自治区精品课程—大学物理学
题库
第三章 功和能
一、 填空 1. 功等于质点受的 和 的标量积,功是 变化的量度。 2. 物理学中用 来描述物体做功的快慢。力的瞬时功率等于 与 的标积。对于一定功率的机械,当速度小时,力就 (填“大”或“小” ) , 速度大时,力必定 (填“大”或“小” ) 。 3. 合外力对质点所做的功等于质点动能的增量,此即 定理。 4. 质点动能定理的微分形式是 。 5. 质点动能定理的积分形式是 。 6. 按做功性质,可以将力分为 和 。 7. 所做的功只取决于受力物体的初末位置,与物体所经过的路径无 关。做功与路径有关的力叫做 。 8. 物体在 力作用下,沿任意闭合路径绕一周所做的功等于零。 9. 保守力做功与物体势能改变量之间的关系是 。 10. 若保守力做正功,则势能 ( “增加”或“减少” ) ,若保守力做负功, 则 势能 ( “增加”或“减少” ) 。 11. 势能的增量与势能零点的选取 (填“有关”或“无关” ) ,势能的大小 与势能零点的选取 (填“有关”或“无关” ) 。 12. 质点系内各质点之间的相互作用力称为 ,质点系以外的其他物体对 质点系内各质点的作用力称为 。 13. 质点系在运动过程中, 所做的功与 所做的功的总 和等于质点系的机械能的增量,此即质点系的 原理。 14. 在只 有 做功 的情 况下, 质点 系的机 械能 保持不 变, 这就是 定律。 15. 行星沿 轨道绕太阳运行, 太阳位于椭圆的一个 上; 对任一行星, 以 太阳 中 心为 参 考点 , 行星 的 位置 矢 量在 相 等的 时 间内 扫 过的 面 积填 ( “相 等 ”或 “ 不 相等 ” ) ; 行星 绕 太阳 运 动的 和 椭圆 轨 道的 成正比。 16. 第一宇宙速度是 所需要 的速度。 17. 第二宇宙速度是 所需要的 最小速度。 18. 第三宇宙速度是 所需的 最小速度。 二、 简答 1. 2. 3. 4. 5. 简述质点动能定理的内容,并写出其微分形式和积分形式。 简述保守力做功与物体势能改变量之间的关系。 简述质点系功能原理的内容。 简述机械能守恒定律的内容。 简述行星运动的三大定律的内容。
数据库答案 第三章习题参考答案

7. 找出没有使用天津产的零件的工程项目代码。 找出没有使用天津产的零件的工程项目代码。 Select jno from j where not exists (Select * from spj where spj.jno=j.jno and sno in (Select sno from s where city=‘天津’) city=‘天津了供应商 所供应的全部零件的工程号 求至少用了供应商S1所供应的全部零件的工程号 求至少用了供应商 所供应的全部零件的工程号JNO。 。 即查找:不存在这样的零件y,供应商S1供应了 供应了y,而工程x 即查找:不存在这样的零件 ,供应商 供应了 ,而工程 为选用y。 为选用 。 Select distinct jno From spj z Where not exists (select * from spj x where sno=‘S1’ and not exists (select * from spj y where y.pno=x.pno and y.jno=z.jno));
习题三
Select sno from spj Where jno=‘J1’;
第 4题
1.求供应工程 零件的供应商号码 求供应工程J1零件的供应商号码 求供应工程 零件的供应商号码SNO。 。
2.求供应工程 零件 的供应商号码 求供应工程J1零件 的供应商号码SNO。 求供应工程 零件P1的供应商号码 。 Select sno from spj Where jno=‘J1’ and pno=‘P1’;
1
3.求供应工程 零件为红色的供应商号码。 求供应工程J1零件为红色的供应商号码 求供应工程 零件为红色的供应商号码。 Select sno from spj, p Where spj.pno=p.pno and jno=‘J1’ and color=‘红 color=‘红’; 或: Select sno from spj Where jno =‘J1’ and pno in (Select pno from p where color=‘红’ ); color=‘红
第三章 编译原理参考答案(1)
一:有语言L={w|w∈{0,1}*,并且w中至少有两个1,又在任何两个1之间有偶数个0 },试写出该语言的正规表达式。
对于语言L,w中至少有两个1,且任意两个1之间必须有偶数个0;也即在第一个1之前和最后一个1之后,对0的个数没有要求。
据此我们求出L的正规式为0*1(00(00)*1)*00(00)*10*二:设语言L是满足下述条件的符号串构成的语言:若出现 a ,则其后至少紧跟两个 c ;请给出识别L 的正规表达式。
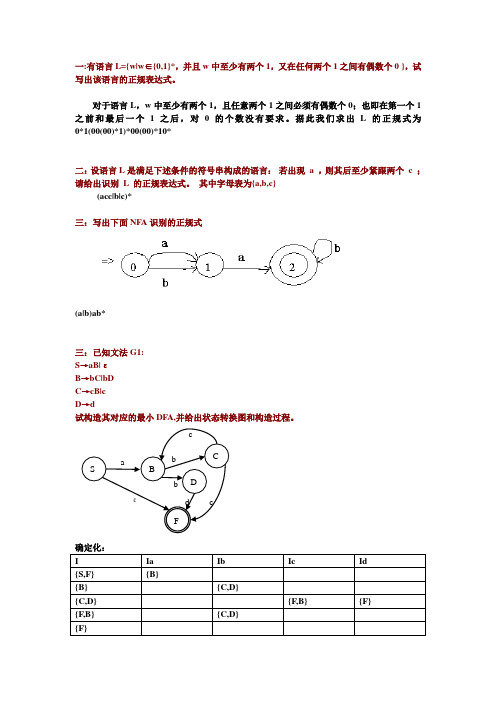
其中字母表为{a,b,c}(acc|b|c)*三:写出下面NFA识别的正规式(a|b)ab*三:已知文法G1:S→aB|εB→bC|bDC→cB|cD→d试构造其对应的最小DFA,并给出状态转换图和构造过程。
确定化:最小化:{1,5,4} {2,3} {1}{5}{4}{2}{3} 上图即为最小DFA四:设有L(G)={a 2n+1b 2m a 2p+1| n ≥0,p ≥0,m ≥1}。
(1) 给出描述该语言的正规表达式; (2) 构造识别该语言的确定有限自动机(可直接用状态图形式给出)并化简。
该语言对应的正规表达式为a(aa)*bb(bb)*a(aa)*,正规表达式对应的NFA 如图:确定化:(按照定义,上图已经是DFA ,所以下面确定化不做也是可以的,直接最小化)由最小化方法得到 {0,2} {1} {3,5} {4,6} {7} 最简的DFA :a重新命名五: 将图所示的非确定有限自动机(NFA)变换成等价的确定有限自动机(DFA)并化简。
其中,X 为初态,Y 为终态。
然后根据最小DFA ,写出对应的正规文法(右线性)b重新命名A->aB|bCB->aF|a|bE|b C->bDD->aD|bF|b E->aF|a|bD F->aF|bF|a|b。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.8 判断下列公式是否为可合一,若可合一,则求出其最一般合一。
(1) P(a, b), P(x, y)(2) P(f(x), b), P(y, z)(3) P(f(x), y), P(y, f(b))(4) P(f(y), y, x), P(x, f(a), f(b))(5) P(x, y), P(y, x)解:(1) 可合一,其最一般和一为:σ={a/x, b/y}。
(2) 可合一,其最一般和一为:σ={y/f(x), b/z}。
(3) 可合一,其最一般和一为:σ={ f(b)/y, b/x}。
(4) 不可合一。
(5) 可合一,其最一般和一为:σ={ y/x}。
3.11 把下列谓词公式化成子句集:(1)(∀x)(∀y)(P(x, y)∧Q(x, y))(2)(∀x)(∀y)(P(x, y)→Q(x, y))(3)(∀x)(∃y)(P(x, y)∨(Q(x, y)→R(x, y)))(4)(∀x) (∀y) (∃z)(P(x, y)→Q(x, y)∨R(x, z))解:(1) 由于(∀x)(∀y)(P(x, y)∧Q(x, y))已经是Skolem标准型,且P(x, y)∧Q(x, y)已经是合取范式,所以可直接消去全称量词、合取词,得{ P(x, y), Q(x, y)}再进行变元换名得子句集:S={ P(x, y), Q(u, v)}(2) 对谓词公式(∀x)(∀y)(P(x, y)→Q(x, y)),先消去连接词“→”得:(∀x)(∀y)(¬P(x, y)∨Q(x, y))此公式已为Skolem标准型。
再消去全称量词得子句集:S={¬P(x, y)∨Q(x, y)}(3) 对谓词公式(∀x)(∃y)(P(x, y)∨(Q(x, y)→R(x, y))),先消去连接词“→”得:(∀x)(∃y)(P(x, y)∨(¬Q(x, y)∨R(x, y)))此公式已为前束范式。
再消去存在量词,即用Skolem函数f(x)替换y得:(∀x)(P(x, f(x))∨¬Q(x, f(x))∨R(x, f(x)))此公式已为Skolem标准型。
最后消去全称量词得子句集:S={P(x, f(x))∨¬Q(x, f(x))∨R(x, f(x))}(4) 对谓词(∀x) (∀y) (∃z)(P(x, y)→Q(x, y)∨R(x, z)),先消去连接词“→”得:(∀x) (∀y) (∃z)(¬P(x, y)∨Q(x, y)∨R(x, z))再消去存在量词,即用Skolem函数f(x)替换y得:(∀x) (∀y) (¬P(x, y)∨Q(x, y)∨R(x, f(x,y))) 此公式已为Skolem标准型。
最后消去全称量词得子句集:S={¬P(x, y)∨Q(x, y)∨R(x, f(x,y))}3-13 判断下列子句集中哪些是不可满足的:(1) {¬P ∨Q, ¬Q, P , ¬P}(2) { P ∨Q , ¬P ∨Q, P ∨¬Q, ¬P ∨¬Q }(3) { P(y)∨Q(y) , ¬P(f(x))∨R(a)}(4) {¬P(x)∨Q(x) , ¬P(y)∨R (y), P(a), S(a), ¬S(z)∨¬R(z)}(5) {¬P(x)∨Q(f(x),a) , ¬P(h(y))∨Q(f(h(y)), a )∨¬P(z)}(6) {P(x)∨Q(x)∨R(x) , ¬P(y)∨R(y), ¬Q(a), ¬R(b)}解:(1) 不可满足,其归结过程为:(2)(3) 不是不可满足的,原因是不能由它导出空子句。
(4) 不可满足,其归结过程略(5) 不是不可满足的,原因是不能由它导出空子句。
(6) 不可满足,其归结过程略3.14 对下列各题分别证明G 是否为F 1,F 2,…,F n的逻辑结论:(1) F: (∃x)(∃y)(P(x, y)G: (∀y)(∃x)(P(x, y)(2) F: (∀x)(P(x)∧(Q(a)∨Q(b)))G: (∃x) (P(x)∧Q(x))(3) F: (∃x)(∃y)(P(f(x))∧(Q(f(y )))G: P(f(a))∧P(y)∧Q(y)(4) F 1: (∀x)(P(x)→(∀y)(Q(y)→⌝L(x.y)))F 2: (∃x) (P(x)∧(∀y)(R(y)→L(x.y)))G: (∀x)(R(x)→⌝Q(x))(5)F1: (∀x)(P(x)→(Q(x)∧R(x)))F2: (∃x) (P(x)∧S(x))G: (∃x) (S(x)∧R(x))解:(1) 先将F和¬G化成子句集:S={P(a,b), ¬P(x,b)}再对S进行归结:所以,G是F的逻辑结论(2) 先将F和¬G化成子句集由F得:S1={P(x),(Q(a)∨Q(b))}由于¬G为:¬(∃x) (P(x)∧Q(x)),即(∀x) (¬ P(x)∨¬ Q(x)),可得:S2={¬ P(x)∨¬ Q(x)}因此,扩充的子句集为:S={ P(x),(Q(a)∨Q(b)),¬ P(x)∨¬ Q(x)}再对S进行归结:所以,G是F的逻辑结论同理可求得(3)、(4)和(5),其求解过程略。
3.15 设已知:(1)如果x是y的父亲,y是z的父亲,则x是z的祖父;(2)每个人都有一个父亲。
使用归结演绎推理证明:对于某人u,一定存在一个人v,v是u的祖父。
解:先定义谓词F(x,y):x是y的父亲GF(x,z):x是z的祖父P(x):x是一个人再用谓词把问题描述出来:已知F1:(∀x) (∀y) (∀z)( F(x,y)∧F(y,z))→G F(x,z))F2:(∀y)(P(x)→F(x,y))求证结论G:(∃u) (∃v)( P(u)→G F(v,u))然后再将F1,F2和¬G化成子句集:①¬F(x,y)∨¬F(y,z)∨G F(x,z)②¬P(r)∨F(s,r)③P(u)④¬G F(v,u))对上述扩充的子句集,其归结推理过程如下:3.16 假设张被盗,公安局派出5个人去调查。
案情分析时,贞察员A说:“赵与钱中至少有一个人作案”,贞察员B说:“钱与孙中至少有一个人作案”,贞察员C说:“孙与李中至少有一个人作案”,贞察员D说:“赵与孙中至少有一个人与此案无关”,贞察员E说:“钱与李中至少有一个人与此案无关”。
如果这5个侦察员的话都是可信的,使用归结演绎推理求出谁是盗窃犯。
解:(1) 先定义谓词和常量设C(x)表示x作案,Z表示赵,Q表示钱,S表示孙,L表示李(2) 将已知事实用谓词公式表示出来赵与钱中至少有一个人作案:C(Z)∨C(Q)钱与孙中至少有一个人作案:C(Q)∨C(S)孙与李中至少有一个人作案:C(S)∨C(L)赵与孙中至少有一个人与此案无关:¬ (C (Z)∧C(S)),即¬C (Z) ∨¬C(S)钱与李中至少有一个人与此案无关:¬ (C (Q)∧C(L)),即¬C (Q) ∨¬C(L)(3) 将所要求的问题用谓词公式表示出来,并与其否定取析取。
设作案者为u,则要求的结论是C(u)。
将其与其否)取析取,得:¬ C(u) ∨C(u)(4) 对上述扩充的子句集,按归结原理进行归结,其修改的证明树如下:因此,钱是盗窃犯。
实际上,本案的盗窃犯不止一人。
根据归结原理还可以得出:因此,孙也是盗窃犯。
3.18 设有子句集:{P(x)∨Q(a, b), P(a)∨⌝Q(a, b), ⌝Q(a, f(a)), ⌝P(x)∨Q(x, b)}分别用各种归结策略求出其归结式。
解:支持集策略不可用,原因是没有指明哪个子句是由目标公式的否定化简来的。
删除策略不可用,原因是子句集中没有没有重言式和具有包孕关系的子句。
单文字子句策略的归结过程如下:用线性输入策略(同时满足祖先过滤策略)的归结过程如下:3.19 设已知:(1)能阅读的人是识字的;(2)海豚不识字;(3)有些海豚是很聪明的。
请用归结演绎推理证明:有些很聪明的人并不识字。
解:第一步,先定义谓词,设R(x)表示x是能阅读的;K(y)表示y是识字的;W(z) 表示z是很聪明的;第二步,将已知事实和目标用谓词公式表示出来能阅读的人是识字的:(∀x)(R(x))→K(x))海豚不识字:(∀y)(¬K (y))有些海豚是很聪明的:(∃z) W(z)有些很聪明的人并不识字:(∃x)( W(z)∧¬K(x)) 第三步,将上述已知事实和目标的否定化成子句集:¬R(x))∨K(x)¬K (y)W(z)¬W(z)∨K(x))第四步,用归结演绎推理进行证明3.20 对子句集:{P∨Q, Q∨R, R∨W, ⌝R∨⌝P, ⌝W∨⌝Q, ⌝Q∨⌝R }用线性输入策略是否可证明该子句集的不可满足性?解:用线性输入策略不能证明子句集{P∨Q, Q∨R, R∨W, ⌝R∨⌝P, ⌝W∨⌝Q, ⌝Q∨⌝R }的不可满足性。
原因是按线性输入策略,不存在从该子句集到空子句地归结过程。
3.23 设已知事实为((P∨Q)∧R) ∨(S∧(T∨U))F规则为S→(X∧Y)∨Z试用正向演绎推理推出所有可能的子目标。
解:先给出已知事实的与/或树,再利用F规则进行推理,其规则演绎系统如下图所示。
由该图可以直接写出所有可能的目标子句如下:P∨Q∨T∨UP∨Q∨X∨ZP∨Q∨Y∨ZR∨T∨UR∨X∨ZR∨Y∨Z3.24 设有如下一段知识:“张、王和李都属于高山协会。
该协会的每个成员不是滑雪运动员,就是登山运动员,其中不喜欢雨的运动员是登山运动员,不喜欢雪的运动员不是滑雪运动员。
王不喜欢张所喜欢的一切东西,而喜欢张所不喜欢的一切东西。
张喜欢雨和雪。
”试用谓词公式集合表示这段知识,这些谓词公式要适合一个逆向的基于规则的演绎系统。
试说明这样一个系统怎样才能回答问题:“高山俱乐部中有没有一个成员,他是一个登山运动员,但不是一个滑雪运动员?”解:(1) 先定义谓词A(x) 表示x是高山协会会员S(x) 表示x是滑雪运动员C(x) 表示x是登山运动员L(x,y) 表示x 喜欢y(2) 将问题用谓词表示出来“张、王和李都属于高山协会A(Zhang)∧A(Wang)∧A(Li)高山协会的每个成员不是滑雪运动员,就是登山运动员(∀x)(A(x)∧¬S(x)→C(x))高山协会中不喜欢雨的运动员是登山运动员(∀x)(¬L(x, Rain)→C(x))高山协会中不喜欢雪的运动员不是滑雪运动员(∀x)(¬L(x, Snow)→¬ S(x))王不喜欢张所喜欢的一切东西(∀y)( L(Zhang, y)→¬ L(Wang ,y))王喜欢张所不喜欢的一切东西(∀y)(¬ L(Zhang, y)→L(Wang, y))张喜欢雨和雪L(Zhang , Rain)∧L(Zhang , Snow)(3) 将问题要求的答案用谓词表示出来高山俱乐部中有没有一个成员,他是一个登山运动员,但不是一个滑雪运动员?(∃x)( A(x)→C(x)∧¬ S(x))(4) 为了进行推理,把问题划分为已知事实和规则两大部分。
