有偏估计之——病态方程的常用解法
范德蒙矩阵形式下的病态线性方程组求解

由表 1 的数据可知,随着范德蒙德矩阵阶数 的增加,其 2- 条件数也越来越大,病态性也越来 越严重参见文献[6-7]。为更直观地了解阶数与条件
基金项目:2018 年长治学院课题“非线性算子的不动点定理及其应用”(ZC201811);长治学院“1331 工程”人才培养质量提升 计划项目(200628)
n
移 bi= aij,i=1,2,…n j=1
下面用新主元加权迭代法对这个线性方程组 进行求解,得到的结果如表 3 所示。
表 3 解的近似值(n=10 加权因子为 籽=1.000001)
近似值 x1 x2 x3 x4 x5 x6 x7 x8 x9 x10
单参数迭代法 0.999999 1 0.999997 1 0.999999 1 1 1 1 1
表 4 加权因子与绝对误差
文章选取以系数矩阵为范德蒙德矩阵的病态 线性方程组,借鉴文献[4]提供的单参数迭代法和文 献[5]中的新主元加权迭代法,对病态线性方程组进 行分析求解。结果表明选取的迭代方法切实可行, 对分析此病态线性方程组有很大帮助。
1 范德蒙德矩阵的病态性分析
选取 n 阶的范德蒙德矩阵如下:
1 杉山
山
1
12
…
1 山
数的增加,2- 条件数越来越大,病态程度也越来越严重。然后选用单参数迭代法和新主元加权迭代法分别
对以系数矩阵是范德蒙德矩阵的病态线性方程组进行求解,从数值结果可以看出,选取适当的加权因子对
求解此病态线性方程组同样有较好的精度和收敛速度。
关键词:病态线性方程组;范德蒙矩阵;单参数迭代法;新主元加权迭代法
2019 年 4 月 第 36 卷 第 2 期
长治学院学报 Journal of Changzhi University
武汉大测绘学院广义测量平差考试复习题

绪论1.平差问题的函数模型的随机模型,无非以下几种:函数模型中系数阵是列满秩还是秩列亏;待估参数是非随机量还是随机量或者两者兼有;观测量的协方差阵是满秩还是奇异;2.以不同的准则来求定未知参数的最佳估计,得到不同的估计方法,经典的测量平差方法都是以最小二乘估计或者极大似然估计为根据导出的;滤波、配置和动态系统的卡尔曼滤波,最初是以极大验后估计或者最小方差估计导出的。
3.有偏估计是为了克服法方程病态的问题的平差方法,病态又称为法方程的复共线性。
P163(论述题)4.简述引起测量平差法方程系数矩阵病态的原因及其后果,通常采用什么方法解决这一问题,采用何种指标评价参数估值的精度?(在第一章讲过)(秩亏是用秩亏自由网平差,病态用有偏估计)原因:误差方程的系数矩阵存在着很弱的弱相关性,弱相关性也称复共线性。
法方程中系数和常数项存在舍入误差而产生微小变化时,引起的解的很大差异。
这种情况下法方程系数阵的性质不好,称为病态方程。
后果:一旦存在病态性,法方程系数上的微小误差会导致方程的解完全被扭曲。
最小二乘解不稳定。
解决方法:采用有偏估计,包括岭估计、广义岭估计、主成分估计等等有偏估计方法。
评定精度的指标:(在经典平差里面用参数估值的方差评定精度,在广义平差里面用参数估计误差的方差评定精度)在有偏估计中采用均方误差MSE(X尖)来评定精度,均方误差用来衡量参数与其真值的偏离程度。
(参数与数学期望间的偏离程度是方差)5.随着测绘科学技术的变革和不断发展,经典测量平差理论已经不能满足现代测量数据处理,根据自己的理解论述现代测量数据处理的发展方向。
(PPT里面有)1.从法方程系数矩阵满秩扩展到法方程系数矩阵亏秩2.从仅处理静态数据扩展到处理动态数据3.从无偏估计扩展到有偏估计4.从线性模型的参数估计扩展到非线性模型的参数估计5.从待估参数为非随机量扩展到待估参数为随机量6.从观测值仅含偶然误差扩展到含有系统误差和粗差7.从主要研究函数模型扩展到深入研究随机模型经典—非随机广义---随机6.经典平差对观测误差的基本假设是?答:观测误差仅含有偶然误差经典平差的基本假设:(局限性)1)系统是静态的2)有足够的起算数据3)观测值是随机变量,参数是非随机变量4)观测误差为偶然误差5)观测值函数独立6)平差准则为V T PV = min7.经典平差---未知参数为非随机参数;第一章极大似然估计P81、正态分布的极大似然估计与最小二乘估计相同————之间的转换,PPT15/16页2、均无法顾及到参数的先验统计性质。
对病态方程组的处理方法研究

对病态方程组的处理方法研究蓝醒龙(广西民族大学数学与计算机科学学院03数本2班,530006)摘 要: 对病态线性方程组解法研究是数值计算方法的一个重要研究课题。
本文分析了病态方程组的特点,介绍了几种有效的解法。
关键词: 病态线性方程组;条件数;预处理;迭代Studying The Algorithm For Solving Ill-conditionedSystem Of EquationsAbstract : Studying the algorithm for solving ill-conditioned system of equations is an important issue. This paper analyses the equations characteristic, and introduces several effective algorithms.Key words :ill-conditioned system of equations; condition number; pretreatment; iteration1 问题的提出一个线性方程组 A X b =,若右端向量b 或系数矩阵A 的微小变化就会引起方程组的解发生很大的变化,则称A X b =为病态方程组。
方程组的系数矩阵A 的条件数()1C o n d A AA -=刻画了方程组的性态,若()1C ond A ≥,则称A X b =为“病态”方程组;若()Cond A 相对较小,则称A X b =为“良态”方程组。
良态方程组用GAUSS 消去法和JACOBI 等简单的迭代法就可以得到比较好的计算解,而对于病态方程组,一般的直接法和迭代法会有较大的误差,甚至严重失真。
所以,在解方程组时,有必要先对方程组的性态进行研究,采用相应的算法,才能得到比较精确的计算解。
利用方程组的条件数来判断就是一个很好的办法。
病态总体最小二乘两步解法-江西信息应用职业技术学院

关键词:约束条件;总体最小二乘;岭估计
The ill-pose total least square with two steps
Tao Wuyong Yu Dongxue Xiong Yongkang
( Jiangxi Vacational & Technical College of Information Application 330043)
101.47943 93.16839 37.36422 10.01004 56.99606 18.03590 10.15063 43.29905 49.25618 22.55966 10.04382
未知参数有 5 个, 为 。 对于观测值 L,其观测噪声 为单位矩阵。 设计矩阵 素与观测值之间的元素相互独立,且其误差
0,0,0)和 ( 7,10,-5),两个未知点之间 设未知点真值分别为 ( 。 要求根据 19 个观测距离确定两个未知点的
4 总结
为了同时考虑系数矩阵和观测向量的误差以及系数矩 ( 下转第 65 页)
2015 年第 2 期 总 第十五期
江西信息应用职业技术学院学报
65
国家安全、恐怖活动犯罪以及特别重大的贿赂犯罪,在其原 本可以适用一般监视居住措施,仅仅因为无固定住所而被指 定居所监视居住,从而限制了更多的人身自由,律师的帮助 权也可能受到限制,出现了 “ 同案不同处理”的情况,这会极 大地损害司法的权威和公正性。
Abstract : In the paper the ill-pose total least square with two steps are proposed on the base of the additional constraint condition,The additional constraint and ridge estimation are cited in. And the method is used to deal with ill-posed problem. At the same time, The article discuss and deduce the theory and formula for the method in dealing with ill-posed problem. At last, Mock experiments are carried out to demonstrate useful and efficiency of the method. Key Words : constraint condition ; Total Least Square ; Ridge estimation
数值分析(hilbert矩阵)病态线性方程组的求解matlab程序

(Hilbert 矩阵)病态线性方程组的求解理论分析表明,数值求解病态线性方程组很困难。
考虑求解如下的线性方程组的求解Hx = b ,期中H 是Hilbert 矩阵,()ij n n Hh ,11ij h i j ,i ,j = 1,2,…,n 1.估计矩阵的2条件数和阶数的关系2.对不同的n ,取(1,1,,1)nx K ?,分别用Gauss 消去,Jacobi 迭代,Gauss-seidel 迭代,SOR 迭代和共轭梯度法求解,比较结果。
3.结合计算结果,试讨论病态线性方程组的求解。
第1小题:condition.m %第1小题程序t1=20;%阶数n=20x1=1:t1;y1=1:t1;for i=1:t1H=hilb(i);y1(i)=log(cond(H));endplot(x1,y1);xlabel('阶数n');ylabel('2-条件数的对数(log(cond(H))');title('2-条件数的对数(log(cond(H))与阶数n 的关系图');t2=200;%阶数n=200x2=1:t2;y2=1:t2;for i=1:t2H=hilb(i);y2(i)=log(cond(H));endplot(x2,y2);xlabel('阶数n');ylabel('2-条件数的对数(log(cond(H))');title('2-条件数的对数(log(cond(H))与阶数n 的关系图');画出Hilbert 矩阵2-条件数的对数和阶数的关系n=200时n=20时从图中可以看出,1)在n小于等于13之前,图像近似直线log(cond(H))~1.519n-1.8332)在n大于13之后,图像趋于平缓,并在一定范围内上下波动,同时随着n的增加稍有上升的趋势第2小题:solve.m%m第2小题主程序N=4000;xGauss=zeros(N,1);xJacobi=zeros(N,1);xnJ=zeros(N,1);xGS=zeros(N,1);xnGS=zeros(N,1);xSOR=zeros(N,1);xnSOR=zeros(N,1);xCG=zeros(N,1);xnCG=zeros(N,1);for n=1:N;x=ones(n,1);t=1.1;%初始值偏差x0=t*x;%迭代初始值e=1.0e-8;%给定的误差A=hilb(n);b=A*x;max=100000000000;%可能最大的迭代次数w=0.5;%SOR迭代的松弛因子G=Gauss(A,b);[J,nJ]=Jacobi(A,b,x0,e,max);[GS,nGS]=G_S(A,b,x0,e,max);[S_R,nS_R]=SOR(A,b,x0,e,max,w);[C_G,nC_G]=CG(A,b,x0,e,max);normG=norm(G'-x);xGauss(n)=normG;normJ=norm(J-x);nJ;xJacobi(n)=normJ;xnJ(n)=nJ;normGS=norm(GS-x);nGS;xGS(n)=normGS;xnGS(n)=nGS;normS_R=norm(S_R-x);nS_R;xSOR(n)=normS_R;xnSOR(n)=nS_R;normC_G=norm(C_G-x);nC_G;xCG(n)=normC_G;xnCG(n)=nC_G;endGauss.m%Gauss消去法function x=Gauss(A,b)n=length(b);l=zeros(n,n);x=zeros(1,n);%消去过程for i=1:n-1for j=i+1:nl(j,i)=A(j,i)/A(i,i);for k=i:nA(j,k)=A(j,k)-l(j,i)*A(i,k);endb(j)=b(j)-l(j,i)*b(i);endend%回代过程x(n)=b(n)/A(n,n);for i=n-1:-1:1c=A(i,:).*x;x(i)=(b(i)-sum(c(i+1:n)))/A(i,i);endJacobi.m%Jacobi迭代,x0表示迭代初值,e表示允许误差(迭代停止条件),n表示迭代次数,m 可能最大的迭代次数function [x,n]=Jacobi(A,b,x0,e,m)n=length(A);D=diag(diag(A));U=-triu(A,1);L=-tril(A,-1);B=D\(L+U);f=D\b;x=B*x0+f;n=1;while norm(x-x0)>ex0=x;x=B*x0+f;n=n+1;if n>mdisp('Jacobi迭代次数过多,迭代可能不收敛');break;endendG_S.m%Gauss-Seidel迭代,x0表示迭代初值,e表示允许误差(迭代停止条件),n表示迭代次数,m可能最大的迭代次数function [x,n]=G_S(A,b,x0,e,m)n=length(A);D=diag(diag(A));U=-triu(A,1);L=-tril(A,-1);B=(D-L)\U;f=(D-L)\b;x=B*x0+f;n=1;while norm(x-x0)>ex0=x;x=B*x0+f;n=n+1;if n>mdisp('Gauss-Seidel迭代次数过多,迭代可能不收敛');break;endendSOR.m%SOR超松弛迭代,x0表示迭代初值,e表示允许误差(迭代停止条件),n表示迭代次数,m可能最大的迭代次数,w松弛因子function [x,n]=SOR(A,b,x0,e,m,w)n=length(A);D=diag(diag(A));U=-triu(A,1);L=-tril(A,-1);B=(D-w*L)\((1-w)*D+w*U);f=(D-w*L)\b*w;x=B*x0+f;n=1;while norm(x-x0)>ex0=x;x=B*x0+f;n=n+1;if n>mdisp('SOR超松弛迭代次数过多,迭代可能不收敛');break;endendCG.m%CG共轭梯度法,x0表示迭代初值,e表示允许误差(迭代停止条件),n表示迭代次数,m可能最大的迭代次数function [x,n]=CG(A,b,x0,e,m)r=b-A*x0;p=r;alpha=(r'*r)/(p'*(A*p));x=x0+alpha*p;r1=b-A*x;n=1;while norm(r1)>ebelta=(r1'*r1)/(r'*r);p=r1+belta*p;r=r1;x0=x;alpha=(r'*r)/(p'*(A*p));x=x0+alpha*p;r1=b-A*x;n=n+1;if n>mdisp('CG共轭梯度法迭代次数过多,迭代可能不收敛');break;endend。
INS_GPS组合导航中的病态问题及其处理方法_金际航

中, 采用的就是平方根形式的 KF。然而, 一方面平方 根 KF 仅能使矩阵的条件数减半, 一定程度地解决病 态问题, 在病态非常严重的场合, 平方根 KF 将可能 无法解决病态问题; 另一方面, 平方根 KF 虽然减弱 了病态性, 但同时也明显增加了计算量, 不利于实时 。 应用 第二种方法是对需要求逆的矩阵进行正则化 如采用 Tikhonov 正则化方法、 岭估计方法、 截断 处理, [ 8 - 10 ] 。然而正则化方法本质上是一 奇异值分解法等 种有偏方法, 正则化 KF 实际上破坏了标准 KF 的最 优性前提, 因而其在解决病态问题的同时, 将影响滤 波精度。鉴于上述方法在计算量或最优性方面的缺 陷, 并考虑到与其采用某种修正的 KF 对存在病态问 题的模型进行滤波, 不如构建一种能够避免病态问题 的模型, 并采用标准的 KF 进行滤波解算。通过引入 尺度化因子( 即平均地球半径) 对传统 INS / GPS 组合 导航模型进行线性变换, 构建了避免病态问题的模 型, 采用标准 KF 进行滤波解算, 在不明显增加计算 量的前提下保证了滤波解的最优性质。
( 10 ) ( 11 ) ( 12 ) ( 13 )
Kk = P H ( Hk P H + Rk )
- k
T k
- k
T k
-1
^ k+ = x ^ k- + K k ( y k - H k x ^ k- ) x
P k+ = P k- - K k H k P k-
- k + k
- ^ 、 ^ 分别为 k 时刻的状态先验、 x x 式中, 后验估计; Pk 、
δv N · · , δL = δl = RN + h
数值求解Hilbert病态线性方程组
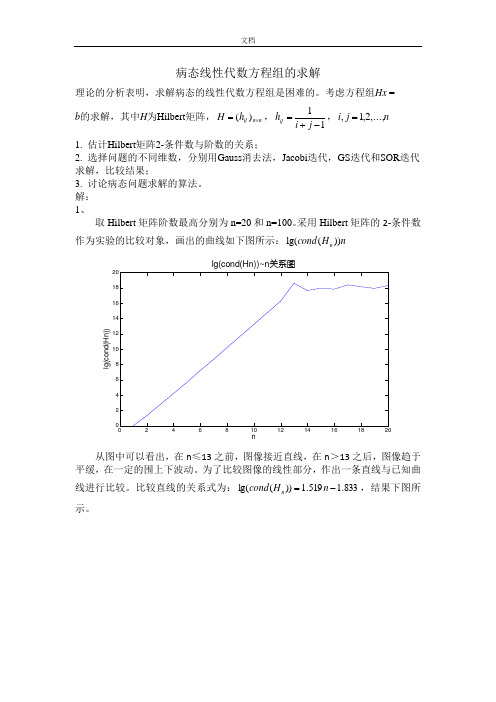
病态线性代数方程组的求解理论的分析表明,求解病态的线性代数方程组是困难的。
考虑方程组Hx = b 的求解,其中H 为Hilbert 矩阵,n n ij h H ⨯=)(,11-+=j i h ij ,n j i ,...,2,1,=1. 估计Hilbert 矩阵2-条件数与阶数的关系;2. 选择问题的不同维数,分别用Gauss 消去法,Jacobi 迭代,GS 迭代和SOR 迭代求解,比较结果;3. 讨论病态问题求解的算法。
解: 1、取Hilbert 矩阵阶数最高分别为n=20和n=100。
采用Hilbert 矩阵的2-条件数作为实验的比较对象,画出的曲线如下图所示:lg(())n cond H n从图中可以看出,在n ≤13之前,图像接近直线,在n >13之后,图像趋于平缓,在一定的围上下波动。
为了比较图像的线性部分,作出一条直线与已知曲线进行比较。
比较直线的关系式为:833.1519.1))(lg(-=n H cond n ,结果下图所示。
nl g (c o n d (H n ))lg(cond(Hn))~n 关系图从图2中可以看出,当n 较小时,n H cond n ~))(lg(之间近似满足线性关系。
当n 继续增大到100时,n H cond n ~))(lg(关系图下图所示:从图中可以看出,图像的走势符合在n=20时的猜想,在n 大于一定的值之后,图像趋于平缓,且在一定围震荡,同时又有一定上升趋势,但上升速度很慢。
2、选择不同的阶数n ,设方程组的精确解为xz=(1,1,…,1)T进行计算,用四种方法解x_Guass1、x_Jacobi1、x_GS1、x_SOR1对比表如下nl g (c o n d (H n ))lg(cond(Hn))~n关系图nl g (c o n d (H n ))lg(cond(Hn))~n 关系图Gauss消去法求解:选择问题的阶数为3~8时,用Gauss消去法求得的解与精确解一致,当阶数为9~14时,解开始出现偏差,而且n越大,偏差越大。
仿真模型与建模方法论

例:环形罗宾服务(Round Robin Service)
USR1 USR5 CPU USR2
USR4
USR3
某计算机系统有一台主 机与5个终端用户组成, 主机依次顺时针为每一 个用户服务。轮到某用 户时,传递数据给主机 CPU并等待回答,接收 到回答后准备下一轮数 据。建模研究用户如何 迅速的完成其程序编制
可信性的检验应贯穿在整个建模阶段,并且与建 模方法相互结合 演绎中的可信性:前提的正确性,前提的其他 结果的检验 归纳中的可信性:偏差估计,统计方法 目的方面的可信性:是否满足目标
三、模型的分类
常用分类
根据模型的时间集合:连续时间模型、离散 时间模型 根据模型的状态变量:连续变化模型、离散 变化模型
非存储系统 存储系统
输出仅与同时刻的输入有关 某时刻输出依赖于到该时刻为止的某区 间上的输入
代数方程 非代数方程
第二节 建模方法学
为方便理解和交流,对建模与仿真的研 究报告内容也有规范,一般包括
模型和针对模型构造的假设的非形式描述 模型结构的形式描述 执行仿真的程序设计 仿真试验,仿真结果分析 模型应用的范围与有效性 现在的模型与过去的和将来的模型的关系
第二章 仿真模型与建模方法论
本章主要内容
建模基本原理 模型的非形式化描述 模型的形式化表示 基于计算机的建模方法学* 解释结构建模* 仿真模型的确认
第一节 建模原理
一、模型与建模
建模:通过观测和检测,在忽略次要因素及 不可检测变量的基础上,用数学的方法对实 际系统进行描述,从而获得简化近似模型的 过程 在系统研究中,模型用来收集系统有关信息 和描述系统有关实体 模型是用以产生行为数据的一组指令
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
b、条件数法 K cond N N N 1
max min
一般认为K 100时没有复共线性; K 1000 时存在严重的复共线性 ,系统 呈病态。这个指标是在 对数据中心化标准化的 前提下得到的。但在测 量 数据处理实际应用中, 如GP S快速定位中,条件数大 致在1013 左右。所以 对上述准则应根据实际 情况修正取舍。 条件数法的缺点是不能 判定设计矩阵B中有几个复共线性关系 。 c、CTVDP法 条件指标 方差分解比方法。
岭参数有多种选取法,常用的 有L曲线法、岭迹法及 GCV 法等。在
ˆ V T PV x ˆT x ˆ min中,V T PV和x ˆT x ˆ均为岭参数的函数,选 式 x
ˆ x ˆT x ˆ 为纵坐标作图,得一条 择不同的值,以 V T PV 为横坐标, x L曲线法的关键是定 L曲线法上曲率
常用均方误差MSE来评价病态情形下参数的估值质量。
由均方误差公式:
2 T 2 ~ ~ ~ ˆ ˆ ˆ ˆ MSE x E x x x x 0 tr Qx ˆx ˆ E x x
1 2 tr B B
2 0 T
T T
所以正则化法单位权方 差无偏估计的计算公式 为 2 ~ V T PV 2 ~ x T Q Q x ˆ0 n t 2tr Q2
ˆ代替。 计算时,由于无法得到 参数真值~ x ,可以用参数估值 x
岭参数(正则化参数)的选取—L曲线法(1)
根据二次型的期望公式 ,有
E V T PV tr PE V T V tr PDVV tr PEV E V 而
T 2 ~ tr PEV E V 2 ~ x T Q Q x
T
2 tr PDVV n t 2tr Q 02
1
ቤተ መጻሕፍቲ ባይዱ2 0
i 1
t
1
i
ˆ是真值~ 上式的条件为 x x 的无偏估值,即 2 0。而若法矩阵 N的最小特征 ˆ 很大,此时LS估值x ˆ不再是~ 值较小,会导致 MSE x x 的一个良好估值了。
i
ˆ ~ 用解病态方程法得到的 参数估值将不再是无偏 估值,即E x x。 有偏估计实质:适当增 大偏差2部分,换取方差部分 1的减小。
max cond2 A min
(3)、奇异值分解的扰动 。 若A与A E A均属于R nt n t ,则对p 1,2, t,有
p A E A p A E A
2
此特性说明当矩阵 A有扰动E A时,奇异值的变化不会 超过 E A 2,可见奇异值 分解法是求线性方程组 、特别是线性病态方程 组的数值稳定的方法。 线性方程组Ax L的通解为:x A L 而 A UV
t 1 i 1 t 1 1n n1
截断原则:选择一个阈 值,舍去小于的奇异值 i 及其相关的特征向
量,这相当于舍去了相 关性很强的约束,降低 了条件数,提高了稳定 性。
平差中,设计矩阵B为病态,其秩为R(B)=t。通过截断,适当去除 (t-T)个大误差项,恢复了一些解的主要特性,但也丧失了一些 解的精确性。
例:有方程组 Ax b,即 1 x1 2 1 1 1.0001 x 2 2 当常数项b有微小变化时,有 1 y1 2 1 1 1.0001 y 2.0001 2
T
2 其精确解为 x 0
2
max min
其中,max和min分别是正定对称矩阵 A中最大和最小的特征值 。
不稳定模型:输入数据很小的误差会引起待估参数很大的误差。所以病态方程也是 不稳定模型。
解释:复共线性
复共线性,指的是平差参数之间具有近似相关关系,反映在 误差方程的设计矩阵上,就是列向量间的某些数据列可以由其余 的数据列近似(非精确)地线性表示。
2 DVV P 1 2 BQ B T BQ NQ B T 0
有 E V PV tr PEV E V tr PDVV 2 ~ 2 即 E V T PV 2 ~ x T Q Q x n t 2tr Q 02
拟合曲线,用这条曲线 选定岭参数的方法称为L曲线法。
最大的那个点的 值,该值即为所求的岭
如图, 2.0943 参数。
其中考虑了:Q N Q N I t I t I t Q
3、正则化解的单位权方差无偏估计
正则化解的残差及自由度与最小二乘解不同,因此其单位 权方差估计式也不同。 由 Q N I t Q
及残差的期望: E V BQ B T P I n E l BQ N B ~ x 上两式合并,有: E V BQ ~ x
二、病态方程的解法
1、病态方程的截断奇异值解法
奇异值分解技术(Singular Value Decomposintion Technique,简记为SVD法)
设有观测方程(式中观 测值向量L的权阵P已经单位化): A x L e
n t t 1 n1 n1
A是设计矩阵,e是误差向量。得 x的最小二乘最小范数解 为 ˆ LS A L x A 是A的广义逆。 下面对A进行奇异值分解: ( 1)当rank( A) p p minn, t 时,对A阵可分解为
nt
A U VT
nn nt t t
式中为半正定的对角阵; U、V均为正交矩阵。
D 阵的分块形式为 nt 0 其中: D diag 1 , 2 , p
0 0
, p R A min(n, t )
且 1 2 p 0. i是A阵全部的非零奇异值。 奇异值 i与矩阵 A或AT A 的特征值i的关系为: i i。 将U和V阵按列划分,为: U u1 u2 un ,V v1 v2 vt (2)奇异值与条件数的关 系: A为长方阵时,得其条件 数与奇异值的关系为:
T 1
V U T
D 1 0 1 1 1 1 , D diag , , , 1 2 p t n 0 0 有 1 2 p 0
,R A p minn, t
由A UV T
2、病态方程的正则化解法
ˆ l 有误差方程: V Bx
( 1)
13
若上式病态,则法矩阵 N的特征值单调地趋向于 0,此时可取
ˆ V T PV x ˆ T Rx ˆ min x
Tikhonov 的正则化准则作用于( 1 )式:
ˆ Tikhononv x 光滑函数。 正则化参数满足 0 R 正则化矩阵。当 R I时,正则化估计也称为 岭估计。(以下 内容R均为单位阵)
1
看出,SVD法可解算满秩、秩亏和 近似秩亏的线性方程组 。
A的奇异值分解式可写为 A V U i1vi uiT
T i 1 p
得解为:
ˆ LS A L i1 vi uiT L x
t 1 i 1 T
p
t 1 1n n1
在第T步对其截断,得病态方 程的截断奇异值法解: ˆT i1 vi uiT L x
ˆ 为 考虑E l B~ x , 有参数的期望值与其真 值~ x 的偏差Bias x ˆ E x ˆ ~ Bias x x Q ~ x 评定精度的均方误差矩 阵为
2 ˆ 0 MSEM x Q NQ 2Q ~ x~ x T Q
得正则化参数解为: ˆ B T PB +I t x
2
1
B T Pl
可见 ,正则化方法的核心是通过附加“全部或部分参数(或 其改正数)加权平方和极小”的条件,增加约束,补充(先验) 信息,来克服不适定性,使解唯一且稳定。
设 Q
1 N I t
14
参数估值及残差可表示 为 ˆ Q B T Pl x ˆ l BQ B T P I n l V Bx
5、什么样的方程可能是病态的?
1)行列式的值很大或很小(如某些行、列近代相关); 2)元素间相差大数量级,且无规则; 3)主元消去过程中出现小主元; 4)特征值相差大数量级。
问题的适定性: 人们根据已获取的观测数据和物理规律,列出的数学模型,当这些模型具有下述性质: 1、解存在; 2、解唯一; 3、解稳定。 则这个问题称为适定性问题。 不适定性: 不满足上面三个条件中的任意一个或多个。 不适定问题通常是病态的,但病态问题不一定就是不适定问题。不适定问题通常是求方 程的稳定近似解。
方程组的解变为: y x x 1 1
0 , 其中b 0 . 0001
若系数阵A或常数项b的微小变化,会引起方程组的解x有巨大变化,则这种方程组称为 “病态方程组”。A称为病态矩阵。
在方程组Ax b中,讨论: 1)A非奇异,设正常, b有误差b,导致解x有多大误差? 即 A x x b b Ax b x A1b A 1 b A x (范数特性) x b
x 1 b 所以: A A x b 2)设A、b均有误差时,解 x有多大误差? 即
A Ax x b b
x 得解的相对误差为: x
A A1 1 A A1
b A A b A A
定义
对非奇异阵A,称乘积 A A1 为矩阵A的 矩阵的条件数: 条件数。它刻画了方程 组的解对原始数据的敏 感程度。 当A为正定实对称矩阵时, (如法方程的 N阵),A阵的谱条件 数为 cond A2 A 2 A1
